Усеченная пирамида егэ задачи

Геометрия 10-11 класс. Усеченная пирамидаadmin2022-11-30T22:09:37+03:00

Скачать файл в формате pdf.

Геометрия 10-11 класс. Усеченная пирамида

Плоскость, параллельная плоскости основания пирамиды и пересекающая ее боковые ребра, отсекает от нее подобную пирамиду. Другая часть представляет собой многогранник, который называется усеченной пирамидой. Грани усеченной пирамиды, лежащие в параллельных плоскостях, называются основаниями; остальные грани называются боковыми гранями.

Объем усеченной пирамиды вычисляется по формуле:    (V = frac{1}{3}Hleft( {,{S_1} + {S_2} + sqrt {,{S_1} cdot {S_2}} ,} right)), где H – высота усеченной пирамиды; ({S_1}) и ({S_2}) – площади ее оснований.

Задачи для самостоятельного решения

Задача 1. Дана треугольная усеченная пирамида ABCA1B1C1, A1B1 = 10, B1C1 = 22, BC = 33. Найдите AB.

Задача 2. Дана правильная четырехугольная усеченная пирамида ABCDA1B1C1D1, A1C1 = 8, CC1 = 5, AC = 16. Найдите высоту данной пирамиды.

Задача 3. Дана правильная четырехугольная усеченная пирамида ABCDA1B1C1D1,  B1C1 = 6,  CC1 = 10, AD = 18. Найдите площадь боковой поверхности.

Задача 4. Дана правильная треугольная усеченная пирамида ABCA1B1C1, A1B1 = 2, BC = 6, (A{A_1} = sqrt 8 .) Найдите площадь боковой поверхности.

Задача 5. Дана правильная треугольная усеченная пирамида ABCA1B1C1, высота которой равна 4. Точки O и O1 – центры оснований, (A{A_1} = sqrt {19} ,,,,{A_1}{O_1} = 2sqrt 3 .) Найдите AC.

Задача 6. Дана правильная треугольная усеченная пирамида ABCA1B1C1, высота которой равна 4, (AB = 6sqrt 3 ,,,,{A_1}{B_1} = 3sqrt 3 .) Найдите AA1.

Задача 7. Дана правильная треугольная усеченная пирамида ABCA1B1C1, (A{C_1} = 4,,,,A{C_1} bot {A_1}C.) Найдите площадь боковой поверхности.

Задача 8. Стороны оснований правильной четырехугольной усеченной пирамиды 3 и 5, боковое ребро равно (sqrt {17} ). Найдите площадь полной поверхности усеченной пирамиды.

Задача 9. Стороны оснований правильной треугольной усеченной пирамиды равны 6 и 12, высота равна 1. Найдите площадь боковой поверхности усеченной пирамиды.

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Многогранник, у которого одна из граней – многоугольник, а все остальные грани – треугольники с общей вершиной, называется пирамидой.

Эти треугольники, из которых составлена пирамида, называют боковыми гранями, а оставшийся многоугольник – основанием пирамиды.

В основании пирамиды лежит геометрическая фигура – n-угольник. В таком случае пирамиду называют еще n-угольной.

Треугольную пирамиду, все ребра которой равны, называют тетраэдром.

Ребра пирамиды, которые не принадлежат основанию, называются боковыми, а их общая точка – это вершина пирамиды. Другие ребра пирамиды обычно называют сторонами основания.

Пирамиду называют правильной, если у нее в основании лежит правильный многоугольник, а все боковые ребра равны между собой.

Расстояние от вершины пирамиды до плоскости основания называется высотой пирамиды. Можно сказать, что высота пирамиды есть отрезок, перпендикулярный основанию, концы которого находятся в вершине пирамиды и на плоскости основания.

Для любой пирамиды имеют место следующие формулы: 

1) S_полн = S _бок + S_осн, где

S_полн – площадь полной поверхности пирамиды;

S_бок – площадь боковой поверхности, т.е. сумма площадей всех боковых граней пирамиды;

S _осн – площадь основания пирамиды.

2) V = 1/3 S_осн · Н, где

V – объем пирамиды;

Н – высота пирамиды.

Для правильной пирамиды имеет место:

S_бок = 1/2 P_осн h, где

P_осн – периметр основания пирамиды;

h – длина апофемы, то есть длина высоты боковой грани, опущенной из вершины пирамиды.

Часть пирамиды, заключенная между двумя плоскостями – плоскостью основания и секущей плоскостью, проведенной параллельно основанию, называют усеченной пирамидой.

Основание пирамиды и сечение пирамиды параллельной плоскостью называются основаниями усеченной пирамиды. Остальные грани называют боковыми. Расстояние между плоскостями оснований называют высотой усеченной пирамиды. Ребра, которые не принадлежат основаниям, называются боковыми.

Кроме того, основания усеченной пирамиды подобные n-угольники. Если основания усеченной пирамиды – правильные многоугольники, а все боковые ребра равны между собой, то такая усеченная пирамида называется правильной.

Для произвольной усеченной пирамиды имеют место следующие формулы: 

1) S_полн = S_бок + S₁ + S₂, где

S_полн – площадь полной поверхности;

S_бок – площадь боковой поверхности, т.е. сумма площадей всех боковых граней усеченной пирамиды, которые представляют собой трапеции;

S₁, S₂ – площади оснований;

2) V = 1/3( S₁ + S₂  + √(S₁ · S₂ ))H, где

V – объем усеченной пирамиды;

H – высота усеченной пирамиды.

Для правильной усеченной пирамиды также имеем:

S_бок = 1/2(P₁ + P₂) · h, где

P₁ , P₂ – периметры оснований;

h – апофема (высота боковой грани, представляющей собой трапецию).

Рассмотрим несколько задач на усеченную пирамиду.

Задача 1.

В треугольной усеченной пирамиде с высотой, равной 10, стороны одного из оснований равны 27, 29 и 52. Определите объем усеченной пирамиды, если периметр другого основания равен 72.

Решение.

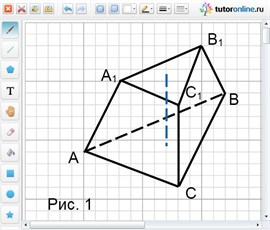
Рассмотрим усеченную пирамиду АВСА₁В₁С₁, изображенную на рисунке1.

1. Объем усеченной пирамиды может быть найден по формуле

V = 1/3H · (S₁ + S₂ + √(S₁ · S₂)), где S₁ – площадь одного из оснований, можно найти по формуле Герона

S = √(p(p – a)(p – b)(p – c)),

т.к. в задаче даны длины трех сторон треугольника.

Имеем: p₁ = (27 + 29 + 52)/2 = 54.

S₁ = √(54(54 – 27)(54 – 29)(54 – 52)) = √(54 · 27 · 25 · 2) = 270.

2. Пирамида усеченная, а значит, в основаниях лежат подобные многоугольники. В нашем случае треугольник АВС подобен треугольнику А₁В₁С₁. Кроме того, коэффициент подобия можно найти как отношение периметров рассматриваемых треугольников, а отношение их площадей будет равно квадрату коэффициента подобия. Таким образом, имеем:

S₁/S₂ = (P₁)²/(P₂)² = 108²/72² = 9/4. Отсюда S₂ = 4S₁/9 = 4 · 270/9 = 120.

Итак, V = 1/3 · 10(270 + 120 + √(270 · 120)) = 1900.

Ответ: 1900.

Задача 2.

В треугольной усеченной пирамиде через сторону верхнего основания проведена плоскость параллельно противоположному боковому ребру. В каком отношении разделился объем усеченной пирамиды, если соответственные стороны оснований относятся как 1 : 2?

Решение.

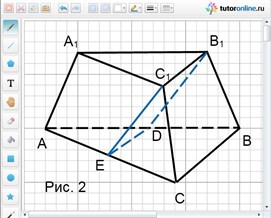
Рассмотрим АВСА₁В₁С₁ – усеченную пирамиду, изображенную на рис. 2.

Так как в основаниях стороны относятся как 1 : 2, то площади оснований относятся как 1 : 4 (треугольник АВС подобен треугольнику А₁В₁С₁).

Тогда объем усеченной пирамиды равен:

V = 1/3h · (S₁ + S₂ + √(S₁ · S₂)) = 1/3h · (4S₂ + S₂ + 2S₂) = 7/3 · h · S₂, где S₂ – площадь верхнего основания, h – высота.

Но объем призмы АDEA₁B₁C₁ составляет V₁ = S₂ · h и, значит,

V₂ = V – V₁ = 7/3 · h · S₂ — h · S₂ = 4/3 · h · S₂.

Итак, V₂ : V₁ = 3 : 4.

Ответ: 3 : 4.

Задача 3.

Стороны оснований правильной четырехугольной усеченной пирамиды равны 2 и 1, а высота равна 3. Через точку пересечения диагоналей пирамиды параллельно основаниям пирамиды проведена плоскость, делящая пирамиду на две части. Найти объем каждой из них.

Решение.

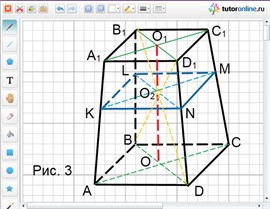
Рассмотрим усеченную пирамиду АВСDА₁В₁С₁D₁, изображенную на рис. 3.

Обозначим О₁О₂ = х, тогда ОО₂ = О₁О – О₁О₂ = 3 – х.

Рассмотрим треугольник В₁О₂D₁ и треугольник ВО₂D:

угол В₁О₂D₁ равен углу ВО₂D как вертикальные;

угол ВDO₂ равен углу D₁B₁O₂ и угол O₂ВD равен углу B₁D₁O₂ как накрест лежащие при B₁D₁ || BD и секущих B₁D и BD₁ соответственно.

Следовательно, треугольник В₁О₂D₁ подобен треугольнику ВО₂D и имеет место отношение сторон:

В1D₁/ВD = О₁О₂/ОО₂ или 1/2 = х/(х – 3), откуда х = 1.

Рассмотрим треугольник В₁D₁В и треугольник LО₂B: угол В – общий, а так же имеется пара односторонних углов при B₁D₁ || LM, значит, треугольник В₁D₁В подобен треугольнику LО₂B, откуда В₁D : LO₂ = OO₁ : OO₂ = 3 : 2, т.е.

LO₂ = 2/3 · B₁D₁, LN = 4/3 · B₁D₁.

Тогда S_KLMN = 16/9 · S_A1B1C1D1 = 16/9.

Итак, V₁ = 1/3 · 2(4 + 16/9 + 8/3) = 152/27.

V₂ = 1/3 · 1 · (16/9 + 1 + 4/3) = 37/27.

Ответ: 152/27; 37/27.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Зачет по теме усеченная пирамида

Задача 1

Высота правильной четырехугольной усеченной пирамиды равна 7 см. Стороны оснований 10см и 2см.

Найти боковое ребро пирамиды.

Задача 2

Стороны оснований правильной треугольной усеченной пирамиды 4 дм и 1 дм.

Боковое ребро 2 дм. Найти высоту пирамиды.

Задача 3

Определить высоту правильных усеченных пирамид 1) треугольной

2) четырехугольной

3) шестиугольной,

если даны боковое ребро с и стороны а и в нижнего и верхнего оснований.

Задача 4

В правильной четырехугольной усеченной пирамиде высота равна 63 см, апофема 65 см, а стороны оснований относятся как 7:3. Определите эти стороны.

Задача 5

В правильной четырехугольной усеченной пирамиде высота равна 2 см, а стороны оснований 3 см и 5 см. Определить диагональ этой усеченной пирамиды.

Задача 6

Определить стороны оснований правильной четырехугольной усеченной пирамиды, если ее высота равна 7 см, боковое ребро 9 см, диагональ 11 см.

Задача 7

Высота правильной четырехугольной усеченной пирамиды равна 4 см, диагональ 5 см.

Найти площадь диагонального сечения.

Задача 8

Высота правильной четырехугольной усеченной пирамиды равна 4 . Стороны оснований равны 2 и 8.

Найти площадь диагонального сечения.

Задача 9

В правильной четырехугольной усеченной пирамиде высота равна 4 см, стороны оснований 8 см и 2 см. Найти полную поверхность.

Задача 10

Стороны оснований правильной треугольной усеченной пирамиды 9 дм и 12 дм, высота равна 1 дм. Найти площадь боковой поверхности.

              Тема.
«Пирамида. Усеченная  пирамида».

Записать ответы на вопросы.

1.      Рисунок
любой пирамиды с обозначением всех вершин.

2.      Определение
пирамиды. Перечислить по рисунку: основание, вершину, боковые ребра, боковые
грани, высоту.

3.      Определение
правильной пирамиды. Записать два обязательных условия, чтобы пирамида была
правильной.

4.      Что
такое апофема правильной пирамиды? Как
обозначается?

5.      Что
такое поверхность фигуры?

6.      Что
такое объем?

7.      Выписать
формулу боковой поверхности правильной пирамиды, описать все входящие туда
понятия.

8.       Выписать
формулу полной поверхности правильной пирамиды, описать все входящие туда
понятия.

9.       Выписать
формулу объема пирамиды, описать все входящие туда понятия.

10.   Какие
две разные высоты входят в формулы боковой поверхности и объема пирамиды?

11.   Что
такое усеченная пирамида? Сделать рисунок правильной четырехугольной усеченной
пирамиды.

12.   Выписать
формулы для вычисления боковой, полной поверхности и объема усеченной пирамиды.

Решить задачи.
( к каждой задаче должен быть выполнен рисунок, обозначения, краткое условие).

Задача 1. 
В правильной четырехугольной пирамиде боковое  ребро равно 5, сторона основания
равна 6.   Найти  а) боковую поверхность, б) полную поверхность, в) объем пирамиды
( результат умножить на √7).

Задача 2. 
В правильной треугольной пирамиде боковая поверхность равна 18, апофема равна
4. Найти сторону основания.

Задача 3. 
Площадь полной поверхности тетраэдра 128. Все ребра увеличили в 3 раза. Какова
стала поверхность?

Задача 4. 
Все ребра октаэдра равны 12√2 . Найти его объем. (
Примечание: радиус описанной  окружности около квадрата вычисляется по формуле:
R= a √2 / 2 , а
– сторона квадрата).

Задача 5. 
В правильной шестиугольной пирамиде сторона основания равна 18, а боковое ребро
равно 41.   Найти  а) боковую поверхность.

Задача 6. 
Даны две правильные четырехугольные пирамиды. Объем первой равен 16. У  второй
высота в 2 раза меньше, чем у первой, а сторона основания в 1,5 раза больше,
чем у первой. Чему равен объем второй пирамиды.

Задача 7. 
В основании пирамиды  SABC
 лежит
правильный треугольник ABC
со стороной 10. Высота пирамиды обозначена буквой S.
Боковое ребро SA перпендикулярно
плоскости основания и равно 7√3. Вычислить объем пирамиды.

Задача 8. 
В основании пирамиды лежит прямоугольник со сторонами 3 и 4. Объем пирамиды
равен 32. Вычислить высоту пирамиды.

Задача 9. 
Объем тетраэдра равен 216. Все ребра уменьшили в 2 раза. Какой будет объем?

Задача 10. 
В правильной четырехугольной пирамиде полная поверхность равно 40, сторона
основания равна 2. Найти апофему пирамиды.

Пояснения
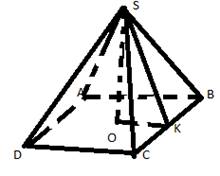
к задачам.    Задача
№ 1.        Дано: SB
=5,  AD=6   Найти а) Sбок.

б)
Sпол.       в) V

                                                                                                                
План решения.

                                                                                                     а)
Sбок= 
½· Pосн
·hбок,         hбок
=SK  —
апофема,  ее находим по т. Пифагора из

 ∆ SKB,    
Pосн. – периметр
основания( сумма всех сторон основания- квадрата)

б) Sпир
=  Sбок + Sосн          
Sосн – площадь
основания, т.е. площадь квадрата.

в)  V=
1/
3· Sосн·h       
h=SO
—  высота самой пирамиды, ее находим по т. Пифагора из

 ∆ SOK
, 
SK – апофема найдена
выше, OK =r
–радиус
вписанной окружности в основание, для квадрата   r=a
/2
, где а – сторона квадрата.(результат
умнож.на √7.)

Задача № 2.  
 В
формулу  боковой поверхности подставьте заданные величины, найдите оттуда
неизвестную величину —  периметр основания (сумму всех одинаковых трех сторон).
Найдите одну сторону.

Задача № 3 и №9. Это
на работу с формулами. Надо посмотреть, в какой степени в формуле находится та
величина, которая изменяется (увеличивается или уменьшается), в эту степень
возводится величина, на которую происходит изменение.  При
вычислении площадей эта величина возводится в квадрат, при вычислении объемов в
куб. Далее «увеличение» означает умножение на
эту величину, «уменьшение» означает деление на это число. Например,
поверхность пирамиды была равна 1200. Все ребра уменьшили в 5 раз.   а) Какая
стала поверхность?  б) Какой стал объем?

Решение:    а)  5 в квадрате =
25.          1200 / 25 =  48         Ответ:
48.

                     б)  5 в кубе =
125                 1200 /125
= 9,6         Ответ: 9,6.

Задача № 4.
 Сделайте
рисунок. Октаэдр рассматриваем как две одинаковые четырехугольные
пирамиды, соединенные своими основаниями. Находим объем одной и умножаем на
два. Для нахождения высоты одной пирамиды по т. Пифагора нужен R
— радиус описанной окружности около квадрата в основании пирамиды R=
a·√2
/
2. Ребро
октаэдра – гипотенуза, R
– катет, находим высоту. По формуле вычисляем объем

( Sосн
– площадь квадрата). Не забудьте удвоить результат!!!

Задача № 5. 
Сделайте рисунок. Найдите апофему по т.Пифагора как в зад. №1, зная
гипотенузу-это боковое ребро, оно  равно 41 и половину стороны основания  18/2
=9. Найдите периметр основания (там правильный шестиугольник).Подставьте
найденные величины в формулу Sбок.

Задача № 6. В 
этом образце условие другое, но подобное, как№6 . Даны  две правильные
треугольные пирамиды (какие пирамиды роли не играет). Объем первой равен 600. У
второй высота в 4 раза меньше, а сторона основания в 3 раза больше. Чему равен
объем второй.      Решение.   В формулу объема пирамиды высота входит в
первой степени, а в площади основания сторона входит  всегда в квадрате.
Поэтому,  600 делим на 4 (т.к. в 4 раза меньше высота), а умножаем на 3 в
квадрате)   (600 / 4)·9=2025.

Задача № 7.  
Сделать рисунок. Выписать формулу для объема пирамиды. Площадь основания в этой
формуле — это площадь правильного треугольника:          S
=
сторона треугольника в квадрате умножить на √3
все разделить на 4. Боковое ребро в этой задаче – это высота, т.к. по условию
ребро SA перпендикулярно
основанию. Подставить величины в формулу.

Задача № 8.  
Сделать
рисунок как в зад.№1. Выписать формулу объема пирамиды.

Вычислить площадь основания, как площадь
прямоугольника. Подставить в формулу объема: в левую часть формулы величину
объема, заданную по условию, в правую часть вычисленную площадь основания,
выразить оттуда и вычислить высоту.

Задача № 10. Выписать
формулу полной поверхности пирамиды.                           S
пол.=Sбок + Sосн
= ½· Pосн
·hбок + Sквадрата.      
Зная сторону основания  а=2, вычислить Pосн.
( периметр, как сумму всех четырех сторон) и площадь квадрата.

Подставить в левую часть формулы 
известную Sпол
=40, в правую часть -вычисленные периметр  и площадь квадрата, найти
единственную неизвестную величину hбок 
— апофему.

Самостоятельная работа.

	Вариант 1		Вариант 2
1	В правильной треугольной пирамиде SABC медианы треугольника АВС пересекаются в точке О. Площадь треугольника АВС равна 2, объем пирамиды равен 6. Найти SO.	1	В правильной треугольной пирамиде SABC медианы треугольника АВС пересекаются в точке О. Площадь треугольника АВС равна 9, объем пирамиды равен 6. Найти SO.
2	В правильной треугольной пирамиде SABC  L – середина ребра АС, сторона ВС равна 6, отрезок SL равен 5. Найти боковую поверхность пирамиды.	2	В правильной треугольной пирамиде SABC  L – середина ребра АС, сторона ВС равна 12, отрезок SL равен 10. Найти боковую поверхность пирамиды.
3	В правильной четырехугольной  пирамиде SABCD точка О – центр основания ABCD. Ребро SD равно 10, отрезок SO равен 6. Найти АС.	3	В правильной четырехугольной  пирамиде SABCD точка О – центр основания ABCD. Ребро SD равно 13, отрезок SO равен 5. Найти АС.
4	В правильной четырехугольной пирамиде сторона основания равна 8, а длина бокового ребра равна 9. Найти высоту пирамиды.	4	В правильной треугольной  пирамиде сторона основания равна 6, а длина бокового ребра равна 4. Найти высоту пирамиды.
5	Высота правильной четырехугольной пирамиды равна 10, а сторона основания равна 15. Найти длину апофемы этой пирамиды.	5	Высота правильной треугольной пирамиды равна 2, а сторона основания равна 12. Найти длину апофемы этой пирамиды.
6	Радиус окружности, вписанной в основание правильной четырехугольной пирамиды равен 4√5,а длина бокового ребра пирамиды равна 14. Найти высоту пирамиды.	6	Радиус окружности, вписанной в основание правильной треугольной пирамиды равен 12,а длина бокового ребра пирамиды равна 26. Найти высоту пирамиды.
7	Плоскость, параллельная плоскости основания правильной четырехугольной пирамиды, делит высоту пирамиды в отношении 1:2, считая от вершины. Апофема полученной усеченной пирамиды равна 4дм, а площадь ее полной поверхности равна 186 дм2. Найдите объем  усеченной пирамиды.	7	Плоскость, параллельная плоскости основания правильной четырехугольной пирамиды, делит высоту пирамиды в отношении 1:4, считая от вершины. Апофема полученной усеченной пирамиды равна 16 дм, а площадь ее полной поверхности равна 744 дм2. Найдите объем  усеченной пирамиды.
8	Стороны основания правильной  треугольной усеченной пирамиды  40 см и 20 см, а боковое ребро равно 20 см. Найдите объем и боковую поверхность пирамиды.	8	Основаниями усеченной пирамиды являются правильные треугольники со сторонами 5 см и 3 см. Одно из боковых ребер перпендикулярно к плоскости основания и равно 1 см. Найдите площадь боковой поверхности и объем пирамиды.
9	В правильной усеченной  четырехугольной пирамиде стороны основания 6 см и 4 см, а площадь сечения пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани, равна 15 см2. Найдите объем усеченной пирамиды.	9	В правильной усеченной  четырехугольной пирамиде радиусы вписанных окружностей в основания 12 см и 8 см, а боковое ребро 5 см. Найдите объем усеченной пирамиды.