Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Найдите объём усечённой пирамиды, если площади оснований усечённой пирамиды равны 245 и 80, а высота полной пирамиды равна 35.
2
Найдите объём усечённой пирамиды, если площади оснований усечённой пирамиды равны 18 и 25, а высота полной пирамиды равна 35.
Аналоги к заданию № 682: 683 Все
3
Найдите объём усечённой пирамиды, если боковое ребро правильной четырёхугольной усечённой пирамиды равно 3, стороны оснований 5 и 1.
4
Найдите объём усечённой пирамиды, если боковое ребро правильной четырёхугольной усечённой пирамиды равно 3, стороны оснований 3 и 7.
Аналоги к заданию № 684: 685 Все
5
Найдите объём усечённой пирамиды, если в основаниях лежат правильные шестиугольники со сторонами 4 и 6, а боковые рёбра составляют с нижним основанием.
Пройти тестирование по этим заданиям
Описание презентации по отдельным слайдам:
-
1 слайд
Задания по теме «Пирамида»
из курса ЕГЭ за 2016 — 2017 г.
Тип задания: 8 -
2 слайд
Боковое ребро правильной четырехугольной пирамиды равно 7,5, а сторона основания равна 10. Найдите высоту пирамиды.
Основанием правильной четырехугольной пирамиды является квадрат. По теореме Пифагора найдем диагональ квадрата, центр которой пересекает вершина пирамиды.
d=10√2
Рассмотрим прямоугольный треугольник, в котором один катет является половиной диагонали квадрата основания пирамиды, а гипотенуза равна ее боковому ребру. По теореме Пифагора найдем второй катет, являющийся высотой пирамиды:
h=√6,25=2,5
Ответ 2,5 -
-
-
-
-
7 слайд
Сторона оснований правильной усеченной четырехугольной пирамиды равны 3 и 9 см. Высота пирамиды 4 см. найдите площадь боковой поверхности.
Проведя перпендикуляры. Получим, что большее основание разбивается на отрезки по три сантиметра. Рассмотрим прямоугольный треугольник , катеты в нем известны, это египетский треугольник, по теореме Пифагора определяем длину гипотенузы: 5 см. -
8 слайд
Высота правильной четырехугольной усеченной пирамиды равна 7 см. Вычислите длину бокового ребра пирамиды, если длины сторон ее оснований равны 2 см и 10 см.
Рассмотрим треугольник CFC1.
По теореме Пифагора CC1 = ?Найдем CF =?
CF=(AC — A1C1)/2=?
Ответ: 9 см
Многогранник, у которого одна из граней – многоугольник, а все остальные грани – треугольники с общей вершиной, называется пирамидой.
Эти треугольники, из которых составлена пирамида, называют боковыми гранями, а оставшийся многоугольник – основанием пирамиды.
В основании пирамиды лежит геометрическая фигура – n-угольник. В таком случае пирамиду называют еще n-угольной.
Треугольную пирамиду, все ребра которой равны, называют тетраэдром.
Ребра пирамиды, которые не принадлежат основанию, называются боковыми, а их общая точка – это вершина пирамиды. Другие ребра пирамиды обычно называют сторонами основания.
Пирамиду называют правильной, если у нее в основании лежит правильный многоугольник, а все боковые ребра равны между собой.
Расстояние от вершины пирамиды до плоскости основания называется высотой пирамиды. Можно сказать, что высота пирамиды есть отрезок, перпендикулярный основанию, концы которого находятся в вершине пирамиды и на плоскости основания.
Для любой пирамиды имеют место следующие формулы:
1) Sполн = S бок + Sосн, где
Sполн – площадь полной поверхности пирамиды;
Sбок – площадь боковой поверхности, т.е. сумма площадей всех боковых граней пирамиды;
S осн – площадь основания пирамиды.
2) V = 1/3 Sосн · Н, где
V – объем пирамиды;
Н – высота пирамиды.
Для правильной пирамиды имеет место:
Sбок = 1/2 Pосн h, где
Pосн – периметр основания пирамиды;
h – длина апофемы, то есть длина высоты боковой грани, опущенной из вершины пирамиды.
Часть пирамиды, заключенная между двумя плоскостями – плоскостью основания и секущей плоскостью, проведенной параллельно основанию, называют усеченной пирамидой.
Основание пирамиды и сечение пирамиды параллельной плоскостью называются основаниями усеченной пирамиды. Остальные грани называют боковыми. Расстояние между плоскостями оснований называют высотой усеченной пирамиды. Ребра, которые не принадлежат основаниям, называются боковыми.
Кроме того, основания усеченной пирамиды подобные n-угольники. Если основания усеченной пирамиды – правильные многоугольники, а все боковые ребра равны между собой, то такая усеченная пирамида называется правильной.
Для произвольной усеченной пирамиды имеют место следующие формулы:
1) Sполн = Sбок + S1 + S2, где
Sполн – площадь полной поверхности;
Sбок – площадь боковой поверхности, т.е. сумма площадей всех боковых граней усеченной пирамиды, которые представляют собой трапеции;
S1, S2 – площади оснований;
2) V = 1/3( S1 + S2 + √(S1 · S2 ))H, где
V – объем усеченной пирамиды;
H – высота усеченной пирамиды.
Для правильной усеченной пирамиды также имеем:
Sбок = 1/2(P1 + P2) · h, где
P1 , P2 – периметры оснований;
h – апофема (высота боковой грани, представляющей собой трапецию).
Рассмотрим несколько задач на усеченную пирамиду.
Задача 1.
В треугольной усеченной пирамиде с высотой, равной 10, стороны одного из оснований равны 27, 29 и 52. Определите объем усеченной пирамиды, если периметр другого основания равен 72.
Решение.
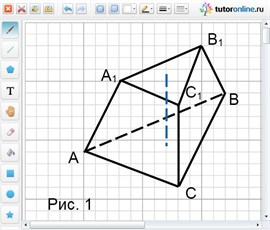
Рассмотрим усеченную пирамиду АВСА1В1С1, изображенную на рисунке1.
1. Объем усеченной пирамиды может быть найден по формуле
V = 1/3H · (S1 + S2 + √(S1 · S2)), где S1 – площадь одного из оснований, можно найти по формуле Герона
S = √(p(p – a)(p – b)(p – c)),
т.к. в задаче даны длины трех сторон треугольника.
Имеем: p1 = (27 + 29 + 52)/2 = 54.
S1 = √(54(54 – 27)(54 – 29)(54 – 52)) = √(54 · 27 · 25 · 2) = 270.
2. Пирамида усеченная, а значит, в основаниях лежат подобные многоугольники. В нашем случае треугольник АВС подобен треугольнику А1В1С1. Кроме того, коэффициент подобия можно найти как отношение периметров рассматриваемых треугольников, а отношение их площадей будет равно квадрату коэффициента подобия. Таким образом, имеем:
S1/S2 = (P1)2/(P2)2 = 1082/722 = 9/4. Отсюда S2 = 4S1/9 = 4 · 270/9 = 120.
Итак, V = 1/3 · 10(270 + 120 + √(270 · 120)) = 1900.
Ответ: 1900.
Задача 2.
В треугольной усеченной пирамиде через сторону верхнего основания проведена плоскость параллельно противоположному боковому ребру. В каком отношении разделился объем усеченной пирамиды, если соответственные стороны оснований относятся как 1 : 2?
Решение.
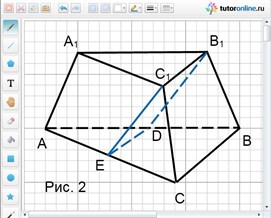
Рассмотрим АВСА1В1С1 – усеченную пирамиду, изображенную на рис. 2.
Так как в основаниях стороны относятся как 1 : 2, то площади оснований относятся как 1 : 4 (треугольник АВС подобен треугольнику А1В1С1).
Тогда объем усеченной пирамиды равен:
V = 1/3h · (S1 + S2 + √(S1 · S2)) = 1/3h · (4S2 + S2 + 2S2) = 7/3 · h · S2, где S2 – площадь верхнего основания, h – высота.
Но объем призмы АDEA1B1C1 составляет V1 = S2 · h и, значит,
V2 = V – V1 = 7/3 · h · S2 — h · S2 = 4/3 · h · S2.
Итак, V2 : V1 = 3 : 4.
Ответ: 3 : 4.
Задача 3.
Стороны оснований правильной четырехугольной усеченной пирамиды равны 2 и 1, а высота равна 3. Через точку пересечения диагоналей пирамиды параллельно основаниям пирамиды проведена плоскость, делящая пирамиду на две части. Найти объем каждой из них.
Решение.
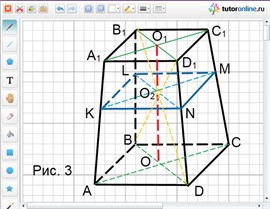
Рассмотрим усеченную пирамиду АВСDА1В1С1D1, изображенную на рис. 3.
Обозначим О1О2 = х, тогда ОО₂ = О1О – О1О2 = 3 – х.
Рассмотрим треугольник В1О2D1 и треугольник ВО2D:
угол В1О2D1 равен углу ВО2D как вертикальные;
угол ВDO2 равен углу D1B1O2 и угол O2ВD равен углу B1D1O2 как накрест лежащие при B1D1 || BD и секущих B₁D и BD₁ соответственно.
Следовательно, треугольник В1О2D1 подобен треугольнику ВО2D и имеет место отношение сторон:
В1D1/ВD = О1О2/ОО2 или 1/2 = х/(х – 3), откуда х = 1.
Рассмотрим треугольник В1D1В и треугольник LО2B: угол В – общий, а так же имеется пара односторонних углов при B1D1 || LM, значит, треугольник В1D1В подобен треугольнику LО2B, откуда В1D : LO2 = OO1 : OO2 = 3 : 2, т.е.
LO2 = 2/3 · B1D1, LN = 4/3 · B1D1.
Тогда SKLMN = 16/9 · SA1B1C1D1 = 16/9.
Итак, V1 = 1/3 · 2(4 + 16/9 + 8/3) = 152/27.
V2 = 1/3 · 1 · (16/9 + 1 + 4/3) = 37/27.
Ответ: 152/27; 37/27.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Видео по теме
Задача 1. В правильной четырехугольной пирамиде точка
– центр основания,
– вершина,
Найдите длину отрезка
.
Решение: + показать
Задача 2. В правильной четырехугольной пирамиде точка
– центр основания,
– вершина,
Найдите боковое ребро
Решение: + показать
Задача 3. Стороны основания правильной четырехугольной пирамиды равны боковые ребра равны
Найдите площадь поверхности этой пирамиды.
Решение: + показать
Задача 4. В правильной четырёхугольной пирамиде точка
— центр основания,
— вершина,
Найдите длину отрезка
Решение: + показать
Задача 5. Основанием пирамиды является прямоугольник со сторонами и
Ее объем равен
Найдите высоту этой пирамиды.
Решение: + показать
Задача 6. В правильной четырёхугольной пирамиде с основанием
боковое ребро
равно
сторона основания равна
Найдите объём пирамиды.
Решение: + показать
Задача 7. В правильной четырёхугольной пирамиде все рёбра равны Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер.
Решение: + показать
Задача 8. Даны две правильные четырёхугольные пирамиды. Объём первой пирамиды равен У второй пирамиды высота в
раза больше, а сторона основания в
раза больше, чем у первой. Найдите объём второй пирамиды.
Решение: + показать
Задача 9. В правильной четырёхугольной пирамиде боковое ребро равно а тангенс угла между боковой гранью и плоскостью основания равен
Найти сторону основания пирамиды.
Решение: + показать
Задача 10. Основанием пирамиды является прямоугольник со сторонами и
Ее объем равен
Найдите высоту этой пирамиды.
Решение: + показать
Задача 11. Стороны основания правильной четырехугольной пирамиды равны боковые ребра равны
Найдите площадь поверхности этой пирамиды.
Решение: + показать
Задача 12. В правильной треугольной пирамиде медианы основания
пересекаются в точке
. Площадь треугольника
равна
объем пирамиды равен
Найдите длину отрезка
.
Решение: + показать
Задача 13. В правильной треугольной пирамиде точка
— середина ребра
— вершина. Известно, что
а
. Найдите площадь боковой поверхности пирамиды.
Решение: + показать
Задача 14. Найдите объем правильной треугольной пирамиды, стороны основания которой равны а высота равна
Решение: + показать
Задача 15. Найдите высоту правильной треугольной пирамиды, стороны основания которой равны а объем равен
Решение: + показать
Задача 16. Стороны основания правильной шестиугольной пирамиды равны боковые ребра равны
Найдите площадь боковой поверхности этой пирамиды.
Решение: + показать
Задача 17. Объем правильной шестиугольной пирамиды Сторона основания равна
Найдите боковое ребро.
Решение: + показать
Задача 18. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в два раза?
Решение: + показать
Задача 19. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в раз?
Решение: + показать
Задача 20. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в пять раз?
Решение: + показать
Задача 21. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом °. Высота пирамиды равна
Найдите объем пирамиды.
Решение: + показать
Задача 22. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно Найдите объем пирамиды.
Решение: + показать
Задача 23. От треугольной призмы, объем которой равен отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.
Решение: + показать
Задача 24. Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен Найдите объем шестиугольной пирамиды. Видео по теме 1 2
Решение: + показать
Задача 25. Сторона основания правильной шестиугольной пирамиды равна 8, боковое ребро равно 16. Найдите объём пирамиды.
Решение: + показать
Задача 26. Сторона основания правильной шестиугольной пирамиды равна а угол между боковой гранью и основанием равен
Найдите объем пирамиды.
Решение: + показать
Задача 27. Найдите объём правильной шестиугольной пирамиды если объём треугольной пирамиды
равен
Решение: + показать
Задача 28. Объем параллелепипеда равен
Найдите объем треугольной пирамиды
Решение: + показать
Задача 29. Объем куба равен Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Решение: + показать
Задача 30. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно
Решение: + показать
Задача 31. Объем правильной четырехугольной пирамиды равен
Точка
— середина ребра
. Найдите объем треугольной пирамиды
.
Решение: + показать
Задача 32. От треугольной пирамиды, объем которой равен отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
Решение: + показать
Задача 33. Ребра тетраэдра равны Найдите площадь сечения, проходящего через середины четырех его ребер.
Решение: + показать

Геометрия 10-11 класс. Усеченная пирамида
Скачать файл в формате pdf.
Геометрия 10-11 класс. Усеченная пирамида
Плоскость, параллельная плоскости основания пирамиды и пересекающая ее боковые ребра, отсекает от нее подобную пирамиду. Другая часть представляет собой многогранник, который называется усеченной пирамидой. Грани усеченной пирамиды, лежащие в параллельных плоскостях, называются основаниями; остальные грани называются боковыми гранями.
Объем усеченной пирамиды вычисляется по формуле: (V = frac{1}{3}Hleft( {,{S_1} + {S_2} + sqrt {,{S_1} cdot {S_2}} ,} right)), где H – высота усеченной пирамиды; ({S_1}) и ({S_2}) – площади ее оснований.
Задачи для самостоятельного решения
| Задача 1. Дана треугольная усеченная пирамида ABCA1B1C1, A1B1 = 10, B1C1 = 22, BC = 33. Найдите AB. |
| Задача 2. Дана правильная четырехугольная усеченная пирамида ABCDA1B1C1D1, A1C1 = 8, CC1 = 5, AC = 16. Найдите высоту данной пирамиды. |
| Задача 3. Дана правильная четырехугольная усеченная пирамида ABCDA1B1C1D1, B1C1 = 6, CC1 = 10, AD = 18. Найдите площадь боковой поверхности. |
| Задача 4. Дана правильная треугольная усеченная пирамида ABCA1B1C1, A1B1 = 2, BC = 6, (A{A_1} = sqrt 8 .) Найдите площадь боковой поверхности. |
| Задача 5. Дана правильная треугольная усеченная пирамида ABCA1B1C1, высота которой равна 4. Точки O и O1 – центры оснований, (A{A_1} = sqrt {19} ,,,,{A_1}{O_1} = 2sqrt 3 .) Найдите AC. |
| Задача 6. Дана правильная треугольная усеченная пирамида ABCA1B1C1, высота которой равна 4, (AB = 6sqrt 3 ,,,,{A_1}{B_1} = 3sqrt 3 .) Найдите AA1. |
| Задача 7. Дана правильная треугольная усеченная пирамида ABCA1B1C1, (A{C_1} = 4,,,,A{C_1} bot {A_1}C.) Найдите площадь боковой поверхности. |
| Задача 8. Стороны оснований правильной четырехугольной усеченной пирамиды 3 и 5, боковое ребро равно (sqrt {17} ). Найдите площадь полной поверхности усеченной пирамиды. |
| Задача 9. Стороны оснований правильной треугольной усеченной пирамиды равны 6 и 12, высота равна 1. Найдите площадь боковой поверхности усеченной пирамиды. |
Задание. В правильной треугольной усечённой пирамиде ABCA1B1C1 площадь нижнего основания ABC в девять раз больше площади меньшего основания A1B1C1. Через ребро AВ проведена плоскость α, которая пересекает ребро СС1 в точке N и делит пирамиду на два многогранника равного объема.
а) Докажите, что точка N делит ребро CC1 в отношении 5 : 13, считая от точки C1.
б) Найдите площадь сечения усечённой пирамиды плоскостью α, если высота пирамиды равна 13, а ребро меньшего основания равно 3.
Решение:
а) Докажите, что точка N делит ребро CC1 в отношении 5 : 13, считая от точки C1.
Пусть площадь нижнего основания SABC = S, площадь верхнего основания SA1B1C1 = S1, высота усечённой пирамиды ABCA1B1C1 равна C1H1 = h, высота пирамиды NABC равна NH = h1.
По условию площадь нижнего основания ABC в девять раз больше площади меньшего основания A1B1C1, т. е. S = 9S1.
Плоскость α, которая пересекает ребро СС1 в точке N, делит пирамиду на два многогранника равного объема, т. е. Vус.пир. = 2VNABC, или
Объем усеченной пирамиды VABCA1B1C1 вычисляется по формуле
Объем пирамиды VNABC вычисляется по формуле
Подставим найденные объемы в формулу (1), получим
Треугольники ΔC1H1C и ΔNHC подобны (по первому признаку подобия треугольников; ∠C – общий, ∠H1 = ∠H – прямые углы), следовательно,
т. е.
б) Найдите площадь сечения усечённой пирамиды плоскостью α, если высота пирамиды равна 13, а ребро меньшего основания равно 3.
Ребро меньшего основания правильной треугольной усечённой пирамиды А1C1 = А1B1 = B1C1 = 3,
а высота пирамиды C1Н1 = 13.
По условию ABCA1B1C1– правильная усеченная пирамида, поэтому треугольники ΔАВС и ΔА1В1С1 подобны.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия, т. е.
Значит,
Медиана CF треугольника ΔАВС является его высотой.
Из прямоугольного треугольника ΔАCF (ÐF = 900) найдем CF:
Точки О и О1 – центры треугольников ΔАВС и ΔА1В1С1, т. е. точки О и О1 – точки пересечения медиан, биссектрис и высот треугольников ΔАВС и ΔА1В1С1.
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины, т. е.
Так как треугольники ΔАВС и ΔА1В1С1 подобны (k = 3), то
Тогда H1C = CO – OH1 = 3√3 — √3 = 2√3
Так как треугольники ΔC1H1C и ΔNHC подобны, найдем NH и HC:
Из прямоугольного треугольника ΔNFH (ÐH = 900) найдем NF:
Площадь сечения усечённой пирамиды плоскостью α (ΔABN) равна
Ответ: 48,5
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи по теме «Пирамида»
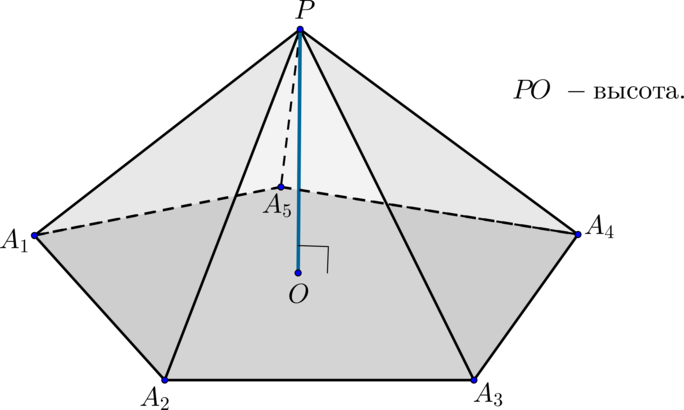
Пирамида (PA_1A_2…A_n):
(blacktriangleright) Многоугольник (A_1…A_n) – основание;
треугольники (PA_1A_2, PA_2A_3) и т.д. – боковые грани;
точка (P) – вершина;
отрезки (PA_1, PA_2, …, A_1A_2) и т.д. – ребра.
(blacktriangleright) Если в основании пирамиды лежит треугольник, то она называется тетраэдром.
(blacktriangleright) Высота пирамиды – перпендикуляр, опущенный из вершины (P) к основанию.
(blacktriangleright) Объем пирамиды ({Large{V=dfrac{1}{3}S_{text{осн}}h}}) , где (S_{text{осн}}) – площадь основания, (h) – высота.
(blacktriangleright) Площадь боковой поверхности – сумма площадей всех боковых граней.
Площадь полной поверхности – сумма площади боковой поверхности и площади основания.
Заметим, что принято записывать название пирамиды, начиная с вершины.
Задание
1
#2878
Уровень задания: Равен ЕГЭ
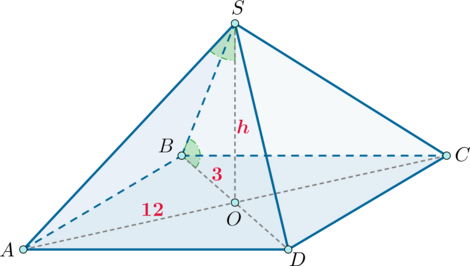
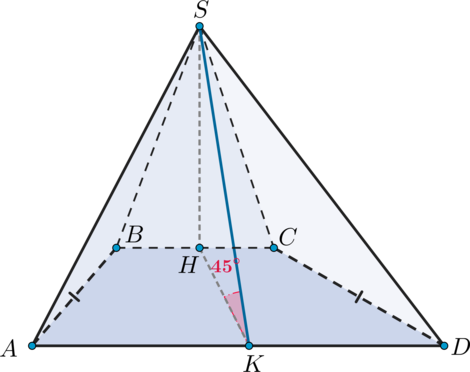
Дана пирамида (SABCD), вершиной которой является точка (S), в основании лежит ромб, а высота (SO) пирамиды падает в точку пересечения диагоналей ромба. Найдите объем пирамиды, если известно, что угол (ASO) равен углу (SBO), а диагонали основания равны (6) и (24).
Так как диагонали ромба точкой пересечения делятся пополам, то (AO=12), (BO=3).
Заметим, что так как (SO) – высота пирамиды, то (triangle ASO) и (triangle BSO) – прямоугольные. Так как у них есть равные острые углы, то они подобны. Пусть (SO=h), тогда из подобия имеем: [dfrac{BO}{h}=dfrac{h}{AO} quadRightarrowquad h=6.] Так как площадь ромба равна полупроизведению диагоналей, то объем пирамиды равен [V=dfrac13cdot hcdot dfrac12cdot 24cdot 6=144.]
Ответ: 144
Задание
2
#2879
Уровень задания: Равен ЕГЭ
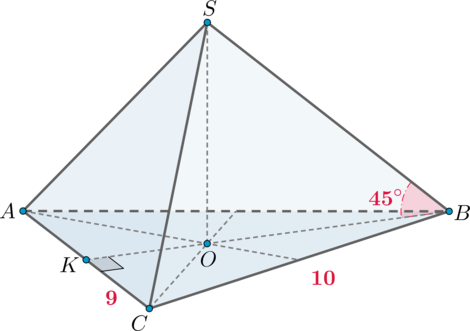
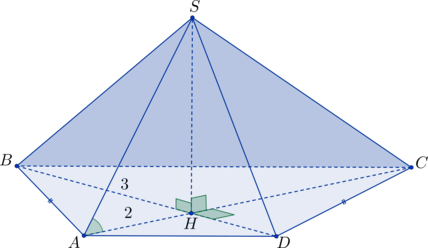
В пирамиде (SABC) высота (SO) падает в точку пересечения медиан основания. Треугольник (ABC) равнобедренный, боковые стороны равны (10), а основание (AC=18). Найдите объем пирамиды, если известно, что угол между боковым ребром (SB) и плоскостью основания равен (45^circ).
Пусть (BK) – высота в (triangle ABC), а значит и медиана. Тогда из прямоугольного (triangle BKC): [BK=sqrt{BC^2-KC^2}=sqrt{10^2-9^2}=sqrt{19}.] Тогда площадь основания равна [S_{ABC}=dfrac12cdot ACcdot
BK=9sqrt{19}.] Так как (O) – точка пересечения медиан, то (O) лежит на (BK). Так как медианы точкой пересечения делятся в отношении (2:1), считая от вершины, то [BO=dfrac23BK=dfrac23sqrt{19}.] Заметим, что угол между прямой и плоскостью – это угол между прямой и ее проекцией на плоскость, следовательно, (angle SBO=45^circ) и есть угол между (SB) и основанием (так как (BO) – проекция (SB) на плоскость (ABC)). Так как к тому же (triangle SBO) прямоугольный, то он равнобедренный, следовательно, [SO=BO=dfrac23sqrt{19}.] Тогда объем пирамиды равен [V=dfrac13cdot SOcdot S_{ABC}=38.]
Ответ: 38
Задание
3
#2880
Уровень задания: Равен ЕГЭ
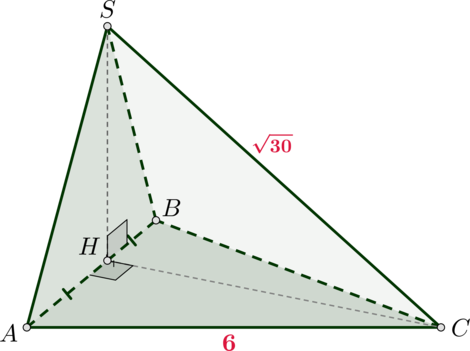
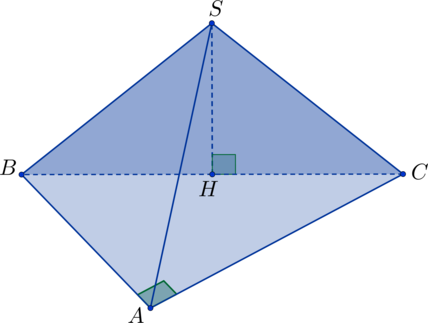
Высота (SH) треугольной пирамиды (SABC) падает на середину стороны (AB), (ABC) – правильный треугольник со стороной (6). Найдите объем пирамиды, если (SC=sqrt{30}).
Так как (H) – середина (AB) и треугольник правильный, то (CH) – высота. Следовательно, [CH=dfrac{sqrt3}2AB=3sqrt3.] Так как (SH) – высота пирамиды, то (triangle SHC) – прямоугольный, следовательно, [SH=sqrt{SC^2-CH^2}=sqrt{30-27}=sqrt3.] Следовательно, объем равен [V=dfrac13cdot SHcdot S_{ABC}=
dfrac13cdot SHcdot dfrac12cdot CHcdot AB=9.]
Ответ: 9
Задание
4
#2881
Уровень задания: Сложнее ЕГЭ
В основании пирамиды (SABCD) лежит равнобедренная трапеция (ABCD), (AD) – большее основание. Высота пирамиды падает на отрезок (BC). Апофема грани (ASD) равна (10) и образует угол (45^circ) с плоскостью трапеции. Найдите объем пирамиды, если средняя линия трапеции равна (9).
Пусть (SH) – высота пирамиды. Проведем (HKperp AD). Следовательно, по теореме о трех перпендикулярах (SK) (наклонная) также перпендикулярна (AD) (так как (HK) – ее проекция на плоскость (ABC)). Следовательно, (SK) и есть апофема грани (ASD). Также отсюда следует, что (angle SKH=45^circ) (так как угол между прямой и плоскостью – это угол между прямой и ее проекцией на плоскость). Следовательно, (triangle SHK) прямоугольный и равнобедренный, значит, [SH=HK=SKdiv sqrt2=dfrac{10}{sqrt2}] По определению получается, что (HK) также высота трапеции. Так как площадь трапеции равна полусумме оснований, умноженной на высоту, а полусумма оснований в свою очередь равна средней линии, то [S_{ABCD}=9cdot dfrac{10}{sqrt2}] А значит объем пирамиды равен [V=dfrac13cdotdfrac{10}{sqrt2}cdot9cdot dfrac{10}{sqrt2}=150.]
Ответ: 150
Задание
5
#1857
Уровень задания: Сложнее ЕГЭ
В основании пирамиды (SABCD) лежит равнобедренная трапеция с основаниями (AD) и (BC). (H) – точка пересечения диагоналей трапеции, а (SH) – высота пирамиды. Диагонали трапеции перпендикулярны, (mathrm{tg}, angle SAC = 3), (BH = 3), (AH = 2). Найдите объем пирамиды.
(triangle AHD) и (triangle BHC) – равнобедренные треугольники, т.к. трапеция (ABCD) равнобедренная (Rightarrow) (AH = HD), (BH = HC) (Rightarrow) (AC = BD = 2 + 3 = 5) (Rightarrow)
[S_{ABCD} = S_{ABC} + S_{ADC} = frac{1}{2}cdot ACcdot BH + frac{1}{2}cdot ACcdot HD = frac{1}{2}cdot ACcdot(BH + HD) = frac{1}{2}cdot ACcdot BD.]
В (triangle SAH): (SH = AHcdot mathrm{tg}, angle SAC = 6), т.к. (triangle SAH) – прямоугольный. Тогда объем пирамиды можно найти следующим образом: [V_{text{пир.}} = frac{1}{3}cdot S_{ABCD}cdot SH = frac{1}{3}cdotfrac{1}{2}cdot5cdot5cdot6 = 25].
Ответ: 25
Задание
6
#1858
Уровень задания: Сложнее ЕГЭ
В основании пирамиды (SABC) лежит прямоугольный треугольник с прямым углом (angle A). Точка (H) – центр описанной вокруг треугольника (triangle ABC) окружности, (SH) – высота пирамиды. Найдите объем пирамиды, если известно, что (AB = 6), (AC = 
Центр описанной вокруг прямоугольного треугольника окружности лежит на гипотенузе и делит ее пополам (Rightarrow) (BH = AH = CH) – радиусы описанной окружности. В прямоугольном треугольнике (triangle BAC) по теореме Пифагора: (BC^2 = AB^2 + AC^2 = 6^2 + 8^2 = 100) (Rightarrow) (BC = 10) (Rightarrow) (AH = frac{BC}{2} = frac{10}{2} = 5). Треугольник (triangle AHS) – прямоугольный, т.к. (SH perp ABC) ((SH) – высота), тогда по теореме Пифагора можно найти (SH): (SH^2 = AS^2 — AH^2 = (5sqrt5)^2 — 5^2 = 100) (Rightarrow) (SH = 10). Теперь найдем объем пирамиды: [V_{text{пир.}} = frac{1}{3}cdot SHcdot S_{triangle BAC} = frac{1}{3}cdot SHcdotfrac{1}{2}cdot ABcdot AC = frac{1}{3}cdot10cdotfrac{1}{2}cdot6cdot8 = 80.]
Ответ: 80
Задание
7
#2769
Уровень задания: Сложнее ЕГЭ
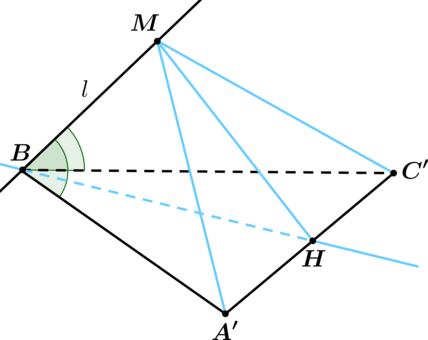
Точки (A), (B) и (C) лежат в плоскости (pi). Прямая (l) образует с плоскостью (pi) угол в (45^circ) и проходит через точку (B) так, что (angle(l; AB) = angle(l; BC)). Через (l’) обозначим проекцию (l) на (pi). Найдите (angle(l’; AB)), если (angle ABC = 80^circ). Ответ дайте в градусах.
Докажем, что (l’) содержит биссектрису угла (ABC). Выберем на (AB) точку (A’), а на (BC) точку (C’) так, чтобы (A’B = BC’). Построим прямую, проходящую через точку (B) и точку (H) – середину (A’C’).
Отметим на (l) точку (M). Треугольник (A’BC’) – равнобедренный, тогда (BH) – высота.
Рассмотрим треугольники (A’BM) и (C’BM): они равны по двум сторонам и углу между ними, тогда (MA’ = MC’) и треугольник (A’MC’) – равнобедренный, тогда (MH) – его высота.
В итоге (A’C’perp BH) и (A’C’perp MH), следовательно, (A’C’perp (MBH)). Если предположить, что (M’) – проекция точки (M) на ((A’BC’)), не попадает на прямую, содержащую (BH), то получим, что (A’C’perp M’M) и (A’C’perp MH), откуда следует, что (A’C’perp (MM’H)). Но тогда плоскости ((MM’H)) и ((MBH)) перпендикулярны к одной прямой, пересекаются, но не совпадают, чего быть не может.
Таким образом, (M’) лежит на прямой, содержащей (BH), но тогда (l’) совпадает с прямой, содержащей (BH). В итоге, (angle(l’; AB) = 0,5angle ABC = 40^circ).
Ответ: 40
При подготовке к ЕГЭ по математике старшеклассникам следует особое внимание уделить теме «Пирамида», так как задачи, связанные с расчетом объема и площади данного многогранника, непременно встретятся на финальной аттестации. Весь необходимый для повторного изучения материал вы найдете в данном разделе. Специалисты образовательного проекта «Школково» предлагают пойти от простого к сложному: сначала мы даем теорию и элементарные упражнения, а затем постепенно переходим к заданиям экспертного уровня.
Базовая информация
Пирамида — многогранник, образованный благодаря соединению всех точек плоского многоугольника с точкой, выходящей за пределы плоскости данного многоугольника.
Пирамиду называют n-угольной по количеству углов в основании. Если последним является правильный многоугольник, а основание высоты совпадает с его центром, фигуру называют правильной.
Все боковые грани пирамиды — треугольники.
Подробная теоретическая часть приведена в начале страницы. Вы также можете сразу приступить к практике. Задачи, представленные в данном разделе, помогут вам найти объем пирамиды, длину ее определенных отрезков и т. д. Каждое упражнение содержит подробный алгоритм решения и правильный ответ. Таким образом, разобраться в теме вы сможете самостоятельно, без помощи репетитора.
Как часто следует тренироваться?
Чтобы на ЕГЭ ребенок смог легко решить задачи по стереометрии (а определение площади и других параметров пирамиды относятся к данному разделу геометрии), мы рекомендуем выполнять по 2—3 упражнения каждый день. Таким образом, знания будут лучше усваиваться и вам будет проще переходить от простого к сложному.
Проверьте, легко ли вы рассчитаете площадь пирамиды, прямо сейчас. Разберите любое задание онлайн. Если решение дастся вам легко, значит, шансы на высокие экзаменационные баллы по математике достаточно велики. А при возникновении затруднений планируйте свой день таким образом, чтобы в ежедневное расписание был включен дистанционный образовательный проект «Школково». Мы поможем вам восполнить пробелы в знаниях!

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ