Видеоурок 1: Перемещение, скорость, ускорение
Видеоурок 2: Равноускоренное движение — Физика в опытах и экспериментах
Лекция: Ускорение материальной точки

Ускорение — это векторная ФВ, характеризующая быстроту изменения скорости во времени.
Ускорение — это первая производная от скорости, а также вторая — от перемещения.
Данная физическая величина показывает, насколько быстро изменяется скорость со временем.
Следует помнить, что ускорением обладает то тело, на которое действует сила.
Основной единицей ускорения является 1м/с^2.
В отличие от скорости, направление ускорения не всегда совпадает с направлением движения тела. Если тело ускоряется, то ускорение имеет положительное значение, если же тело замедляется, то ускорение — отрицательно. Иными словами, ускорение имеет то же направление, что и результирующая сила, которая действует на тело.
Если тело двигается по окружности, то ускорение направлено к её центру.

Геометрическим смыслом ускорения является площадь под прямой графика движения в координатах V(t).
Механика — раздел физики, который изучает механическое движение физических тел и взаимодействие между ними.
Основная задача механики — определение положение тела в пространстве в любой момент времени.
Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение и его виды
По характеру движения точек тела выделяют три вида механического движения:
- Поступательное. Это движение, при котором все точки тела движутся одинаково. Если через тело мысленно провести прямую, то после изменения положения этого тела в пространстве данная прямая останется параллельной самой себе.
- Вращательное. Это движение, при котором все точки тела движутся, описывая окружности.
- Колебательное. Это движение тела, которое повторяется точно или приблизительно через определенные интервалы времени. От вращательного движения его отличает то, что при колебаниях тело перемещается в двух взаимно противоположных направлениях.
По типу линии, вдоль которой движется тело, выделяют два вида движения:
- Прямолинейное — тело движется по прямой линии.
- Криволинейное — тело движется по кривой линии, в том числе замкнутой.
По скорости выделяют два вида движения:
- Равномерное — скорость движущегося тела остается неизменной.
- Неравномерное — скорость движущегося тела с течением времени меняется.
По ускорению выделяют три вида движения:
- Равноускоренное — тело движется неравномерно с постоянным ускорением (положительным). Скорость увеличивается.
- Равнозамедленное — тело движется неравномерно с постоянным замедлением (отрицательным ускорением). Скорость уменьшается.
- Ускоренное — тело движется неравномерно с меняющимся ускорением. Скорость может, как увеличиваться, так и уменьшаться.
Что нужно для описания механического движения?
Для описания механического движения нужно выбрать, относительно какого тела оно будет рассматриваться. Движение одного и того же объекта относительно разных тел неодинаковое. К примеру, идущий человек относительно дерева движется с некоторой скоростью. Но относительно сумки, которую он держит в руках, он находится в состоянии покоя, так как расстояние между ними с течением времени не изменяется.
Решение основной задачи механики — определения положения тела в пространстве в любой момент времени — заключается в вычислении координат его точек. Чтобы вычислить координаты тела, нужно ввести систему координат и связать с ней тело отсчета. Также понадобится прибор для измерения времени. Все это вместе составляет систему отсчета.
Система отсчета — совокупность тела отсчета и связанных с ним системы координат и часов.
Тело отсчета — тело, относительно которого рассматривается движение.
Часы — прибор для отсчета времени. Время измеряется в секундах (с).
При описании движения тела важно учитывать его размеры, так как характер движения его отдельных точек может различаться. Но в рамках некоторых задач размер тела не влияет на результат решения. Тогда его можно считать пренебрежительно малым. Тогда тело рассматривают как движущуюся материальную точку.
Материальная точка — это тело, размерами которого можно пренебречь в условиях конкретной задачи. Допустимо принимать тело за точку, если оно движется поступательно или его размеры намного меньше расстояний, которые оно проходит.
Виды систем координат
В зависимости от характера движения тела для его описания выбирают одну из трех систем координат:
- Одномерную. Используется, когда положение материальной точки можно задать только одной координатой x — M(x) . В этом случае тело движется прямолинейно.
- Двумерную. Используется, когда положение материальной точки можно задать двумя координатами x и y — M(x,y). Тело в этом случае движения по плоскости.
- Трехмерную. Используется, когда положение материальной точки можно задать тремя координатами x, y и z — M(x,y,z). Тело в этом случае изменяет положение в трехмерном пространстве.
Способы описания механического движения
Описать механическое движение можно двумя способами:
- координатным
- векторным
Координатный способ
Указать положение материальной точки в пространстве можно, используя трехмерную систему координат. Если эта точка движется, то ее координаты с течением времени меняются. Так как координаты точки зависят от времени, можно считать, что они являются функциями времени. Математически это записывается так:
Эти уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме.
Векторный способ
Радиус-вектор точки — вектор, начало которого совпадает с началом системы координат, а конец — с положением этой точки.
Указать положение точки в трехмерном пространстве также можно с помощью радиус-вектора. При движении точки радиус-вектор со временем изменяется. Он может менять направление и длину. Это значит, что радиус-вектор тоже можно принять за функцию времени. Математически это записывается так:
Эта формула называется кинематическим уравнением движения точки, записанным в векторной форме.
Характеристики механического движения
Движение материальной точки характеризуют три физические величины:
- перемещение
- скорость
- ускорение
Перемещение
Определение
Перемещение (вектор перемещения) — направленный отрезок, начало которого совпадает с начальным положением точки, а конец — с его конечным положением. Обозначается как S.
Перемещение точки определяется как изменение радиус-вектора. Это изменение обозначается как Δr. С точки зрения геометрии вектор перемещения равен разности радиус-векторов, задающих конечное и начальное положение точки:
Траектория — линия, которую описывает тело во время движения.
Путь — длина траектории. Обозначается буквой s. Единица измерения — метры (м).
Путь есть функция времени:
Модуль перемещения — длина вектора перемещения. Обозначается как |Δr|. Единица измерения — метры (м).
Внимание!
Модуль перемещения необязательно должен совпадать с длиной пути.
Пример №1. Человек обошел круглое поле диаметром 1 км. Чему равны пройденный путь и перемещение, которое он совершил.
Путь равен длине окружности. Поэтому:
Человек, обойдя круглое поле, вернулся в ту же точку. Поэтому его начальное положение совпадает с конечным. В этом случае человек совершил перемещение, равное нулю.
Пример №2. Точка движется по окружности радиусом 10 м. Чему равен путь, пройденный этой точкой, в момент, когда модуль перемещения равен диаметру окружности?
Диаметр — это отрезок, который соединяет две точки окружности и проходит через центр. Перемещение равно длине этого отрезка в случае, если один из концов этого отрезка является началом вектора перемещения, а другой — его концом. Траекторией движения в этом случае является дуга, равная половине окружности. А длина траектории есть путь:
Скорость
Определение
Скорость — векторная физическая величина, характеризующая быстроту перемещения тела. Численно она равна отношению перемещения за малый промежуток времени к величине этого промежутка.
В физике скорость обозначается V. Математически скорость определяется формулой:
Скорость характеризуется не только направлением вектора скорости, но и его модулем.
Модуль скорости — расстояние, пройденное точкой за единицу времени. Обозначается буквой V и измеряется в метрах в секунду (м/с).
Математическое определение модуля скорости:
Величина скорости тела в данный момент времени есть первая производная от пройденного пути по времени:
Ускорение
Определение
Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости тела. Численно она равна отношению изменения скорости за малый промежуток времени к величине этого промежутка.
В физике ускорение обозначается a. Математически оно определяется формулой:
Модуль ускорения — численное изменение скорости в единицу времени. Обозначается буквой a. Единица измерения — метры в секунду в квадрате (м/с2).
Математическое определение модуля скорости:
v — скорость тела в данный момент времени, v0— его скорость в начальный момент времени, t — время, в течение которого эта скорость менялась.
Ускорение тела есть первая производная от скорости или вторая производная от пройденного пути по времени:
Проекция вектора перемещения на ось координат
Определение
Проекция вектора перемещения на ось — это скалярная величина, численно равная разности конечной и начальной координат.
Проекция вектора на ось OX:
Проекция вектора на ось OY:
Знаки проекций перемещения
- Проекция является положительной, если движение от начала проекции вектора к проекции конца происходит сонаправленно оси координат.
- Проекция является отрицательной, если движение от начала проекции вектора к проекции конца направлено в сторону, противоположную направлению координатной оси.
Внимание!
Проекция вектора перемещения на ось считается нулевой, если вектор расположен перпендикулярно этой оси.
Модуль перемещения — длина вектора перемещения:
Модуль перемещения измеряется в метрах (м).
Вместе с собственными проекциями модуль перемещения образует прямоугольный треугольник. Сам он является гипотенузой этого треугольника. Поэтому для его вычисления можно применить теорему Пифагора. Выглядит это так:
Выразив проекции вектора перемещения через координаты, эта формула примет вид:
Выражение проекций вектора перемещения через угол его наклона по отношению к координатным осям:
Общий вид уравнений координат:
Пример №3. Определить проекции вектора перемещения на ось OX, OY и вычислить его модуль.
Определяем координаты начальной точки вектора:
Определяем координаты конечной точки вектора:
Проекция вектора перемещения на ось OX:
Проекция вектора перемещения на ось OY:
Применяем формулу для вычисления модуля вектора перемещения:
Пример №4. Определить координаты конечной точки B вектора перемещения, если начальная точка A имеет координаты (–5;5). Учесть, что проекция перемещения на OX равна 10, а проекция перемещения на OY равна 5.
Извлекаем известные данные:
Для определения координаты точки В понадобятся формулы:
Выразим из них координаты конечного положения точки:
Точка В имеет координаты (5; 10).
Задание EF17612
Тело начинает двигаться из состояния покоя с ускорением 4 м/с2. Через 2 с его скорость будет равна…
Алгоритм решения
- Записать исходные данные в определенной системе отсчета.
- Записать формулу ускорения.
- Выразить из формулы ускорения скорость.
- Найти искомую величину.
Решение
Записываем исходные данные:
- Тело начинает двигаться из состояния покоя. Поэтому его начальная скорость v0 = 0 м/с.
- Ускорение, с которым тело начинает движение, равно: a = 4 м/с2.
- Время движения согласно условию задачи равно: t = 2 c.
Записываем формулу ускорения:
Так как начальная скорость равна 0, эта формула принимает вид:
Отсюда скорость равна:
v = at
Подставляем имеющиеся данные и вычисляем:
v = 4∙2 = 8 (м/с)
Ответ: 8
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 37.2k
1. Ускорением (или мгновенным ускорением) называется векторная величина a, характеризующая быстроту изменения скорости движущейся точки и равная первой производной от скорости по времени:
a = dv/dt
Вектор ускорения лежит в соприкасающейся плоскости, проходящей через главную нормаль и касательную к траектории, и направлен в сторону вогнутости траектории.
Проекции ax, ay, az ускорения на оси прямоугольной декартовой системы координат равны:
ax=dvx/dt, ay=dvy/dt, az=dvz/dt
2. Движение точки называется ускоренным, если численное значение ее скорости возрастает с течением времени, т.е. a > 0. Движение точки называется замедленным, если численное значение ее скорости убывает с течением времени, т. е. a < 0. В случае равномерного движения a = 0. При ускоренном движении вектор at совпадает по направлению с вектором v скорости движения точки, а при замедленном он направлен в сторону, противоположную направлению вектора v.
3. Средним ускорением точки в промежутке времени от t до t +Dt называется вектор acp, равный отношению приращения Dv скорости v точки за этот промежуток времени к его продолжительности Dt:
aср(t,Dt) =Dv/Dt
CP ‘ Д/ ДЯ
В пределе при Д/ -> О среднее ускорение совпадает с мгновенным ускорением в момент времени t:
| Ускорение | |
 |
|
| Размерность |
LT−2 |
|---|---|
| Единицы измерения | |
| СИ |
м/с² |
| СГС |
см/с² |
Падающий мяч при отсутствии сопротивления воздуха ускоряется, то есть движется все быстрее и быстрее.
Ускоре́ние (обычно обозначается 

Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,8 м/с каждую секунду, то есть, его ускорение равно 9,8 м/с².
Единицей ускорения в Международной системе единиц (СИ) служит метр в секунду за секунду (m/s2, м/с2), существует также внесистемная единица Гал (Gal), применяемая в гравиметрии и равная 1 см/с2.
Производная ускорения по времени, то есть величина, характеризующая скорость изменения ускорения, называется рывок:
, где:
— вектор рывка.
Содержание
- 1 Кинематика точки
- 1.1 Ускорение точки при прямолинейном движении
- 1.2 Ускорение точки при движении по окружности
- 1.3 Ускорение точки при движении по кривой
- 2 Ускорения в твёрдом теле
- 3 Ускорение при сложном движении
- 4 Динамика точки
- 5 Единицы измерения ускорения
- 6 Измерение ускорения
- 7 Примеры ускорений
- 8 См. также
- 9 Примечания
- 10 Ссылки
Кинематика точки
Вектор ускорения материальной точки в любой момент времени находится путём дифференцирования вектора скорости материальной точки по времени:
.
Ускорение точки при прямолинейном движении
Если вектор 
.
Из вышеприведённых двух формул можно вывести ещё одну, связывающую скалярные величины:
Здесь 



Частным случаем равноускоренного движения является случай, когда ускорение равно нулю в течение всего времени движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), поэтому такое движение называют прямолинейным и равномерным.
Равноускоренное движение точки всегда является плоским, а твёрдого тела — плоскопараллельным (поступательным). (Обратное, вообще говоря, не верно).
Ускорение точки при движении по окружности
Вектор ускорения
при движении точки по окружности можно разложить на два слагаемых (компоненты):
Тангенциальное ускорение — 

Центростремительное или Нормальное ускорение 

Угловое ускорение — показывает, на сколько изменилась угловая скорость за единицу времени, и, по аналогии с линейным ускорением, равно:
Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и скорости сонаправлены, значение скорости растёт, и наоборот.
Ускорение точки при движении по кривой
Вектор ускорения 

,
где


Векторы 

Итак, учитывая сказанное выше, вектор ускорения всегда можно записать как:
,
Ускорения в твёрдом теле
Связь ускорений двух точек можно получить, продифференцировав формулу Эйлера для скоростей по времени:
,
где 

Второе слагаемое называется осестремительным ускорением.
Ускорение при сложном движении
Говорят, что материальная точка (тело) совершает сложное движение, если она движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. Тогда абсолютное ускорение тела равно сумме относительного, переносного и кориолисова:
.
Динамика точки
Первый закон Ньютона постулирует существование инерциальных систем отсчёта. В этих системах отсчёта равномерное прямолинейное движение имеет место в том случае, когда тело (материальная точка) не подвергается никаким внешним воздействиям в процессе своего движения. На основе этого закона возникает ключевое для механики понятие силы как такого внешнего воздействия на тело, которое выводит его из состояния покоя или влияет на скорость его движения. Таким образом, постулируется, что причиной возникновения ненулевого ускорения в инерциальной системе отсчёта всегда является некоторое внешнее силовое воздействие.
Второй закон Ньютона утверждает, что ускорение материальной точки всегда пропорционально приложенной к ней и порождающей ускорение силе, причём коэффициент пропорциональности всегда один и тот же независимо от вида силового воздействия (он называется массой материальной точки):
Единицы измерения ускорения
- метр на секунду в квадрате (метр в секунду за секунду), м/с², производная единица системы СИ
- сантиметр на секунду в квадрате (сантиметр в секунду за секунду), см/с², производная единица системы СГС
| м/с2 | фут/с2 | g0 | см/с2 | |
|---|---|---|---|---|
| 1 м/с2 = | 1 | 3.28084 | 0.101972 | 100 |
| 1 фут/с2 = | 0.304800 | 1 | 0.0310810 | 30.4800 |
| 1 g0 = | 9.80665 | 32.1740 | 1 | 980.665 |
| 1 см/с2 = | 0.01 | 0.0328084 | 0.00101972 | 1 |
Измерение ускорения
Приборы для измерения ускорения называются акселерометрами. Они не измеряют ускорение непосредственно, а измеряют силу реакции (укр.)русск. опоры, которая возникает при ускоренном движении. Поскольку аналогичные силы сопротивления возникают также и в поле тяготения, то с помощью акселерометров можно измерять также и гравитацию.
Акселерографы — приборы, измеряющие и автоматически записывающие (в виде графиков) значения ускорения поступательного и вращательного движения.
Примеры ускорений
Значения ускорений различных движений:[1]
| Вид движения | Ускорение, м/с2 |
|---|---|
| Аварийное торможение автомобиля | 4—6 |
| Автомобиль «Жигули» | 1,5 |
| Бегун на коротких дистанциях | 1,5 |
| Велосипедист | 1,7 |
| Гоночный автомобиль | 8—9 |
| Запуск и торможение космического корабля | 4—6 g |
| Конькобежец | 1,9 |
| Манёвр реактивного самолёта | до 10 g |
| Микрочастицы в ускорителе | (2—50) · 1014 |
| Мотоцикл | 3—6 |
| Пассажирский лифт | 0,9—1,6 |
| Поезд метро | 1 |
| Поршень двигателя внутреннего сгорания | 3 · 103 |
| Пуля в стволе винтовки | 2,5 · 105 |
| Свая после удара копром | 300 |
| Торможение при открытии парашюта | 3 g |
Примечание: g ≈ 9,81 м/с2.
См. также
| Ускорение в Викисловаре? | |
| Ускорение в Викитеке? | |
| Ускорение на Викискладе? |
- Ускорение свободного падения
- Релятивистски равноускоренное движение
Примечания
- ↑ Кошкин Н.И., Ширкевич М.Г. Справочник по элементарной физике. — 10-е, испр. и доп.. — М.: Наука, 1988. — С. 61. — 256 с. — ISBN 5-02-013833-9
Ссылки
- Ландау, Л. Д., Лифшиц, Е. М. Механика. — Издание 5-е, стереотипное. — М.: Физматлит, 2004. — 224 с. — («Теоретическая физика», том I). — ISBN 5-9221-0055-6
§1. Вектор ускорения точки
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. Оно показывает, на какую величину изменяется скорость тела за единицу времени.
В СИ единицей ускорения является метр на секунду в квадрате .
Пусть в некоторый момент времени t движущаяся точка находится в положении М и имеет скорость v, а в момент t1 приходит в положение M1 и имеет скорость v1 (рис. 1).
Рис.1. Движение точки М с ускорением
Тогда за промежуток времени ∆t=t1-t скорость точки получает приращение . Для построения вектора отложим от точки М вектор, равный v1, и построим параллелограмм, в котором диагональю будет
, a одной из сторон . Тогда, очевидно, вторая сторона и будет изображать вектор . Заметим, что вектор всегда направлен в сторону вогнутости траектории.
Отношение приращения вектора скорости к соответствующему промежутку времени ∆t определяет вектор среднего ускорения точки за этот промежуток времени:
Вектор среднего ускорения имеет то же направление, что и вектор , т.е. направлен в сторону вогнутости траектории.
Ускорение точки равно нулю лишь тогда, когда скорость точки v постоянна как по величине, так и по направлению: это соответствует только прямолинейному и равномерному движению.
Найдем, как располагается вектор по отношению к траектории точки. При прямолинейном движении вектор направлен вдоль прямой, по которой движется точка.
При прямолинейном движении с возрастающей по модулю скоростью (рис. 2, а) векторы и сонаправлены () и проекция ускорения на направление движения положительна.
При прямолинейном движении с убывающей по модулю скоростью (рис. 2, б) направления векторов и противоположны () и проекция ускорения на направление движения отрицательна.
Рис.2. Направление вектора ускорения:
а) — равноускоренное движение; б) — равнозамедленное движение
§2. Определение ускорения при координатном способе задания движения
Вектор ускорения точки в проекции на оси получаем:
Или
т.е. проекция ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени. Модуль и направление ускорения найдутся из формул
где α1, β1, γ1 — углы, образуемые вектором ускорения с координатными осями.
§3. Касательное и нормальное ускорение точки Полное ускорение
можно разложить на две состовляющие: касательную и нормальную составляющие ускорения точки (рис. 3) При этом составляющая
будет всегда направлена в сторону вогнутости кривой (величина a всегда положительна), а составляющая
может быть направлена или в положительном, или в отрицательном направлении оси Mτ в зависимости от знака проекции aτ (см. рис.3, а и б).
Рис.3. Направление нормального и касательного ускорений
Вектор ускорения точки из ображается диагональю параллелограмма, построенного на составляющих и . Так как эти составляющие взаимно перпендикулярны, то по модулю:





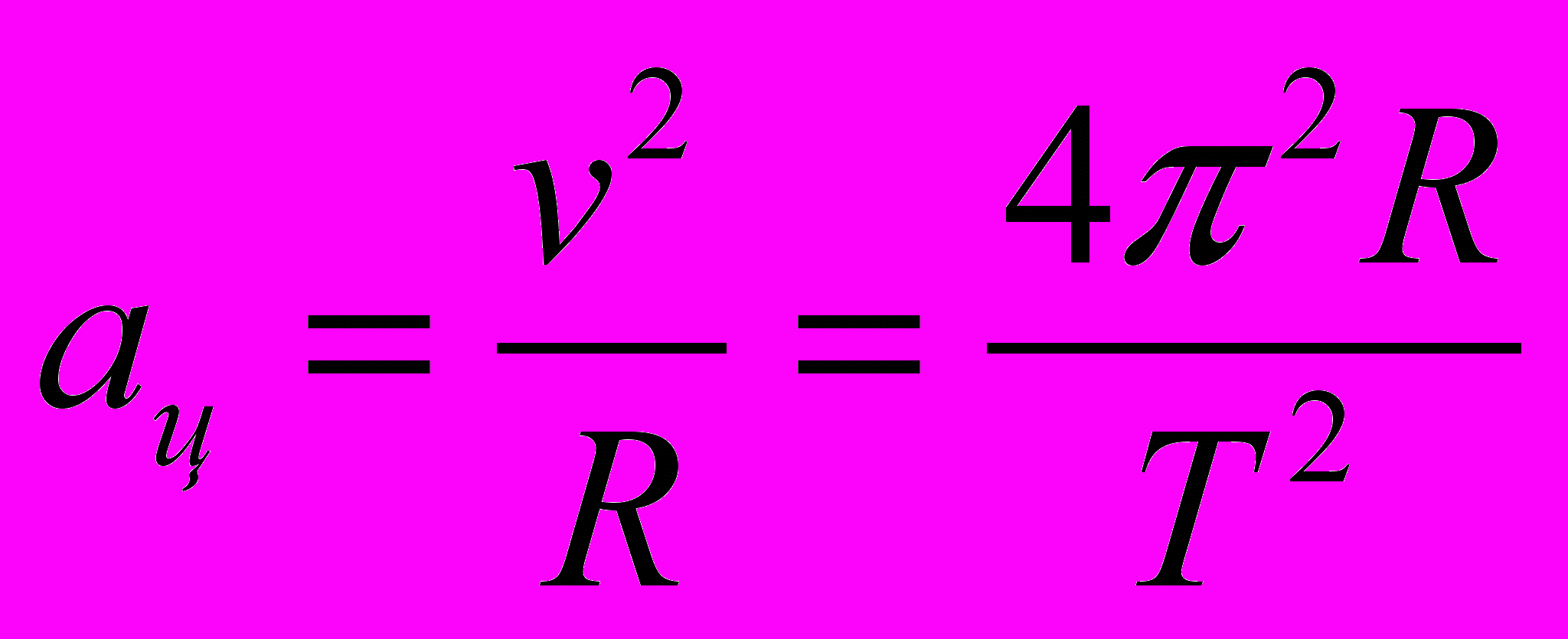














 , где:
, где:  — вектор рывка.
— вектор рывка. .
.
 .
.






 ,
, ,
,![vec{w}_B = vec{w}_A + left[vec{omega}, left[ vec{omega}, vec{AB}right] right] + left[ varepsilon, vec{AB} right]](https://dic.academic.ru/dic.nsf/ruwiki/3e27aa54ea841bf57cd0aa5554e07bf5.png) ,
,![vec a_a=vec {a}_r + vec {a}_e + 2left[vec omega times vec {v}_r right]](https://dic.academic.ru/dic.nsf/ruwiki/2bb4936c467fcb4f36cd35d23434328c.png) .
.