Устная математика вступительный экзамен

Программа вступительных испытаний по математике

Настоящая программа состоит из трех разделов.

В первом разделе перечислены основные математические понятия, которыми должен владеть поступающий как на письменном, так и на устном экзамене.

Второй раздел представляет собой перечень вопросов теоретической части устного экзамена. При подготовке к письменному экзамену целесообразно познакомиться с формулировками утверждений этого раздела.

В третьем разделе указано, какие навыки и умения требуются от поступающего на письменном и устном экзаменах.

Объем знаний и степень владения материалом, описанным в программе, соответствуют курсу математики средней школы. Поступающий может пользоваться всем арсеналом средств из этого курса, включая и начала анализа. Однако для решения экзаменационных задач достаточно уверенного владения лишь теми понятиями и их свойствами, которые перечислены в настоящей программе. Объекты и факты, не изучаемые в общеобразовательной школе, также могут использоваться поступающими, но при условии, что он способен их пояснять и доказывать.

В связи с обилием учебников и регулярным их переизданием отдельные утверждения второго раздела могут в некоторых учебниках называться иначе, чем в программе, или формулироваться в виде задач, или вовсе отсутствовать. Такие случаи не освобождают поступающего от необходимости знать эти утверждения.

I. Основные понятия

1. Натуральные числа. Делимость. Простые и составные числа. Наибольший общий делитель и наименьшее общее кратное.
2. Целые, рациональные и действительные числа. Проценты. Модуль числа, степень, корень, арифметический корень, логарифм. Синус, косинус, тангенс, котангенс числа (угла). Арксинус, арккосинус, арктангенс, арккотангенс числа.
3. Числовые и буквенные выражения. Равенства и тождества.
4. Функция, ее область определения и область значений. Возрастание, убывание, периодичность, четность, нечетность.
   Наибольшее и наименьшее значения функции. График функции.

5. Линейная, квадратичная, степенная, показательная, логарифмическая, тригонометрические функции.
6. Уравнение, неравенства, система. Решения (корни) уравнения, неравенства, системы. Равносильность.
7. Арифметическая и геометрическая прогрессии.
8. Прямая на плоскости. Луч, отрезок, ломаная, угол.
9. Треугольник. Медиана, биссектриса, высота.
10. Выпуклый многоугольник. Квадрат, прямоугольник, параллелограмм, ромб, трапеция. Правильный многоугольник. Диагональ.
11. Окружность и круг. Радиус, хорда, диаметр, касательная, секущая. Дуга окружности и круговой сектор. Центральный и вписанные углы.
12. Прямая и плоскость в пространстве. Двугранный угол.
13. Многогранник. Куб, параллелепипед, призма, пирамида.
14. Цилиндр, конус, шар, сфера.
15. Равенство и подобие фигур. Симметрия.
16. Параллельность и перпендикулярность прямых, плоскостей. Скрещивающиеся прямые. Угол между прямыми, плоскостями, прямой и плоскостью.
17. Касание. Вписанные и описанные фигуры на плоскости и в пространстве. Сечение фигуры плоскостью.
18. Величина угла. Длина отрезка, окружности и дуги окружности. Площадь многоугольника, круга и кругового сектора.
    Площадь поверхности и объем многогранника, цилиндра, конуса, шара.

19. Координатная прямая. Числовые промежутки. Декартовы координаты на плоскости и в пространстве. Векторы.

II. Содержание теоретической части устного экзамена

Алгебра

1. Признаки делимости на 2, 3, 5, 9, 10.
2. Свойства числовых неравенств.
3. Формулы сокращенного умножения.
4. Свойства линейной функции и ее график.
5. Формула корней квадратного уравнения. Теорема о разложении квадратного трехчлена на линейные множители. Теорема
   Виета.

6. Свойства квадратичной функции и ее график.
7. Неравенство, связывающее среднее арифметическое и среднее геометрическое двух чисел. Неравенство для суммы двух взаимно обратных чисел.
8. Формулы общего члена и суммы n первых членов
   арифметической прогрессии.

9. Формулы общего члена и суммы n первых членов геометрической прогрессии.
10. Свойства степеней с натуральными и целыми показателями. Свойства арифметических корней n-й степени. Свойства степеней с рациональными показателями.
11. Свойства степенной функции с целым показателем и ее график.
12. Свойства показательной функции и ее график.
13. Основное логарифмическое тождество. Логарифмы произведения, степени, частного. Формула перехода к новому
    основанию.
14. Свойства логарифмической функции и ее график.
15. Основное тригонометрическое тождество. Соотношения между тригонометрическими функциями одного и того же аргумента. Формулы приведения, сложения, двойного и половинного аргумента, суммы и разности тригонометрических функций. Выражение тригонометрических функций через тангенс половинного аргумента. Преобразование произведения синусов и косинусов в сумму. Преобразование выражения asinx + bcosx с помощью вспомогательного аргумента.
16. Формулы решений простейших тригонометрических уравнений.
17. Свойства тригонометрических функций и их графики.

Геометрия

1. Теоремы о параллельных прямых на плоскости.
2. Свойства вертикальных и смежных углов.
3. Свойства равнобедренного треугольника.
4. Признаки равенства треугольников.
5. Теорема о сумме внутренних углов треугольника. Теорема о внешнем угле треугольника. Свойства средней линии треугольника.
6. Теорема Фалеса. Признаки подобия треугольников.
7. Признаки равенства и подобия прямоугольных треугольников. Пропорциональность отрезков в прямоугольном треугольнике. Теорема Пифагора.
8. Свойство серединного перпендикуляра к отрезку. Свойство биссектрисы угла.
9. Теоремы о пересечении медиан, пересечении биссектрис и пересечении высот треугольника.
10. Свойство отрезков, на которые биссектриса треугольника делит противоположную сторону.
11. Свойство касательной к окружности. Равенство касательных, проведенных из одной точки к окружности. Теоремы о вписанных углах. Теорема об угле, образованном касательной и хордой. Теоремы об угле между двумя пересекающимися хордами и об угле между двумя секущими, выходящими из одной точки. Равенство произведений отрезков двух пересекающихся хорд. Равенство квадрата касательной произведению секущей на ее внешнюю часть.
12. Свойство четырехугольника, вписанного в окружность. Свойство четырехугольника, описанного около окружности.
13. Теорема об окружности, вписанной в треугольник. Теорема об окружности, описанной около треугольника.
14. Теоремы синусов и косинусов для треугольника.
15. Теорема о сумме внутренних углов выпуклого многоугольника.
16. Признаки параллелограмма. Свойства параллелограмма.
17. Свойства средней линии трапеции.
18. Формула для вычисления расстояния между двумя точками на координатной плоскости. Уравнение окружности.
19. Теоремы о параллельных прямых в пространстве. Признак параллельности прямой и плоскости. Признак параллельности плоскостей.
20. Признак перпендикулярности прямой и плоскости. Теорема об общем перпендикуляре к двум скрещивающимся прямым. Признак перпендикулярности плоскостей. Теорема о трех перпендикулярах.

III. Требования к поступающему

На экзамене по математике поступающий должен уметь:

1. выполнять (без калькулятора) действия над числами и числовыми выражениями; преобразовывать буквенные выражения; производить операции над векторами (сложение, умножение на число, скалярное произведение); переводить одни единицы измерения величин в другие;
2. сравнивать числа и находить их приближенные значения (без калькулятора); доказывать тождества и неравенства для буквенных выражений;
3. решать уравнения, неравенства, системы (в том числе с параметрами) и исследовать их решения;
4. исследовать функции; строить графики функций и множества точек на координатной плоскости, заданные уравнениями и неравенствами;
5. изображать геометрические фигуры на чертеже; делать дополнительные построения; строить сечения; исследовать взаимное расположение фигур; применять признаки равенства, подобия фигур и их принадлежности к тому или иному виду;
6. пользоваться свойствами чисел, векторов, функций и их графиков, свойствами арифметической и геометрической прогрессий;
7. пользоваться свойствами геометрических фигур, их характерных точек, линий и частей, свойствами равенства, подобия и взаимного расположения фигур;
8. пользоваться соотношениями и формулами, содержащими модули, степени, корни, логарифмические, тригонометрические выражения, величины углов, длины, площади, объемы;
9. составлять уравнения, неравенства и находить значения величин, исходя из условия задачи;
10. излагать и оформлять решение логически правильно, полно и последовательно, с необходимыми пояснениями.

    На устном экзамене поступающий должен дополнительно уметь:

11. давать определения, формулировать и доказывать утверждения (формулы, соотношения, теоремы, признаки, свойства и т.п.), указанные во втором разделе настоящей программы;
12. анализировать формулировки утверждений и их доказательства;
13. решать задачи на построение циркулем, линейкой; находить геометрические места точек.

В данной статье представлен пример устного вступительного экзамена по математике в 9 класс лицея «Вторая школа», проходившего в 2017 году, с разбором всех заданий от профессионального репетитора, занимающегося подготовкой школьников к поступлению в этот лицей. Разбор варианта письменного вступительного экзамена во «Вторую школу» вы можете найти на этой странице.

Разбор заданий устного вступительного экзамена по математике в лицей «Вторая школа»

Всего на устном экзамене по математике в лицей «Вторая школа» в 2017 году абитуриентам было предложено 10 задач. Решение каждой задачи абитуриент должен был защитить перед экзаменатором. На защиту каждой задачи отводилось по 3 попытки. Если за первый час сдающий не смог защитить решение по крайней мере 3-х задач из первой пятёрки, экзамен считался не сданным. Ниже приведены цитаты формулировок заданий, предложенных в одном из вариантов, а также их подробное решение.

1. Соревновались 4 команды, каждая с каждой сыграла 1 раз. За победу давалось 3 очка, за ничью — 1 очко, за поражение — 0 очков. Команды набрали 5, 3, 3, 2 очка. Сколько было ничьих?

По результатам каждой игры в общую копилку очков добавлялось 3 очка (если одна команда победила другую) или 2 очка (если команды сыграли вничью). Всего было сыграно 6 матчей (1-я команда со 2-й, с 3-й, с 4-й; 2-ая команда с 3-й и с 4-й; 3-я команда с 4-й). Мы видим, что после всех игр в общей копилке оказалось 13 очков. Это нечётное число. Значит, была по крайней мере 1 победа, за которую какая-то команда получила 3 очка. Осталось 10 очков. Предположим, что они получились в общей копилке за 2-х побед и 2-х ничьих. Но тогда общее количество игр будет 5. Значит, единственно возможным вариантом остаётся, что эти 10 очков оказалось в общей копилке в результате 5-ти ничейных матчей. Других вариантов быть не может. То есть всего ничьих было 5.

Примечание. Результаты матчей были следующими: 1-я команда одержала победу в матче с 4-й, остальные 5 игр между командами прошли с ничейным результатом.

2. Чётное натуральное число n имеет 7 делителей, включая 1 и n. Сколько делителей имеет число 2n?

Представим чётное натуральное число n в каноническом разложении на простые сомножители:

   

Здесь — простые числа, большие 2 и меньшие либо равные n, а — неотрицательные целые числа.

Тогда количество делителей числа n определяется по формуле:

   

Первая скобка не может быть равна 1. Но поскольку 7 — простое число, то и , а остальные скобки равны 1. То есть . Значит, . У этого числа 7+1=8 делителей.

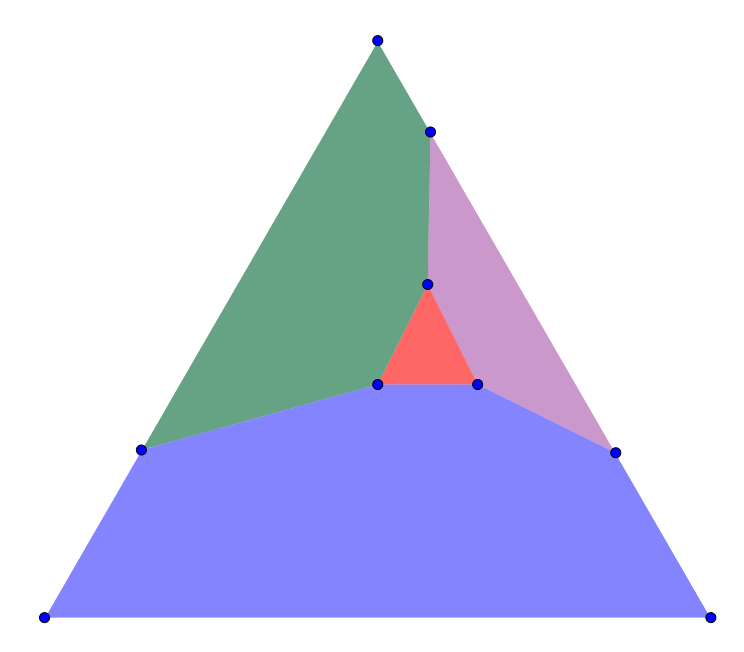
3. Разрежьте равносторонний треугольник на 4 выпуклые фигуры: шестиугольник, пятиугольник, четырёхугольник и треугольник.

Можно, например, разрезать его так:

4. По кругу лицом в центр круга стоят мальчики и девочки, всего 20 детей (есть и те, и другие). У каждого мальчика справа стоит ребёнок в синей футболке, а у каждой девочки слева стоит ребёнок в красной футболке. Сколько в круге мальчиков?

Расположения типа МАЛЬЧИК — НЕИЗВЕСТНЫЙ РЕБЁНОК — ДЕВОЧКА невозможны, так как цвет футболки НЕИЗВЕСТНОГО РЕБЁНКА должен быть одновременно и красным, и синим. Значит, мальчики в круге должны стоять через одного, и их не меньше 10. По аналогичным соображениям девочек в круге тоже не меньше 10. Следовательно, и девочек, и мальчиков в круге по 10. Мальчики и девочки чередуются, все мальчики в красных футболках, все девочки в синих футболках.

5. Разместите в квадрате со стороной 1 несколько непересекающихся квадратов, так чтобы сумма их периметров была больше 2017. Квадраты могут иметь общую границу, но не могут иметь общих внутренних точек.

Пусть это будут одинаковые квадраты, каждый со стороной 0,001. Тогда периметр такого квадрата равен 0,004. Всего внутри исходного квадрата, согласно условиям задачи, можно разместить 1 000 000 таких квадратов. Сумма их периметров будет равна 4 000, что больше 2017.

6. В вершинах квадрата расставили натуральные числа a, b, c, d, а на сторонах написали произведения на концах. Сумма на рёбрах — 77. Найти сумму в вершинах.

Именно эту формулировку использовали авторы-составители. Стороны квадрата здесь обозвали «рёбрами». Но имелись ввиду именно стороны. Я это знаю точно, потому что мой ученик решал на экзамене эту задачу, исходя из того, что под рёбрами они понимали стороны квадрата. И эту задачу ему зачли. Ну и плюс к тому, по смыслу здесь больше ничего не подходит.

Итак, имеем, что ab + bc + cd + da = (a + c)(b + d) = 77. Так как у числа 77 только 4 натуральных делителя (1, 7, 11 и 77), то для натуральных чисел a, b, c, d возможно только, что a + c = 7 и b + d = 11 либо a + c = 11 и b + d = 7. В обоих случаях сумма в вершинах равна 18.

7. Есть 5 разных станков. Обучение одного рабочего на одном станке стоит N рублей. С какими наименьшими затратами можно обучить 8 рабочих так, чтобы при отсутствии любых трёх из них можно было использовать все 5 станков?

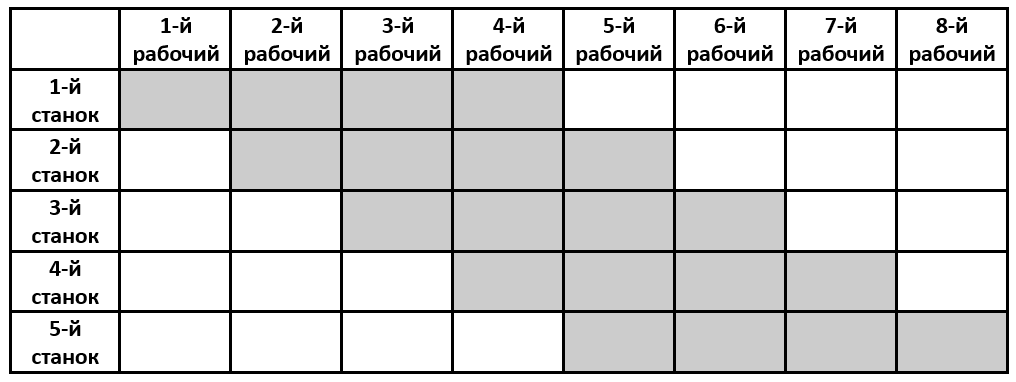
На каждом станке должны научиться работать как минимум по 4 рабочих. В противном случае возникает вероятность, что среди трёх отсутствующих рабочих окажутся все те, которые умеют работать на каком-то станке. То есть как минимум потребуется 5×4=20 циклов обучения, на которые будет потрачено 20N рублей. Приведём пример необходимого плана обучения рабочих. В приведённой ниже таблице строки соответствуют станкам, а столбцы — рабочим:

Как видно, при удалении любых трёх столбцов из этой таблицы среди рабочих останутся те, которые смогут работать на каждом из 5 станков.

8. Пусть M — точка внутри параллелограмма ABCD. Что больше: сумма расстояний от точки M до вершин параллелограмма или его периметр?

Эта задача — яркое демонстрация того, что только школьными знаниями при поступлении в лицей «Вторая школа» вам не обойтись. Вот смотрите, что вам понадобится для её решения. Во-первых, неравенство треугольника. Согласно этому неравенству длина любой стороны треугольника меньше суммы длин двух других сторон. Эту теорему ещё худо-бедно проходят на уроках в школе. Правда иногда уделяют этому настолько мало времени, что некоторые ученики, даже хорошие, просто проходят мимо этой теорема, вообще не понимая зачем она нужна. Но это отдельный вопрос. Главное проходят.

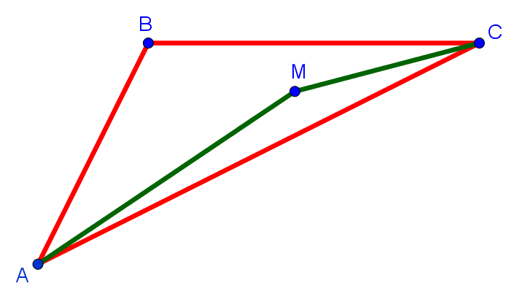
Вот собственно и всё, что дают в школе на эту тему на уроках геометрии в 7 классе. Но проблема в том, что очень малое количество школьников сможет решить эту задачу сходу, зная только теорему о неравенстве треугольника. И причина этого в том, что для решения этой задачи требуется знание ещё одного факта из геометрии, доказательство которого основано на неравенстве треугольника. И этот факт заключается в следующем. Если взять точку внутри треугольника, то сумма расстояний от этой точки до двух вершин треугольника, между которыми находится какая-то его сторона, меньше суммы двух других сторон этого треугольника. Чтобы стало понятно, изобразим это на рисунке:

То есть на изображённом рисунке AM + MC < AB + BC. Казалось бы, что это очевидный факт. Но он не оформлен в школе как теорема, поэтому его обязательно нужно доказывать. Если вы его не докажите, то задача не будет решена. Вам за неё поставят 0 баллов. Как же нам доказать этот факт? Для этого продлим отрезок CM до пересечения со стороной AB в точке F:

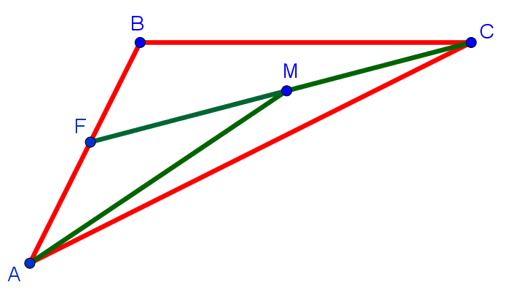
Применим теперь неравенство треугольника для треугольников FBC и AFM. Получим следующие неравенства: FC < BF + BC и AM < AF + FM. Сложим их почленно и представим FC как FM + MC. Получим следующее неравенство: FM + MC + AM < BF + BC + AF + FM. С учётом того, что BF + AF = AB. Получаем MC + AM < AB + BC, а это как раз то самое неравенство, которое нам нужно было доказать.

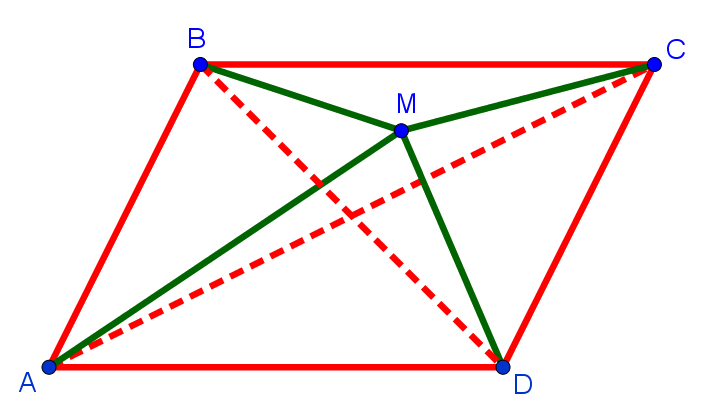
И только теперь, доказав эту лемму (теорему, необходимую для доказательства основной теоремы), мы готовы решить данную задачу. Изобразим ситуацию на рисунке:

Для треугольника ABC получаем AM + MC < AB + BC. Для треугольника BCD получаем BM + MC < BC + CD или, с учётом BC = AD (так как это противоположные стороны параллелограмма), BM + MC < AD + CD. Складываем почленно полученные неравенства и получаем: AM + MC + BM + MD < AB + BC + AD + CD. То есть сумма расстояний от точки внутри параллелограмма до его вершин меньше периметра этого параллелограмма.

Вот такое решение. Получается, что эту задачу можно решить, зная только неравенство треугольника, изучающееся в школьном курсе геометрии. То есть формально содержание задачи не выходит за рамки школьной программы. Но по факту очень мало кто из школьников может решить эту задачу. Даже из отличников, которые прекрасно знают, что такое неравенство треугольника. И это не из-за того, что они какие-то глупые или не обладают математическими способностями. Просто их в школе этому не научили. Ну а самостоятельно подготовиться в этом возрасте школьники не могут. Это нереально, да и времени всегда очень мало. Так что без дополнительной специальной подготовки не обойтись. И лучше всего, конечно, с профессиональным репетитором, который знаком со спецификой заданий из вступительных экзаменов.

9. Разложите 56 конфет по 14 пакетам так, чтобы с помощью этих пакетов можно было разделить конфеты поровну как между 7-ю, так и между 8-ю детьми. Перекладывать конфеты нельзя. В разных пакетах может быть одинаковое число конфет.

Нужно положить по 7 конфет в 7 пакетов, а в оставшиеся 7 пакетов положить по 1 конфете. Тогда, чтобы разделить конфеты поровну между 7-ю детьми, нужно каждому ребёнку выдать по 2 пакета: первый — с 7 конфетами, второй — с 1 конфетой. А для того, чтобы разделить конфеты поровну между 8-ю детьми, нужно 7 из них выдать по пакету с 7-ю конфетами, а оставшемуся ребёнку выдать оставшиеся 7 пакетов, в каждом из которых лежит по 1 конфете.

Введём обозначение:

Тогда верно также следующее:

При этом из условия задачи следует, что . Из этого следует, что если принимает наибольшее значение, то и также принимает наибольшее значение. Найдём это значение.

При любом выражение принимает наибольшее значение при Действительно, абсцисса вершины параболы , ветви которой направлены вниз, находится в точке (условие соблюдено). Соответствующая ордината равна Это и есть наибольшее значение данной квадратичной функции. Наибольшее значение примет в том случае, если при любом все произведения типа одновременно примут свои наибольшие значения Поскольку таких произведений , то наибольшее значение равно Тогда наибольшее значение равно

Вот такого уровня задания предлагаются на устном вступительном экзамене по математике в лицей «Вторая школа». И практика показывает, что очень часто школьники не могут решить те или иные задачи, не потому что они не способны к серьёзному изучению математики, а потому что они не знали к чему готовиться, что и как изучать, чтобы успешно сдать этот экзамен. Ну а школа не в состоянии дать необходимую подготовку, тем более если ученик учится в слабом классе. Так что специальная подготовка крайне необходима. И лучше всего — с профессиональным репетитором по математике и физике, который имеет большой опыт подготовки к вступительным экзаменам в лицей «Вторая школа» и знает, как в ограниченные сроки эффективно подготовиться к вступительному экзамену. И лучше всего начинать подготовку заранее. Чем раньше она начнётся, тем выше вероятность успеха.

Если вам была интересна эта статья, возможно вас заинтересую также следующие:

• Лицей вторая школа. Вступительный по математике 2017 года
• Репетитор для поступления в лицей «Вторая школа»
• Вступительный экзамен в лицей «Вторая школа»

Подготовка к вступительным экзаменам в МГУ — Задачи устного экзамена по математике — Федотов М.В., Хайлов Е.Н. — 2000.

Настоящее пособие составлено для подготовительных курсов факультета вычмслительной математики и кибернетики МГУ имени М.В. Ломоносова. Может быть полезно абитуриентам при подготовке к поступлению как на факультет ВМиК, так и на другие факультеты МГУ, где есть устный экзамен по математике.

Содержание

Часть I. Задачи по алгебре

§ 1 Действительные числа 
п. 1.1. Целые числа. Делимость
п. 1.2. Рациональные и иррациональные числа
п. 1.3. Сравнение чисел
§2. Квадратный трехчлен и его свойства. Теорема Виета
§3. Тригонометрические задачи
§4. Логарифмические и показательные задачи
§5. Решение уравнений и неравенств
п. 5.1. Рациональные уравнения и неравенства
п. 5.2. Иррациональные уравнения и неравенства
п. 5.3. Тригонометрические уравнения и неравенства
п. 5.4. Логарифмические и показательные уравнения и неравенства
п. 5.5. Решение уравнений и неравенств в целых числах
§6. Решение систем уравнений и неравенств
§7. Доказательства неравенств и тождеств
§8. Задачи на арифметические и геометрические прогрессии
§9. Функции и их графики
§10. Изображение множества точек на плоскости
§11. Многочлены
§12. Задачи последних лет
п. 12.1. Факультет ВМиК МГУ (1997 — 1999 гг.)
п. 12. 2. Геологический факультет МГУ (1997 — 1999 гг.)
п. 12.3. Механико-математический факультет МГУ (1998- 1999гг.)
Ответы

Часть П. Задачи по геометрии
§ 1. Задачи, связанные с треугольниками
§2. Задачи, связанные с четырехугольниками
§3. Задачи, связанные с окружностью
§4. Площади фигур
§5. Задачи на построение
Ответы

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:

Скачать книгу Подготовка к вступительным экзаменам в МГУ — Задачи устного экзамена по математике — Федотов М.В., Хайлов Е.Н. — fileskachat.com, быстрое и бесплатное скачивание.

Скачать djvu
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу

Скачать Книгу Подготовка к вступительным экзаменам в МГУ — Задачи устного экзамена по математике — Федотов М.В., Хайлов Е.Н.

Дата публикации: 12.06.2010 06:59 UTC

Теги:

математика :: экзамен по математике :: МГУ :: вступительный экзамен в МГУ по математике :: задачи устного экзамена по математике :: Федотов :: Хайлов :: книга :: скачать

Вступительные испытания в ВУЗ по математике. Примеры с ответами

Высшее Учебное Заведение. Россия. ВИ. ЕГЭ. 2019, 2020, 2021, 2022 год

Если вы в этом году решили поступить в ВУЗ на очное обучение или заочное отделение, тогда вам придется сдавать Вступительные испытания ВИ. Если вы не сдавали ЕГЭ в школе, тогда вам пригодится эта информация для поступления в ВУЗ

На этой страницу вы можете бесплатно скачать тесты, задания и примеры вступительных экзаменов в ВУЗ, а так же подробное решение и ответы на задания.

Вступительные испытания в ВУЗ по математике. Примеры с ответами

Процедура проведения вступительного испытания

1. Вступительное испытание проводится в соответствии с действующими Правилами приема в бакалавриат и специалитет и Положением о порядке проведения вступительных испытаний МФТИ.

2. Вступительное испытание по математике проводится с совмещением письменной и устной форм.

3. Вступительное испытание состоит из четырех частей.

4. Первые три части вступительного испытания – решение задач с численным ответом. Длительность каждой части – 45 минут.

5. Первая часть вступительного испытания вступительного испытания, проводимого с использованием дистанционных технологий, проверяется программно-аппаратным способом.

6. Допуск ко второй письменной части и последующим частям вступительного испытания проводится по результатам проверки первой письменной части. Недопущенным ко второй и последующим частям вступительного испытания выставляется балл на основании проверки первой части вступительного испытания.

7. Четвертая часть вступительного испытания – устный опрос по задачам и программе вступительного испытания. Длительность устной части – до 30 минут.

Программа вступительного испытания

1. Натуральные числа. Делимость. Простые и составные числа. Признаки делимости. Наибольший общий делитель и наименьшее общее кратное.

2. Целые, рациональные, действительные числа и операции с ними.

3. Преобразование арифметических и алгебраических выражений. Формулы сокращённого умножения.

4. Числовые неравенства и их свойства.

5. Функция. Область определения и множество значений. График функции. Чётность, нечётность, периодичность функций. Линейная, квадратичная, степенная, дробно-рациональная функции и их свойства.

6. Линейные уравнения. Квадратные уравнения. Рациональные уравнения. Уравнения с модулем. Уравнения высших степеней. Разложение многочленов на множители.

7. Линейные неравенства. Квадратные неравенства. Рациональные неравенства. Неравенства с модулем.

8. Корень из числа и его свойства. Арифметический корень. Иррациональные уравнения. Иррациональные неравенства.

9. Арифметическая и геометрическая прогрессии и их свойства.

10. Комбинаторика. Правила суммы и произведения. Перестановки, размещения, сочетания.

11. Задачи на составление уравнений (задачи на движение, на проценты, на совместную работу, на смеси и пр.).

12. Тригонометрические формулы. Тригонометрические и обратные тригонометрические функции и их свойства. Преобразование тригонометрических выражений. Тригонометрические уравнения и неравенства.

13. Свойства степеней. Логарифмы и их свойства. Показательная и логарифмическая функции и их свойства. Показательные и логарифмические уравнения и неравенства.

14. Производная. Исследование функций с помощью производных.

15. Задачи с параметром.

16. Системы уравнений и неравенств.

17. Множества точек на координатной плоскости.

18. Планиметрия:

— смежные и вертикальные углы,

— признаки и свойства равнобедренного треугольника, признаки равенства треугольников,

— теоремы о параллельных прямых, сумма углов треугольника, сумма углов выпуклого многоугольника,

— геометрические места точек (множество внутренних точек угла, равноудалённых от его сторон, множество точек, равноудалённых от концов отрезка),

— медианы, биссектрисы, высоты треугольника и их свойства,

— подобие треугольников, теорема Фалеса, теорема о пропорциональных отрезках,

— четырёхугольники; параллелограмм, прямоугольник, ромб, квадрат, трапеция и их свойства,

— пропорциональные отрезки в прямоугольном треугольнике, теорема Пифагора,

— площадь и её свойства,

— формулы площади треугольника, параллелограмма, трапеции,

— точки пересечения высот, медиан, биссектрис, серединных перпендикуляров треугольника,

— теоремы синусов, косинусов и Менелая для треугольника,

— окружность и её свойства,

— касательная к окружности и её свойства,

— теоремы о пропорциональных отрезках в окружности,

— теоремы об углах, связанных с окружностью (вписанный угол, центральный угол, угол между касательной и хордой),

— окружность, описанная около треугольника; окружность, вписанная в треугольник,

— окружность, описанная около четырёхугольника; окружность, вписанная в четырёхугольник,

— правильные многоугольники и их свойства,

— длина окружности, площадь круга и его частей,

— векторы, скалярное произведение векторов,

— метод координат на плоскости.

19. Стереометрия. Параллельность прямых и плоскостей, перпендикулярность прямых и плоскостей. Объём фигуры; площадь поверхности фигуры. Куб, параллелепипед, призма, пирамида, шар, цилиндр, конус и их свойства. Векторы и координаты в пространстве. Сечения многогранников. Углы и расстояния в пространстве.

.