По теме: методические разработки, презентации и конспекты
Тренировочные задания для подготовки к ГИА по ИНФОРМАТИКЕ и ИКТ (Задание № 11)
Решение задания № 11 Задание: На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.Скол…
Творческие и системные задания для подготовки к ЕГЭ естественно-научного цикла со способами решений и ответами. Познавательные задания по зоологии позвоночных
Рациональное сочетание различных приемов и средств обучения помогает нам организовать так работу детей, чтобы интерес, как к предмету, так и ко всему живому на планете не пропадал на…
Задания для подготовки к ЕГЭ математика профильный уровень 10 задание
Задания ЕГЭ №10 по математике с решением…
Задания для подготовки к ЕГЭ математика профильный уровень 10 задание
Задания ЕГЭ №10 по математике с решением…
тренировочные задания для подготовки в ОГЭ по химии 15 тестовых заданий
тестовые задания направлены повторение материала и проверку знаний части А в ОГЭ по химии…
Первое задание из открытого банка заданий для подготовки к ЕГЭ по математике(профильный уровень).
Первое задание из открытого банка заданий для подготовки к ЕГЭ по математике (профильный уровень)…
задание для подготовки ОГЭ по информатике (задание по Exel, задание 19)
Данный фал может использоваться как для подготовки, так и для итоговой проверки по 19 заданию ОГЭ по информатике. На закладках файла собраны тексты и сами задания для школьников….
31 марта 2015
В закладки
Обсудить
Жалоба
Тренажёр устных упражнений для подготовки к ЕГЭ по математике
Предназначен для подготовки учащихся 11 классов к ЕГЭ по математике. Может быть использован для отработки навыков устных вычислений.
Автор: Дмитренко Людмила Ивановна.
trenazher.docx
Мастер класс: Устные упражнения на уроках математики в старшей школе.
Методика применения: Устная работа на уроках математики играет важную роль в проработке элементарных математических действий, но чем старше становятся ребята, тем большее количество учащихся, стараются отсидеться во время устной работы. Если в среднем звене (5-6 класс) при устной работе еще приемлем стандартный подход, но и в этих классах на второй-третий урок целесообразно «выключить» отличников во время устной работы с помощью индивидуальных карточек, то в следующих, более старших классах такая работа уже не приносит должного эффекта. Поэтому я практикую увиденную в начальных классах «систему реагирования». Ранее я пыталась внедрить известный всем «светофор». Ребята заводили карточки зеленого и красного цвета (согласен и не согласен), наклеивали их на линейку, чтобы не потерять, но все не то! Теперь если учащийся согласен, то он поднимает руки перед грудью, а если не согласен — поднимает руку. Класс как на ладони, тут уже не отсидеться. Один-двое отвечают, остальные — реагируют. Я фиксирую.
Также для проведения устной работы я использую планшет. Это лист белого картона в файле. У каждого есть маркер для белой доски. Задания высвечиваются на доске, ответы ребята пишут на планшете и поднимают. Очень удобно при подготовке к экзамену выделять таким образом однородные по подготовке группы учащихся, а также своевременно выявить появившиеся затруднения. В период устной работы я часто прошу двух человек (у меня 2 обычных доски) оформить домашнее задание, остальные работают устно. Так сразу после устной работы можно проверять выполнение Д/з. Так что такой вид работы идеально вписывается в любой урок.
Егэ профиль №1
ЗАДАНИЕ 1
Процент и его
история
Обозначение процента как % связано с следующей историей. В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» В одном месте речь шла о процентах которые тогда обозначали «cto» — сокращенно от cento Однако наборщик принял это «cto» за дробь и напечатал «%.
Запись отношений стала удобнее, исчезли нули и запятая, а символ % сразу указывает, что перед нами относительная величина, а не граммы, литры, рубли или метры.
Как найти 1% от числа?
Раз 1% это одна сотая часть, надо число разделить на 100. Деление на 100 можно заменить умножением на 0,01. Поэтому, чтобы найти 1% от данного числа, нужно умножить его на 0,01. А если нужно найти 5% от числа, то умножаем данное число на 0,05 и т.д.
Пример . Найти: 25% от 120
С помощью процентов люди могут определять сколько соли в морской воде, сколько меди в сплаве и т.д.В математике существует множество задач на тему процентов.
Давайте рассмотрим несколько из таких задач:
Решение задач
Задача 1
Флеш-карта для компьютера стоила 800 рублей.Она подешевела на 15%.Сколько флеш карт можно купить на 2000 рублей?
Решение:
После снижение цены на товар на 15% его цена стала
100%-15%=85%,соответственно можем составить пропорцию
800 рублей-100%
Х рублей-85%
Найдем х=(800*85)/100=680 рублей стоит одна флеш-карта
Соответственно на 2000 рублей можно купить
2000/680=2(флеш-карты)
Ответ:2 флеш-карты
Задача 2
Пакет молока стоил 26 рублей.Сколько можно купить пакетов молока на 50 рублей после повышения цены на 15%?
Решение:
После повышения цены на товар он стал стоить:
100%+15%=115%,из всего этого можем составить пропорцию
26рублей-100%
Х рублей-115%,
Найдем х=(26*115%)/100=29,9рублей(один пакет молока после повышения цены)
Значит на 50 рублей можно купить
50:29,9=1(пакет молока)
Ответ:1 пакет молока.
Задача 3
Диск с компьютерной программой стоит 220 рублей.На специальной выставке он стоит на 30% дешевле.Сколько дисков можно купить на 1000 рублей?
Решение:
После понижения цены на товар,его цена стала
100%-30%=70%,соответственно составляем пропорцию
220рублей-100%
Х рублей-70%
Найдем х=(220*70)/100=154рубля(цена одного диска).
Значит на 1000 рублей можно купить
1000/154=6 дисков
Ответ:6 дисков
Задача 4.
Свежие грибы содержат 98% воды и весят 100 кг. При хранении они усохли и воды оказалось 96%. Найдите массу грибов после высыхания. Решение: Свежие грибы содержат сухого вещества 2% от всей массы грибов, что составляет 2 кг. В сухих грибах масса сухого вещества не изменилась. Но 2 кг сухого вещества составляют теперь 4% от массы сухих грибов. (2/4) 100 = 50 (кг) – масса сухих грибов. Ответ: масса грибов после высыхания составляет 50 кг.
Что развивает решение
Таких задач
- оказывает положительное влияние на всестороннее развитие школьников, выработку у них полезных навыков и качеств.
- развивают логическое мышление
- заставляет мыслить неординарно
- адаптирует к жизни
Вернуться к списку заданий
ЗАДАНИЯ 2
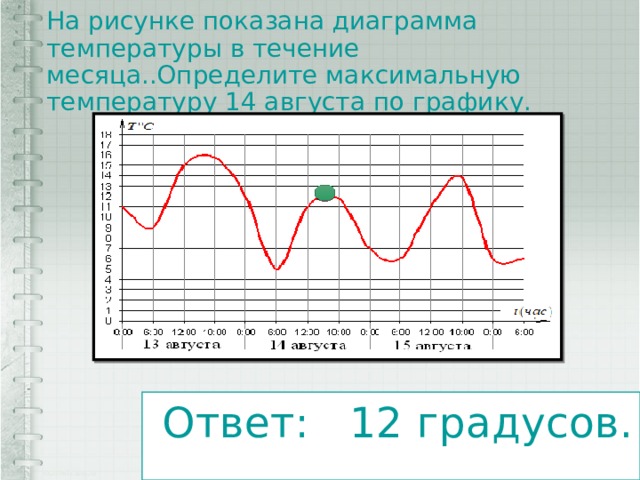
На рисунке показана диаграмма температуры в течение месяца..Определите максимальную температуру 14 августа по графику.
Ответ: 12 градусов.
На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 23 января. Ответ дайте в градусах Цельсия.
Ответ: -13.
На графике показано изменение напряжения на батарейке (в вольтах) в зависимости от времени её использования. Чему было равно напряжение через 2 часа 5 минут после начала её использования? Ответ дайте в вольтах.
Вернуться к списку заданий
Ответ: 1,1.
ЗАДАНИЕ 3
ОДЗ:
удовлетворяет ОДЗ
Ответ: 3
ОДЗ :
, т.к. D (log)=R+
удовлетворяет ОДЗ
Ответ: 1
ОДЗ:
не удовлетворяет ОДЗ
Ответ:6
ОДЗ:
, т.к. D (log)=R+
удовлетворяет ОДЗ
Ответ:18
ОДЗ:
, т.к. D (log)=R+
удовлетворяет ОДЗ
Ответ:41
Вернуться к списку заданий
ЗАДАНИЕ 4
Тригонометрия — раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии
Основные понятия:
- тригонометрическая окружность
- градусы и радианы
- синус и косинус
- тангенс и котангенс
- формулы
Числовая окружность – единичная окружность,
с установленным соответствием
( между действительными числами и точками окружности).
На числовой окружности находятся числа, выраженные в долях числа «пи». ( «пи» — это математическая константа, выражающая отношение длины окружности к длине ее диаметра. Эта константа приближенно равна 3,14.)
Знаки тригонометрических функций по четвертям
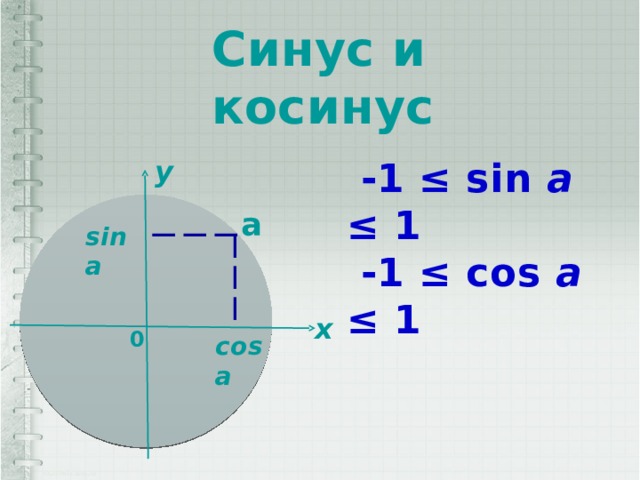
Синус и косинус
y
-1 ≤ sin a ≤ 1
-1 ≤ cos a ≤ 1
a
sin a
x
0
cos a
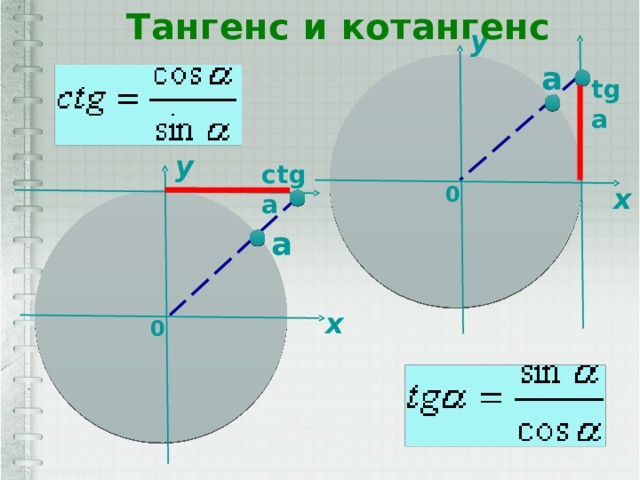
Тангенс и котангенс
y
a
tg a
y
ctg a
x
0
a
x
0
arccos a
arcsin a
π/2
arcsin a
π/2
arccos a
0
π
π
[- π/2 ; π/2 ]
0
arcsin a ϵ
arccos a ϵ
[ 0 ; π ]
— π/2
— π/2
arcctg a
arctg a
π/2
π/2
arctga ϵ
(- π/2 ; π/2 )
π
0
π
0
0
0
arcctg a ϵ
( 0 ; π )
— π/2
— π/2
Задание 4(1): Решите уравнение.
2sin x*cos x = sin x – cos x + 1/2
2sin x*cos x — sin x + cos x – 1/2
2sin x*(cos x -1/2) + (cos x – 1/2) =0
(2sin x + 1)*(cos x –1/2) = 0
(2sin x + 1) = 0
(cos x -1/2) = 0
sin x = -1/2
cos x = 1/2
x=(-1) n arcsin a + π n , n ϵz
x=±arccosa+2 π n , n ϵz
x= ± π /3+2 π n , n ϵ z
x = (-1)*(- π/6 ) + πn , n ϵz
x=(-1) n+1 π /6+ π n , n ϵz
Задание 4(2): Вычислите значение выражения 12s in 2 a , если ctg= 3
1 + 3 =
s in 2 a = 1/4
12* 1/4=3
Ответ : 3
Задание 4(3): Решите уравнение
sin2α = 2sinα*cosα
sin x +sin 2x = cos x *2 cos 2 x
sin x + 2sin x *cos x = cos x *2 cos 2 x
sin x + (1 + 2cos x) = cos x (1+2 cos 2 x)
(1 + 2cos x) (sin x – cos x) = 0
1 + 2cos x = 0
sin x – cos x = 0
(: cos x )
2cos x = -1
sin x/cos x – 1 = 0
cos x = -1/2
tg x = 1
x=±arccosa+2 π n
x = arctg a + π n , n ϵ z
x= ± 2 π /3+2 π n , n ϵ z
x = π/4+ πn , n ϵ z
Задание 4(4): Вычислите значение выражения
cos 2 π/6 + ctg π/4 – sin π/6
(cos 2*π/6 + 1)/2 + ctg π/4 — sin π/6 = 1,25
2* π/6= π/3
cos π/3 =1/2
ctg π/4= 1
Ответ : 1,25
sin π/6 =1/2
Вернуться к списку заданий
ЗАДАНИЕ 5
Задача №1
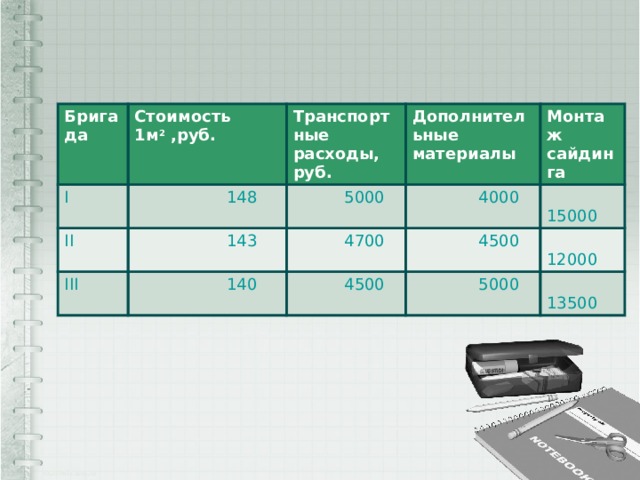
- Хозяин дома решил обшить свой дом сайдингом и обратился в три фирмы, чтобы выбрать самый дешёвый вариант. Площадь обшивки составляет 120м 2 . Стоимость работы, материалов и транспортные расходы приведены в таблице. Какова стоимость самого дешёвого варианта?
Бригада
Стоимость 1м 2 ,руб.
I
II
148
Транспортные расходы, руб.
Дополнительные материалы
143
5000
III
Монтаж
140
4000
4700
сайдинга
4500
4500
15000
12000
5000
13500
Решение№1
1)120*148+5000+4000+15000=41760
2)120*143+4700+4500+12000=36360
3)120*140+4500+5000+13500=39800
Ответ:36360.
Задача№2
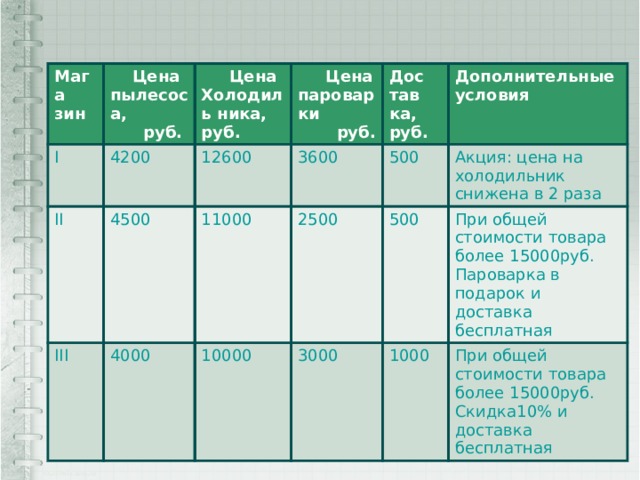
- Мария Ивановна собирается купить через интернет пылесос, холодильник и пароварку. Она изучает цены и сравнивает доставки в трех фирмах. Цены товара и условия доставки приведены в таблице. Сколько рублей заплатит Мария Ивановна за самый дешёвый вариант покупки?
Мага
I
зин
Цена
II
4200
Цена
пылесоса,
Холодиль ника, руб.
4500
Цена
III
руб.
12600
3600
Дос
пароварки
11000
4000
Дополнительные условия
тав
500
руб.
2500
10000
3000
Акция: цена на холодильник снижена в 2 раза
ка, руб.
500
При общей стоимости товара более 15000руб. Пароварка в подарок и доставка бесплатная
1000
При общей стоимости товара более 15000руб. Скидка10% и доставка бесплатная
Решение№2
1)4200+6300+3600+500=14600
2)4500+11000=15500
3)4000+10000+3000=17000
17000 – 100%
1700 – 10% 17000-1700=15300
X – 10% Ответ:14600.
Задача№3
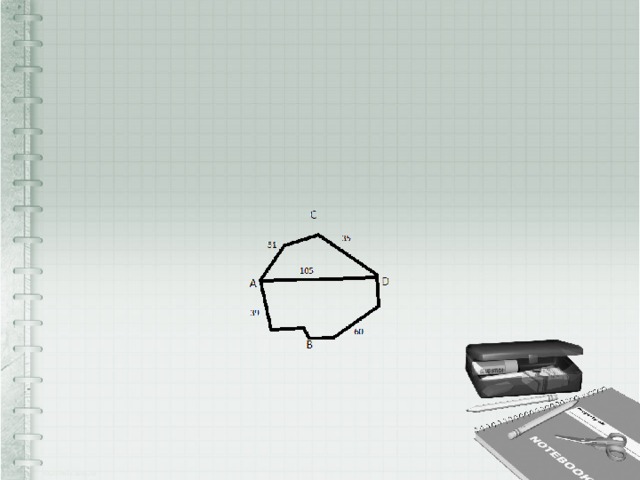
- Из пункта А в пункт D ведут три дороги. Через пункт В едет грузовик со скоростью 44 км/ч, через пункт С едет автобус со средней скоростью 43 км/ч. Третья дорога — без промежуточных пунктов, и по ней движется легковой автомобиль со средней скоростью 70 км/ч. На рисунке показана схема дорог и раcстояние в километрах между пунктами по дорогам.
- Все три автомобиля одновременно выехали из А. Какой автомобиль добрался до D позже других? В ответе укажите, сколько часов он находился в дороге.
Решение№3
Через В, груз. 99км/44кмч=2,25часов
Через С, авто. 86км/43кмч=2часа
На прямую легковой авто. 105км/70кмч=1,5часа
Ответ:2,25часа
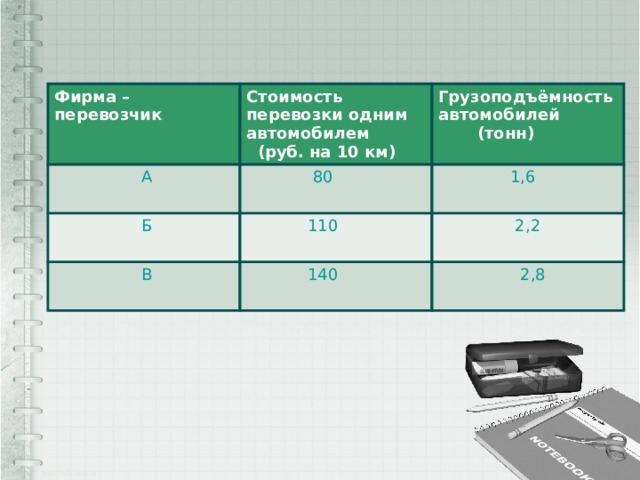
Задача №4
- Для транспортировки 5 тонн груза на 350 км можно воспользоваться услугами одной из трёх фирм – перевозчиков. Стоимость перевозки и грузоподъёмность автомобилей для каждого перевозчика указана в таблице. Сколько рублей придется заплатить за самую дешёвую перевозку?
Фирма – перевозчик
Стоимость перевозки одним автомобилем
А
(руб. на 10 км)
Грузоподъёмность автомобилей
80
Б
(тонн)
1,6
110
В
2,2
140
2,8
Решение№4
А 2800*4=11200руб.
Б 3850*3=11550руб.
В 4900*2=9800руб.
Ответ:9800руб.
Вернуться к списку заданий
ЗАДАНИЕ 6
Площадь треугольника, формула.
Треугольник образуется соединением отрезками трех точек, не лежащих на одной прямой. При этом точки называются вершинами треугольника, а отрезки — его сторонами. Площадь треугольника равна произведению основания треугольника (a) на его высоту (h):
Площадь треугольника, формула.
На клетчатой бумаге с клетками размером 1 см * 1 см изображен треугольник . Найдите его площадь в квадратных сантиметрах.
Решение:
a= 9;
h= 3;
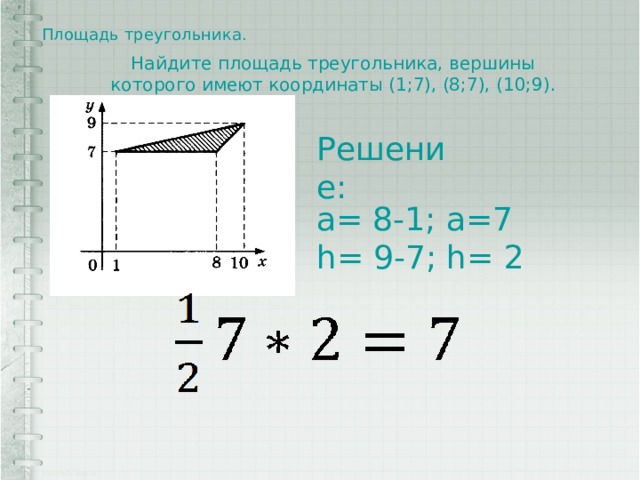
Площадь треугольника.
Найдите площадь треугольника, вершины которого имеют координаты (1;7), (8;7), (10;9).
Решение:
a= 8-1; a=7
h= 9-7; h= 2
Площадь прямоугольника.
Прямоугольником называется четырехугольник, у которого все углы равны. Площадь прямоугольника равна произведению его сторон (a, b):
Площадь прямоугольника.
Найдите площадь прямоугольника, вершины которого имеют координаты (2;1), (10;1), (10;7), (2;7).
Решение:
a= 7-1; a=6
b= 10-2; b= 8
Площадь трапеции.
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны. Площадь трапеции равна произведению полу-суммы ее оснований (a, b) на высоту (h):
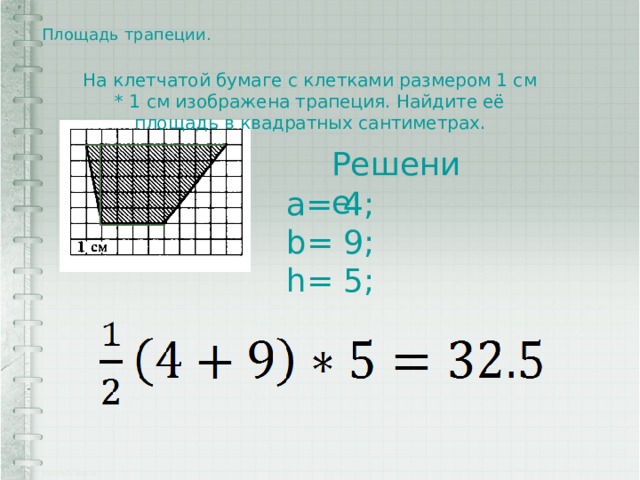
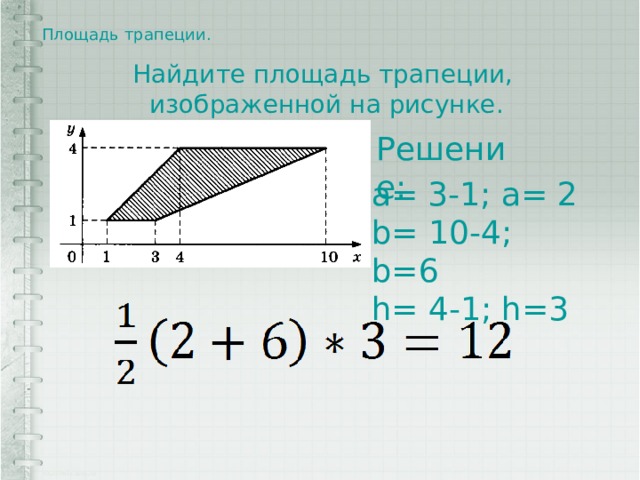
Площадь трапеции.
На клетчатой бумаге с клетками размером 1 см * 1 см изображена трапеция. Найдите её площадь в квадратных сантиметрах.
Решение:
a= 4;
b= 9;
h= 5;
Площадь трапеции.
Найдите площадь трапеции,
изображенной на рисунке.
Решение:
a= 3-1; a= 2
b= 10-4; b=6
h= 4-1; h=3
Площадь параллелограмма.
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны. Площадь параллелограмма равна произведению его основания (a) на высоту (h):
Площадь параллелограмма.
На клетчатой бумаге с клетками размером 1 см * 1 см изображен параллелограмм. Найдите его площадь в квадратных сантиметрах.
Решение:
a= 3;
h=4;
Площадь параллелограмма.
Найдите площадь параллелограмма,
изображенного на рисунке.
Решение:
a=3-1; a=2
h=7-3; h= 4
Площадь ромба
Ромбом называется параллелограмм с равными сторонами. Квадрат есть частный вид ромба. Площадь ромба равна половине произведения его диагоналей:
Площадь ромба
Найдите площадь четырёхугольника , изображенного на рисунке.
Решение:
По теореме Пифагора найдём диагонали :
Площадь круга.
Окружность есть геометрическое место точек плоскости, равноудаленных от одной ее точки. Равные отрезки, соединяющие центр с точками окружности, называются радиусами.
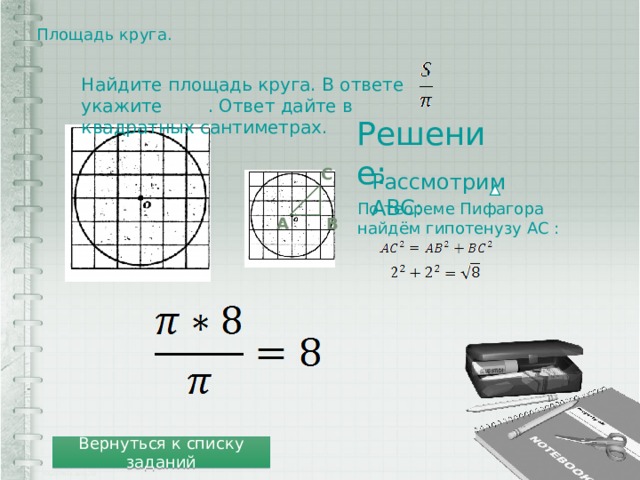
Площадь круга.
Найдите площадь круга. В ответе укажите . Ответ дайте в квадратных сантиметрах.
Решение:
C
Рассмотрим ABC:
По теореме Пифагора
найдём гипотенузу AC :
B
A
Вернуться к списку заданий
ЗАДАНИЕ 7
Определение. Логарифмом положительного числа b по положительному и отличному от 1 основания а называют показатель степени, в которую нужно возвести число а , чтобы получилось число b.
Формулы логарифма
1=0
a=1
x+
y
xy=
y
=
x-
b=1:
a
Задание №1
Найдите значение выражения:
Log₇441- Log₇9= Log₇441/9= Log₇49= Log₇7²=2
x-
y=
Задание №2
19+
4=
19*4=
76=1
xy
y=
x+
Вернуться к списку заданий
ЗАДАНИЕ 8
Производной функции f(x) в точке x называется предел отношения приращения функции к приращению аргумента при х 0
lim f(x + x) – f(x ) / x, где х=х-х – приращение аргумента, а разность f(x + x) – f(x )= f(x ) называется приращением функции.
Обозначается производная f’(x)=lim f(x )/ x при х 0
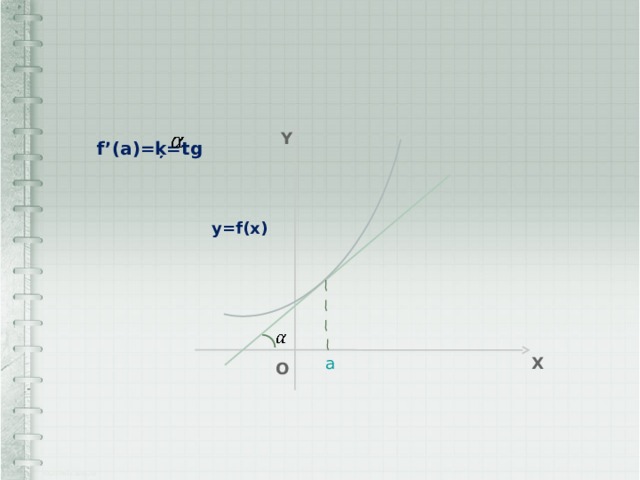
Геометрический смысл производной состоит в том, что значение производной функции у=f(x) в точке х=а равно угловому коэффициенту касательной к графику функции у=f(x) в точке х=а
f’(a)=ķ=tg
y
у=f(x)
a
x
o
Физический смысл производной состоит в следующем. Если s(t) –закон прямолинейного движения тела, то производная выражает мгновенную скорость в момент времени t: U = s’(t)
Для нахождения производной функции f(x) пользуются не определением производной, а правилами и формулами дифференцирования .
Основные правила дифференцирования :
1Производная суммы(разности) равна сумме(разностей) производных (U ± V)’=U’ ± V’
2Производная произведения равна: (UV )’=U’V + V’U
3Производная частного равна: ( U/V)’ = U’V – V’U/V², при V ≠ 0
4Производная сложной функции:
( f (φ(x)))’ = f’(φ(x)) * φ’(x)
Основные формулы дифференцирования :
1 (c)’=0
2 (xⁿ)’=nxⁿ¯¹
3 ( )’=
4 ( )’= lna
5(ln x)’=
6(lg x)’= lg e
7( )’=
8(sin x)’=cos x
9(tg x)’=1/cos x
10(cos x)’=-sin x
11(ctg x)’=-1/sin x
12(arcsin x)’=1/
13(arccos x)’=-1/
14(arctg x)’=
15(arcctg)’=-
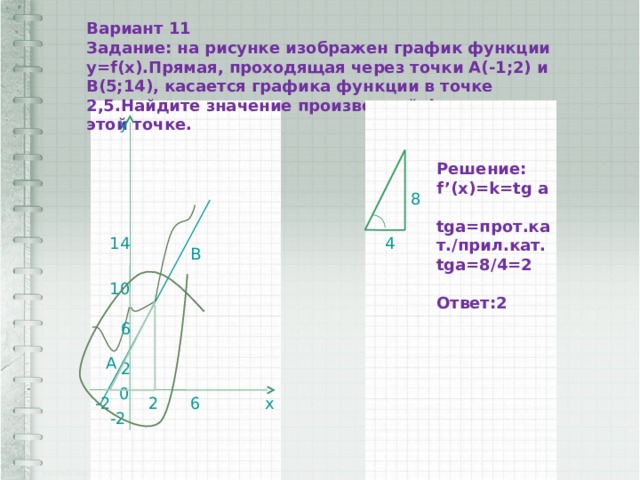
Вариант 11
Задание: на рисунке изображен график функции у=f(x).Прямая, проходящая через точки А(-1;2) и В(5;14), касается графика функции в точке 2,5.Найдите значение производной функции в этой точке.
y
Решение:
f’(x)=k=tg a
tga=прот.кат./прил.кат.
tga=8/4=2
Ответ:2
8
14
4
B
10
6
A
2
0
6
x
-2
2
-2
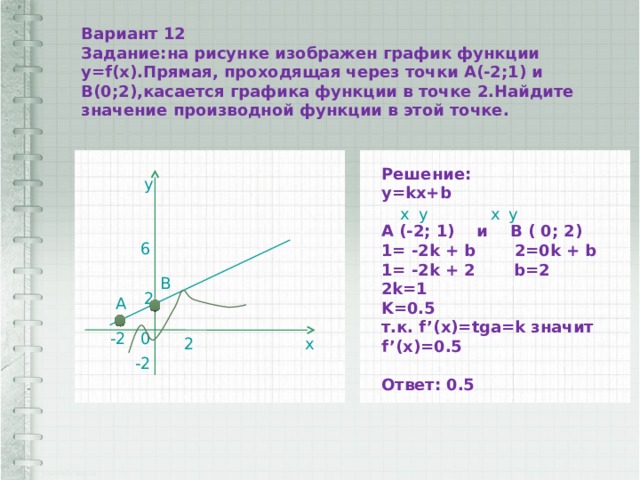
Вариант 12
Задание:на рисунке изображен график функции у=f(x).Прямая, проходящая через точки А(-2;1) и В(0;2),касается графика функции в точке 2.Найдите значение производной функции в этой точке.
Решение:
y=kx+b
A (-2; 1) и В ( 0; 2)
1= -2k + b 2=0k + b
1= -2k + 2 b=2
2k=1
K=0.5
т.к. f’(x)=tga=k значит f’(x)=0.5
Ответ: 0.5
y
y
y
x
x
6
B
2
A
0
-2
2
x
-2
Вариант 32
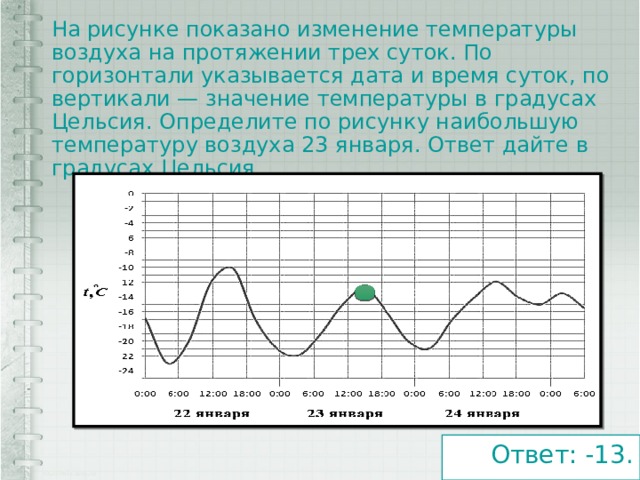
Задание:на рисунке изображен график производной функции у=f’(x), которая задана на промежутке [-4; 5].Укажите точку, в которой функция достигает наибольшее значение.
Решение:
+
y’
y
y
у=f’(x)
В точке х=5 функция y=f(x) достигнет наибольшее значение.
4
у=f(x)
2
5
-4
0
5
x
4
-2
-4
2
-2
Ответ: 5
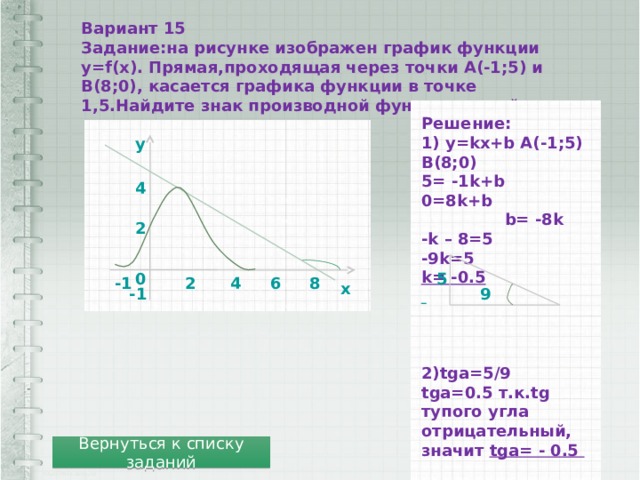
Вариант 15
Задание:на рисунке изображен график функции y=f(x). Прямая,проходящая через точки А(-1;5) и В(8;0), касается графика функции в точке 1,5.Найдите знак производной функции в этой точке.
Решение:
1) y=kx+b A(-1;5) B(8;0)
5= -1k+b 0=8k+b
b= -8k
-k – 8=5
-9k=5
k= -0.5
2)tga=5/9 tga=0.5 т.к.tg тупого угла отрицательный, значит tga= — 0.5
Ответ: -0.5
y
4
2
5
0
8
2
4
6
-1
x
9
-1
Вернуться к списку заданий
ЗАДАНИЕ 9
Справка:
S треугольника =(a*h a )/2
S трапеции =((а+в)/2)*h
S круга =πR 2
S куба =6а 2
S бок.цилиндра =2πRh
S шара =4 πR 2
V цилиндра = πR 2 *h
V призмы =S осн. *h
V куба =а 3
V пирамиды =1/3*S осн. *h
V конуса =1/3 πR 2 *h
V шара =4/3 πR 3
Демо-вариант 2011
Диагональ куба равна 11. Найдите площадь его поверхности.
Решение:
Пусть ребро куба равно а
Сумма квадратов ребер параллелепипеда равна квадрату диагонали параллелепипеда
Но у куба все ребра равны
3а 2 =11 2
а 2 =11 2 /3
S= 6а 2 =6*11 2 /3=242
Ответ: 242
Демо-вариант 2010
Объем конуса равен 64. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Решение:
Обозначим объем большого конуса V 1
(πR 2 *h)/3=64
В маленьком конусе: r=R/2 h=H/2
V мал.конуса = (π(R/2) 2 *H/2)/3= ((πR 2 *h)/3):8=64:8=8
Ответ: 8
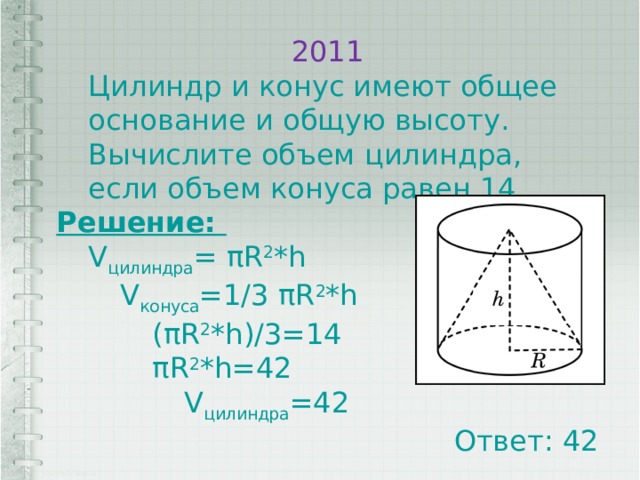
2011
Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 14.
Решение:
V цилиндра = πR 2 *h
V конуса =1/3 πR 2 *h
(πR 2 *h)/3=14
πR 2 *h=42
V цилиндра =42
Ответ: 42
2010
В сосуд, имеющий форму правильной треугольной призмы, налили 1900 см 3 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 20 см до отметки 22 см. найдите объем детали. Ответ выразите в см 3.
Решение:
Обозначим первоначальный объем воды V 1 , а объем воды после погружения детали V 2
Пусть площадь основания призмы равна S см 2
h 1 = 20 h 2 =22 – по условию
Вычислим площадь основания S:
V=S* h 1
1900=S*20
S=1900/20=95 см 3
Объем детали равен:
V 2 — V 1 = S*h 2 — S* h 1 = S(h 2 — h 1 )= 95(22-20) =190 см 3
Ответ: 190 см 3
2011
Даны пара цилиндров .Объем первого равен12 м 3 . У второго радиус основания уменьшен в 2 раза, а высота в 3 раза увеличена.
Необходимо вычислить объем второго цилиндра.
Решение:
Объем цилиндра вычисляется по формуле:
Следует отметить что, радиус основания первого цилиндра r а высоту h. Получили что радиус основания второго цилиндра равен r/2, а высота 3h. Применим формулу и получим:
Немного преобразуем полученное выражение:
Объем 2ого цилиндра равен 9 м 3 .
Ответ: 9
Вернуться к списку заданий
ЗАДАНИЕ 10
Задание B10 – это прикладная задача на нахождение наибольшего или наименьшего значения, моделирующая реальную или близкую к реальности ситуацию. Для решения ученик должен составить и решить по условию задачи линейное или квадратное неравенство.
Задача №1.
В розетку электросети подключены приборы, общее сопротивление которых составляет 90 Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите (в омах) наименьшее возможное сопротивление этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями R1 и R2 их общее сопротивление задаётся формулой , а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 30 Ом.
По условию задачи, общее сопротивление 2-х проводников задаётся формулой:
Введем переменную.
Пусть сопротивление обогревателя будет – x Ом. Из условия задачи нам известно, что общее сопротивление двух проводников = 90 Ом. Но обогреватель является ещё одним проводником.
Тогда имеем:
Далее решаем это неравенство. Перенесем 30 в левую часть с противоположным знаком и приведем к общему знаменателю.
Получим:
В числителе приведем подобные. Получим:
Решим неравенство методом интервалов.
Найдем точки в которых оно равно нулю и не существует:
Эти точки разбивают координатную прямую на отрезки, в каждом из которых выражение сохраняет свой знак.
Просчитаем знак.
Пусть x=1.
Т.к. знак неравенства больше или равно, то
+ — +
45
-90
Воспользуемся знакочередованием.
Ответ: 45 Ом.
Задача №2.
Для определения эффективной температуры звёзд используют закон Стефана-Больцмана, согласно которому мощность излучения нагретого тела прямо пропорциональна площади его поверхности и четвертой степени температуры:
, где — числовой коэффициент, площадь измеряется в квадратных метрах, температура – в градусах Кельвина, а мощность – в ваттах. Известно, что некоторая звезда имеет площадь ,
а излучаемая ею мощность P не менее Определите наименьшую возможную температуру этой звезды.
По условию задачи имеем формулу: .
Данные:
P не менее
Подставим данные в формулу, получим неравенство, так как P должно быть не менее
Решим неравенство:
Ответ: 600 К.
Задача №3.
Для одного из предприятий-монополистов зависимость объема спроса на продукцию q (единиц в месяц) от её цены p (тыс. р.) задается формулой: q=210-15p.
Определите максимальный уровень цены p (тыс.р.),при котором значение выручки предприятия за месяц r=q*p составит не менее 360 тыс. р.
Итак, мы имеем:
Формулу: q=210-15p
r=q*p не менее 360.
Значение q*p должно быть больше или равно 360.
В это неравенство подставим значение q. Получим:
Раскроем скобки: .
Разделим на -1 при этом сменив знак неравенства на противоположный, получим:
Разделим на 15.
Неравенство примет вид: .
Решим квадратное уравнение, для этого приравняем левую часть неравенства к нулю:
. a=1, b=-14, c=24. Найдём дискриминант по формуле:
Найдём корни уравнения по формуле:
p принадлежит промежутку
Цена должна быть не меньше 2 тыс. р., но не больше 12 тыс. р.
ОТВЕТ: 12 тыс. руб.
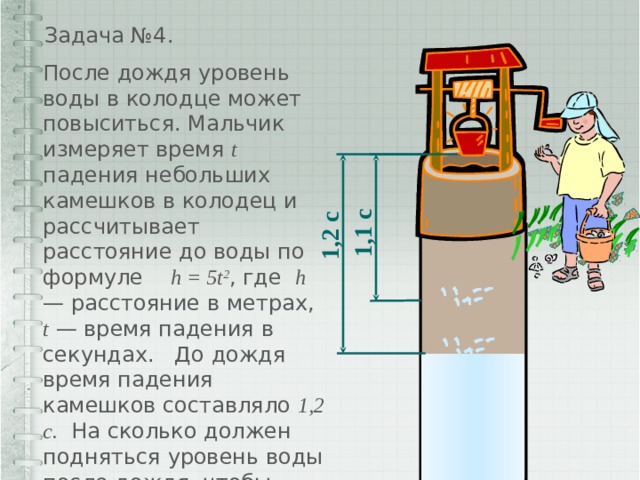
1,2 с
1,1 с
Задача №4.
После дождя уровень воды в колодце может повыситься. Мальчик измеряет время t падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле h = 5t 2 , где h — расстояние в метрах, t — время падения в секундах. До дождя время падения камешков составляло 1,2 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,1 с ?
Функция:
Данные:
Найти:
Решение.
Найдём h(1,2), подставив значение в данную функцию:
Затем найдем h(1,1), подставив в данную функцию:
Найдем по формуле
м
м
м
Ответ: 1,15 м.
Задача №5.
Автомобиль, движущийся в начальный момент времени со скоростью v 0 = 24 м/с , начал торможение с постоянным ускорением a = 3 м/с 2 . За t секунд после начала торможения он прошёл путь (м).
Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 90 метров . Ответ выразите в секундах.
at 2
v 0 t
S
=
2
Данные:
Функция:
Найти:
Решение.
Подставим в функцию данные:
Приравняем к 90:
Перенесем 90 в левую часть с противоположным знаком и разделим уравнение на 3.
Затем умножим на 2
Получим квадратное уравнение.
а=1, b=-16, c=60
Найдем дискриминант по формуле:
Найдем корни уравнения по формуле:
Выбираем наименьший корень-это 6 . Значит он и пойдет в ответ.
Ответ: 6
Вернуться к списку заданий
ЗАДАНИЕ 11
Определение множества значений функции (min, max функции, наибольшее, наименьшее значения, экстремумы) Точка x 0 называется точкой максимума функции f(x), если существует такая окрестность точки x 0 , что для всех x ≠ x 0 из этой окрестности выполняется неравенство f(x) f(x 0 ). Точки минимума и точки максимума называются точками экстремума.
Теорема. Если x 0 – точка экстремума дифференцируемой функции f(x), то f ′(x 0 ) =0. Точки, в которых функция имеет производную, равную нулю, или недифференцируема (не имеет производной), называют критическими точками. Точки, в которых производная равна 0, называют стационарными. Геометрический смысл: касательная к графику функции y=f(x) в экстремальной точке параллельна оси абсцисс (OX), и поэтому ее угловой коэффициент равен 0 ( k = tg α = 0). Теорема: Пусть функция f(x) дифференцируема на интервале (a;b), x 0 С (a;b), и f ′(x0) =0. Тогда: 1) Если при переходе через стационарную точку x 0 функции f(x) ее производная меняет знак с «плюса» на «минус», то x 0 – точка максимума. 2) Если при переходе через стационарную точку x0 функции f(x) ее производная меняет знак с «минуса» на «плюс» , то x 0 – точка минимума.
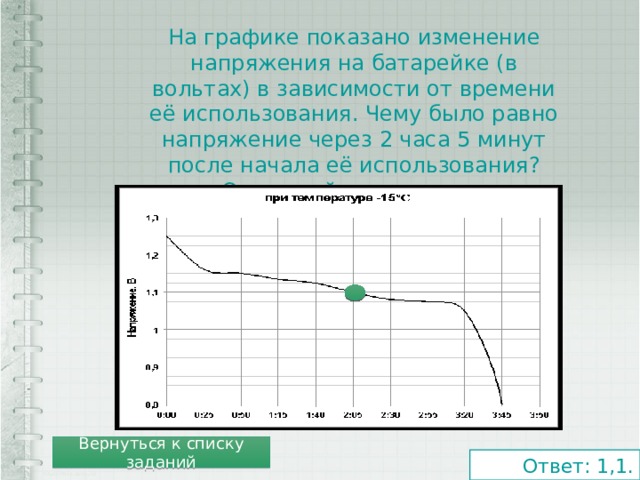
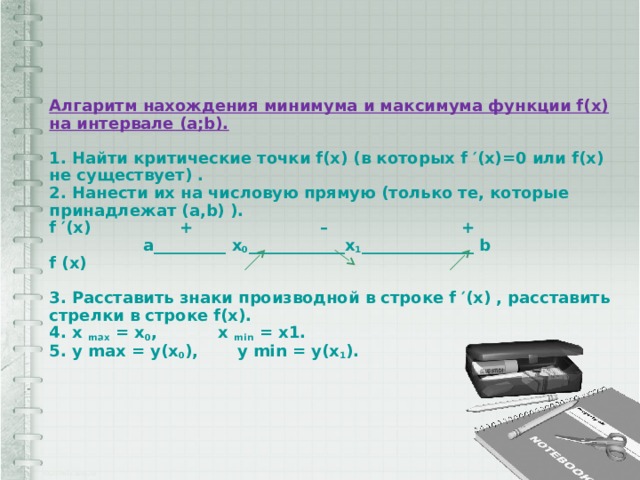
Алгаритм нахождения наибольшего и наименьшего значения функции f(x) на отрезке [a;b]. 1. Найти призводную функции и приравнять нулю. Найти критические точки . 2. Найти значения функции на концах отрезка, т.е. числа f(a) и f(b). 3. Найти значения функции в тех критических точках, которые принадлежат [a;b]. 4. Из найденных значений выбрать наибольшее и наименьшее.
Алгаритм нахождения минимума и максимума функции f(x) на интервале (a;b). 1. Найти критические точки f(x) (в которых f ′(x)=0 или f(x) не существует) . 2. Нанести их на числовую прямую (только те, которые принадлежат (a,b) ). f ′(x) + – + a_________ x 0 ____________x 1 ______________ b f (x) 3. Расставить знаки производной в строке f ′(x) , расставить стрелки в строке f(x). 4. x max = x 0 , x min = x1. 5. y max = y(x 0 ), y min = y(x 1 ).

В11.Найдите наибольшее значение функции f(x) = 3sin x + 30/п *x + 4 на отрезке [5п/6; 0]. Решение. Найдем критические точки. f´(x) = 3cos x + 30/π = 0 (1); 3·cos x=-30/π; cos x = –10/π , где π≈3.14. cos(x) ≈–3.18… Но |cos(x)| ≤ 1 , значит уравнение (1) решения не имеет. Это значит, что f´(x) не обращается в 0, а следовательно, функция f(x) не имеет критических точек. Очевидно, что f´(x)0 при любых x. Значит, f(x) возрастает на всей области определения , и на промежутке [-5π / 6; 0], а значит, своего наибольшего значения f(x) достигает на правом конце промежутка, т.е. при х=0. f(0) = 3sin0 + 0 + 4 = 4. Ответ: 4.
В11.Найдите точку минимума функции у=(х-3) 2 (х+1). Решение. Возьмем производную: у’ = 2(x-3)(x+1) + (x-3) 2 =0, (x-3)*(2x+2+x-3) = 0, Свернем формулу:( x-3)(3x-1)=0, x1=3, x0=1/3. x1 и x0 — критические точки. Высчитаем знак производной. у’ + – + ___________ 1/3 ___________3 ____________ у Точка х0=х max =1/3. Точка х1= х min = 3 Ответ: 3.

В11. Найдите наибольшее значение функции f ( x ) = 3sin x + 30х/π + 4 на отрезке [ − 5π/ 6 ; 0 ] Решение . Найдем критические точки. f´(x)=3cos(x)+30/π=0 ; 3cos(x)=-30/π; cos(x)=-10/π , где π≈3.14. cos(x)=-3.18… Но |cos(x)|≤1 , значит уравнение решения не имеет. Это значит, что f´(x) не обращается в 0, а следовательно, функция f(x) не имеет критических точек. Очевидно, что f´(x)0 при любых x. Значит, f(x) возрастает на всей области определения , в т.ч. и на промежутке [-5π/6; 0], а значит, своего наибольшего значения f(x) достигает на правом конце промежутка, т.е. при х=0. f(0) = 3sin0 + 0 + 4 = 4. Ответ: 4. Примечание: если не очевидно, что f´(x)0 для всех х, то найдите значения f(x) на обоих концах промежутка и выберите наибольшее.

В11.Найдите точку максимума функции у = −х/(х 2 +289) Решение. Применим ф-лу для нахождения производной частного: (u/v)’ = (u’v — uv’) / v 2 . Y’ =(-(x 2 + 289)+x*2x) /(x 2 +289) 2 =0 -x 2 — 289 + 2x 2 =0 — x 2 — 289 =0 — x =±17 — критические точки. y’ =(x 2 — 289)/(x 2 + 289) 2 y’ + • – • + _____ y -17 +17 Ответ: х = -17 — точка максимума
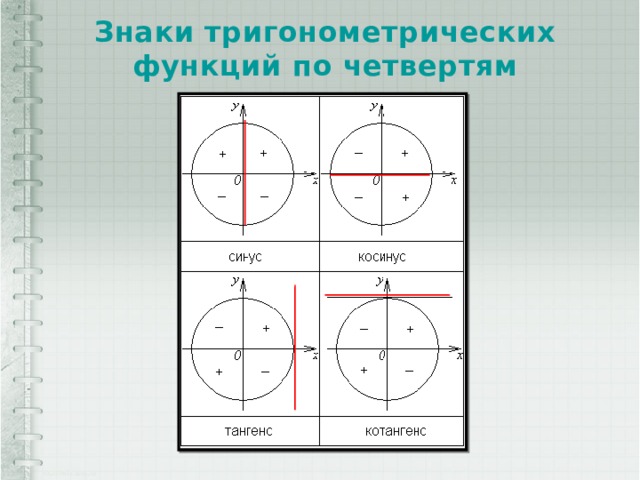
Найдите наибольшее и наименьшее значение функции y=x 2 — 2x — 3 на отрезке [-5;-1] Найдем производную, прировняем её к нулю. y’ = 2x — 2 = 0, 2x = 2, x = 1 — критическая точка функции, но она не принадлежит [-5;-1]. Значит просчитаем значение функции на концах отрезка. y(-5) = 25 +10 — 3 = 32 — наибольшее значение у(х), y(-1) = 1 + 2 — 3 = — 1 — наименьшее значение у(х) на [-5; -1]. Ответ: 32 — наибольшее значение — 1 — наименьшее значение
Вернуться к списку заданий
ЗАДАНИЕ 12
Под строительную площадку отвели участок прямоугольной формы, длина которого на 30 метров больше его ширины. При утверждении плана застройки выяснилось, что граница участка проходит по территории водоохранной зоны, поэтому его ширину уменьшили на 20 метров. Найдите длину участка, если после утверждения плана застройки площадь участка составила 2400 кв.м.
Дано: ABCD – прямоугольник,
S ( ABCD) = 2400
Найти дину прямоугольника.
х + 30
B
C
K
M
х
Решение:
х-20
S = 2400
1)Пусть x – ширина прямоугольника,
Тогда (х + 30) – длина прямоугольника
D
A
2)S = a*b
S AMKD = (x-20)*(x+30)
X 1 =60
X 2 =-50 не подходит по смыслу
(x-20)*(x+30)=2400
3) 60 + 30 = 80 — длина прямоугольника
Ответ:80
Смешали 8 литров 15-процентного водного раствора некоторого вещества с 12 литрами 40-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
8 литров
12 литров
20 литров
15%
40%
?
+
=
1,2+4,8=6 — кислоты
8 – 100%
12 – 100%
х – 15%
у – 40%
у = 4,8 — кислоты
х = 1,2 — кислоты
в растворе
в растворе
20 – 100%
6 – z%
z =30% — концентрация
получившегося раствора
Ответ:30
Численность волков в двух заповедниках в 2009 году составляла 220 особей. Через год обнаружили, что в первом заповеднике численность волков возросла на 10%, а во втором – на 20%. В результате общая численность волков в двух заповедниках составила 250 особей. Сколько волков было в первом заповеднике в 2009 году?
1 заповедник
2 заповедник
В 2 заповедниках
220
y
x
В 2009 году
1,2y
1,1x
250
В 2010 году
2)y – 100%
1)x – 100%
x 2 – 10%
y 2 – 20%
y 2 = 0,2x
x 2 = 0,1x
3)
Ответ:140
Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 60км/ч, а вторую половину времени – со скоростью 46 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Время
Расстояние
Скорость
t
60t
60
1 половина
t
46t
46
2 половина
Решение:
𝝊 ср
𝝊 ср
,
Ответ:53
Моторная лодка прошла против течения 24 км и вернулась обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите скорость (в км/ч) лодки в неподвижной воде, если скорость течения равна 3 км/ч.
Время
Расстояние
Скорость
(𝝊-3)
24
против течения
24
(𝝊+3)
по течению
Решение:
𝝊≠ 3, 𝝊≠-3
𝝊 =21
𝝊 =-21 — не подходит по смыслу
Ответ:21
Вернуться к списку заданий
ЗАДАНИЕ 13
Задача №1
Решение:
1.
значит siny
2. Введем новую переменную cosy=a, |a|меньше или равно 1.
Теперь второе уравнение можно привести к виду:
Корни:
a_1=3/2;
a_2=-1/2;
Первый корень не удовлетворяет условию
|a|меньше или равно 1.Вернемся к прежней переменной.
3. т.к. siny
4.
x=1/2
Ответ: x=1/2,
Задача №2
Решение:
Возведем в квадрат.
Приравняем y^2 из первого уравнения
cos x=2 решений не имеет т.к. значения cosx находятся в пределах от -1 до 1.
cos x=0
y+1=2cos x
y=-1
Ответ: y=-1,
Задача №3
Решение:
1. Сделаем замену sin x = t, значения t находятся в пределах от -1 до 1. Тогда второе уравнение можно привести к виду:
Корни: t_1=2; t_2=-1/2
Первый корень не удовлетворяет условию.
2. Вернемся к прежней переменной: sin x=-1/2
т.к. левая часть первого уравнения системы положительна, то для того чтобы уравнение имело решение необходимо чтобы cos x
3. Подставим значение x в первое уравнение:
y= 1/2
Ответ: y= 1/2,
Задача №4
Решение:
Ответ:
Задача №5
Решение:
1. Введем новую переменную
2.
t_1=3
t_2=27
, решений нет
Ответ:
Вернуться к списку заданий
ЗАДАНИЕ 14
ОДЗ
- √ (x+2) → x≥-2;
- √ (8-x) → x≤8;
- √ (8-x) — |x-2|≠0 → x≠-1,
x≠4 (вычисления далее);

Решение
Т.е. при условии
x²-3x-4
выполняется
√ (8-x) — |x-2|0.
Тогда:
√ (8-x) — |x-2|0
√ (8-x)|x-2|
8-xx²-4x+4
x²-3x-4
x₁=-1; x₂=4
+
+
—
—
—
+
100
√ (x+2)-|x-2|
√ (8-x)-|x-2|
≥ 1, домножим на знаменатель правую часть
√ (x+2)-|x-2|-√(8-x)+|x-2|
≥ 0
√ (8-x)-|x-2|
√ (x+2)-√(8-x)≥0
x≥3
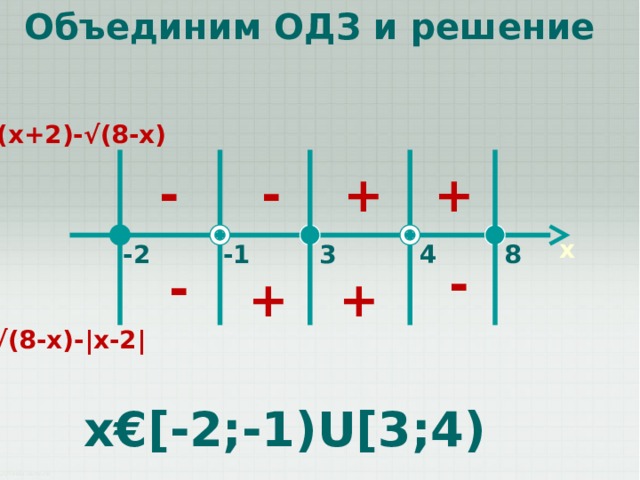
Объединим ОДЗ и решение
√ (x+2)-√(8-x)
+
—
+
—
x
3
8
4
-1
-2
—
—
+
+
√ (8-x)-|x-2|
x€[-2;-1)U[3;4)
Решите неравенство:
√ (x+3-4√(x-1))+√(x+8-6√(x-1))≥3
ОДЗ
√ (x-1) → x≥1
x+3-4√(x-1)≥0, … x 2 -10x+25≥0; x=5 (ноль уравнения x 2 -10x+25=0 один), тогда x€R.
x+8-6√(x-1)≥0, … x 2 -20x+100≥0; x=10 (ноль уравнения x 2 -10x+25=0 один), тогда x€R.
- √ (x+3-4√(x-1))+√(x+8-6√(x-1))≥3
- √ ( √(x-1)²-2*2√(x-1)+2²)+√( √(x-1)²-2*3√(x-1)+3²)≥3
- √ ( (√(x-1)-2)²) + √( (√(x-1)-3)²) ≥3
(по формуле квадрата разности)
4. |√(x-1)-2|+|√(x-1)-3| ≥3
Найдём нули модулей
√ (x-1)-2=0, x=5; √(x-1)-3=0, x=10
Расставим знаки модулей на промежутках
+
+
—
|√(x-1)-2|
x
5
1
10
+
—
—
|√(x-1)-3|
x€[1;5]
x€[1;5]
x€[1;3]
2-√(x-1)+3-√(x-1)≥3
x≤3
x€(5;10)
x€(5;10)
1≥3
√ (x-1)-2+3-√(x-1)≥3
x€[10;∞)
x€[10;∞)
x€[17;∞)
√ (x-1)-2+√(x-1)-3≥3
x≥17
x€[1;3]U[17;∞)

Решите неравенство:
x 2/x — 4
0
(x-2)*log 2x (3x-2)

ОДЗ
x≠0
2/x≠0
x-2 ≠0
x ≠2
2x ≠1
x ≠0,5
x0
2×0
3x-20
x2/3
2/3
1
2
Найдём нули выражений и их знаки на промежутках
x 2/x — 4=0, x=1
x-2=0, x=2
log 2x (3x-2)=0, x=1
—
—
+
x 2/x — 4
—
+
—
x-2
+
+
—
log 2x (3x-2)
2
1
2/3
x€(2/3;1)U(1;2)
Вернуться к списку заданий
Спасибо за внимание!
Удачи при сдаче ЕГЭ!
Экзамен по математике в форме ЕГЭ требует от школьников умения выполнять быстро и правильно задания первой части экзамена. Школьники должны владеть высоким уровнем вычислений без использования электронных средств подсчёта. Устный счет является одним из важнейших приемов развития вычислительных навыков учащихся при подготовке к ЕГЭ. Нередко даже высокомотивированные учащиеся к выходу на итоговую аттестацию утрачивают навыки устного счета, сформированные в начальной школе.
Начиная с 6 класса на уроках математики все реже применяются формы устного счета. К концу основной школы учащиеся затрудняются в выполнении простейших устных вычислений и не имеют возможности сделать быстро и правильно расчёты в уме без использования средств вычисления, что отражается на результатах ЕГЭ и на самой успеваемости. Еще одна проблема современных учащихся, которая напрямую связана с вычислительной культурой, – нерациональность вычислений.
В начальной школе учащиеся обучаются выполнению арифметических действий над натуральными числами. Формирование навыков письменных вычислений, а в простейших случаях, и устных, следует довести до уровня, обеспечивающего беглое и безошибочное выполнение вычислений. В 5–6-х классах учащиеся овладевают навыками вычисления с натуральными и целыми числами, с обыкновенными и десятичными дробями. При этом алгоритмы вычислений должны быть отработаны с учащимися до автоматизма; их включение в выполнение более сложных вычислений не должно затруднять учащихся. В 7–11-х классах обобщаются и систематизируются сведения о действительных числах, развиваются и закрепляются вычислительные навыки. При этом не следует ослаблять внимание к поддержанию достаточно высокого уровня техники вычислений и повышению уровня вычислительной культуры учащихся (рационализация вычислений, их организация, применение приближенных вычислений). Эта задача должна решаться путем последовательного увеличения доли вычислений при изучении основного материала курса. Вычислительные навыки учащихся должны получить дальнейшее развитие при изучении вопросов, связанных с приближенными вычислениями, где, помимо дальнейшей отработки вычислительных алгоритмов, должны быть сформированы навыки прикидки и оценки результатов вычислений.
Вычислительные навыки и умения можно считать сформированными только в том случае, если учащиеся умеют с достаточной беглостью выполнять математические действия с натуральными числами, десятичными и обыкновенными дробями, рациональными и иррациональными числами, производить тождественные преобразования различных числовых и буквенных выражений и приближенные вычисления, рационально организовывать ход вычислений, а также убеждать в правильности полученных результатов.
Обучение приемам устного счета имеет большой развивающий потенциал. Его применение создает условия для развития учащихся, повышения мотивационного компонента в обучении математике, а также для использования приобретенного в школе опыта деятельности в реальной жизни, за рамками учебного процесса.
Устные упражнения активизируют мыслительную деятельность учащихся, развивают внимание, наблюдательность, память, речь, быстроту реакции, повышают интерес к изучаемому материалу. Как этап урока устные упражнения имеют свои задачи:
1) воспроизводство и корректировка знаний, умений и навыков учащихся, необходимых для их самостоятельной деятельности на уроке или осознанного восприятия объяснения учителя;
2) контроль состояния знаний учащихся;
3) автоматизация навыков простейших вычислений и преобразований.
Для достижения правильности и беглости устных вычислений, преобразований, решения задач в течение всех лет обучения на каждом уроке необходимо отводить 5-7 минут для проведения упражнений в устных вычислениях, предусмотренных программой каждого класса.
Главное условие здесь — систематичность, работа на каждом уроке. Устный счет следует проводить так, чтобы ребята начинали с легкого, затем выполняли более сложное.
Развитие у учащихся навыков устных вычислений и преобразований является одним из важных факторов их успешной сдачи обязательных экзаменов.
Предлагаем систему заданий, предназначенных для устных упражнений на уроках математики в старших классах, по теме «Арифметический корень натуральной степени» и «Логарифмы».
Арифметический корень натуральной степени
Логарифмы
Поговорим о том, как проходят индивидуальные занятия при соблюдении для них комфортных учебных условий. Жаль, что репетитор по математике находится в прямой зависимости от возможностей и планов родителей, от их убеждений в том, как именно следует организовывать учебный процесс и насколько рано начинать заниматься. В планы репетитора вмешиваются различные факторы и условия: финансовые, временные, программные (школьные), часто мешающие развернуться с методиками на долгосрочную перспективу. В сложных и нестабильных условиях репетитор по математике лишен тех возможностей, которыми наделен школьный преподаватель: занятия проходят не регулярно (даже при на графике «раз в неделю»), из-за школьной нагрузки и низкого уровня мотивации обучающегося, несмотря на плачевное состояние его знаний, домашние задания не всегда выполняются. Одним словом — проблем множество.
Писать о методах индивидуальной репетиторской помощи приходится с оговоркой на некие идеальные условия, на практике редко реализуемые. Почему? Родители не всегда следуют рекомендациям репетитора и предоставляют для занятий математикой такое количество часов, при котором трудно заниматься методически правильно. Нет времени на всестороннее и неспешное умственное развитие учащихся, их навыков и способностей. Приходится срочно латать дыры в знаниях, ибо главной целью частных уроков у большинства родителей становится подготовка к ЕГЭ по математике.
По статистике только в одном из четырех случаев репетитор по математике получает необходимую свободу действий и, несмотря на занятость и загруженность ребенка по школе, несмотря на его низкую мотивацию и финансовые трудности, родителям все же удается организовать постоянные занятия с хорошей частотой их проведения. И даже с выездом к репетитору на дом задолго до подготовки к ЕГЭ. Именно в этих случаях удается внести существенные изменения в характер учебы слабого школьника и добиться качественного изменения ситуации не только с оценками, но и дать необходимое развитие его математическим способностям. О таких занятиях и пойдет речь. Их всегда интересно готовить и проводить, писать о методиках, повышающих эффективность индивидуальных уроков. Поговорим об одном из приемов неспешной работы репетитора, а именно об устном счете. К сожалению, не всегда репетитор по математике использует устные задания. И не только по вышеизложенным причинам, но также из-за нежелания или неумения их готовить. Низкий уровень педагогической подготовки многих репетиторов не позволяет строить занятия максимально разнообразно. Более того, большинство репетиторов по математике Интернета не имеют прямого отношения к преподаванию вообще и берутся работать с детьми только потому, что ладили с математикой и в школе и в ВУЗе.
Вернемся к теме статьи. Устный счет является разновидностью более широкого направления учебной работы, а именно устной и может включать в себя не только вычислительные задания, но и задания на запоминание математических фактов, на тренировку памяти и мышления. Какие особенности имеют устные задания и когда их нужно предлагать в качестве отдельных упражнений? Надо понимать, что хороший репетитор по математике всегда планирует занятие заранее и имеет в этом случае возможность продумать содержание устного счет в соответствии с темой урока. Практически для каждого параграфа удается найти соответствующие задания. Надо только иметь определенный талант их составления. Материалы могут иметь разное тематическое содержание и в рамках практически любой темы от 5 класса и до 11-го. Требования репетитора к подаче заданий и характеру их выполнения тоже могут быть разными, даже в том случае, когда работа направлена исключительно на тренировку вычислений. Замечу, что применение устного счета на ранних этапах обучения математике дает в долгосрочной перспективе значительно больший эффект, чем обычное монотонное решение номеров из учебника.
Если репетитор по математике уделяет внимание устной работе, то она, как правило, проводится преимущественно с маленькими учениками (5 — 6 класс). Однако в определенных ситуациях применение методики в старших классах также дает значительный эффект. Даже при подготовке к ЕГЭ по математике. Элементы и этапы выполнения некоторых алгоритмов, знание которых проверяется на ЕГЭ, могут быть локализованы репетитором в отдельные задания для выдачи учащимся мгновенного решения (ответа). Например, на этапе, предшествующем решению вариантов ЕГЭ, слабому абитуриенту можно готовить карточки с изображенными на них знаками производной некоторой функции.
Пример устного задания для подготовки к ЕГЭ:
Ученик указывает репетитору по математике характер каждой изображенной критической точки: является ли она точкой минимума, максимума или не является ни одной из них.
Почему репетитор по математике использует устные задания?
1) Очевидно, что устные упражнения выполняются значительно быстрее письменных. Репетитору удается сэкономить драгоценные минуты, теряемые в ином случае на оформление решений. Есть возможность увеличить объем и спектр повторяемого материала.
2) Дети часто спрашивают репетитора: «Сегодня будет устный счет?». Почему они задают такой вопрос? Очевидно, многим не нравится писать. Процесс размышления оказывается куда более приятным видом деятельности. Применяя устную форму, репетитор по математике некоторым образом повышает желание ребенка заниматься.
3) Отдельные устные упражнения не обязательно связывать друг с другом. Поэтому комплекты заданий легче подстраивать под индивидуальные цели занятий и способности школьника.
3) Устную работу удается проводить целенаправленно. Именно здесь репетитор по математике имеет неоспоримые преимущества перед школьным устным счетом, ибо он видит проблемы конкретного ученика. Например, если ребенок плохо складывает десятичные дроби, но ему предоставляется большее количество заданий «на запятые». Если плохо знает обыкновенные – пусть выделяет целые части, сокращает и т.д.
4) Возможность объединять задания на разные темы. В рамках одного списка они могут иметь различное расположение в программе. Например, уже в 8 — 9 классе можно включать номера на знание таблицы значений тригонометрических функций, перемешивая содержание упражнений с вычислениями, извлечением корней, логическими вопросами, вопросами по теории.
В какой форме репетитор по математике предлагает устные задания?
Я не рекомендую зачитывать примеры с расчетом на их зрительное представление. Они трудно запоминаются и поэтому трудно «перевариваются». Лучше всего их написать и положить перед глазами ученика. Каждый отдельный номер можно оформить на отдельном листочке (особенно для невнимательных учеников). Кроме этого нужны четкие инструкции по выполнению самой работы: «ты смотришь, думаешь, но ничего не пишешь (и даже ничего не говоришь) кроме ответа. Все выполняется в уме».
Виды устных заданий:
1) на вычисление
2) на запоминание (степеней, дробей, значений тригонометрических функций…)
3) на логику
4) на знание теорем и формул.
Устный счет с комментариями и рассужденими
Одна из форм устной работы – выполнение заданий с обсуждением правил. Репетитор по математике озвучивает все этапы вычислительных, логических или смысловых операций. Роль «транслятора» можно передавать ученику в зависимости от его уровня и степени подготовленности к тому или иному типу заданий. Приведем пример, когда репетитор по математике самостоятельно комментирует ход выполнения вычислений. Мы тренируем умение умножать двузначные числа на однозначные посредством представления первых в виде суммы разрядных слагаемых. Допустим, это 
Устный счет на время
Медлительным ученикам нужно ставить временные границы для каждого примера. Я говорю «у тебя есть n секунд. Постарайся уложиться». Такие условия предъявляют репетитору по математике жесткие требования к подбору заданий. Они должны быть примерно равны по сложности и, как следствие, по расчетному времени выполнения. Иначе придется каждый раз объявлять о том, сколько секунд для каждого из них выделяется.
На каком этапе урока репетитор по математике проводит устный счет?
Почему-то многие преподаватели считают, что эту работу нужно проводить в качестве разминки в начале урока. Я не согласен с таким мнением и часто предлагаю устные задания в тот момент, когда чувствую, что ребенок устал писать. Некоторым ученикам вообще лучше предлагать устные упражнения ближе к концу занятия, ибо они послужат отдыхом от монотонной письменной работы. Особенно это актуально для 5 класса и 6 класса. Реже для старших. Маленьким математикам можно готовить сразу несколько коротких «устных перерывов» (при условии проведения стандартного полуторачасового репетиторского урока).
Пример устного счета для 5 класса ( 6 класса). Без временных ограничений.
1) Запиши число, которое больше 14 во столько же раз, во сколько 27 больше 9.
2) В коробке 24 шарика, а в ящике в 2 раза меньше. Взяли дну четверть всех имеющихся в них шариков. Сколько взято шаров?
3) Произведение трех множителей равно 240, а произведение двух из их равно 80. Найдите третий множитель.
4) На какое одно и то же число делятся без остатка все данные числа 18, 24, 36, 15
5) Запиши два любых числа, которые делятся на 7 с остатком 2.
6) Во сколько раз 105 больше чем 7?
7) На сколько надо умножить 14, чтобы получилось 84?

9) Задуманы два числа. Одно из них 40. Если его увеличить на 50, то оно будет меньше другого на 30. Найдите второе число.
10) У Маши было 48 открыток. Ей подарили еще 26 открыток, а она подарила Ире 36 открыток. Сколько открыток стало у Маши?
Как мы видим, материал не содержит примеров на прямые арифметические действия. Их еще нужно составить. Такой подход позволяет преподавателю окунуть ученика 5 класса в условия, в которых эти действия применяются. При этом значительно расширяется спектр тренируемых навыков и знаний.
Весьма эффективным может стать проведение устного счета в геометрии для 8 — 9 класса. Репетитор по математике составляет карточки:
с изображенными на них простейшими фигурами (квадрат, прямоугольный или равносторонний треугольник, описанную или вписанную окружность) и просит найти тот элемент, который выделен красным цветом.
Карточка на нахождение высоты:
Можно составлять комбинации из двух фигур. Для подготовленного к такой работе ученика не требется никаких дополнительных инструкций со стороны преподавателя. Все данные об отрезках, углах и площадях предоставлены на рисунке. Ищем то, что показано красным.
Колпаков А.Н. Репетитор по математике, работающий с методикой устных заданий.



























![arccos a arcsin a π/2 arcsin a π/2 arccos a 0 π π [- π/2 ; π/2 ] 0 arcsin a ϵ arccos a ϵ [ 0 ; π ] - π/2 - π/2 arcctg a arctg a π/2 π/2 arctga ϵ (- π/2 ; π/2 ) π 0 π 0 0 0 arcctg a ϵ ( 0 ; π ) - π/2 - π/2](https://fsd.multiurok.ru/html/2020/02/05/s_5e3a84313fd7d/img28.jpg)






































![Вариант 32 Задание:на рисунке изображен график производной функции у=f’(x), которая задана на промежутке [-4; 5].Укажите точку, в которой функция достигает наибольшее значение. Решение: + y’ y y у=f’(x) В точке х=5 функция y=f(x) достигнет наибольшее значение. 4 у=f(x) 2 5 -4 0 5 x 4 -2 -4 2 -2 Ответ: 5](https://fsd.multiurok.ru/html/2020/02/05/s_5e3a84313fd7d/img78.jpg)























![Алгаритм нахождения наибольшего и наименьшего значения функции f(x) на отрезке [a;b]. 1. Найти призводную функции и приравнять нулю. Найти критические точки . 2. Найти значения функции на концах отрезка, т.е. числа f(a) и f(b). 3. Найти значения функции в тех критических точках, которые принадлежат [a;b]. 4. Из найденных значений выбрать наибольшее и наименьшее.](https://fsd.multiurok.ru/html/2020/02/05/s_5e3a84313fd7d/img105.jpg)

![Найдите наибольшее и наименьшее значение функции y=x 2 - 2x - 3 на отрезке [-5;-1] Найдем производную, прировняем её к нулю. y' = 2x - 2 = 0, 2x = 2, x = 1 - критическая точка функции, но она не принадлежит [-5;-1]. Значит просчитаем значение функции на концах отрезка. y(-5) = 25 +10 - 3 = 32 — наибольшее значение у(х), y(-1) = 1 + 2 - 3 = - 1 — наименьшее значение у(х) на [-5; -1]. Ответ: 32 — наибольшее значение - 1 — наименьшее значение Вернуться к списку заданий](https://fsd.multiurok.ru/html/2020/02/05/s_5e3a84313fd7d/img111.jpg)

















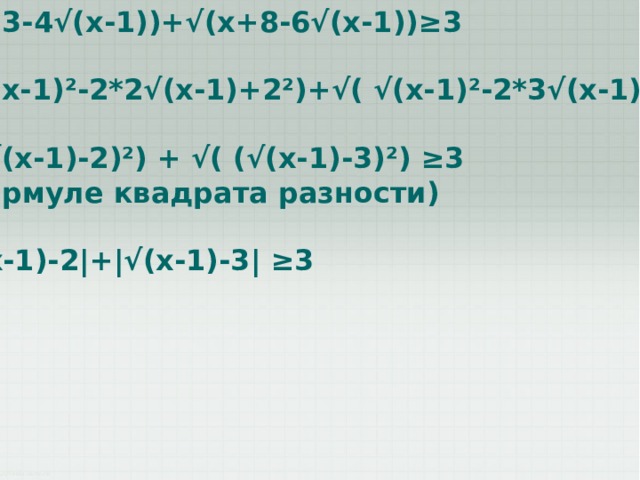

![x€[1;5] x€[1;5] x€[1;3] 2-√(x-1)+3-√(x-1)≥3 x≤3 x€(5;10) x€(5;10) 1≥3 √ (x-1)-2+3-√(x-1)≥3 x€[10;∞) x€[10;∞) x€[17;∞) √ (x-1)-2+√(x-1)-3≥3 x≥17 x€[1;3]U[17;∞)](https://fsd.multiurok.ru/html/2020/02/05/s_5e3a84313fd7d/img133.jpg)





