Переводной экзамен по геометрии за 8 класс
Билеты по геометрии для переводного экзамена в 8 классе
(учебник Геометрия 7 – 9 Л. С. Атанасян.)
Каждый билет содержит 4 вопроса. В первом вопросе предлагается сформулировать и доказать теорему. Во втором вопросе даётся одно из следующих заданий: дать определение понятия, указать его основные свойства или привести примеры, описать этапы построения геометрических фигур. Третий и четвертый вопросы — практические, они содержат задачи за курс 8 класса. Задачи к билетам необходимо решить в тетради. К каждой задаче выполнить рисунок и необходимые пояснения. На экзамен надо принести эту тетрадь с решением и необходимые инструменты: линейка, карандаш, циркуль, ручка. Все билеты надо выучить, уметь ответить у доски и быть готовым к дополнительным вопросам.
Билет №1.
1.Параллелограмм. Свойства параллелограмма. Доказать, что диагонали параллелограмма точкой пересечения делятся пополам.
2.Определение синуса острого угла прямоугольного треугольника. Чему равны значения синуса для углов 300 , 450 , 600?
3. В выпуклом пятиугольнике длины сторон относятся как 5: 7: 8 : 9: 10, а его периметр равен 117 см. Найти наибольшую сторону пятиугольника.
4. В трапеции АВСД с большим основанием АД диагональ АС перпендикулярна к боковой стороне СД, углы ВАС и САД равны. Найти АД, если периметр трапеции равен 20см, а угол Д равен 600.
Билет №2.
1.Параллелограмм. Признаки параллелограмма (доказать один из признаков).
2.Определение косинуса острого угла прямоугольного треугольника. Чему равны значения косинуса для углов 300 , 450 , 600?
3. В параллелограмме АВСД высота, опущенная на сторону СД, делит её пополам и образует со стороной ВС угол 300, АВ = 12см. Найти периметр параллелограмма.
4. Дан треугольник, стороны которого равны 5см, 8см, 7см. Найти периметр треугольника, вершинами которого являются середины сторон данного треугольника.
Билет №3.
1.Прямоугольник. Свойства прямоугольника. Доказать, что диагонали прямоугольника равны.
2.Определение тангенса острого угла прямоугольного треугольника. Чему равны значения тангенса для углов 300 , 450 , 600?
3. В равнобедренной трапеции АВСД диагональ ВД перпендикулярна боковой стороне, угол А равен 600 , АД = 24см., ВС = 12см. Найти периметр трапеции.
4. Центральный угол АОВ на 300 больше вписанного угла, опирающегося на дугу АВ. Найти каждый из этих углов.
Билет №4.
1.Ромб. Свойства ромба. Доказать, что диагонали ромба взаимно перпендикулярны.
2.Определение подобных треугольников. Признаки подобия треугольников.
3.В ромбе АВСД биссектриса угла ВАС пересекает сторону ВС и диагональ ВД соответственно в точках М и К, угол АМС равен 1200 . Найти величину угла АКВ.
4. Через концы хорды АВ, равной радиусу окружности, проведены две касательные, пересекающие в точке С. Найти угол АСВ.
Билет №5.
1.Квадрат. Свойства квадрата. Доказать, что если в ромбе диагонали равны, то ромб является квадратом.
2.Центральный угол. Свойство центрального угла.
3. Высота ВД треугольника АВС делит сторону АС на отрезки, равные 7 см. и 4 см. Площадь треугольника равна 55см» . Найти длину ВД.
4. В окружность вписан равнобедренный треугольник АВС с основанием ВС. Найти углы треугольника, если дуга ВС равна 1020.
Билет №6.
1.Доказать теорему о вычислении площади параллелограмма.
2. Вписанная окружность, центр вписанной окружности. Свойство сторон четырёхугольника, описанного около окружности.
3.В треугольнике АВС угол А = 750 , угол В = 300 , АВ = 10см. Найти площадь треугольника.
4. Найти сторону равностороннего треугольника, если радиус описанной окружности около него окружности равен 10см.
Билет №7.
1.Доказать теорему о вычислении площади треугольника. Как вычислить площадь прямоугольного треугольника?
2. Описанная окружность, центр описанной окружности. Свойство углов четырёхугольника, вписанного в окружность.
3. Основания прямоугольной трапеции равны 10см и 22см, а большая боковая сторона15см. Найти площадь трапеции.
4. Трапеция ВСНМ с основанием ВМ вписана в окружность. Найти углы С, Н, М, если угол В равен 760 , и определите вид трапеции.
Билет №8.
1.Доказать теорему о вычислении площади трапеции.
2.Вписанный угол. Следствия, вытекающие из теоремы о вписанном угле.
3. Периметр треугольника равен 40см, две его стороны равны 15см и 9см. Найти отрезки, на которые биссектриса треугольника делит его третью сторону.
4. Найти площадь прямоугольника, если одна из его сторон 5 см, а угол между диагоналями равен 600.
Билет №9.
1.Доказать теорему Пифагора.
2.Биссектриса угла. Свойство биссектрисы угла.
3. Стороны параллелограмма равны 6см и 7см, угол между ними 600 . Найти высоты параллелограмма.
4. Площадь прямоугольной трапеции равна 120см2 , а её высота равна 8см. Найти все стороны трапеции, если одно из оснований больше другого на 6см.
Билет №10.
1.Определение средней линии треугольника. Доказать теорему о средней линии треугольника.
2.Серединный перпендикуляр. Свойство серединного перпендикуляра к отрезку.
3. АВ и ВС отрезки касательных, проведённых к окружности с центром О радиуса 6см. Найти периметр четырёхугольника АВСО, если угол АВС равен 600 .
4. Смежные стороны параллелограмма равны 32см и 26см., а один из его углов равен 1500 . Найти площадь параллелограмма.
Билет №11.
1.Доказать, что высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на подобные треугольники. Сформулировать утверждения о пропорциональных отрезках в прямоугольном треугольнике.
2.Сформулировать теорему обратную теореме Пифагора.
3. Хорды АВ и СД пересекаются в точке Е. Найти длину АВ, если СЕ = 8см, ДЕ = 9см, а длина АЕ в 2 раза больше длины ВЕ.
4. Одна из диагоналей ромба на 4см больше другой, а площадь ромба равна 96см2 . Найти сторону ромба.
Билет №12.
1.Касательная к окружности, точка касания прямой к окружности. Доказать теорему о свойстве касательной.
2.Дать определение подобных треугольников. Теорема об отношении площадей подобных треугольников.
3. В равнобедренном треугольнике основание равно 20см. а угол между боковыми сторонами равен 1200 . Найти высоту, проведённую к основанию.
4. Площадь прямоугольного треугольника равна 24см2 , а один из его катетов равен 6см. Найти длину средней линии, параллельной другому катету.
Билет №13.
1.Доказать, что отрезки касательных к окружности, проведённые из одной точки, равны и составляют углы с прямой, проходящей через эту точку и центр окружности.
2.Сформулировать свойство медиан треугольника пересекающихся в одной точке.
3. Один из углов ромба на 400 больше другого. Найти углы треугольника ВОС, если О – точка пересечения диагоналей.
4. Найти площадь равнобедренной трапеции, если её основания равны 5см и 17см, а боковая сторона равна 10см.
Билет №14.
1.Вписанный угол. Теорема о вписанном угле.
2.Трапеция. Виды трапеции. Свойства равнобокой трапеции.
3. Найти площадь равнобедренного треугольника, если его основание равно 30см, боковая сторона равна 17см.
4. Треугольник АВС – равнобедренный с основанием АС, АД – его высота, ВД = 16см,
ДС =4см. Найти основание АС и высоту АД.
Билет №15.
1.Доказать теорему об отрезках пересекающихся хорд.
2.Теорема Фалеса. Деление отрезка на п-равных отрезков.
3. Найдите периметр прямоугольника, если его площадь равна 40 см2 и одна сторона больше другой на 3 см
4. АМ и ВК – медианы треугольника АВС. Определить вид четырёхугольника АВМК и найти его периметр, если АВ =14см, ВС = 12см, АС = 18см.
Задачи к билетам
1.В выпуклом пятиугольнике длины сторон относятся как 5:7:8:9:10, а его периметр равен 117 см. Найти наибольшую сторону пятиугольника.
2.В параллелограмме АВСД высота, опущенная на сторону СД, делит её пополам и образует со стороной ВС угол 300, АВ = 12см. Найти периметр параллелограмма.
3.В равнобедренной трапеции АВСД диагональ ВД перпендикулярна боковой стороне, угол А равен 600 , АД = 24см., ВС = 12см. Найти периметр трапеции.
4.В ромбе АВСД биссектриса угла ВАС пересекает сторону ВС и диагональ ВД соответственно в точках М и К, угол АМС равен 1200 . Найти величину угла АКВ.
5.Высота ВД треугольника АВС делит сторону АС на отрезки, равные 7 см. и 4 см. Площадь треугольника равна 55см» . Найти длину ВД.
6.В треугольнике АВС угол А = 750 , угол В = 300 , АВ = 10см. Найти площадь треугольника.
7.Основания равнобедренной трапеции равны 10см и 24см, а большее основание 15см. Найти площадь трапеции.
8.Периметр треугольника равен 40см, две его стороны равны 15см и 9см. Найти отрезки, на которые биссектриса треугольника делит его третью сторону.
9.Стороны параллелограмма равны 6см и 7см, угол между ними 600 . Найти высоты параллелограмма.
10.АВ и ВС отрезки касательных, проведённых к окружности с центром О радиуса 6см. Найти периметр четырёхугольника АВСО, если угол АВС равен 600 .
11.Хорды АВ и СД пересекаются в точке Е. Найти длину АВ, если СЕ = 8см, ДЕ = 9см, а длина АЕ в 2 раза больше длины ВЕ.
12.В равнобедренном треугольнике основание равно 20см. а угол между боковыми сторонами равен 1200 . Найти высоту, проведённую к основанию.
13.Один из углов ромба на 400 больше другого. Найти углы треугольника ВОС, если О – точка пересечения диагоналей.
14.Найти площадь равнобедренного треугольника, если его основание равно 30см, боковая сторона равна 17см.
15.АМ и ВК – медианы треугольника АВС. Определить вид четырёхугольника АВМК и найти его периметр, если АВ =14см, ВС = 12см, АС = 18см.
16. Найдите периметр прямоугольника, если его площадь равна 40 см2 и одна сторона больше другой на 3 см
Задачи к билетам
1.АВСД – ромб, угол АВС равен 1400 . Найти углы треугольника СОД, где точка О – пересечение диагоналей.
2.Треугольник АВС – равнобедренный с основанием АС, АД – его высота, ВД = 16см, ДС =4см. Найти основание АС и высоту АД.
3.Найти площадь равнобедренной трапеции, если её основания равны 5см и 17см, а боковая сторона равна 10см.
4.Площадь прямоугольного треугольника равна 24см2 , а один из его катетов равен 6см. Найти длину средней линии, параллельной другому катету.
5.Одна из диагоналей ромба на 4см больше другой, а площадь ромба равна 96см2 . Найти сторону ромба.
6.Смежные стороны параллелограмма равны 32см и 26см., а один из его углов равен 1500 . Найти площадь параллелограмма.
7.Площадь прямоугольной трапеции равна 120см2 , а её высота равна 8см. Найти все стороны трапеции, если одно из оснований больше другого на 6см.
8.Найти площадь прямоугольника, если одна из его сторон 5 см, а угол между диагоналями равен 600.
9.Трапеция ВСНМ с основанием ВМ вписана в окружность. Найти углы С, Н, М, если угол В равен 760 , и определите вид трапеции.
10.Найти сторону равностороннего треугольника, если радиус описанной окружности около него окружности равен 10см.
11.В окружность вписан равнобедренный треугольник АВС с основанием ВС. Найти углы треугольника, если дуга ВС равна 1020.
12.Центральный угол АОВ на 300 больше вписанного угла, опирающегося на дугу АВ. Найти каждый из этих углов.
13.Через концы хорды АВ, равной радиусу окружности, проведены две касательные, пересекающие в точке С. Найти угол АСВ.
14.Дан треугольник, стороны которого равны 5см, 8см, 7см. Найти периметр треугольника, вершинами которого являются середины сторон данного треугольника.
15.В трапеции АВСД с большим основанием АД диагональ АС перпендикулярна к боковой стороне СД, углы ВАС и САД равны. Найти АД, если периметр трапеции равен 20см, а угол Д равен 600.
Билеты по геометрии для 8 класса (Атанасян) 2018 год
Билет №1.
-
Определение четырёхугольника. Виды четырёхугольников.
-
Доказать теорему Фалеса.
-
Задача.
Найти площадь ромба, если его высота 15 см, а острый угол 30°.
-
В треугольнике АВС
=90
,sinА=
, АС=4
Найдите АВ.
Билет №2.
-
Параллелограмм. Определение. Свойства параллелограмма.
-
Доказать теорему о средней линии треугольника.
-
Задача. В равнобокой трапеции боковая сторона 17 см, основания равны 10 см и 26 см. Найти площадь трапеции.
-
В треугольнике АВС
=90
,sinА=
, АС=5
Найдите АВ.
Билет №3.
-
Квадрат. Определение. Свойства.
-
Вписанная окружность. Доказать теорему об окружности, вписанной в треугольник.
-
Задача. В равнобедренном треугольнике основание равно 80 см, и угол при нём 45°. Найти площадь треугольника.
-
В треугольнике АВС
=90
,АВ=182, АС=70. Найдите tgА.
Билет №4.
-
Пропорциональность отрезков в прямоугольном треугольнике.
-
Прямоугольник. Доказательство теоремы о равенстве диагоналей прямоугольника.
-
Задача. Площадь равнобедренного треугольника равна 4800 см2, а его высота, проведённая к основанию, равна 80 см. Найти боковую сторону треугольника.
-
В треугольнике АВС
=90
,ВС=28, АВ=35. Найдите sinВ.
Билет №5.
-
Соотношения между сторонами и углами в прямоугольном треугольнике (определение синуса, косинуса и тангенса острого угла в прямоугольном треугольнике). Основное тригонометрическое тождество.
-
Ромб. Доказательство теоремы о диагоналях ромба.
-
Задача. В окружности проведены две пересекающиеся хорды. Одна из них делится на отрезки 3 см и 12 см, а другая – пополам. Найдите длину второй хорды.
-
В треугольнике АВС
=90
,cosВ=
, АВ=5
Найдите АС.
Билет № 6.
-
Касательная к окружности. Свойства.
-
Параллелограмм. Свойства параллелограмма. Доказательство одного из свойств параллелограмма (на выбор учащегося).
-
Задача. Определить площадь равнобедренного треугольника, если его основание 8 см и боковая сторона 5 см.
-
В треугольнике АВС
=90
,cosВ=
, АВ=45
Найдите АС.
Билет № 7.
-
Площадь четырехугольников: параллелограмма, трапеции
-
Значения синуса, косинуса и тангенса некоторых углов. Вывод нахождения значений синуса, косинуса и тангенса углов в 45°, 30° и 60°.
-
Задача. В равнобедренный треугольник с основанием 12 см и периметром 32 см вписана окружность. Найдите радиус этой окружности.
-
В треугольнике АВС
=90
,ВС=
21, АВ=5. Найдите sinВ.
Билет №8.
-
Вписанная и описанная окружности в треугольники и четырехугольники.
-
Докажите свойство противолежащих сторон и углов параллелограмма.
-
Задача. Периметр равнобедренного треугольника равен 50 см, а его боковая сторона на 11 см меньше основания. Найти высоту треугольника, опущенную на основание.
-
В треугольнике АВС
=90
,АВ=13, АС=5. Найдите tgА.
Билет №9.
-
Признаки параллельности прямых.
-
Докажите теорему об отношении площадей треугольников.
-
Задача. Меньшее основание трапеции относится к средней линии как 1:3, а большее основание равно 30 см. Найдите среднюю линию трапеции.
-
В треугольнике АВС
=90
,cosВ=
, АВ=25
Найдите АС.
Билет №10.
-
Вписанная и описанная окружности в треугольники и четырехугольники.
-
Площадь треугольника. Формулы для вычисления площади треугольника (общие и частные случаи).
-
Задача. Одна из сторон параллелограмма в 3 раза больше проведённой к ней высоты. Вычислите их, если площадь параллелограмма равна 48 см2.
-
В треугольнике АВС
=90
,АВ=15, АС=12. Найдите tgА.
Билет №11.
-
Вписанный и центральный углы, дуга окружности.
-
Признаки подобия треугольников. Докажите один из признаков подобия треугольников (по выбору учащегося).
-
Задача. Боковая сторона равнобокой трапеции образует с большим её основанием угол 45°. Вычислите площадь трапеции, если основания её равны 24 см и 60 см.
-
В треугольнике АВС
=90
,АВ=20, АС=12. Найдите sinА
Билет №12.
-
Признаки равенства треугольников.
-
Вписанный угол. Докажите теорему о вписанном угле.
-
Задача. Длины диагоналей ромба относятся, как 3 : 4. Площадь ромба равна 150 см2. Вычислить высоту ромба.
-
В треугольнике АВС
=90
,sinА=
, АС=4
Найдите АВ.
Билет № 13.
-
Понятие площади многоугольника. Свойства площадей.
-
Докажите теорему Пифагора.
-
Задача. В треугольник, углы которого относятся как 1:3:5, вписана окружность. Найдите углы между радиусами, проведёнными в точки касания.
-
В треугольнике АВС
=90
,sinА=
, АС=5
Найдите АВ.
Билет №14.
-
Формулы для вычисления площади параллелограмма.
-
Касательная к окружности. Докажите теорему о свойстве касательной к окружности.
-
Задача. В равнобокой трапеции, один из углов которой равен 45°, большее основание равно 70 см, высота равна 10 см. Вычислить площадь трапеции.
-
В треугольнике АВС
=90
,АВ=182, АС=70. Найдите tgА.
Билет №15.
-
Признаки равенства прямоугольных треугольников.
-
Вписанный угол. Докажите теорему о вписанном угле.
-
Задача. Боковая сторона равнобокой трапеции, равная 20 см, образует с меньшим её основанием угол 150°. Вычислите площадь трапеции, если её основания равны 12 см и 30 см.
-
В треугольнике АВС
=90
,ВС=28, АВ=35. Найдите sinВ.
Билет №16.
-
Треугольник. Свойства равнобедренного треугольника.
-
Описанная окружность. Докажите теорему об окружности, описанной около треугольника.
-
Задача. Площадь параллелограмма равна 24 см2, каждая из его сторон равна 6 см. Найти расстояние между противоположными сторонами.
-
В треугольнике АВС
=90
,cosВ=
, АВ=5
Найдите АС.
Вопросы, предлагаемые для устного экзамена по геометрии в 8 классах
1 часть
1.Определение четырёхугольника. Виды четырёхугольников.
2.Параллелограмм. Определение. Свойства параллелограмма.
3.Квадрат. Определение. Свойства.
4. Пропорциональность отрезков в прямоугольном треугольнике.
5. Соотношения между сторонами и углами в прямоугольном треугольнике (определение синуса, косинуса и тангенса острого угла в прямоугольном треугольнике). Основное тригонометрическое тождество.
6. Касательная к окружности. Свойства
7. Площадь четырехугольников: параллелограмма, трапеции
8. Вписанная и описанная окружности в треугольники и четырехугольники.
9. Признаки параллельности прямых
10. Вписанный и центральный углы, дуга окружности.
11. Признаки равенства треугольников.
12. Понятие площади многоугольника. Свойства площадей.
13. Формулы для вычисления площади параллелограмма
14. Признаки равенства прямоугольных треугольников.
15. Треугольник. Свойства равнобедренного треугольника.
2 часть.
1. Доказать теорему Фалеса.
2. Доказать теорему о средней линии треугольника.
3. Вписанная окружность. Доказать теорему об окружности, вписанной в треугольник.
4. Прямоугольник. Доказательство теоремы о равенстве диагоналей прямоугольника.
5. Ромб. Доказательство теоремы о диагоналях ромба.
6. Параллелограмм. Свойства параллелограмма. Доказательство одного из свойств параллелограмма (на выбор учащегося).
7. Значения синуса, косинуса и тангенса некоторых углов. Вывод нахождения значений синуса, косинуса и тангенса углов в 45°, 30° и 60°.
8. Докажите свойство противолежащих сторон и углов параллелограмма.
9. Докажите теорему об отношении площадей треугольников.
10. Площадь треугольника. Формулы для вычисления площади треугольника (общие и частные случаи).
11. Площадь треугольника. Формулы для вычисления площади треугольника (общие и частные случаи).
12. Признаки подобия треугольников. Докажите один из признаков подобия треугольников (по выбору учащегося).
13. Докажите теорему Пифагора.
14. Касательная к окружности. Докажите теорему о свойстве касательной к окружности.
15. Вписанный угол. Докажите теорему о вписанном угле.
16. Описанная окружность. Докажите теорему об окружности, описанной около треугольника.
В данной работе представлен комплект билетов к устному экзамену по геометрии за курс восьмого класса ( к учебнику Атанасяна Л.С. «Геометрия. 7 — 9 классы».
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
04.01.2018
Билеты по геометрии для проведения устного
экзамена в 8 классе.
Оценить
2287
Содержимое разработки
Билеты по геометрии для проведения устного
экзамена в 8 классе.
Билет № 1
Касательная к окружности: определение и свойства.
Сформулируйте определение трапеции. Сформулируйте определение средней линии трапеции.
Билет № 2
Сформулируйте определение синуса острого угла прямоугольного треугольника. Вывод значения синуса, косинуса, тангенса для углов 30°, 45°, 60°.
Параллелограмм: Определение, свойства. Доказать одно свойство на выбор
Билет № 3
1.Сформулируйте свойство медианы равнобедренного треугольника.
2.Сформулируйте определение параллелограмма. Сформулируйте
и докажите свойство диагоналей параллелограмма.
Билет № 4
Прямоугольник: Определение, свойства. Доказать одно свойство на выбор.
Сформулируйте определение медианы треугольника.
Билет № 5
1. Приведите формулы площади прямоугольника и площади параллелограмма. Приведите примеры применения площади прямоугольника либо площади параллелограмма.
2.. Сформулируйте и докажите теорему Пифагора.
Билет № 6
1. Приведите формулу площади трапеции. Приведите пример ее применения.
2. Сформулируйте определение подобных треугольников. Сформулируйте признаки подобия треугольников и докажите один из них по выбору.
Билет № 7
1. Сформулируйте определение вектора. Сформулируйте определение суммы векторов. Приведите примеры сложения векторов.
2. Сформулируйте теоремы о пропорциональных отрезках в прямоугольном треугольнике и докажите один из них по выбору.
Билет № 8
1. Ромб: Определение, свойства. Доказать одно свойство на выбор.
2. Сформулируйте определение прямоугольного треугольника.
Билет № 9
1. Сформулируйтепризнак параллелограмма по выбору учащегося.
2. Сформулируйте определение средней линии треугольника. Сформулируйте и докажите теорему о средней линии треугольника.
Билет № 10
Площадь трапеции. Доказательство.
Сформулируйте определение ромба. Сформулируйте свойство диагоналей ромба.
Билет № 11
1. Сформулируйте определение выпуклого многоугольника. Сформулируйте теорему о сумме углов выпуклого многоугольника.
2. Сформулируйте определение прямоугольника. Сформулируйте и докажите свойство диагоналей прямоугольника.
Билет № 12
Приведите формулы площади треугольника. Приведите примеры их
применения.
Сформулируйте определение параллелограмма и докажите его.
Билет № 13
Сформулируйте определение тангенса острого угла прямоугольного
треугольника.
2. Сформулируйте определение параллелограмма. Сформулируйте
и докажите свойства углов и сторон параллелограмма.
Билет № 14
Квадрат: Определение, признаки. Доказать один признак на выбор
Подобные треугольники: определение и признаки (без доказательства).
Билет № 15
1. Прямоугольник: Определение, признаки. Доказать один признак на выбор
2. Сформулируйте определение косинуса острого угла прямоугольного
треугольника .
Билет №16
1. Площадь равностороннего треугольника. Вывод формулы.
2. Квадрат: Определение, свойства. Доказать одно свойство на выбор.
Билет № 17
Ромб: Определение, признаки. Доказать один признак на выбор.
Площадь параллелограмма. Доказательство.
Практическая часть.
1. Биссектриса угла А прямоугольника ABCD делит сторону ВС на отрезки ВЕ = 3,5 см и ЕС = 7 см. Вычислить периметр прямоугольника.
2 Периметр параллелограмма равен 33 см. Длина одной из его сторон в два раза меньше другой. Найти стороны параллелограмма.
3. В равнобедренный прямоугольный треугольник с катетами по 2 см вписан квадрат, имеющий с ним один общий угол. Найти периметр квадрата.
4. Величина тупого угла равнобокой трапеции втрое больше величины острого угла. Вычислить углы трапеции.
5. . В ромбе ABCD точка М – середина стороны DC. Выразить вектор через векторы и .
6. . Даны два неколлинеарных вектора и . Построить вектор 2 + 3.
7. Основания трапеции относятся как и разнятся на 3,2 м. Найти среднюю линию.
8. Основания трапеции относятся как , а ее средняя линия равна 104 см. Вычислить основания трапеции.
9. Один из углов параллелограмма составляет 25 % другого. Вычислить углы параллелограмма.
10 В равнобокой трапеции высота, проведенная из вершины тупого угла, делит большее основание на отрезки 6,5 см и 29,5 см. Вычислить среднюю линию трапеции.
11 В ромбе одна из диагоналей равна его стороне. Найти углы ромба.
12 Найдите углы В,С и D четырехугольника ABCD, если А = В,С = D и А = 35°.
13 ABCD – параллелограмм. АВ = 10 см, ВС = 15 см. Найти AD и CD.
14. . Большее основание трапеции равно 8 см, а меньшее – на 3 см меньше средней линии. Определите меньшее основание и среднюю линию.
15. ОтрезокМК параллелен стороне АС треугольника АВС (). Найдите длину отрезка СК, если АМ = 6 см, ВМ = 9 см, ВК = 12 см.
16.ABCD – равнобокая трапеция. AD – большее основание. Разность между периметрами треугольников ACD и ВАС равна 6 см, средняя линия – 12 см. Вычислить основания.
17. . В равнобокой трапеции диагональ делит острый угол пополам, периметр ее равен 54 дм, большее основание ее – 1,8 м. Вычислить меньшее основание трапеции
ключи к задачам
Задача 1. Биссектриса угла А прямоугольника ABCD делит сторону ВС на отрезки ВЕ = 3,5 см и ЕС = 7 см. Вычислить периметр прямоугольника.
Решение.
ВЕ = 3,5 см; ЕС = 7 см; ВАЕ = ЕАD (по условию);
ВЕА = EAD (ВС || AD,АЕ – секущая) ВЕА = ВАЕ
АВЕ – равнобедренный, АВ = ВЕ = 3,5 см.
ВС = 10,5 см; Р = 2(АВ + ВС) = 2(3,5 + 10,5) = 28 см.
Ответ:Р = 28 см.
Задача 2. Периметр параллелограмма равен 33 см. Длина одной из его сторон в два раза меньше другой. Найти стороны параллелограмма.
Решение.
АВ = х;ВС = 2х
(х + 2х) 2 = 33
х= 5,5 см
АВ = 5,5 см; ВС = 11 см
Ответ:АВ = 5,5 см; ВС = 11 см.
Задача 3. В равнобедренный прямоугольный треугольник с катетами по 2 см вписан квадрат, имеющий с ним один общий угол. Найти периметр квадрата.
Решение.
В = ВЕD = EAF = 45
BD = DE;FE = FA
РCDEF = CD + DE + EF + CF = CD + DB + FA + CF = BC + CA = 4
Ответ:РCDEF = 4 см.
Задача 3. Величина тупого угла равнобокой трапеции втрое больше величины острого угла. Вычислить углы трапеции.
Решение.
х+ 3х = 180
4х = 180
х = 45
Ответ: величина острого угла 45, тупого 135.
Задача 4. Вычислить периметр и площадь прямоугольника, сторона которого равна 9 см, а диагональ – 15 см.
Решение.
АВ = 9 см; ВС = = 12 см
Р = 2(12 + 9) = 42 см
S = 9 12 = 108 см2
Ответ: 42 см; 108 см2.
Задача 5. В ромбе ABCD точка М – середина стороны DC. Выразить вектор через векторы и .
Решение.
= – +
Задача 6. Даны два неколлинеарных вектора и . Построить вектор 2 + 3.
Решение.
Задача 7.. Основания трапеции относятся как и разнятся на 3,2 м. Найти среднюю линию.
Решение.
В трапеции ABCD имеем .
м; ; ; .
4х = 3,2.
х = 0,8 (м).
AD = 5 м; DC = 2,4 м.
м.
Ответ:MN = 4 м.
Задача8. Основания трапеции относятся как , а ее средняя линия равна 104 см. Вычислить основания трапеции.
Решение.
В трапеции ABCD .
Средняя линия .
; ;
(см); см
Ответ: 96 см; 112 см.
Задача9.Один из углов параллелограмма составляет 25 % другого. Вычислить углы параллелограмма.
Решение.
; .
Ответ: 144; 36.
. Задача 10 В равнобокой трапеции высота, проведенная из вершины тупого угла, делит большее основание на отрезки 6,5 см и 29,5 см. Вычислить среднюю линию трапеции.
см
О т в е т: 29,5 см.
Задача 11 В ромбе одна из диагоналей равна его стороне. Найти углы ромба.
Решение.
АВ = AD = BDABD – равносторонний;
, .
Задача 12. Найдите углы В,С и D четырехугольника ABCD, если А = В,С = D и А = 35°.
Решение. Так как по условию А = В и А = 35°, то А + В = 35°. Сумма углов четырехугольника равна 360, поэтому С + D = 360° – 70° = 290°. По условию С = D, значит, каждый из них равен 145.
Ответ:В = 35°;С = 145°;D = 145°.
Задача 13. Дано: ABCD – параллелограмм. АВ = 10 см, ВС = 15 см. Найти AD и CD.
ВС и AD,AB и DC – противолежащие стороны.
ВС = AD = 15 см.
АВ = CD = 10 см.
Ответ:АD = 15 см, CD = 10 см.
Задача 14.Большее основание трапеции равно 8 см, а меньшее – на 3 см меньше средней линии. Определите меньшее основание и среднюю линию.
Дано:
ABCD – трапеция.
AD = 8 см.
ВС – ? на 3 см меньше МК
Найти:ВС,МК.
Решение.
Пустьхсм – меньшее основание, тогда
ВС = 2 см
МК = 5 см
Ответ: 2 см, 5 см.
Задача 15. Отрезок МК параллелен стороне АС треугольника АВС (). Найдите длину отрезка СК, если АМ = 6 см, ВМ = 9 см, ВК = 12 см.
Дано:
ABC, .
Найти:СК.
Решение.
Ответ: 8 см.
Задача 16.ABCD – равнобокая трапеция. AD – большее основание. Разность между периметрами треугольников ACD и ВАС равна 6 см, средняя линия – 12 см. Вычислить основания.
Решение.
см
MN = 12 см
см
см
Ответ: 9 см; 15 см.
Задача 17. В равнобокой трапеции диагональ делит острый угол пополам, периметр ее равен 54 дм, большее основание ее – 1,8 м. Вычислить меньшее основание трапеции.
1 = 2;1 = 32 = 3
АВС – равнобедренный
АВ = ВС
АВ = х
Р = AD + BC + 2AB
3х + 18 = 54
3х= 36
х = 12 дм
Ответ: 12 дм.
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/290592-bilety-po-geometrii-8-klass

«Свидетельство участника экспертной комиссии»
Оставляйте комментарии к работам коллег и получите документ
БЕСПЛАТНО!

 =90
=90 ,
,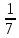 , АС=4
, АС=4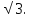 Найдите АВ.
Найдите АВ.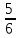 , АС=5
, АС=5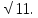 Найдите АВ.
Найдите АВ.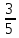 , АВ=5
, АВ=5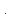 Найдите АС.
Найдите АС.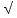 21, АВ=5. Найдите
21, АВ=5. Найдите 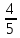 , АВ=25
, АВ=25