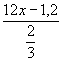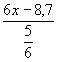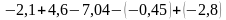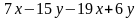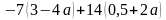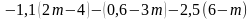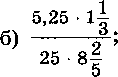Устный экзамен по математике 6 класс билеты

Вопросы к промежуточной аттестации

по математике

в 6 классе

(по учебнику А.Г. Мерзляка)

Вопросы для устного экзамена по математике в 6 классе.

Каждый билет состоит из двух вопросов, первый – теория по курсу математики 5-6 классов, второй – практическое задание.

  1. Определение натурального числа. Законы сложения и умножения: переместительный, сочетательный, распределительный (формулы и правила).

  2. Обыкновенные дроби. Правильные и неправильные дроби. Сложение и вычитание дробей с одинаковым знаменателем. Смешанные числа. Перевод из неправильной дроби в смешанное число (выделить целую часть) и из смешанного числа в неправильную дробь.

  3. Десятичные дроби. Представление десятичной дроби в виде обыкновенной и обыкновенной в виде десятичной. Сложение и вычитание десятичных дробей.

  4. Умножение и деление десятичных дробей на 10, 100, 1000 и т.д. Умножение и деление десятичной дроби на десятичную дробь.

  5. Делители и кратные. Признаки делимости на 2, 3, 5, 9, 10, 4, 8.

  6. Простые и составные числа, взаимно простые числа. Разложение на простые множители. Нахождение НОД и НОК чисел.

  7. Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю.

  8. Правила сложения, вычитания, умножения и деления обыкновенных дробей.

  9. Взаимно обратные числа. Правила нахождения дроби (процентов) от числа и числа по значению его дроби (процентов).

  10. Преобразование обыкновенной дроби в десятичную дробь. Бесконечные периодические десятичные дроби (примеры). Рациональные числа.

  11. Отношения и пропорция. Основное свойство пропорции.

  12. Прямая и обратная пропорциональные зависимости. Случайные события и вероятность случайного события.

  13. Окружность и круг (понятия радиуса, диаметра, хорды). Длина окружности и площадь круга (формулы). Площадь квадрата и прямоугольника (формулы). Объем куба и прямоугольного параллелепипеда (формулы).

  14. Целые числа. Противоположные числа. Понятие модуля числа. Сравнение положительных и отрицательных чисел.

  15. Правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.

  16. Переместительное, сочетательное и распределительное свойства умножения рациональных чисел. Коэффициент. Правила раскрытия скобок, перед которыми стоит знак «плюс» или знак «минус».

  17. Решение уравнений. Что значит «решить уравнение». Что такое «корень уравнения».

  18. Прямая, отрезок, луч. Перпендикулярные и параллельные прямые. Свойство параллельных прямых.

  19. Центральная и осевая симметрии (примеры).

  20. Представление о координатной плоскости. Координаты точки на плоскости. График.

Практические задания к экзамену.

  1. Задачи на проценты.

  1. За контрольную работу по математике было поставлено 15% пятёрок. Сколько учеников писало контрольную работу, если пятёрки получили 6 человек?

(Ответ. 40 учеников)

  1. Из 76 м2 площади квартиры кухня занимает 12%. Найдите площадь кухни.

(Ответ. 9,12 м2)

  1. Примеры на действия с положительными и отрицательными числами.

  1. Задание на нахождение длины окружности и площади круга.

Найдите длину окружности и площадь круга, если диаметр круга равен 15 см. (Число 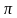округлите до сотых).

(Ответ. C = 47,1 см, S = 176,625 см2)

  1. Задачи на масштаб.

а) На чертеже изображен прямоугольник, площадь которого 216 см2. Найдите площадь этого прямоугольника в действительности, если чертеж выполнен в масштабе 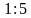. (Ответ. 1080 см2)

б) Расстояние между двумя городами равно 615 км. Каким будет это расстояние на карте, если масштаб карты 1:1500000? (Ответ. 41 см)

  1. Координатная плоскость: построение точек с указанными координатами и нахождение координат указанных точек.

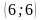
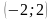
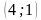
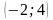
Отметьте на координатной плоскости точки M , N , K и P . Укажите в какой четверти лежит каждая точка. Проведите прямые MN и KP. Найдите координаты точки пересечения:

а) прямых MN и KP;

б) прямой MN с осью абсцисс;

в) прямой KP с осью ординат.

(Ответ. Точки K, M – 1 ч. и точки N, P – 2 ч.; а) (0;3); б) (-6;0); в) (0;3))

  1. Задача на формулу объёма прямоугольного параллелепипеда.

Ширина прямоугольного параллелепипеда 12 дм, длина в 3 раза больше, а высота на 3 дм больше ширины. Найдите объем прямоугольного параллелепипеда. (Ответ. 6480 дм3).

  1. Задание на понятие модуля числа.

Найдите значение выражения:

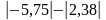
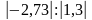
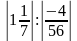
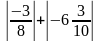
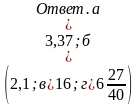
а) б) в) г)

  1. Упростить выражения.

  1. Текстовая задача на движение.

Из двух пунктов, расстояние между которыми 40 км, навстречу друг другу одновременно отправились пешеход и велосипедист. Скорость велосипедиста в 4 раза больше скорости пешехода. Найдите скорости пешехода и велосипедиста, если известно, что они встретились через 2,5 ч после своего выхода.

(Ответ. 3,2 км/ч и 12,8 км/ч)

  1. Текстовая задача на составление уравнения.

На пришкольном участке было собрано 360 кг овощей. Картофеля было собрано в 5 раз больше, чем свёклы, а капусты – на 80 кг больше, чем свёклы. Сколько кг каждой культуры было собрано?

(Ответ. 40 кг свёклы, 200 кг картофеля, 120 кг капусты)

  1. Задание на нахождение НОД и НОК чисел.

Найдите наименьшее общее кратное и наибольший общий делитель чисел:

а) 68 и 170;

б) 792 и 1188.

(Ответ. а) НОД = 34, НОК = 340; б) НОД = 396, НОК = 2376)

  1. Примеры на действия с обыкновенными дробями.

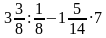
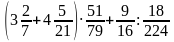
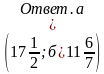
а) б)

  1. Решение уравнений.

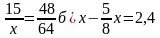
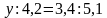
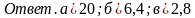
а) в)

( )

  1. Задачи на пропорции.

  1. 24 человека за 6 дней пропололи участок клубники. За сколько дней выполнят ту же работу 36 человек, если будут работать с такой же производительностью? (Ответ. 4 дня)

  2. Для изготовления 14 деталей требуется 16,8 кг металла. Сколько металла пойдет на изготовление 27 таких деталей? (Ответ. 32,4 кг металла)

  1. Примеры на действия с десятичными дробями.

а) ;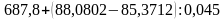

б)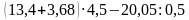

(Ответ. а) 748; б) 36,76)

  1. Задания на сравнение чисел.

Сравните числа:

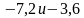
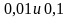
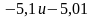
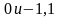
а) ; б) ; в) ; г) ;

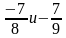
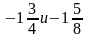
д) ; е) .

  1. Примеры на действия с обыкновенными, десятичными дробями и квадрат, куб числа.

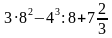
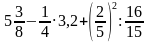
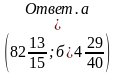
а) 1 ; б)

  1. Задание на раскрытие скобок.

Раскройте скобки и найдите значение выражения:

а) ;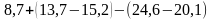

б) .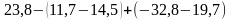

(Ответ. )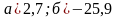

  1. Решение уравнений.

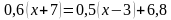
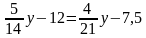
а) ; б)

(Ответ. )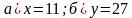

  1. Задачи на нахождение дроби от числа и числа по его дроби.

1) Рабочие засадили пшеницей 0,6 часть участка, что составляет 132 га. Какова площадь всего участка, который нужно засадить? (Ответ. 220 га)

2) В магазине 1 кг конфет стоит 318 рублей. Сколько стоят 0,4 кг этих конфет? (Ответ. 127,2 р.)

  1. Определение натурального числа. Законы арифметических действий: переместительный, сочетательный, распределительный.

  1. Обыкновенные дроби. Правильные и неправильные дроби. Смешанные числа.

  1. Определение десятичной дроби. Представление десятичной дроби в виде обыкновенной и обыкновенной в виде десятичной.

  1. Арифметические действия с десятичными дробями (правила сложения, вычитания, умножения, деления).

  1. Определения уравнения и корня уравнения. Перенос слагаемых из одной части уравнения в другую.

  1. Проценты. Нахождение процента от величины, величины по её проценту.

  1. Определение целого числа. Правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.

  1. Определение простого и составного числа, взаимно простых чисел. НОД и НОК чисел.

  2. Признаки делимости на 2, 3, 5, 9,10, 4, 8.

  1. Правила сложения, вычитания, умножения и деления обыкновенных дробей.

  1. Правила нахождения части от целого и целого по его части.

  1. Представление об отношении и о пропорции. Основное свойство пропорции.

  1. Понятие модуля числа. Противоположные числа.

  1. Представление о координатной плоскости. Координаты точки.

  1. Прямая, отрезок, луч как геометрические понятия. Перпендикулярные и параллельные прямые.

  1. Определение угла. Виды углов. Биссектриса угла.

  1. Треугольник. Виды треугольников. Сумма углов треугольника.

  1. Окружность, круг как геометрические фигуры. Длина окружности и площадь круга.

  1. Правила раскрытия скобок, перед которыми стоит знак «плюс» или знак «минус». Подобные слагаемые.

  1. Прямоугольный параллелепипед и куб. Формулы объёма.

  1. Задачи на проценты.

1) За контрольную работу по математике было поставлено 15% пятёрок. Сколько учеников писало контрольную работу, если пятёрки получили 6 человек?

2) Из 76 м2 площади квартиры кухня занимает 12%. Найдите площадь кухни.

  1. Примеры на действия с положительными и отрицательными числами.

  1. Задание на нахождение длины окружности и площади круга.

Найдите длину окружности и площадь круга, если диаметр круга равен 15 см. (Число 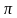округлите до сотых).

  1. Задачи на масштаб.

а) На чертеже изображен прямоугольник, площадь которого 216 см2. Найдите площадь этого прямоугольника в действительности, если чертеж выполнен в масштабе .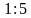

б) Расстояние между двумя городами равно 615 км. Каким будет это расстояние на карте, если масштаб карты 1:1500000?

  1. Координатная плоскость: построение точек с указанными координатами и нахождение координат указанных точек.

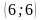
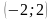
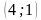
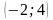
Отметьте на координатной плоскости точки M , N , K и P . Укажите в какой четверти лежит каждая точка. Проведите прямые MN и KP. Найдите координаты точки пересечения: а) прямых MN и KP; б) прямой MN с осью абсцисс; в) прямой KP с осью ординат.

  1. Задача на формулу объёма прямоугольного параллелепипеда.

Ширина прямоугольного параллелепипеда 12 дм, длина в 3 раза больше, а высота на 3 дм больше ширины. Найдите объем прямоугольного параллелепипеда.

  1. Задание на понятие модуля числа.

Найдите значение выражения:

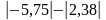
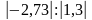
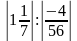
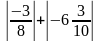
а) б) в) г)

  1. Упростить выражения.

  1. Текстовая задача на движение.

Из двух пунктов, расстояние между которыми 40 км, навстречу друг другу одновременно отправились пешеход и велосипедист. Скорость велосипедиста в 4 раза больше скорости пешехода. Найдите скорости пешехода и велосипедиста, если известно, что они встретились через 2,5 ч после своего выхода.

  1. Текстовая задача на составление уравнения.

На пришкольном участке было собрано 360 кг овощей. Картофеля было собрано в 5 раз больше, чем свёклы, а капусты – на 80 кг больше, чем свёклы. Сколько кг каждой культуры было собрано?

  1. Задание на нахождение НОД и НОК чисел.

Найдите наименьшее общее кратное и наибольший общий делитель чисел:

а) 68 и 170;

б) 792 и 1188.

  1. Примеры на действия с обыкновенными дробями.

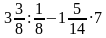
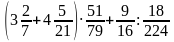
а) б)

  1. Решение уравнений.

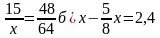
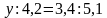
а) в)

  1. Задачи на пропорцию.

1) 24 человека за 6 дней пропололи участок клубники. За сколько дней выполнят ту же работу 36 человек, если будут работать с такой же производительностью?

2) Для изготовления 14 деталей требуется 16,8 кг металла. Сколько металла пойдет на изготовление 27 таких деталей?

  1. Примеры на действия с десятичными дробями.

а) ;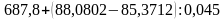

б)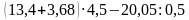

  1. Задание на сравнение чисел.

Сравните числа:

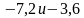
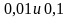
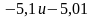
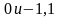
а) ; б) ; в) ; г) ;

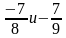
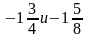
д) ; е) .

  1. Примеры на действия с обыкновенными, десятичными дробями и квадрат, куб числа.

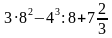
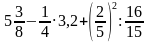
а) 1 ; б)

  1. Задание на раскрытие скобок.

а) ;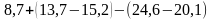

б) .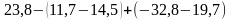

  1. Решение уравнений.

а) ;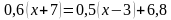

б)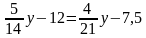

  1. Задачи на нахождение части от целого и целого по его части.

1) Рабочие засадили пшеницей 0,6 часть участка, это составляет 132 га. Какова площадь всего участка, который нужно засадить?

2) В магазине килограмм конфет стоит 318 рублей. Сколько стоят 400 грамм этих конфет?

Источник

Игнатьева Марина Васильевна

Данный материал поможет провести устный экзамен по математике в 6 классе.

Скачать:

Предварительный просмотр:

Билет №1

  1. Какие числа называются противоположными?
  2. Что показывает масштаб?
  3. Укажите модули чисел: 25; -9,71; -78; 0

Билет №2

  1. Что называется пропорцией? Правило вычисления пропорций.
  2. Определение коэффициента.
  3. Укажите число противоположное b, если b=+1,2; b=-2; b=4

Билет №3

  1. Определение модуля числа.
  2. Определение делителя, кратного.
  3. Укажите все целые числа, расположенные на координатной прямой между числами -8,2 и 3,4

Билет №4

  1. Признаки делимости на 2,3,4,5,9,10.
  2. Как найти сумму отрицательных чисел?
  3. Сравните числа: а) -5/12 и -7/12;

                                б) -2, 4 и 2;

                                 в) 0, 1 и — 12

Билет №5

  1. Как найти сумму чисел с разными знаками?
  2. Определение простого, составного числа.
  3. Расположите числа в порядке возрастания: 2/3, 5/6, 7/12

Билет №6

  1. Определение наибольшего общего делителя, наименьшего общего кратного.
  2. Как найти произведение (частное) отрицательных чисел, чисел с разными знаками?
  3. Укажите наименьшее и наибольшее целое число, принадлежащее данному числовому промежутку: а) [-2; 8,2) б) [-5,2; 2] в) (0; 6,5)

Билет № 7

  1. Правило раскрытия скобок по распределительному закону.
  2. Определение взаимно простых чисел.
  3. Вычислите: а) -6*(-2,5) ; б) 7,2:(-3); в) 2/5*5

Билет № 8

  1. Основное свойство дроби.
  2. Какие слагаемые называются подобными? Правило приведения подобных слагаемых.
  3. Упростите выражения: а) (-3)*6а; б) -7х*(-5); в) 7с*(-4)

Билет № 9

  1. Правила, применяемые при решении уравнений:

а) перенос слагаемых;

б) умножение на число.

2. Правило сложения смешанных чисел.

3. Вычислите: а) |-5,6+2,8|; б) |7|*|-3,5|; в) 6-|-6,7|

Билет № 10

  1. Правило вычитания смешанных чисел.
  2. Определение перпендикулярных прямых.
  3. Вычислите: а) 5/7*7/10; б) 2 ½*(-4/5); в) (-14/20)*(-4/7)

Билет № 11

  1. Определение параллельных прямых.
  2. Правило умножения обыкновенных дробей, смешанных чисел.
  3. Вычислите: а) 2 ½- 2 ¼; б) (-5 2/4)-3 3/5

Билет № 12

  1. Правило деления обыкновенных дробей, смешанных чисел.
  2. Что называется координатной плоскостью, системой координат? Как называются координаты точки?
  3. Раскройте скобки и упростите: а) 2(3+а)-10; б) -12-7(а+1); в) –(а+5)+а

Билет №13

  1. Формулы нахождения длины окружности и площади круга (через радиус и через диаметр).
  2. Определение взаимно обратных чисел.
  3. Решите уравнения: а) 4х-7=2х+15; б) -24+3х=9х+18

Билет №14

  1. Как найти часть, процент от  числа?
  2. Что показывает масштаб?
  3. Вычислите площадь круга, длину окружности , если R=3см, π=3,14

Билет №15

  1. Как найти число по его части, проценту?
  2. Как найти вероятность события?
  3. Найдите НОД, НОК чисел 56 и 196

По теме: методические разработки, презентации и конспекты

  • Мне нравится 

 

Источник

Подборка по базе: Экзаменационные билеты для подготовки аппаратчиков химводоочистк, Экзамен билет.docx, 1 билет.docx, новый билет по мсфо 2023.docx, IDEF5 билет.docx, бх рк билет КЗС.docx, Қазақстан тарихынан емтихан билеттері 9-сынып.docx, тех прог билеты.docx, Өндіріс емтихан билеттері 2023.docx, 5 билет..docx

Билет №1

1. Делители и кратные. Простые и составные числа.

2. Отметьте на координатной плоскости точки А (-2; 4), В (-4; -5), С (8; 0), D (-4; 4).

Найдите координаты точки пересечения прямых АВ и СD.

Билет №2

1. Признаки делимости на 10, на 5, на 2, на 3 и на 9.

2. Найдите значение дробного выражения:

Билет №3

1. Разложение на простые множители. Наименьшее общее кратное.

2. Комбайнер перевыполнил план на 15% и убрал зерновые на площади 230 га. Сколько гектаров по плану должен убрать комбайнер?

Билет №4

1. Наибольший общий делитель. Взаимно простые числа.

2. Найдите значение выражения: -2,6 (3 — 3,8) + 4,2 • (4 — 2,7)

Билет №5

1. Основное свойство дроби. Сокращение дробей.

2. В двух строительных бригадах 88 человек. В первой бригаде в 2 раза меньше людей, чем во второй. Сколько человек в каждой бригаде?

Билет №6

1. Приведение дробей к общему знаменателю. Сравнение, сложение и вычитание дробей с разными знаменателями.

2. Увеличив производительность труда на 7%, рабочий сделал за этот же срок на 98 деталей больше, чем намечалось по плану. Сколько деталей рабочий должен был сделать по плану?

Билет №7

1. Сложение и вычитание смешанных чисел. Применение распределительного свойства умножения.

2. Огород занимает 8 га. Картофелем занято 45% площади этого огорода. Сколько гектаров занято картофелем?

Билет №8

1. Умножение дробей. Нахождение дроби от числа.

2. Найдите наименьшее общее кратное чисел: 20, 70 и 15.

Найдите наибольший общий делитель чисел 15, 45, и 75.

Билет №9
1. Взаимно обратные числа. Деление.

2. По норме рабочий должен изготовить 72 детали, а он изготовил 90 деталей. На сколько процентов рабочий выполнил норму и на сколько процентов он перевыполнил норму?

Билет №10

1. Нахождение числа по его дроби. Дробные выражения.

2. Какие из чисел 72; 33339; 5 402 070 делятся на 3? Какие из них делятся на 9?

Билет №11

1. Отношения. Пропорции.

2. Постройте столбчатую диаграмму по данным: наибольшая глубина озера Байкал 1620 м, Онежского озера 127 м, озера Иссык-Куль 668 м, Ладожского озера 225 м.

Билет №12

1. Прямая и обратная пропорциональные зависимости. Масштаб.

2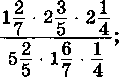 . Найдите значение выражения:

Билет №13

1. Длина окружности и площадь круга. Шар.

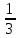
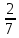
2. Решите уравнение: (3х – 6) – (7х – 21) = 9.

Билет №14

1. Координаты на прямой. Противоположные числа.

2. Выезжая из села, велосипедист заметил на мосту пешехода, идущего в том же направлении, и догнал его через 12 мин. Найдите скорость пешехода, если скорость велосипедиста 15 км/ч, а расстояние от села до моста 1 км 800 м.

Билет №15

1. Модуль числа. Сравнение чисел.

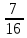
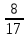
2. Два одинаковых сосуда заполнены жидкостью. Из первого сосуда взяли имевшейся там жидкости, а из второго — . В каком сосуде осталось жидкости больше?

Билет №16

1. Изменение величин. Сложение чисел с помощью координатной прямой.

2. Длина дома на плане 25 см. Чему равна длина дома на местности, если план сделан в масштабе 1 : 300?

Билет №17

1. Сложение отрицательных чисел. Сложение чисел с разными знаками.

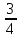
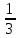
2. В трёх бидонах 10 л молока. В первом и втором бидонах было 6 л, а во втором и в третьем – 5 л молока. Сколько литров молока было в каждом бидоне?

Билет №18

1. Рациональные числа. Вычитание рациональных чисел.

2. Решите уравнение: 2,45 — (х — 8,8) = 4,4

Билет №19

1. Умножение и деление рациональных чисел.

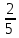
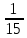
2. Площадь прямоугольника 2 м2. Длина одной стороны 1 м. Найдите длину другой стороны.

Билет №20

1. Рациональные числа. Свойства действий с рациональными числами.

2. Крутизной лестницы называют отношение высоты ступеньки к её глубине. Чему равна крутизна лестницы, если высота ступеньки 18 см, а глубина 30 см?

Билет №21

1. Раскрытие скобок. Коэффициент.

2. Окружность арены во всех цирках мира имеет длину 40,8 м.

Найдите диаметр и площадь арены (π ≈ 3).

Билет №22

1. Подобные слагаемые. Решение уравнений.

2. Площадь прямоугольника 11,7 дм2, а ширина этого прямоугольника 2,6 дм. Все его стороны увеличили на 0,2 дм. Найдите площадь нового прямоугольника.

Билет №23

1. Перпендикулярные прямые. Параллельные прямые. Координатная плоскость.

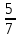
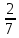
2. В трёх ящиках 21 кг гвоздей. В первом ящике в 1 раза больше гвоздей, чем во втором. Масса гвоздей третьего ящика составляет массы гвоздей второго ящика. Сколько килограммов гвоздей было в каждом ящике?

Источник

Данный зачет является продолжением работы,
выполненной в прошлом году и опубликованной на
сайте Фестиваля педагогических идей “Открытый
урок” (сайт www. festival. 1 september. ru. газеты “Первое
сентября”).

В 2003-2004 учебном году зачет был проведен в 5
классе, причем во втором полугодии (вторая часть
зачета) более успешно, чем в первом. По-видимому,
это объясняется тем, что учащиеся осознали
необходимость знания точных формулировок
определений и правил, а также математических
терминов.

В 6 классе предполагается проводить зачет один
раз в конце года после прохождения программы во
время итогового повторения. Это позволит выявить
недостаточно усвоенные в процессе обучения темы
и скорректировать знания.

Зачет состоит из двух теоретических вопросов,
которые открыты для учащихся за 1,5 – 2 месяца до
проведения, и одного практического задания,
которое выдается в процессе сдачи зачета только
после успешного выполнения двух первых.

Данный зачет составлен к учебнику “Арифметика
– 6” С.М.Никольский, М.К.Потапов, Н.Н.Решетников,
А.В.Шевкин. – 2-е изд. – М.: Просвещение, 2000. – 308 с.:
ил.

Примеры для третьих заданий билетов взяты из
сборника “Самостоятельные и контрольные работы
по математике для 6 класса” А.П.Ершова,
В.В.Голобородбко. – М.: Илекса, 2003.

БИЛЕТ №1

1. Отношения и пропорции. Основное свойство
пропорции. Доказательства пропорции.
2. Числовые неравенства. Строгие и нестрогие
неравенства. Преобразование неравенств.
3. Решите уравнение.

БИЛЕТ №2

1. Прямая и обратная пропорциональные
зависимости.
2. Системы счисления. Сложение и вычитание чисел в
различных системах счисления.
3. Преобразуйте выражение.

БИЛЕТ №3

1. Деление целого на пропорциональные части.
2. Множества. Способы задания множеств.
Подмножества.
3. Вычислите длину отрезка.

БИЛЕТ №4

1. Масштаб.
2. Пересечение и объединение множеств. Разбиение
множеств на подмножества. Дополнения множества.
3. Решите уравнение.

БИЛЕТ №5

1. Положительные и отрицательные числа на
координатной прямой. Противоположные числа.
2. Линейная функция.
3. Решите задачу.

БИЛЕТ №6

1. Модуль числа. Сравнение чисел.
2. Прямая пропорциональность.
3. Решите задачу.

БИЛЕТ №7

1. Сложение отрицательных чисел.
2. График функции.
3. Решите уравнение.

БИЛЕТ №8

1. Сложение чисел с разными знаками.
2. Функция, способы задания функции.
3. Решите задачу.

БИЛЕТ №9

1. Вычитание положительных и отрицательных
чисел.
2. Координатная плоскость.
3. Решите задачу.

БИЛЕТ №10

1. Умножение и деление положительных и
отрицательных чисел.
2. Уравнение, корень уравнения, линейное
уравнение.
3. Решите задачу.

БИЛЕТ №11

1. Рациональные числа. Конечная и бесконечная
десятичная дробь. Периодическая десятичная
дробь.
2. Методы решения линейных уравнений.
3. Сравните значения выражений.

БИЛЕТ №12

1. Алгебраические выражения: числовые и
буквенные. Свойства действий над рациональными
числами.
2. Преобразование выражений: раскрытие скобок,
приведение подобных слагаемых. Коэффициент.
3. Решите уравнение.

 Задания №3 к билетам.

№1. Решите уравнение: 0,2* (3¦х¦ — 5) – 3*(0,4 – 0,3¦х¦) =
-0,7.

№2. Преобразуйте выражение: — 2,8 – (4,2 – (1,7 + (-1))).

№3. Найдите расстояние между точками А и В, если
А(а + 0,8), В(b – 4,2), b – a = -3.

№4. Решите уравнение: х = 4х + .

№5. Решите задачу.

Воду из котлована планировали откачать за 50
дней с помощью 60 насосов. Сколько насосов
необходимо привлечь дополнительно, чтобы
закончить работу на 10 дней раньше?

№6. Решите задачу.

Длины сторон треугольника относятся как 3:4:5.
Найдите периметр треугольника, если разность его
наибольшей и наименьшей сторон равна 12 см.

№7. Решите уравнение: 11 — 3¦2х + 1¦ = 5.

№8. Решите задачу.

Агрофирма, имеющая 20 комбайнов, планировала
убрать урожай яровых за 8 дней. Сколько дней
понадобится дополнительно, если 4 комбайна
оказались неисправными?

№9. Решите задачу.

В двух мешках 140 кг муки. После того, как часть
муки из первого мешка переложили во второй, муки
в мешках стало поровну. Сколько килограммов муки
было в каждом мешке первоначально?

№10. Решите задачу.

Велосипедист проехал участок шоссе со
скоростью 18 км/час и участок проселочной дороги
со скоростью 12 км/час. Всего он проехал 78 км.
Сколько времени велосипедист затратил на весь
путь, если по проселочной дороге он ехал на 0,5
часа дольше, чем по шоссе?

№11. Сравните значения выражений: (2 — (-1)2) *
1,5 и —.

№12. Решите уравнение: = .

Источник

Понравилась статья? Поделить с друзьями:
  • Устный экзамен по литературе 6 класс с ответами
  • Устный экзамен по китайскому языку
  • Устный экзамен по истории казахстана
  • Устный экзамен по истории егэ
  • Устный экзамен по истории 9 класс