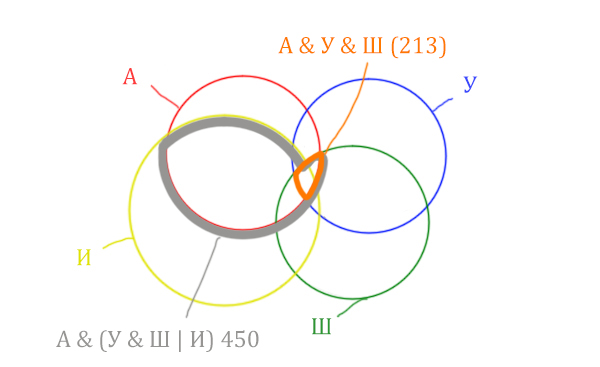Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:
| Ключевое слово | Найдено страниц |
|---|---|
| сканер | 200 |
| принтер | 250 |
| монитор | 450 |
Сколько сайтов будет найдено по запросу «(принтер | сканер) & монитор», если по запросу «принтер | сканер» было найдено 450 сайтов, по запросу «принтер & монитор» — 40, а по запросу «сканер & монитор» — 50.
2
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество страниц (тыс.) |
|---|---|
| торты | пироги | 12000 |
| торты & пироги | 6500 |
| пироги | 7700 |
Сколько страниц (в тысячах) будет найдено по запросу торты
3
Некоторый сегмент сети Интернет состоит из 5000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:
| Ключевое слово | Количество сайтов,для которых данное слово является ключевым |
|---|---|
| принтеры | 400 |
| сканеры | 300 |
| мониторы | 500 |
Сколько сайтов будет найдено по запросу (принтеры | мониторы) & сканеры
если по запросу принтеры | сканеры было найдено 600 сайтов,
по запросу принтеры | мониторы – 900,
а по запросу сканеры | мониторы – 750.
4
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Лебедь & (Рак | Щука) | 320 |
| Лебедь & Рак | 200 |
| Лебедь & Рак & Щука | 50 |
Какое количество страниц (в тысячах) будет найдено по запросу
Лебедь & Щука
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
5
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Пекин & (Москва | Токио) | 338 |
| Пекин & Москва | 204 |
| Пекин & Москва & Токио | 50 |
Какое количество страниц (в тысячах) будет найдено по запросу Пекин & Токио?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Пройти тестирование по этим заданиям
(Старый формат ЕГЭ) 17. Запросы в поисковых системах
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{ноутбук}&100\
hline
text{монитор}&200\
hline
text{стол}&350\
hline
text{ноутбук | стол}&450\
hline
text{ноутбук} & text{монитор}&50\
hline
text{стол} & text{монитор}&40\
hline
end{array}]
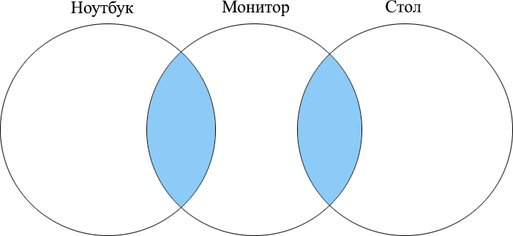
Сколько страниц будет найдено по запросу (ноутбук | стол) & монитор?
Если сложить количество страниц, найденных отдельно по запросам ”ноутбук” и ”монитор”, получим 450. Можно заметить, что (ноутбук | стол) так же равно 450. Это значит, что эти два множества не пересекаются, то есть (text{(ноутбук} & text{монитор)}=0).
Отметим на кругах Эйлера то, что нам необходимо найти по условию задачи:
Исходя из рисунка, нам нужно найти сумму (text{(ноутбук} & text{монитор)}+text{(стол} & text{монитор)}). Все данные приведены в таблице, значит, наш ответ (50+40=90).
Ответ: 90
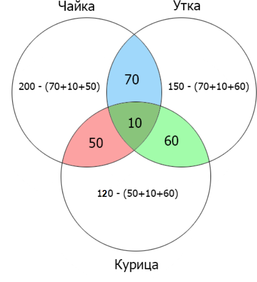
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{чайка}&200\
hline
text{утка}&150\
hline
text{курица}&120\
hline
text{чайка} & text{утка}&80\
hline
text{утка} & text{курица}&70\
hline
text{чайка} & text{курица}&60\
hline
text{чайка} & text{курица} & text{утка}&10\
hline
end{array}]
Сколько страниц будет найдено по запросу (чайка | утка)?
Первый способ решения
Отметим на кругах Эйлера то, что нам необходимо найти по условию задачи:
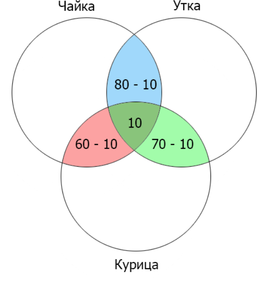
Посчитаем количество найденных страниц для каждого пересечения:
Посчитаем оставшиеся данные:
Затем складываем все данные, входящие в круги ”чайка” и ”утка”: (70+70+50+10+60+10=270)
Второй способ решения
Чтобы найти объединение (операция «ИЛИ») множеств, необходимо сложить отдельно количество страниц, найденных по каждому запросу, а затем вычесть их пересечение (операция «И»): (200+150-80=270)
Ответ: 270
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{карандаш}&300\
hline
text{линейка}&200\
hline
text{ручка}&280\
hline
text{ручка} & text{линейка}&80\
hline
text{ручка} & text{карандаш}&70\
hline
text{линейка} & text{карандаш}&0\
hline
end{array}]
Сколько страниц будет найдено по запросу (линейка | ручка | карандаш)?
Первый способ решения
Отметим на кругах Эйлера то, что нам необходимо найти по условию задачи:
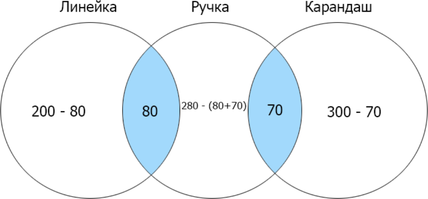
Отметим известные данные и посчитаем недостающее:
Затем складываем все данные, входящие в искомую область: (120+130+230+80+70=630).
Второй способ решения
Заметим, что по условию нам необходимо найти сумму всех найденных страниц по введенным запросам. Если мы сложим все отдельные значения найденных страниц, мы учтем по 2 раза каждое из двух пересечений. Таким образом, можем посчитать искомое по формуле: (линейка) + (ручка) + (карандаш) — (ручка & линейка) — (ручка & карандаш) (=300+200+280-80-70=630).
Ответ: 630
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{конверт}&100\
hline
text{книга}&200\
hline
text{журнал}&400\
hline
text{конверт | книга}&300\
hline
text{конверт} & text{журнал}&50\
hline
text{журнал} & text{книга}&60\
hline
end{array}]
Сколько страниц будет найдено по запросу (конверт | книга | журнал)?
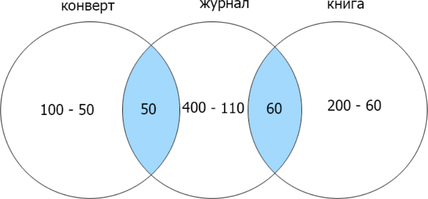
Заметим, что если сумма найденных страниц по каждому отдельному запросу равна их объедиению (операция «ИЛИ»), то их пересечение (операция «И») равно нулю. Т.к. сумма количества страниц, найденных по запросам конверт и книга = 300, а (конверт | книга) = 300, (конверт & книга) = 0. Теперь отобразим известные данные:
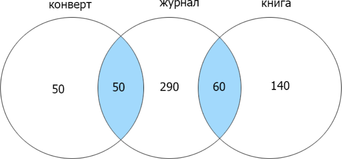
Отметим найденные данные и сложим каждую отдельную область для нахождения объедиения трех множеств:
(50+50+290+60+140=590).
Ответ: 590
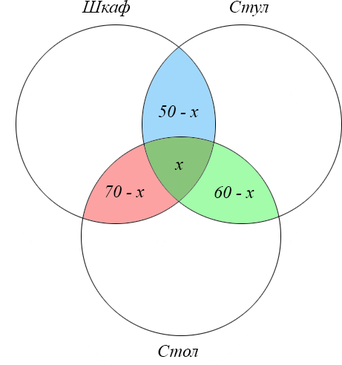
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{шкаф} & text{стул}&50\
hline
text{стул} & text{стол}&60\
hline
text{стол} & text{шкаф}&70\
hline
text{(шкаф} & text{стул) | (стул} & text{стол) | (стол} & text{шкаф)}&120\
hline
end{array}]
Сколько страниц будет найдено по запросу (шкаф & стул & стол)?
Обозначим искомую область за (x) и выразим данные через (x):
Из последней строки таблицы нам известно, что сумма всех отмеченных элементов равна 120. Значит, можем найти (x) через следующее уравнение:
((50-x)+(70-x)+(60-x)+x=120)
(180-2x=120)
(2x=60)
(x=30)
Ответ: 30
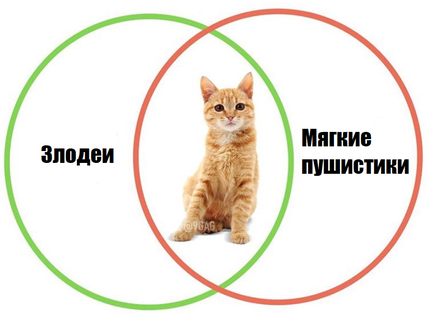
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{злодеи}&150\
hline
text{мягкие пушистики}&210\
hline
text{злодеи | мягкие пушистики}&300\
hline
end{array}]
Сколько страниц будет найдено по запросу кот, если известно, что коты находятся на пересечении множеств злодеев и мягких пушистиков?
Отметим искомую область:
Заметим, что кот = (злодеи & мягкие пушистики) = злодеи + пушистики — (злодеи | мягкие пушистики) = (150+210-300=60).
Ответ: 60
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
textbf{Запрос} & textbf{Найдено страниц (в тысячах)}\
hline
text{сок}&100\
hline
text{фрукты}&100\
hline
text{сахар | фрукты | сок}&300\
hline
text{сок | фрукты}&200\
hline
text{сок} ; & ; text{сахар}&20\
hline
text{сахар} ; & ; text{фрукты}&30\
hline
end{array}]
Сколько страниц будет найдено по запросу сахар?
Заметим, что если сумма найденных страниц по каждому отдельному запросу равна их объедиению (операция «ИЛИ»), то их пересечение (операция «И») равно нулю. Т.к.сумма количества страниц, найденных по запросам сок и фрукты = 200, а (сок | фрукты) = 200, (сок & фрукты) = 0. Теперь отобразим известные данные: 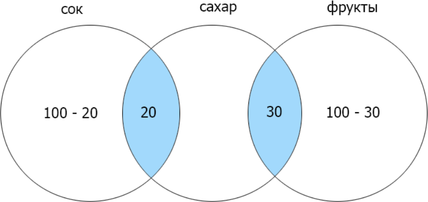
Ответ: 150

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Задание 17. Логические выражения и запросы для поисковых систем: Демоверсия егэ по информатике 2020: объяснение и решение
Разбор 17 задания. Демоверсия егэ по информатике 2020, ФИПИ:
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
| Запрос | Найдено страниц (в сотнях тысяч) |
|---|---|
| Поле | 54 |
| Пшеница | 40 |
| Напряжённость | 44 |
| Поле & Пшеница | 30 |
| Напряжённость & Поле | 14 |
| Напряжённость & Пшеница | 0 |
Какое количество страниц (в сотнях тысяч) будет найдено по запросу
Напряжённость | Поле | Пшеница?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
📹 Видеоразбор подобного 17 задания ЕГЭ
✍ Решение:
- Поскольку запрос Напряжённость & Пшеница возвращает значение 0, это значит, что в схеме кругов Эйлера-Вена два данных сектора пересекаться НЕ будут! Учитывая данный факт, отобразим круги Эйлера для решения, обозначив цифрами каждую составляющую:
- Получим значения отдельных секторов схемы, исходя из условий задачи:
1. №2 + №3 + №4 = 54 2. №4 + №5 = 40 3. №1 + №2 = 44 4. №4 = 30 5. №2 = 14
Искомый запрос: №1 + №2 +№3 + №4 + №5 = ?
44 + 54 + 40 - 14 - 30 = 94
Результат: 94
Сегодня разберём задачи на круги Эйлера в информатике.
Леонард Эйлер — швейцарский, немецкий и российский математик и механик, сыгравший огромную роль в развитии этих наук.
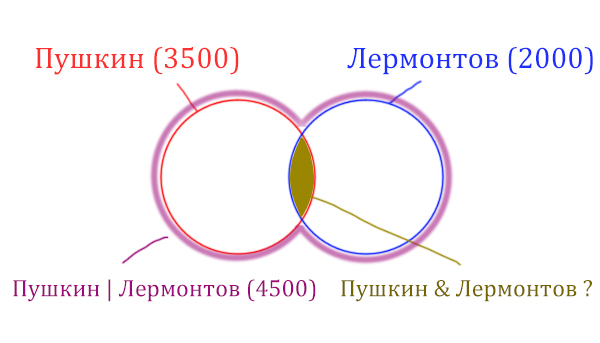
Задача (Простая)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Пушкин | 3500 |
| Лермонтов | 2000 |
| Пушкин | Лермонтов | 4500 |
Какое количество страниц (в тысячах) будет найдено по запросу Пушкин & Лермонтов? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
Видим, что по запросу «Пушкин» в поисковике нашлось 3500 страниц. По запросу «Лермонтов» — 2000 страниц.
Запрос «Пушкин | Лермонтов» обозначает, что поисковик выдаст страницы, где есть слова про «Пушкина», и страницы, где есть слова про «Лермонтова», а так же могут быть страницы, где написано и про «Пушкина», и про «Лермонтова» одновременно.
Если сложить страницы, в которых написано про «Пушкина» и про «Лермонтова» получается 3500 + 2000 = 5500 страниц. Но почему же при запросе «Пушкин | Лермонтов» получается меньше страниц, всего 4500 ?
Этот факт обозначает то, что когда мы подсчитывали страницы про «Пушкина» (3500 страниц), мы подсчитали и те страницы, где было написано и про «Пушкина», и про «Лермонтова» одновременно.
Тоже самое и для количества страниц, где написано про «Лермонтова» (2000 страниц). В этом числе находятся и те, в которых одновременно упоминается и про «Пушкина», и про «Лермонтова».
В вопросе спрашивается, сколько страниц будет по запросу «Пушкин & Лермонтов«. Это обозначает, что как раз нужно найти количество страниц, где будет одновременно написано и про «Пушкина», и про «Лермонтова».
Отсюда получается:
Пушкин & Лермонтов = (3500 + 2000) — 4500 = 5500 — 4500 = 1000 страниц.
Это и будет ответ!
Теперь решим эту задачу с помощью Кругов Эйлера!
У нас всего есть две сущности: «Пушкин» и «Лермонтов». Поэтому рисуем два пересекающихся круга, желательно разными цветами.
Объединение двух кругов в общую фигуру (показано фиолетовым цветом), показывает операцию «Пушкин | Лермонтов». Эта операция всегда стремится увеличить площадь, объединить площади других фигур!
Обратите внимание, что круги пересекаются, из-за этого сумма площадей двух кругов по отдельности (3500 + 2000 = 5500) больше чем у фигуры, которая характеризует логическую операцию «ИЛИ» «Пушкин | Лермонтов» (4500).
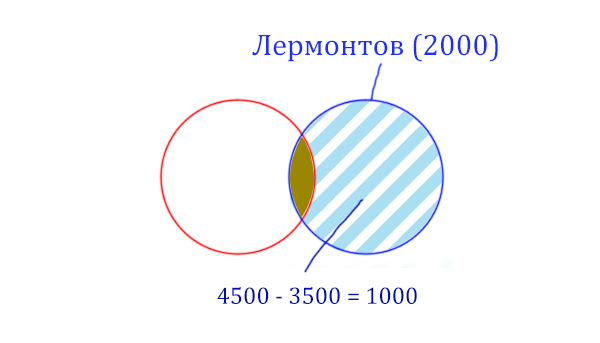
Нужно найти площадь фигуры Пушкин & Лермонтов, которая закрашена золотистым цветом. Данная логическая операция «И» стремится уменьшить площадь. Она обозначает общую площадь других фигур.
Найдём сначала заштрихованную часть синего круга. Она равна: площадь фиолетовой фигуры (4500) минус площадь красного круга (3500).
Теперь легко найти площадь золотистой фигуры. Для этого нужно от площади синего круга вычесть площадь заштрихованной части. Получается:
Пушкин & Лермонтов (Количество страниц) = 2000 — 1000 = 1000
Получается, что по запросу Пушкин & Лермонтов будет найдено 1000 страниц.
Ответ: 1000
Рассмотрим ещё одну не сложную разминочную задачу.
Задача (Разминочная)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Кокос | Ананас | 3400 |
| Кокос & Ананас | 900 |
| Кокос | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Ананас?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
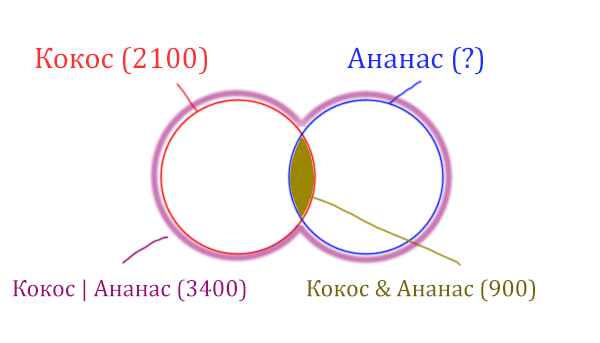
У нас две сущности: Кокос и Ананас. Нарисуем два круга Эйлера, которые пересекаются между собой. Так же отменим все имеющееся данные.
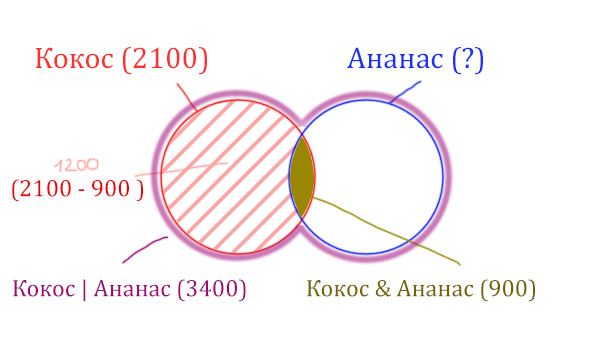
Найдём заштрихованную часть красного круга.
Весь красный круг 2100. Золотистая область равна 900. Заштрихованная часть равна 2100 — 900 = 1200.
После того, как нашли заштрихованную часть (такой полумесяц), можно найти уже площадь синего круга. Для этого нужно от площади фиолетовой фигуры отнять площадь заштрихованной части!
Ананас (Количество страниц) = 3400 — 1200 = 2200
Ответ: 2200
Разберём классическую задачу из информатики по кругам Эйлера.
Задача (Классическая)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| (Космос & Звезда) | (Космос & Планета) | 1100 |
| Космос & Планета | 600 |
| Космос & Планета & Звезда | 50 |
Какое количество страниц (в тыс.) будет найдено по запросу Космос & Звезда?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
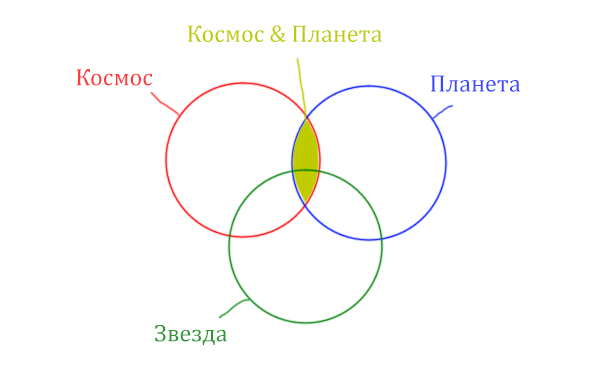
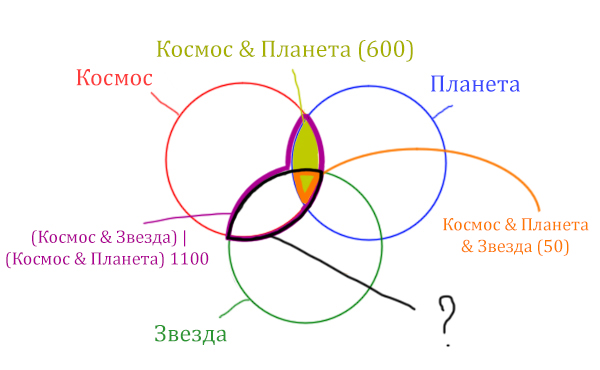
В этой задаче у нас три сущности: Космос, Планета, Звезда. Поэтому рисуем три круга Эйлера, которые пересекаются между собой.
Могут ли круги не пересекаться ? Могут! Если мы докажем, что площади по отдельности двух кругов в сумме дают площадь фигуры, которая получается при применении операции логического «ИЛИ».
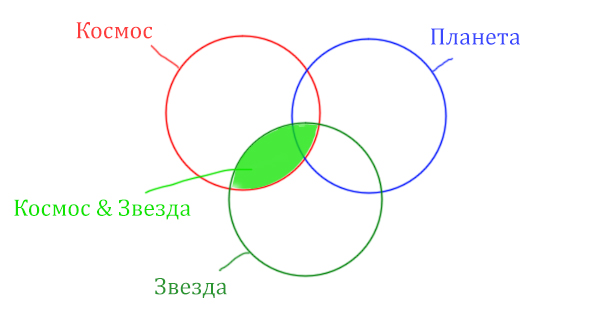
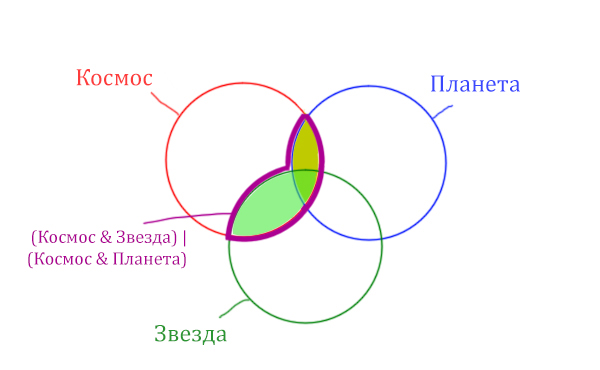
Теперь отметим на нашем рисунке запрос (Космос & Звезда) | (Космос & Планета).
Сначала отменим для себя то, что находится в скобках. Первое Космос & Звезда
Теперь отметим вторую скобку Космос & Планета.
В выражении (Космос & Звезда) | (Космос & Планета) две скобки соединяет знак логического «ИЛИ». Значит, эти две области нужно объединить! Область (Космос & Звезда) | (Космос & Планета) отмечена фиолетовым цветом!
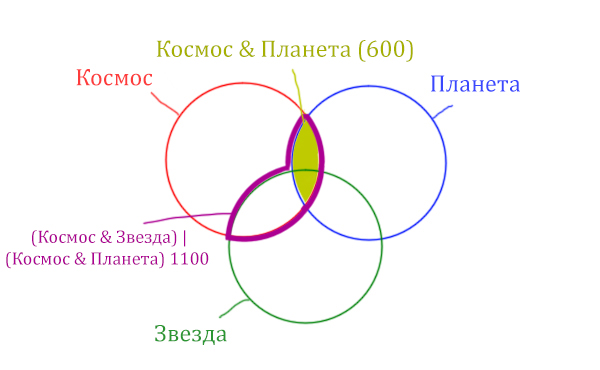
Отметим Космос & Планета ещё раз, т.к. для этого выражения известно количество страниц.
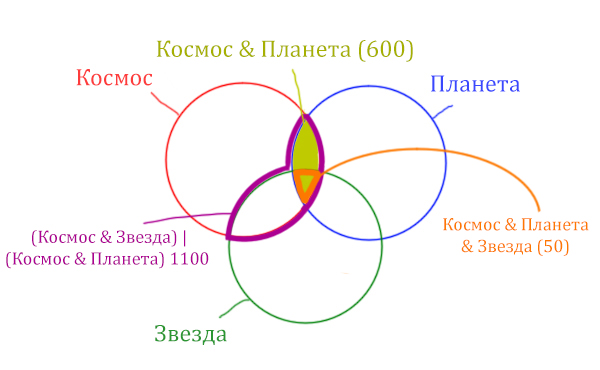
Площадь фигуры для выражения Космос & Планета & Звезда будет очень маленькая. Это общая часть для всех трёх кругов. Отметим её оранжевым цветом! Каждая точка этой фигуры должна одновременно быть в трёх кругах!
Найти нужно Космос & Звезда. Отменим на рисунке чёрным цветом ту область, которую нужно найти. Мы эту область уже отмечали салатовым цветом.
Теперь у нас есть все компоненты, чтобы решить эту задачу.
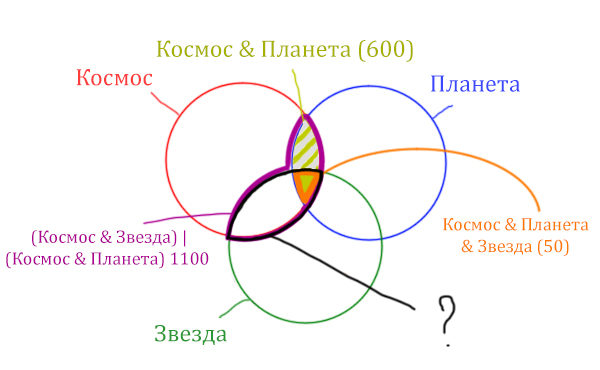
Найдём заштрихованную область.
Вся область Космос & Планета равна 600. А заштрихованная часть равна: область Космос & Планета (600) минус оранжевая область (50).
Количество страниц в заштрихованной части = 600 — 50 = 550
Тогда черная область легко находится: фиолетовая область (1100) минус заштрихованная область (550).
Количество страниц (при запросе Космос & Звезда) = 1100 — 550 = 550
Ответ: 550
Закрепляем материал по задачам на Круги Эйлера.
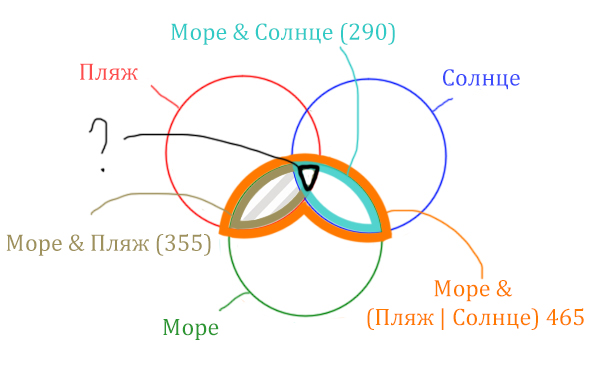
Задача (На закрепление)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
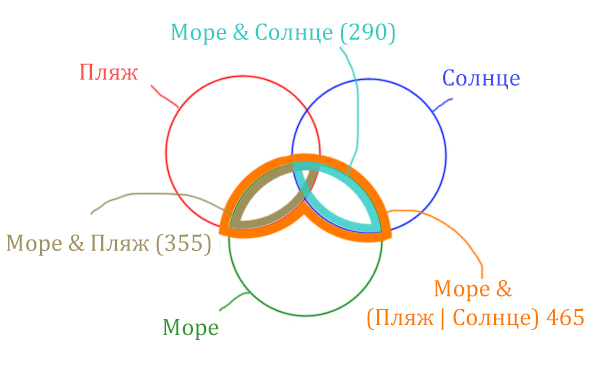
| Запрос | Найдено страниц (в тысячах) |
| Море & Солнце | 290 |
| Море & Пляж | 355 |
| Море & (Пляж | Солнце) | 465 |
Какое количество страниц (в тысячах) будет найдено по запросу Море & Пляж & Солнце? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
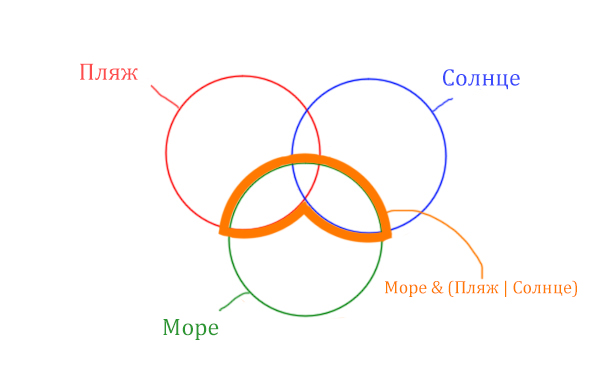
В задаче используются три сущности: Море, Пляж, Солнце. Поэтому нарисуем три пересекающихся круга Эйлера.
Отметим все области для которых нам даны количество страниц.
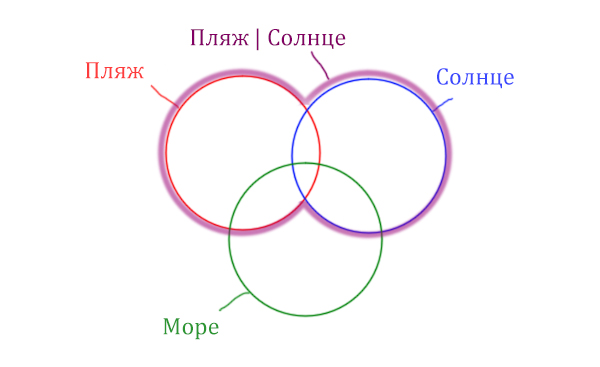
В начале отметим Море & (Пляж | Солнце). Для начало нарисуем область, которая в скобках (Пляж | Солнце)
Теперь нужно очертить общую часть фиолетовой области и зелёного круга и получится Море & (Пляж | Солнце). Отметим оранжевым цветом.
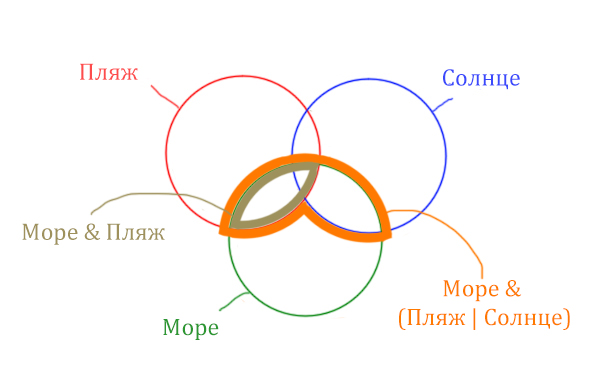
Теперь отметим Море & Пляж.
Теперь отметим Море & Солнце.
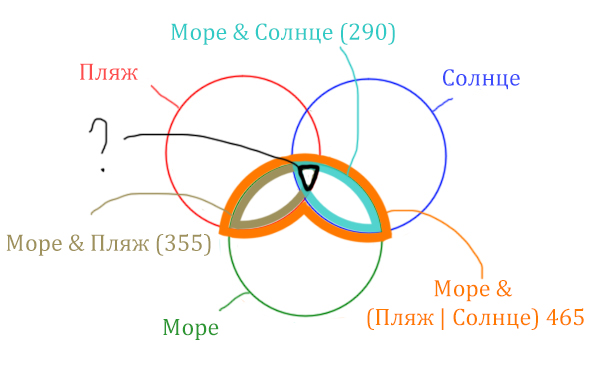
Найти нужно ту область, которая получается в результате выделения общей части для всех трёх кругов! Обозначим её чёрным цветом!
Найдём заштрихованную область!
Количество страниц (в заштрихованной области) =
= Количество страниц (В оранжевой области) — Море & Солнце =
= 465 — 290 = 175
Чтобы найти искомую чёрную область, нужно из Море & Пляж (355) вычесть заштрихованную область (175).
Количество страниц (Море & Пляж & Солнце) =
= Море & Пляж (355) — Количество страниц (в заштрихованной области) 175 =
= 355 — 175 = 180
Ответ: 180
Решим ещё одну тренировочную задачу из информатики на Круги Эйлера.
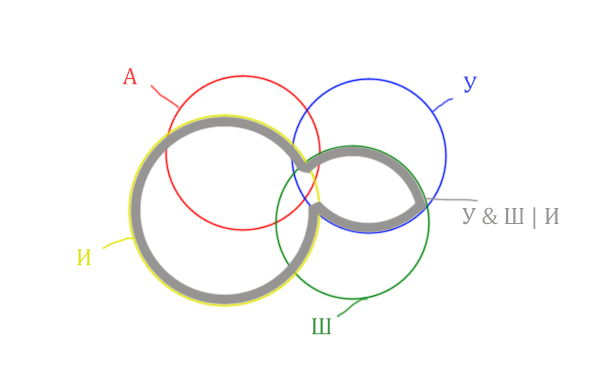
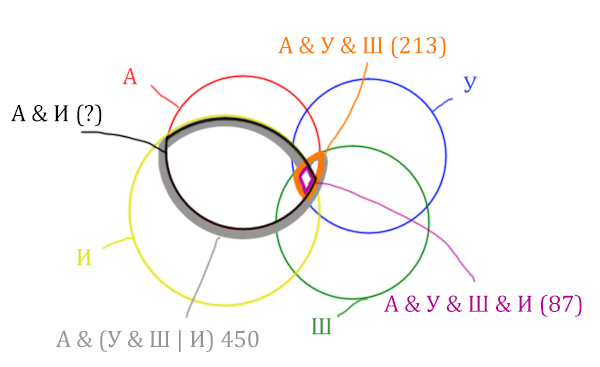
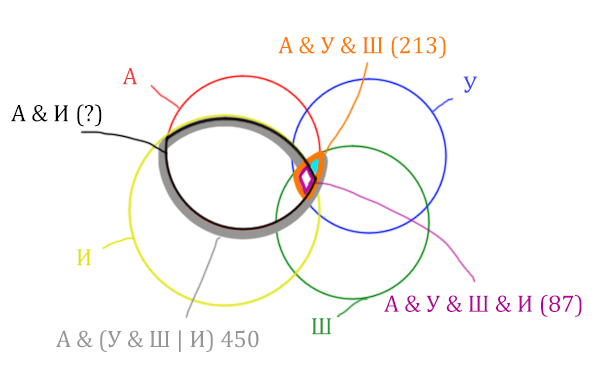
Задача (с 4 сущностями)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
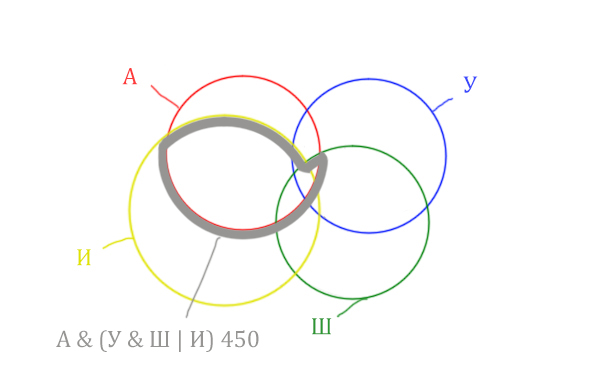
| Англия & (Уэльс & Шотландия | Ирландия) | 450 |
| Англия & Уэльс & Шотландия | 213 |
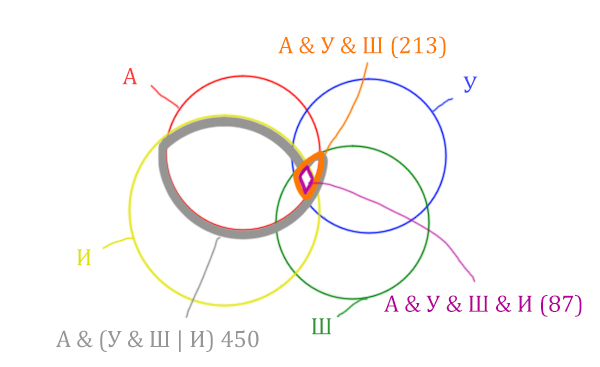
| Англия & Уэльс & Шотландия & Ирландия | 87 |
Какое количество страниц (в тысячах) будет найдено по запросу
Англия & Ирландия?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
Нужно нарисовать 4 пересекающихся круга. Сначала нарисуем три круга, как обычно, оставив немного места для четвёртого круга.
Четвёртый круг для Ирландии нужно нарисовать так, чтобы он проходил через область (Англия & Уэльс & Шотландия). Это нам подсказывает сама таблица, где есть количество страниц для Англия & Уэльс & Шотландия, а так же для Англия & Уэльс & Шотландия & Ирландия.
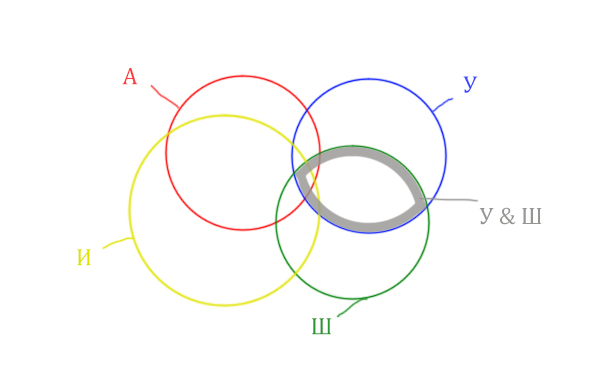
Нужно отметить на рисунке Англия & (Уэльс & Шотландия | Ирландия). Это будем делать, как всегда поэтапно.
Область Уэльс & Шотландия выглядит так:
Добавим к этой области Ирландию через логическое «ИЛИ». Получается область (Уэльс & Шотландия | Ирландия). Произошло объединение серой области и жёлтого круга!
Теперь нужно сделать операцию логического «И» получившийся области с «Англией». Тогда область Англия & (Уэльс & Шотландия | Ирландия) примет вид:
Т.е. это общее между предыдущем серым контуром и красным кругом!
Отметим Англия & Уэльс & Шотландия — это общая территория трёх кругов: Красного, Синего и Зелёного. Отмечено оранжевым цветом.
Отметим Англия & Уэльс & Шотландия & Ирландия — это общая территория четырёх кругов. Область получается ещё меньше. Если взять точку в этой области, то мы будем находится сразу в четырёх кругах одновременно. Отмечено фиолетовым цветом.
Отметим то, что нужно найти Англия & Ирландия чёрным цветом.
Искомую чёрную область легко найти, если из серой области вычесть кусочек, окрашенный в бирюзовый цвет!
Найдём, сколько страниц приходится на бирюзовый кусочек:
Количество страниц (для бирюзового кусочка) =
= Англия & Уэльс & Шотландия (213) — Англия & Уэльс & Шотландия & Ирландия (87) =
= 213 — 87 = 126
Найдём искомую чёрную область.
Количество станиц (для чёрной области) =
= Англия & (Уэльс & Шотландия | Ирландия) (450) — Количество (для бирюзового кусочка) =
450 — 126 = 324
Это и будет ответ!
Ответ: 324.
Разберём задачу из реального экзамена по информатике, которая была в 2019 году в Москве! (Сейчас в 2021 задачи не встречаются на Круги Эйлера)
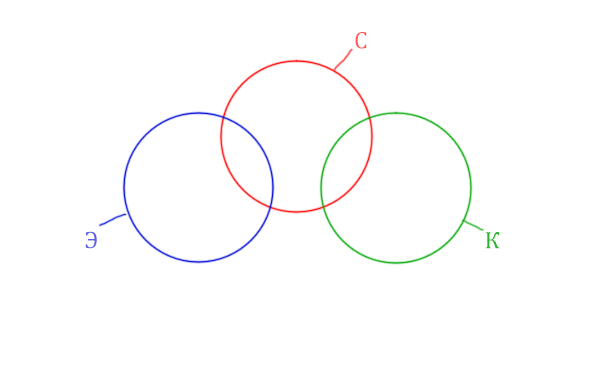
Задача (ЕГЭ по информатике, 2019, Москва)
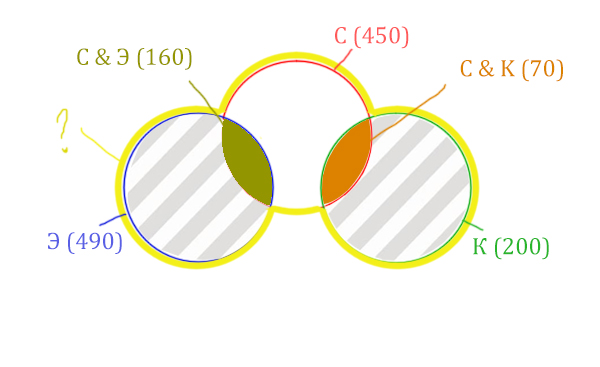
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Суфле | 450 |
| Корзина | 200 |
| Эклер | 490 |
| Суфле & Корзина | 70 |
| Суфле & Эклер | 160 |
| Корзина & Эклер | 0 |
Сколько страниц (в тысячах) будет найдено по запросу
Суфле | Корзина | Эклер
Решение:
Видим, что у нас три поисковых разных слова, поэтому будет три разных круга Эйлера!
Так же видим, что логическое «И» между словами Корзина и Эклер даёт 0 страниц. Это значит, что эти круги не пересекаются! Так же круги бы не пересекались, если бы операция логического «ИЛИ» совпадала бы с суммой этих кругов.
Видим, что Суфле имеет с двумя кругами пересечения, а Корзина и Эклер не пересекаются.
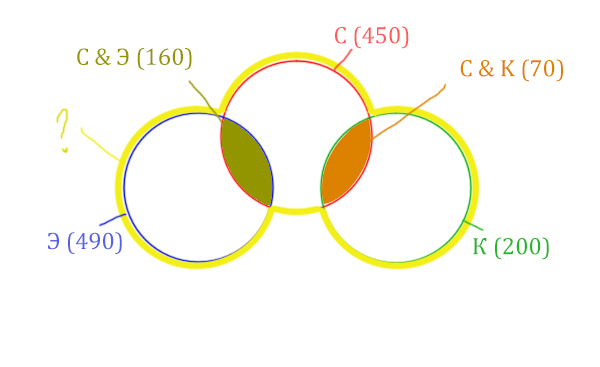
Отметим всё, что нам дано в условии.
Жёлтым цветом отмечено Суфле | Корзина | Эклер . Объединение всех трёх кругов. Это то, что нужно найти.
Искомая жёлтая фигура складывается из заштрихованных областей и красного круга! Площадь красного круга мы знаем. Нужно найти площади заштрихованных частей.
Левая заштрихованная область находится просто:
Количество страниц (лев. заштрих. область) =
= Эклер (490) — Суфле & Эклер (160) = 330
Так же найдём площадь правой заштрихованной области:
Количество страниц (прав. заштрих. область) =
= Корзина (200) — Суфле & Корзина (70) = 130
Теперь можно найти искомую жёлтую область
Количество страниц (Суфле | Корзина | Эклер) =
= Красный круг (450) + лев. заштрих. область (310) + прав. заштрих. область (130) =
= 450 + 330 + 130 = 910
Задача решена, можно писать ответ.
Ответ: 910
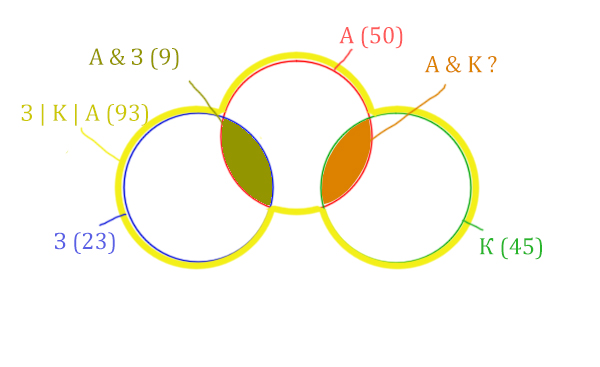
Разберём ещё одну задачу из реального ЕГЭ уже 2020 года
Задача (ЕГЭ по информатике, 2020, Москва)
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Аврора | 50 |
| Крейсер | 45 |
| Заря | 23 |
| Аврора & Заря | 9 |
| Заря & Крейсер | 0 |
| Заря | Крейсер | Аврора | 93 |
Сколько страниц (в тысячах) будет найдено по запросу
Аврора & Крейсер
Решение:
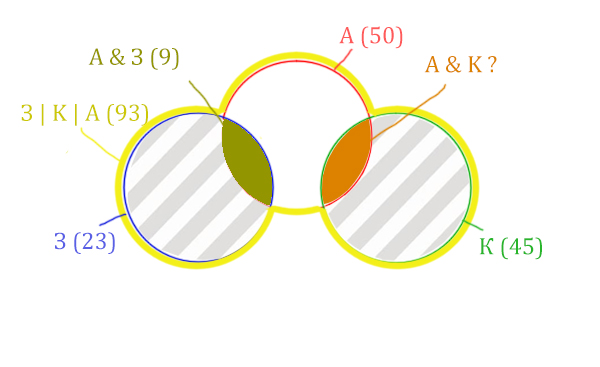
Количество страниц при запросе Заря & Крейсер равно нулю. Значит, эти два круга не будут пересекаться.
Нарисуем все данные на рисунке.
Нужно найти для начала заштрихованную правую часть.
Количество страниц (для двух заштрих. частей) =
З | К | А (93) — Красный круг (50) = 43
Левую заштрихованную область легко найти.
Количество страниц (для левой заштрих. части) =
Синий круг (23) — А & З (9) = 14
Тогда для правой заштрихованной области получается:
Колич. страниц (для правой заштрих. части) =
Колич. страниц (для двух заштрих. частей) (43) — Колич. страниц (для лев. заштрих. части) (14) =
= 43 — 14 = 29
Тогда искомую область легко найти:
Колич. страниц (А & K) =
Зелёный круг (45) — Колич. страниц (для правой заштрих. части) (29) =
45 — 29 = 16
Ответ: 16
На этом всё! Надеюсь, вы теперь будете с удовольствием решать задачи по информатике с помощью Кругов Эйлера.
Интересно…
как быть , когда идет произведение3 предметов + произведниее 3 педметов..
ОГРОМНОЕ СПАСИБО за Ваш труд!!! Всё очень понятно и доходчиво. +++++++++++++++
Перейти к контенту

Решение ГИА в форме ОГЭ по информатике 8 задание из демоверсии 2021 года. Задание на понимание принципов поиска информации в Интернете.
Давайте познакомимся с условием задания.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
Какое количество страниц (в тысячах) будет найдено по запросу Рыбка?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Ответ: 570.
По запросу Рыбак ИЛИ Рыбка могут появиться результаты одновременно — 780.
Рыбак И Рыбка, только Рыбак или только Рыбка — 50.
Запрос Рыбак — выдал 260.
По формуле включений и исключений имеем:
m(Рыбак | Рыбка ) = m(Рыбак) + m(Рыбка) — m(Рыбак & Рыбка),
780 = 260 + ? — 50.
Следовательно, m(Рыбка) = 780 + 50 — 260 = 570.
Ответ: 570.
Изменения структуры и содержания КИМ 2021 отсутствуют.
Программа формирующие задания, аналогичные демо ОГЭ 2021.
ПОДГОТОВКА К ОГЭ 2021 ПО ИНФОРМАТИКЕ. ПРОГРАММА «КОГЭ ТРЕНЕР»
Решение №1
Для решения данной задачи полезно воспользоваться визуализацией в виде кругов Эйлера. Разберём эту визуализацию подробнее.
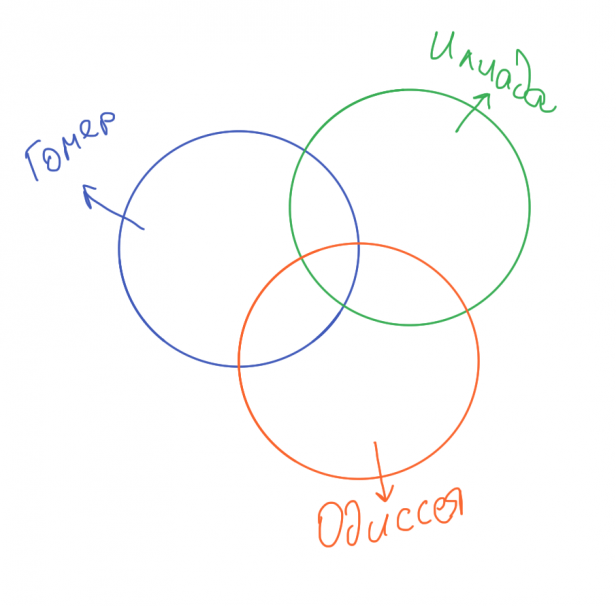
У нас имеются три разных слова в запросах:
- Гомер
- Илиада
- Одиссея
Обозначим страницы, в которых встречаются эти слова, за круги. При этом сделаем так, чтобы эти круги пересекались.
Круги Эйлера
Что нам известно по условию согласно таблице?
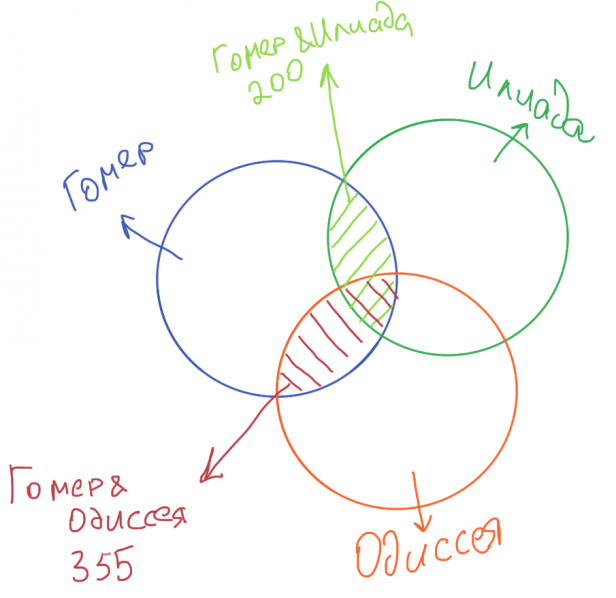
- Гомер & Илиада = 200. Что это означает?
- Что количество страниц, где встречаются одновременно слова и Гомер, и Илиада («и», так как используется &), равно 200.
- Что на рисунке соответствует таким страницам?
- Им соответствует область, которая лежит и в Гомере, и в Илиаде (см. светло-зелёную область).
- Теперь по аналогии отметим красным область Гомер & Одиссея:
- Теперь давайте разберём строку Гомер & (Одиссея | Илиада). Это пересечение двух областей, одна из которых понятна (Гомер). Давайте разберёмся со второй: Одиссея | Илиада.
- Одиссея | Илиада — это Одиссея или Илиада. То есть, это страницы, на которых есть или Одиссея, или Илиада, или обе. То есть, это — объединение Одиссеи и Илиады.
- Это объединение пересекается с Гомером в общих областях (см. картинку, розовый цвет).
- Что нам надо сосчитать? — Гомер & Одиссея & Илиада. То есть, пересечение всех трёх областей (маленький «псевдотреугольник» в центре).
- Давайте посмотрим внимательно, как мы его можем посчитать.
- Если мы в уме сложим области «Гомер & Одиссея» (бордовый) и «Гомер & Илиада» (зелёный), то получится, что мы охватили все пересечения (розовый), но при этом маленький треугольник мы посчитали два раза.
- То есть, если из суммы бордового и зелёного отнять розовый, получится как раз один маленький треугольничек (так как все области кроме него сократятся).
- Значит, Гомер & Одиссея & Илиада = 355 + 200 — 470 = 85
Ответ: 65 тысяч страниц.
Немного теории
17.1 17.2 17.3 17.4 17.5 17.6
17.1 (ege.yandex.ru-2) В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц(в тысячах) |
| Пушкин | 3500 |
| Лермонтов | 2000 |
| Пушкин |Лермонтов | 4500 |
Какое количество страниц (в тысячах) будет найдено по запросу
Пушкин & Лермонтов?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение: Через Ответ(Z) будем обозначать множество страниц, найденных по запросу Z, а через N(Z) – размер множества Ответ(Z), то есть количество страниц, найденных по запросу Z. В этих обозначениях множество Ответ(X&Y) — это пересечение множеств Ответ(X) и Ответ(Y), а множество Ответ(X | Y) – объединение Ответ(X) и Ответ(Y).
По запросу Пушкин |Лермонтов было найдено 4500 страниц. Среди них были страницы, содержавшие либо оба этих слова, либо только одно из них. Если сложить количество страниц, найденных по запросу Пушкин и количество страниц, найденных по запросу Лермонтов, то страницы, найденные по запросу Пушкин & Лермонтов будут учтены дважды. Поэтому верна формула:
N(Пушкин |Лермонтов) = N(Пушкин) + N(Лермонтов) –N(Пушкин & Лермонтов)
В соответствии с этой формулой и условием задачи получаем:
4500 = 3500+2000- N(Пушкин & Лермонтов)
N(Пушкин & Лермонтов) = 3500+2000-4500 = 1000
Ответ: 1000
Замечание. Приведенные рассуждения отражают следующий простой факт из теории множеств. Применительно к нашей задаче его можно записать так. Для любых запросов X и Y выполнено:
N(X | Y) = N(X)+N(Y) – N(X&Y)
17.2 (ege.yandex.ru-2) В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц(в тысячах) |
| Сербия&Хорватия | 500 |
| Сербия|Хорватия | 3000 |
| Сербия | 2000 |
Какое количество страниц (в тысячах) будет найдено по запросу
Хорватия?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение: Через Ответ(Z) будем обозначать множество страниц, найденных по запросу Z, а через N(Z) – размер множества Ответ(Z), то есть количество страниц, найденных по запросу Z. В этих обозначениях множество Ответ(X&Y) — это пересечение множеств Ответ(X) и Ответ(Y), а множество Ответ(X | Y) – объединение Ответ(X) и Ответ(Y).
По запросу Сербия|Хорватия было найдено 3000 страниц. Среди них были страницы, содержавшие либо оба этих слова, либо только одно из них. Если сложить количество страниц, найденных по запросу Сербия и количество страниц, найденных по запросу Хорватия, то страницы, найденные по запросу Сербия&Хорватия будут учтены дважды. Поэтому верна формула:
N(Сербия | Хорватия) = N(Сербия) + N(Хорватия) –N(Сербия & Хорватия)
В соответствии с этой формулой и условием задачи получаем:
3000 = 2000 + N(Хорватия) – 500
N(Хорватия) = 3000 – 2000 + 500 = 1500
Ответ: 1500
Замечание. Приведенные рассуждения отражают следующий простой факт из теории множеств. Применительно к нашей задаче его можно записать так. Для любых запросов X и Y выполнено:
N(X | Y) = N(X)+N(Y) – N(X&Y)
17.3 (ege.yandex.ru-3) В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц(в тысячах) |
| Швеция | 3200 |
| Финляндия | 2300 |
| Швеция&Финляндия | 100 |
Какое количество страниц (в тысячах) будет найдено по запросу
Швеция | Финляндия?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение: Через Ответ(Z) будем обозначать множество страниц, найденных по запросу Z, а через N(Z) – размер множества Ответ(Z), то есть количество страниц, найденных по запросу Z. В этих обозначениях множество Ответ(X&Y) — это пересечение множеств Ответ(X) и Ответ(Y), а множество Ответ(X | Y) – объединение Ответ(X) и Ответ(Y).
Нам нужно найти количество N(Швеция | Финляндия), найденных по запросу Швеция | Финляндия. Среди этих страниц есть страницы, содержащие оба этих слова, и страницы, содержащие только одно из них. Если сложить количество страниц, найденных по запросу Швеция и количество страниц, найденных по запросу Финляндия, то страницы, найденные по запросу Швеция&Финляндия будут учтены дважды. Поэтому верна формула:
N(Швеция | Финляндия) = N(Швеция) + N(Финляндия) –N(Швеция&Финляндия)
В соответствии с этой формулой и условием задачи получаем:
N(Швеция | Финляндия) = 3200 + 2300 – 100
N(Швеция | Финляндия) = 5400
Ответ: 5400
Замечание. Приведенные рассуждения отражают следующий простой факт из теории множеств. Применительно к нашей задаче его можно записать так. Для любых запросов X и Y выполнено:
N(X | Y) = N(X)+N(Y) – N(X&Y)
17.4 (ege.yandex.ru-4) В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц(в тысячах) |
| Сербия&Хорватия | 650 |
| Сербия|Хорватия | 3100 |
| Хорватия | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу
Сербия?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение: Через Ответ(Z) будем обозначать множество страниц, найденных по запросу Z, а через N(Z) – размер множества Ответ(Z), то есть количество страниц, найденных по запросу Z. В этих обозначениях множество Ответ(X&Y) — это пересечение множеств Ответ(X) и Ответ(Y), а множество Ответ(X | Y) – объединение Ответ(X) и Ответ(Y).
По запросу Сербия|Хорватия было найдено 3000 страниц. Среди них были страницы, содержавшие либо оба этих слова, либо только одно из них. Если сложить количество страниц, найденных по запросу Сербия и количество страниц, найденных по запросу Хорватия, то страницы, найденные по запросу Сербия&Хорватия будут учтены дважды. Поэтому верна формула:
N(Сербия | Хорватия) = N(Сербия) + N(Хорватия) –N(Сербия &∓ Хорватия)
В соответствии с этой формулой и условием задачи получаем:
3100 = N(Сербия) + 2100 – 650
N(Сербия) = 3100 – 2100 + 650 = 1650
Ответ: 1650
Замечание. Приведенные рассуждения отражают следующий простой факт из теории множеств. Применительно к нашей задаче его можно записать так. Для любых запросов X и Y выполнено:
N(X | Y) = N(X)+N(Y) – N(X&Y)
17.5 (ege.yandex.ru-5) В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
|
Запрос |
Найдено страниц (в тысячах) |
|
Байрон &Пушкин |
330 |
|
Байрон &Лермонтов |
220 |
|
Байрон &(Пушкин |Лермонтов) |
440 |
Какое количество страниц (в тысячах) будет найдено по запросу
Байрон &Пушкин & Лермонтов?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение: Через Ответ(Z) будем обозначать множество страниц, найденных по запросу Z, а через N(Z) – размер множества Ответ(Z), то есть количество страниц, найденных по запросу Z. В этих обозначениях множество Ответ(X&Y) — это пересечение множеств Ответ(X) и Ответ(Y), а множество Ответ(X | Y) – объединение Ответ(X) и Ответ(Y).
Заметим, что во всех запросах рассматриваются только страницы, содержащие слово Байрон. Поэтому ниже мы при обозначении запросов для краткости будем опускать это слово. Можно считать, что поиск ведется по запросам, в которых упоминаются только Пушкин и Лермонтов, но область поиска ограничена страницами, которые содержат слово Байрон.
В новых обозначениях, по запросу Пушкин |Лермонтов найдено 440 страниц.Среди этих страниц есть страницы, содержащие оба этих слова, и страницы, содержащие только одно из них. Если сложить количество страниц, найденных по запросу Пушкин и количество страниц, найденных по запросу Лермонтов, то страницы, найденные по запросу Пушкин & Лермонтов будут учтены дважды. Поэтому верна формула:
N(Пушкин |Лермонтов) = N(Пушкин) + N(Лермонтов) –N(Пушкин & Лермонтов)
В соответствии с этой формулой и условием задачи получаем:
440 = 330+220- N(Пушкин & Лермонтов)
N(Пушкин & Лермонтов) = 330+220-440 = 110
Ответ: 110
Замечание. Приведенные рассуждения отражают следующий простой факт из теории множеств. Применительно к нашей задаче его можно записать так. Для любых запросов X, Yи Zвыполнено:
N(X | Y) = N(X)+N(Y) – N(X&Y)
N(Z & (X | Y) )= N(Z & X)+N(Z & Y) – N(Z & X&Y)
17.6 (ege.yandex.ru-3) В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц(в тысячах) |
| Швеция&Норвегия | 330 |
| Финляндия&Норвегия | 255 |
| Швеция&Финляндия&Норвегия | 220 |
Какое количество страниц (в тысячах) будет найдено по запросу
Швеция&Норвегия | Финляндия&Норвегия ?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение: Запрос (Швеция & Норвегия) | (Финляндия & Норвегия) можно переписать в виде
(Швеция | Финляндия) & Норвегия
Таким образом, во всех запросах рассматриваются только страницы, содержащие слово Норвегия. Поэтому ниже мы при обозначении запросов для краткости будем опускать это слово. Можно считать, что поиск ведется по запросам, в которых упоминаются Швеция и Финляндия, но область поиска ограничена страницами, которые содержат слово Норвегия. Поэтому далее мы слово «Норвегия» при описании запросов будем опускать.
Пусть N(Z) обозначает количество страниц, найденных по запросу Z. Для любых двух запросов Z1 и Z2 выполнено:
N(Z1 | Z2) = N(Z1) + N(Z2) – N(Z1&Z2)
(при подсчете страниц, которые содержат текст Z1 или текст Z2 путем сложения N(Z1) и N(Z2) мы учитываем страницы, содержащие оба текста дважды).
Поэтому (подсчет ведется в тысячах страниц)
N(Швеция | Финляндия) = N(Швеция) + N(Финляндия) — N(Швеция & Финляндия) = 330+255-220 = 365
Ответ: 365