Задание 1
Основания равнобедренной трапеции равны 45 и 14. Высота трапеции равна 9,3. Найдите тангенс острого угла.
Ответ: 0,6
Скрыть
Задание 2
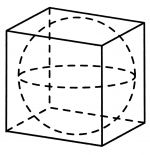
Прямоугольный параллелепипед описан около сферы радиуса 2,5. Найдите площадь его поверхности.
Ответ: 150
Скрыть
Задание 3
Рассмотрим случайный телефонный номер. Какова вероятность того, что среди трёх последних цифр этого номера хотя бы две цифры одинаковы?
Ответ: 0,28
Скрыть
Задание 4
Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью 0,34. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Ответ: 0,17
Скрыть
Задание 5
Найдите корень уравнения $$sqrt{frac{50}{5x+45}}=1frac{1}{4}$$
Ответ: -2,6
Скрыть
Задание 6
Найдите значение выражения $$2^{12log_{8}5}$$
Ответ: 625
Скрыть
Задание 7
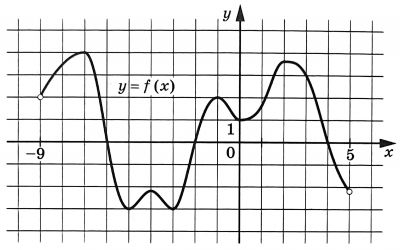
На рисунке изображён график функции $$y=f(x)$$, определённой на интервале $$(-9;5)$$. Найдите сумму точек экстремума функции $$f(x)$$.
Ответ: -18
Скрыть
Задание 8
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 217 МГц. Скорость погружения батискафа $$v$$ вычисляется по формуле $$v=ccdotfrac{f-f_{0}}{f+f_{0}}$$ где $$c=1500$$ м/с — скорость звука в воде, $$f_{0}$$ — частота испускаемых импульсов, $$f$$ — частота отражённого от дна сигнала, регистрируемая приёмником (в МГц). Определите частоту отражённого сигнала в МГц, если скорость погружения батискафа равна 12 м/с.
Ответ: 220,5
Скрыть
Задание 9
Боря и Ваня могут покрасить забор за 10 часов. Ваня и Гриша могут покрасить этот же забор за 15 часов, а Гриша и Боря — за 18 часов. За сколько часов мальчики покрасят забор, работая втроём?
Ответ: 9
Скрыть
Задание 10
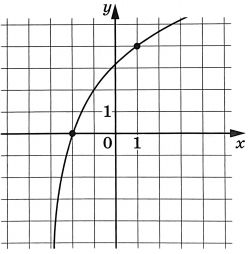
На рисунке изображён график функции $$f(x)=log_{a}(x+3)$$. Найдите значение $$x$$, при котором $$f(x)=16$$.
Ответ: 253
Скрыть
Задание 11
Найдите наименьшее значение функции $$y=e^{2x}-9e^{x}-3$$ на отрезке $$[0; 3]$$.
Ответ: -23,25
Скрыть
Задание 12
а) Решите уравнение $$2sin xcdot sin 2x=2cos x+cos 2x$$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[-frac{5pi}{2};pi]$$.
Ответ: а) $$frac{pi}{4}+frac{pi n}{2};$$$$-frac{2pi}{3}+2pi m;$$$$frac{2pi}{3}+2pi k,$$$$m,n,kin Z$$ б)$$-frac{9pi}{4};-frac{7pi}{4};-frac{4pi}{3};-frac{5pi}{4}$$
Скрыть
Задание 13
Грань ABCD прямоугольного параллелепипеда $$ABCDA_1B_1C_1D_1$$ является вписанной в основание конуса, а сечением конуса плоскостью $$A_1B_1C_1$$ является круг, вписанный в четырёхугольник $$A_1B_1C_1D_1$$: $$AB=a$$, $$AA_1=sqrt{2}$$.
а) Высота конуса равна $$h$$. Докажите, что $$4,5a<h<5a$$.
б) Найдите угол между плоскостями $$ABC$$ и $$SD_1C_1$$, где $$S$$ — вершина конуса.
Ответ: $$arctg(2sqrt{6}+2sqrt{3})$$
Скрыть
Задание 14
Решите неравенство $$log_{5}x^{2}+4log_{25}(6-2x)geqlog_{sqrt{5}}(x^{2}-4)+2log_{0,2}(2-x)$$.
Ответ: $$(-infty;-2)$$
Скрыть
Задание 15
В июле Анна планирует взять кредит на 3 года на целое число миллионов рублей. Два банка предложили Анне оформить кредит на следующих условиях:
— в январе каждого года действия кредита долг увеличивается на некоторое число процентов (ставка плавающая — может быть разным для разных годов);
— в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
В первом банке процентная ставка по годам составляет 10, 20 и 15 процентов соответственно, а во втором — 15, 10 и 20 процентов. Анна выбрала наиболее выгодное предложение. Найдите сумму кредита, если эта выгода по общим выплатам по кредиту составила от 14 до 15 тысяч рублей.
Ответ:
Задание 16
На сторонах $$AB$$ и $$CD$$ четырёхугольника $$ABCD$$, около которого можно описать окружность, отмечены точки $$K$$ и $$N$$ соответственно. Около четырёхугольников $$AKND$$ и $$BCNK$$ также можно описать окружность. Косинус одного из углов четырёхугольника $$ABCD$$ равен 0,2.
а) Докажите, что прямые $$KN$$ и $$AD$$ параллельны.
б) Найдите радиус окружности, описанной около четырёхугольника $$BCNK$$, если радиус окружности, описанной около четырёхугольника $$ABCD$$, равен 7, $$AK:KB=9:10$$, a $$BC<AD$$ и $$BC=10$$.
Ответ: $$frac{5sqrt{22}}{4}$$
Скрыть
Задание 17
Найдите все такие значения $$a$$, при каждом из которых уравнение $$sqrt{10x^{2}-19x-15}cdotlog_{3}(7-(a-4)cdot(x+2))$$ имеет ровно два различных корня.
Ответ: $$4;[frac{16}{3};frac{50}{9});(frac{58}{7};9)$$
Скрыть
Задание 18
Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 7 раз больше, либо в 7 раз меньше предыдущего. Сумма всех членов последовательности равна 7735.
а) Может ли последовательность состоять из трёх членов?
б) Может ли последовательность состоять из шести членов?
в) Какое наибольшее количество членов может быть в последовательности?
Ответ: а)нет б)нет в)1933
Скрыть
Основания равнобедренной трапеции равны 45 и 14. Высота трапеции равна 9,3. Найдите тангенс острого угла.
Прямоугольный параллелепипед описан около сферы радиуса 2,5. Найдите площадь его поверхности.
Рассмотрим случайный телефонный номер. Какова вероятность того, что среди трёх последних цифр этого номера хотя бы две цифры одинаковы?
Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,34. Шахматисты А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Найдите корень уравнения (sqrt{dfrac{50}{5x+45}}=1dfrac14)
Найдите значение выражения (2^{12log_85})
На рисунке изображен график функции y=f(x), определенной на интервале (-9;5). Найдите сумму точек экстремума функции f(x).
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 217 МГц. Скорость погружения батискафа (v) вычисляется по формуле (v=ccdotdfrac{f-f_0}{f+f_0}), где (c=1500) м/с – скорость звука в воде, (f_0) – частота испускаемых импульсов, (f) – частота отраженного от дна сигнала, регистрируемая приемником (в МГц). Определите частоту отраженного сигнала в МГц, если скорость погружения батискафа равна 12 м/с.
Боря и Ваня могут покрасить забор за 10 часов. Ваня и Гриша могут покрасить этот же забор за 15 часов, а Гриша и Боря – за 18 часов. За сколько часов мальчики покрасят забор, работая втроём?
На рисунке изображен график функции (f(x)=log_a(x+3)). Найдите значение (x), при котором (f(x)=16)
Найдите наименьшее значение функци (y=e^{2x}-9e^x-3) на отрезке [0;3].
а) Решите уравнение (2sin xcdotsin2x=2cos x+cos2x)
б) Укажите все корни этого уравнения, принадлежащие отрезку (left[-dfrac{5pi}{2};-piright])
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4.π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -5π/2 | 18. -7π/3 | 19. -9π/4 | 20. -13π/6 |
| 21. -2π | 22. -11π/6 | 23. -7π/4 | 24. -5π/3 |
| 25. -3π/2 | 26. -4π/3 | 27. -5π/4 | 28. -7π/6 |
| 29. -π |
Грань ABCD прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ является вписанной в основание конуса, а сечением конуса плоскостью A₁B₁C₁ является круг, вписанный в четырехугольник A₁B₁C₁D₁; AB=a, AA₁=√2a.
а) Высота конуса равна h. Докажите, что 4,5a< h< 5a.
б) Найдите угол между плоскостями ABC и SD₁C, где S – вершина конуса.
Решите неравенство (log_5x^2+4log_{25}(6-2x)geqslantlog_{sqrt5}(x^2-4)+2log_{0{,}2}(2-x))
В июле Анна планирует взять кредит на 3 года на целое число миллионов рублей. Два банка предложили Анне оформить кредит на следующих условиях:
– в январе каждого года действия кредита долг увеличивается на некоторое число процентов (ставка плавающая – может быть разным для разных годов);
– в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причем последний платеж должен погасить долг по кредиту полностью.
В первом банке процентная ставка по годам составляет 10, 20 и 15 процентов соответственно, а во втором – 15, 10 и 20 процентов. Анна выбрала наиболее выгодное предложение. Найдите сумму кредита, если эта выгода по общим выплатам по кредиту составила от 14 до 15 тысяч рублей. В ответ запишите количество миллионов.
На сторонах AB и CD четырёхугольника ABCD, около которого можно описать окружность, отмечены точки K и N соответственно. Около четырёхугольников AKND и BCNK также можно описать окружность. Косинус одного из углов четырёхугольника ABCD равен 0,2.
а) Докажите, что прямые KN и AD параллельны.
б) Найдите радиус окружности, описанной около четырёхугольника BCNK, если радиус окружности, описанной около четырёхугольника ABCD, равен 7, AK:KB=9:10, а BC< AD и BC=10.
Найдите все такие значения (a), при каждом из которых уравнение (sqrt{10x^2-19x-15}cdotlog_3(7-(a-4)(x+2))=0) имеет ровно два различных корня.
Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 7 раз больше, либо в 7 раз меньше предыдущего. Сумма всех членов последовательности равна 7735.
а) Может ли последовательность состоять из трёх членов?
б) Может ли последовательность состоять из шести членов?
в) Какое наибольшее количество членов может быть в последовательности?
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.
Решение и ответы заданий № 1–12 варианта №10 из сборника ЕГЭ 2021 по математике (профильный уровень) И.В. Ященко. ГДЗ профиль для 11 класса.
Задание 1.
Для приготовления маринада для огурцов на 1 литр воды требуется 15 г лимонной кислоты. Лимонная кислота продаётся в пакетиках по 10 г. Анна Петровна собирается законсервировать четыре 3-литровые банки огурцов. В 3-литровых банках огурцы обычно занимают 60 % объёма, остальное – маринад. Какое наименьшее число пакетиков лимонной кислоты нужно купить Анне Петровне?
Задание 2.
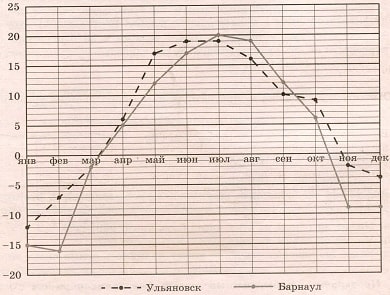
На рисунке показано изменение средней температуры за каждый месяц 2019 года в Ульяновске и Барнауле. По горизонтали указаны месяцы, по вертикали – значение температуры в градусах Цельсия. Определите по рисунку, на сколько градусов средняя температура февраля в Ульяновске была выше соответствующей температуры в Барнауле. Ответ дайте в градусах Цельсия.
Задание 3.
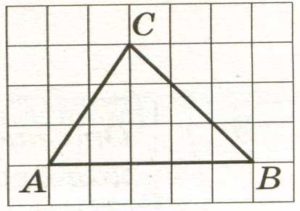
На клетчатой бумаге с размером клетки 1х1 изображён треугольник АВС. Найдите длину его средней линии, параллельной стороне АВ.
Задание 4.
В магазине в одной коробке лежат вперемешку ручки с чёрными, синими или красными чернилами одинаковые на вид. Покупатель случайным образом выбирает одну ручку. Вероятность того, что она окажется чёрной, равна 0,37, а того, что она окажется синей, равна 0,45. Найдите вероятность того, что ручка окажется красной.
Задание 5.
Найдите корень уравнения (х – 11)4 = (х + 3)4.
Задание 6.
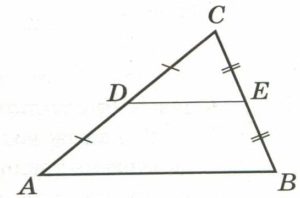
В треугольнике АВС средняя линия DЕ параллельна стороне АВ. Найдите площадь треугольника АВС, если площадь трапеции АВЕD равна 48.
Задание 7.
Материальная точка движется прямолинейно по закону х(t) = 
t3 – 2t2 + 6t + 25, где за x – расстояние от точки отсчёта в метрах, t – время в секундах, прошедшее с момента начала движения. Найдите её скорость (в метрах в секунду) в момент времени t = 4.
Задание 8.
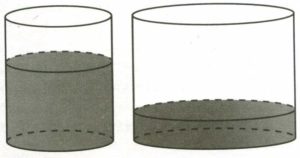
В цилиндрическом сосуде уровень жидкости достигает 25 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2,5 раза больше диаметра первого? Ответ дайте в сантиметрах.
Задание 9.
Найдите значение выражения
Задание 10.
Водолазный колокол, содержащий v = 2 моль воздуха при давлении p1 = 2,4 атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления p2 в атмосферах. Работа, совершаемая водой при сжатии воздуха, вычисляется по формуле ‚ где α = 13,5 Дж/моль·К – постоянная, Т = 300 К – температура воздуха. Найдите, какое давление p2 будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 16200 Дж. Ответ дайте в атмосферах.
Задание 11.
Первая труба заполняет резервуар объёмом 440 литров на 4 минуты медленнее, чем вторая труба заполняет резервуар объёмом 396 литров. Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба?
Задание 12.
Найдите точку минимума функции y = (x + 
2·e– x – 3
Источник варианта: Сборник ЕГЭ 2021 по математике профильный уровень. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 1 / 5. Количество оценок: 1
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Канал видеоролика: Ломоносов клуб
Смотреть видео:
#математикаогэ #гвэ #егэответы #числа #математика #алгебра #подготовкакогэ #ответы_огэ #подготовкакегэ
Свежая информация для ЕГЭ и ОГЭ по Математике (листай):
С этим видео ученики смотрят следующие ролики:
1 вариант ЕГЭ Ященко 2023 математика профильный уровень
Ломоносов клуб
2 вариант ЕГЭ Ященко 2023 математика профильный уровень
Ломоносов клуб
3 вариант ЕГЭ Ященко 2023 математика профильный уровень
Ломоносов клуб
4 вариант ЕГЭ Ященко 2023 математика профильный уровень
Ломоносов клуб
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
21.12.2022
Ответы к 36 вариантам профильного ЕГЭ по математике. Сборник ЕГЭ-2023 «Типовые экзаменационные варианты».
Вариант 1
1) 5,5
2) 2048
3) 0,06
4) 0,89
5) -0,2
6) 0,5
7) 5
5,832
9) 2
10) -4
11) -2910
Вариант 2
1) 7,5
2) 4
3) 0,12
4) 0,91
5) -0,9
6) 0,2
7) 1
0,216
9) 16
10) -8
11) 12,25
Вариант 3
1) 2,5
2) 30
3) 0,37
4) 0,375
5) -2,5
6) 4
7) 2
51,2
9) 14
10) 32
11) 204
Вариант 4
1) 1,5
2) 12
3) 0,24
4) 0,125.
5) 0,375
6) 125
7) 8
281,25
9) 18
10) -56
11) -10,9
Вариант 5
1) 99,5
2) 12
3) 0,004 /или/ -0,004
4) 0,9409
5) -0,5
6) 2
7) -19
60
9) 17
10) 16
11) -52
Вариант 6
1) 55
2) 18
3) 0,006 /или/ -0,006
4) 0,8464
5) -5,5
6) 3
7) -4
30
9) 24
10) -1
11) -6
Вариант 7
1) 0,2
2) 10
3) 0,2
4) 0,56
5) -0,4
6) -1
7) 9
0,6
9) 55
10) 6
11) 0,5
Вариант 8
1) 0,4
2) 5
3) 0,125
4) 0,46
5) -7
6) -1
7) 7
1,8
9) 11
10) 0,25
11) 17
Вариант 9
1) 3
2) 15 625
3) 0,01
4) 0,28
5) -12
6) 144
7) -1
756
9) 20
10) -3
11) 9
Вариант 10
1) 0,6
2) 150
3) 0,28
4) 0,17
5) -2,6
6) 625
7) -18
220,5
9) 9
10) 253
11) -23,25
Вариант 11
1) -0,7
2) 72
3) 0,25
4) 0,043
5) -0,2
6) -5
7) -1
50
9) 17,5
10) 78
11) 6,75
Вариант 12
1) 0,75
2) 24
3) 0,55
4) 0,02
5) -1,5
6) -4
7) 4
40
9) 13,5
10) -23
11) 6,25
Вариант 13
1) 8
2) 48
3) 0,4
4) 0,6
5) -9
6) 0,5
7) 4
33
9) 9
10) -0,5
11) 77
Вариант 14
1) 14
2) 40,5
3) 0,28
4) 0,78
5) -2
6) 0,04
7) 39
23
9) 24
10) 0,4
11) 37
Вариант 15
1) 11,55
2) 432
3) 0,014
4) 0,06
5) -9
6) 0,25
7) 2
0,32
9) 3
10) 2,5
11) 208
Вариант 16
1) 12
2) 192
3) 0,29
4) 0,02
5) -8
6) 0,125
7) 4
1,16
9) 1
10) -15
11) 5
Вариант 17
1) 10
2) 80
3) 0,08
4) 0,2
5) -2,5
6) 216
7) -2
175
9) 18
10) 16
11) -24
Вариант 18
1) 35
2) 10
3) 0,2
4) 0,24
5) -0,2
6) 3,5
7) 28
43,75
9) 21
10) 2,25
11) -15
Вариант 19
1) 2,5
2) 7,28
3) 0,25
4) 0,22
5) -1,5
6) 1
7) 0,2
115
9) 135
10) 2
11) -34
Вариант 20
1) 6
2) 7,68
3) 0,75
4) 0,27
5) -4,5
6) 10
7) -0,25
220
9) 52
10) 27
11) 0
Вариант 21
1) 113
2) 60
3) 0,2
4) 0,973
5) 5,5
6) 324
7) 2
6250
9) 14
10) 15
11) 7
Вариант 22
1) 0,75
2) 45
3) 0,3
4) 0,9744
5) 11
6) -7,5
7) 7
1,3
9) 5
10) 3,4
11) 1,2
Вариант 23
1) 62
2) 25
3) 0,25
4) 0,3
5) -2
6) 80
7) 6
60
9) 75
10) 28
11) 18
Вариант 24
1) 78
2) 20
3) 0,2
4) 0,82
5) 0
6) 28
7) 6
30
9) 10
10) -28
11) -2
Вариант 25
1) 37
2) 135
3) 0,18
4) 3
5) 0,8
6) 0,4
7) -0,2
6
9) 1 35
10) -0,4
11) 14
Вариант 26
1) 53
2) 72
3) 0,38
4) 5
5) -4
6) -0,3
7) -0,75
96
9) 28
10) -13
11) 1
Вариант 27
1) 29
2) 315
3) 0,14
4) 0,03
5) 4
6) 2,72
7) 6
7
9) 77
10) 76
11) -3
Вариант 28
1) 6
2) 176
3) 0,375
4) 0,012
5) -1
6) -3
7) -3
28
9) 6
10) -5
11) 38
Вариант 29
1) 60
2) 18
3) 0,24
4) 0,2
5) 3
6) 4
7) 4
6,5
9) 6,4
10) 67
11) -21
Вариант 30
1) 64
2) 4
3) 0,28
4) 0,6
5) 4
6) 8
7) 14
9,6
9) 22
10) 3
11) -8
Вариант 31
1) 6,5
2) 54
3) 0,98
4) 0,2
5) 2
6) -10
7) 2
25
9) 54
10) -7
11) 8
Вариант 32
1) 30
2) 27
3) 0,024
4) 0,15
5) -2
6) 91
7) 3
17
9) 12
10) 13
11) -9
Вариант 33
1) 72,5
2) 47
3) 0,28
4) 0,097
5) -5
6) 65
7) 3
8
9) 48
10) -2,5
11) 26
Вариант 34
1) 68
2) 76
3) 0,16
4) 0,068
5) 6
6) 16
7) 6
633
9) 64
10) -0,25
11) -1
Вариант 35
1) 21
2) 200
3) 0,56
4) 0,9
5) -2
6) 7,5
7) 0,5
0,31
9) 20
10) 0,75
11) 9
Вариант 36
1) 35
2) 88
3) 0,12
4) 12
5) -5
6) 2,5
7) 5,5
1,728
9) 756
10) -0,5
11) 30
Наверх
Скачать бесплатно сборник Ященко И.В. ЕГЭ 2023 профильный уровень математика 11 класс 36 тренировочных вариантов с ответами и решением.
Скачать сборник Ященко ЕГЭ 2023 в PDF
Аннотация к сборнику «ЕГЭ 2023. Математика. Профильный уровень. Типовые экзаменационные варианты. 36 вариантов» Серия подготовлена разработчиками контрольных измерительных материалов (КИМ) единого государственного экзамена.
Ященко ЕГЭ 2023 математика профиль 36 вариантов
В сборнике представлены: -36 типовых экзаменационных вариантов, составленных в соответствии с проектом демоверсии КИМ ЕГЭ по математике профильного уровня 2023 года; — инструкция по выполнению экзаменационной работы; — ответы ко всем заданиям; — решения и критерии оценивания заданий 12-18.
Выполнение заданий типовых экзаменационных вариантов предоставляет обучающимся возможность самостоятельно подготовиться к государственной итоговой аттестации, а также объективно оценить уровень своей подготовки.
Учителя могут использовать типовые экзаменационные варианты для организации контроля результатов освоения школьниками образовательных программ среднего общего образования и интенсивной подготовки обучающихся к ЕГЭ. Под редакцией И. В. Ященко.
-
Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением
-
Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Перейти к содержимому
ЕГЭ-2023. Сборник тренировочных вариантов. Книга предназначена для подготовки учащихся к ЕГЭ по математике. В сборнике представлены: 36 типовых экзаменационных вариантов, составленных в соответствии с демоверсиями КИМ ЕГЭ 2023 года; ответы ко всем заданиям и критерии оценивания.
Читать онлайн и скачать сборник в формате PDF: Скачать
* Еще больше пособий ЕГЭ и ОГЭ
* Учебные материалы
Поделиться: