При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Один острый угол прямоугольного треугольника в 4 раза больше другого. Найдите больший острый угол. Ответ дайте в градусах.
Ответ:
2
В треугольнике ABC угол C равен 90°, синус внешнего угла при вершине A равен 
Найдите 
Ответ:
3
4
5
В ромбе ABCD угол ACD равен 43°. Найдите угол ABC. Ответ дайте в градусах.
Ответ:
Завершить тестирование, свериться с ответами, увидеть решения.
109
вариант
Единый
государственный экзамен по МАТЕМАТИКЕ Профильный уровень
Инструкция
по выполнению работы
Экзаменационная работа состоит из
двух частей, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого
числа или конечной десятичной дроби; – часть 2 содержит 7 заданий (задания
12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных
действий)
На
выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235
минут).
Задание с кратким ответом (1–11) считается
выполненным, если в бланке ответов № 1 зафиксирован верный ответ в виде целого
числа или конечной десятичной дроби. Задания 12–18 с развёрнутым ответом, в
числе которых 5 заданий повышенного уровня и 2 задания высокого уровня
сложности, предназначены для более точной дифференциации абитуриентов вузов..
Все
бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование
гелевой или капиллярной ручки. При выполнении заданий можно пользоваться
черновиком. Записи в черновике, а также в тексте контрольных измерительных
материалов не учитываются при оценивании работы. Баллы, полученные Вами за
выполненные задания, суммируются. Постарайтесь выполнить как можно больше
заданий и набрать наибольшее количество баллов. После завершения работы
проверьте, что ответ на каждое задание в бланках ответов №1 и №2 записан под
правильным номером.
Желаем успеха!
Справочные
материалы
sin 2𝛼 = 2 sin 𝛼 ⋅ cos 𝛼
sin(𝛼 + 𝛽) = sin 𝛼 ⋅ cos 𝛽 + cos 𝛼 ⋅ sin 𝛽
Ответом
к заданиям 1–11 является целое число или конечная десятичная дробь. Запишите
число в поле ответа в тексте работы, затем перенесите его в БЛАНК ОТВЕТОВ № 1
справа от номера соответствующего задания, начиная с первой клеточки. Каждую
цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с
приведёнными в бланке образцами. Единицы измерений писать не нужно.
Часть
1
1.
Решите
уравнение 
2. В сборнике билетов по философии всего 25 билетов, в 7 из них
встречается вопрос по теме «Онтология». Найдите вероятность того, что
в случайно выбранном на экзамене билете школьнику не достанется вопроса
по теме «Онтология».
3.
В треугольнике ABC угол C равен
90°, CH — высота, 
Найдите BH.
4. Найдите значение выражения 
5. 
Около куба с
ребром 
описан шар. Найдите объем этого шара, деленный
на 
6.
На рисунке изображен график функции y = f(x),
определенной на интервале (−3; 9). Найдите количество точек, в которых
касательная к графику функции параллельна прямой y = 12 или
совпадает с ней.
7. Камнеметательная машина выстреливает камни под некоторым острым
углом к горизонту. Траектория полeта камня описывается формулой 
где 
м
– постоянные параметры, 
–
смещение камня по горизонтали, 
– высота камня над землeй. На
каком наибольшем расстоянии (в метрах) от крепостной стены высотой 8 м нужно
расположить машину, чтобы камни пролетали над стеной на высоте не менее 1
метра?
8. Теплоход, скорость которого в неподвижной воде равна 15 км/ч,
проходит по течению реки и после стоянки возвращается в исходный пункт.
Скорость течения равна 3 км/ч, стоянка длится 3 часа, а в исходный пункт
теплоход возвращается через 58 часов после отплытия из него. Сколько километров
прошел теплоход за весь рейс?
9. 
На рисунке
изображён график функции вида 
где
числа a, b и c — целые. Найдите 
10. Игральную кость бросили два раза. Известно, что три очка не выпали
ни разу. Найдите при этом условии вероятность события «сумма выпавших очков
окажется равна 8».
11. Найдите точку минимума функции 
12. а) Решите уравнение: 
б) Укажите корни этого уравнения, принадлежащие отрезку 
13. В основании правильной четырёхугольной пирамиды MABCD лежит
квадрат ABCD со стороной 8. Противоположные боковые рёбра
пирамиды попарно перпендикулярны. Через середины рёбер MA и MB проведена
плоскость 
параллельная ребру MС.
а) Докажите, что сечение плоскостью 
пирамиды MABC является
параллелограммом.
б) Найдите площадь сечения пирамиды MABC плоскостью 
14. Решите неравенство 
15. В июле планируется взять кредит в банке на сумму 20 млн рублей на
некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 30% по сравнению с концом
предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину
меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если известно, что общая сумма
выплат после его погашения равнялась 47 млн рублей?
16. Прямая, проходящая через середину M гипотенузы AB прямоугольного
треугольника ABC, перпендикулярна CM и пересекает
катет AC в точке K. При этом AK : KC =
1 : 2.
а) Докажите, что 
б) Пусть прямые MK и BC пресекаются
в точке P, а прямые AP и BK — в
точке Q. Найдите KQ, если BC = 
17. Найдите все значения параметра а, при каждом из
которых уравнение 
имеет
ровно два неотрицательных решения.
18. Известно, что a, b, c, и d — попарно
различные положительные двузначные числа.
а) Может ли выполняться равенство 
б) Может ли дробь 
быть в 11 раз
меньше, чем сумма 
в) Какое наименьшее значение может принимать дробь 
если 
и 
ответ
109 вариант
|
№ п/п |
Ответ |
|
1 |
10 |
|
2 |
0,72 |
|
3 |
9,6 |
|
4 |
702 |
|
5 |
3280,5 |
|
6 |
5 |
|
7 |
90 |
|
8 |
792 |
|
9 |
-0,75 |
|
10 |
0,12 |
|
11 |
2 |
|
12 |
а) |
|
13 |
|
|
14 |
|
|
15 |
8. |
|
16 |
|
|
17 |
|
|
18 |
а) Да, например, если a = 11, b = 30, c = 16 |
б) 
![( минус логарифм по основанию 2 6; минус логарифм по основанию 2 3].](https://documents.infourok.ru/0d09f09f-decb-4a84-a0cb-d0f316e227ff/0/image041.png){kind=small}
ЕГЭ, Математика, 11 класс, Вариант №109, 2010.
На выполнение экзаменационной работы по математике дается 4 часа (240 мин). Работа состоит из двух частей и содержит 18 заданий.
Часть 1 содержит 12 заданий с кратким ответом (В1-В12) базового уровня по материалу курса математики. Задания части 1 считаются выполненными, если экзаменуемый дал верный ответ в виде целого числа или конечной десятичной дроби.
Часть 2 содержит 6 более сложных заданий (С1-С6) по материалу курса математики. При их выполнении надо записать полное решение и ответ.
Советуем для экономии времени пропускать задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.
Примеры.
На рисунке жирными точками показана цена золота на момент закрытия биржевых торгов во все рабочие дни с 6 но 19 ноября 2008 года. По горизонтали указываются числа месяца, по вертикали — цена унции золота в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена золота на момент закрытия торгов была наибольшей.
В треугольнике AВС угол С равен 90°, AВ = 30, АС = 24. Найдите sin A.
Строительной фирме нужно приобрести 60 кубометров строительного бруса у одного из трех поставщиков. Сколько рублей придется заплатить за самую дешевую покупку с доставкой? Цены и условия доставки приведены в таблице.
На рисунке изображены график функции у = f(х) и касательная к этому графику, проведенная в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу ЕГЭ, Математика, 11 класс, Вариант №109, 2010 — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу
Скачать книгу ЕГЭ, Математика, 11 класс, Вариант №109, 2010 — pdf — depositfiles.
Скачать книгу ЕГЭ, Математика, 11 класс, Вариант №109, 2010
— pdf — Яндекс.Диск.
Дата публикации: 09.07.2013 07:00 UTC
Теги:
ЕГЭ по математике :: математика :: 11 класс
Следующие учебники и книги:
- ЕГЭ, Математика, 11 класс, Вариант №113, 2010
- ЕГЭ, Математика, 11 класс, Вариант №112, 2010
- ЕГЭ, Математика, 11 класс, Вариант №111, 2010
- ЕГЭ, Математика, 11 класс, Вариант №110, 2010
Предыдущие статьи:
- ЕГЭ, Математика, 11 класс, Вариант №108, 2010
- ЕГЭ, Математика, 11 класс, Вариант №107, 2010
- ЕГЭ, Математика, 11 класс, Вариант №106, 2010
- ЕГЭ, Математика, 11 класс, Вариант №105, 2010
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2022 из различных источников.
Тренировочные варианты ЕГЭ 2022 по математике (профиль)
| egemath.ru | |
| Вариант 1 | скачать |
| Вариант 2 | скачать |
| Вариант 3 | скачать |
| Вариант 4 | скачать |
| Вариант 5 | скачать |
| Вариант 6 | скачать |
| Вариант 7 | скачать |
| variant 8 | скачать |
| variant 9 | скачать |
| variant 10 | скачать |
| variant 11 | скачать |
| variant 12 | скачать |
| variant 13 | скачать |
| variant 14 | скачать |
| variant 15 | скачать |
| variant 16 | скачать |
| variant 17 | скачать |
| variant 18 | скачать |
| variant 19 | скачать |
| variant 20 | скачать |
| yagubov.ru | |
| вариант 21 | ege2022-yagubov-prof-var21 |
| вариант 22 | ege2022-yagubov-prof-var22 |
| вариант 23 | ege2022-yagubov-prof-var23 |
| вариант 24 | ege2022-yagubov-prof-var24 |
| вариант 25 | ege2022-yagubov-prof-var25 |
| вариант 26 | ege2022-yagubov-prof-var26 |
| вариант 27 | ege2022-yagubov-prof-var27 |
| вариант 28 | ege2022-yagubov-prof-var28 |
| Досрочный Москва 28.03.2022 | скачать |
| egemathschool.ru | |
| вариант 1 | ответ |
| вариант 2 | ответ |
| вариант 3 | ответ |
| вариант 4 | ответ |
| ЕГЭ 100 баллов (с решениями) | |
| Вариант 1 | скачать |
| Вариант 2 | скачать |
| Вариант 3 | скачать |
| Вариант 4 | скачать |
| Вариант 5 | скачать |
| Вариант 6 | скачать |
| Вариант 7 | скачать |
| Вариант 8 | скачать |
| Вариант 9 | скачать |
| Вариант 10 | скачать |
| variant 11 | скачать |
| variant 12 | скачать |
| variant 13 | скачать |
| variant 14 | скачать |
| variant 15 | скачать |
| variant 16 | скачать |
| variant 17 | скачать |
| variant 18 | скачать |
| variant 20 | скачать |
| variant 21 | скачать |
| variant 23 | скачать |
| variant 24 | скачать |
| variant 25 | скачать |
| variant 26 | скачать |
| variant 29 | скачать |
| variant 30 | скачать |
| math100.ru (с ответами) | |
| Вариант 140 | скачать |
| Вариант 141 | скачать |
| Вариант 142 | скачать |
| Вариант 143 | math100-ege22-v143 |
| Вариант 144 | math100-ege22-v144 |
| Вариант 145 | math100-ege22-v145 |
| Вариант 146 | math100-ege22-v146 |
| variant 147 | math100-ege22-v147 |
| variant 148 | math100-ege22-v148 |
| variant 149 | math100-ege22-v149 |
| variant 150 | math100-ege22-v150 |
| variant 151 | math100-ege22-v151 |
| variant 152 | math100-ege22-v152 |
| variant 153 | math100-ege22-v153 |
| variant 154 | math100-ege22-v154 |
| variant 155 | math100-ege22-v155 |
| variant 156 | math100-ege22-v156 |
| variant 157 | math100-ege22-v157 |
| variant 158 | math100-ege22-v158 |
| variant 159 | math100-ege22-v159 |
| variant 160 | math100-ege22-v160 |
| variant 161 | math100-ege22-v161 |
| variant 162 | math100-ege22-v162 |
| variant 163 | math100-ege22-v163 |
| variant 164 | math100-ege22-v164 |
| variant 165 | math100-ege22-v165 |
| variant 166 | math100-ege22-v166 |
| variant 167 | math100-ege22-v167 |
| variant 168 | math100-ege22-v168 |
| variant 169 | math100-ege22-v169 |
| variant 170 | math100-ege22-v170 |
| variant 171 | math100-ege22-v171 |
| variant 172 | math100-ege22-v172 |
| variant 173 | math100-ege22-v173 |
| variant 174 | math100-ege22-v174 |
| alexlarin.net | |
| Вариант 358 |
скачать |
| Вариант 359 | скачать |
| Вариант 360 | скачать |
| Вариант 361 | скачать |
| Вариант 362 | проверить ответы |
| Вариант 363 | проверить ответы |
| Вариант 364 | проверить ответы |
| Вариант 365 | проверить ответы |
| Вариант 366 | проверить ответы |
| Вариант 367 | проверить ответы |
| Вариант 368 | проверить ответы |
| Вариант 369 | проверить ответы |
| Вариант 370 | проверить ответы |
| Вариант 371 | проверить ответы |
| Вариант 372 | проверить ответы |
| Вариант 373 | проверить ответы |
| Вариант 374 | проверить ответы |
| Вариант 375 | проверить ответы |
| Вариант 376 | проверить ответы |
| Вариант 377 | проверить ответы |
| Вариант 378 | проверить ответы |
| Вариант 379 | проверить ответы |
| Вариант 380 | проверить ответы |
| Вариант 381 | проверить ответы |
| Вариант 382 | проверить ответы |
| Вариант 383 | проверить ответы |
| Вариант 384 | проверить ответы |
| Вариант 385 | проверить ответы |
| Вариант 386 | проверить ответы |
| Вариант 387 | проверить ответы |
| Вариант 388 | проверить ответы |
| vk.com/ekaterina_chekmareva (задания 1-12) | |
| Вариант 1 | ответы |
| Вариант 2 | |
| Вариант 3 | |
| Вариант 4 | |
| Вариант 5 | |
| Вариант 6 | |
| Вариант 7 | ответы |
| Вариант 8 | |
| Вариант 9 | |
| Вариант 10 | |
| vk.com/matematicalate | |
| Вариант 1 | matematikaLite-prof-ege22-var1 |
| Вариант 2 | matematikaLite-prof-ege22-var2 |
| Вариант 3 | matematikaLite-prof-ege22-var3 |
| Вариант 4 | matematikaLite-prof-ege22-var4 |
| Вариант 5 | matematikaLite-prof-ege22-var5 |
| Вариант 6 | matematikaLite-prof-ege22-var6 |
| Вариант 7 | matematikaLite-prof-ege22-var7 |
| Вариант 8 | matematikaLite-prof-ege22-var8 |
| vk.com/pro_matem | |
| variant 1 | pro_matem-prof-ege22-var1 |
| variant 2 | pro_matem-prof-ege22-var2 |
| variant 3 | pro_matem-prof-ege22-var3 |
| variant 4 | разбор |
| variant 5 | разбор |
| vk.com/murmurmash | |
| variant 1 | otvet |
| variant 2 | otvet |
| → Купить сборники тренировочных вариантов ЕГЭ 2022 по математике |
Структура варианта КИМ ЕГЭ
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.
Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Связанные страницы:
Средний балл ЕГЭ 2021 по математике
Решение задач с параметром при подготовке к ЕГЭ
Изменения в КИМ ЕГЭ 2022 года по математике
Купить сборники типовых вариантов ЕГЭ по математике
Как решать экономические задачи ЕГЭ по математике профильного уровня?
Решение и ответы заданий варианта 2210109 СтатГрад 28 сентября ЕГЭ 2023 по математике (профильный уровень). ГДЗ профиль для 11 класса.
Все материалы получены из открытых источников и публикуются после окончания тренировочного экзамена в ознакомительных целях.
Задания №13,16,17,18 долго оформлять, решу их позже, если будет время и желание. Решены те задания, у которых кнопка «Смотреть решение» зелёная.
Задание 1.
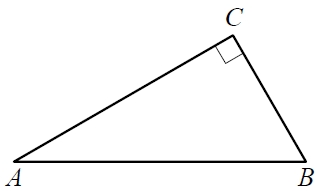
В треугольнике ABC угол C равен 90°, AB = 4, sinA=frac{sqrt{19}}{10}. Найдите AC.
Задание 2.
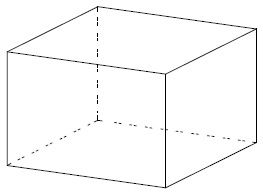
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 7 и 4. Объём параллелепипеда равен 140. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
Задание 3.
При производстве в среднем из 2000 насосов 4 неисправных. Найдите вероятность того, что случайно выбранный насос окажется неисправным.
Задание 4.
Игральную кость бросили два раза. Известно, что четыре очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 11».
Задание 5.
Найдите корень уравнения sqrt{frac{7x+13}{19}}=5.
Задание 6.
Найдите значение выражения frac{a^{-1}b^{-1}}{(2a)^{2}b^{-3}}cdot frac{11}{a^{-3}b^{2}}.
Задание 7.
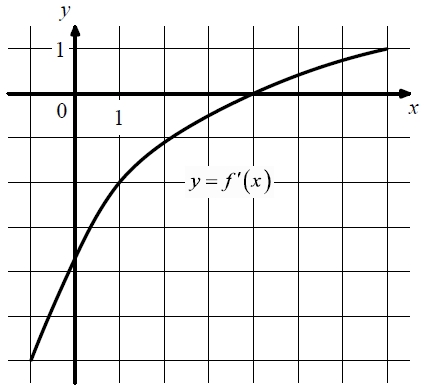
На рисунке изображён график функции y = f ‘(x) – производной функции f(x). Найдите абсциссу точки, в которой касательная к графику функции y = f(x) параллельна прямой y = 6 − 2x или совпадает с ней.
Задание 8.
Рейтинг R интернет-магазина вычисляется по формуле , R=r_{пок}–frac{r_{пок}–r_{экс}}{(K+1)^{m}}, где m=frac{0,02K}{r_{пок}+0,1}, rпок – средняя оценка магазина покупателями, rэкс – оценка магазина, данная экспертами, K – число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 15, их средняя оценка равна 0,5, а оценка экспертов равна 0,22.
Задание 9.
Расстояние между пристанями A и B равно 60 км. Из A в B по течению реки отправился плот, а через 3 часа вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот проплыл 44 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч.
Задание 10.
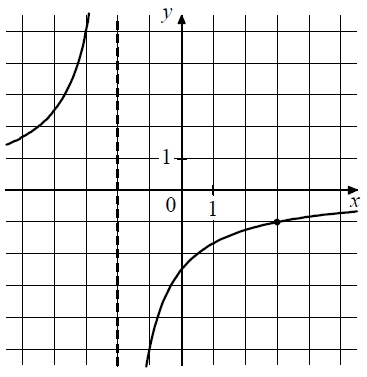
На рисунке изображён график функции вида f(x)=frac{k}{x+a}. Найдите значение x, при котором f(x) = –0,125.
Задание 11.
Найдите точку минимума функции y = x3 − 6x2 + 15.
Задание 12.
а) Решите уравнение cos2 x − cos2x = 0,75.
б) Найдите все корни этого уравнения, принадлежащие отрезку [frac{3pi}{2};3pi].
Задание 13.
Ребро куба ABCDA1B1C1D1 равно 2. На ребре BB1 отмечена точка K так, что KB = 1,6. Через точки K и C1 проведена плоскость α , параллельная прямой BD1.
а) Докажите, что A1P : PB1 = 3:1, где P – точка пересечения плоскости α с ребром A1B1.
б) Найдите угол между плоскостями α и BB1C1.
Задание 14.
Решите неравенство frac{(3x–4)^{2}}{x–3}ge frac{16–24x+9x^{2}}{15–8x+x^{2}}.
Задание 15.
15 января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 40 % больше суммы, взятой в кредит. Найдите r.
Задание 16.
Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N.
а) Докажите, что прямые MN и BO параллельны.
б) Найдите площадь четырёхугольника BOMN, если CN = 9 и AM:MC = 1:8.
Задание 17.
Найдите все значения a, при каждом из которых уравнение
(|x + 2| + |x – a|)2 – 4(|x + 2| + |x – a|) + 3a(4 – 3a) = 0
имеет ровно два решения.
Задание 18.
На сайте проводится опрос, кого из 156 футболистов посетители сайта считают лучшим по итогам сезона. Каждый посетитель голосует за одного футболиста. На сайте отображается рейтинг каждого футболиста – доля голосов, отданных за него, в процентах, округлённая до целого числа. Например, числа 9,3, 10,5 и 12,7 округляются до 9, 11 и 13 соответственно.
а) Всего проголосовало 11 посетителей сайта, и рейтинг первого футболиста стал равен 45. Увидев это, Вася отдал свой голос за другого футболиста. Чему теперь равен рейтинг первого футболиста?
б) Вася проголосовал за некоторого футболиста. Могла ли после этого сумма рейтингов всех футболистов уменьшиться на 150 или больше?
в) Какое наибольшее значение может принимать сумма рейтингов всех футболистов?
Источник варианта: СтатГрад/statgrad.org.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.2 / 5. Количество оценок: 10
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.