Вариант 12 егэ математика профиль ященко 2021 год решение - Помощь в подготовке к экзаменам и поступлению

Задание 1

В магазине вся мебель продаётся в разобранном виде. Покупатель может заказать сборку мебели на дому, стоимость которой составляет 10% от стоимости купленной мебели. Шкаф стоит 2400 рублей. Во сколько рублей обойдётся покупка этого шкафа вместе со сборкой?

Ответ: 2640

Задание 2

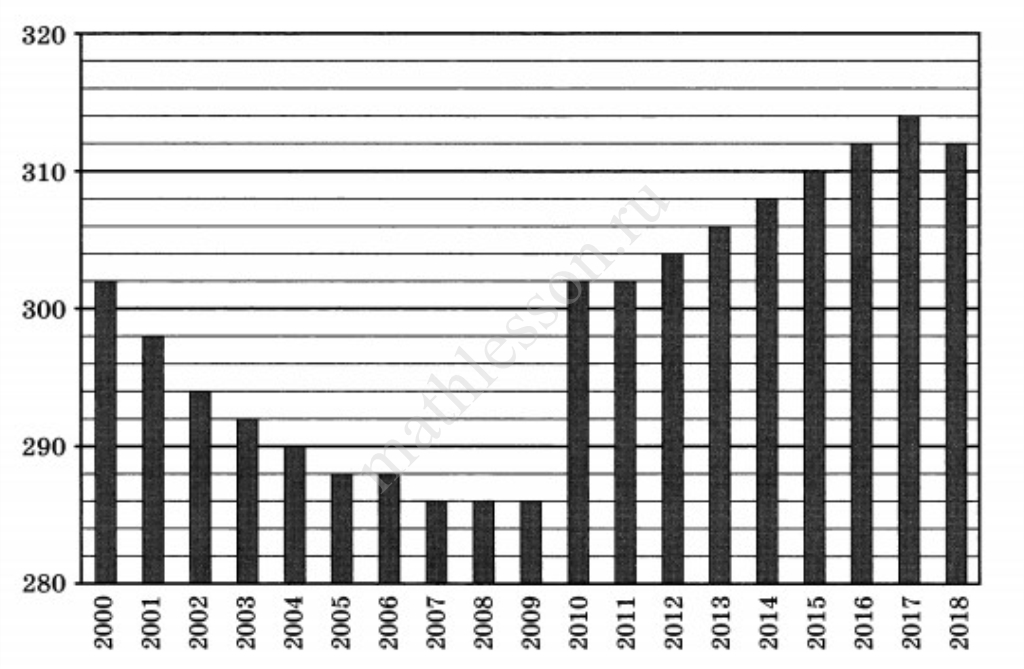
На диаграмме приведены данные о численности населения в Вологде на конец каждого года с 2000 года по 2018 год (в тыс. чел.).

Определите, на сколько тысяч человек выросла численность населения в Вологде за период с конца 2008 года по конец 2018 года.

Ответ: 26

Задание 3

На клетчатой бумаге с размером клетки 1×1 изображён четырёхугольник. Найдите его площадь.

Ответ: 27

Задание 4

Всего в группе туристов 51 человек, в том числе Иван и Егор. Группу случайным образом делят на три подгруппы по 17 человек для посадки в три автобуса. Известно, что Иван оказался в третьем автобусе. Какова вероятность того, что при этом условии Егор окажется в первом автобусе?

Ответ: 0,34

Задание 5

Найдите корень уравнения $${0,2}^{5+4x}=125$$

Ответ: -2

Задание 6

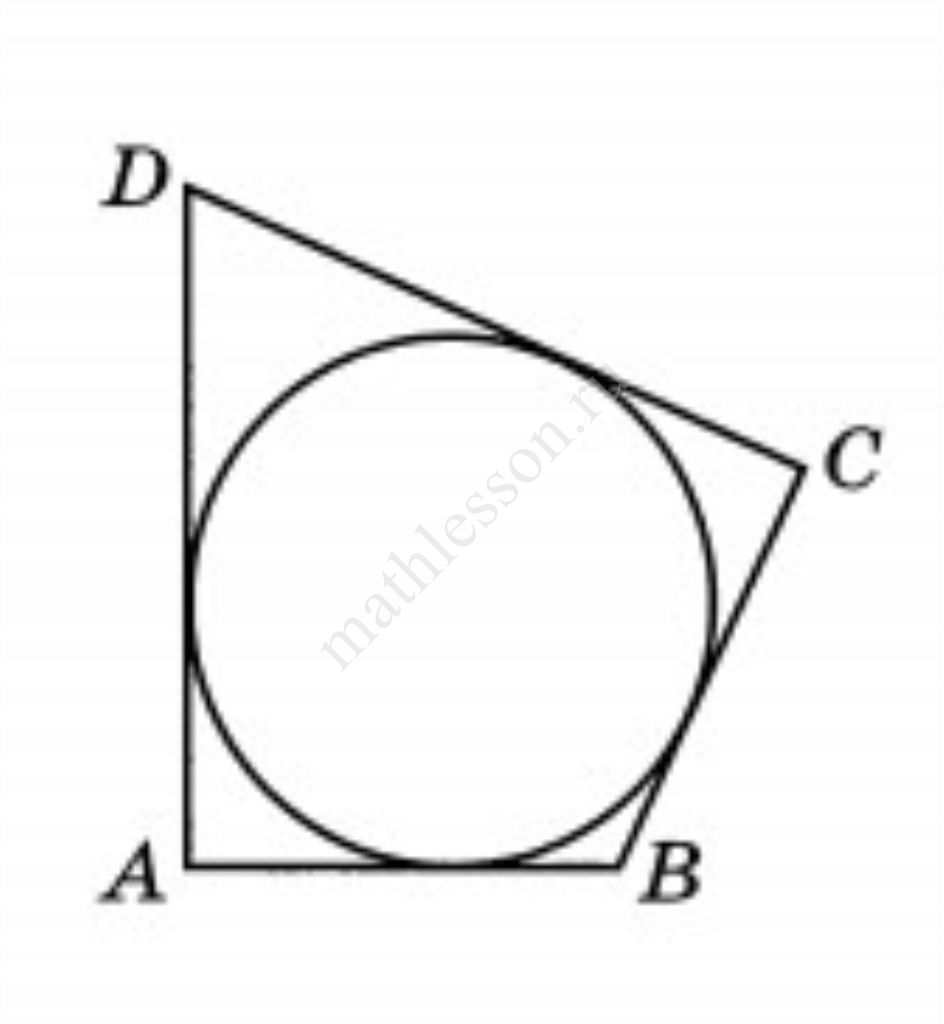
В четырёхугольник ABCD вписана окружность, $$AB = 8, BC = 5 и CD = 27.$$ Найдите четвёртую сторону четырёхугольника.

Ответ: 30

Задание 7

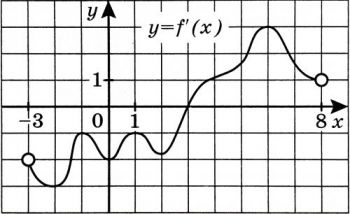
На рисунке изображён график $$y= f'(x)$$ — производной функции $$f(x)$$, определённой на интервале (-3; 8). В какой точке отрезка [-2; 3] функция $$f(x)$$ принимает наименьшее значение?

Ответ: 3

Задание 8

Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна $$27sqrt{2}.$$ Найдите площадь боковой поверхности конуса.

Ответ: 27

Задание 9

Найдите значение выражения $$left(3frac{1}{8}-1,5right):frac{1}{56}$$

Ответ: 91

Задание 10

В телевизоре ёмкость высоковольтного конденсатора $$C = 5cdot {10}^{-6}$$ Ф. Параллельно с конденсатором подключён резистор с сопротивлением $$R=6cdot {10}^6$$ Ом. Во время работы телевизора напряжение на конденсаторе $$U_0 = 34 $$кВ. После выключения телевизора напряжение на конденсаторе убывает до значения $$U$$ (кВ) за время, определяемое выражением $$t = aRC{log}_2frac{U_o}{U}$$ (с), где $$alpha =1,7$$ — постоянная. Определите напряжение на конденсаторе, если после выключения телевизора прошла 51 с. Ответ дайте в киловольтах.

Ответ: 17

Задание 11

Плиточник должен уложить 120 м$${}^{2}$$ плитки. Если он будет укладывать на 8 м$${}^{2}$$ в день больше, чем запланировал, то закончит работу на 4 дня раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник?

Ответ: 12

Задание 12

Найдите точку максимума функции $$y = x^3 + 18x^2 + 81x + 23.$$

Ответ: -9

Задание 13

а) Решите уравнение $$2{{sin }^2 x }-3sqrt{3}{sin left(frac{pi }{2}+xright) }-5=0$$

б) Укажите корни этого уравнения, принадлежащие отрезку $$[-frac{5pi }{2};-pi ]$$

Ответ: $$pm frac{5pi }{6}+2pi n, n in Z$$; б) $$-frac{7pi }{6}$$

Задание 14

В правильной четырёхугольной пирамиде SABCD сторона основания АВ равна 4, а боковое ребро SA равно 5. На ребре SC отмечена точка К, причём $$SK: KC=1:3.$$ Плоскость $$alpha $$ содержит точку К и параллельна плоскости SAD.

а) Докажите, что сечение пирамиды SABCD плоскостью $$alpha $$ — трапеция.

б) Найдите объём пирамиды, вершиной которой является точка S, а основанием — сечение пирамиды SABCD плоскостью $$alpha $$.

Ответ: $$frac{5sqrt{17}}{8}$$

Задание 15

Решите неравенство $${log}_2left(18-9xright)-{log}_2left(x+2right)>{log}_2(x^2-6x+8)$$

Ответ: (-2;1); (1;2)

Задание 16

Точка О — центр вписанной в треугольник АВС окружности. Прямая ВО вторично пересекает описанную около этого треугольника окружность в точке Е.

а) Докажите, что $$angle EOC= angle ECO.$$

б) Найдите площадь треугольника АСЕ, если радиус описанной около треугольника АВС окружности равен $$6sqrt{3}, angle ABC = 60{}^circ .$$

Ответ: $$27sqrt{3}$$

Задание 17

15 января планируется взять кредит в банке на 49 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 2 млн рублей? (Считайте, что округления при вычислении платежей не производятся.)

Ответ: 1,6 млн. руб.

Задание 18

Найдите все значения a, при каждом из которых уравнение

$$frac{left|x-6right|+a-6}{x^2-10x+a^2}=0$$

имеет ровно два различных корня.

Ответ: $$a<0; 0<a<3; 3<a<4; 4<a<5; 5<a<6$$

Скрыть

Преобразуем исходное уравнение:

$$frac{|x-6|+a-6}{x^2-10x+a^2}=0Leftrightarrowleft{begin{matrix} |x-6|=6-a,\ x^2-10x+a^2neq0 end{matrix}right.Leftrightarrowleft{begin{matrix} left[begin{matrix} x=a,\ x=12-a, end{matrix}right.\ aleq6,\ x^2-10x+a^2neq0. end{matrix}right.$$

Чтобы уравнение имело два различных корня, числа a и 12 − a должны быть различны, поэтому $$aneq12-a,$$ откуда $$aneq6.$$ Таким образом, $$a<6$$ и ни одно из чисел a и 12 − a не должно являться корнем уравнения $$x^2-10x+a^2=0.$$ Подставляя эти числа в уравнение $$x^2-10x+a^2,$$ найдем, при каких a они являются корнями:

1) из $$a^2-10a+a^2=0,$$ получаем: a=0 или a=5;

2) из $$(12-a)^2-10(12-a)+a^2=0,$$ получаем:

$$2a^2-14a+24=0Leftrightarrow a^2-7a+12=0Leftrightarrowleft[begin{matrix} a=3,\ a=4. end{matrix}right.$$

Тем самым одновременно: $$a<6,aneq0,aneq3,aneq4,aneq5.$$

Задание 19

а) Могло ли в ящике оказаться поровну овощей массой меньше 1000 г и овощей массой больше 1000 г?

б) Могло ли в ящике оказаться ровно 12 овощей, масса каждого из которых равна 1000 г?

в) Какую наименьшую массу может иметь овощ в этом ящике?

Ответ: а) нет; б) нет; в) 240 г.

Источник

ЕГЭ Ященко 2021 вариант 12 математика профильный уровень uchus.online

ЕГЭ Ященко 2021 вариант 12 математика профильный уровень uchus.online. Разбор варианта ЕГЭ по математике 2021. егэ математика профиль 2021 тренировочные варианты

Смотрите также:

ЕГЭ Ященко 2021 вариант 10 математика профильный уровень uchus.online

Консультация по подготовке к ЕГЭ по математике 2021 — «На все 100»

Источник

В магазине вся мебель продаётся в разобранном виде. Покупатель может заказать сборку мебели на дому, стоимость которой составляет 10 % от стоимости купленной мебели. Шкаф стоит 2400 рублей. Во сколько рублей обойдётся покупка этого шкафа вместе со сборкой?

На диаграмме приведены данные о численности населения в Вологде на конец каждого года с 2000 года по 2018 год (в тыс. чел.). Определите, на сколько тысяч человек выросла численность населения в Вологде за период с конца 2008 года по конец 2018 года.

На клетчатой бумаге с размером клетки 1×1 изображён четырёхугольник. Найдите его площадь.

Найдите корень уравнения (0{,}2^{5+4x}=125).

В четырёхугольник ABCD вписана окружность, АВ=8, ВС=5 и CD=27. Найдите четвёртую сторону четырёхугольника.

На рисунке изображён график (y = f'(x)) производной функции (f(x)), определённой на интервале ((-3; 8)). В какой точке отрезка ([-2; 3]) функция (f(x)) принимает наименьшее значение?

Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 27√2. Найдите площадь боковой поверхности конуса.

Найдите значение выражения (left(3dfrac{1}{8}-1{,}5right):dfrac{1}{56}).

В телевизоре ёмкость высоковольтного конденсатора (C=5cdot10^{-6}Ф). Параллельно с конденсатором подключён резистор с сопротивлением (R=6cdot10^{6}Ом). Во время работы телевизора напряжение на конденсаторе (U_0=34 кВ). После выключения телевизора напряжение на конденсаторе убывает до значения (U (кВ))за время, определяемое выражением (t=alpha RClog_{2}{dfrac{U_0}{U}} (с)), где (alpha=1{,}7) — постоянная. Определите напряжение на конденсаторе, если после выключения телевизора прошла 51 с. Ответ дайте в киловольтах.

Плиточник должен уложить 120 м² плитки. Если он будет укладывать на 8 м² в день больше, чем запланировал, то закончит работу на 4 дня раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник?

Найдите точку максимума функции (y=x^{3}+18x^{2}+81x+23).

а) Решите уравнение (2sin^2x-3sqrt3sinleft(dfrac{pi}{2}+xright)-5=0).
б) Укажите все корни этого уравнения, принадлежащие отрезку (left[-dfrac{5pi}{2};-pi right] ).

Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)

1. 2πn, n∈Z	2. π/6+2πn, n∈Z	3. π/4+2πn, n∈Z	4.π/3+2πn, n∈Z
5. π/2+2πn, n∈Z	6. 2π/3+2πn, n∈Z	7. 3π/4+2πn, n∈Z	8. 5π/6+2πn, n∈Z
9. π+2πn, n∈Z	10. -π/6+2πn, n∈Z	11. -π/4+2πn, n∈Z	12. -π/3+2πn, n∈Z
13. -π/2+2πn, n∈Z	14. -2π/3+2πn, n∈Z	15. -3π/4+2πn, n∈Z	16. -5π/6+2πn, n∈Z

б)

17. -5π/2	18. -7π/3	19. -9π/4	20. -13π/6
21. -2π	22. -11π/6	23. -7π/4	24. -5π/3
25. -3π/2	26. -4π/3	27. -5π/4	28. -7π/6
29. -π

В правильной четырёхугольной пирамиде SABCD сторона основания АВ равна 4, а боковое ребро SA равно 5. На ребре SC отмечена точка K, причём SK:KC = 1:3. Плоскость (alpha) содержит точку K и параллельна плоскости SAD.
а) Докажите, что сечение пирамиды SABCD плоскостью (alpha) — трапеция.
б) Найдите объём пирамиды, вершиной которой является точка S, а основанием — сечение пирамиды SABCD плоскостью (alpha).

Решите неравенство (log_{2}{(18-9x)}-log_{2}{(x+2)}>log_{2}{(x^2-6x+8)})

Точка O — центр вписанной в треугольник ABC окружности. Прямая BO вторично пересекает описанную около этого треугольника окружность в точке E.
а) Докажите, что углы ∠EOC=∠ECO.
б) Найдите площадь треугольника ACE, если радиус описанной около треугольника ABC окружности равен 6√3, ∠ABC=60°.

15 января планируется взять кредит в банке на 49 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Какую сумму в рублях планируется взять в кредит, если общая сумма выплат после полного его погашения составит 2 млн рублей?
(Считайте, что округления при вычислении платежей не производятся.)

Найдите все значения (a), при каждом из которых уравнение (dfrac{|x-6|+a-6}{x^2-10x+a^2}=0) имеет ровно два различных корня.

В ящике лежит 58 овощей, масса каждого из которых выражается целым числом граммов. В ящике есть хотя бы два овоща различной массы, а средняя масса всех овощей равна 1000 г. Средняя масса овощей, масса каждого из которых меньше 1000 г, равна 976 г. Средняя масса овощей, масса каждого из которых больше 1000 г, равна 1036 г.
а) Могло ли в ящике оказаться поровну овощей массой меньше 1000 г и овощей массой больше 1000 г?
б) Могло ли в ящике оказаться ровно 12 овощей, масса каждого из которых равна 1000 г?
в) Какую наименьшую массу может иметь овощ в этом ящике?

Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.

Источник

Канал видеоролика: Ломоносов клуб

Смотреть видео:

#математикаогэ #гвэ #егэответы #числа #математика #алгебра #подготовкакогэ #ответы_огэ #подготовкакегэ

Свежая информация для ЕГЭ и ОГЭ по Математике (листай):

С этим видео ученики смотрят следующие ролики:

Решаем ЕГЭ 2021 Ященко Математика профильный Вариант 1 (повышенная сложность)

Математик МГУ

Решаем ЕГЭ 2021 Ященко Математика профильный Вариант 2

Математик МГУ

9 вариант ЕГЭ Ященко 2021| Задачи 1-17 математика профильный уровень

Ломоносов клуб

16 задача ЕГЭ | Планиметрия 4 вариант Ященко 2021 математика профильный уровень

Ломоносов клуб

Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):

08.12.2020

Источник

Решение и ответы заданий Варианта №12 из сборника ЕГЭ 2023 по математике (профильный уровень) И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ профиль для 11 класса. Полный разбор.

Задание 1.
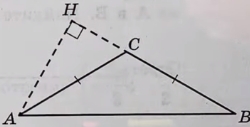
В тупоугольном треугольнике ABC известно, что AC = BC, высота AH равна 3, СН = √7. Найдите синус угла ACB.

Задание 2.
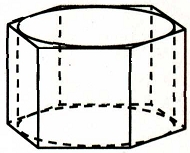
Цилиндр вписан в правильную шестиугольную призму. Радиус основания цилиндра равен √3, а высота равна 2. Найдите площадь боковой поверхности призмы.

Задание 3.
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Вписанная окружность», равна 0,25. Вероятность того, что это вопрос по теме «Площадь», равна 0,3. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Задание 4.
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 25% этих стекол, вторая – 75%. Первая фабрика выпускает 5% бракованных стекол, а вторая – 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Задание 5.
Найдите корень уравнения 9^2х+5 = 3,24·5^2х+5.

Задание 6.
Найдите значение выражения frac{4cos121°}{cos59°}.

Задание 7.
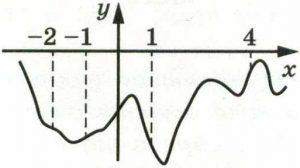
На рисунке изображён график функции y = f(x). На оси абсцисс отмечены точки −2, –1, 1, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

Задание 8.
При температуре 0°С рельс имеет длину l₀= 15 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону l(𝑡°) = l₀(1 + α∙t°), где α = 1,2∙10⁻⁵(°С )⁻¹ – коэффициент теплового расширения, t° – температура (в градусах Цельсия). При какой температуре рельс удлинится на 7,2 мм? Ответ дайте в градусах Цельсия.

Задание 9.
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 135 км. На следующий день он отправился обратно в А со скоростью на 9 км/ч больше прежней. По дороге он сделал остановку на 4 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в B. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.

Задание 10.
На рисунке изображён график функции вида f(x) = ax² + bx + c, где числа a, b и c – целые. Найдите значение f(−9).

Задание 11.
Найдите точку минимума функции y = frac{4}{3}x√x – 5x + 4.

Задание 12.
а) Решите уравнение 2cos³(x – π) = sin(frac{3pi}{2} + x).
б) Найдите все корни уравнения, принадлежащие отрезку [frac{9pi}{2};frac{11pi}{2}].

Задание 13.
В правильной четырёхугольной пирамиде SABCD сторона основания AD равна 10, высота SH равна 12. Точка К – середина бокового ребра SD. Плоскость АКВ пересекает боковое ребро SC в точке Р.

а) Докажите, что площадь четырёхугольника CDKP составляет frac{3}{4} площади треугольника SCD.
б) Найдите объем пирамиды ACDKP.

Задание 14.
Решите неравенство (25^х – 4·5^х)² + 8·5^х< 2·25^x + 15.

Задание 15.
В июле 2023 года планируется взять кредит на 10 лет. Условия его возврата таковы:
– каждый январь с 2024 по 2028 год долг возрастает на 18% по сравнению с концом предыдущего года;
– каждый январь с 2029 по 2033 год долг возрастает на 16% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года должен быть на одну и ту же величину меньше долга на июль предыдущего года;
– к июлю 2033 года долг должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат по кредиту должна составить 1470 тысяч рублей?

Задание 16.
Точки A, B, C, D и E лежат на окружности в указанном порядке, причем BC = CD = DE, а AC⊥BE. Точка K – пересечение прямых BE и AD.

а) Докажите, что прямая EC делит отрезок KD пополам.
б) Найдите площадь треугольника ABK, если AD = 4, DC = √3.

Задание 17.
Найдите все значения 𝑎, при каждом из которых уравнение

|x^{2}-a^{2}|=|x+a|cdot sqrt{x^{2}-5ax+4a}

имеет ровно два различных корня.

Задание 18.
На доске написаны три различных натуральных числа. Второе число равно сумме цифр первого, а третье равно сумме цифр второго.

а) Может ли сумма этих чисел быть равна 3456?
б) Может ли сумма этих чисел быть равна 2345?
в) В тройке чисел первое число трёхзначное, а третье равно 5. Сколько существует таких троек?

Источник варианта: Сборник ЕГЭ 2023. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 5 / 5. Количество оценок: 2

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Решаем задачи из сборника : 30 тренировочных вариантов ЕГЭ под редакцией И. В. Ященко» – 2021. Все задачи №13 (Уравнения)

Разбираем все типы задач № 13 (в новой нумерации №12) из сборника: 30 тренировочных вариантов ЕГЭ под редакцией И. В. Ященко» – 2021.
Подробно объясняем ход решения и показываем оформление задач.
Полное название сборника:
«Математика. Профильный уровень. Единый Государственный Экзамен. Готовимся к итоговой аттестации. 2021 год. 30 вариантов».
Как правило, задания из таких сборников немного сложнее, чем реальные задачи ЕГЭ. Зато, решая такие задачи, вы сможете отлично подготовиться к любым возможным неожиданностям на экзамене.
В задании 13 вариантов ЕГЭ вам могут встретиться уравнения различных типов: тригонометрические, показательные, логарифмические.

1. Вариант 1

а) Решите уравнение $displaystyle (x^2+2x-2)(log_3(x^2-5)log_{frac{1}{3}}(sqrt{5}-x))=0.$
б) Найдите все корни этого уравнения, принадлежащие отрезку [-3,5; -2,8].

Посмотреть решение

2. Вариант 6

а) Решите уравнение $4 cdot 256^{sin x}-65 cdot 16^{sin x} +16 =0.$

б) Найдите все корни этого уравнения, принадлежащие отрезку $displaystyle [- frac{5 pi}{2};-pi].$

Посмотреть решение

3. Вариант 11.

а) Решите уравнение $(-2 cos^2 x+ sin x+1) cdot log_{0,5}(- cos x)=0.$
б) Найдите все корни уравнения, принадлежащие отрезку

Посмотреть решение

4. Вариант 17.

а) Решите уравнение $16^x - 7 cdot 8^x - 2^{x+3}+56=0.$
б) Укажите корни этого уравнения, принадлежащие отрезку $[2; log_{2} 10].$

Посмотреть решение

5. Вариант 22

а) Решите уравнение $displaystyle (3 sin (frac{3 pi}{2}+3x)+4 cos^3 3x)sqrt{tg 3x}=0.$
б) Укажите корни этого уравнения, принадлежащие отрезку $displaystyle [pi; frac{3pi}{2}]$

Посмотреть решение

6. Вариант 28.

а) Решите уравнение $(sqrt{2} cos^2 x- cos x)sqrt{- 6 sin x}=0.$

б) Укажите все корни этого уравнения, принадлежащие промежутку $displaystyle [frac{5 pi}{2};4 pi)$

Посмотреть решение

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задачи из сборников Ященко, 2021 год» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Ответы к 36 вариантам профильного ЕГЭ по математике. Сборник ЕГЭ-2023 «Типовые экзаменационные варианты».

Вариант 1

1) 5,5
2) 2048
3) 0,06
4) 0,89
5) -0,2
6) 0,5
7) 5
5,832
9) 2
10) -4
11) -2910

Вариант 2

1) 7,5
2) 4
3) 0,12
4) 0,91
5) -0,9
6) 0,2
7) 1
0,216
9) 16
10) -8
11) 12,25

Вариант 3

1) 2,5
2) 30
3) 0,37
4) 0,375
5) -2,5
6) 4
7) 2
51,2
9) 14
10) 32
11) 204

Вариант 4

1) 1,5
2) 12
3) 0,24
4) 0,125.
5) 0,375
6) 125
7) 8
281,25
9) 18
10) -56
11) -10,9

Вариант 5

1) 99,5
2) 12
3) 0,004 /или/ -0,004
4) 0,9409
5) -0,5
6) 2
7) -19
60
9) 17
10) 16
11) -52

Вариант 6

1) 55
2) 18
3) 0,006 /или/ -0,006
4) 0,8464
5) -5,5
6) 3
7) -4
30
9) 24
10) -1
11) -6

Вариант 7

1) 0,2
2) 10
3) 0,2
4) 0,56
5) -0,4
6) -1
7) 9
0,6
9) 55
10) 6
11) 0,5

Вариант 8

1) 0,4
2) 5
3) 0,125
4) 0,46
5) -7
6) -1
7) 7
1,8
9) 11
10) 0,25
11) 17

Вариант 9

1) 3
2) 15 625
3) 0,01
4) 0,28
5) -12
6) 144
7) -1
756
9) 20
10) -3
11) 9

Вариант 10

1) 0,6
2) 150
3) 0,28
4) 0,17
5) -2,6
6) 625
7) -18
220,5
9) 9
10) 253
11) -23,25

Вариант 11

1) -0,7
2) 72
3) 0,25
4) 0,043
5) -0,2
6) -5
7) -1
50
9) 17,5
10) 78
11) 6,75

Вариант 12

1) 0,75
2) 24
3) 0,55
4) 0,02
5) -1,5
6) -4
7) 4
40
9) 13,5
10) -23
11) 6,25

Вариант 13

1) 8
2) 48
3) 0,4
4) 0,6
5) -9
6) 0,5
7) 4
33
9) 9
10) -0,5
11) 77

Вариант 14

1) 14
2) 40,5
3) 0,28
4) 0,78
5) -2
6) 0,04
7) 39
23
9) 24
10) 0,4
11) 37

Вариант 15

1) 11,55
2) 432
3) 0,014
4) 0,06
5) -9
6) 0,25
7) 2
0,32
9) 3
10) 2,5
11) 208

Вариант 16

1) 12
2) 192
3) 0,29
4) 0,02
5) -8
6) 0,125
7) 4
1,16
9) 1
10) -15
11) 5

Вариант 17

1) 10
2) 80
3) 0,08
4) 0,2
5) -2,5
6) 216
7) -2
175
9) 18
10) 16
11) -24

Вариант 18

1) 35
2) 10
3) 0,2
4) 0,24
5) -0,2
6) 3,5
7) 28
43,75
9) 21
10) 2,25
11) -15

Вариант 19

1) 2,5
2) 7,28
3) 0,25
4) 0,22
5) -1,5
6) 1
7) 0,2
115
9) 135
10) 2
11) -34

Вариант 20

1) 6
2) 7,68
3) 0,75
4) 0,27
5) -4,5
6) 10
7) -0,25
220
9) 52
10) 27
11) 0

Вариант 21

1) 113
2) 60
3) 0,2
4) 0,973
5) 5,5
6) 324
7) 2
6250
9) 14
10) 15
11) 7

Вариант 22

1) 0,75
2) 45
3) 0,3
4) 0,9744
5) 11
6) -7,5
7) 7
1,3
9) 5
10) 3,4
11) 1,2

Вариант 23

1) 62
2) 25
3) 0,25
4) 0,3
5) -2
6) 80
7) 6
60
9) 75
10) 28
11) 18

Вариант 24

1) 78
2) 20
3) 0,2
4) 0,82
5) 0
6) 28
7) 6
30
9) 10
10) -28
11) -2

Вариант 25

1) 37
2) 135
3) 0,18
4) 3
5) 0,8
6) 0,4
7) -0,2
6
9) 1 35
10) -0,4
11) 14

Вариант 26

1) 53
2) 72
3) 0,38
4) 5
5) -4
6) -0,3
7) -0,75
96
9) 28
10) -13
11) 1

Вариант 27

1) 29
2) 315
3) 0,14
4) 0,03
5) 4
6) 2,72
7) 6
7
9) 77
10) 76
11) -3

Вариант 28

1) 6
2) 176
3) 0,375
4) 0,012
5) -1
6) -3
7) -3
28
9) 6
10) -5
11) 38

Вариант 29

1) 60
2) 18
3) 0,24
4) 0,2
5) 3
6) 4
7) 4
6,5
9) 6,4
10) 67
11) -21

Вариант 30

1) 64
2) 4
3) 0,28
4) 0,6
5) 4
6) 8
7) 14
9,6
9) 22
10) 3
11) -8

Вариант 31

1) 6,5
2) 54
3) 0,98
4) 0,2
5) 2
6) -10
7) 2
25
9) 54
10) -7
11) 8

Вариант 32

1) 30
2) 27
3) 0,024
4) 0,15
5) -2
6) 91
7) 3
17
9) 12
10) 13
11) -9

Вариант 33

1) 72,5
2) 47
3) 0,28
4) 0,097
5) -5
6) 65
7) 3
8
9) 48
10) -2,5
11) 26

Вариант 34

1) 68
2) 76
3) 0,16
4) 0,068
5) 6
6) 16
7) 6
633
9) 64
10) -0,25
11) -1

Вариант 35

1) 21
2) 200
3) 0,56
4) 0,9
5) -2
6) 7,5
7) 0,5
0,31
9) 20
10) 0,75
11) 9

Вариант 36

1) 35
2) 88
3) 0,12
4) 12
5) -5
6) 2,5
7) 5,5
1,728
9) 756
10) -0,5
11) 30

Источник