Векторно координатный метод при решении задач егэ

Всего: 117    1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 117    1–20 | 21–40 | 41–60 | 61–80 …

Цели:

• выработать умение рассматривать различные подходы к решению задач и
  проанализировать “эффект” от применения этих способов решения;
• выработать умение учащегося выбирать метод решения задачи в соответствии
  со своими
  математическими предпочтениями, базирующимися на более прочных знаниях и
  уверенных навыка;
• выработать умение составить план последовательных этапов для достижения
  результата;
• выработать умение обосновать все предпринимаемые шаги и вычисления;
• повторить и закрепить различные темы и вопросы стереометрии и
  планиметрии, типовые стереометрические конструкции, связанные с решением
  текущих задач;
• развить пространственное мышление.

Задачи:

• анализ различных методов решения задачи: координатно-векторный метод,
  применение теоремы косинусов, применение теоремы о трех перпендикулярах;
• сравнение преимуществ и недостатков каждого метода;
• повторение свойств куба, треугольной призмы, правильного шестигранника;
• подготовка к сдаче ЕГЭ;
• развитие самостоятельности при принятии решения.

Схема урока

Задача 1.

В кубе ABCDA₁B₁C₁D₁
с ребром 1 точка О – центр грани ABCD.

Найти:

а) угол между прямыми A₁D и BO;

б) расстояние от точки B до середины отрезка A₁D.

Решение пункта а).

1 способ. Координатно-векторный метод

Поместим наш куб в прямоугольную систему координат как показано на рисунке,
вершины A₁ (1; 0; 1), D (1; 1; 0), B₁
(0; 0; 1), O (½; ½; 0).

Направляющие векторы прямых A₁D и B₁O:

{0; 1; -1} и
{½;
½; -1};

искомый угол φ между ними находим по формуле:

cos∠φ =
,
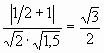
откуда∠φ = 30°.

2 способ. Используем теорему косинусов.

1) Проведем прямую В₁С параллельно прямой
A₁D. Угол CB₁O будет искомым.

2) Из прямоугольного треугольника BB₁O по теореме Пифагора:

B₁O =
.

3) По теореме косинусов из треугольника CB₁O
вычисляем угол CB₁O:

cos
CB₁O
=
,
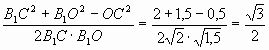
искомый угол составляет 30°.

Замечание. При решении задачи 2-м способом можно заметить, что по теореме
о трех перпендикулярах
COB₁ = 90°,
поэтому из прямоугольного ∆ CB₁O также легко вычислить косинус
искомого угла.

 Решение пункта б).

1 способ. Воспользуемся формулой расстояния между двумя
точками

Пусть точка E – середина A₁D, тогда координаты E (1; 1/2; ½), B (0; 0; 0).

BE =
.

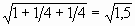
2 способ. По теореме Пифагора

Из прямоугольного ∆ BAE с прямым
BAE
находим BE =
.

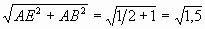
Задача 2.

В правильной треугольной призме ABCA₁B₁C₁
все ребра равны a. Найти угол между прямыми AB и A₁C.

Решение.

1 способ. Координатно-векторный метод

Координаты вершин призмы в прямоугольной системе при расположении призмы, как
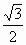
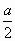
на рисунке: A (0; 0; 0), B (a;
;
0),
A₁(0; 0; a), C (0; a; 0).

Направляющие векторы прямых A₁C и AB:

{0; a; -a} и

{a;
;
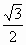
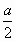
0} ;

cos φ =
;

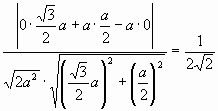
φ
= arccos
.

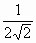
2 способ. Используем теорему косинусов

Рассматриваем ∆ A₁B₁C, в котором
A₁B₁ || AB. Имеем

 cos φ =
.

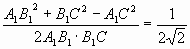
Задача 3.

(Из сборника ЕГЭ-2012. Математика: типовые экзаменационные варианты под ред.
А.Л.Семенова, И.В.Ященко)

В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁,
все рёбра которой равны 1, найдите расстояние от точки E до прямой B₁C₁.

Решение

1 способ. Координатно-векторный метод

1) Поместим призму в прямоугольную систему координат, расположив координатные
оси, как показано на рисунке. СС₁,
СВ и СЕ попарно перпендикулярны, поэтому можно направить вдоль них
координатные оси. Получаем координаты:

С₁ (0; 0; 1), Е (;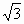
0; 0), В₁ (0;1;1).

2) Найдем координаты направляющих векторов для прямых С₁В₁
и С₁Е:

(0;1;0),

(;0;-1).

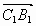
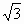
3) Найдем косинус угла между С₁В₁
и С₁Е, используя скалярное произведение векторов
и
:

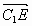
 cos β =
=
0 => β = 90° => C₁E – искомое расстояние.

4) С₁Е =
= 2.

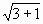
Вывод: знание различных подходов к решению стереометрических задач
позволяет выбрать предпочтительный для любого учащегося способ, т.е. тот,
которым ученик владеет уверенно, помогает избежать ошибок, приводит к успешному
решению задачи и получению хорошего балла на экзамене. Координатный метод имеет
преимущество перед другими способами тем, что требует меньше стереометрических
соображений и видения, а основывается на применении формул, у которых много
планиметрических и алгебраических аналогий, более привычных для учащихся.

Форма проведения урока – сочетание объяснения учителя с фронтальной
коллективной работой учащихся.

На экране с помощью видеопроектора демонстрируются рассматриваемые
многогранники, что позволяет сравнивать различные способы решения.

Домашнее задание: решить задачу 3 другим способом, например, с помощью
теоремы о трех перпендикулярах.

Литература

1. Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по
геометрии для 11 класса.– М.: ИЛЕКСА, – 2010. – 208 с.

2. Геометрия, 10-11: учебник для общеобразовательных учреждений: базовый и
профильный уровни / Л.С.Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.:
Просвещение, 2007. – 256 с.

3. ЕГЭ-2012. Математика: типовые экзаменационные варианты: 10 вариантов/ под
ред. А.Л.Семенова, И.В.Ященко. – М.: Национальное образование, 2011. – 112 с. –
(ЕГЭ-2012. ФИПИ – школе).

Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №2

Мастер-класс по теме 
«Применение координатно-векторного метода при решении стереометрических задач»

Подготовила

учитель математики МБОУ СОШ №2

Гергель Анна Анатольевна

11 ноября 2020

 Если ученик берется за решение стереометрической задачи, то в большинстве случаев действует поэтапно-вычислительным методом, используя определения, признаки и свойства различных фигур. Однако этот метод требует безупречного знания и понимания основных теорем, связанных с взаимным расположением прямых и плоскостей в пространстве и не всегда оказывается эффективным.

Целью моего выступления является рассмотреть и проанализировать координатно-векторный метод решения стереометрических задач. Координатный метод позволяет избежать указанных трудностей. Основная нагрузка при решении задачи координатным методом приходится на вычислительную часть. Практика показывает, что учащиеся быстро осваивают метод координат, так как при его использовании необходимо придерживаться общего алгоритма:

– рационально расположить фигуру относительно системы координат;

– вычислить координаты необходимых точек, расположенных на многогранниках;

– применить соответствующую формулу.

Координатным методом можно вычислять расстояния: между скрещивающимися прямыми, между точкой и плоскостью, между плоскостями. Следует отметить, что координатный метод в чистом виде применяется редко. На практике используют комбинированный, то есть координатно-векторный метод, который позволяет расширить спектр решаемых задач. Использование векторов позволяет находить углы между прямыми, между прямой и плоскостью, между плоскостями. Рассмотрим использование координатно-векторного метода для решения стереометрических задач, предлагаемых на ЕГЭ по математике профильного уровня. Для начала разберем наиболее удобные способы расположения системы координат относительно различных видов многогранников. 

1. Куб.

При таком расположении системы координат (рис. 4) вершины куба будут иметь следующие координаты: А(0;0;0), В(0;а;0), С(а;а;0), D(а;0;0), А1(0;0;а), В1(0;а;а), С1(а;а;а), D1(а;0;а).

Такое же расположение системы координат удобно использовать для прямоугольного параллелепипеда. Еще один вариант расположения кубаотносительно системы координат связан с размещением начала координат в точке пересечения диагоналей основания.

2. Правильная треугольная призма. Пусть в правильной треугольной призме АВСDА1В1С1D1 сторона основания равна а, а боковое ребро равно b. Разместим начало координат в точке А, ось абсцисс будет направлена вдоль ребра АС, ось ординат проходит через точку А перпендикулярно АС, ось Оz направлена вдоль бокового ребра АА1 (см. рис. 5).

Тогда вершины призмы будут иметь координаты: А(0;0;0), В(𝑎/2; 𝑎 √3/2;0), C(a;0;0), A1(0;0;b), B1(𝑎/2;𝑎√3/2;𝑏), C1(a;0;b).

Другой возможный вариант расположения правильной треугольной призмы относительно прямоугольной декартовой системы координат показан на рисунке 6.

3. Правильная шестиугольная призма.

Пусть в правильной шестиугольной призме АВСDЕFА1В1С1D1Е1F1 сторона основания равна а, а боковое ребро равно b. Разместим начало координат в точке А, ось абсцисс направим вдоль ребра АF, ось Оу – через точку А перпендикулярно АF, ось Оz – вдоль бокового ребра АА1 (смотри рисунок 7).

Тогда вершины призмы будут иметь координаты: А(0;0;0), В(−𝑎/2;𝑎√3/2;0),

C(0; a√3;0), D(а; a√3;0), Е(3а/2;𝑎√3/2;0), F(а;0;0), A1(0;0;b), B1(−𝑎/2;𝑎√3/2;𝑏),

C1(0; a√3;b), D1(а; a√3;b), Е1(3а/2;𝑎√3/2;𝑏), F1(а;0;b).

Другой вариант расположения правильной шестиугольной призмы относительно прямоугольной декартовой системы координат представлен на рисунке 8.

4. Правильная треугольная пирамида.

Пусть в правильной треугольной пирамиде МАВС сторона основания равна а, а высота равна h. Разместим начало координат в точке А, ось абсцисс

направим вдоль ребра АС, ось Оу – через точку А перпендикулярно АС, ось Оz– через точку А перпендикулярно плоскости АВС (смотри рисунок 9).

Тогда вершины пирамиды имеют координаты: А(0;0;0), В(𝑎/2;𝑎√3/2;0), C(а;0;0), М(𝑎/2;𝑎√3/6;ℎ).

Еще один вариант расположения правильной треугольной пирамиды относительно системы координат представлен на рисунке.

5. Правильная четырехугольная пирамида.

Пусть в правильной четырехугольной пирамиде МАВСD сторона основания равна а, а высота равна h.

Разместим начало координат в точке А, ось абсцисс направим вдоль ребра АD, ось Оу – вдоль ребра АВ, ось Оz – через точку А перпендикулярно плоскости АВС. Тогда вершины пирамиды имеют координаты: А(0;0;0), В(0;а;0), С(а;а;0), D(а;0;0), М(𝑎/2;𝑎/2;ℎ).

6. Правильная шестиугольная пирамида. Пусть в правильной шестиугольной пирамиде МАВСDЕF сторона основания равна а, а высота равна h. Разместим начало координат в точке А, ось абсцисс направим вдоль ребра АС, ось Оу – через точку А перпендикулярно АС, ось Оz – проходит через точку А перпендикулярно плоскости АВС (смотри рисунок 12).

Тогда вершины пирамиды имеют координаты А(0;0;0), В(−𝑎/2;𝑎√3/2;0),

C(0; a√3;0), D(а; a√3;0), Е(3𝑎/2;𝑎√3/2;0), F(а;0;0), М(𝑎/2;𝑎√3/2;ℎ).

Еще один вариант расположения правильной шестиугольной пирамиды относительно прямоугольной декартовой системы координат показан на рисунке 13

Примеры решения задач

(Сборник Лысенко Ф. Ф., Кулабухова С. Ю. Математика. Подготовка к ЕГЭ 2021. Профильный уровень.)

1. Вариант 16 № 14.

ABCDA1B1C1D1  — правильная четырехугольная призма, на ребре СС1 отмечена точка Р такая, что СР:РС1  =3:5. Плоскость проходит через точки D  и Р и параллельна прямой АС. Эта плоскость пересекает ребро ВВ1 в точке F.

а) Докажите, что сечение призмы плоскостью  является ромбом.

б) Найдите длину ребра ВВ1, если АВ=6, а площадь сечения призмы плоскостью  равна 72.

а) Т. к. противоположные грани параллелепипеда параллельны, то по свойству параллельных плоскостей сечение является параллелограммом. Для доказательства перпендикулярности диагоналей воспользуемся методом координат.

Введем прямоугольную систему координат, как показано на рисунке. Тогда D (6;0;0), К (0; 0; 3а), Р (6; 6; 3а), F (0; 6; z).  Значение z вычислим из равенства векторов DK и PF. DK{-6; 0; 3a},  PF {-6; 0 z-3a}. Z=6a.

 Вычислим скалярное произведение DF * KP. DF {-6; 6; 6a}, KP {6; 6; 0}.
DF * KP= -36+36+0=0, значит DF  KP, а значит параллелограмм DKFP – ромб.

б) Sp = .

 (по условию)

2 + а2 =8

, ВВ1 = 8а = 8

Ответ: 8

2. Вариант 33 №14

Диаметр АВ верхнего основания цилиндра перпендикулярен диаметру СD нижнего основания, при этом диаметр основания цилиндра в раз больше высоты цилиндра. Докажите, что тетраэдр АВСD – правильный.

Задачи для самостоятельного решения

1. В единичном кубе АВСDА1В1С1D1 найти угол между прямой АD1 и плоскостью α, проходящей через точки А1, Е и М, где точка Е – середина ребра С1D1, а точка М лежит на ребре DD1, так, что D1М = 2DМ.

2. В правильной шестиугольной призме АВСDЕFА1В1С1D1Е1F1, все ребра которой равны 1, найти угол между прямой АВ1 и плоскостью АСЕ1.

3. В правильной четырехугольной пирамиде МАВСК, все ребра которой равны 1, найти угол между прямой КЕ, где Е – середина апофемы МР грани АМВ, и плоскостью АМС.

Справочный материал

1. Отрезок, для которого указано, какой из его концов считается началом, а какой – концом, называется вектором  

2. Длиной ненулевого вектора АВ называется длина отрезка АВ

3. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых

4. Векторы называются равными, если они сонаправлены и их длины равны.

5. Сложение векторов:

Правило треугольника:

— отложить от какой-нибудь точки А вектор АВ, равный а (см. рис.);

— отложить от точки В вектор ВС, равный в;

— вектор АС , называется суммой векторов а и в .

Правило параллелограмма

— отложить векторы а   и в  от одной точки;

— построить на векторах а и в  параллелограмм;

— диагональ полученного параллелограмма будет суммой векторов 𝑎а  и в (см. рис.).

Правило многоугольника:

построение суммы трех и более векторов выполняют по правилу

многоугольника, состоящему в использовании правила треугольника нужное число раз.

6. Произведением ненулевого вектора а  на число к называется такой вектор в , длина которого равна |к|∙|в |, причем векторы а и в сонаправлены при k > 0 и противоположно направлены при k < 0.

7. На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом

8. Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними

9. Условие перпендикулярности векторов: два вектора перпендикулярны, если их скалярное произведение равно нулю.

10. Скалярный квадрат вектора равен квадрату его длины

11. Координаты вектора. Каждая координата вектора равна разности соответствующих координат его конца и начала.

12. Длина вектора  вычисляется по формуле

13. Координаты середины отрезка.

Каждая координата середины отрезка равна полусумме соответствующих координат его концов, т.е. если С(х; у) – середина отрезка АВ, А(х1; у1) и В(х2; у2) – его концы, то х=(х1+х2)/2, у=(у1+у2)/2

14. Расстояние между двумя точками.

Если М1(х1; у1) и М2(х2; у2), то М1М2 =

15. Уравнение окружности радиуса r с центром в точке О(х0; у0) имеет вид (х – х0)2 + (у – у0)2 = r2.

16. Уравнение прямой ах + by + c = 0.

17. Направляющим вектором прямой l называют ненулевой вектор р(а;в) лежащий на данной прямой l

18. Расстояние от точки М(х0; у0) до прямой ах + by + c = 0 вычисляется по формуле

19. Угол между прямыми. Если 𝑎 (𝑥1;𝑦1;𝑧1) и 𝑏⃗ (𝑥2;𝑦2;𝑧2) – направляющие векторы прямых a и b, φ – угол между прямыми a и b, то

20. Ненулевой вектор п , перпендикулярный к плоскости α, называют нормальным вектором плоскости α.

21. Расстояние от точки до плоскости. Если М(х0, у0, z0) — данная точка,
aх + bу +сz +d = 0 – уравнение данной плоскости α, то

Литература

1. Атанасян, Л.С., Бутузов, В.Ф., Кадомцев С.Б. и др. Геометрия. 7-9 классы: учеб. для общеобразоват. организаций. – М.: Просвещение, 2018

2. Александров А.Д. Геометрия. 9 класс: учеб. для общеобразоват. организаций. – М.: Просвещение, 2014.

3. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия. 10-11 классы: учеб. для общеобразоват. организаций. – М.: Просвещение, 2020.

4. Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения. – 102

5. Лысенко Ф. Ф., Кулабухова С. Ю. Математика. Подготовка к ЕГЭ 2021. Профильный уровень.

8 ноября 2020

В закладки

Обсудить

Жалоба

С помощью данных методических рекомендаций можно научиться решать задачи на вычисление углов и расстояний в стереометрии координатно-векторным методом.

Координатно-векторный метод основан на введении прямоугольной системы координат и создании геометрически-алгебраической модели решения задач, тем самым упрощая громоздкие и достаточно сложные преобразования и выкладки.

Достоинство метода координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных конфигураций.

→ 14kvm.doc
→ Другое пособие по теме
→ Пособие к 14 задаче
→ Экзаменационные задачи

«Использование метода координат в пространстве для решения задачи №13 Единого государственного экзамена»

Как всем известно, для учеников старших классов самой насущной проблемой является Единый государственный экзамен. Причём, тех учеников, которые с уверенностью могут сказать: «Я могу решить 13 или 16 задачу», всего единицы. Да и те, кто действительно могут решить их, об этом громко не заявляют.

Анализируя данную проблему, можно сказать, что большая часть выпускников ограничивается заданием 13 пункта а). А при решении пункта б) уже возникают проблемы.

Как вы знаете, в задании 13 чаще всего требуется найти:

1) угол между двумя скрещивающимися прямыми, между прямой и плоскостью, между двумя плоскостями;

2) расстояние между двумя скрещивающимися прямыми, расстояние от точки до прямой, от точки до плоскости.

В своей работе я предлагаю использовать один из универсальных приёмов решения геометрических задач – метод координат в пространстве. Мы уже хорошо знакомы с векторами, координатами и их свойствами. Цель моей работы: научиться применять знания для решения задач стереометрии.

Однако формальное применение координатно-векторного метода может значительно затруднить решение даже самой простой задачи. Поэтому я привожу несколько общих указаний, которые помогут сориентироваться и решить, можно ли в данной задаче использовать векторы и координаты.

Во-первых, естественно, нужно применять координатный или векторный метод, если в условиях задачи говорится о векторах или координатах;

Во-вторых, очень полезно применить координатный метод, если из условия задачи не понятно, как расположены те или иные точки;

В-третьих, что для нас особенно важно, полезно и удобно применять координаты и векторы для вычисления углов и расстояний;

В-четвертых, вообще, часто, когда не видно ни каких подходов к решению задачи, можно попробовать применить координатный метод. Он не обязательно даст решение, но поможет разобраться с условиями и даст толчок к поиску другого решения.

2.1. Кратко из теории⁴

Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки. Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Существует множество систем координат: аффинная, полярная, биполярная, коническая, параболическая, проективная, сферическая, цилиндрическая и др. Наиболее используемая из них — прямоугольная система координат (также известная как декартова система координат). Ею мы и будем пользоваться для решения задач.

Прямоугольная (декартова) система координат – совокупность точки О (называемой началом координат), единицы измерения и трёх попарно перпендикулярных прямых Ox, Oy и Oz (называемых осями координат: Ox – ось абсцисс, Oy – ось ординат, Oz – ось аппликат), на каждой из которых указано направление положительного отсчёта. Плоскости хОу, уОz и zOx называют координатными плоскостями. Каждой точке пространства ставится в соответствие тройка чисел, называемых её координатами.

Применение метода координат даёт нам множество возможностей для решения задач.

1. Нахождение расстояния между двумя точками, заданными своими координатами.

где d=AB, A(x₁; y₁; z₁), B(x₂; y₂; z₂)

2. Нахождение координаты середины С(x; y; z) отрезка АВ, A(x₁; y₁; z₁), B(x₂; y₂; z₂). , ,

3. Нахождение косинуса, а, следовательно, и самого угла, между двумя векторами, заданными своими координатами.

где .

4. Нахождение угла между плоскостями путем составления уравнения каждой плоскости Ах+Ву+Сz+D=0 и определения угла между нормалями к плоскостям. Нормаль n при этом имеет координаты .

5.Нахождение расстояния от произвольной точки М₀(х₀, у₀, z₀)  до плоскости Ах+Ву+Сz+D=0 равно.

6. Координаты x, y, z точки М, которая делит отрезок , ограниченный точками (, , ) и (, , ), в отношении , определяется по формулам

, , .

2.2. Нахождение угла между скрещивающимися прямыми

• Углом между скрещивающимися прямыми называется угол между двумя прямыми, параллельными им и проходящими через произвольную точку.
• 0˚<(a,α)<90˚.

При нахождении угла между прямыми используют:

формулу или в координатной форме

для нахождения угла φ между прямыми m и l, если векторы и параллельны соотвественно этим прямым; в частности, для того чтобы прямые m и l были перпендикулярны, необходимо и достаточно, чтобы или .

Пример 1.⁵ Сторона основания правильной четырехугольной призмы ABCDA₁B₁C₁ D₁ равна 2, высота — 4. Точка E — середина отрезка CD, точка F — середина отрезка AD. Найдите угол между прямыми CF и B₁E.

х

у

z

B₁

A₁

C₁

D₁

B C

A E

F D

Решение.

Для начала сделаем чертёж и проанализируем задачу.

Прямые CF и B₁E являются скрещивающимися, поэтому, чтобы найти угол между ними геометрическим способом, было бы необходимо параллельно перенести одну из прямых так, чтобы обе прямые лежали на одной плоскости. При этом было бы довольно сложно определить, в каком соотношении они будут пересекаться, и решить эту задачу поэтапно-вычислительным методом.

Я предлагаю поместить параллелепипед в прямоугольную систему координат, как показано на рисунке, и найти искомый угол как угол между векторами.

Выпишем координаты точек B₁, E, C, F в этой системе координат:

B₁ (0; 0; 4), E(1; 2; 0), C(0; 2; 0), F (2; 1; 0).

Тогда {2; -1; 0}, {1; 2; -4}. Найдём угол между этими векторами по формуле:

То есть искомый угол α=90˚.

Как видите, задачу, которую довольно-таки сложно решить геометрическим путём, можно быстро и красиво решить аналитически.

Ответ: 90˚.

Пример 2.² Точка О лежит на ребре DD₁ куба ABCDA₁B₁C₁ D₁, точка Р является точкой пересечения диагоналей грани ABCD. DO : DD₁ = 1 : 5. Найдите косинус угла между прямой ОР и прямой, содержащей диагональ куба, выходящую из вершины С.

Решение.

Поместим куб в прямоугольную систему координат, как показано на рисунке. Условно обозначим грани куба за единицу. Если обозначить её какой-либо буквой, она всё равно сократится. Определим координаты точек Р, О, С и А₁:

О

Р

Р(0,5; 0,5; 0), О(1; 1; 0,5), С(0; 1; 0), А₁(1; 0; 1).

Отсюда .

Ответ: .

Пример 3.⁵ Основанием пирамиды SABC является равносторонний треугольник ABC, сторона которого равна . Боковое ребро SC перпендикулярно плоскости основания и равно 1. Найдите угол между скрещивающимися прямыми, одна из которых проходит через точку S и и середину ребра DC, а другая проходит через точку C и середину ребра AB.

Решение.

Поместим пирамиду в декартову систему координат. Найдём координаты точек S, L, C и M: S(0;0;1), L(0;;0), C(0;0;0). Чтобы найти координаты точки М, воспользуемся геометрией: в равностороннем треугольнике все углы равны 60˚, а т.М, которая делит сторону АВ пополам, является не только медианой, но и биссектрисой, поэтому .

Для равностороннего треугольника , х(СМ)=СМ·соs60˚=, у(СМ)=СМ·соs30˚=, {}, SL{0;;-1}

Решая аналогично предыдущим примерам, находим, что .

Ответ: 45˚.

2.3. Нахождение угла между прямой и плоскостью

• Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и её проекцией на данную плоскость.
• 0˚<(a,α)<90˚.

Угол между прямой l и плоскостью α можно вычислить:

по формуле или в координатах , где

— вектор нормали к плоскости α,

— направляющий векор прямой l;

Пример 4.⁵ В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ рёбра АВ и АА₁ равны 1, а ребро АD=2. Точка Е – середина ребра В₁С₁. Найдите угол между прямой ВЕ и плоскостью АВ₁С.

Решение. Для решения этой задачи необходимо воспользоваться уравнением плоскости, имеющим общий вид

ах+bу+cz+d=0, где a, b и c – координаты нормали к плоскости.

Чтобы составить это уравнение, необходимо определить координаты трёх точек, лежащих в данной плоскости: А(1; 0; 0), В₁(0;0;1), С(0;2;0).

Решая систему

находим коэффициенты а, b и с уравнения ах+bу+cz+d=0: а= -d, b=,

c=-d. Таким образом, уравнение примет вид или, после упрощения, 2х+у+2z-2=0. Значит нормаль n к этой плоскости имеет координаты .

Длину вектора легко найти геометрически: . Но его координаты нам всё равно необходимы. Из простых вычислений находим, что .

Найдем угол между вектором и нормалью к плоскости по формуле скалярного произведения векторов:

.

Ответ: 45˚

2.4. Нахождение угла между двумя плоскостями

• Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру.
• Величина двугранного угла принадлежит промежутку(0˚; 180˚)
• Величина угла между пересекающимися плоскостями принадлежит промежутку (0˚; 90˚].
• Угол между двумя параллельными плоскостями считается равным 0˚.

Угол между двумя пересекающимися плоскостями можно вычислить:

как угол между нормалями по формуле или в координатной форме , где — вектор нормали плоскости А₁х+В₁у+С₁z+D₁=0, — вектор нормали плоскости A₂x+B₂y+C₂z+D₂=0.

Пример 5.¹ В единичном кубе АВСDA₁В₁С₁D₁ найдите угол между плоскостями АD₁ Е и D₁FC, где точки Е и F-середины ребер А₁В₁ и В₁С₁ соответственно.

Решение.

Введём прямоугольную систему координат. Тогда А(0;0;0), С(1;1;0), D₁(1;0;1), E(0;0,5;1), F(0,5;1;1).

1) Решая систему

, составляем уравнение плоскости (АD₁E): x+2y-z=0.

2) плоскость CFD₁:

отсюда находим уравнение 2x+y+z-3=0. Найдём искомый угол как угол между нормалями плоскостей.

, , откуда φ=60˚ Ответ: 60˚

2.5. Нахождение расстояния между двумя точками.

Расстояние между точками А и В можно вычислить:

по формуле ,

где A(x₁; y₁; z₁), B(x₂; y₂; z₂);

по формуле .

Пример 6.⁶ В основании пирамиды SABCD лежит ромб со стороной 2 и острым углом в 60˚. Боковое ребро SA перпендикулярно основанию пирамиды и равно 4. Найдите расстояние от середины Н ребра SD и серединой М ребра ВС.

Решение. Поместим пирамиду в прямоугольную систему координат, как показано на рисунке.

Найдём координаты точки Н как координаты середины отрезка SD: S(0; 0; 4), D(0; 2; 0).

Чтобы найти координаты точек В и С, найдём координаты их проекций на оси. АВ_х=AC_x=2·cos30˚=, AB_y=AC_у–2=2·cos60˚=1.

Отсюда В(; 1; 0), С(; 3;0). Тогда координаты точки М равняются:

.

Теперь находим расстояние между точками, заданными своими координатами:

Ответ: .

Пример 7.¹ В единичном кубе АВСDA₁В₁С₁D₁ точки Е и К – середины ребер АА₁ и СD соответственно, а точка М расположена на диагонали В₁D₁ так, что В₁М = 2МD₁. Найдите расстояние между точками Q и L, где Q – середина отрезка ЕМ, а L – точка отрезка МК такая, что ML=2LK

Решение. Введём декартову систему координат. E(1;0;0,5), K(0,5;1,0), В₁(0;0;1), D₁(1;1;1). Чтобы вычислить координаты т.М, воспользуемся формулой для нахождения координат точки, которая делит отрезок B₁D₁ в отношении λ=2:1:

, , .

Аналогично находим координаты точки L:

.

Координаты точки Q находим по формуле координат середины отрезка:

, , .

Ответ: .

2.6. Нахождение расстояния от точки до плоскости.

Расстояние от точки до плоскости , не содержащей эту точку , есть длина отрезка перпендикуляра , опущенного из этой точки на плоскость .

Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра.

Расстояние между прямой и параллельной ей плоскостью равно расстоянию от любой точки этой прямой до плоскости.

Расстояние между двумя параллельными плоскостями равно длине их общего перпендикуляра.

Расстояние между двумя параллельными плоскостями равно расстоянию между точкой одной из этих плоскостей и другой плоскостью.

Расстояние от точки М до плоскости α

вычисляется по формуле , где М(х₀;у₀;z₀), плоскость α задана уравнением ax+by+cz+d=0;

Пример 8.² В кубе АВСDA₁B₁C₁D₁ проведена диагональ B₁D. В каком отношении, считая от вершины B₁, плоскость А₁BC₁ делит диагональ B₁D?

Решение. Составим уравнение плоскости А₁BC₁ и найдём расстояние от этой плоскости до каждой из точек B₁ и D. Пусть l – ребро куба.

В(0;0;0), А₁(l;0;l), С₁(0;l;l).

Решив систему определяем, что уравнение плоскости имеет вид: x+y–z=0 → а=1, b=1, c= –1. B₁(0;0;1), D(1;1;0).

Теперь найдём расстояние от каждой точки до плоскости по формуле

:

Ответ: 2:1.

Пример 9.⁵ Основание прямой призмы АВСА₁В₁С₁ – равнобедренный треугольник АВС, основание АС и высота ВD которого равны 4. Боковое ребро равно 2. Через середину К отрезка В₁С проведена плоскость, перпендикулярная к этому отрезку. Найдите расстояние от вершины А до этой плоскости.

Решение. Выберем систему координат как показано на рисунке и выпишем координаты вершин данной призмы и точки К в этой системе координат: А(0;–2;0), В(0;0;0), С(0;2;0), В₁(4;0;2), К(2;1;1). Тогда . Этот вектор перпендикулярен плоскости, значит, он является его нормалью. К тому же плоскость проходит через точку К. То есть уравнение плоскости имеет вид –2(x–2)+2(у–1)–2(z–1)=0 или, после упрощения, 2x–y+z-4=0.

Теперь находим расстояние от т.А(0;-2;0) до плоскости:

. Ответ: .

Заключение

Представляю вашему вниманию свою работу, которой я занималась в течение последних месяцев: я искала формулы, подбирала для каждого случая именно те задачи, геометрическое решение которых перегружено формулами, редко используемыми теоремами, сложными преобразованиями и вычислениями.

Конечно, эту работу нельзя считать авторитетным пособием по решению задания 13 ЕГЭ, так как в ней рассмотрено лишь небольшое количество задач, и ограниченное количество приёмов.

Конечно, я не настаиваю на том, что все задачи стереометрии надо решать методом координат, иногда это просто нецелесообразно. Но согласитесь, настолько простое и изящное решение не только освободит время для решения других заданий, но и будет высоко оцениваться проверяющим учителем.

Список использованной литературы

1. Самое полное издание типовых вариантов реальных заданий ЕГЭ 2010: Математика /авт.-сост . И.Р.Высоцкий, Д.Д.Гущин, П.И.Захаров и др.; под ред. А.Л.Семенова, И.В.Ященко. – М.: АСТ: Астрель , 2009. – (ФИПИ).

2. Математика. Подготовка к ЕГЭ-2011: учебно-методическое пособие/ под ред. Ф.Ф.Лысенко, С.Ю.Калабухова. – Ростов-на-Дону: Легион – М., 2010.

3. Единый государственный экзамен 2010. Математика. Универсальные материалы для подготовки учащихся / ФИПИ – М.: Интеллект -Центр, 2010.

4. Большая универсальная школьная энциклопедия/ гл. редактор М.Аксёнова – М.: Мир энциклопедий Аванта+, Астрель, 2008.

5. www.fmclass.ru – образовательный портал «Физ/мат класс»

6. www.mathege.ru – открытый банк заданий.

7. www.problems.ru – каталог задач.

1. Стереометрия

Векторно- координатный
метод в решении задач
№14 ЕГЭ

2.

Угол между прямыми
а
р
q
b
р
q
cos =
р
— направляющий вектор прямой а
q
— направляющий вектор прямой b
— угол между прямыми
p x1 ; y1 ; z1
q x2 ; y2 ; z2
| x1 x2 + y1 y2 + z1 z 2 |
x12 + y12 + z12 x22 + y22 + z 22

3.

Задача 1. В единичном кубе A…D1 найдите угол
между прямыми AE и BF, где Е – середина
ребра А1В1 , а F – середина ребра B1С1
А1
K
Е
A1D1
KAE
К — середина
B1 F
D
А
Решение (1 способ)
С1
D1
AK || BF
С
5
AE AK
2
2
KE
2
По теореме косинусов для
B
AKE
KE AE AK 2 AE AK cos
cos 0,8
arccos 0,8
2
2
2

4.

z
Решение (2 способ)
1
А(1;0;0)
Е (1; ;1)
B1 F
2
1
В(1;1;0)
F ( ;1;1)
2
С
1
1
y АЕ 0; ;1
BF ;0;1
2
2
B
С1
D1
А1
Е
D
А
x
cos =
1 1
| 0 0 1 1 |
2 2
2
2
1
1
2
2
2
0 1 0 1
2
2
2
0,8

5. Задача2. Точка К – середина ребра АА1 куба АВСDA1B1C1D1. Найдите угол между прямыми А1В и СК.

1способ
С1
D1
1
А1
1
2
В1
5
2
a
D
1
2
А
1
В
KD1 KA1 A1 D1 ;
2
2
2
2
2
К
Из KA1 D1 :
1
2
KD1 12 ;
2
1
2
Из CC1 D1 :
KD1 1 ;
2
2
2
4
CD1 CC1 C1 D1 ;
5
KD1 ; CD12 12 12 ;
С
4
2
CD
1
1 2;
5
KD1
.
CD1 2 ;
2
CD1 2 .

6.

Точка К – середина ребра АА1 куба АВСDA1B1C1D1. Найдите угол
между прямыми А1В и СК.
Из треугольника
KBC
D1
С1Составляем теорему косинусов для
стороны KD1:
1
А1
1
2
5
2
5 3 2
2 2
2
3
2
D
А
2
В1
К
1
2
3
KC
2
a
5
2
1
1
В
2 2 32
2
1
3 2 cos a 3
С
cos a
cos a
3
3 2
2
2
a 450
2 cos a

7.

Задача 2. Точка К – середина ребра АА1 единичного куба
АВСDA1B1C1D1. Найдите угол между прямыми А1В и СК.
2 способ
x x y y z z
1
2
1
2
1
2
BA1{z0; 1;1}; KC{ 1;1; 1 } cos
2
2
2
2
2
2
2
x
y
z
x
y
z
1
1
1
2
2
2
D1
С
1
1
(1;0;1)
А1?
В1
cos
1
0 1 1 1 1
2
1
2
2
0 2 1 12 1 12
2
1
(1;0; 2 )
К?
С(?0;1;0)
cos
D
1
х
А
1
1
?
В(1;1;0)
1
1
2
1
2 2
4
2
cos
2
3
2
9
2
4
3
2
2
450
3
2
2

8.

Задача 3 В правильной треугольной призме
ABCA1B1C1
все ребра которой равны 1, найдите косинус угла
между прямыми AD и CE, где D и E — соответственно
середины реберA1C1 иB1C1
z С
1
С
E
D
А1
А
1
3
2
B
1
y
B
x
y
1
2
B1
С
Решение.
А
x

9.

Координаты правильной треугольной
призмы
z С (0;0;1)
1
1 3
B1 ( ; ;1)
2 2
А1 (1;0;1)
С (0;0;0)
y
x
А(1;0;0)
1 3
B( ; ;0)
2 2

10.

Решение.
1
D( ;0;1)
2
z С1 (0;0;1)
1 3
Е ( ; ;1)
4 4
1 3
B1 ( ; ;1)
2 2
А1 (1;0;1)
С (0;0;0)
y
x
А(1;0;0)
1 3
B( ; ;0)
2 2
1
АD ;0;1
2
1 3
СЕ ;
;1
4 4

11.

1
АD ;0;1
2
cos =
1 3
СЕ ;
;1
4 4
1 1
3
| 0
1 1 |
2 4
4
2
1
1 3
2
2
2
1
0 1
2
4 4
2
cos =
2
7
8
5
5
2
2
0,7

12.

Задача 4. В правильной шестиугольной призме A…F1
все ребра которой равны 1, найдите косинус угла между
прямыми AB1 и BD1
Решение.
z
F1
Е
D1
E1
А1
E
F
x
А
B
1
1
2
F
D
D
y
С1
B1
1
С
3
2
1
С
3
2
y
А
x
В

13.

Координаты правильной шестиугольной
призмы
D
(
0
;
1
;
1
)
E
(
0
;
0
;
1
)
1
1
z
F1
E1
А1
D1
B1
Е
x
С1
D
y
F
А
В
С
А1 ( 3;0;1)
3 3
С1 ( ; ;1)
2 2
B1 ( 3;1;1)
E (0;0;0)
D(0;1;0)
3 1
F1 ( ; ;1)
2 2
3 3
3 1
F ( ; ;0) С ( ; ;0)
2 2
2 2
А( 3;0;0)
B ( 3;1;0)

14.

Решение.
z
F1
D1
E1
А1
С1
B1
E
С
F
x
B1 ( 3;1;1)
D1 (0;1;1)
АВ1 0;1;1
D
А
А( 3;0;0)
B ( 3;1;0)
y
ВD1 3;0;1
B
| 0 ( 3 ) 1 0 1 1 |
cos =
0 1 1
2
2
2
3 0
2
2
1
2
1
2 2

15.

Задача 5. В правильной четырехугольной пирамиде
SABCD, все ребра которой равны 1, отмечены точки Е и
F – середины сторон SB и SC соответственно. Найдите
угол между прямыми AE и BF.
z
Решение.
S
F
E
D
О
x
А
В
AC 12 12 2
2
С
AО
2
y
2
2
2
2
SO 1
2
2

16.

Координаты правильной четырехугольной
пирамиды
z
D(0;0;0)
1 1 2
S( ; ;
)
2 2 2
С (0;1;0)
y
x А(1;0;0)
В(1;1;0)

17.

z
D
1 1 2
S( ; ;
)
2 2 2
F
E
С (0;1;0)
y
x
А(1;0;0)
В(1;1;0)
1 3 2
АE ; ;
4 4 4
Решение.
Е- середина SB
3 3 2
Е( ; ;
)
4 4 4
F- середина SC
1 3 2
F( ; ;
)
4 4 4
3 1 2
BF ; ;
4 4 4

18.

1 3 2
АE ; ;
4 4 4
cos =
3 1 2
BF ; ;
4 4 4
1 3 3 1
2 2
|
|
4 4 4 4 4 4
2
1 3 2
3 1 2
4 4 4
4 4 4
2
2
1
cos
6
2
2
1
arccos
6
2

19.

Угол между прямой и плоскостью
р х1; у1; z1 — направляющий вектор прямой
n x2 ; у2 ; z2 — нормальный вектор плоскости
а
n a
n
р
a
sin
| x1 x2 y1 y2 z1 z 2 |
x y z x y z
2
1
2
1
2
1
2
2
2
2
2
2

20.

Задача 6. Дан прямоугольный параллелепипед
АВСDA1B1C1D1
(АВ = AD = 2, АА1 = 1). Найти угол между прямой АС1 и
плоскостью
АВ1С.
z
B1
C1
D1
C (0;0;0), A(2;2;0) C1 0;0;1 B1 0;2;1
x y 2 z 0 n 1; 1;2
A1
C
B
у
D
A
х
Ответ:
6
arcsin
9
sin AC1 ; AB1C cos AC1 ; n
2 2 2
6
9
4 4 1 1 1 4

21.

Задача 7. В правильной четырехугольной пирамиде
SABCD , все ребра которой равны 1, найдите угол
между прямой DE, где Е- середина апофемы SF грани
ASB и плоскостью ASC
Решение.
z
S(0;0;
1
4
О
1
2
1
2
x
ОВ — вектор нормали
Е(0; ;
С
D( ; ;0)
ОВ ASC
2
)
2
А
ASC
DE — направляющий вектор прямой
2
) 1 1
4 В( ; ;0)
2 2
1
F(0; ;0)
2
плоскости
y
1 1
ОВ ; ;0
2 2
1 3 2
DE ; ;
2 4 4

22.

1 1
ОВ ; ;0 — вектор нормали плоскости ASC
2 2
1 3 2
DE ; ;
— направляющий вектор прямой DE
2 4 4
sin
2
1 1 1 3
| 0
|
4
2 2 2 4
1 1
1 3 2
2
0
2
2
2
4
4
2
5
8
2
5
sin
2 15
30
2
4
2
2
5
arcsin
30
2

23.

Уравнение плоскости, проходящей через
данную точку перпендикулярно данному
вектору
n{a; b; c}
А( x0 ; у0 ; z0 ) a
В( x; y; z )
a
n a
n{a; b; c}-нормальный
вектор плоскости
А( x0 ; у0 ; z0 )
В( x; y; z ) a
АB x x0 ; y y0 ; z z0
n АB 0
a( x x0 ) b( y y 0 ) c( z z0 ) 0
ax by cz d 0
, где
d (ax0 by0 cz0 )

24.

Уравнение плоскости
a( x x0 ) b( y y 0 ) c( z z0 ) 0
ax by cz d 0
, где
d (ax0 by0 cz0 )
Если плоскость проходит через начало координат, то d=0
z
С
Если плоскость пересекает оси
координат в точках А, В, С, то
В
x
А
y
x y z
1
A B C
уравнение плоскости в отрезках

25.

Задача 8. Составить уравнение плоскости,
проходящей через точки А(-2;3;5), В(4;-3;0), С(0;6;-5)
и найти координаты вектора нормали.
Решение.
ax by cz d 0
2a 3b 5c d 0
4a 3b d 0
6b 5c d 0
d 5c 6b
2a 3b 10c 0
4a 9b 5c 0
5
5
a c, b c, d 5c
2
3
5
5
cx cy cz 5c 0
2
3
15 x 10 y 6 z 30 0
n{15;10;6}

26.

Расстояние от точки до плоскости
M ( x0 ; у0 ; z0 )
n{a; b; c}
a
(M ,a )
| ax0 by0 cz0 d |
a b c
2
2
2

27.

Расстояние между
параллельными плоскостями
a
ax by cz d1 0
ax by cz d2 0
(a , )
| d 2 d1 |
a b c
2
2
2

28.

Задача 9. В правильной четырехугольной пирамиде
SABCD, все ребра которой равны 1, найдите расстояние
от середины ребра ВС до плоскости SCD
Решение.
z
S
y
y
А
D
В
M
С
x
А
О
2
D (0;
;0)
2
2
2
С(
;0;0)
В (0;
;0)
2
2
2
2
М(
;
;0)
4
4
x

29.

z
Решение.
2
S (0;0;
)
2
(M ,a )
| ax0 by0 cz0 d |
a 2 b2 c2
y
А
В
2
2
M(
;
;0)
4
4
2
D (0;
;0)
2
2
С(
;0;0)
2
x
x
y
z
1
2
2
2
2
2
2
2x 2 y 2z 1 0
2
2
2 0 1|
| 2
2
4
4
1
( M , SCD)
2
2
2
6
2 2 2

30.

Угол между плоскостями
a : a1x b1 y c1z d1 0
Вектор нормали плоскости a : n1{a1 ; b1 ; c1}
: a2 x b2 y c2 z d2 0
Вектор нормали плоскости : n2 {a2 ; b2 ; c2 }
cos
| a1 a2 b1 b2 c1 c2 |
a1 b1 c1 a2 b2 c2
2
2
2
2
2
2

31.

Угол между плоскостями равен углу между
перпендикулярами к этим плоскостям.
a1 x b1 y c1 z d1 0 уравнение плоскости a
a2 x b2 y c2 z d 2 0 уравнение плоскости
m a1 ; b1 ; c1 a
n
n a2 ; b2 ; c2
cos m;n
m
a1a2 b1b2 c1c2
a b c
2
1
2
1
2
1
a b c
2
2
2
2
2
2

32.

Задача 10. В единичном кубеA…D1
найдите угол
между плоскостями AD1 E и D1FC , где Е – середина
ребра А1В1 , а F – середина ребра B1С1
Решение.
z
Е
А1
B1
A(0;0;0)
С1
B
А
D
x
С
D1 (1;0;1)
ax by cz d 0
F
D1
1
Е (0; ;1)
2
y
d 0
a c d 0
1
b c d 0
2
Уравнение плоскости
с а
b 2a
ax 2ay az 0
AD1E : x 2 y z 0
Вектор нормали плоскости
AD1E :
n1{1;2; 1}

33.

z
Е
А1
D1 (1;0;1)
B1
С1
B
А
D
x
С (1;1;0)
ax by cz d 0
F
D1
1
F ( ;1;1)
2
а с d 0
1
a b c d 0
2
a b d 0
y
С
a 2c
b c
d 3c
2cx cy cz 3c 0
Уравнение плоскости
Вектор нормали плоскости
D1FC : 2 x y z 3 0
D1FC : n2{2;1;1}

34.

cos
| a1 a2 b1 b2 c1 c2 |
a1 b1 c1 a2 b2 c2
2
2
2
n1{1;2; 1}
2
2
2
n2 {2;1;1}
| 1 2 2 1 1 1 |
1
cos
12 2 2 ( 1) 2 2 2 12 12 2
3

35. Задача 11. В единичном кубе найдите угол между плоскостями (АСD1) и (ВDC1).

A (1; 0; 0) D1 (0; 0; 1)
C (0; 1; 0)
z
D (0; 0; 0) C1 (0; 1; 1)
B (1; 1; 0)
у
х
Запишем уравнения
плоскостей (АСD1) и
(BDC1):

36.

ax by cz d 0
a d 0
b d 0
c d 0
a d
b d
c d
dx dy dz d 0
d 0
a b d 0
b c d 0
d 0
a b
c b
bx by bz 0
A (1; 0; 0)
C (0; 1; 0)
D1 (0; 0; 1)
D (0; 0; 0)
B (1; 1; 0)
C1 (0; 1; 1)
cos m;n
x y z 1 0
m 1;1;1 ACD1
x y z 0
n 1; 1;1 DBC1
1 1 1 1 1 1
1 1 1 1 1 1
m; n arccos
2
1
3
2
2
2
2
1
Ответ: arccos
3
2
1
3

37. Задача 12. В правильной треугольной призме все ребра равны 1. Найдите угол между плоскостями (АВС1) и (А1В1С).

z
С1
В1
А1
С
А
х
В
3
1
A ;0;0 B 0;
;0
2
2
1
C1 ;0;1
2
3
1
A1 ;0;1
B1 0;
;1
2
2
1
C ;0;0
2
Запишем уравнения
плоскостей (АBС1) и
у (A1B1C):

38.

1
A ;0;0
2
ax by cz d 0
1
2 a d 0
3
B 0;
;0 3 b d 0
2 2
1
1 a c d 0
C1 ;0;1
2
2
1
A1 ;0;1
2
3
B1 0;
;1
2
1
C ;0;0
2
1
2 a c d 0
3
b c d 0
2
1
2 a d 0
a 2d
2
b
d
3
c 2d
a 2d
2
d
b
3
c 2d
2
dy 2dz d 0
3
2
2x
y 2z 1 0
3
2dx
2
m 2;
; 2 ABC1
3
2
2dx
dy 2dz d 0
3
2x
2
y 2z 1 0
3
2
n 2;
; 2 A1 B1C
3

39.

2
n 2;
; 2
3
2
m 2;
; 2
3
cos m;n
2 2
2 2
2 2
3 3
2
1
2
2
7
2
2
2
2
2
22
2
2
3
3
1
m; n arccos
7
1
Ответ: arccos
7

40. Задача 13. В правильной шестиугольной призме ребро основания равно 1, а боковое ребро – 2. Найдите угол между плоскостями

(ВА1D1) и
(АА1Е1).
1 3
z
1 3
B ;
;0
2 2
1 3
A1 ;
; 2
2 2
A ;
;0
2 2
1
3
E ;
;0
2
2
C (1; 0;0)
х
у
Запишем уравнения
плоскостей (А1BC) и
(AA1E):

41.

ax by cz d 0
1 3
B ;
;0
2 2
1 3
A1 ;
; 2
2 2
C (1; 0;0)
1
3
b d 0
a
2
2
1
3
a
b 2c d 0
2
2
a d 0
1
1
dx
dy dz d 0
2
3
1
1
x
y z 1 0
2
3
a d
1
b
d
3
1
c d
2
1 1
m 1;
; A1 BC
3 2

42.

1
A ;
2
1
A1 ;
2
3
;0
2
3
; 2
2
1
3
E ;
;0
2
2
ax by cz d 0
1
a
2
1
a
2
1
a
2
3
b d 0
2
3
b 2c d 0
2
3
b d 0
2
2dx 0 y 0 z d 0
2x 0 y 0 z 1 0
n 2; 0; 0 A1 AE
a 2d
b 0
c 0

43.

1 1
m 1;
;
3 2
cos m;n
n 2; 0; 0
1
1
1 2
0 0
2
3
2
2
1 1
2
2
2
12
2
0
0
3 2
12
19
12
m; n arccos
19
12
Ответ: arccos
19

44.

Задача 14. В правильной четырехугольной призме АВСDA1B1C1D1
стороны основания равны 2, а боковые ребра равны 5. На ребре АА1
отмечена точка Е так, что АЕ : ЕА1 = 3 : 2. Найдите угол между
плоскостями АВС и ВЕD1. (Обсудить нахождение линейного угла
двугранного угла).
D1
FPC – линейный
C1
A1
угол
двугранного угла
FBOC
3
B1
2
F
5E
2
3
a
2
А
O
C
D
2
В
P

45.

В правильной четырехугольной призме АВСDA1B1C1D1 стороны
основания равны 2, а боковые ребра равны 5. На ребре АА1 отмечена
точка Е так, что АЕ : ЕА1 = 3 : 2. Найдите угол между плоскостями АВС и
ВЕD1.
2 способ.
a : a x b y c z d 0
1
1
1
1
Вектор нормали плоскости
D1
:
z
n1{a1 ; b1 ; c1}
a2 x b2 y c2 z d 2 0
Вектор нормали плоскости
:
n2 {a2 ; b2 ; c2 }
C1
cos
A1
B1
2
| a1 a2 b1 b2 c1 c2 |
a1 b1 c1
2
2
E(2;0;3), B(2;2;0),
F
2
n ( BED1 )
a2 b2 c2
2
2
a=c
d=-5c
b=1,5c
n
2x+3y+2z-10=0
{2;3;2}
D
2
А
x
2
В
y
cos
2
DD1 {0; 0;5},
D1 (0;0;5).
2a+3c+d=0
5c+d=0
2a+2b+d=0
E
5
3
a:
0 2 0 3 5 2
0 2 0 2 5 2 2 2 32 2 2
2
17

46. Использование ИКТ при подготовке к ЕГЭ.

Название сайта
Материалы сайта
Электронный адрес
Все задачи открытого банка
http://reshuege.ru/
заданий ЕГЭ по математике 2013
года с образцами решений.
ALEXLARIN.NET
Материалы прошлых лет.
Диагностические и
тренировочные работы.
АВ Alleng
Учебные материалы (книги,
http://www.alleng.ru
учебники, пособия, справочники
и т.п.) размещенные на самом
сайте.
Открытый банк заданий ЕГЭ по математике
Задания, тренировочные работы, http://mathege.ru
документы
МИФИст
Решённые задачи открытого
банка
Документы, КИМы
http://live.mephist.ru/sho
w/mathege2010/
http://www.fipi.ru/
Документы, новости,
мероприятия
http://ege.edu.ru/
Федеральный институт педагогических измерений
Официальный информационный портал ЕГЭ
http://alexlarin.net/