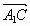Векторный метод в стереометрии егэ

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора:

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Сумма векторов:

Разность векторов:

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

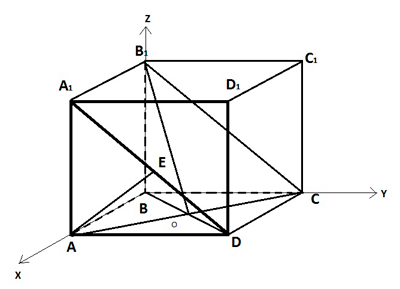
1.  В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2.  В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и :

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму.

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

Для точки M:

То есть A + C + D = 0.

Для точки N:

Аналогично для точки K:

Получили систему из трех уравнений:

.

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

;

.

Выразим C и B через A и подставим в третье уравнение:

.

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Упростим систему:

.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике»

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Итак, AA₁ = √3

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор  или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

  

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

Цели:

• выработать умение рассматривать различные подходы к решению задач и
  проанализировать “эффект” от применения этих способов решения;
• выработать умение учащегося выбирать метод решения задачи в соответствии
  со своими
  математическими предпочтениями, базирующимися на более прочных знаниях и
  уверенных навыка;
• выработать умение составить план последовательных этапов для достижения
  результата;
• выработать умение обосновать все предпринимаемые шаги и вычисления;
• повторить и закрепить различные темы и вопросы стереометрии и
  планиметрии, типовые стереометрические конструкции, связанные с решением
  текущих задач;
• развить пространственное мышление.

Задачи:

• анализ различных методов решения задачи: координатно-векторный метод,
  применение теоремы косинусов, применение теоремы о трех перпендикулярах;
• сравнение преимуществ и недостатков каждого метода;
• повторение свойств куба, треугольной призмы, правильного шестигранника;
• подготовка к сдаче ЕГЭ;
• развитие самостоятельности при принятии решения.

Схема урока

Задача 1.

В кубе ABCDA₁B₁C₁D₁
с ребром 1 точка О – центр грани ABCD.

Найти:

а) угол между прямыми A₁D и BO;

б) расстояние от точки B до середины отрезка A₁D.

Решение пункта а).

1 способ. Координатно-векторный метод

Поместим наш куб в прямоугольную систему координат как показано на рисунке,
вершины A₁ (1; 0; 1), D (1; 1; 0), B₁
(0; 0; 1), O (½; ½; 0).

Направляющие векторы прямых A₁D и B₁O:

{0; 1; -1} и
{½;
½; -1};

искомый угол φ между ними находим по формуле:

cos∠φ =
,
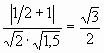
откуда∠φ = 30°.

2 способ. Используем теорему косинусов.

1) Проведем прямую В₁С параллельно прямой
A₁D. Угол CB₁O будет искомым.

2) Из прямоугольного треугольника BB₁O по теореме Пифагора:

B₁O =
.

3) По теореме косинусов из треугольника CB₁O
вычисляем угол CB₁O:

cos
CB₁O
=
,
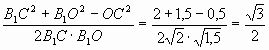
искомый угол составляет 30°.

Замечание. При решении задачи 2-м способом можно заметить, что по теореме
о трех перпендикулярах
COB₁ = 90°,
поэтому из прямоугольного ∆ CB₁O также легко вычислить косинус
искомого угла.

 Решение пункта б).

1 способ. Воспользуемся формулой расстояния между двумя
точками

Пусть точка E – середина A₁D, тогда координаты E (1; 1/2; ½), B (0; 0; 0).

BE =
.

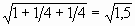
2 способ. По теореме Пифагора

Из прямоугольного ∆ BAE с прямым
BAE
находим BE =
.

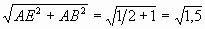
Задача 2.

В правильной треугольной призме ABCA₁B₁C₁
все ребра равны a. Найти угол между прямыми AB и A₁C.

Решение.

1 способ. Координатно-векторный метод

Координаты вершин призмы в прямоугольной системе при расположении призмы, как
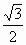
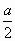
на рисунке: A (0; 0; 0), B (a;
;
0),
A₁(0; 0; a), C (0; a; 0).

Направляющие векторы прямых A₁C и AB:

{0; a; -a} и

{a;
;
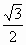
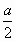
0} ;

cos φ =
;

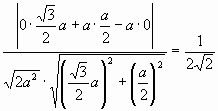
φ
= arccos
.

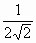
2 способ. Используем теорему косинусов

Рассматриваем ∆ A₁B₁C, в котором
A₁B₁ || AB. Имеем

 cos φ =
.

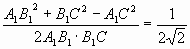
Задача 3.

(Из сборника ЕГЭ-2012. Математика: типовые экзаменационные варианты под ред.
А.Л.Семенова, И.В.Ященко)

В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁,
все рёбра которой равны 1, найдите расстояние от точки E до прямой B₁C₁.

Решение

1 способ. Координатно-векторный метод

1) Поместим призму в прямоугольную систему координат, расположив координатные
оси, как показано на рисунке. СС₁,
СВ и СЕ попарно перпендикулярны, поэтому можно направить вдоль них
координатные оси. Получаем координаты:

С₁ (0; 0; 1), Е (;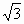
0; 0), В₁ (0;1;1).

2) Найдем координаты направляющих векторов для прямых С₁В₁
и С₁Е:

(0;1;0),

(;0;-1).

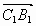
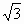
3) Найдем косинус угла между С₁В₁
и С₁Е, используя скалярное произведение векторов
и
:

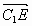
 cos β =
=
0 => β = 90° => C₁E – искомое расстояние.

4) С₁Е =
= 2.

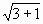
Вывод: знание различных подходов к решению стереометрических задач
позволяет выбрать предпочтительный для любого учащегося способ, т.е. тот,
которым ученик владеет уверенно, помогает избежать ошибок, приводит к успешному
решению задачи и получению хорошего балла на экзамене. Координатный метод имеет
преимущество перед другими способами тем, что требует меньше стереометрических
соображений и видения, а основывается на применении формул, у которых много
планиметрических и алгебраических аналогий, более привычных для учащихся.

Форма проведения урока – сочетание объяснения учителя с фронтальной
коллективной работой учащихся.

На экране с помощью видеопроектора демонстрируются рассматриваемые
многогранники, что позволяет сравнивать различные способы решения.

Домашнее задание: решить задачу 3 другим способом, например, с помощью
теоремы о трех перпендикулярах.

Литература

1. Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по
геометрии для 11 класса.– М.: ИЛЕКСА, – 2010. – 208 с.

2. Геометрия, 10-11: учебник для общеобразовательных учреждений: базовый и
профильный уровни / Л.С.Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.:
Просвещение, 2007. – 256 с.

3. ЕГЭ-2012. Математика: типовые экзаменационные варианты: 10 вариантов/ под
ред. А.Л.Семенова, И.В.Ященко. – М.: Национальное образование, 2011. – 112 с. –
(ЕГЭ-2012. ФИПИ – школе).

Всего: 117    1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 117    1–20 | 21–40 | 41–60 | 61–80 …

 Решение задач  из материалов ЕГЭ векторно-координатным методом 

Задание С2 Единого государственного экзамена по математике с 2010 года представляет стереометрическую задачу на определение расстояний или углов в пространстве между объектами, связанными с некоторым многогранником.  За этот период по итогам ЕГЭ —  только около 5% представленных решений были оценены в два балла.

Как научить выпускников решать задачи C2 из ЕГЭ по математике?  Существует три основных метода решения задач C2.  Условно назовем их «методом построений», «векторно-координатным методом» и «методом объемов». Каждый из них удобен в том или ином случае, поэтому лучше знать и уметь использовать все три.                      

Наиболее универсальным является «метод построений», с его помощью можно решить практически любую задачу по стереометрии из тех, что предлагаются в вариантах ЕГЭ по математике. Однако, он не всегда целесообразен с точки зрения временных и вычислительных затрат. Учащийся должен иметь хорошее пространственное воображение, помнить алгоритмы решения для каждого вида задач. Чтобы решать задачи этим методом необходимым (но, конечно, не достаточным) условием является безупречное знание и понимание основных теорем стереометрии, связанных с взаимным расположением прямых и плоскостей в пространстве, которые непременно сопровождают решение практически любой задачи C2, без которых часть баллов за это задание на экзамене может быть потеряна.  Второй случай, когда не всегда целесообразно использовать «метод построений», связан с нахождением расстояний от точки до прямой  или от точки до плоскости. Тогда  на помощь приходят два оставшихся метода.

Векторно-координатный метод позволяет избежать вышеуказанные  трудности. От учащегося требуются знания нескольких формул и навыки в решении простейших задач, основная  нагрузка при решении задачи приходится на вычислительную часть.

           Векторно-координатные приемы изучаются в школе в весьма ограниченном количестве. В базовый учебник стереометрии Л.С. Атанасяна включен целый параграф «скалярное произведение векторов» и даже отдельно рассматривается нахождение углов между объектами. Однако дальше темы «вычисление угла между прямыми» и осторожного намека на аналогичный алгоритм для прямой и плоскости материал не рассматривается. И даже не вводится такое понятие, как «нормаль».

Как правило учитель выбирает  одну из трех стратегий подготовки к задаче С2 на ЕГЭ:

 1) Полный отказ от векторно- координатных приемов

 2) Изучение отдельных алгоритмов

 3) Демонстрация всех приемов (без доказательств) для самых сильных учеников.

           Преимущество методов аналитической геометрии перед альтернативным решением средствами дополнительных построений состоит в том, что удается полностью отстраниться от чертежа и заниматься исключительно числами (координатами). Поэтому в определенных условиях подготовки к ЕГЭ по математике удается натаскать ученика на стандартные решения. Причем за весьма короткий срок и в обход большого количества тем.

     Если у школьника имеются серьезные проблемы с пониманием определений, с чтением или построением сложного стереометрического рисунка, если ему никак не удается подобрать необходимые дополнительные построения, то можно построить работу по С2 на векторах и координатах. Особенно это актуально в условиях экстренной помощи, когда на подготовку к ЕГЭ отводится всего лишь 2-3 месяца. Если у преподавателя нет времени на неспешный комплексный подход, то лучше всего сразу обратиться к координатам.

Практика показывает, что учащиеся быстро осваивают метод координат, так как при его использовании необходимо придерживаться общего алгоритма: вычислить координаты необходимых точек, расположенных на многогранниках, и применить соответствующую формулу. Для некоторых задач дополнительно требуется умение составлять уравнение плоскости.

Какую подготовку к восприятию векторно-координатных приемов должен провести учитель?

Необходимо повторить следующие темы:

1) Координаты точки и координаты вектора.

 2) Длина вектора.

 3) Скалярное произведение векторов.

 4) Координаты середины отрезка (на случай, если плоскость или прямая будут заданы серединами каких-нибудь диагоналей или ребер у пирамид).

Удачный выбор системы координат (некоторые вершины многогранника находятся на координатных осях) позволяет значительно упростить вычисления.

Первая группа подготовительных задач.

Изобразите многогранник, указанную прямоугольную систему координат и определите координаты вершин многогранника.

1. Куб A… с ребром a. Начало координат — в точке A; прямая AD — ось x; прямая AB — ось y; прямая — ось z.

2. Правильная треугольная призма, сторона основания которой равна a, а боковое ребро b. Начало координат — в точке A; прямая AC — ось x; прямая, проходящая через точку A в плоскости ABC перпендикулярно прямой AC, — ось y; прямая — ось z. 

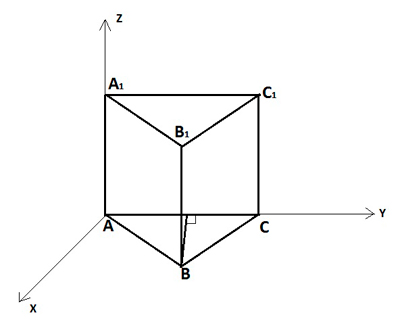
3. Правильная шестиугольная призма A…, сторона основания которой равна a, а боковое ребро b. Начало координат — в центре O шестиугольника ABCDEF; прямая CF — ось x; прямая, проходящая через точку O в плоскости ABC перпендикулярно прямой CF, — ось y; прямая  — ось z, где  — центр шестиугольника.  

  4. Правильная треугольная пирамида MABC, сторона основания которой равна a, а высота h. Начало координат — в точке A; прямая AC — ось x; прямая, проходящая через точку A в плоскости ABC перпендикулярно прямой AC, — ось y; прямая, проходящая через точку A перпендикулярно плоскости ABC, — ось z. 

5. Правильная четырехугольная пирамида MABCD, сторона основания которой равна a, а высота h. Начало координат — в центре O квадрата ABCD; прямая, проходящая через точку O параллельно AD, — ось x; прямая OM — ось z. 

6. Правильная шестиугольная пирамида MABCDEF, сторона основания которой равна a, а высота h. Начало координат — в центре O шестиугольника ABCDEF; прямая CF — ось x; прямая, проходящая через точку O в плоскости ABC перпендикулярно прямой CF, — ось y; прямая OM — ось z.

Векторно-координатный метод позволяет рассматривать множество самых трудных задач на вычисление всех видов углов (между прямыми, между прямой и плоскостью, между плоскостями) и любых расстояний (от точки до плоскости, между параллельными плоскостями, между скрещивающимися прямыми). С тремя последними работать сложнее всего, ибо приходится затрагивать тему «уравнение плоскости».  

Расстояние от точки до плоскости

Решение данной задачи позволяет решать задачи о нахождении расстояния между параллельными плоскостями, между параллельными прямой и плоскостью, между скрещивающимися прямыми. Поэтому необходимо подробнее остановиться на отработке учащимися навыков решения задач о нахождении расстояния от точки до плоскости.

Пусть дана точка M(; ; ) и плоскость α, заданная уравнением

Ax + By + Cz + D = 0 в прямоугольной декартовой системе координат. Расстояние от точки M до плоскости α можно вычислить по формуле:

,   (1)

где  координаты вектора нормали к плоскости (то есть вектора, перпендикулярного плоскости α).

Подготовительные упражнения для отработки навыков применения формулы  для данных точки и плоскости.

1. Найдите расстояние от точки M(–3; 1; 2) до плоскости, заданной уравнением 3x + 4y – 12z + 2 = 0.

2. Вычислите расстояние от начала координат до плоскости, заданной уравнением 2x + 3y – 6z + 14 = 0.

3. Вычислите расстояние между параллельными плоскостями, заданными уравнениями 3x + 2y + 4z + 11 = 0 и 9x + 6y + 12z – 5 = 0.

Указание. Для этого достаточно выбрать точку первой плоскости,

например,  

4. Докажите, что в общем случае расстояние между параллельными плоскостями α и β:

:   :

вычисляется по формуле:      

Указание. Используйте алгоритм решения задачи 3.

Следующая система упражнений направлена на составление уравнения плоскости, проходящей через три точки. Один из способов получения уравнения плоскости, если известны координаты трех ее точек не лежащих на одной прямой: M(; ; ), N(; ; ), P(; ; ). Для этого нужно в общий вид  уравнения плоскости Ax + By + Cz + D = 0, подставить координаты точек M, N, P, получим систему уравнений

Решив ее, найдем A = pD, B = qD, C = rD  (если окажется, что D = 0, то            A = pC, B = qC; если D = C = 0, то A = pB).  Подставив в исходное уравнение и  разделив на D ≠ 0, получим уравнение  px + qy + rz + 1 = 0.

Иногда удобно использовать уравнение плоскости в отрезках:

,  если известны координаты точек (A; 0; 0), (0; B; 0), (0; 0; C) пересечения данной плоскости с координатными осями Ox, Oy, Oz соответственно.

Пример 1. Напишите уравнение плоскости, проходящей через три точки, M(0; 1; 0), N(1; 0; 0), P(1; 1; 1).

Решение.  В общий вид уравнения плоскости Ax + By + Cz + D = 0  подставим  координаты этих точек, получим:

Отсюда B = –D, A = –D и C = D. Уравнение плоскости MNP имеет вид

–Dx – Dy + Dz + D = 0, или x + y – z – 1 = 0, после деления на – D ≠ 0.

Пример 2. В правильной шестиугольной призме , все ребра которой равны 1, найдите расстояние от точки A до плоскости  DE.

Решение. Введем систему координат, как показано на рисунке, и найдем координаты точек:                                      

                                                                                                               

                                                                                                                                                   

   Пусть Ax + By + Cz + D = 0  — уравнение плоскости DE. Подставляя в него координаты точек D, E, , получим:

Отсюда имеем: A = 0, B = —   C=-D

Уравнение плоскости DE примет вид  Вычислим расстояние от точки A до плоскости DE по формуле (1):

                                                                                                 Ответ:

Расстояние между скрещивающимися прямыми

Задачу данного вида можно свести к задаче о вычислении расстояния от точки до плоскости, поэтому можно применить формулу расстояния от точки до плоскости, применяя координатный метод.

Пример 3. В единичном кубе A… найдите расстояние между прямыми  и BD.

Решение. Так как     Поэтому расстояние

ρ(; ) = ρ(; )=  ρ(; ).

Введем систему координат, как показано на рисунке, и определим координаты точек:                                       (0; 0; 0),  (0; 1; 0),  (1; 0; 0), (1; 1; 1).

Плоскость, проходящая через точки , имеет вид x + y – z – 1 = 0 (см. пример 1). Расстояние между прямыми  и  равно расстоянию от точки   до плоскости

                                                                                                          Ответ:

Угол между двумя прямыми

         На каждой прямой AB и CD выбираются удобные точки, определяются  координаты их направляющих векторов. Пусть  

 — искомый угол между двумя прямыми AB и CD.

                Формула:.     (2)

Пример 4. В правильной шестиугольной призме, ребра которой равны 1, найдите угол между прямыми и .

Решение. Введем прямоугольную систему координат, как указано на рисунке.

 Тогда  

           ,

       Отсюда

            где  — искомый угол.

                                      Ответ:

Угол между прямой и плоскостью

         Пусть даны вектор , перпендикулярный к некоторой плоскости  (ее нормаль) и направляющий вектор  прямой.  — искомый угол между прямой  и плоскость  

Уравнение плоскости имеет вид:                                    ,

Синус угла  между прямой  и вектором  равен модулю косинуса угла между нормалью  и направляющим вектором  прямой , так  как углом между двумя прямыми называется меньший из углов.           Формула: .    (3)

В задачах на вычисление угла между прямой и плоскостью или угла между пересекающимися плоскостями в общем случае уравнение плоскости находить не требуется. Координаты вектора нормали можно вывести, если известны координаты трех точек плоскости M, N, P, не лежащих на одной прямой. Для этого находим координаты двух векторов плоскости:

Предположим, что вектор с координатами = {p; q; r} (здесь p, q, r — неизвестные числа, которые нужно найти) перпендикулярен любому вектору плоскости α, в том числе векторам  

Его координаты можно найти из условий равенства нулю скалярных произведений с векторами   из следующей системы уравнений:

Эта система имеет бесконечное множество решений, так как векторов, перпендикулярных плоскости α, бесконечно много. Выразив, например, из системы координаты  p и q через r,  выберем ненулевой вектор                        = {p(r); q(r); r}, взяв в качестве r какое-нибудь число (обычно берут такое число, чтобы в координатах не было дробей или радикалов).

Пример 5. В единичном кубе  найти угол между прямой  и плоскостью α, проходящей через точки , E и F, где точка E — середина ребра , а точка F лежит на ребре так, что  .

Решение. Введем прямоугольную систему координат, как на рисунке.  Тогда

 (0; 0; 0),   (0; 0; 1),   (1; 0; 1),  

Пусть   {x; y; z} — вектор, перпендикулярный плоскости α. Найдем его координаты из условий перпендикулярности этого вектора векторам  и  то есть из условийПусть x = 2, тогда y = –4, z = 3 и  {2; − 4; 3},   .

Так как  то

=   Отсюда

                                                                                                    Ответ:

Угол между плоскостями

Задачу о нахождении угла между плоскостями α и β, заданными в прямоугольной декартовой системе координат уравнениями

  и   соответственно, удобнее свести к задаче о нахождении угла между векторами их    нормалей    и , используя формулу

 α и β

Прежде чем перейти к содержательным задачам, с учащимися необходимо рассмотреть простейшие задачи следующего вида: найти угол между плоскостями, заданными уравнениями  2x + 3y + 6z – 5 = 0 и                4x + 4y + 2z – 7 = 0.

Пример 6. (ЕГЭ 2012) В правильной четырёхугольной призме A…стороны основания равны 1, а боковые рёбра равны 3. На ребре отмечены точка Е так, что . Найдите угол между плоскостями   .

Решение. Введем прямоугольную систему координат, как на рисунке.  Тогда

B (0; 0; 0),   (1; 1; 3),         В общий вид уравнения плоскости           Ax + By + Cz + D = 0  подставим  координаты этих точек, получим:

Отсюда D = 0, A = –2C, B = – C.  Уравнение плоскости  имеет вид

–2C x – C y + Cz  = 0, или –2 x –  y + z  = 0, после деления на   C ≠ 0.

Вектор нормали  плоскости

Уравнение плоскости :   z = 0, её вектор нормали

                                                            

                                                                      Ответ:

 Источники:

1. Атанасян Л.С.и др. Геометрия, 10-11: учеб. для общеобразоват. учреждений: базовый и профил. уровни.- 17 – е изд.- М. : Просвещение, 2008.

2. Беликова И. Задание С2: Решаем методом координат // Математика, 2010, № 20.

3. Смирнов В.А. ЕГЭ-2011. Математика. Задача С2. Геометрия.    Стереометрия / под ред. А.Л. Семенова, И.В. Ященко. — М.: МЦНМО, 2011.

4. Шабунин М.И. Математика для поступающих в вузы: пособие. — 2-е изд., испр. и доп. — М.: БИНОМ, 2003.

5. http://ege-ok.ru/ 

6. http://nsportal.ru/