СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика базового уровня
Математика базового уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Справочник
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Векторы
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Задания Д15 № 27663
Найдите длину вектора
(6; 8).
Аналоги к заданию № 27663: 58455 58497 58457 58459 58461 58463 58465 58467 58469 58471 … Все
Решение
·
·
Сообщить об ошибке · Помощь
2
Задания Д15 № 27664
Найдите квадрат длины вектора
Аналоги к заданию № 27664: 26395 Все
Решение
·
·
Сообщить об ошибке · Помощь
3
Задания Д15 № 27720
Стороны правильного треугольника ABC равны
Найдите длину вектора
Аналоги к заданию № 27720: 60805 26453 60807 60809 60811 60813 60815 60817 60819 60821 … Все
Решение
·
·
Сообщить об ошибке · Помощь
4
Задания Д15 № 27721
Стороны правильного треугольника ABC равны 3. Найдите длину вектора
Аналоги к заданию № 27721: 60855 60857 60859 60861 60863 60865 60867 60869 60871 60873 … Все
Решение
·
·
Сообщить об ошибке · Помощь
5
Задания Д15 № 27722
Стороны правильного треугольника ABC равны 3. Найдите скалярное произведение векторов
и
Аналоги к заданию № 27722: 60905 60907 60909 60911 60913 60915 60917 60919 60921 60923 … Все
Решение
·
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
Контрольная работа «ВЕКТОРА»
ВАРИАНТ 1
1.
Найдите квадрат длины вектора +
.

2.
Стороны правильного
треугольника равны
.
Найдите
длину вектора .
3.
Найдите длину отрезка, соединяющего
точки A(6;

(−2; 2).
4.
Найдите угол между векторами и
.

в градусах.
5.
Диагонали изображенного на рисунке
ромба равны 12 и
16.

+
.
6.
Точки O(0; 0), A(10; 8), C(2;
6) и B являются вершинами параллелограмма. Найдите
абсциссу точки B.
Контрольная работа «ВЕКТОРА»
ВАРИАНТ 2
1. Найдите
квадрат длины вектора .

Точки O(0; 0), A(10; 8), B(8; 2) и C являются вершинами параллелограмма.
Найдите абсциссу точки C.
3. Найдите квадрат
длины вектора .

равны
6 и 8. Диагонали пересекаются в точке .Найдите
длину разности векторов и
.
5. Найдите расстояние от точки A с координатами
(6; 
6. Найдите угол между
векторами и
.
Ответ
дайте в градусах.
Контрольная работа «ВЕКТОРА»
|
Вариант 1 |
Вариант 2 |
|
|
1 |
200 |
40 |
|
2 |
6 |
2 |
|
3 |
10 |
40 |
|
4 |
45 |
8 |
|
5 |
16 |
6 |
|
6 |
8 |
45 |
Задачи с векторами — ЕГЭ по математике
- 09.11.2015
Решённые задания открытого банка заданий ЕГЭ по математике на тему «Задачи с векторами».
Напомним, что ФИПИ создан открытый банк заданий по математике. В нашем документе содержатся эти задания, к каждому из которых приложен правильный ответы.
Разбор заданий ОБЗ помогает в качественной подготовке к ЕГЭ по математике.
Автор-составитель: Александр и Наталья Крутицких.
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Тема «Векторы на координатной плоскости» достаточно подробно рассматривается в рамках школьного курса учащихся старших классов. Однако практика показывает, что, сталкиваясь с нетипичным заданием, выпускники часто теряются и не могут быстро найти правильный ответ.
Чтобы задачи, в которых требуется построить векторы на координатной плоскости, не вызывали сложностей при написании профильного уровня ЕГЭ по математике, необходимо понять, как они решаются.
Вместе с образовательным порталом «Школково» подготовка к прохождению аттестационного испытания будет легкой и качественной! Сайт поможет учащимся выявить пробелы в знаниях и успешно справиться с аттестационным испытанием.
Чтобы разобраться в теме «Координаты вектора на координатной плоскости», рекомендуем вначале вспомнить весь базовый материал. Он представлен в разделе «Теоретическая справка». Учащиеся смогут освежить в памяти основные теоремы, свойства координат вектора, определение скалярного произведения векторов и другие понятия, которые помогут при решении заданий ЕГЭ.
Для того чтобы закрепить усвоенный материал, мы рекомендуем попрактиковаться в выполнении соответствующих упражнений. Большая подборка задач по теме «Векторы на координатной плоскости», а также по правилам сложения и вычитания векторов представлена в разделе «Каталог». Для качественной подготовки к ЕГЭ лучше всего переходить от простых упражнений к более сложным. В каждом задании на сайте представлен алгоритм решения и дан правильный ответ.
Практиковаться в выполнении задач выпускники из Москвы и других российских городов могут в онлайн-режиме. В случае необходимости любое упражнение можно сохранить в разделе «Избранное». В дальнейшем к этому заданию можно будет вернуться и, к примеру, обсудить алгоритм его решения с преподавателем.
Векторы | ЕГЭ по математике (профильной)
Отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом, называется вектором.
Вектор с началом в точке A и концом в точке B обозначают ${(АВ)}↖{→}$ или строчной (маленькой) буквой, например ${а}↖{→}$
Любая точка плоскости является вектором. В этом случае вектор называется нулевым.
Модуль (длину) вектора обозначают $|АВ|↖{→}$.
Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.
Два коллинеарных вектора называются сонаправленными, если они направлены в одну сторону.
Векторы называются равными, если они сонаправлены и их длины равны.
Сумма векторов — это вектор, который можно получить двумя способами.
- Правило треугольника (А)
- Правило параллелограмма (Б)
Для любых векторов $a↖{→}, b↖{→}, c↖{→}$ справедливы равенства:
- $a↖{→}+b↖{→}=b↖{→}+a↖{→}$(переместительный закон)
- $(a↖{→}+b↖{→})+c↖{→}=a↖{→}+(b↖{→}+c↖{→})$ (сочетательный закон)
Разность векторов тоже можно получить двумя способами:
Если надо найти разность двух векторов, их необходимо отложить из одной точки. Результирующий вектор направлен к уменьшаемому.
Для любых $a↖{→}$ и $b↖{→}$ справедливо равенство $a↖{→}-b↖{→}=a↖{→}+({-b}↖{→})$
Скалярное произведение векторов равно произведению длин векторов на косинус угла между ними.$a↖{→}⋅b↖{→}=|a↖{→}|·|b↖{→}|·cosα$
Ненулевые векторы $a↖{→}$ и $b↖{→}$ перпендикулярны, если их произведение равно нулю.
Координаты вектора равны разностям соответствующих координат конца и начала данного вектора.
Для того чтобы векторы $a↖{→}$ и $b↖{→}$ были коллинеарными, необходимо и достаточно, чтобы выполнялось равенство $a↖{→}=k·b↖{→}$, где $k$ — это некоторое число.
Координаты середины вектора равны средним арифметическим координат его концов.
Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.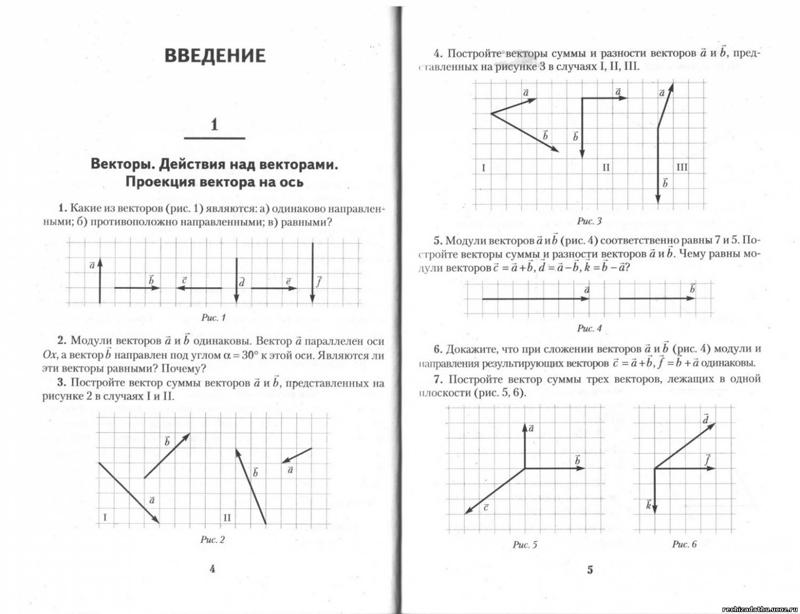
Найдите угол между векторами $a↖{→}$ и $b↖{→}$
Решение:
- Сначала нужно найти координаты векторов $a↖{→}$ {2-0;6-0} $b↖{→}${8-0;4-0}
- Найдем скалярное произведение векторов $a↖{→}·b↖{→} = 2·8+6·4=16+24=40$
- Найдем длины каждого вектора $|a↖{→}|= √{4+36}=√{40}; |b↖{→}|=√{64+16}=√{80}$
- Найдем косинус угла между векторами $cosα={40}/{√{40}·√{80}}={40}/{√{40·40·2}}={1}/{√2}={√2}/{2}$
- Найдем угол $α=arccos{√2}/{2}=45$
Ответ: 45
Практика: решай 3 задание и тренировочные варианты ЕГЭ по математике (профильной)
Векторы. Решение заданий №3 по ЕГЭ
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6.
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Решение заданий
№3
ВЕКТОРЫ
по материалам открытого банка
задач ЕГЭ по математике 2016года
http://mathege.ru/or/ege/Main.html
Прототип задания B3(№ 27717)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и
16. Найдите длину вектора АО ВО .
Решение.
По правилу треугольника:
С
AO BO AO OD AD
Найдём длину AD из п/у ∆AOD
(т.к. ABCD – ромб, то АС ⊥ BD
и ВО = ОD = 6, АО = ОС = 
D
O
В
2
AD AD 2 AO 2 OD 2
АD 2 82 62 100
AD 100 10
А
Ответ: 10.
Прототип задания B3 (27709)
Две стороны прямоугольника ABCD равны 60 и 45. Найдите
длину разности векторов AB и AD .
Решение.
D
С
По правилу треугольника:
AB AD AB DA
А
60
45
DA AB DB
В
DB DB
AB 2 AD 2
DB 602 452 5625 75
Ответ: 75.
Прототип задания B3 (27710)
Две стороны прямоугольника ABCD равны 17 и 26. Найдите
скалярное произведение векторов AB и AD.
D
А
26
С
Решение.
17
Т.к. векторы AB ⊥AD , то
их скалярное произведение
В
AB AD 0
Ответ: 0.
Прототип задания B3 (27711)
Две стороны прямоугольника равны 15 и 23. Диагонали
пересекаются в точке О. Найдите длину суммы векторов
и . AО ВО
Решение.
D
С
О
А
23
15
В
По правилу треугольника:
AО ВО AО ОD AD
АD 15
Ответ: 15.
Прототип задания B3 (27712)
Две стороны прямоугольника равны 13 и 25.
Диагонали пересекаются в точке О. Найдите длину
разности векторов AО и ВО.
Решение.
D
С
О
А
25
13
В
По правилу треугольника:
AО ВО AО ОВ AВ
АВ 25
Ответ: 25.
Прототип задания B3(№ 27713)
Диагонали ромба ABCD равны 54 и 72. Найдите длину
вектора АВ .
Решение.
С
B
O
Найдём длину АВ из п/у ∆AOB
(т.
и ВО = ОD = 27, АО = ОС = 36)
AВ 2 AO 2 OВ 2
D
АВ AВ
AO 2 OВ 2
AВ 272 362 45
А
Ответ: 45.
Прототип задания B3 (№ 27714)
Диагонали ромба ABCD равны 44 и 66. Найдите длину
вектора АВ AD .
Решение.
С
По правилу параллелограмма
АВ AD АС
AС 66
B
O
А
D
Ответ: 66.
Прототип задания B3(27720)
Стороны правильного треугольника ABC равны 45 3.
Найдите длину вектора AВ АС.
М
С
AВ АС АМ 2 AО ,
где АО – высота, медиана,
биссектриса р/с ∆ АВС
О
а
Решение.
По правилу параллелограмма:
2
А
а
В
а 3
а
АО а
2
2
2
45 3 3 45 3
АО
67,5
2
2
АМ 135
Ответ: 135.
Прототип задания B3(27722)
Стороны правильного треугольника ABC равны 18.
Найдите скалярное произведение векторов AВ и АС.
Решение.
С
По определению скалярного
произведения, имеем:
18
AВ АС AВ АС cos А,
60°
А
18
В
AВ АС 18 18 cos 60
1
AВ АС 324 162
2
Ответ: 162.
Прототип задания B3 (№ 00000)
Дан вектор a.
Найдите: 1) координаты вектора; 2) длину вектора.
Решение.
1) координаты вектора a:
y
a x2 x1; y2 y1 ;
8
a
2
0 1
8–2
a 9 1; 8 2 ;
a 8; 6 .
2) длина вектора: a
или: a
9–1
9 x
x2 х1
2
x2 y2 ;
y2 у1 ;
a 82 62 100 10.
Ответ: 1) {8; 6}; 2) 10.
2
Прототип задания B3 (№ 00000)
Даны векторы a и b .
Найдите: 1) скалярное произведение; 2) длины векторов.
Решение.
Координаты векторов a и b: a 2; 6 ; b 8; 4
1) скалярное произведение: a b x x y y
1
2
1
2
2) длины векторов: a x 2 y 2 ; b x 2 y 2
1
1
2
2
y
6
4
0
a
1) a b 2 8 6 4 40
b
2
2) a 22 62 40 ;
8 x
b 82 42 80 .
Ответ: 1) 40; 2) √40; √80.
Прототип задания B3 (№ 00000)
Даны векторы a и b .
Найдите: 1) сумму координат вектора a b ;
2) найдите квадрат длины вектора a b .
Решение.
Координаты векторов a и b: a 2; 6 ; b 8; 4
1) сумма координат вектора a b: x1 x2 y1 y2
y
2
2) квадрат длины вектора: a b х 2 у 2
6
4
0
1) сумма векторов a b:
a
b
2
8 x
Ответ: 1) 20; 2) 200.
a 2; 6
b 8; 4
a b 10; 10
сумма координат вектора a b:
10 10 20
2
2) a b 102 102 200
Прототип задания B3 (№ 27735)
Найдите угол между векторами a и b .
Ответ дайте в градусах.
Решение.
Координаты векторов a и b: a 2; 6 ; b 8; 4
Найдём угол между ними через скалярное
произведение:
y
6
4
0
cos φ
a
b
a b
a b
x1 x2 y1 y2
2
1
2
1
2
x y x2 y 2
2 8 6 4
2
40
40 80
2 2 6 2 82 4 2
40
40
1
2
8 x
⇒
3200 40 2
2
Ответ: 45.
⇒ φ 45
Используемые материалы
http://mathege.ru/or/ege/Main.html − ????????? ????????? ????? ??????? ?? ??????????
2015 ????
English
Русский
Правила
12.

Значки выпускного экзамена задают простой вектор. студенческий колледжPREMIUM
Набор значков дистанционного обученияPREMIUM
Векторный набор линейных значков, связанных с образовательным процессом, обучением, репетиторством и дистанционным онлайн-образованием. монолинейные пиктограммы и элементы дизайна инфографикиPREMIUM
Иконки линий онлайн-образования. векторная иллюстрация включала иконку в виде интернета, видео, аудио пиктограмму личного кабинета для школы, колледжа, университетского обучения. Идеальный редактируемый штрих 64×64 пикселей. ПРЕМИУМ
Иконка выпускного экзамена простой вектор. академическое исследованиеПРЕМИУМ
Значок экзамена диссертации простой вектор. final studyPREMIUM
Векторная иконка экзамена на белом фоне. Знак символа плоского векторного экзамена из коллекции современного образования для дизайна мобильных концепций и веб-приложений.
Школьный тест подготовки к экзамену. контрольный список концепции экзамена и песочные часы, выбор формы анкеты ответов, векторная плоская иллюстрация образования. онлайн-курс обучения экзамен. заполнить анкету резюмеPREMIUM
Группа студентов за столом занимается. вид сверху.PREMIUM
Значок почтового экзамена простой вектор. окончательное исследованиеPREMIUM
Номер раскраски для детей. рабочий лист для дошкольного, детского сада и школьного возраста. вычитание. считать и раскрашивать. бабочки.PREMIUM
Онлайн-экзамен, контрольный список и карандаш, сдача теста, выбор ответа, форма анкеты, концепция образования, векторная плоская иллюстрацияPREMIUM
Значок бумажного диплома простой вектор. книга финалПРЕМИУМ
У грустных детей плохая оценка на экзамене.PREMIUM
3D контрольный список задач по управлению задачами с мобильным телефоном, держащим руку, эффективная работа над планом проекта, быстрый прогресс, концепция повышения уровня, задание и экзамен.
Иконка концепции графиков экзаменов. дистанционный образовательный процесс. промежуточные и итоговые экзамены. учебный план. идея академического календаря тонкая линия иллюстрации. вектор изолированный контур rgb цветной рисунокPREMIUM
Быстрый выпускной экзамен значок контур вектор. академическое исследованиеPREMIUM
Стрессовая девочка-подросток делает школьное задание векторный мультфильм illustrationPREMIUM
Девушка сидит на полу в окружении ноутбука, книг и бумаг и пишет заметки. женщина учится или готовится к экзаменам дома. студент-подросток усердно учится в скандинавском интерьере дома. PREMIUM
Иконка выпускного экзамена простой вектор. учебная тетрадьPREMIUM
Симпатичный маленький мальчик чувствует себя счастливым, потому что получил хорошую оценку на экзаменеPREMIUM
Красочные школьные принадлежности и канцелярские принадлежности на белом фоне. векторный бесшовный рисунок для баннера, плаката, магазина канцелярских товаров, веб-сайта и оберточной бумаги.
Нарисованные от руки быстрые услуги, контрольный список и секундомер, план действий, промедление и эффективность, управление проектами, быстрый опрос, краткий опрос, doodlePREMIUM
Персонаж молодой женщины держит ручку перед огромной книгой, готовится к экзамену по грамматике или делает домашнее задание. студентка читает и учится. образование в университете или колледже концепции. Cartoon vector illustrationPREMIUM
Трудно учиться у подростка. трудности в учебе. уставший ребенок не хочет учиться. концепция вектора образования студенту нужна помощь, чтобы сделать домашнюю работуPREMIUM
Значок задания в виде песочных часов, изометрический стильPREMIUM
Значок задания в виде песочных часов, изометрический стильPREMIUM
Веб-баннер или набор целевых страниц. деловые люди перед коллегами.PREMIUM
Скучающий школьник с рукой на лице сидит за партой и пишет в блокнотеPREMIUM
Подготовка к экзаменам, школьный тест векторная плоская иллюстрация.
Нарисованный от руки онлайн-экзамен, контрольный список и карандаш, прохождение теста, выбор ответа, форма анкеты, концепция образования, вектор каракулейPREMIUM
Учитель-мужчина проводит онлайн-уроки для школьников или студентов университетов. видеокурс, веб-семинар, интернет-класс, услуги личного учителя для индивидуального дистанционного домашнего самообразования. ПРЕМИУМ
Студентка, стоящая перед доской. ПРЕМИУМ
Концепция университетского обучения.0003
Вектор контура значка диплома. студенческая книжкаПРЕМИУМ
Обучение времени по часам. рабочий лист образовательной деятельности для детей и малышей. овощная морковь. игра для детей. простая плоская изолированная цветная векторная иллюстрация в стиле милого мультфильма. школьники. набор мультяшных клипартов для детской раскраски, печати на футболках, значков, логотипов, этикеток, патчей или наклеек.
Онлайн-репетитор абстрактная концепция векторной иллюстрации. ПРЕМИУМ
Онлайн-тест для шаблона баннеров, флаеров, книг и обложек журналов векторная иллюстрация. work testPREMIUM
Вектор контура иконки почтового экзамена. выпускное исследованиеPREMIUM
Студент стоит перед доскойPREMIUM
Молодая женщина Джейн держит ручку перед огромной книгой. готовьтесь к экзамену, делайте домашнее задание, читайте и учитесь. образование, университет, концепция колледжа. 3d векторная иллюстрация персонажей людей. ПРЕМИУМ
Проверка значка буфера обмена простой вектор. final bookPREMIUM
У африканского мальчика много вопросов vector cartoonPREMIUM
Жизнерадостная девушка, работающая журналистом, наслаждается отдыхом в столовой. рисованной в стиле тонкой линии, векторные иллюстрации.ПРЕМИУМ
Изучайте английский язык. студенты учатся с книгами. группа людей в классеPREMIUM
Школьник с вопросами делает домашнее задание vector cartoonPREMIUM
Студент готовится к тесту в последний момент.
Счастливый милый маленький мальчик учится для тестаPREMIUM
Вектор контура иконки экзамена. final studyPREMIUM
Бумажный вектор контура значка диплома. book finalPREMIUM
Изучение вектора контура иконки папируса. выпускной экзаменPREMIUM
Вид сверху на молодых людей, сидящих за столом и изучающих английский язык. студенты учатся вместеPREMIUM
Развивающая детская игра. соответствующий игровой лист для детей. совпадают по цвету. найти пары птиц и скворечник. учим цвета, тема животныхPREMIUM
Плоский вектор значка выпускного экзамена. учебная тетрадьPREMIUM
Время выучить баннер. девушка-брюнетка сидит на стопке разноцветных книг и читает учебное пособие, готовится к следующему уроку или выпускному экзамену. плоская векторная целевая страница с копией пространства для дополнительного текста.
Значок академического экзамена простой вектор. book finalPREMIUM
Снова в школу векторная абстрактная плоская иллюстрация. значки образования и учебы, этикетки, наклейки и элементы дизайна.0003
Домашнее задание. концепция электронного обучения, онлайн-образования, домашнего обучения, веб-курсов, учебных пособий. 3d реалистичная векторная иллюстрация. PREMIUM
Студентка и стопка книг векторная иллюстрацияPREMIUM
Дети учатсяPREMIUM
Развивающая детская игра для детей и малышей. что не подходит логическая игра. найти нечетный, дополнительный объект. тема насекомых. обучающие насекомыеPREMIUM
Значок диплома об окончании школы плоский вектор. студенческая тетрадьPREMIUM
Милый маленький мальчик чувствует себя счастливым, потому что получил хорошую оценку на экзаменеPREMIUM
Значок бумажного диплома плоский вектор. book finalPREMIUM
Значок выпускного студента простой вектор. Study finalPREMIUM
Милому маленькому мальчику грустно из-за плохой оценки на экзаменеPREMIUM
Студенты учатся онлайн дома.
Онлайн-курс в университете, видеоурок, подготовка к экзаменам, дистанционный урок грамматики для студентов. человек изучают иностранный язык дистанционно, используя современные интернет-технологии, онлайн-сервис обученияPREMIUM
Симпатичная девушка задает вопросы векторный персонажPREMIUM
Университетский онлайн-курс, видеоурок, подготовка к экзаменам, дистанционный урок грамматики для студентов. люди изучают иностранный язык удаленно, используя современные интернет-технологии, сервис веб-образования. секундомер, план выполнения, прокрастинация и эффективность, управление проектами, быстрая анкета, краткий опрос, doodlePREMIUM
Счастливый милый маленький мальчик, думающий на экзаменеPREMIUM
Значок экзамена с черным рисунком на белом фонеPREMIUM
Женщина из комиксов, улыбающаяся блондинка с книгой на английском языке.
Школьники. студенты в классе, ученики готовятся к дню знаний, учатся в школе, готовят набор векторных иллюстраций домашних заданий. символы школьного образованияPREMIUM
Образование и работа в Интернете, занятия через ИнтернетPREMIUM
Значок экзамена ноутбука плоский вектор. рабочий тестПРЕМИУМ
Значок академического выпуска простой вектор. book studyPREMIUM
Векторные плоские люди усердно учатся. измученная уставшая девушка, студентка или работница, сидящая за столом, чашка кофе, переутомление, изучение экзаменов, мужчина, держащий волосы, девушка, взбирающаяся на стопку, мужчина, бегущий с книгами. ПРЕМИУМ
Удивленный мужчина, список дел, задание контрольного списка, управление задачами, концепция прокрастинации, низкий балл теста , векторная плоская иллюстрацияPREMIUM
Вектор контура значка выпускного экзамена. учебникПРЕМИУМ
Счастливая милая девочка учится усердно думаетPREMIUM
Логический ребенок описывает игру с картинками шаблон для печатиPREMIUM
Концепция быстрого образования, подготовка к экзаменам, учебный предмет, крайний срок школьного задания, обзор знаний, самообучение, время учиться, контрольный список, векторный значок, плоская иллюстрацияPREMIUM
Мальчик учитсяPREMIUM
Бумажный вектор контура значка экзамена.
Иллюстрация концепции изометрических исследованийPREMIUM
Улыбающийся студент мужского пола сидит за партой и пишет векторную плоскую иллюстрацию школьного теста. красочный счастливый парень на экзамене в колледже, изолированные на белом фоне. счастливый подросток за столом в университетеПРЕМИУМ
Вектор контура значка диплома о высшем образовании. экзамен PREMIUM
Концепция изометрического дизайна онлайн-библиотеки со стопкой учебных пособий, покрытых шляпой магистратуры под облачными значками, изометрическая векторная иллюстрацияPREMIUM
Веб-баннер библиотекаря или целевая страница. каталогизация персонала библиотекиPREMIUM
Счастливая милая девочка изучает математикуPREMIUM
Исчисление III
Математика 333 — Календарь
Исчисление III
Исчисление III
Неделя
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17
| Неделя | Дата | Тема | Домашнее задание (оплачивается в начале занятий) |
|---|---|---|---|
| 1 | Понедельник 26.  08.13 08.13 |
Ориентация курса &раздел 11.1. Векторы в плоскости. |
Домашнее задание не сдано. |
| Вторник 27.08.13 |
&раздел 11.2. Космические координаты и векторы в пространстве. | Упражнения, отмеченные знаком (*), являются задачами для предварительного чтения. | |
| Четверг 29.08.13 |
&раздел 11.3. Скалярный продукт двух векторов. |   | |
| 2 | Понедельник 02.09.13 |
День труда — без класса |   |
| Вторник 04.09.13 |
&раздел 11. 4. Перекрестное произведение двух векторов в пространстве. 4. Перекрестное произведение двух векторов в пространстве.902:30 |
  | |
| Четверг 06.09.13 |
&раздел 11.5. Линии и плоскости в пространстве. |   | |
| 3 | Понедельник 9/9/13 |
&раздел 11.6. Поверхности в космосе. |   |
| Вторник 10.09.13 |
&раздел 11.7. Цилиндрические и сферические координаты. |   | |
| Четверг 12.09.13 |
&раздел 12.1. Векторнозначные функции. |   | |
| 4 | Понедельник 16.09.13 |
&раздел 12. 2. Дифференцирование и интегрирование вектор-функций. 2. Дифференцирование и интегрирование вектор-функций.902:30 |
  |
| Вторник 17.09.13 |
&раздел 12.3. Скорость и ускорение. |   | |
| Четверг 19.09.13 |
&раздел 12.4. Касательные векторы и нормальные векторы. |   | |
| 5 | Понедельник 23.09.13 |
Экзамен I — главы 11 и 12 | Домашнее задание не сдано. |
| Среда 26.09.13 |
&раздел 3.2. Сложение и вычитание целых чисел |
&раздел 3.1. Упражнения 15, 18, 19, 24, 25, 32, 33; стр. 108-111. &раздел 3.2. Упражнение 1*; стр.  119-122. 119-122.
|
|
| 6 | Понедельник 01.10.13 |
Экзамен I — главы 11 и 12 &раздел 3.3. Умножение и деление целых чисел |
&раздел 3.2. Упражнения 3, 9, 11, 12, 13, 14, 17, 20, 32; стр. 119-122. &раздел 3.3. Упражнение 1*; стр. 133-138. |
| Среда 03.10.13 |
&раздел 3.4. Свойства операций с целыми числами |
&раздел 3.3. Упражнения 3, 5, 6, 7, 8, 13, 14, 23, 27, 28, 29, 30, 31, 32, 35, 36, 47, 48; стр. 133-138. &раздел 3.4. Упражнение 1*; стр. 146-150. |
|
| 7 | Понедельник 8.10.13 |
&раздел 3.5. Алгоритмы сложения и вычитания целых чисел |
&раздел 3.4. Упражнения 3, 4, 9, 14, 19, 22, 28; стр. 147-150. &раздел 3.  5. Упражнения 1*; стр. 158-161. 5. Упражнения 1*; стр. 158-161.
|
| Среда 10.10.13 |
&раздел 3.6. Алгоритмы умножения и деления целых чисел |
&раздел 3.5. Упражнения 6, 7, 11, 13, 18, 23, 33, 34; стр. 158-161. &раздел 3.6. Упражнение 1*; стр. 167-170. |
|
| 8 | Понедельник 15.10.13 |
&раздел 3.8. Поместите ценность и алгоритмы в другие базы |
&раздел 3.6. Упражнения 2, 5, 10, 12, 14, 17, 18, 19, 27, 28; стр. 167-170. &раздел 3.8. Упражнение 1*; стр. 187-190. |
| Среда 17.10.13 |
Видео и обсуждение — Совместное использование бутербродов с подводной лодкой |
&раздел 3.8. Упражнения 5, 6, 7, 8, 11, 17, 18, 19, 20, 24, 25, 26; стр. 187-190. Подготовка к просмотру видео. 
|
|
| 9 | Понедельник 22.10.13 |
Экзамен II — Глава 3 | Домашнее задание не сдано. |
| Среда 24.10.13 |
&раздел 4.1. Факторы &раздел 4.2. Делимость 902:30 |
Домашнее задание не сдано. | |
| 10 | Понедельник 29.10.13 |
&раздел 4.3. Простые и составные числа &раздел 4.4. Общие факторы и мультипликаторы |
&раздел 4.1. Упражнения 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22; стр. 201-202. &раздел 4.2. Упражнения 6, 7, 9, 10, 14, 15, 19, 20, 21, 22; стр. 210-212. 902:30 |
| Среда 31.10.13 |
&раздел 5. 1. Сложение и вычитание целых чисел 1. Сложение и вычитание целых чисел
|
&раздел 4.3. Упражнения 5, 7, 9, 15, 18; стр. 218-220. &раздел 4.4. Упражнения 2, 3, 4, 10, 13, 15, 21, 23; стр. 226-228 &раздел 5.1. Упражнение 2*; стр. 242-245. |
|
| 11 | Понедельник 5/11/13 |
&раздел 5.2. Умножение и деление целых чисел &раздел 5.3. Свойства целочисленных операций |
&раздел 5.1. Упражнения 4, 5, 6, 11, 16, 17, 25, 29, 37, 38, 41; стр. 242-245. |
| Среда 7/11/13 |
&раздел 6.1. Рациональное число |
&раздел 5.2. Упражнения 1, 3, 4, 5, 11, 12, 13, 16, 19; стр. 249-250. &раздел 5.3. Упражнения 6, 7, 8, 10, 12, 15; стр. 254-255. 902:30 |
|
| 12 | Понедельник 13.11.13 |
&раздел 6. 2. Сложение и вычитание рациональных чисел 2. Сложение и вычитание рациональных чисел
|
&раздел 6.1. Упражнения 4, 5, 8, 9, 10, 15, 20, 22, 24, 35, 37, 38, 41, 44; стр. 268-272. &раздел 6.2. Упражнения 6, 7, 9, 11, 12, 17, 18, 19, 25, 30; стр. 280-283. &раздел 6.3. Упражнения 3*; стр. 291-295. |
| Среда 14.11.13 |
&раздел 6.3. Умножение и деление рациональных чисел &раздел 6.4. Рациональные числа: свойства, оценка и шаблоны ошибок |
Домашнее задание не сдано. | |
| 13 | Понедельник 19.11.13 |
Экзамен III — главы 4, 5 и 6 |
&раздел 6.3. Упражнения 8, 13, 14, 20, 22, 32, 35, 41, 54, 55, 56; стр. 291-295. &раздел 6.4. Упражнения 5, 9, 36, 37, 38, 39, 40; стр. 301-303. |
| Среда 21.  11.13 11.13 |
Перерыв на День Благодарения — без класса |   | |
| 14 | Понедельник 26.11.13 |
Видео и обсуждение — Изучение игровых площадок § 7.1 Десятичные числа: разрядное значение, оценка и вычисление в уме &раздел 7.2. Десятичная арифметика и шаблоны ошибок |
Домашнее задание не сдано. |
| Среда 28.11.13 |
&раздел 7.3. Соотношение и пропорция |
&раздел 7.1. Упражнения 11, 12, 25, 26, 27, 30, 38, 42; стр. 318-321. &раздел 7.2. Упражнения 3, 11, 12, 22, 23, 33, 41, 42, 54, 55; стр. 331-335. &раздел 7.3. Упражнение 1*; стр. 341-345. |
|
| 15 | Понедельник 03.12. 
No related posts. |
 
 
Задачи по теме «Векторы»(для подготовки к ЕГЭ по математике профильный уровень)
консультация по математике (11 класс) на тему
Скачать:
| Вложение | Размер |
|---|---|
| vektory.docx | 479.51 КБ |
Предварительный просмотр:
- Найдите квадрат длины вектора .
- Стороны правильного треугольника ABC равны . Найдите длину вектора + .
- Найдите сумму координат вектора .
Вектор с началом в точке A (2, 4) имеет координаты (6, 2). Найдите ординату точки B .
Вектор с концом в точке B (5, 3) имеет координаты (3, 1). Найдите абсциссу точки A .
Вектор с концом в точке B (5, 4) имеет координаты (3, 1). Найдите сумму координат точки A .
Найдите квадрат длины вектора + .
Найдите квадрат длины вектора .
Найдите длину вектора (6; 8).
Найдите квадрат длины вектора .
Стороны правильного треугольника равны . Найдите длину вектора .
Стороны правильного треугольника равны 3. Найдите длину вектора .
Стороны правильного треугольника равны 3. Найдите скалярное произведение векторов и .
. Найдите сумму координат вектора .
. Вектор с началом в точке (2; 4) имеет координаты (6; 2). Найдите абсциссу точки .
Вектор с началом в точке (2; 4) имеет координаты (6; 2). Найдите ординату точки .
Вектор с началом в точке (3; 6) имеет координаты (9; 3). Найдите сумму координат точки .
Вектор с концом в точке (5; 3) имеет координаты (3; 1). Найдите абсциссу точки .
Вектор с концом в точке (5; 3) имеет координаты (3; 1). Найдите ординату точки .
Вектор с концом в точке (5; 4) имеет координаты (3; 1). Найдите сумму координат точки .
Найдите сумму координат вектора + .
Найдите квадрат длины вектора + .
. Найдите сумму координат вектора .
Найдите квадрат длины вектора .
Найдите скалярное произведение векторов и .
Найдите угол между векторами и . Ответ дайте в градусах.
Найдите сумму координат вектора + .
Найдите квадрат длины вектора + .
Найдите сумму координат вектора .
Найдите квадрат длины вектора .
Найдите скалярное произведение векторов и .
Найдите угол между векторами и . Ответ дайте в градусах.
Векторы
Отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом, называется вектором.
Вектор с началом в точке A и концом в точке B обозначают $<(АВ)>↖<→>$ или строчной (маленькой) буквой, например $<а>↖<→>$
Любая точка плоскости является вектором. В этом случае вектор называется нулевым.
Модуль (длину) вектора обозначают $|АВ|↖<→>$.
Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.
Два коллинеарных вектора называются сонаправленными, если они направлены в одну сторону.
Векторы называются равными , если они сонаправлены и их длины равны.
Сумма векторов — это вектор, который можно получить двумя способами.
- Правило треугольника (А)
- Правило параллелограмма (Б)
Для любых векторов $a↖<→>, b↖<→>, c↖<→>$ справедливы равенства:
Разность векторов тоже можно получить двумя способами:
Если надо найти разность двух векторов, их необходимо отложить из одной точки. Результирующий вектор направлен к уменьшаемому.
Для любых $a↖<→>$ и $b↖<→>$ справедливо равенство $a↖<→>-b↖<→>=a↖<→>+(<-b>↖<→>)$
Скалярное произведение векторов равно произведению длин векторов на косинус угла между ними.$a↖<→>⋅b↖<→>=|a↖<→>|·|b↖<→>|·cosα$
Ненулевые векторы $a↖<→>$ и $b↖<→>$ перпендикулярны, если их произведение равно нулю.
Метод координат
Координаты вектора равны разностям соответствующих координат конца и начала данного вектора.
Для того чтобы векторы $a↖<→>$ и $b↖<→>$ были коллинеарными, необходимо и достаточно, чтобы выполнялось равенство $a↖<→>=k·b↖<→>$, где $k$ — это некоторое число.
Координаты середины вектора равны средним арифметическим координат его концов.
Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Скалярное произведение векторов $a↖<→>$ и $b↖<→>$ в координатах находится по формуле $a↖<→>·b↖<→>= x1·x2+y1·y2$
Длина вектора $a↖<→>$ вычисляется по формуле: $|a↖<→>|=√$
Расстояние между двумя точками $M1(x1;y1)$ и $M2(x2; y2)$ находится по формуле $|M1M2|=√<(x2-x1)^2+(y2-y1)^2>$
Найдите угол между векторами $a↖<→>$ и $b↖<→>$
- Сначала нужно найти координаты векторов $a↖<→>$ <2-0;6-0>$b↖<→>$
- Найдем скалярное произведение векторов $a↖<→>·b↖ <→>= 2·8+6·4=16+24=40$
- Найдем длины каждого вектора $|a↖<→>|= √<4+36>=√<40>; |b↖<→>|=√<64+16>=√<80>$
- Найдем косинус угла между векторами $cosα=<40>/<√<40>·√<80>>=<40>/<√<40·40·2>>=<1>/<√2>=<√2>/<2>$
- Найдем угол $α=arccos<√2>/<2>=45$
Сборник «Решение задач №14 ЕГЭ по математике координатно-векторным методом»
Серия «Школьник — школьнику»
Решение заданий №14 ЕГЭ по математике координатно-векторным методом
С помощью данных методических рекомендаций можно научиться решать задачи на вычисление углов и расстояний в стереометрии с помощью координатно-векторного метода. Для учеников 10-11 классов самой главной проблемой является подготовка к ЕГЭ. Причем не все ученики уверенно решают задания II части , а некоторые и не берутся за их решение.
Координатно-векторный метод основан на введении прямоугольной системы координат и создании геометрически-алгебраической модели решения задач, тем самым упрощая громоздкие и достаточно сложные преобразования и выкладки.
Достоинство метода координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных конфигураций.
Выражаю огромную благодарность своим ученикам 11 класса 2016 – 2017 учебного года: Комаровой Ангелине, Тарбаеву Наилю, Бекмурзаеву Тимуру, Утегеновой Аимгуль, Абылхатаевой Карине, Кункашевой Арине, Юсуповой Аделине, Успанову Гелиму , которые сыграли большую роль в создании данного методического сборника
Если у вас имеются серьезные проблемы с пониманием определений, с чтением или построением сложного стереометрического рисунка, если вам никак не удается подобрать необходимые дополнительные построения, мне кажется, что стоит заняться изучением координатно-векторного метода. Особенно это актуально в условиях экстренной помощи, когда до ЕГЭ остается всего лишь 2-3 месяца.
Данный курс не претендует на научность, а является небольшим методическим пособием при подготовке к ЕГЭ для выпускника, нацеленного на высокий балл при сдаче экзамена. Курс является кратким, в нем рассмотрены лишь наиболее часто встречающиеся типы заданий, как в сборниках, так и в контрольно-измерительных материалах.
Метод координат — это довольно несложный способ, но в настоящих задачах №14 никаких координат и векторов нет. Поэтому их придется вводить: указать начало отсчета, единичный отрезок и направление осей x, y и z.
Самое замечательное свойство этого метода заключается в том, что не имеет никакого значения, как именно вводить систему координат. Если все вычисления будут правильными, то и ответ будет правильным.
Метод координат —эффективный и универсальный способ нахождения любых углов или расстояний между стереометрическими объектами в пространстве. Данный метод заключается во введении декартовой системы координат, а затем – нахождение образующихся векторов (их длин и углов между ними). Достоинство метода координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных конфигураций. Алгоритм применения метода координат к решению геометрических задач сводится к следующему:
— Выбираем в пространстве систему координат
— Находим координаты необходимых, по условию задачи, точек.
— Решаем задачу, используя основные задачи метода координат.
— Переходим от аналитических соотношений к геометрическим.
Для начала разбора метода координат для стереометрических задач рассмотрим, что же представляет собой прямоугольная (декартова) система координат в пространстве. Прямоугольная (декартова) система координат в пространстве – совокупность точки О (называемой началом координат), единицы измерения и трёх попарно перпендикулярных прямых Ox, Oy иOz (называемых осями координат: Ox – ось абсцисс, Oy – ось ординат, Oz – ось аппликат), на каждой из которых указано направление положительного отсчёта. Плоскости хОу, уОz и zOx называют координатными плоскостями. Каждой точке пространства ставится в соответствие тройка чисел, называемых её координатами.


Для того чтобы использовать метод координат, надо хорошо знать формулы:
1. Нахождение расстояния между двумя точками, заданными своими координатами.

2. Нахождение координат середины отрезка
A ( x 1 ; y 1 ; z 1 ), B ( x 2 ; y 2 ; z 2 ) 
3. Нахождение косинуса угла между векторами

4. Координаты x, y, z точки М , которая делит отрезок , ограниченный точками А(х 1 , у 1 , z 1 ) и B ( x 2 ,y 2 , z 2 ), в отношении , определяется по формулам
5. Расстояние от точки до плоскости
Для решения задач необходимо научиться находить координаты вершин основных многогранников при помещении их в прямоугольную систему координат.
Ниже представлены координаты вершин некоторых многогранников, помещенных в систему координат.
Это самый простой многогранник, все двугранные углы которого равны 90°.
Система координат также вводится очень просто:
Начало координат — в точке A;
Чаще всего ребро куба не указано, поэтому принимаем его за единичный отрезок;
Ось x направляем по ребру AB, y — по ребру AD, а ось z — по ребру AA 1 .
Обратите внимание: ось z направляется вверх! После двумерной системы координат это несколько непривычно, но на самом деле очень удобно и логично.
Итак, теперь у каждой вершины куба есть координаты. Соберем их в таблицу — отдельно для нижней плоскости куба:
И для верхней: Несложно заметить, что точки верхней плоскости отличаются от соответствующих точек нижней только координатой z. Например, B = (1; 0; 0), B 1 = (1; 0; 1).
Координаты правильной треугольной призмы
При правильном подходе достаточно знать координаты только нижнего основания — верхнее будет считаться автоматически.
В задачах №14 встречаются исключительно правильные трехгранные призмы (прямые призмы, в основании которых лежит правильный треугольник). Для них система координат вводится почти так же, как и для куба.
Вводим систему координат:
Начало координат — в точке A;
Сторону призмы принимаем за единичный отрезок, если иное не указано в условии задачи;
Ось x направляем по ребру AB, z — по ребру AA 1 , а ось y расположим так, чтобы плоскость OXY совпадала с плоскостью основания ABC.
Получаем следующие координаты точек:
Как видим, точки верхнего основания призмы снова отличаются от соответствующих точек нижнего лишь координатой z. Основная проблема — это точки C и C 1 . У них есть иррациональные координаты, и для того чтобы довольно просто решить задание №14 эти иррациональные координаты надо просто запомнить. Или можно вывести.
Координаты правильной шестиугольной призмы
Шестиугольная призма — это «клонированная» трехгранная. Можно понять, как это происходит, если взглянуть на нижнее основание — обозначим его ABCDEF. Проведем дополнительные построения: отрезки AD, BE и CF. Получилось шесть треугольников, каждый из которых (например, треугольник ABO) является основанием для трехгранной призмы.
Теперь введем систему координат. Начало координат — точку O — поместим в центр симметрии шестиугольника ABCDEF. Ось x пойдет вдоль FC, а ось y — через середины отрезков AB и DE. Получим такую картинку:
Нужно обратить внимание на то, что начало координат не совпадает с вершиной многогранника. На самом деле, при решении настоящих задач выясняется, что это очень удобно, поскольку позволяет значительно уменьшить объем вычислений. Осталось добавить ось z. Проводим ее перпендикулярно плоскости OXY и направляем вертикально вверх. Получим картинку:
Запишем теперь координаты точек. Предположим, что все ребра нашей правильной шестигранной призмы равны 1. Итак, координаты нижнего основания:
Координаты верхнего основания сдвинуты на единицу по оси z:
Координаты правильной четырехугольной пирамиды
Итак, правильная четырехугольная пирамида. Обозначим ее SABCD, где S — вершина. Введем систему координат: начало в точке A, единичный отрезок AB = 1, ось x направим вдоль AB, ось y — вдоль AD, а ось z — вверх, перпендикулярно плоскости OXY. Для дальнейших вычислений нам потребуется высота SH — вот и построим ее. Получим следующую картинку:
Теперь найдем координаты точек. Для начала рассмотрим плоскость OXY. Здесь все просто: в основании лежит квадрат, его координаты известны. Проблемы возникают с точкой S. Поскольку SH — высота к плоскости OXY, точки S и H отличаются лишь координатой z. Длина отрезка SH — это и есть координата z для точки S, поскольку H = (0,5; 0,5; 0).
Заметим, что треугольники ABC и ASC равны по трем сторонам (AS = CS = AB = CB = 1, а сторона AC — общая). Следовательно, SH = BH. Но BH — половина диагонали квадрата ABCD, т.е. BH = AB · sin 45°. Получаем координаты всех точек:
Ниже представлено, как найти определитель третьего порядка по правилу Саррюса, составить уравнение плоскости и найти вектор нормали.
§2 Практическая часть
Ниже представлены задачи:
— на нахождение угла между прямыми;
— угла между прямой и плоскостью;
— угла между плоскостями;
— расстояния от точки до прямой;
— расстояния от точки до плоскости.
Эти задачи решили мои ученики 11 класса
Вариант 13. Задача №14 по сборнику Ф.Ф.Лысенко
В кубе ABCDA 1 B 1 C 1 D 1 , ребро которого равно 4, точка М является серединой отрезка BC 1 . Найдите расстояние между прямыми А 1 В и АМ.
Задача №14 по сборнику ФИПИ 2016
В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 все рёбра равны 1. Найдите расстояние от точки В до прямой C 1 F .
Задача №14 по сборнику ФИПИ 2017
Дана правильная четырёхугольная призма ABCDA 1 B 1 C 1 D 1 . Найдите расстояние от точки B 1 до плоскости AD 1 C , если АВ равно 5, АА 1 равно 6.
Задача №14 ЕГЭ по сборнику ФИПИ 2017
В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 все рёбра равны 4.
а) Докажите, что угол между прямыми А D 1 и DC 1 равен 90 0 .
б) Найдите угол между плоскостями FAC 1 и AA 1 D .
Задача №14 ЕГЭ по сборнику ФИПИ 2017
Мы изучили метод координат на более высоком уровне по сравнению со школьной программой по геометрии. Познакомились и научились применять новые формулы: на нахождение расстояния от точки до плоскости, от точки до прямой, угла между прямыми, угла между прямой и плоскостью, угла между плоскостями. Мы узнали, что для составления уравнения плоскости можно использовать матрицу и определитель третьего порядка, который можно посчитать правилом Саррюса.
Мы пришли к выводу, что использование метода координат требует от ученика внимательности, хороших вычислительных навыков. Мы убеждены в том, что координатно-векторный метод в школьном курсе геометрии необходимо изучать на глубоком уровне и увеличить количество часов на изучение данной темы.
Нами подобраны задания из сборников ФИПИ 2016г и 2017г, которые мы самостоятельно решили и которые помогут отработать полученные навыки, и тем самым более качественно подготовиться к сдаче экзамена.
Мы надеемся, что изложенная в работе информация поможет выпускникам решать задание №14 и достичь более высоких результатов на ЕГЭ по математике
ЕГЭ 2017. Математика. И.В. Ященко. 36 вариантов. Профильный уровень
ru . wikipedia . org – Система координат.
Смирнова, И.М. C 50 Геометрия. Расстояния и углы в пространстве: учебно-методическое пособие / И.М. Смирнова, В.А. Смирнов. – 2-е изд., перераб. И доп. – М.: Издательство «Экзамен», 2009. – 158, [2] с. (Серия «ЕГЭ. 100 баллов»)
Геометрия, 10 – 11 : Учеб. Для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 13-е изд. – М.: Просвещение, 2014. – 206 с.: ил.
Корянов А.Г, Прокофьев А.А. Многогранники: виды задач и методы их решения . МАТЕМАТИКА ЕГЭ 2013 (типовые задания С2) « Многогранники: виды задач и методы их решения » www.alexlarin.narod.ru
Корянов А.Г, « Расстояния и углы в пространстве» МАТЕМАТИКА ЕГЭ 2010 (типовые задания С2) www.alexlarin.narod.ru
В.В. Леваков «Решение задач координатно-векторным методом»
источники:
http://examer.ru/ege_po_matematike/teoriya/vector
http://infourok.ru/sbornik-reshenie-zadach-14-ege-po-matematike-koordinatno-vektornym-metodom-4377304.html





























































