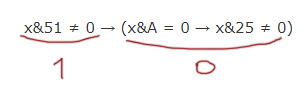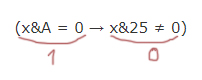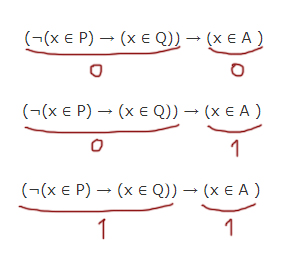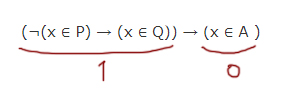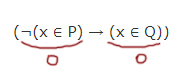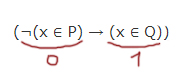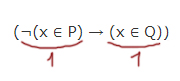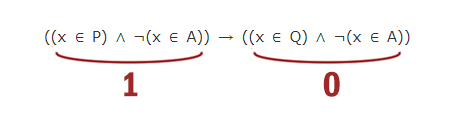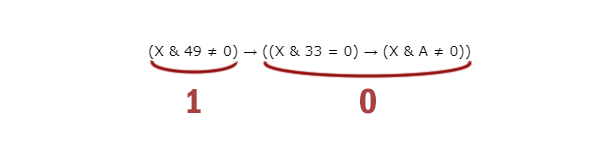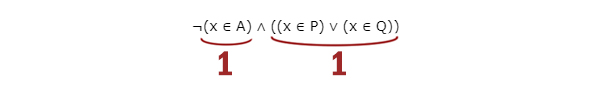-
Главная
-
Пробные и реальные тесты ЕГЭ
-
ЕГЭ по информатике
-
Тренировочный вариант Статград №2 ЕГЭ 2023 по информатике от 15.12.2022
- 28.12.2022
Вариант Статграда по информатике для 11 класса в формате ЕГЭ 2023 года
Работа проводилась 15 декабря 2022 года.
- Другие варианты по информатике
Вариант полностью соответствует демоверсии ФИПИ и кодификатору. Замечательный материал для самоподготовки.
Мы сделали для вас видеоразбор этого варианта. Смотрите ниже.
Есть вопросы? Задавайте в комментариях ниже!
Вариант №1
Вариант №2
Вариант №3
Сохранить ссылку:
Комментарии (1)
Добавить комментарий
Комментарии
+1
#1
Лидия Морозова
10.03.2023 09:38



Цитировать
Обновить список комментариев
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Имя (обязательное)
E-Mail
Подписаться на уведомления о новых комментариях
Отправить
Сегодняшний урок посвящён 15 заданию из ЕГЭ по информатике 2022.
Темой этого урока связана с преобразованием логических выражений.
Теорию для преобразования логических выражений Вы можете посмотреть в этой статье. Как можно работать с логическими выражениями на питоне, можно прочитать в этой статье.
Перейдём к практике решения задач 15 задания из ЕГЭ по информатике 2022.
Задача (Неравенство, одна переменная)
Какое количество натуральных чисел удовлетворяет логическому условию:
¬(X2 ≥ 9) ∨ ¬((X < 7) ∨ (X ≥ 10)) ?
Решение:
Первый способ (с помощью питона).
k=0 for x in range(1, 1000): if not(x**2 >= 9) or not((x < 7) or (x>=10)): k = k + 1 print(k)
Здесь перебираем с помощью цикла for натуральные числа от 1 до 1000.
Если логическое выражение выдаёт истину, то мы подсчитываем такой вариант.
Программа напечатает число 5.
Второй способ (с помощью рассуждений).
Натуральные числа — это целые, положительные числа. Например: 1, 2, 3, 4, и т. д.
Преобразуем первое выражение ¬(X2 ≥ 9) = (X2 < 9). Отрицание внесли в скобки. В этом случае знак, который находится в скобках, нужно поменять на противоположный.
Важно: Если было строгое неравенство, то оно станет нестрогим, и наоборот, если было неравенство нестрогим, то оно станет строгим.
Получается, что выражение (X2 < 9) будет истинно только при двух значениях: X = 1, X = 2.
Во втором выражении ¬((X < 7) ∨ (X ≥ 10)) удобно применить формулу Де Моргана.
Формула де Моргана:
¬(A ∨ B) = ¬A ∧ ¬B
¬(A ∧ B) = ¬A ∨ ¬B
Преобразуем выражение по формуле де Моргана и внесём отрицание в скобки:
¬((X < 7) ∨ (X ≥ 10)) = ¬(X < 7) ∧ ¬(X ≥ 10) = (X ≥ 7) ∧ (X < 10)
Получилось выражение (X ≥ 7) ∧ (X < 10). Между двумя выражениями стоит логическое умножение. Значит, одновременно должны выполняться и первое неравенство, и второе. Таким образом, получается, что подходят три значение для выражения (X ≥ 7) ∧ (X < 10). Это X = 7, X = 8, X = 9.
Обратимся к самому начальному логическому условию. Там два выражения соединятся логическим сложением. Значит, мы должны объединить те случаи, когда у нас первое выражение становится истинным (X=1, X=2), и те случаи, когда второе выражение становится истинным (X = 7, X = 8, X = 9).
Получается всего 5 натуральных чисел удовлетворяют изначальному логическому условию.
Ответ: 5
Разберём ещё одну разминочную задачу для подготовки к ЕГЭ по информатике 2022.
Задача (Неравенство, две переменные)
Для какого наибольшего целого неотрицательного числа A выражение
(x ≥ A) ∨ (y ≥ A) ∨ (x * y ≤ 205)
тождественно истинно, т.е. принимает значение 1 при любых целых положительных x и y ?
Решение:
Первый способ (с помощью питона).
for A in range(0, 300): k=0 for x in range(1, 301): for y in range(1, 301): if (x >= A) or (y >= A) or (x * y <= 205): k=k+1 if k==90000: print(A)
В первом цикле перебираем значения для A. Здесь мы пытаемся подобрать ответ в диапазоне от 0 до 300. Этот диапазон меньше, чем в прошлой задаче. Потому что здесь три вложенных цикла, и если перебирать числа от 0 до 1000, то программа может работать очень долго. При необходимости можно указать другой диапазон.
Для каждого A устанавливаем счётчик k в ноль.
Затем перебираем все числа в диапазоне от 1 до 300 (включительно) для переменных x и y, тем самым имитируем фразу «для любых x и y».
Если логическое выражение сработает при каждом значении x и y, то считается, что значение A нам подходит, и в счётчике по окончанию вложенных циклов будет значение 90000 (300 * 300 = 90000).
Наибольшее число, которое напечатает программа равно 15.
Второй способ (с помощью рассуждений).
Здесь есть три выражения в скобках, которые соединены логическим сложением. При логическом сложении достаточно хотя бы одного выражения, где будет истина, чтобы всё общее выражение было истинно.
Если мы сделаем A слишком большим, к примеру A = 250, то найдутся такие x = 16, y = 16, при которых все три условия в скобках не будут выполняться, и, значит, всё общее выражение будет ложным.
Следовательно, нам нужно выбрать таким A, чтобы не было возможности подобрать x, y, при которых все три выражения ложны.
Сделаем так: пока x и y меньше A, должно «работать» третье выражение в скобках. Как только x или y сравняются с A — начинают «работать» первое или второе выражение.
До какого же максимального значения могут дойти x и y, чтобы перемножение этих двух чисел было меньше или равно 205 (x * y <= 205) ?
15 * 15 = 225
14 * 14 = 196
Получается, пока числа x и y меньше 15, «выручает» третье выражение (x * y ≤ 205), как только станут x ≥ 15 и y ≥ 15, будут «работать» первое и второе выражение.
Отсюда получаем, что максимальное число A = 15
Ответ: 15
Задача (Функция ДЕЛ)
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула
¬ДЕЛ(x, А) → (ДЕЛ(x, 6) → ¬ДЕЛ(x, 9))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?
Решение:
Первый способ (с помощью питона).
def D(n, m): if n%m==0: return True else: return False for A in range(1, 1000): k=0 for x in range(1, 1001): if D(x, A) or (not(D(x, 6)) or not(D(x, 9))): k=k+1 if k==1000: print(A)
Здесь мы формируем функцию ДЕЛ (функцию D). Если n делится на m, то функция возвращает Истину, в противном случае функция возвращает Ложь.
Далее решаем примерно так же, как и в прошлых задачах: для каждого числа A перебираем все значения x. Следование расписываем по формуле A ⟶ B = ¬A ∨ B.
Наибольшее число здесь получается равно 18.
Второй способ (с помощью рассуждений).
Рассмотрим случай, когда в левой части логического выражения будет 1, а в правой 0. В остальных случаях беспокоится не за что, потому что вся формула будет выдавать истину.
Посмотрим, когда в правой части получается ноль. Функция ДЕЛ(x, 6) должна выдавать истину. Т.е. x должен делится на 6. А функция ¬ДЕЛ(x, 9) должна выдавать ноль. Т.е. без отрицания ДЕЛ(x, 9) должна выдавать истину. Значит, x так же делится на 9.
x делится на 6 => x = 2*3*n, n ∈ N
x делится на 9 => x = 3*3*n, n ∈ N
Чтобы выполнялся случай, когда в правой части получается ноль, икс должен быть равен x = 3*3*2*n (n ∈ N). Т.е. получается, что икс должен быть кратен 18.
Т.е. получается, что когда x делится на 18, в правой части логического выражения будет получатся ноль. Чтобы спасти ситуацию, мы должны в левой части логического выражения не получать 1. Следовательно, ¬ДЕЛ(x, А) должно выдавать ноль. Значит, ДЕЛ(x, А) должно выдавать 1. Таким образом, приходим к выводу, что A должно равняться 18.
Если получится опасная ситуация, когда x кратен 18, то она будет нейтрализована, ведь в левой части будет получатся ноль.
Ответ: 18
Ещё один важный тип задач 15 задания ЕГЭ по информатике 2022
Задача (Поразрядная конъюнкция)
Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14&5 = 11102 & 01012 = 4
Для какого наименьшего неотрицательного целого числа A формула
x&51 ≠ 0 → (x&A = 0 → x&25 ≠ 0)
тождественно истинна (то есть принимает значение 1 при любом неотрицательном целом значении переменной x)?
Решение:
Первый способ (с помощью питона).
for A in range(0, 1000): k=0 for x in range(0, 1000): if x&51==0 or (x&A!=0 or x&25!=0): k=k+1 if k==1000: print(A)
Здесь следование преобразовываем по формуле: A ⟶ B = ¬A ∨ B. Так же и A, и x неотрицательные числа. Поэтому мы перебираем их диапазон, начиная с нуля. Из-за этого в цикле, который перебирает переменную x, мы устанавливаем верхнюю границы равной 1000, а не 1001. Тогда тоже будет 1000 повторений в этом цикле.
Наименьшее число равно 34.
Второй способ (с помощью рассуждений).
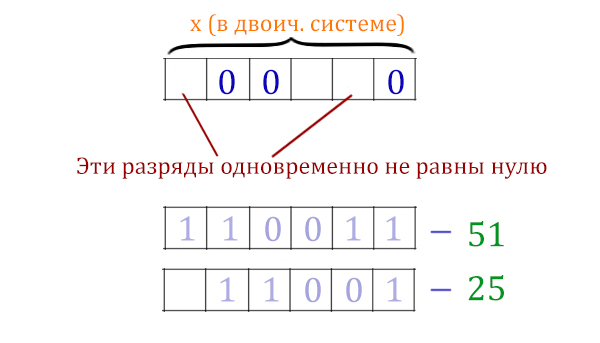
Переведём числа 51 и 25 в двоичную систему.
51 = 1100112
25 = 110012
Формула будет тождественно ложна, когда
Этого допустить нельзя!
При каком x получается в левой выражении формулы истина ? Если у икса в двоичном представлении в тех разрядах, где у числа 51 стоят 1, будет хотя бы в одном месте 1.
Рассмотрим правое выражение формулы. Ноль получается в единственном случае:
Рассмотрим выражение x&25 ≠ 0. Чтобы в этом логическом выражении получился ноль, нужно x&25 = 0. Посмотрим на двоичное представление числа 25. В тех разрядах, где стоят единицы, у икс должны быть нули (для x&25 = 0).
Сформулируем окончательное условие для x, при котором возникает опасность превращение общей формулы в ложь.
Нам нужно «поломать эту песенку» с помощью x&A = 0. Т.е. нельзя допускать, чтобы это выражение было истинно.
Получается, что A = 1000102. Это наименьшее из возможных число, при котором мы точно себя обезопасим от того, что вся формула будет ложна.
A = 1000102 в десятичной системе будет 34.
Ответ: 34
Ещё один тип задач 15 задания ЕГЭ по информатике
Задача (числовая прямая)
На числовой прямой даны отрезки P=[5, 13] и Q=[8, 19]. Укажите наименьшую возможную длину такого отрезка A, что формула (¬(x ∈ P) → (x ∈ Q)) → (x ∈ A ) верна при любых значениях x.
Решение:
Первый способ (с помощью питона).
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 200): for b in range(a, 200): k=0 for i in range(-200, 200): x = i / 2 if not((F(5, 13, x) or F(8, 19, x))) or F(a, b, x): k=k+1 if k==400: mn= min(mn, b-a) print(mn)
Получается ответ 14. Более подробно, как решать задачи на ОТРЕЗКИ из 15 задания ЕГЭ по информатике на Python, можете посмотреть в этой статье.
Второй способ (с помощью рассуждений).
Если будут такие варианты:
То нам беспокоится не о чём. Потому что формула всегда будет истинна! (см. таблицу истинности для следования →)
Нас же будет интересовать этот случай.
При таком раскладе вся формула будет ложна! Нам нужно этого не допустить при любом значении x!
Единица получается в первом подвыражении в трёх случаях:
1) Случай
Выражение ¬(x ∈ P) получается ложно, когда (x ∈ P) будет истинно! Получается при x ∈ [5, 13] выражение ¬(x ∈ P) — ложно!
Выражение (x ∈ Q) ложно, когда x ∉ [8, 19]
Какой же минимальной длины должен быть отрезок A, чтобы этот случай не проходил при любом x ? При этом случае отрезок A должен быть равен [5, 8). Тогда левое выражение пусть и может стать единицей при x ∈ [5, 8), но выражение (x ∈ A) будет также равно 1 при x ∈ [5, 8)! И схема 1 → 0 не пройдёт. Будет 1 → 1.
Для 1 случая A=[5, 
2) Случай
При каких x выражение ¬(x ∈ P) обращается в ноль, мы уже рассматривали: x ∈ [5, 13].
Второе выражение «выдаёт» 1 при x ∈ [8, 19].
Получается, что при при x ∈ [8; 13] первое выражение в скобках в главной формуле будет тождественно истинно!
С помощью отрезка A нужно это нейтрализовать путём превращения второго выражения в скобках в главной формуле в 1, пока x ∈ [8; 13]. Значит, для этого случая A = [8; 13]
3) Случай
В выражении ¬(x ∈ P) единица получается, когда в выражении (x ∈ P) получается ноль. Тогда x ∉ [5, 13]!
Чтобы во втором выражении (x ∈ Q) была единица, нужно, чтобы x ∈ [8, 19].
Получается, что 3 случай выполняется, если x ∈ (13, 19].
С помощью отрезка A нужно этому противодействовать! Нужно чтобы выражение (x ∈ A) было всегда 1 при x ∈ (13, 19]. Тогда A должно быть (13, 19].
Следовательно, для третьего случая A=(13, 19].
Нам нельзя допустить ни одного случая! Поэтому, объединив все случаи, получаем, что A=[5, 19].
Длина отрезка равна 14.
Ответ: 14
Ещё одна задача про числовую прямую из банка тренировочных заданий ЕГЭ по информатике 2021.
Задача (Числовая прямая, закрепление)
На числовой прямой даны отрезки P=[5, 13] и Q=[8, 19]. Укажите наименьшую возможную длину такого отрезка A, что формула ((x ∈ P) ∧ ¬(x ∈ A)) → ((x ∈ Q) ∧ ¬(x ∈ A)) верна при любых значениях x.
Решение:
Первый способ (с помощью питона).
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 200): for b in range(a, 200): k=0 for i in range(-200, 200): x = i / 2 if not((F(5, 13, x) and not(F(a, b, x)))) or (F(8, 19, x) and not(F(a, b, x))): k=k+1 if k==400: mn=min(mn, b-a) print(mn)
Второй способ (с помощью рассуждений).
Формула может быть ложна, когда
Во всех остальных случаях, формула всегда верна.
Чтобы выражение ((x ∈ P) ∧ ¬(x ∈ A)) было тождественно 1, выражение (x ∈ P) обязательно должно быть тождественно 1. А, значит, x ∈ [5, 13] — это опасная зона, при которой появляется возможность обратить всю формулу в ноль!
Мы можем сразу пресечь эту опасность с помощью отрезка A. Выбрать такой отрезок, чтобы он всегда «выдавал» ложь при x ∈ [5, 13]. Для этого достаточно выбрать A=[5, 13]! Но вдруг его можно сделать ещё более маленьким за счёт правой части формулы ?
Предположим, что отрезок A сделали ещё меньшим. Тогда при каком-то x (x ∈ [5, 13]) выражение ¬(x ∈ A) будет «выдавать» 1! Причём такое же выражение стоит и в правой части формулы! Там тоже будет 1 для выражения ¬(x ∈ A).
Нас же в этом случае должно выручить выражение (x ∈ Q). Если оно «выдаст» 1 в этот «сложный» момент, то мы спасены! Ведь тогда получается, что правая часть всей формулы будет «выдавать» не 0, а 1. Посмотрим при каких x из отрезка [5, 13] приходит это спасение.
Видим, что в интервале x ∈ [8, 13] нас спасает выражение (x ∈ Q).
Значит, отрезок A можно сократить до A=[5, 8).
Длина отрезка будет равна 3!
Ответ: 3
Задачи для закрепления
Задача (Неравенство, две переменные, закрепление)
Для какого наибольшего целого неотрицательного числа A выражение
(x < A) ∧ (y < A) ∧ (x * y > 603)
тождественно ложно, т.е. принимает значение 0 при любых целых положительных x и y ?
Решение:
Первый способ (с помощью питона).
for A in range(0, 300): k=0 for x in range(1, 301): for y in range(1, 301): if not( (x < A) and (y < A) and (x * y > 603) ): k=k+1 if k==90000: print(A)
Т.к. выражение должно быть ЛОЖНО, то обернём логическое выражение в функцию not(). Видим, что программа не сильно отличается от прошлой задачи. Данный шаблон подходит для большинства задач подобного типа.
Наибольшее число получается равно 25.
Второй способ (с помощью рассуждений).
В этой задаче нужно, чтобы общее выражение было ложно!
Если мы поставим отрицание над всем выражением, то можно искать такое максимальное A, при котором всё выражение тождественно истинно, а не ложно!
¬((x < A) ∧ (y < A) ∧ (x * y > 603)) = ¬(x < A) ∨ ¬(y < A) ∨ ¬(x * y > 603)
Здесь применили формулу де Моргана! Т.е. каждое подвыражение получило отрицание + соединительная логическая операция (логическое умножение) сменилась на противоположную операцию (логическое сложение).
Внесём отрицание в скобки. Получается:
(x ≥ A) ∨ (y ≥ A) ∨ (x * y ≤ 603)
Получили ситуацию, как в прошлой задаче! Напомню, что теперь нужно, чтобы общее выражение было истинно.
Найдём максимальное число, до которого могут «подняться» x и y, чтобы ещё работало третье выражение!
Обратите внимание, что x и y — симметричны. Значит, что верхняя планка для x и y будет одно и тоже число.
Поэтому вспоминаем таблицу квадратов.
25 * 25 = 625
24 * 24 = 576
Получается, что максимальное число до которого могут «дойти» x и y, чтобы «работало» третье выражение, равно 24.
Тогда, начиная с 25 для x и y, должны работать первое и второе выражение.
Получается, что максимальное число для A равно 25.
Ответ: 25
Ещё одна задачка подобного типа из тренировочных упражнений 15 задания ЕГЭ по информатике.
Задача (Неравенство, две переменные, закрепление)
Для какого наименьшего целого числа A формула
(3 * x + y < A) ∨ (x < y) ∨ (16 ≤ x)
тождественно истинна, т.е. принимает значение 1 при любых целых неотрицательных x и y ?
Решение:
Первый способ (с помощью питона).
for A in range(-300, 300): k=0 for x in range(1, 301): for y in range(1, 301): if (3*x + y < A) or (x < y) or (16 <= x): k=k+1 if k==90000: print(A)
Наименьшее число равно 61. Здесь не сказали, что A принимает неотрицательные значения, поэтому мы включили в диапазон для A числа, которые меньше нуля. Из-за этого увеличилось время выполнения программы, но ответ получим за приемлемое время.
Второй способ (с помощью рассуждений).
Чтобы вся формула была тождественно истинна, нужно, чтобы хотя бы одно выражение «выдавало» истину, т.к. выражения в формуле соединяются с помощью логического сложения!
Взглянем на третье выражение. Пока x ≥ 16, всё идёт как надо. Третье выражение будет истинно, и, значит, вся формула будет истинна.
Но если x ≤ 15, то нужно, чтобы нас «спасало» первое или второе выражение.
Рассмотрим второе выражение. Пока y > x (x ≤ 15) => y > 15, у нас всё нормально, второе выражение будет истинно, и вся формула будет истинна.
Теперь обратим внимание на первое выражение. Оно должно нас «спасать», когда третье и второе выражение «не спасло»! Это возможно, если x ≤ 15 (иначе «спасло» бы третье выражение), а так же y ≤ 15 (иначе «спасало» бы второе выражение).
Но, чтобы первое выражение было всегда истинно при x ≤ 15 и y ≤ 15, мы должны подобрать число A при максимальных x и y (x=15, y=15)! Ведь для более маленьких значений выражение (3 * x + y < A) точно будет истинно.
Получается:
3 * 15 + 15 < A
60 < A
Нужно найти наименьшее число для A, при котором A > 60. Тогда там, где не «спасли» третье и второе выражение, точно «спасёт» первое выражение. Получается A = 61.
Ответ: 61
Задача (ЕГЭ по информатике, Москва, 2020)
Для какого наибольшего целого неотрицательного числа A выражение
(x > A) ∨ (y > x) ∨ (2 * y + x < 110)
тождественно истинно, то есть принимает значение 1 при любых целых неотрицательных x и y ?
Решение:
Первый способ (с помощью питона).
for A in range(0, 300): k=0 for x in range(1, 301): for y in range(1, 301): if (x > A) or (y > x) or (2 * y + x < 110): k=k+1 if k==90000: print(A)
Максимальное число получается равно 36.
Второй способ (с помощью рассуждений).
Пока y > x, второе подвыражение всегда истинно, значит, и всё выражение истинно.
Теперь будем рассматривать случай y ≤ x.
Рассмотрим третье подвыражение. Найдём максимальные значения для x и для y, которые они одновременно могут принимать, и при которых ещё выполняется третье условие.
Т.к. мы рассматриваем случай y ≤ x, то максимальное число для y будет xmax т.е. ymax = xmax.
Тогда
2 * xmax + xmax < 110
3 * xmax < 110
36 * 3 = 108
37 * 3 = 111
xmax = ymax = 36
Если x «перевалит» за 36, и при этом y ≤ x (иначе «спасает» второе подвыражение), то должно «спасать» первое выражение.
Получается, что наибольшее значение A будет равно 36.
Ответ: 36
Следующий тип задач часто можно встретить в тренировочных вариантах ЕГЭ по информатике 2022.
Задача (С функцией ДЕЛ, закрепление)
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа A формула
ДЕЛ(120, A) ∧ ((ДЕЛ(x, 70) ∧ ДЕЛ(x, 30)) → ДЕЛ(x, A))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Решение:
Первый способ (с помощью питона).
def D(n, m): if n%m==0: return True else: return False for A in range(1, 1000): k=0 for x in range(1, 1001): if D(120, A) and (not(D(x, 70) and D(x, 30)) or D(x, A)): k=k+1 if k==1000: print(A)
Наибольшее число получается равно 30.
Второй способ (с помощью рассуждений).
Рассмотрим левую часть логического выражения. Мы видим, что число 120 должно делится на A. Значит, для A уже есть некоторое ограничение (A <= 120).
Рассмотрим правую часть выражения. Изучим, когда она превращается в ноль. Тогда
Т.е. x должен делится на 70 и одновременно x должен делится на 30.
x = 70*n = 2*5*7*n (n ∈ N)
x = 30*n = 2*5*3*n (n ∈ N)
Чтобы одновременно выполнялись два условия, икс должен быть равен x = 2*5*7*3*n (n ∈ N).
Для того, чтобы правое выражение не превращалось в ноль, x как раз должен делится на число 2*5*7*3. Тогда будет 1->1. Т.е. число A должно равняться 2*5*7*3. Но мы сказали, что A <= 120, плюс, должно являться делителем числа 120. Значит, должны снизить значение для A.
Рассмотрим значение 2*5*7 для числа A (Предыдущее число, но без тройки). Для правой части оно подходит, т.к. «при малейшей» возможности превращения правого выражения в ноль (т.е. ДЕЛ(x, 70) = True), у нас будет спасаться ситуация, т.к. ДЕЛ(x, A) так же
будет равно 1. И снова получаем 1->1. Но это значение не подходит для левой части, ведь тогда A не является делителем числа 120.
Приходится брать число 2*5*3 (без семёрки). Здесь ситуация аналогично предыдущему случаю, только теперь это число является делителем числа 120.
В ответе напишем 30.
Ответ: 30
Задача (Поразрядная конъюнкция, закрепление)
Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K (логическое «И» между соответствующими битами двоичной записи). Определите наименьшее натуральное число A, такое что выражение
(X & 49 ≠ 0) → ((X & 33 = 0) → (X & A ≠ 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)?
Решение:
Первый способ (с помощью питона).
for A in range(1, 1000): k=0 for x in range(1, 1001): if (x&49==0) or ((x&33!=0) or (x&A!=0)): k=k+1 if k==1000: print(A)
Наименьшее число равно 16.
Второй способ (с помощью рассуждений).
Переведём числа 49 и 33 в двоичную систему.
4910 = 1100012
3310 = 1000012
Рассмотрим случай, когда функция стремится превратится в ноль.
Чтобы левое выражение выдавало истину, икс должен иметь 1 (единицу) в первом разряде или во второй разряде, или в последнем разряде (в 6-ти битном числе).
Рассмотрим правое выражение. Посмотрим, когда выражение (X & 33 = 0) выдаёт истину. Первый бит и последний бит должен быть равен нулю. Т.е получается, что в 6-ти битном числе нас интересует второй бит. Если он будет равен 1 и при этом первый бит и последний будут равны 0, то возникает опасная ситуация, которую нужно спасть.
При выше описанных условиях выражение (X & A ≠ 0) должно выдавать истину. Тогда наименьшее A равно 100002 = 162.
Ответ: 16
Задача (числовая прямая, закрепление 2)
На числовой прямой даны два отрезка: P = [20, 30] и Q = [35, 60]. Найдите наименьшую возможную длину отрезка A, при котором формула
¬(x ∈ A) ∧ ((x ∈ P) ∨ (x ∈ Q))
тождественно ложна, то есть принимает значение 0 при любых x.
Решение:
Первый способ (с помощью питона).
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 200): for b in range(a, 200): k=0 for i in range(-200, 200): x = i / 2 if not(not(F(a, b, x)) and (F(20, 30, x) or F(35, 60, x))): k=k+1 if k==400: mn=min(mn, b-a) print(mn)
Ответ будет 40.
Второй способ (с помощью рассуждений).
Рассмотрим наоборот, когда логическое выражение выдаёт истину.
В правой части получается 1, когда x ∈ P или x ∈ Q. Именно в эти моменты выражение ¬(x ∈ A) должно спасать ситуацию и выдавать 0. Тогда без отрицания (x ∈ A) должно выдавать 1. Чтобы покрыть два отрезка, берём A=[20; 60].
Минимальная длина получается 60-20=40.
Ответ: 40
На этом всё! Увидимся в новых уроках по подготовке к ЕГЭ по информатике!
Добрый день! А как в 5 задаче (про числовую прямую) получился ответ 14?
В конце же получается, что A принадлежит [5, 19], то есть длина отрезка 15.
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 — 15 штук
Или я что-то неправильно понял?
Считается количество единиц, а не сколько целых чисел в этом отрезке.
И в самой последней задаче на закрепление, у вас, видимо, та же ошибка. Не 40, а 41 должно быть?
Как решать 15 задание с «~» тильдой на питоне?
Как например это задание:
На числовой прямой даны два отрезка: P = [7, 14] и Q = [9, 11]. Укажите наибольшую возможную длину промежутка A, для которого формула
((x ∈ P) ~ (x ∈ Q)) → ¬(x ∈ A)
Грамотное объяснение. Безумно здорово, что есть объяснения как на питон (перебором) так и чисто в математической форме, потому что в информатике оба подхода, мне кажется, равносильны. Спасибо
1.
1 задание. Демо ЕГЭ 2022 информатика, ФИПИ:
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|
| 1 | — | 3 | 4 | ||||
| 2 | 3 | — | 12 | 13 | |||
| 3 | — | 10 | 11 | ||||
| 4 | 10 | — | 9 | 7 | |||
| 5 | 4 | 12 | 11 | 9 | — | 8 | 6 |
| 6 | 13 | 8 | — | 5 | |||
| 7 | 7 | 6 | 5 | — |
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе.
Определите, какова сумма протяжённостей дорог из пункта Б в пункт В и из пункта Г в пункт Д.
В ответе запишите целое число.
Ответ: 20
🎦
Видео на RuTube здесь
2.
2 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Миша заполнял таблицу истинности логической функции F
¬(y → (x ≡ w)) / (z → x)
но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | Функция |
| ??? | ??? | ??? | ??? | F |
| 1 | 1 | 1 | ||
| 0 | 0 | 1 | ||
| 0 | 1 | 0 | 1 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.).
Ответ: wxyz
🎦
Решение подобного задания (программирование):
3.
3 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
В файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц.
Таблица «Движение товаров» содержит записи о поставках товаров в магазины в течение первой декады июня 2021 г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок, шт. занесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня. Заголовок таблицы имеет следующий вид.
| ID операции | Дата | ID магазина | Артикул | Тип операции | Количество упаковок, шт. | Цена, руб./шт. |
Таблица «Товар» содержит информацию об основных характеристиках каждого товара. Заголовок таблицы имеет следующий вид.
| Артикул | Отдел | Наименование | Ед. изм. | Количество в упаковке | Поставщик |
Таблица «Магазин» содержит информацию о местонахождении магазинов. Заголовок таблицы имеет следующий вид.
На рисунке приведена схема указанной базы данных.
Используя информацию из приведённой базы данных, определите на сколько увеличилось количество упаковок яиц диетических, имеющихся в наличии в магазинах Заречного района, за период с 1 по 10 июня включительно.
В ответе запишите только число.
Ответ: 966
🎦
Видео на RuTube здесь
4.
4 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Для кодирования некоторой последовательности, состоящей из букв Л, М, Н, П, Р, решили использовать неравномерный двоичный код, удовлетворяющий условию, что никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Для букв Л, М, Н использовали соответственно кодовые слова 00, 01, 11. Для двух оставшихся букв – П и Р – кодовые слова неизвестны.
Укажите кратчайшее возможное кодовое слово для буквы П, при котором код будет удовлетворять указанному условию. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Ответ: 100
🎦
Видео на RuTube здесь
5.
5 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1. Строится двоичная запись числа N.
2. К этой записи дописываются справа ещё два разряда по следующему правилу:
а) складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа).
Например, запись 11100 преобразуется в запись 111001;
б) над этой записью производятся те же действия – справа дописывается остаток от деления суммы её цифр на 2.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.
Укажите такое наименьшее число N, для которого результат работы данного алгоритма больше числа 77. В ответе это число запишите в десятичной системе счисления.
-
✎ Решение аналитическим способом:
- Заметим, что после второго пункта условия задачи получаются только четные числа (т.к. если число в двоичной системе заканчивается на 0, то оно четное). Таким образом, нас будут интересовать только четные числа.
- Наименьшим возможным числом, превышающим 77, является число 78. С ним и будем работать.
- Переведем 78 в двоичную систему счисления. Используя компьютер это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать bin(78). Получим:
1001110
N. Значит, необходимое нам двоичное число — это 10011. После первого пункта задачи к данному числу должна была добавиться справа единица, так и есть: 100111. А затем добавляется 0: 1001110. Соответственно, оно подходит.int('10011',2)
✎ Решение с использованием программирования:
PascalAbc.NET:
uses school; begin var n_ := 1; while True do begin var n := n_; var ost := bin(n).CountOf('1') mod 2; //в двоичной с.с. добавляем разряд (*2) и остаток к этому разряду (+ost) n := 2 * n + ost; // получаем остаток при делении на 2 : ost := bin(n).CountOf('1') mod 2; n := 2 * n + ost; if n > 77 then begin println(n_); break end; n_ += 1; end; end. |
Python:
n_ = 1 while True: n = n_ r = str(bin(n)) r = r[2:] for i in range(2): if r.count('1') % 2 == 0: r+='0' else: r+='1' n = int(r, base=2) if n > 77: print(n_,n) break n_+=1 |
Ответ: 19
🎦 -> аналитическое решение
Видео на RuTube здесь
🎦 -> решение с программированием (на Паскале) подобного задания
Видео на RuTube здесь
6.
6 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Определите, при каком наименьшем введённом значении переменной s программа выведет число 64. Для Вашего удобства программа представлена на четырёх языках программирования.
Паскаль:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
var s, n: integer; begin readln(s); s := s div 10; n := 1; while s < 51 do begin s := s + 5; n := n * 2 end; writeln(n) end. |
Алгоритмический язык:
алг нач цел n, s ввод s s := div(s, 10) n := 1 нц пока s < 51 s := s + 5 n := n * 2 кц вывод n кон |
Python:
s = int(input()) s = s // 10 n = 1 while s < 51: s = s + 5 n = n * 2 print(n) |
С++:
#include <iostream> using namespace std; int main() { int s, n; cin >> s; s = s / 10; n = 1 ; while (s < 51) { s = s + 5; n = n * 2; } cout << n << endl; return 0; } |
Ответ: 259
✍ Решение:
-
✎ Способ 1 (программный):
- Поскольку условие цикла
s < 51, а по условию задания следует найти наименьшее значениеs, то можно начать сs=509, так как далее идет операторs := s div 10;, который присваиваетsзначение 50 (<51). Во внешнем цикле необходимо постоянно уменьшать значениеsна единицу. - Важно для внешнего цикла использовать другую переменную, т.к. во внутреннем цикле переменная
sменяется, а нам следует каждый шаг внешнего цикла сохранить предыдущее значениеs, уменьшив его всего на 1. Используем переменнуюS1для этих целей.
Pascalabc.net:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
begin var s1 := 509; while true do // внешний цикл, бесконечный begin var s := s1; s := s div 10; // --- код из условия задания --- // var n := 1; while s < 51 do begin s := s + 5; n := n * 2; if n = 64 then // если найдено, то выводим соответствующее s begin print(s1); exit; // выход из бесконечного цикла end; end; s1 := s1 - 1; end; end. |
Пояснение:
| Бейсик: |
Python:
s1 = 509 while True: # внешний цикл, бесконечный s = s1 # --- код из условия задания --- s = s//10 n = 1 while s < 51: s = s + 5 n = n * 2 # --- конец кода из условия задания --- if n == 64: print(s1) quit() s1 -= 1 |
| С++: |
Ответ: 259
🎦
Видео на RuTube здесь
7.
7 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Для хранения произвольного растрового изображения размером 128×320 пикселей отведено 20 Кбайт памяти без учёта размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков.
Какое максимальное количество цветов можно использовать в изображении?
Ответ: 16
🎦
Видео на RuTube здесь
8.
8 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Все четырёхбуквенные слова, в составе которых могут быть только буквы Л, Е, М, У, Р, записаны в алфавитном порядке и пронумерованы, начиная с 1.
Ниже приведено начало списка.
1. ЕЕЕЕ 2. ЕЕЕЛ 3. ЕЕЕМ 4. ЕЕЕР 5. ЕЕЕУ 6. ЕЕЛЕ …
Под каким номером в списке идёт первое слово, которое начинается с буквы Л?
Ответ: 126
✍ Решение:
✎ Решение с использованием программирования:
|
PascalABC.net (использование LINQ, быстрое решение): Способ 1:
Cartesian(3) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 3-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
|
PascalABC.net (приближенный к традиционному, долгое решение): Способ 2:
|
||
|
PascalABC.net (приближенный к традиционному, долгое решение): Способ 3:
|
||
Python:
|
||
| С++: |
🎦 (программный способ)
Видео на RuTube здесь
🎦 (теоретический способ)
Видео на RuTube здесь
9.
9 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
Откройте файл электронной таблицы, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел может являться сторонами треугольника, то есть удовлетворяет неравенству треугольника.
В ответе запишите только число.
Ответ: 2453
🎦
Видео на RuTube здесь
10.
10 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
С помощью текстового редактора определите, сколько раз, не считая сносок, встречается слово «долг» или «Долг» в тексте романа в стихах А.С. Пушкина «Евгений Онегин». Другие формы слова «долг», такие как «долги», «долгами» и т.д., учитывать не следует. В ответе укажите только число.
Ответ: 1
🎦
Видео на RuTube здесь
11.
11 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
При регистрации в компьютерной системе каждому объекту сопоставляется идентификатор, состоящий из 15 символов и содержащий только символы из 8-символьного набора: А, В, C, D, Е, F, G, H. В базе данных для хранения сведений о каждом объекте отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование идентификаторов, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно идентификатора, для каждого объекта в системе хранятся дополнительные сведения, для чего отведено 24 байта на один объект.
Определите объём памяти (в байтах), необходимый для хранения сведений о 20 объектах. В ответе запишите только целое число – количество байт.
Ответ: 600
🎦 (теоретическое решение)
Видео на RuTube здесь
12.
12 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150.Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
…
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 70 идущих подряд цифр 8? В ответе запишите полученную строку.
НАЧАЛО
ПОКА нашлось (2222) ИЛИ нашлось (8888)
ЕСЛИ нашлось (2222)
ТО заменить (2222, 88)
ИНАЧЕ заменить (8888, 22)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
✎ Решение с использованием программирования:
PascalABC.NET:
Вариант 1:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
begin var s := '8'*70; var p2 := Pos('2222',s); var p8 := Pos('8888',s); while (p2 > 0) or (p8 > 0) do begin if p2 > 0 then begin Delete( s, p2, 4 ); Insert( '88', s, p2 ); end else begin Delete( s, p8, 4 ); Insert( '22', s, p8 ); end; p2 := Pos('2222',s); p8 := Pos('8888',s); end; write(s); end. |
Вариант 2:
1 2 3 4 5 6 7 8 9 10 11 |
begin var s: string := '8' * 70; while ('2222' in s) or ('8888' in s) do // ИЛИ: while (s.contains('2222')) or (s.contains('8888')) do begin if ('2222' in s) then // ИЛИ: if (s.contains('2222')) then s := s.replace('2222', '88') else s := s.replace('8888', '22'); end; writeln(s); end. |
Питон:
1 2 3 4 5 6 7 |
s = 70 * '8' while "2222" in s or "8888" in s: if "2222" in s: s = s.replace( "2222", "88", 1 ) else: s = s.replace( "8888", "22", 1 ) print(s) |
🎦
Видео на RuTube здесь
13.
13 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город М, проходящих через город В?
Ответ: 24
Разбор
подобного
задания смотрите в видео:
🎦 Видео
Видео на RuTube здесь
14.
14 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Значение арифметического выражения:
3*438 + 2*423 + 420 + 3*45 + 2*44 + 1
записали в системе счисления с основанием 16. Сколько значащих нулей содержится в этой записи?
Ответ: 15
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.NET:
begin var numb: Biginteger; numb := 3*Biginteger.Pow(4,38) + 2*Biginteger.Pow(4,23)+Biginteger.Pow(4,20) + 3*Biginteger.Pow(4,5) +2*Biginteger.Pow(4,4) +1; var digit: biginteger; var n := 0; while numb > 0 do begin digit := numb mod 16; if digit = 0 then n += 1; numb := numb div 16 end; print(n) end. |
Python:
x = 3*4**38 + 2*4**23 + 4**20+3*4**5 +2*4**4 +1 k = 0 while x: if x % 16 == 0: k += 1 x //= 16 print( k ) |
| С++: |
✎ Решение аналитическим способом:
- По возможности приведем каждое слагаемое к степеням 16. Учтем, что:
4n=16n/2
3*1619 + 2*(41*1611) + 3*(41*162) + 2*162 + 1
3*1619:Формула: 16n=10..0[n штук]16 (в 16 с.с.) 3*1619 = 3*10..016 -> 19 нулей + 1 другая цифра(3), т.е. всего 20 цифр
2*(41*1611) = 2*(4*10..0[11 штук]16=80..0[11 штук]16 -> одна другая цифра 41*162 = 4*10016 = 400 -> одна другая цифра 3*(41*162) = 3*4*10016 = С0016 -> одна другая цифра 2*162 =2*10016 = 20016 -> одна другая цифра 1 -> одна другая цифра
20-5=15
Ответ: 15
🎦 (программное решение)
Видео на RuTube здесь
15.
15 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
На числовой прямой даны два отрезка: D = [17; 58] и C = [29; 80].
Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение
(x ∈ D) → ((¬(x ∈ C) / ¬(x ∈ A)) → ¬(x ∈ D))
истинно (т.е. принимает значение 1) при любом значении переменной х.
Ответ: 12
✍ Решение:
🎦 (теоретическое решение)
Видео на RuTube здесь
16.
16 задание. Демоверсия варианта ЕГЭ по информатике 2021, ФИПИ:
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1 при n = 1; F(n) = n + F(n − 1), если n – чётно, F(n) = 2 × F(n − 2), если n > 1 и при этом n – нечётно
Чему равно значение функции F(26)?
✎ Решение с использованием программирования:
PascalABC.NET:
1 2 3 4 5 6 7 8 9 10 11 12 13 |
function F(n: integer): integer; begin if n <= 1 then F := 1; if n mod 2 = 0 then F := n + F(n - 1); if (n > 1) and (n mod 2 <> 0) then F := 2 * F(n - 2) end; begin print(F(26)) end. |
Питон:
1 2 3 4 5 6 7 8 |
def F( n ): if n <= 1: return 1 if (n % 2 == 0): return n + F(n-1) if (n>1 and n % 2 != 0): return 2 * F(n-2) print (F(26)) |
C++:
Ответ: 4122
🎦 (программное решение)
Видео на RuTube здесь
17.
17 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите и запишите в ответе сначала количество пар элементов последовательности, в которых хотя бы одно число делится на 3, затем максимальную из сумм элементов таких пар.
В данной задаче под парой подразумевается два идущих подряд элемента последовательности.
Например, для последовательности из пяти элементов:
6; 2; 9; –3; 6 – ответ: 4 11
Ответ: 2802 1990
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.NET: LINQ-метод
1 2 3 4 5 6 7 8 |
## var data := ReadLines('17.txt').Select(t -> t.ToInteger).ToArray; var twins := data.NWise(2).Select(ar->ar.Order.ToArray) .Where(ar->(ar[0].Divs(3)) or (ar[1].Divs(3))); twins.Take(4).Print; // [786,835] [-457,786] [-457,495] [-699,495] twins.Count.Print; var sums:=twins.Select(t->t[0]+t[1]); // массив сумм sums.max.print; |
PascalABC.NET: быстрое решение
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
## нужно открыть файл и посмотреть кол-во строк в нем, 5000 Assign(input, '17.txt'); var a := ReadArrInteger(5000); var k := 0; var max := integer.MinValue; for var i := 0 to a.Length - 2 do begin if (a[i] mod 3 = 0) or (a[i + 1] mod 3 = 0) then begin if a[i] + a[i + 1] > max then max := a[i] + a[i + 1]; k += 1; end; end; print(k, max); |
PascalABC.NET: Классическое решение
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
begin var f: text; var i, k, max, len: integer; assign(f, '17.txt'); reset(f); var data: array of integer; data := new integer[100000]; i := 0; while not EOF(f) do begin readln(f, data[i]); inc(i); end; len := i - 1; k := 0; max := -100; for i := 1 to len do begin if (data[i] mod 3 = 0) or (data[i - 1] mod 3 = 0) then begin inc(k); if data[i] + data[i - 1] > max then max := data[i] + data[i - 1]; end; end; print(k, max) end. |
Питон:
1 2 3 4 5 6 7 8 9 |
f = open('17.txt') data =[int(x) for x in f] k = 0 m = -100 for i in range(len(data)-1): if data[i]%3==0 or data[i+1]%3==0: k+=1 m = max(m, data[i]+data[i+1]) print (k,m) |
C++:
✎ Решение в Excel:
- Запустите программу Excel.
- В меню Файл выберите пункт Открыть и щелкните Обзор.
- Рядом с полем Имя файла выберите в списке Все файлы
(*|*). Откройте файл задания (17.txt— Далее, Далее, Готово). - В столбце
Bбудем искать подходящие пары: если одно число из пары кратно трём, то будем выводить сумму рассматриваемой пары, а иначе – выводить пустое значение («»)
B1
=ЕСЛИ(ИЛИ(ОСТАТ(A1;3)=0;ОСТАТ(A2;3)=0);A1+A2;"")
B до конца и сотрите значение в самой последней ячейке (B5000), если оно там есть (сравнение идет со следующей пустой ячейкой)!!!С1 введем формулу для поиска количества подходящих пар:С1
=СЧЁТ(B:B)
2802
D1 найдем максимальное значение из найденного ряда (максимальную сумму пары):D1
=МАКС(B:B)
1990
🎦
Видео на RuTube здесь
18.
18 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.
Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю.
В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
Для указанных входных данных ответом должна быть пара чисел:
38 22
Ответ: 721 640
🎦 (решение Excel)
Видео на RuTube здесь
19.
19 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 29 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 28.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.
Ответ: 14
✍ Решение 1:
- Ваня может выиграть первым ходом (как бы ни играл Петя), если в куче будет
S = 14камней. Тогда после первого хода Пети в куче будет 15 или 28 камней. В обоих случаях Ваня удваивает кучу и выигрывает в один ход.
S = 14 Петя: 14 + 1 = 15 выигрышная позиция (см. п. а). Выигрывает Ваня Петя: 14 * 2 = 28 выигрышная позиция (см. п. а). Выигрывает Ваня
14 — проигрышная позиция
Ответ: 14
✍ Решение 2 (Excel):
🎦 (решение Excel)
Видео на RuTube здесь
20.
20 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
Найденные значения запишите в ответе в порядке возрастания.
Ответ: 7 13
✍ Решение 1:
- Возможные значения
S: 7, 13. В этих случаях Петя, очевидно, не может выиграть первым ходом. Однако он может получить кучу из 14 камней (из задания № 19 мы знаем, что это проигрышная позиция): в первом случае удвоением, во втором — добавлением одного камня. Эта позиция разобрана в задании 19. В ней игрок, который будет ходить (теперь это Ваня), выиграть не может, а его противник (то есть Петя) следующим ходом выиграет.
S = 7 Петя: 7 * 2 = 14 проигрышная позиция (см. п. 1 б). Выигрывает Петя S = 13 Петя: 13 + 1 = 14 проигрышная позиция (см. п. 1 б). Выигрывает Петя
7, 13 — выигрышные позиции со второго хода
Ответ: 7 13
✎ Решение 2 (Excel)
21.
21 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Для игры, описанной в задании 19, найдите значение S, при котором одновременно выполняются два условия:
Если найдено несколько значений S, в ответе запишите минимальное из них.
✍ Решение:
- Возможные значения
S: 12. После первого хода Пети в куче будет 13 или 24 камня. Если в куче их станет 24, Ваня удвоит количество камней и выиграет первым ходом. Ситуация, когда в куче 13 камней, разобрана в задании 20. В этой ситуации игрок, который будет ходить (теперь это Ваня), выигрывает своим вторым ходом.
S = 12 Петя: 12 + 1 = 13 Ваня: 13 + 1 = 14 проигрышная позиция (см. задание 19). Выигрывает Ваня вторым ходом!
Ответ: 12
22.
22 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Ниже на четырёх языках программирования записан алгоритм. Получив на вход число x, этот алгоритм печатает два числа: L и M. Укажите наибольшее число x, при вводе которого алгоритм печатает сначала 4, а потом 5.
Паскаль:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
var x, L, M, Q: integer; begin readln(x); Q := 9; L := 0; while x >= Q do begin L := L + 1; x := x - Q; end; M := x; if M < L then begin M := L; L := x; end; writeln(L); writeln(M); end. |
Алгоритмический язык:
алг
нач
цел x, L, M, Q
ввод x
Q := 9
L := 0
нц пока x >= Q
L := L + 1
x := x - Q
кц
M := x
если M < L
то
M := L
L := x
все
вывод L, нс, M
кон
|
Python:
x = int(input()) Q = 9 L = 0 while x >= Q: L = L + 1 x = x - Q M = x if M < L: M = L L = x print(L) print(M) |
С++:
#include <iostream> using namespace std; int main() { int x, L, M, Q; cin >> x; Q = 9; L = 0; while (x >= Q){ L = L + 1; x = x - Q; } M = x; if (M < L){ M = L; L = x; } cout <<L <<endl <<M <<endl; return 0; } |
Ответ: 49
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.NET:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
var x, l, M, q: longint; begin for var x_ := 1 to 5000 do begin x := x_; q := 9; l := 0; while x >= q do begin l := l + 1; x := x - q; end; M := x; if M < l then begin M := l; l := x; end; if (l = 4) and (M = 5) then print(x_) end; end. |
23.
23 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Исполнитель преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Программа для исполнителя – это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 20, и при этом траектория вычислений содержит число 10?
Траектория вычислений программы – это последовательность результатов выполнения всех команд программы.
Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 16, 17.
- Сначала найдём количество программ для перехода от числа 1 к числу 10, а затем от числа 10 к 20.
- Будем использовать разные рекуррентные формулы для чётных и нечётных
N. - Напишем программу, реализующую алгоритм поиска результата, вычисления по рекуррентным формулам организуем с помощью рекурсии.
- Рекурсивная функция, которая возвращает количество программ для преобразования числа
startв числоx:
Паскаль. Решение 1:
function f(start, x: integer): integer; begin var k: integer; if start > x then result := 0 else if start = x then result := 1 else begin // обязательные операторные скобки k := k + f(start + 1, x) + f(start *2, x); result := k; end; end; begin writeln(f(1, 10)*f(10, 20)); end.
Паскаль. Решение 2:
function func( start, x: integer ): integer; var k: integer; begin if x < start then func := 0 // если число x меньше нач. значения, кол-во программ равно 0 else if x = start then func := 1 // если число x = нач. значению, кол-во программ равно 1 else begin k := func( start, x-1 ); //учитываем кол-во программ предыдущего числа // если число чётное, нужно добавить ещё кол-во программ для числа x//2: if x mod 2 = 0 then k := k + func( start, x div 2 ); func := k; end; end; begin writeln( func(1,10) * func(10,20) ); end.
Ответ: 28
24.
24 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
Текстовый файл состоит из символов P, Q, R и S.
Определите максимальное количество идущих подряд символов, среди которых нет идущих подряд символов P.
Для выполнения этого задания следует написать программу.
Ответ: 188
✍ Решение:
-
Паскаль:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
var f: text; i, k, max: integer; s: string; begin assign(f, '24.txt'); reset(f); readln(f, s); max := 1; k := 1; // кол-во подряд идущих без PP for i := 2 to length(s) do begin if (not ((s[i] = 'P') and (s[i - 1] = 'P'))) then begin inc(k); if k > max then max := k; end else k := 1; end; write(max) end. |
Python:
1 2 3 4 5 6 7 8 9 10 11 12 |
f=open('24.txt') s=f.readline() m=1 k=1 for i in range(2,len(s)): if not(s[i]=='P' and s[i-1]=='P'): k+=1 if k > m: m = k else: k=1 print(m) |
25.
25 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Пусть M – сумма минимального и максимального натуральных делителей целого числа, не считая единицы и самого числа. Если таких делителей у числа нет, то значение M считается равным нулю.
Напишите программу, которая перебирает целые числа, бо́льшие 700 000, в порядке возрастания и ищет среди них такие, для которых значение M оканчивается на 8. Выведите первые пять найденных чисел и соответствующие им значения M.
Формат вывода: для каждого из пяти таких найденных чисел в отдельной строке сначала выводится само число, затем – значение М.
Строки выводятся в порядке возрастания найденных чисел.
Количество строк в таблице для ответа избыточно.
Ответ:
700005 233338 700007 100008 700012 350008 700015 140008 700031 24168
✍ Решение:
✎ Метод полного перебора, неоптимизированный:
PascalABC.net:
|
||
| Python: | ||
| С++: |
26.
26 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный объём архивируемых файлов.
Известно, какой объём занимает файл каждого пользователя.
По заданной информации об объёме файлов пользователей и свободном объёме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Входные данные.
В первой строке входного файла находятся два числа: S – размер свободного места на диске (натуральное число, не превышающее 10 000) и N – количество пользователей (натуральное число, не превышающее 1000). В следующих N строках находятся значения объёмов файлов каждого пользователя (все числа натуральные, не превышающие 100), каждое в отдельной строке.
Запишите в ответе два числа: сначала наибольшее число пользователей, чьи файлы могут быть помещены в архив, затем максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Пример входного файла:
100 4 80 30 50 40
При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объёмы этих двух файлов 30 и 40, 30 и 50 или 40 и 50. Наибольший объём файла из перечисленных пар – 50, поэтому ответ для приведённого примера:
2 | 50
Ответ: 568 50
✍ Решение:
-
Проанализируем возможное решение:
- Чтобы вычислить максимальное число пользователей, чьи файлы можно сохранить в архиве, необходимо брать файлы с наименьшим объемом, пока суммарный объем этих файлов меньше свободного объема диска. Т.е. для нижеуказанного примера, будем брать
30 + 40. Файл объемом 50 мы взять уже не сможем, так как70 + 50 = 120, а это уже больше указанного объема диска (100):
100 4 80 30 50 40
100 - 70 = 30
30 - 40 <= запаса (30) 40 - 40 <= запаса (30) 50 - 40 <= запаса (30) 80 - 40 > запаса (30), не подходит
✎ Решение с использованием программирования:
Теперь построим алгоритм на языках программирования:
PascalABC.net:
|
||
Python:
|
||
| С++: |
✎ Решение в Excel:
- Запустите программу Excel.
- В меню Файл выберите пункт Открыть и щелкните Обзор.
- Рядом с полем Имя файла выберите в списке Все файлы(*|*).
- Щёлкните Далее, а затем установите флажок рядом с пунктом Пробел:
- Затем Готово.
- В открытом файле перенесите первую строку с двумя заполненными ячейками в ячейки
I2иJ2(или любое свободное место). - Удалите первую строку.
- Отсортируйте столбец
Апо возрастанию: Данные — Сортировка - В ячейку
B1занесите число, стоящее вА1. - В ячейку
B2вставим формулу для подсчета суммы размеров файлов, прибавляя каждое последующее значение до тех пор, пока эта сумма меньше или равна свободному объему диска (I1). Не забываем зафиксировать значение ячейки, чтобы при копировании формулы адрес ячейки не менялся:
=ЕСЛИ(И(A2+B1<=I$1;B1<>0);A2+B1;0)
B, до тех пор, пока не появится значение 0. Последнее заполненное значение — 8176 — это сумма объемов файлов, которые вместились с учетом свободного объема диска. А номер строки — 568 — это максимальное число пользователей, чьи файлы можно сохранить в архиве (первое значение для ответа).С1): =I1-B568
D1 внесем формулу для поиска максимального размера файла в архиве (с учетом рассчитанного запаса). Будем выводить значение подходящего размера файла, а как только размер уже будет не подходить — выведем 0. Поскольку формулу будем копировать, не забудьте зафиксировать ячейку с запасом (C$1) и с максимальным объемом файла из ряда подходиящих файлов (A$568)=ЕСЛИ(A1-A$568<=C$1;A1;0)
D не равны 0. Находим последнее значение — 50 — это и есть максимальный размер файла, который можно поместить в архив.
Ответ: 568 | 50
Видео на RuTube здесь
27.
27 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
A
B
Задание выполняется с использованием прилагаемых файлов
Дана последовательность из N натуральных чисел. Рассматриваются все её непрерывные подпоследовательности, такие что сумма элементов каждой из них кратна k = 43. Найдите среди них подпоследовательность с максимальной суммой, определите её длину. Если таких подпоследовательностей найдено несколько, в ответе укажите количество элементов самой короткой из них.
Входные данные
Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество чисел N (1 ≤ N ≤ 10 000 000). Каждая из следующих N строк содержит одно натуральное число, не превышающее 10 000.
7 21 13 9 19 17 26 95
В этом наборе можно выбрать последовательности 21+13+9 (сумма 43) и 17+26 (сумма 43). Самая короткая из них, 17 + 26, имеет длину 2. Для указанных программа должна вывести число 2.
В ответе укажите два числа: сначала значение искомой суммы для файла А, затем – для файла B.
Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Ответ: 185 329329
✍ Решение:
Решение для файла А (27-75a.txt), полный перебор:
PascalABC.net:
|
||
| Python: | ||
| С++: |
ЕГЭ по информатике -> демоверсия ЕГЭ 2022
Канал видеоролика: Evgenij Jobs
Смотреть видео:
#информатика #егэинформатика #икт #экзамены #егэ_2020 #мгту #школьникам #помощь_студентам #поступление
Свежая информация для ЕГЭ и ОГЭ по Информатике (листай):
С этим видео ученики смотрят следующие ролики:

Разбор варианта 15062022 | КЕГЭ по информатике 2022
Evgenij Jobs

Разбор варианта 05012020 | ЕГЭ по информатике
Evgenij Jobs

Разбор варианта 03022020 | ЕГЭ по Информатике
Evgenij Jobs

Разбор варианта досрочной волны ЕГЭ по информатике 2020
Алекс ЕГЭ Информатика
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
14.06.2022
22 июля 2022
В закладки
Обсудить
Жалоба
Вариант с ЕГЭ по информатике от 20.06.2022.
Вариант: stepik.org/lesson/748682/step/1
Файлы к заданиям: drive.google.com/drive…
Таймкоды
00:00 Вступление
00:11 Номер 1 (ответ:66)
06:33 Номер 2 (ответ:wzyx)
11:36 Номер 3 (ответ:1610)
20:38 Номер 4 (ответ:14)
30:32 Номер 5 (ответ:8)
40:32 Номер 6 (ответ:81)
46:23 Номер 7 (ответ:2048)
53:05 Номер 8 (ответ:2961)
01:05:58 Номер 9 (ответ:104)
01:13:19 Номер 10 (ответ:26)
01:14:13 Номер 11 (ответ:1388)
01:19:57 Номер 12 (ответ:299)
01:22:31 Номер 13 (ответ:21)
01:27:19 Номер 14 (ответ:1891)
01:28:53 Номер 15 (ответ:74)
01:39:40 Номер 16 (ответ:578)
01:47:32 Номер 17 (ответ:175 173738)
01:54:34 Номер 18 (ответ:2628 1659)
02:05:52 Номер 19-21 ответ:19)61 20)112 120 21)111
02:33:09 Номер 22 (ответ:71)
02:41:22 Номер 23 (ответ:376)
02:48:55 Номер 24 (ответ:174)
02:59:20 Номер 25
03:09:01 Номер 26 (ответ:2767 51)
03:20:13 Номер 27 (ответ:51063 5634689219329)
Не потерять время на задачу 3 через Excel | ЕГЭ 2022 по информатике
Флеш НОВОЕ ЗАДАНИЕ №3 на базы данных | ЕГЭ информатика 2022
2020-2021
ДЕМО 2022 ПОЛНЫЙ РАЗБОР PYTHON PASCAL C++ | ЕГЭ информатика 2022
https://www.youtube.com/watch?v=tUood_s6A38&t=20s
Реальный ЕГЭ 24 июня 2021 года
!!! Разбор 27 реального егэ 24 июня 2021г.
№ 5 Статград от 26 апреля 2021
Дневник эксперта
Флеш
Статград 26.04.2021 2 вариант 1 часть| ЕГЭ информатика 2021
https://www.youtube.com/watch?v=RZw7eUnfaeY
________________________________________________________________
№ 4 Статград от 17 марта 2021
Статград 17.03.2021| 1 часть | ЕГЭ информатика 2021
Статград 17.03.2021 2 часть| ЕГЭ информатика 2021
Дневник эксперта ЕГЭРазбор задач 1-27 2 варианта СТАТГРАД № 4 от 17.03.2021 ЕГЭ по информатике 2021 разбор
_______________________________________________________________
№ 3 Статград 2.02. 2021 г.
Статград от 02.02.2021 1 часть ЕГЭ Информатика 2021
(18-ладья)
2 часть Статград 02.02.2021 ЕГЭ информатика 2021
Дневник эксперта
Разбор статград 02.02.2021 1 часть 1 вариант без 18 ЕГЭ по информатике 2021
Разбор статград 02.02.2021 2 часть 1 вариант ЕГЭ по информатике 2021
Разбор 2 варианта статград 02.02.2021 ЕГЭ по информатике 2021
____________________________________________________________________________
№ 2 Статград 10.12. 2020 г.
_____________________________________________________________________
№1 Статград от 22 октября 2020 ЕГЭ информатика 22.10.2020
_________________________________________________________________
Дневник эксперта егэ Задание 18 (2 стены)
Информатик БУ разбор егэ 27 делится на 5
ЕГЭ 19-20-21 через рекурсию
ЕГЭ 19-20-21 через Excel общая таблица
ЕГЭ 19-20-21 через Excel ФЛЭШ
Вебинары (комбинаторика):
Полезный сайт. Подборка пробных заданий Статграда
Комбинатрика
разбор демо версии 2021
№18
Аналог «Сдам ЕГЭ» https://yandex.ru/tutor/subject/?subject_id=6
ЕГЭ 2019 г.
Разбор заданий Демо (без №23, 26, 27)
Разбор задания Демо №23
тренировочная работа 14.09.2018
ЕГЭ 2018 г.
Светлана Майер — разбор досрочного
не досрочный разбор Светлана Майер
Полезные ссылки:
ЕГЭ 24
Стрим #13
Стрим #39 (системы счисления)
Стрим #40
стрим 41-1https://www.youtube.com/watch?v=TJOlRmpWXgk&index=43&list=PLgvtHXe0kJXZXDBqDx0CuZ3l3k-cmGm01
стрим #41-2 https://www.youtube.com/watch?v=ryz7QhnF0aE&index=44&list=PLgvtHXe0kJXZXDBqDx0CuZ3l3k-cmGm01 (разбор досрочного Задачи: 2, 5, 6, 9, 10, 11, 12, 14, 16, 18, 20, 21, 22, 24, 25)
стрим #42 https://www.youtube.com/watch?v=r3rjHlV4x2s&t=25s (что было на досрочке, какие были задачи)
стрим #43 https://www.youtube.com/watch?v=Pl5Fen79GRk&t=12s (Решаем задачки: 3, 5, 6, 11, 13, 14, 17, 18, 21, 22, 23, 25)
стрим#45 https://www.youtube.com/watch?v=34d-Q98_aF0&index=48&list=PLgvtHXe0kJXZXDBqDx0CuZ3l3k-cmGm01 (Фано Алгоритм Хаффмана , маски, динамическое программирование, 23 три задачи)
стрим #46 https://www.youtube.com/watch?v=Tv52a-gnnzE ( 2, 9, 12, 14, 16, 20, 21, 22, 23)
(робот, исполнитель)
Робот 39 минута
стрим #47 https://www.youtube.com/watch?v=Ycy2lgtVUvU (2, 5, 10, 17, 18, 21, 23, 26, 27)
ЕГЭ 10
Задание №1701/10
Задание
Сколько существует способов разместить на книжной полке шесть книг, среди которых имеются четыре тома романа «Война и мир», которые должны стоять рядом?
Решение
Представим четыре тома романа «Война и мир» в виде единого блока, внутрь которого не должны попасть никакие другие книги. Тогда необходимо расположить на полке этот блок и две другие книги, что можно сделать 3!=1⋅2⋅3=6 способами.
Для определения количества способов расположить четыре тома «Войны и мира» внутри блока снова воспользуемся формулой количества перестановок без повторений, согласно которой имеется 4!=1⋅2⋅3⋅4=24 таких способов.
Учитывая, что расположение томов романа «Война и мир» внутри блока не зависит от расположения всего блока на полке, применимо правило произведения, откуда искомое количество способов 3!⋅4!=6⋅24=144.
Задание №1702/10
Задание
Сколько существует различных символьных последовательностей длины 5, которые содержат ровно 3 символа из алфавита {A,B} и 2 символа из алфавита {C,D,E,F}?
Решение
Имеется C53 способов выбрать три позиции из пяти возможных для размещения трёх символов из алфавита {A,B}. На каждой из этих позиций может находиться любой из двух символов данного алфавита.
Далее, для размещения двух символов из алфавита {C,D,E,F} остаются две позиции, выбрать которые можно C22 способами. На каждой из этих позиций может находиться любой из четырёх символов данного алфавита.
Учитывая, что символы располагаются в последовательности независимо друг от друга, можно применить правило произведения:N=C53⋅23⋅C22⋅42=5!3!⋅(5−3)!⋅23⋅2!2!⋅(2−2)!⋅42=
67)
(прислал
А.Н. Носкин) Палиндром – это
символьная строка, которая читается одинаково в обоих направлениях. Сколько
различных 6-символьных палиндромов можно составить из строчных латинских букв?
(В латинском алфавите 26 букв).
В Латинском алфавите 26 букв
Если они симметричные то решить можно так
26*26*26=17576
Ответ: 17576
51)
Вася
составляет 5-буквенные слова, в которых есть только буквы К, А, Т, Е, Р, причём
буква Р используется в каждом слове хотя бы 2 раза. Каждая из других допустимых
букв может встречаться в слове любое количество раз или не встречаться совсем.
Словом считается любая допустимая последовательность букв, не обязательно
осмысленная. Сколько существует таких слов, которые может написать Вася?
Решила другим способом.
Две буквы Р: 1*1*4*4*4 =64 Количество сочетаний 2 из 5 =10 итого10*64=640
Три буквы Р: 1*1*1*4*4 =16 Количество сочетаний 3 из 5 =10 итого10*16=160
Четыре буквы Р: 1*1*1*1*4 =4 Количество сочетаний 4 из 5 =5 итого5*4=20
Пять букв Р: 1 способ
итого 821
ЕГЭ №14
115
161
103
60
Об изменениях в ЕГЭ по информатике в 2022 году
ЕГЭ по информатике состоит из следующих тем: «Системы счисления», «Базы данных», «Поиск информации в текстовых документах», «Электронные таблицы», «Алгебра логики», «Графы», «Комбинаторика», «Алгоритмизация и программирование», «Теория игр», «Кодирование и декодирование».
По сравнению с прошлым годом контрольные измерительные материалы изменились. Например, задание №3 теперь нужно выполнять на компьютере, так как оно предполагает работу с файлами импровизированной базы данных. В задании №9 учащимся придется вспомнить логические функции при работе с формулами в электронных таблицах, а задание №17 потребует от выпускников выполнить анализ числовой информации из файла.
Напомним, что на протяжении всего экзамена у участников все так же будет доступ к компьютеру с установленным прикладным программным обеспечением и средами программирования.
Основное отличие нынешнего ЕГЭ по информатике от экзаменов прошлых лет состоит в том, что практически все задания в нем можно выполнить на компьютере.
И это, к сожалению, иногда может сбивать выпускников с правильного пути.
Приведем примеры ошибок, которые допускали участники экзамена в прошлом году, для того чтобы помочь избежать их нынешним старшеклассникам.
Ошибка № 1. Попытка выполнить все задания с использованием компьютера
Хотя большинство задач в ЕГЭ по информатике построено таким образом, что их можно решить как в черновике, так и при помощи офисных приложений или сред программирования, нужно понимать, что решение с использованием компьютера не всегда приводит к быстрому результату.
Учительница перед началом сдачи ЕГЭ по информатике в средней общеобразовательной школе №13 Владивостока, 3 июля 2020 года
Виталий Аньков/РИА «Новости»
Например, выпускник может потратить значительное количество времени на написание программного кода для решения задачи, которая аналитическим методом при помощи ручки и листа бумаги решилась бы намного быстрее, и возможно, проще.
В качестве примера приведем задание №8.
Все 5-буквенные слова, составленные из 4 букв ВЕРТ, записаны в алфавитном порядке.
Вот начало списка:
1. ВВВВВ
2. ВВВВЕ
3. ВВВВР
4. ВВВВТ
5. ВВВЕВ
…
На каком месте от начала списка стоит слово «ВЕТЕР»?
Решение
Представим все буквы как цифры системы счисления с основанием 4. Тогда В – 0, Е – 1, Р – 2, Т – 3.
Слово «ВЕТЕР» будет выглядеть как число 01312. Переведем его в десятичную систему счисления — это число 118 (это можно сделать, например, функцией print(int(‘01312’,4)) всего в одну строку на языке Python. Таким образом, слово «ВЕТЕР» должно находиться на 118 месте. Однако мы видим, что слово ВВВВВ — это 00000 (ноль) в четверичной системе счисления и оно находится на месте 1. Значит, есть сдвиг на одну позицию. Таким образом, слово «ВЕТЕР» находится не на 118, а на 119 месте.
Теперь решим это задание вторым способом — напишем программу на языке Python.
Личный архив Николая Никулина
Оба представленных способа решения данной задачи приведут к верному результату, но первый займет у подготовленного ученика меньше времени.
И таких заданий на экзамене достаточно. А ведь на ЕГЭ каждая минута времени может принести дополнительный балл.
Ошибка № 2. Неверная последовательность выполнения заданий
Эта ошибка характерна не только для ЕГЭ по информатике, но и для других предметов. Прежде всего необходимо выполнять те задачи, которые хорошо знакомы и не требуют значительных временных затрат. Часто участники выполняют задания подряд и, увидев новое для себя задание, пытаются его решить, тратя большую часть времени и усилий. На все остальные задачи у них остается уже меньше ресурсов.
Поэтому, если задание показалось сложным, следует его пропустить и постараться выполнить более простые.
Таким образом можно набрать основное количество баллов и оставить большую часть времени для спокойного размышления над сложными заданиями.
Ошибка № 3. Ложная надежда на компьютерные технологии
Некоторые выпускники думают, что наличие компьютера на экзамене со всевозможными офисными программами и средами программирования сразу избавит их практически от всех проблем, связанных с решением задач. Но всеми этими технологиями еще нужно научиться грамотно пользоваться. При этом необходимо знать теорию по конкретным темам курса информатики.
Например, одна из задач, которая, на наш взгляд, стала решаться гораздо быстрее с использованием компьютера — это задание 14. Приведем пример и решение с использованием алгоритма, записанного на языке программирования Python.
Личный архив Николая Никулина
Для написания подобного программного кода необходимо помнить стандартный алгоритм перевода числа в систему счисления с произвольным основанием. Также нужно знать такие темы из курса информатики, как циклы, работа со строками, операции деления. Еще можно запомнить некоторые стандартные функции языков программирования (например, count для языка Python).
Рекомендации по подготовке к экзамену
Очень важно научиться правильно выбирать методику решения каждого конкретного задания. Некоторые задачи проще и быстрее выполнять без использования компьютерных программ, прибегая к аналитическому подходу.
С другой стороны, на экзамене есть и такие задания, которые невозможно решить вручную за отведенное время, и без написания программного кода или использования прикладного программного обеспечения уже не обойтись. Поэтому попробуйте проверить свои знания, провести самодиагностику. Для этого можно выполнить демонстрационный вариант с последующей проверкой ответов, отметить задания и темы, которые вызывают затруднения. Например, воспользоваться виртуальной лабораторией по информатике в Библиотеке МЭШ, открытыми вариантами контрольных измерительных материалов ЕГЭ на сайте ФИПИ или пройти диагностику в формате ЕГЭ. Проверить свои знания и потренироваться в заполнении экзаменационных бланков вы можете в Центре независимой диагностики Московского центра качества образования. Запись открыта в разделе Центра на сайте МЦКО.
Большое значение имеет повторение тем, относящихся к практическому программированию. Знание одного или нескольких языков программирования на базовом или углубленном уровнях поможет решить не только задачи, относящиеся непосредственно к теме «Алгоритмизация и программирование», но и многие другие задания быстро и оптимально. Изучить необходимые языки программирования помогут в школе на уроках информатики. Также можно воспользоваться учебными материалами в Библиотеке «Московской электронной школы».
Каждую неделю, в разные дни, уделяйте внимание изучению новых материалов и повторению того, что вы уже знаете. Старайтесь еженедельно решать разные варианты из ЕГЭ.