ПРОГРАММА ВНЕУРОЧНОЙ ДЕЯТЕЛЬНОСТИ
«ПОДГОТОВКА К ЕГЭ ПО МАТЕМАТИКЕ»
ДЛЯ 11КЛАССА
Учитель
Омарова З.М.
2020 – 2021 учебный год
Пояснительная записка
Программа предназначена для работы с учащимися 11 класса с целью повышения эффективности обучения их математике, предусматривает подготовку их к государственной (итоговой) аттестации по математике за курс полной средней школы и к дальнейшему математическому образованию. Программа рассчитана на 34 учебных часа (1 час в неделю). Содержание программы соответствует по тематическому содержанию программе по математике для 5-11 классов общеобразовательных школ.
Данный курс в 11 классе представляет собой повторение, обобщение и углубленное изучение теоретического материала укрупненными блоками по наиболее значимым темам: «Выражения», «Уравнения и неравенства», «Функции и графики», «Элементы статистики, комбинаторики и теории вероятностей», «Решение задач по геометрии». Курс рассчитан на обучающихся, желающих хорошо подготовиться к ЕГЭ и к дальнейшему изучению математики в ВУЗах.
В процессе изучения данного курса будут использованы приемы индивидуальной, парной, групповой деятельности для осуществления самооценки, взаимоконтроля; развиваться умения и навыки работы с математической литературой и использования интернет-ресурсов.
Цели курса:
- Коррекция и углубление конкретных математических знаний, необходимых для прохождения государственной (итоговой) аттестации за курс средней полной школы в форме и по материалам ЕГЭ, для изучения смежных дисциплин, для продолжения образования.
- Интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе.
Задачи курса:
- Систематическое повторение учебного материала по основным темам курса алгебры и начал анализа и геометрии.
- Оказание практической коррекционной помощи учащимся в изучении отдельных тем предмета.
- Формирование поисково-исследовательского метода.
- Акцентирование внимания учащихся на единых требованиях к правилам оформления решения различных заданий.
- Осуществление тематического контроля на основе мониторинга выполнения учащимися типовых экзаменационных заданий.
- Получение школьниками дополнительных знаний по математике.
- Воспитание культуры личности, отношения к математике как части общечеловеческой культуры, играющей особую роль в общественном развитии.
Планируемые результаты изучения курса
В результате изучения курса учащиеся 11 класса должны уметь:
- находить значения корня натуральной степени, степени с рациональным показателем, логарифма, значения тригонометрических выражений на основе определений и основных свойств, пользоваться оценкой и прикидкой при практических расчетах;
- выполнять тождественные преобразования тригонометрических, иррациональных, степенных, показательных и логарифмических выражений;
- вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
- определять значения функции по значению аргумента при различных способах задания функции;
- строить графики линейной, квадратичной, тригонометрических, степенной, показательной и логарифмической функций;
- решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
- решать рациональные, тригонометрические, иррациональные, показательные и логарифмические уравнения, их системы;
- решать рациональные, показательные и логарифмические неравенства, их системы;
- вычислять производные и первообразные элементарных функций;
исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций;
- решать геометрические задачи с применением соотношений и пропорциональных отрезков в прямоугольном треугольнике, основных теорем для произвольного треугольника;
- решать геометрические задачи на клетчатой бумаге.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни.
Особенности курса:
— интеграция разных тем;
— практическая значимость для учащихся.
Требования к уровню подготовленности учащихся.
- В результате изучения курса учащиеся должны уметь:
- вычислять значения корня, степени, логарифма;
- находить значения тригонометрических выражений;
- выполнять тождественные преобразования тригонометрических, иррациональных, показательных, логарифмических выражений;
- решать тригонометрические, иррациональные, показательные, логарифмические уравнения, неравенства, системы, включая с параметром и модулем, а также комбинирование типов аналитическими и функционально-графическими методами,
- строить графики элементарных функций, проводить преобразования графиков, используя изученные методы описывать свойства функций и уметь применять их при решении задач,
- применять аппарат математического анализа к решению задач;
- решать различные типы текстовых задач с практическим содержанием на проценты, движение, работу, концентрацию, смеси, сплавы, десятичную запись числа, на использование арифметической и геометрической прогрессии;
- уметь соотносить процент с соответствующей дробью;
- знать широту применения процентных вычислений в жизни, решать основные задачи на проценты, применять формулу сложных процентов;
- решать планиметрические задачи, связанные с нахождением площадей, линейных или угловых величин треугольников или четырехугольников;
- решать стереометрические задачи, содержащие разный уровень необходимых для решения обоснований и количество шагов в решении задач, включенных в часть I и часть II экзаменационной работы, часто требующие построения вспомогательных элементов и сечений, сопровождаемых необходимыми доказательствами;
- производить прикидку и оценку результатов вычислений;
- при вычислениях сочетать устные и письменные приемы, использовать приемы, рационализирующие вычисления.
Содержание обучения
Текстовые задачи 5ч
Дроби и проценты. Смеси и сплавы. Движение. Работа. Задачи на анализ практической ситуации.
. Выражения и преобразования 5ч
. Тождественные преобразования иррациональных и степенных выражений. Тождественные преобразования логарифмических выражений. Тождественные преобразования тригонометрических выражений
Функции и их свойства 4ч
Исследование функций элементарными методами. Производная функции, ее геометрический и физический смысл. Исследование функций с помощью производной.
Уравнения, неравенства и их системы 6ч
Рациональные уравнения, неравенства и их системы. Иррациональные уравнения и их системы. Тригонометрические уравнения и их системы. Показательные уравнения,
неравенства и их системы. Логарифмические уравнения, неравенства и их системы. Комбинированные уравнения и смешанные системы.
Задания с параметром 3 ч
Уравнения и неравенства. Уравнения и неравенства с модулем.
Планиметрия 3ч
Треугольники. Четырехугольники. Окружность. Окружности, вписанные в треугольник и четырехугольник. Окружности, описанные около треугольника и четырехугольника.
Стереометрия 3 ч
Углы и расстояния. Сечения многогранников плоскостью. Площади поверхностей тел. Объемы тел.
Календарно-тематическое планирование курса
1 час в неделю, всего 34 часа
|
№/п |
Тема урока |
Кол-во часов |
дата |
примечание |
|
|
План |
Факт |
||||
|
1.Текстовые задачи – 5 часов |
|||||
|
1 |
Задачи практического содержания (дроби, проценты, смеси и сплавы). |
2 |
|||
|
3 |
Задачи на работу и движение. |
1 |
|||
|
4 |
Задачи на анализ практической ситуации. |
1 |
|||
|
5 |
Задачи на анализ практической ситуации |
1 |
|||
|
2.Выражения и преобразования – 5 часов. |
|||||
|
1 |
Тождественные преобразования иррациональных и степенных выражений |
1 |
|||
|
2 |
Тождественные преобразования логарифмических выражений. |
1 |
|||
|
3 |
Преобразования тригонометрических выражений. |
1 |
|||
|
4 |
Преобразование тригонометрических выражений. |
1 |
|||
|
5 |
Преобразование выражений. |
1 |
|||
|
3.Функции и их свойства – 4 часа. |
|||||
|
1 |
Исследование функций элементарными методами. |
1 |
|||
|
2 |
Производная, ее геометрический и физический смысл. |
1 |
|||
|
3 |
Исследование функции с помощью производной. |
1 |
|||
|
4 |
Исследование функции с помощью производной. |
1 |
|||
|
4.Уравнения, неравенства и их системы –6 часов |
|||||
|
1 |
Рациональные уравнения, неравенства и их системы |
1 |
|||
|
2 |
Иррациональные уравнения и их системы. |
1 |
|||
|
3 |
Тригонометрические уравнения и их системы. |
1 |
|||
|
4 |
Показательные уравнения, неравенства и их системы. |
1 |
|||
|
5 |
Логарифмические уравнения, неравенства и их системы. |
1 |
|||
|
6 |
Комбинированные уравнения и смешанные системы |
1 |
|||
|
5. Задания с параметром – 3 часа. |
|||||
|
1 |
Уравнения и неравенства |
1 |
|||
|
2 |
Уравнения и неравенства |
1 |
|||
|
3 |
Уравнения и неравенства с модулем. |
1 |
|||
|
6. Планиметрия – 3 часа |
|||||
|
1 |
Треугольники. Четырехугольники. Окружность. |
1 |
|||
|
2 |
Окружности, вписанные в треугольник и четырехугольник. |
1 |
|||
|
3 |
Окружности, описанные около треугольника и четырехугольника. |
1 |
|||
|
7. Стереометрия – 3 часа |
|||||
|
1 |
Углы и расстояния. Сечения многогранников плоскостью. |
1 |
|||
|
2 |
Площади поверхностей и объемы тел. |
1 |
|||
|
3 |
Площади поверхностей и объемы тел. |
1 |
|||
|
8. Структура и содержание контрольно — измерительных материалов ЕГЭ – 5 часов |
|||||
|
1 |
Система оценивания. Решение заданий с кратким ответом (I часть). |
1 |
|||
|
2 |
Решение заданий с развернутым ответом (II часть). |
1 |
|||
|
3 |
Решение заданий с развернутым ответом (II часть). |
1 |
|||
|
4 |
Тренировочные варианты ЕГЭ 2020-2021г |
1 |
|||
|
5 |
Тренировочные варианты ЕГЭ 2020-2021г |
1 |
Список литературы
- сборник ЕГЭ 2021 Ященко И.В 36 типовых тренировочных вариантов с ответами по математике 11 класс — база .
- 36 типовых экзаменационных вариантов (задания и ответы)Ященко И.В. 2021, 256с.- профиль.
- Лысенко Ф. Ф., Калабухова С. О. Математика. Подготовка к ЕГЭ 2021. Учебно-методическое пособие./ Ростов на Дону. Легион, 2020
Информационные ресурсы интернет
- http://fipi.ru/ . Сайт ФИПИ. Открытый банк заданий ЕГЭ по математике.
- http://reshuege.ru/ . Сайт для подготовки учащихся к ЕГЭ и проведения он-лайн тестирования
и др
РЕСПУБЛИКА
СЕВЕРНАЯ ОСЕТИЯ — АЛАНИЯ
МУНИЦИПАЛЬНОЕ
БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«СРЕДНЯЯ
ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА ИМЕНИ ГЕРОЯ
СОЦИАЛИСТИЧЕСКОГО ТРУДА САЛАМГЕРИ КОКАЕВА С. ХУМАЛАГ»


ПРОГРАММА
ВНЕУРОЧНОЙ ДЕЯТЕЛЬНОСТИ
«ПОДГОТОВКА
К ЕГЭ ПО МАТЕМАТИКЕ»
ДЛЯ
11 КЛАССА
Учитель
Сидакова
Жанна
Насрбековна
2020
– 2021 учебный год
Пояснительная записка
Программа предназначена для работы с учащимися 11 класса с
целью повышения эффективности обучения их математике, предусматривает
подготовку их к государственной (итоговой) аттестации по математике за курс
полной средней школы и к дальнейшему математическому образованию. Программа
рассчитана на 34 учебных часа (1 час в неделю). Содержание программы
соответствует по тематическому содержанию программе по математике для 5-11
классов общеобразовательных школ.
Данный курс в 11 классе представляет собой повторение,
обобщение и углубленное изучение теоретического материала укрупненными блоками
по наиболее значимым темам: «Выражения», «Уравнения и неравенства», «Функции и
графики», «Элементы статистики, комбинаторики и теории вероятностей»,
«Решение задач по геометрии». Курс рассчитан на обучающихся, желающих хорошо
подготовиться к ЕГЭ и к дальнейшему изучению математики в ВУЗах.
В процессе
изучения данного курса будут использованы приемы индивидуальной, парной, групповой
деятельности для осуществления самооценки, взаимоконтроля; развиваться умения и
навыки работы с математической литературой и использования интернет-ресурсов.
Цели курса:
·
Коррекция и углубление
конкретных математических знаний, необходимых для прохождения государственной
(итоговой) аттестации за курс средней полной школы в форме и по материалам ЕГЭ,
для изучения смежных дисциплин, для продолжения образования.
·
Интеллектуальное развитие
учащихся, формирование качеств мышления, характерных для математической
деятельности и необходимых для продуктивной жизни в обществе.
Задачи
курса:
·
Систематическое повторение
учебного материала по основным темам курса алгебры и начал анализа и геометрии.
·
Оказание практической
коррекционной помощи учащимся в изучении отдельных тем предмета.
·
Формирование
поисково-исследовательского метода.
·
Акцентирование внимания
учащихся на единых требованиях к правилам оформления решения различных заданий.
·
Осуществление тематического
контроля на основе мониторинга выполнения учащимися типовых экзаменационных
заданий.
·
Получение школьниками
дополнительных знаний по математике.
·
Воспитание культуры личности,
отношения к математике как части общечеловеческой культуры, играющей особую
роль в общественном развитии.
Планируемые
результаты изучения курса
В результате изучения
курса учащиеся 11 класса должны уметь:
·
находить значения корня
натуральной степени, степени с рациональным показателем, логарифма, значения
тригонометрических выражений на основе определений и основных свойств, пользоваться
оценкой и прикидкой при практических расчетах;
·
выполнять тождественные
преобразования тригонометрических, иррациональных, степенных, показательных и
логарифмических выражений;
·
вычислять значения числовых и
буквенных выражений, осуществляя необходимые подстановки и преобразования;
·
определять значения функции по
значению аргумента при различных способах задания функции;
·
строить графики линейной,
квадратичной, тригонометрических, степенной, показательной и логарифмической
функций;
·
решать уравнения, простейшие
системы уравнений, используя свойства функций и их графиков;
·
решать рациональные,
тригонометрические, иррациональные, показательные и логарифмические
уравнения, их системы;
·
решать рациональные,
показательные и логарифмические неравенства, их системы;
·
вычислять производные и
первообразные элементарных функций;
исследовать в простейших
случаях функции на монотонность, находить наибольшие и наименьшие значения
функций;
·
решать геометрические задачи с
применением соотношений и пропорциональных отрезков в прямоугольном
треугольнике, основных теорем для произвольного треугольника;
·
решать геометрические задачи на
клетчатой бумаге.
Использовать
приобретенные знания и умения в практической деятельности и повседневной жизни.
Особенности курса:
—
интеграция разных тем;
—
практическая значимость для учащихся.
Требования к уровню подготовленности учащихся.
·
В результате изучения курса
учащиеся должны уметь:
·
вычислять значения корня,
степени, логарифма;
·
находить значения
тригонометрических выражений;
·
выполнять тождественные
преобразования тригонометрических, иррациональных, показательных,
логарифмических выражений;
·
решать тригонометрические,
иррациональные, показательные, логарифмические уравнения, неравенства, системы,
включая с параметром и модулем, а также комбинирование типов аналитическими и
функционально-графическими методами,
·
строить графики элементарных
функций, проводить преобразования графиков, используя изученные методы
описывать свойства функций и уметь применять их при решении задач,
·
применять аппарат
математического анализа к решению задач;
·
решать различные типы текстовых
задач с практическим содержанием на проценты, движение, работу, концентрацию,
смеси, сплавы, десятичную запись числа, на использование арифметической и
геометрической прогрессии;
·
уметь соотносить процент с
соответствующей дробью;
·
знать широту применения
процентных вычислений в жизни, решать основные задачи на проценты, применять
формулу сложных процентов;
·
решать планиметрические задачи,
связанные с нахождением площадей, линейных или угловых величин треугольников
или четырехугольников;
·
решать стереометрические
задачи, содержащие разный уровень необходимых для решения обоснований и
количество шагов в решении задач, включенных в часть I и часть II
экзаменационной работы, часто требующие построения вспомогательных элементов и
сечений, сопровождаемых необходимыми доказательствами;
·
производить прикидку и оценку
результатов вычислений;
·
при вычислениях сочетать устные
и письменные приемы, использовать приемы, рационализирующие вычисления.
Содержание
обучения
Текстовые задачи 5ч
Дроби и проценты. Смеси и
сплавы. Движение. Работа. Задачи на анализ практической ситуации.
. Выражения
и преобразования 5ч
.
Тождественные преобразования иррациональных и степенных выражений.
Тождественные преобразования логарифмических выражений. Тождественные
преобразования тригонометрических выражений
Функции и их свойства 4ч
Исследование функций
элементарными методами. Производная функции, ее геометрический и физический
смысл. Исследование функций с помощью производной.
Уравнения, неравенства и их системы 6ч
Рациональные уравнения,
неравенства и их системы. Иррациональные уравнения и их системы.
Тригонометрические уравнения и их системы. Показательные уравнения,
неравенства и их системы.
Логарифмические уравнения, неравенства и их системы. Комбинированные уравнения
и смешанные системы.
Задания с параметром 3 ч
Уравнения и неравенства.
Уравнения и неравенства с модулем.
Планиметрия 3ч
Треугольники.
Четырехугольники. Окружность. Окружности, вписанные в треугольник и
четырехугольник. Окружности, описанные около треугольника и четырехугольника.
Стереометрия 3 ч
Углы и расстояния. Сечения
многогранников плоскостью. Площади поверхностей тел. Объемы тел.
Календарно-тематическое
планирование курса
1 час в неделю, всего 34 часа
|
№/п |
Тема |
Кол-во |
дата |
примечание |
|
|
План |
Факт |
||||
|
1.Текстовые |
|||||
|
1 |
Задачи практического содержания (дроби, |
2 |
|||
|
3 |
Задачи на работу и движение. |
1 |
|||
|
4 |
Задачи на анализ практической ситуации. |
1 |
|||
|
5 |
Задачи на анализ практической ситуации |
1 |
|||
|
2.Выражения |
|||||
|
1 |
Тождественные преобразования |
1 |
|||
|
2 |
Тождественные преобразования |
1 |
|||
|
3 |
Преобразования тригонометрических |
1 |
|||
|
4 |
Преобразование тригонометрических |
1 |
|||
|
5 |
Преобразование выражений. |
1 |
|||
|
3.Функции |
|||||
|
1 |
Исследование функций элементарными |
1 |
|||
|
2 |
Производная, ее геометрический и |
1 |
|||
|
3 |
Исследование функции с помощью |
1 |
|||
|
4 |
Исследование функции с помощью |
1 |
|||
|
4.Уравнения, |
|||||
|
1 |
Рациональные уравнения, неравенства и их |
1 |
|||
|
2 |
Иррациональные уравнения и их системы. |
1 |
|||
|
3 |
Тригонометрические уравнения и их |
1 |
|||
|
4 |
Показательные уравнения, неравенства и |
1 |
|||
|
5 |
Логарифмические уравнения, неравенства и |
1 |
|||
|
6 |
Комбинированные уравнения и смешанные |
1 |
|||
|
5. Задания с |
|||||
|
1 |
Уравнения и неравенства |
1 |
|||
|
2 |
Уравнения и неравенства |
1 |
|||
|
3 |
Уравнения и неравенства с модулем. |
1 |
|||
|
6. Планиметрия |
|||||
|
1 |
Треугольники. Четырехугольники. |
1 |
|||
|
2 |
Окружности, вписанные в треугольник и |
1 |
|||
|
3 |
Окружности, описанные около треугольника |
1 |
|||
|
7. |
|||||
|
1 |
Углы и расстояния. Сечения |
1 |
|||
|
2 |
Площади поверхностей и объемы тел. |
1 |
|||
|
3 |
Площади поверхностей и объемы тел. |
1 |
|||
|
8. Структура |
|||||
|
1 |
Система оценивания. Решение заданий с |
1 |
|||
|
2 |
Решение заданий с развернутым ответом (II |
1 |
|||
|
3 |
Решение заданий с развернутым ответом (II |
1 |
|||
|
4 |
Тренировочные варианты ЕГЭ 2020-2021г |
1 |
|||
|
5 |
Тренировочные варианты ЕГЭ |
1 |
Список
литературы
·
сборник ЕГЭ 2021 Ященко И.В 36 типовых
тренировочных вариантов с ответами по математике 11
класс — база .
- 36 типовых экзаменационных вариантов (задания
и ответы)Ященко И.В. 2021, 256с.- профиль. - Лысенко Ф.
Ф., Калабухова С. О. Математика. Подготовка к ЕГЭ 2021.
Учебно-методическое пособие./ Ростов на Дону. Легион, 2020
Информационные
ресурсы интернет
- http://fipi.ru/
. Сайт ФИПИ. Открытый банк заданий ЕГЭ по математике. - http://reshuege.ru/ .
Сайт для подготовки учащихся к ЕГЭ и проведения он-лайн тестирования
и др
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ГОРОДА РОСТОВА-НА-ДОНУ «ШКОЛА № 73»
|
СОГЛАСОВНА |
Рассмотрена и рекомендована |
УТВЕРЖДЕНА |
||
|
руководитель МО |
к утверждению |
и.о. директора |
||
|
_________________ |
на педагогическом совете |
____________С.В. Козинкова |
||
|
С.В. Козинкова |
Протокол № 1 от 30.08.2021 |
Приказ № 317 от 31.08.2021 |
РАБОЧАЯ ПРОГРАММА
по внеурочной деятельности
«Подготовка к ЕГЭ по математике»
для 11 «Б» класса
|
Учебный год |
2021-2022 |
|
Учитель |
Гончарова Е.В. |
г. Ростов-на-Дону
2021
Данная рабочая программа разработана на основе Федерального государственного образовательного стандарта среднего общего образования, в соответствии с учебным планом и календарным учебным графиком МБОУ «Школа № 73», и требованиями к результатам освоения основной образовательной программы среднего общего образования.
Данный курс систематизирует содержание учебных предметов Алгебра и Геометрия и служит подготовительной базой для учащихся 11 класса при подготовке к государственной итоговой аттестации. Рабочая программа разработана на основе открытого банка заданий по подготовке к государственной итоговой аттестации в форме единого государственного экзамена.
Характерной особенностью данного учебного курса является систематизация и обобщение знаний учащихся, закрепление и развитие умений и навыков по основным темам.
Программа рассчитана на 64 часа (из расчета 2 часа в неделю).
РЕЗУЛЬТАТЫ ОСВОЕНИЯ КУРСА ВНЕУРОЧНОЙ ДЕЯТЕЛЬНОСТИ
Личностные результаты предусматривают умения:
— развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
— формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
— воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
— формирование качеств мышления, необходимых для адаптации в современном информационном обществе; развитие интереса к математическому творчеству и математических способностей.
Метапредметными результатами являются умения:
— формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
— развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
— формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности.
Предметными результатами являются представления:
— овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни;
-создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
СОДЕРЖАНИЕ КУРСА ВНЕУРОЧНОЙ ДЕЯТЕЛЬНОСТИ
|
№ |
Раздел учебной программы |
Кол-во часов |
Характеристика основных содержательных линий |
|
1. |
Подготовка к ЕГЭ по математике |
64 |
Действия с дробями. Округление с недостатком. Округление с избытком. Размеры и единицы измерения. Чтение графиков и диаграмм. Задачи на квадратной решетке. Задачи на проценты, округление. Действия со степенями. Преобразования числовых иррациональных, логарифмических, тригонометрических выражений. Вычисление значений тригонометрических выражений. Действия с формулами. Простейшие уравнения: линейные, квадратные, кубические, иррациональные, показательные, логарифмические. Прикладная геометрия: многоугольники. Начала теории вероятностей. Классическое определение вероятности. Теоремы о вероятностных событиях. Выбор оптимального варианта. Стереометрия: многогранники, куб, прямоугольный параллелепипед, призма, пирамида, площадь поверхности составного многогранника объем составного многогранника круглые тела. Анализ графиков и диаграмм. Планиметрия: треугольники и их элементы четырехугольники и их элементы многоугольники окружность. Задачи по стереометрии: параллелепипед призма пирамида цилиндр конус шар. Решение неравенств. Числовые промежутки. Анализ утверждений. Числа и их свойства. Решение задач на смекалку. Физический смысл производной. Геометрический смысл производной касательная. Применение производной к исследованию функций. Первообразная. Задачи с прикладным содержанием: линейные, квадратные, степенные, рациональные, иррациональные, показательные, логарифмические, тригонометрические уравнения и неравенства. Задачи на проценты, сплавы, смеси. Задачи на движение по прямой, окружности. Задачи на движение по воде. Задачи на совместную работу. Задачи на прогрессии. Графики функций: гиперболы, кусочно-линейная функция, параболы синусоиды. Наибольшее и наименьшее значение функций. Исследование степенных и иррациональных функций. Исследование частных, произведений. Исследование показательных и логарифмических функций. Исследование тригонометрических функций. Исследование функций без помощи производной. Рациональные неравенства. Неравенства, содержащие радикалы. Показательные, логарифмические неравенства. Неравенства с логарифмами по переменному основанию. Неравенства с модулем. Смешанные неравенства. |
|
Итого: |
64 |
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
|
№ |
Раздел учебной программы |
Кол-во часов |
Основные виды учебной деятельности |
Формы текущего контроля |
|
1. |
Подготовка к ЕГЭ по математике |
64 |
Вычисления: действия с дробями. Решение простейших текстовых задач. Чтение графиков и функций. Решение задач на квадратной решетке. Вычисления и преобразования числовых выражений. Решение задач по прикладной геометрии. Решение задач на теорию вероятностей. Выбор оптимального варианта. Решение задач по стереометрии. Решение задач по планиметрии. Анализ графиков и диаграмм. Анализ утверждений. Решение задач на свойства чисел. Решение задач на смекалку. Нахождение производной, первообразной. Решение задач на физический, геометрический смысл производной. Решение задач с прикладным содержанием. Построение и исследование графиков функций. Решение задач на вероятность сложных событий. Исследование функций нахождение наибольшего и наименьшего значения. Решение уравнений неравенств. |
Фронтальный опрос, тематическое тестирование, решение заданий из открытого банка заданий на сайте fipi.ru, https://math8-vpr.sdamgia.ru, платформы Учи.ру, образовательного ресурса ЯКласс |
|
Общее количество часов |
64 |
КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
|
Номер занятия |
Дата |
Тема |
Часы |
|
Подготовка к ЕГЭ по математике |
|||
|
|
04.09 |
Действия с дробями |
1 |
|
|
04.09 |
Округление с недостатком. Округление с избытком |
1 |
|
|
11.09 |
Простейшие текстовые задачи |
1 |
|
|
11.09 |
Размеры и единицы измерения |
1 |
|
|
18.09 |
Чтение графиков и диаграмм |
1 |
|
|
18.09 |
Задачи на квадратной решетке |
1 |
|
|
25.09 |
Задачи на проценты, округление |
1 |
|
|
25.09 |
Действия со степенями |
1 |
|
|
02.10 |
Преобразование числовых иррациональных выражений |
1 |
|
|
02.10 |
Преобразование числовых логарифмических выражение |
1 |
|
|
09.10 |
Вычисление значений тригонометрических выражений. Преобразование числовых тригонометрических выражений |
1 |
|
|
09.10 |
Преобразование выражений. Действия с формулами |
1 |
|
|
16.10 |
Простейшие уравнения. Линейные, квадратные, кубические уравнения. Иррациональные уравнения |
1 |
|
|
16.10 |
Простейшие уравнения. Показательные уравнения. Логарифмические уравнения |
1 |
|
|
23.10 |
Прикладная геометрия. Многоугольники |
1 |
|
|
23.10 |
Начала теории вероятностей. Классическое определение вероятности |
1 |
|
|
13.11 |
Начала теории вероятностей. Теоремы о вероятностных событиях |
1 |
|
|
13.11 |
Решение задач на выбор оптимального варианта |
1 |
|
|
20.11 |
Стереометрия. Многогранники. Куб. Прямоугольный параллелепипед. Призма. Пирамида |
1 |
|
|
20.11 |
Площадь поверхности составного многогранника. Объем составного многогранника. Круглые тела |
1 |
|
|
27.11 |
Анализ графиков и диаграмм |
1 |
|
|
27.11 |
Планиметрия. Треугольники и их элементы. Четырехугольники и их элементы |
1 |
|
|
04.12 |
Многоугольники. Окружность |
1 |
|
|
04.12 |
Решение задач по стереометрии. Параллелепипед. Призма. Пирамида. Цилиндр. Конус. Шар |
1 |
|
|
11.12 |
Решение неравенств |
1 |
|
|
11.12 |
Анализ утверждений |
1 |
|
|
18.12 |
Числа и их свойства |
1 |
|
|
18.12 |
Числа и их свойства |
1 |
|
|
25.12 |
Решение задач на проценты, сплавы, смеси. Решение задач на движение по прямой, окружности |
1 |
|
|
25.12 |
Решение задач на движение по воде. Решение задач на совместную работу. Решение задач на прогрессии |
1 |
|
|
15.01 |
Решение задач на смекалку |
1 |
|
|
15.01 |
Решение задач на смекалку |
1 |
|
|
22.01 |
Решение прямоугольного треугольника |
1 |
|
|
22.01 |
Решение равнобедренного треугольника |
1 |
|
|
29.01 |
Треугольники общего вида |
1 |
|
|
29.01 |
Параллелограммы. Трапеция |
1 |
|
|
05.02 |
Центральные и вписанные углы. Касательная, хорда, секущая |
1 |
|
|
05.02 |
Вписанные окружности. Описанные окружности |
1 |
|
|
12.02 |
Физический смысл производной. Геометрический смысл производной, касательная |
1 |
|
|
12.02 |
Применение производной к исследованию функций. Первообразная |
1 |
|
|
19.02 |
Задачи с прикладным содержанием. Линейные уравнения и неравенства. Квадратные и степенные уравнения и неравенства. Рациональные уравнения и неравенства |
1 |
|
|
19.02 |
Задачи с прикладным содержанием. Иррациональные, Показательные, логарифмические уравнения и неравенства |
1 |
|
|
26.02 |
Задачи с прикладным содержанием. Тригонометрические уравнения и неравенства |
1 |
|
|
26.02 |
Графики функций. Гиперболы. Кусочно-линейная функция |
1 |
|
|
05.03 |
Графики функций. Параболы. Синусоиды |
1 |
|
|
05.03 |
Теоремы о вероятностных событиях |
1 |
|
|
12.03 |
Теоремы о вероятностных событиях |
1 |
|
|
12.03 |
Исследование степенных и иррациональных функций |
1 |
|
|
19.03 |
Исследование частных. Исследование произведений |
1 |
|
|
19.03 |
Исследование показательных и логарифмических функций |
1 |
|
|
09.04 |
Исследование тригонометрических функций |
1 |
|
|
09.04 |
Исследование функций без помощи производной |
1 |
|
|
16.04 |
Развернутая часть. Рациональные, иррациональные уравнения. Логарифмические и показательные уравнения |
1 |
|
|
16.04 |
Развернутая часть. Рациональные, иррациональные уравнения. Логарифмические и показательные уравнения |
1 |
|
|
23.04 |
Развернутая часть. Тригонометрические уравнения, разложение на множители, исследование ОДЗ |
1 |
|
|
23.04 |
Развернутая часть. Тригонометрические уравнения, разложение на множители, исследование ОДЗ |
1 |
|
|
30.04 |
Развернутая часть. Уравнения смешанного типа |
1 |
|
|
30.04 |
Развернутая часть. Уравнения смешанного типа |
1 |
|
|
07.05 |
Развернутая часть. Рациональные неравенства. Неравенства, содержащие радикалы |
1 |
|
|
07.05 |
Развернутая часть. Показательные неравенства. Логарифмические неравенства |
1 |
|
|
14.05 |
Развернутая часть. Неравенства с логарифмами по переменному основанию |
1 |
|
|
14.05 |
Развернутая часть. Неравенства с модулем |
1 |
|
|
21.05 |
Решение типового варианта ЕГЭ |
1 |
|
|
21.05 |
Решение типового варианта ЕГЭ |
1 |
|
Итого: |
64 |
Раздел I. Пояснительная записка
Программа курса разработана в соответствии:
с требованиями Федерального государственного образовательного стандарта среднего (полного) общего образования.;
с особенностями Образовательной программы школы.
В 21 веке — веке новых технологий все больше специальностей требует высокого уровня образования, связанного с непосредственным применением математики. Математические методы исследования используются в различных областях знаний (экономика, бизнес, финансы, техника, информатика, психология и другие). Таким образом, расширяется круг школьников, для которых математика становится профессионально значимым предметом.
Курс «Решение математических задач повышенной сложности» является предметно — ориентированным и предназначен для расширения теоретических и практических знаний учащихся 11 класса универсального направления общеобразовательной школы. Практикум рассчитан на 34 учебных часов, один раз в неделю.
Цель курса
Углубление и расширение знаний учащихся о способах и методах решения нестандартных задач.
Создание условий для формирования у учащихся качеств мышления, характерных для математической деятельности необходимых для изучения смежных дисциплин, продолжения образования и продуктивной жизни в современном обществе.
Задачи курса
-
Расширить знания учащихся о методах и приемах решения алгебраических уравнений высших степеней;
-
Систематизировать теоретические знания учащихся о приемах и методах решения задач различного вида сложности, включая задачи с модулем и параметром;
-
Сформировать практические навыки и умения учащихся по решению:
-уравнений и неравенств, содержащих радикалы; степени, логарифмы, тригонометрические функции;
-уравнений и неравенств, содержащих переменную под знаком модуля;
-уравнений и неравенств, содержащих параметры
-
Повысить математическую культуру учащихся.
Программой курса предусмотрено изучение следующих вопросов выходящих за рамки школьной программы по математике (базового уровня): многочлены и уравнения высших степеней, тригонометрические уравнения и неравенства с модулем и параметрами, иррациональные неравенства, нестандартные методы решения показательных и логарифмических уравнений и неравенств, комбинированных уравнений и неравенств.
Материал курса кроме теоретических сведений, необходимых для решения уравнений, неравенств и их систем, содержит интересные нестандартные задачи, освещает способы и методы решения математических задач не рассматриваемые в школьном курсе математики. Углубление базового материал по математике реализуется за счет обучения методам и приемам решений заданий, требующих применения высокой логической и операционной культуры, развивающим научно-теоретическое и алгоритмическое мышление учащихся.
Для реализации целей и задач курса предполагается использовать следующие формы проведения занятий: лекции, практикумы по решению задач, семинары. Для получения эффективных результатов имеет смысл использовать компьютер интерактивную доску, которые помогут как в реализации результатов работы с данными вопросами, так и при решении математических задач.
Эффективность усвоения изучаемого материала отслеживается через выполнение индивидуальных самостоятельных работ (Приложение 1). Итоговый контроль предусматривает выполнение контрольной работы, включающей разноуровневые задания, рассматриваемые на занятиях. Результат освоения курса считается положительным, если ученик выполнил 75% контрольной работы (Приложение 1).
Программа содержит темы творческих работ (Приложение 2), календарно-тематическое планирование (Приложение 3) и список литературы по предложенным темам.
В результате изучения программы элективного курса учащиеся получают возможность
знать и понимать:
-
основные виды уравнений и неравенств;
-
алгоритмы решения уравнений, неравенств, их систем с модулями и параметрами;
-
различные методы решения тригонометрических, иррациональных, показательных и комбинированных уравнений, неравенств и их систем;
уметь:
-
уметь обобщать и систематизировать сведения об уравнениях, неравенствах, системах уравнений и неравенств и методах их решения;
-
решать уравнения, неравенства, системы уравнений и неравенств, содержащих переменную под знаком модуля;
-
решать уравнения, неравенства, системы уравнений и неравенств, содержащих параметр;
-
применять различные приемы при решении тригонометрических, иррациональных, показательных и комбинированных уравнений и неравенств;
-
выбирать наиболее рациональные способы решения математических задач;
-
уметь извлекать необходимую информацию из учебной, справочной, научной литературы.
-
применять теорию многочленов к нахождению корней рационального уравнения с целыми коэффициентами; усвоить основные методы решения алгебраических уравнений
Содержание основных разделов
Тема 1. Алгебраические уравнения и неравенства 5 ч.
-
Простейшие способы решения алгебраических уравнений;
-
Симметрические и возвратные уравнения;
-
Искусственные методы решения алгебраических уравнений:
-умножение уравнений на функцию;
-использование симметричности уравнений;
-исследование уравнения на промежутках действительной оси
-
Решение алгебраических неравенств. Обобщенный метод интервалов.
Тема 2. Тригонометрические уравнения 6 ч.
-
Методы решения тригонометрических уравнений:
-решение уравнений с помощью универсальной подстановки;
-решение уравнений с помощью введение вспомогательного угла;
-решение уравнений умножением на тригонометрическую функцию;
-искусственные приемы при решении тригонометрических уравнений.
-
Тригонометрические уравнения, содержащие параметры, знак модуля или арифметического корня.
-
Решение систем тригонометрических неравенств методом концентрических окружностей
-
Системы тригонометрических уравнений и неравенств.
Тема 3. Уравнения и неравенства, содержащие радикалы 9ч.
-
Методы решения иррациональных уравнений
-метод исследования области определения функций, входящих в данное иррациональное уравнение;
-метод исследования множества значений функций, входящих в данное иррациональное уравнение (Метод оценки);
-сведение иррационального уравнения к системе уравнений;
-сведение иррационального уравнения к тригонометрическому уравнению;
-искусственные приемы при решении иррациональных уравнений;
-
Иррациональные неравенства.
-
Иррациональные уравнения и неравенства с параметрами
-
Системы иррациональных уравнений и неравенств.
Тема 4. Уравнения и неравенства, содержащие степени и логарифмы 7ч.
-
Метод почленного деления при решении показательного уравнения
-
Показательно-степенное уравнение
-
Метод логарифмирования при решении показательно-степенных уравнений
-
Искусственные методы решения показательных уравнений
-
Уравнения и неравенства, содержащие неизвестную в основании логарифма
-
Показательные и логарифмические уравнения и неравенства с модулями и параметрами
Тема 5. Комбинированные уравнения и неравенства 7ч.
-
Решение уравнений и неравенств с использованием свойств входящих в них функций:
-использование ОДЗ
-использование ограниченности функции
-использование монотонности функции
-использование графиков функций
-метод интервалов для непрерывных функций
-
Решение некоторых уравнений и неравенств сведением их к системе уравнений или неравенств относительно той же неизвестной
-
Применение производной для решения уравнений
Литература
Литература для учащихся:
-
Олехник, С.Н. Уравнения и неравенства. Нестандартные методы решения./ С.Н. Олехник.: Москва, «Дрофа», 2001-189с.
-
Жафяров, А.Ж. Математика ЕГЭ. Решение задач повышенного уровня С3/А.Ж. Жафяров. — Новосибирск: Сиб. унив. изд-во,2010-181с.
-
Жафяров, А.Ж. Математика ЕГЭ. Решение задач уровня /А.Ж. Жафяров. — Новосибирск: Сиб. унив. изд-во,2009-181с.
-
Амелькин, В.В. Задачи с параметрами./ В.В, Амелькин, В.Л. Рабинович В.Л.: Минск, «Асар»,1996г.
Литература для учителя:
-
Айвазян, Д.Ф. Математика.10-11 классы. Решение уравнений и неравенств с параметрами: элективный курс/Д.Ф. Айвазян. Волгоград: Учитель, 2009. -204с.
-
Шахмейстер, А.Х. Иррациональные уравнения и неравенства/ А.Х. Шхмейстер М: МЦНМО 2011.-216с.
-
Шахмейстер, А.Х. Задачи с параметрами на экзаменах/ А.Х. Шахмейстера М: МЦНМО 2011.-248с.
-
Горштейн, П.И., Полонский В.Б., Якир М.С. Задачи с параметрами/ Горштейн П.И., Полонский В.Б., Якир М.С. М.:Просвещение, 2007г.
-
Севрюков, П.Ф., Смоляков А.Н. Показательные и логарифмические уравнения и неравенства, 2006г.
-
Ершова, А.П. Самостоятельные и контрольные работы по алгебре и началам анализа для 10-11 классов./ А.П. Ершова, В.В. Голобородько — М. ИЛЕКС 2004.-176с.
-
Цыпкин, А.Г.Справочник по методам решения задач по математике/ А.Г. Цыпкин, А.И, Пинский -М.:Наука. Гл.ред. физ.-мат. Лит., 1989.-576с.
Приложение 1
Домашняя самостоятельная работа №1
по теме «Уравнения и неравенства, содержащие радикалы»
Вариант 1.
-
Решите уравнение:
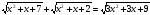
-
Решите неравенство:
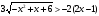
-
Решите неравенство методом интервалов:
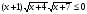
-
Найдите все значения параметра, а при которых уравнение
имеет только одно решение.
Вариант 2.
-
Решите уравнение:
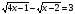
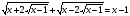
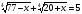
-
Решите неравенство:
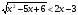
-
Решите неравенство методом интервалов:
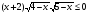
-
Найдите все значения параметра а, при которых уравнение
имеет только одно решение.
Вариант 3*.
-
Решите уравнение:
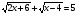
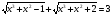
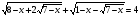
-
Решите неравенство:
-
Найдите все значения параметра а, при которых уравнение
не имеет решений.
Вариант 4*.
-
Решите уравнение:
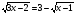
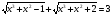
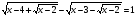
-
Решите неравенство:
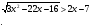
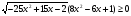
-
Найдите все значения параметра а, при которых уравнение
имеет только два решение.
Домашняя самостоятельная работа № 2
по теме «Методы решения тригонометрических уравнений и неравенств»
Вариант 1.
1. Решите данное уравнение тремя способами (с помощью формул двойного угла, метода вспомогательного угла и универсальной подстановки) и докажите, что полученные ответы совпадают:
2sin x – 3 cos x = 2.
2. Используя умножение на тригонометрическую функцию, решите уравнения:
а) cos x cos 2x cos 4x = 1/8;
б) sin 2x+ sin 4x+ sin 6x =0,5ctgx.
3. Решите уравнение:
а) | sin x| = sin x+2 cos x;
б) | cos x|(2х-4) = |х-2|;
в) cos x = +1;
г) .
-
Используя метод интервалов, решите неравенство cos 3x+ 2cos x
0.
5.Решить систему неравенств методом концентрических окружностей.
6. При каких значениях параметра a уравнение не имеет решений?
Вариант 2.
-
Решите данное уравнение тремя способами (с помощью формул двойного угла, метода вспомогательного угла и универсальной подстановки) и докажите, что полученные ответы совпадают:
3 cos x -4sin x = 5.
-
Используя умножение на тригонометрическую функцию, решите уравнения:
а) 4 cos x cos 2x cos 3x = cos 6x;
б) cos 2x+ cos 4x+ cos 6x =-0,5.
-
Решите уравнение:
а) | cos x|= cos x-2 sin x;
б) |tgx|(х+3) = |х+3|;
в) cos x =1=1/ (+1);
г) .
-
Используя метод интервалов, решите неравенство sin3 x-2 sin x
0.
-
Решить систему неравенств методом концентрических окружностей.
-
Найдите все целые значения параметра a, при каждом из которых уравнение
имеет решения. Найдите эти решения?
Домашняя самостоятельная работа № 3
по теме «Уравнения и неравенства, содержащие степени и логарифмы»
Вариант 1.
-
Решите уравнения:
а) ;
б) ;
в) ;
г) (введение параметра);
д) (введение новой переменной);
е) .
-
Решите неравенства:
а) ;
б) .
-
Найдите все значения параметра а, при которых уравнение
имеет единственный корень.
Вариант 2.
-
Решите уравнения:
а) ;
б) ;
в) ;
г) (введение параметра);
д) (введение новой переменной);
е) .
2. Решите неравенства:
а) ;
б) .
3. Найдите все значения параметра а, при которых уравнение имеет только один корень.
Зачетная контрольная работа
Вариант 1
-
Решить уравнение:
а);
б);
в) .
-
Решите неравенство:
-
Найдите все значения параметра а, при каждом из которых уравнение
имеет единственное решение.
Вариант 2
-
Решить уравнение:
а);
б);
в) .
-
Решите неравенство:
-
Найдите все значения параметра а, при каждом из которых уравнение
не имеет действительных корней.
Приложение 2
Темы творческих работ и сообщений.
-
Формулы Кардана.
-
Метод Феррари для решения уравнений четвертой степени.
-
Теорема Безу.
-
Наибольший общий делитель многочленов. Алгоритм Евклида.
-
Основная теорема алгебры многочленов.
-
Франсуа Виет, жизнь и творчество.
-
Квадратный трёхчлен, расположение корней квадратного трёхчлена.
-
Конструирование задач на изучаемую тему курса.
-
Графический способ решения уравнений и неравенств.
-
Проект опорных сигналов по способам решения уравнений и неравенств с модулем.
Приложение 3
Тематическое планирование курса построено так, что ученики на занятиях углубляют знания, полученные на уроках математики, и приобретают умения решать нестандартные задачи и задачи повышенной сложности.
Календарно-тематическое планирование
|
№ |
Тема урока |
Кол во часов |
Дата проведения |
Виды деятельности учащихся |
Оборудование, контрольно-измерительные материалы |
Примечание |
|
|
План |
Факт |
||||||
|
Алгебраические уравнения и неравенства. |
5 ч. |
||||||
|
Простейшие способы решения алгебраических уравнений. Симметрические и возвратные уравнения |
1 |
Актуализация знаний учащихся о методах решения алгебраических уравнений. |
||||
|
|
Искусственные способы решения алгебраических уравнений. Умножение уравнения на функцию |
1 |
Практикум по решению алгебраических уравнений. |
Раздаточный материал с образцами решения алгебраических уравнений |
|||
|
|
Искусственные способы решения алгебраических уравнений. Использование симметричности уравнения |
1 |
Практикум по решению алгебраических уравнений. |
||||
|
|
Искусственные способы решения алгебраических уравнений. Исследование уравнения на промежутках действительной оси |
1 |
Практикум по решению алгебраических уравнений. Самостоятельная работа по решению алгебраических уравнений |
Раздаточный материал |
|||
|
|
Решение алгебраических неравенств. Обобщенный метод интервалов |
1 |
Составление алгоритма действия по решению алгебраических неравенств методом интервалов. |
Раздаточный материал с образцами решения алгебраических неравенств |
|||
|
Тригонометрические уравнения и неравенства |
6ч. |
||||||
|
|
Методы решения тригонометрических уравнений. |
1 |
Составление памятки по методам решения тригонометрических уравнений. Работа со справочной литературой. Практикум. |
Справочная литература Раздаточный материал Слайд-лекция «Простейшие тригонометрические уравнения. Основные методы решения тригонометрических уравнений» |
|||
|
|
Методы решения тригонометрических уравнений. |
1 |
Практикум по решению тригонометрических уравнений |
Конспекты, памятки по решению тригонометрических уравнений |
|||
|
|
Искусственные приемы при решении тригонометрических уравнений |
1 |
Работа с раздаточным материалом. Практикум по решению тригонометрических уравнений. |
Раздаточный материал |
|||
|
|
Тригонометрические уравнения и неравенства, содержащие параметры, знак модуля или арифметического корня. |
1 |
Составление алгоритма действия для решения тригонометрических уравнений (неравенств), содержащих параметры. |
Слайд-лекция «Уравнения с модулем» |
|||
|
|
Решение систем тригонометрических неравенств методом концентрических окружностей |
1 |
Работают с раздаточным материалом, составление опорного конспекта. |
Слайд «Числовая окружность» Раздаточный материал |
|||
|
|
Решение систем тригонометрических уравнений и неравенств |
1 |
Практикум по решению упражнений повышенного уровня сложности. |
Выполнение домашней самостоятельной работы (Приложение 1) |
|||
|
Уравнения и неравенства, содержащие радикалы |
9 ч |
||||||
|
|
Методы решения иррациональных уравнений (Использование ОДЗ. Метод оценки) |
1 |
Актуализация знаний учащихся о методах решения иррациональных уравнений. |
Раздаточный материал с образцами решения иррациональных уравнений |
|||
|
|
Сведение иррационального уравнения к системе уравнений |
1 |
Практикум по решению упражнений |
||||
|
|
Сведение иррационального уравнения к тригонометрическому |
1 |
Практикум по решению упражнений |
Раздаточный материал |
|||
|
|
Искусственные приемы при решении иррациональных уравнений |
1 |
Практикум по решению упражнений |
Раздаточный материал |
|||
|
|
Иррациональные неравенства |
1 |
Составление алгоритма действия по решению иррациональных неравенств. |
||||
|
|
Иррациональные неравенства |
1 |
Практикум по решению упражнений Решение самостоятельной работы |
Раздаточный материал |
|||
|
|
Иррациональные уравнения и неравенства с параметрами |
1 |
Составление плана исследования уравнения (неравенства) в зависимости от значения параметра |
||||
|
|
Иррациональные уравнения и неравенства с параметрами |
1 |
Практикум по решению упражнений повышенного уровня сложности |
||||
|
|
Системы иррациональных уравнений и неравенств |
1 |
Практикум по решению упражнений |
Раздаточный материал |
Выполнение домашней самостоятельной работы (Приложение 1) |
||
|
Уравнения и неравенства, содержащие степени и логарифмы |
7ч. |
||||||
|
|
Метод почленного деления при решении показательного уравнения |
1 |
Составление опорного конспекта по методам решения уравнений. Работа со справочной литературой |
Раздаточный материал с образцами решения показательных уравнений |
|||
|
|
Показательно-степенное уравнение |
1 |
Практикум по решению упражнений |
||||
|
|
Метод логарифмирования при решении показательно-степенных уравнений |
1 |
Практикум по решению упражнений |
||||
|
|
Искусственные методы решения показательных уравнений |
1 |
Практикум по решению упражнений Решение самостоятельной работы |
Раздаточный материал |
|||
|
|
Уравнения и неравенства, содержащие неизвестную в основании логарифма |
1 |
Практикум по решению упражнений |
||||
|
|
Уравнения и неравенства, содержащие неизвестную в основании и показателе степени |
1 |
Практикум по решению упражнений |
||||
|
|
Показательные и логарифмические уравнения и неравенства с модулями и параметрами |
1 |
Составление плана исследования уравнения (неравенства) в зависимости от значения параметра |
Выполнение домашней самостоятельной работы (Приложение 1) |
|||
|
Комбинированные уравнения и неравенства |
7ч. |
||||||
|
|
Решение уравнений и неравенств с использованием ОДЗ входящих в них функций. |
1 |
Актуализация знаний учащихся об основных свойствах функций. Работа с раздаточным материалом |
Раздаточный материал Слайд – лекция «Свойства функций» |
|||
|
|
Решение уравнений и неравенств с использованием монотонности и ограниченности входящих в них функций. |
1 |
Практикум по решению упражнений повышенного уровня сложности. Выполнение самостоятельной работы |
Раздаточный материал |
|||
|
|
Решение уравнений и неравенств с использованием графиков входящих в них функций. |
1 |
Практикум по решению упражнений |
Раздаточный материал |
|||
|
|
Решение уравнений и неравенств с использованием метода интервалов |
1 |
Практикум по решению упражнений |
Раздаточный материал |
|||
|
|
Решение некоторых уравнений и неравенств сведением их к системе уравнений или неравенств относительно той же неизвестной |
1 |
Практикум по решению упражнений |
||||
|
|
Применение производной для решения уравнений |
1 |
Составление опорного конспекта. Решение упражнений |
||||
|
|
Итоговое занятие |
1 |
Выполнение контрольной работы. |
Раздаточный материал |
Приложение 1 |
МУНИЦИПАЛЬНОЕ АВТОНОМНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ
«Средняя общеобразовательная школа совхоза им. Ленина»
|
УТВЕРЖДАЮ ________________ Приказ |
Рабочая программа внеурочной деятельности
«Математика. Повторение курса в формате ЕГЭ»
название
16-18 лет, 10 – 11 класс (11 «А»)
возраст, класс
2020-2021 учебный год
срок реализации программы
Учитель: Дроздова
Ирина Михайловна , учитель математики, высшая
ФИО,
должность, кв. категория
Поселок совхоза им. Ленина
2020
Раздел I. Пояснительная записка
Программа внеурочной
деятельности для 10 – 11 классов «Математика.
Повторение курса в формате ЕГЭ» разработана в соответствии с требованиями
Федерального государственного образовательного стандарта основного общего образования. Программа содержит все
необходимые разделы и соответствует современным требованиям, предъявляемым к
программам внеурочной деятельности.
Данный курс является
предметно- ориентированным и направлен на повторение и углубленное изучение
отдельных разделов основного курса математики. Он также расширяет базовую программу
по математике, не нарушая её целостности.
Данная
программа позволяет учащимся ознакомиться со многими интересными вопросами математики
на данном этапе обучения, выходящими за рамки школьной программы, расширить целостное
представление о проблеме данной науки. Решение математических задач, связанных
с логическим мышлением закрепит интерес детей к познавательной деятельности,
будет способствовать развитию мыслительных операций и общему интеллектуальному
развитию.
Место курса внеурочной деятельности «Математика после уроков» в учебном плане
МАОУ «СОШ совхоза им. Ленина» определяется Федеральным базисным учебным планом
для образовательных учреждений Российской Федерации 2012 года. Курс
предназначен для обеспечения школьного компонента учебного плана и рассчитана на
35 часов (1 час в неделю) в 10 классе и 34 часа (1 час в неделю) в 11 классе, всего
69 часов.
Цель
курса:
Ø повторение, углубление и расширение знаний по математике, развитие
логического мышления и познавательного интереса;
Ø
формирование у учащихся навыков
решения заданий повышенной сложности;
Ø
решение уравнений, содержащих одно
выражение под знаком модуля с точки зрения геометрического смысла модуля и
алгебраического определения модуля;
Ø
применение этих методов при
решении уравнений, содержащих неизвестное под знаком модуля;
Ø
решение уравнений, содержащих
несколько выражений под знаком модуля;
Ø
применение знаний при решении
задач.
Основные
задачи:
Ø
активизировать познавательную
деятельность школьников;
Ø
интегрировать знания по
разнообразию методов решения уравнений;
Ø
повышать информационную и
коммуникативную компетентность учащихся;
Ø
развивать у школьников логическое
мышление, интерес к предмету;
Ø расширить представления учащихся о математике как науке;
Ø подготовить учащихся к итоговой аттестации;
Ø научить решать нестандартные задачи;
Ø научить различным приемам, помогающим успешно справиться с
заданиями второй части ЕГЭ.
Новизна программы заключается в
том, что содержание построено таким образом, что изучение всех последующих тем
обеспечивается знаниями по ранее изученным темам базовых курсов. Предполагаемая
методика изучения и структура программы позволяют наиболее эффективно организовать
учебный процесс, в том числе и обобщающее повторение учебного материала. В процессе
занятий вводятся новые методы решения, но вместе с тем повторяются, углубляются
и закрепляются знания, полученные ранее, развиваются умения применять эти
знания на практике в процессе самостоятельной работы.
Общая характеристика
В курсе
присутствуют темы и задания, которые стимулируют учащихся к проведению несложных
обоснований, к поиску тех или иных закономерностей. Все это направлено на
развитие способностей детей к применению математических знаний в различных
жизненных ситуациях.
Во время занятий у
ребенка происходит становление развитых форм самосознания, самоконтроля и
самооценки. Отсутствие отметок снижает тревожность и необоснованное беспокойство
учащихся, исчезает боязнь ошибочных ответов. В результате у детей формируется
отношение к данным занятиям как к средству развития своей личности. Данный курс
состоит из системы тренировочных упражнений, практических заданий, проектных
задач, дидактических и развивающих игр.
В курсе
используются задачи разной сложности, поэтому слабые дети, участвуя в занятиях, могут почувствовать уверенность в своих силах (для таких учащихся подбираются
задачи, которые они могут решать успешно).
Ребенок на этих занятиях сам
оценивает свои успехи. Это создает особый положительный эмоциональный фон: раскованность, интерес, желание научиться выполнять
предлагаемые задания.
Задания построены таким образом, что один вид деятельности сменяется
другим, различные темы и формы подачи материала активно чередуются в течение
урока. Это позволяет сделать работу динамичной, насыщенной и менее утомляемой.
В системе заданий реализован принцип «спирали», то есть возвращение к
одному и тому же заданию, но на более высоком уровне трудности. Задачи по
каждой из тем могут быть включены в любые занятия другой темы в качестве закрепления.
Возраст
детей,
участвующие в реализации данной программы 16-18 лет.
Срок
реализации
данной образовательной программы 2020-2021 учебный год.
Занятия
внеурочной деятельности проводятся 1 раз в неделю, всего 35
часов
Наполняемость
группы 25 человек.
Планируемые результаты изучения учебного предмета, курса
Данный
курс позволяет добиваться следующих результатов освоения образовательной
программы ООО.
В личностном направлении:
G
формирование
ответственного отношения к учению, готовности и способности к саморазвитию;
G
формирование
умения ясно, точно и грамотно излагать свои мысли в устной речи;
G
развитие
логического и критического мышления, культуры речи, способности к умственному
эксперименту;
G
формирование
у учащихся интеллектуальной честности и объективности, способности к
преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
G
воспитание
качеств личности, обеспечивающих социальную мобильность, способность принимать
самостоятельные решения;
G
формирование
качеств мышления, необходимых для адаптации в современном информационном
обществе;
G
развитие
интереса к математическому творчеству и математических способностей.
В метапредметном направлении:
G
формирование
представлений о математике как части общечеловеческой культуры, о значимости
математики в развитии цивилизации и современного общества;
G
умения
осуществлять контроль по образцу и вносить коррективы;
G
умения
устанавливать причинно-следственные связи, строить логические рассуждения и
выводы;
G
умения
понимать и использовать математические средства наглядности (чертежи, схемы);
G
умения
самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных
задач.
G
развития
способности организовывать сотрудничество и совместную деятельность с учителем
и сверстниками.
В предметном направлении:
G
овладение
математическими знаниями и умениями, необходимыми для продолжения обучения в
старшей школе или иных общеобразовательных учреждениях, изучение смежных
дисциплин, применение в повседневной жизни;
G
умение
работать с математическим текстом (структурирование, извлечение информации),
точно и грамотно выражать свои мысли в устной и письменной речи, применять
математическую терминологию и символику, использовать различные языки
математики (словесный, символический, графический);
G
владение
базовым понятийным аппаратом: иметь представление о числе, дроби, об основных
геометрических объектах;
G
умение
выполнять арифметические преобразования выражений, применять их для решения
учебных математических и задач и задач в смежных учебных предметах.
В ходе реализация программы внеурочной деятельности по учебно-познавательному
направлению «Математика. Повторение курса в формате ЕГЭ» обучающиеся
должны/получат возможность
Знать/понимать
Ø значение
математической науки для решения задач, возникающих в теории и практике;
Ø широту и
ограниченность применения математических методов к анализу и исследованию
процессов и явлений в природе и обществе;
Ø значение практики
и вопросов, возникающих в самой математике, для формирования и развития
математической науки;
Ø идеи расширения
числовых множеств как способа построения нового математического аппарата для
решения практических задач и внутренних задач математики;
Ø значение идей,
методов и результатов алгебры и математического анализа для построения моделей
реальных процессов и ситуаций;
Ø возможности
геометрии для описания свойств реальных предметов и их взаимного расположения;
Ø универсальный
характер законов логики математических рассуждений, их применимость в различных
областях человеческой деятельности;
Ø различие
требований, предъявляемых к доказательствам в математике, естественных, социально-экономических
и гуманитарных науках, на практике;
Ø роль аксиоматики в
математике; возможность построения математических теорий на аксиоматической
основе; значение аксиоматики для других областей знания и для практики;
Ø вероятностных
характер различных процессов и закономерностей окружающего мира.
уметь:
Ø выполнять
арифметические действия, сочетая устные и письменные приемы, применение
вычислительных устройств; находить значения корня натуральной степени, степени
с рациональным показателем, логарифма, используя при необходимости
вычислительные устройства; пользоваться оценкой и прикидкой при практических
расчетах;
Ø применять понятия,
связанные с делимостью целых чисел, при решении математических задач;
Ø находить корни
многочленов с одной переменной, раскладывать многочлены на множители;
Ø выполнять действия
с комплексными числами, пользоваться геометрической интерпретацией комплексных
чисел, в простейших случаях находить комплексные корни уравнений с
действительными коэффициентами;
Ø проводить
преобразования числовых и буквенных выражений, включающих степени, радикалы,
логарифмы и тригонометрические функции;
Ø использовать
приобретенные знания и умения в практической деятельности и повседневной жизни
для:
практических расчетов по формулам, включая формулы, содержащие степени,
радикалы, логарифмы и тригонометрические функции, используя при необходимости
справочные материалы и простейшие вычислительные устройства;
Ø определять
значение функции по значению аргумента при различных способах задания функции;
Ø строить графики
изученных функций, выполнять преобразования графиков;
Ø описывать по
графику и по формуле поведение и свойства функций;
Ø решать уравнения,
системы уравнений, неравенства, используя свойства функций и их графические
представления;
Ø использовать
приобретенные знания и умения в практической деятельности и повседневной жизни
для:
описания и исследования с помощью функций реальных зависимостей, представления
их графически; интерпретации графиков реальных процессов;
Ø находить сумму
бесконечно убывающей геометрический прогрессии;
Ø вычислять
производные и первообразные элементарных функций, применяя правила вычисления
производных и первообразных, используя справочные материалы;
Ø исследовать
функции и строить их графики с помощью производной;
Ø решать задачи с
применением уравнения касательной к графику функции;
Ø решать задачи на
нахождение наибольшего и наименьшего значения функции на отрезке;
Ø вычислять площадь
криволинейной трапеции;
Ø использовать
приобретенные знания и умения в практической деятельности и повседневной жизни
для:
решения геометрических, физических, экономических и других прикладных задач, в
том числе задач на наибольшие и наименьшие значения с применением аппарата
математического анализа;
Ø решать
рациональные, показательные и логарифмические уравнения и неравенства, иррациональные
и тригонометрические уравнения, их системы;
Ø доказывать
несложные неравенства;
Ø решать текстовые
задачи с помощью составления уравнений, и неравенств, интерпретируя результат с
учетом ограничений условия задачи;
Ø изображать на
координатной плоскости множества решений уравнений и неравенств с двумя
переменными и их систем.
Ø находить
приближенные решения уравнений и их систем, используя графический метод;
Ø решать уравнения,
неравенства и системы с применением графических представлений, свойств функций,
производной;
Ø использовать
приобретенные знания и умения в практической деятельности и повседневной жизни
для:
построения и исследования простейших математических моделей.
Методы и формы работы с учащимися с ОВЗ:
Одно из важнейших условий
эффективности учебного процесса — воспитание познавательного интереса у
школьников. Это касается и обучения детей с ограниченными возможностями
здоровья. Важно формировать у них познавательный интерес, желание и привычку
думать, стремление узнать что-то новое. Математика, являясь одним из важных
общеобразовательных предметов, готовит учащихся с ОВЗ к жизни и овладению
доступными профессионально-трудовыми навыками. Поэтому основными задачами
развития познавательной деятельности учащихся с ОВЗ следующие:
ü формирование
мотивации учения, ориентированной на удовлетворение познавательных интересов;
ü развитие памяти и
внимания;
ü формирование
приёмов умственных действий (анализ, сравнение, обобщение);
ü развитие речи,
умения аргументировать свои высказывания, строить простейшие умозаключения;
ü формирование
учебных навыков и умений (умения обдумывать и планировать свои действия,
проверять результат своих действий).
При организации учебно – воспитательного
процесса используется следующие подходы:
v замедленный темп
обучения;
v предупреждение
умственных и физических перегрузок (структурное упрощение содержания обучения;
v дозировка нагрузок
и смена видов деятельности, например, одним видом деятельности учащиеся могут
заниматься не более 10 – 15 минут;
v соблюдение
охранительного режима, например, смена умственной и двигательной активности);
v использование
разнообразных методов, приемов, форм и средств обучения правильное их
сочетание;
v организация
многократных вариативных повторений и упражнений по применению знаний и умений
в разных учебных и жизненных ситуациях;
v наглядно –
практический характер обучения;
v опора на знания и
жизненный опыт учащихся;
v установление
логических связей в изучаемом материале через внутри предметные и межпредметные
связи.
Практическая направленность курса выражена
в следующих положениях:
v сознательное
усвоение учащимися различных приемов вычислений обеспечивается за счет
использования рационально подобранных средств наглядности и моделирования с их
помощью тех операций, которые лежат в основе рассматриваемого приема;
v рассмотрение
теоретических вопросов курса опирается на практические работы, различные
свойства наглядности, подведение детей на основе собственных наблюдений к
выводам, сразу же находящим применение в учебной практике;
v система
упражнений, направленных на выработку навыков, предусматривает их применение в
разнообразных условиях. Тренировочные упражнения рационально распределены во
времени. Усилено внимание к практическим упражнениям с раздаточным материалом,
к использованию схематических рисунков.
Раздел II. Календарно-тематическое планирование.
11 класс
|
№ |
Распределение занятий |
Количество часов |
Дата проведения |
||
|
Всего |
Теоретические занятия |
Практические занятия |
|||
|
Алгебра |
3 |
0,25 |
2,75 |
||
|
1 |
Проценты. Приближенное значение. |
1 |
0,25 |
0,75 |
|
|
2 |
Решение квадратных уравнений и неравенств. |
1 |
— |
1 |
|
|
3 |
Решение задач. Преобразование выражений, включающих |
1 |
— |
1 |
|
|
Функции |
10 |
2 |
8 |
||
|
4 |
Графические зависимости, отражающие реальные |
1 |
1 |
— |
|
|
5 |
Степенная функция, ее свойства и график. |
1 |
0,25 |
0,75 |
|
|
6 |
Преобразование выражений, содержащих радикал. |
1 |
— |
1 |
|
|
7 |
Показательная функция, ее свойства и график. |
1 |
— |
1 |
|
|
8 |
Решение показательных уравнений и систем уравнений. |
1 |
— |
1 |
|
|
9 |
Решение показательных неравенств. |
1 |
0,25 |
0,75 |
|
|
10 |
Понятие логарифма. Свойства логарифмов. |
1 |
0,25 |
0,75 |
|
|
11 |
Логарифмическая функция. |
1 |
0,25 |
0,75 |
|
|
12 |
Решение логарифмических уравнений и систем |
1 |
— |
1 |
|
|
13 |
Решение логарифмических неравенств. |
1 |
— |
1 |
|
|
Тригонометрия |
4 |
0,25 |
3,75 |
||
|
14 |
Тригонометрические функции, их свойства и график. |
1 |
0,25 |
0,75 |
|
|
15 – 16 |
Решение тригонометрических уравнений. |
2 |
2 |
||
|
17 |
Решение систем уравнений. |
1 |
1 |
||
|
Производная |
3 |
0,25 |
2,75 |
||
|
18 |
Производная. Геометрический и физический смысл |
1 |
0,25 |
0,75 |
|
|
19 |
Исследование функции на монотонность и экстремум. |
1 |
1 |
||
|
20 |
Нахождение наибольшего и наименьшего значений |
1 |
— |
1 |
|
|
Прикладные и текстовые |
2 |
— |
2 |
||
|
21 |
Решение прикладных задач. |
1 |
— |
1 |
|
|
22 |
Решение текстовых задач. |
1 |
1 |
||
|
Планиметрия |
4 |
1 |
3 |
||
|
23 |
Треугольники. |
1 |
0,25 |
0,75 |
|
|
24 |
Четырехугольники. |
1 |
0,25 |
0,75 |
|
|
25 |
Подобие. |
1 |
0,25 |
0,75 |
|
|
26 |
Окружность. |
1 |
0,25 |
0,75 |
|
|
Стереометрия |
4 |
1 |
4 |
||
|
27 |
Прямые в пространстве. |
1 |
0,25 |
0,75 |
|
|
28 |
Многогранники. |
1 |
0,25 |
0,75 |
|
|
29 |
Тела вращения. |
1 |
0,25 |
0,75 |
|
|
30 |
Метод координат. |
1 |
0,25 |
0,75 |
|
|
31 – 34 |
Решение вариантов ЕГЭ |
4 |
— |
4 |
|
|
Итого |
34 |
4,75 |
29,25 |
Раздел III.
Содержание изучаемого курса
Основные
методические особенности курса:
1.
Подготовка по тематическому принципу, соблюдая «правила спирали» от простых
типов заданий до заданий со звездочкой;
2.
Максимальное использование наличного запаса знаний, применяя различные
«хитрости» и «правдоподобные рассуждения», для получения ответа простым и
быстрым способом.
Включенный
в программу материал предполагает повторение и углубление следующих разделов
математики:
¯
Рациональные
уравнения и неравенства
¯
Иррациональные
уравнения и неравенства
¯
Системы
уравнений
¯
Показательные
уравнения и неравенства
¯
Логарифмические
уравнения и неравенства
¯
Тригонометрические
уравнения и неравенства
¯
Производная
¯
Планиметрия
¯
Стереометрия
Раздел IV.
Методическое обеспечение образовательной программы.
Разнообразные
формы внеурочной деятельности помогают взаимопониманию между учащимися, учат их
внимательно слушать друг друга, радоваться удачам товарищей и адекватно
оценивать свою работу.
На
занятиях внеурочной деятельности преобладают следующие формы работы:
ü
решение
задач;
ü
участие
в дистанционных математических олимпиадах, международной игре «Кенгуру»,
ü
знакомство
с научно-популярной литературой, связанной с математикой;
ü
проектная
деятельность;
ü
самостоятельная
работа;
ü
работа
в парах, в группах;
ü
творческие
работы;
ü
подготовка
и проведение мероприятий, позволяющих повысить интерес к математике у учащихся
других классов (параллелей).
Раздел V. Перечень
учебно-методического обеспечения для учителя и для учащихся.
·
Федеральный
перечень учебников, рекомендуемых Министерством образования Российской
Федерации к использованию в общеобразовательном процессе в общеобразовательных
учреждениях на 2020 – 2021 учебный год.
·
Программы
для общеобразовательных учреждений. Алгебра и начала анализа. Составитель: Т.
А. Бурмистрова. Москва, «Просвещение»
·
Б.
Г. Зив. Дидактические материалы. Алгебра и начала анализа. 11 класс.
·
М.
И. Шабунин. Алгебра и начала анализа. Дидактические материалы для 10-11
классов.
·
Ю.М.
Калягин, Ю.В. Сидоров, М.В. Ткачёва, Н.Е. Фёдорова и М.И. Шабунин Изучение алгебры
и начал анализа в 10 – 11 классах. Книга для учителя.
·
Ю.П.
Дудницын, А.В. Семенов. Алгебра и начала анализа 11 класс. Контрольные работы в
новом формате.
·
А.В.
Семенов, А.С. Трепалин, И.В. Ященко. ЕГЭ. Математика. Типовые экзаменационные
варианты. 2020.
·
А.В.
Семенов, А.С. Трепалин, И.В. Ященко. ЕГЭ. Математика. Типовые экзаменационные
варианты. 2021.
·
Ф.Ф.
Лысенко и др. ЕГЭ. Математика. Устные вычисления и быстрый счет.
·
А.В.
Семенов, А.С. Трепалин, И.В. Ященко, П.И. Захаров. Оптимальный банк заданий для
подготовки учащихся. ЕГЭ 2020. Математика.
·
Ф.Ф.
Лысенко и др. ЕГЭ. Математика. Повторение курса в форме ЕГЭ.
·
Н.В.
Шевелева и др. Математика. Алгебра, элементы статистики и теории вероятностей.
·
В.С.
Панферов, И.Н. Сергеев. Отличник ЕГЭ. Математика. Решение сложных задач. ФИПИ.
М.: «Интеллект – Центр».
Для обеспечения плодотворного учебного
процесса предполагается использование информации и материалов следующих Интернет
– ресурсов:
·
Министерство
образования РФ: http://www.ed.gov.ru/
; http://www.edu.ru
·
Тестирование
online: 5 – 11 классы: http://www.kokch.kts.ru/cdo
·
Новые
технологии в образовании: http://edu.secna.ru/main
·
Путеводитель
«В мире науки» для школьников: http://www.uic.ssu.samara.ru
·
Мегаэнциклопедия
Кирилла и Мефодия: http://mega.km.ru
·
сайты
«Энциклопедий»: http://www.rubricon.ru/; http://www.encyclopedia.ru
СОГЛАСОВАНО
Руководитель
ШМО
_________________ Л.Н.
Птичкина
Протокол ШМО № _____ от «___»
_______________ 2020 г.
СОГЛАСОВАНО
Зам. директора по УВР
_________________ Е.М.
Путятина
«___» _____________ 2020
МБОУ «Домашовская средняя общеобразовательная школа»
Программа элективного курса
по математике
11 класс
«Система подготовки к ЕГЭ по математике»
Учитель: Федина Марина Вячеславовна
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
На современном этапе развития общества образование призвано обеспечить формирование у учащихся потребности в активном познании окружающего мира; приобретение навыков самоорганизации, обеспечивающих высокую эффективность всех видов учебной и внеурочной деятельности.
Основная задача обучения математике в школе – обеспечить прочное и сознательное овладение учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому члену общества, достаточных для изучения смежных дисциплин и продолжения образования.
Факультативные занятия развивают интерес и склонности учащихся к математике, повышают математическую культуру ученика в рамках школьного курса математики, помогают им систематизировать свои знания при подготовке к поступлению в высшие учебные заведения, в том числе и самого престижного уровня.
Наряду с решением основной задачи изучения математики программа факультатива предусматривает формирование у учащихся устойчивого интереса к предмету, выявление и развитие их математических способностей, ориентацию на профессии, существенным образом связанные с математикой, подготовку к обучению в вузе.
Структура экзаменационной работы требует от учащихся не только знаний на базовом уровне, но и умений выполнять задания повышенной и высокой сложности. В рамках урока не всегда возможно рассмотреть подобные задания, поэтому программа факультатива позволяет решить эту задачу.
Преподавание факультатива строится как углубленное изучение вопросов, предусмотренных программой основного курса. Углубление реализуется на базе обучения методам и приемам решения математических задач, требующих применения высокой логической и операционной культуры, развивающих научно-теоретическое и алгоритмическое мышление учащихся. Тематика задач не выходит за рамки основного курса, но уровень их трудности – повышенный, существенно превышающий обязательный. Особое место занимают задачи, требующие применения учащимися знаний в незнакомой (нестандартной) ситуации.
Литература:
1. Контрольно – измерительные материалы. Алгебра и начала анализа. 11 класс./ Сост. А. Н. Рурукин. – 3-е изд., перераб. – М.: ВАКО, 2013.
2. ЕГЭ 2015. Математика: сборник заданий / В. В. Кочагин, М. Н. Кочагина. – М.: Эксмо, 2014.
3. ЕГЭ-2015: Математика: самое полное издание типовых вариантов заданий для подготовки к ЕГЭ / авт.-сост. И. В. Ященко, И. Р. Высоцкий; под ред. А. Л. Семенова, И. В. Ященко. – Москва: АСТ: Астрель, 2014.
4. ЕГЭ 2015. Математика. Экзаменационные тесты. Базовый уровень. Практикум по выполнению типовых тестовых заданий ЕГЭ / Л. Д. Лаппо, М. А. Попов. – М.: Издательство «Экзамен», 2015.
5. ЕГЭ 2015. Математика. Экзаменационные тесты. Профильный уровень. Практикум по выполнению типовых тестовых заданий ЕГЭ / Л. Д. Лаппо, М. А. Попов. – М.: Издательство «Экзамен», 2015.
Количество часов: всего 68 часов; в неделю 2 час.
Цели:
-
формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов;
-
овладение устным и письменным математическим языком, математическими знаниями и умениями, необходимыми для изучения школьных естественно-научных дисциплин, для продолжения образования в средних учебных заведениях;
-
развитие логического мышления, алгоритмической культуры, развитие математического мышления и интуиции;
-
воспитание средствами математики культуры личности: знакомство с историей математики, эволюцией математики, эволюции математических идей, понимание математики для общественного прогресса.
Задачи:
-
Изучить оригинальные приемы решения тестовых задач
-
Приобрести исследовательские компетенции в решении математических задач
-
Повысить интерес к предмету
-
Приобщить детей к общечеловеческим ценностям
-
Обеспечить эмоциональное благополучие ребенка.
В результате изучения данного курса учащиеся
должны знать:
-
Методы решения различных видов уравнений и неравенств;
-
Основные приемы решения текстовых задач;
-
Элементарные методы исследования функции;
должны уметь:
-
проводить тождественные преобразования иррациональных, показательных, логарифмических и тригонометрических выражений.
-
решать иррациональные, логарифмические и тригонометрические уравнения и неравенства.
-
решать системы уравнений изученными методами.
-
строить графики элементарных функций и проводить преобразования графиков, используя изученные методы.
-
применять аппарат математического анализа к решению задач.
-
применять основные методы геометрии (проектирования, преобразований, векторный, координатный) к решению геометрических задач
-
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для построения и исследования простейших математических моделей..
Для реализации программы факультатива используются лекции, семинары, практикумы по решению задач.
КАЛЕНДАРНО – ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
|
№ п/п |
№ ур. |
Примерная кален. дата |
Фактическая кален. дата |
Название темы урока |
Кол-во часов |
|
1 |
1 |
Преобразование числовых и алгебраических выражений |
1 |
||
|
2-3 |
2-3 |
Преобразование показательных и дробно – иррациональных выражений |
2 |
||
|
4-5 |
4-5 |
Преобразование тригонометрических выражений |
2 |
||
|
6-7 |
6-7 |
Преобразование логарифмических выражений |
2 |
||
|
8 |
8 |
Решение уравнений, общие положения, замена неизвестного, приемы решения уравнений |
1 |
||
|
9 |
9 |
Алгебраические уравнения |
1 |
||
|
10-11 |
10-11 |
Иррациональные уравнения |
2 |
||
|
12-13 |
12-13 |
Показательные и логарифмические уравнения |
2 |
||
|
14-15 |
14-15 |
Уравнения с модулем |
2 |
||
|
16-17 |
16-17 |
Тригонометрические уравнения |
2 |
||
|
18-19 |
18-19 |
Уравнения с параметром |
2 |
||
|
20 |
20 |
Алгебраические неравенства |
1 |
||
|
21-22 |
21-22 |
Неравенства с модулем |
2 |
||
|
23 |
23 |
Тригонометрические неравенства |
1 |
||
|
24 |
24 |
Иррациональные неравенства |
1 |
||
|
25 |
25 |
Показательные и логарифмические неравенства |
1 |
||
|
26-27 |
26-27 |
Неравенства с параметром |
2 |
||
|
28-29 |
28-29 |
Уравнения и неравенства смешанного типа |
2 |
||
|
30-31 |
30-31 |
Метод интервалов |
2 |
||
|
32-33 |
32-33 |
Системы уравнений |
2 |
||
|
34 |
34 |
Графики элементарных функций |
1 |
||
|
35 |
35 |
Область допустимых значений и множество значений функции |
1 |
||
|
36 |
36 |
Периодичность, возрастание (убывание), экстремумы функции |
1 |
||
|
37-38 |
37-38 |
Наибольшее (наименьшее) значение функции |
2 |
||
|
39-40 |
39-40 |
Ограниченность, сохранение знака функции |
2 |
||
|
41-42 |
41-42 |
Связь между свойствами функции и её графиком |
2 |
||
|
43 |
43 |
Правила дифференцирования |
1 |
||
|
44-45 |
44-45 |
Вычисление производных |
2 |
||
|
46-47 |
46-47 |
Производная сложной функции |
2 |
||
|
48-49 |
48-49 |
Применение производной для исследования функции и построения её графика |
2 |
||
|
50 |
50 |
Вторая производная, ее механический смысл; применение производной к исследованию функций |
1 |
||
|
51-52 |
51-52 |
Вычисление площадей с помощью интеграла; использование интеграла в физических задачах |
2 |
||
|
53-54 |
53-54 |
Решение задач планиметрии |
2 |
||
|
55 |
55 |
Расстояние от точки до прямой; от точки до плоскости |
1 |
||
|
56-57 |
56-57 |
Расстояние между прямыми; между прямой и плоскостью; между плоскостями |
2 |
||
|
58-59 |
58-59 |
Сечение многогранников |
2 |
||
|
60-61 |
60-61 |
Тела и поверхности вращения |
2 |
||
|
62-63 |
62-63 |
Методы решения геометрических задач |
2 |
||
|
64 |
64 |
Задачи на части и проценты |
1 |
||
|
65-66 |
65-66 |
Задачи на движение |
2 |
||
|
67-68 |
67-68 |
Задачи с параметрами |
2 |
28.02.2020
Рабочая программа учебного курса по математике для 11 класса по внеурочной деятельности составлена в соответствии с требованиями освоения основной образовательной программы среднего общего образования на основе программы общеобразовательных учреждений по алгебре и началам математического анализа 11 класс (авторы С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин, составитель Т.А. Бурмистрова – М: «Просвещение», 2010 г.), программы общеобразовательных учреждений по геометрии 11 класс (авторы Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, составитель Т.А. Бурмистрова — М.: Просвещение, 2010 г.
На изучение курса отводится 34 часа из расчета 1 ч в неделю. Может быть использована для подготовки учащихся к ЕГЭ по математике.
Оценить
677
Содержимое разработки
1. Пояснительная записка
Рабочая программа учебного курса внеурочной деятельности по математике для 11 класса составлена в соответствии с требованиями освоения основной образовательной программы среднего общего образования на основе следующих нормативных документов:
1. Федеральный закон «Об образовании в Российской Федерации» № 273-ФЗ от 29.12.2012 ( с изменениями)
2. Федеральный государственный образовательный стандарт среднего общего образования, утвержденный Приказом Минобрнауки РФ от 17.05.2012 г. №413 (с изменениями)
3. СанПиН 2.4.2.2821-10 “Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных организациях”, утвержденный Постановлением Главного государственного санитарного врача РФ от 29.12.2010 №189 (с изменениями)
4. Федеральный перечень учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях, реализующих программы начального общего, основного общего, среднего общего образования, утвержденный Приказом Министерства образования и науки РФ от 28.12.2018 г. №345 (с изменениями от 08.05.2019 №233)
5. Письмо Министерства образования и науки Ульяновской области «Об организации 2019/20 учебного года» 73иогв01/4410 исх. от 19.07.2019
6. Устав ОО
7. Основная образовательная программа среднего общего образования
8. Программы общеобразовательных учреждений по алгебре и началам математического анализа 11 класс (авторы С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин, составитель Т.А. Бурмистрова – М: «Просвещение», 2010 г.);
9. Программы общеобразовательных учреждений по геометрии 11 класс (авторы Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, составитель Т.А. Бурмистрова — М.: Просвещение, 2010 г.
Для изучения курса математики на внеурочных занятиях отводится 34 часа из расчета 1 ч в неделю.
Личностные, метапредметные, предметные результаты освоения предмета
К важнейшим результатам обучения математике в 11 классе по данному УМК относятся следующие:
в направлении личностного развития
развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
развитие интереса к математическому творчеству и математических способностей;
в метапредметном направлении
формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;
в предметном направлении
владение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни;
создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности
Содержание тем курса математики
Раздел 1. Выражения и преобразования. (2 ч)
Практика: Свойства степеней и корней, логарифмов. Формулы для преобразования тригонометрических выражений.
Тест.
Раздел 2. Функциональные линии (2 ч)
Теория: Возрастание, убывание, экстремум функции. График функции. Производная функции.
Практика: Возрастание, убывание, экстремум функции. График функции. Производная функции.
Самостоятельная работа.
Раздел 3. Текстовые задачи (3 ч)
Практика: Решение задач на проценты. Решение задач на концентрацию. Решение задач на движение. Решение задач на работу. Решение задач геометрического содержания.
Самостоятельная работа.
Раздел 4. Уравнения и неравенства. Системы уравнений (4ч)
Теория: Тригонометрические уравнения и неравенства Показательные уравнения и неравенства. Логарифмические уравнения и неравенства.
Практика: Линейные и квадратные уравнения. Дробно-рациональные уравнения. Тригонометрические уравнения и неравенства Показательные уравнения и неравенства. Логарифмические уравнения и неравенства. Метод интервалов.
Самостоятельная работа.
Раздел 5. Приемы решения нестандартных уравнений. (3 ч)
Теория: Способы решения нестандартных уравнений: графический, с использованием свойств функций, нахождением производной. Уравнения в целых числах и пути их решения.
Практика: Способы решения нестандартных уравнений: графический, с использованием свойств функций, нахождением производной. Уравнения в целых числах и пути их решения.
Самостоятельная работа.
Раздел 6. Различные способы решения уравнений и неравенств с параметром (3 ч)
Теория: Параметр, его суть в различных случаях. Аналитический и графический способы решения задач с параметром.
Практика: Параметр, его суть в различных случаях. Аналитический и графический способы решения задач с параметром.
Диагностическая работа.
Раздел 7. Планиметрия: нахождение отрезков и углов (3 ч)
Практика: Соотношения между сторонами и углами треугольника. Теорема Пифагора. Тригонометрические функции острого угла прямоугольного треугольника. Сумма углов выпуклого многоугольника. Вписанные и центральные углы.
Тест.
Раздел 8. Планиметрия: нахождение площадей (2ч)
Теория: Формулы площадей известных планиметрических фигур.
Практика: Формулы площадей известных планиметрических фигур.
Решение задач . Тест.
Раздел 9. Планиметрия: многоконфигурационные задачи (4 ч)
Теория: Теорема Менелая.
Практика: Соотношения между сторонами и углами треугольника. Теорема Пифагора. Тригонометрические функции острого угла прямоугольного треугольника. Сумма углов выпуклого многоугольника. Вписанные и центральные углы.
Теоремы о пропорциональных отрезках в круге. Свойство биссектрисы треугольника. Теорема Менелая.
Самостоятельная работа.
Раздел 10. Стереометрия: нахождение отрезков и углов (3 ч)
Практика: Параллельность и перпендикулярность в пространстве. Теорема о трех перпендикулярах. Скрещивающиеся прямые. Линейный угол двугранного угла. Координатный метод нахождения различных отрезков и углов.
Самостоятельная работа.
Раздел 11. Стереометрия: нахождение площадей поверхностей и объемов (4 ч)
Практика: Формулы нахождения площадей поверхностей и объемов известных многогранников и тел вращения.
Диагностическая работа.
Итоговый зачет (1 ч)
Устная работа.
Тематическое планирование
|
Дата |
№ занятий |
Кол-во часов |
Тема занятия |
|
|
по плану |
факт |
|||
|
2 |
Выражения и преобразования. |
|||
|
1 |
Свойства степеней и корней, логарифмов. |
|||
|
2 |
Формулы для преобразования тригонометрических выражений. |
|||
|
2 |
Функциональные линии |
|||
|
3 |
Возрастание, убывание, экстремум функции. График функции |
|||
|
4 |
Производная функции. |
|||
|
3 |
Текстовые задачи |
|||
|
5 |
Решение задач на проценты. |
|||
|
6 |
Решение задач на концентрацию. |
|||
|
7 |
Решение задач на движение. |
|||
|
4 |
Уравнения и неравенства. Системы уравнений |
|||
|
8 |
Линейные и квадратные уравнения. Дробно- рациональные уравнения. |
|||
|
Дробно-рациональные уравнения |
||||
|
9 |
Тригонометрические уравнения и неравенства |
|||
|
10 |
Показательные уравнения и неравенства |
|||
|
11 |
Логарифмические уравнения и неравенства. Метод интервалов. |
|||
|
3 |
Приемы решения нестандартных уравнений. |
|||
|
12 |
Способы решения нестандартных уравнений: графический, с использованием свойств функций, нахождением производной. |
|||
|
13 |
Способы решения нестандартных уравнений: графический, с использованием свойств функций, нахождением производной. |
|
14 |
Уравнения в целых числах и пути их решения. |
|||
|
3 |
Различные способы решения уравнений и неравенств с параметром |
|||
|
15 |
Параметр, его суть в различных случаях. |
|||
|
16 |
Аналитический и графический способы решения задач с параметром |
|||
|
17 |
Аналитический и графический способы решения задач с параметром |
|||
|
3 |
Планиметрия: нахождение отрезков и углов |
|||
|
18 |
Соотношения между сторонами и углами треугольника. Теорема Пифагора |
|||
|
19 |
Тригонометрические функции острого угла прямоугольного треугольника |
|||
|
20 |
Сумма углов выпуклого многоугольника. Вписанные и центральные углы. |
|||
|
3 |
Планиметрия: нахождение площадей |
|||
|
21 |
Формулы площадей известных планиметрических фигур. |
|||
|
22 |
Формулы площадей известных планиметрических фигур. |
|||
|
4 |
Планиметрия: многоконфигурационные задачи |
|||
|
23 |
Теоремы о пропорциональных отрезках в круге. |
|||
|
24 |
Свойство биссектрисы треугольника. |
|||
|
25 |
Теорема Менелая |
|||
|
26 |
Теорема Менелая |
|||
|
3 |
Стереометрия: нахождение отрезков и углов |
|||
|
27 |
Параллельность и перпендикулярность в пространстве |
|||
|
28 |
Теорема о трех перпендикулярах. Скрещивающиеся прямые. |
|||
|
29 |
Координатный метод нахождения различных отрезков и углов |
|||
|
4 |
Стереометрия: нахождение площадей поверхностей и объемов |
|||
|
30 |
Формулы нахождения площадей поверхностей и объемов известных многогранников и тел вращения |
|||
|
31 |
Формулы нахождения площадей поверхностей и объемов известных многогранников и тел вращения |
|||
|
32 |
Формулы нахождения площадей поверхностей и объемов известных многогранников и тел вращения |
|||
|
33 |
Формулы нахождения площадей поверхностей и объемов известных многогранников и тел вращения |
|||
|
34 |
1 |
Итоговый зачет |
||
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/379589-izbrannye-voprosy-matematiki-v-11-klasse-vneu

«Свидетельство участника экспертной комиссии»
Оставляйте комментарии к работам коллег и получите документ
БЕСПЛАТНО!



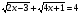
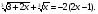
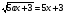 имеет только одно решение.
имеет только одно решение.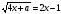 имеет только одно решение.
имеет только одно решение.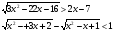
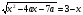 не имеет решений.
не имеет решений.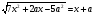 имеет только два решение.
имеет только два решение.