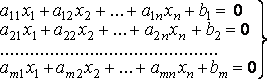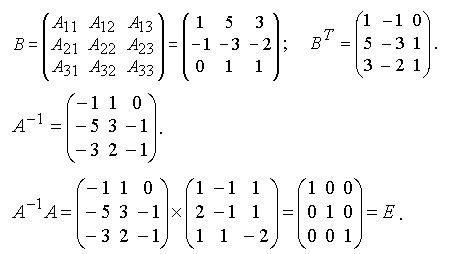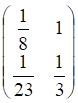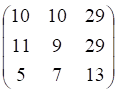Вопросы экзамен матрицы

---

Подборка по базе: ОБЖТестовые вопросы к разделу 1_ просмотр попытки.pdf, englishТестовые вопросы к разделу 7_ просмотр попытки.pdf, Сборник вопросов Газоспасатели с литературой. С выделениями.(1)., Контрольная работа _Разделительные вопросы_ (1).doc, Самые популярные вопросы о Чичикове из поэмы.docx, Примерные вопросы к дифференцированному зачету_Психология общени, Тестовые вопросы к разделу 5_ просмотр попытки.pdf, Тестовые вопросы к разделу 8_ просмотр попытки.pdf, 13 вопросов.docx, Организация на рынке труда 42 вопроса — 1. Рынок труда представл

---

Вопрос №1

Матрицы и многомерные векторы. Матрицей называется прямоугольная таблица чисел, содержащая n строк и m столбцов.

Виды матриц.

Две матрицы называются равными, если их соответствующие элементы равны.

Если в матрице число строк равно числу столбцов (n=m), то матрица называется квадратной.

Матрица, у которой все элементы, стоящие вне главной диагонали равны 0, называется диагональной.

Диагональная матрица, у которой все диагональные элементы равны 1, называется единичной.

Матрица, состоящая из одних нулей, называется нулевой.

Если в квадратной матрице все элементы стоящие ниже (выше) главной диагонали равны 0, то она называется верхний (нижний) треугольник.

Если в матрице А строки записать столбцами с теми же номерами, то полученная матрица будет называться транспонированной к матрице А.

Если матрица А равна транспонированной, то она называется симметричной.

Действия над матрицами:

1) Умножение матрицы на число. В результате умножения матрицы на число получается матрица такой же размерности, что и исходная, каждый элемент которой является результатом произведения соответствующего элемента исходной матрицы на число. Мы получим одинаковый результат, умножая число на матрицу, или матрицу на число. Из определения следует, что общий множитель всех элементов матрицы можно выносить за знак матрицы.

2) Сложение и вычитание матриц. Складывать и вычитать можно только матрицы одинаковой размерности. Суммой (разностью) двух матриц называется матрица той же размерности, что и исходные, каждый элемент которой определяется как сумма (разность) соответствующих элементов матриц. Очевидно, результат сложения не изменится, если слагаемые матрицы поменять местами. Если к матрице прибавить или от нее отнять нулевую матрицу той же размерности, то получим исходную матрицу.

3) Умножение матрицы на матрицу. Умножать друг на друга можно только те матрицы, для которых число столбцов первого сомножителя равно числу строк второго сомножителя. Результатом умножения является матрица, у которой число строк равно числу строк первого сомножителя, а число столбцов совпадает с числом столбцов второго сомножителя. Иными словами, перемножать можно те матрицы, у которых совпадают средние индексы. Крайние индексы определяют размерность получаемого результата.

Свойства операций над матрицами.

1) В общем случае . Если то матрицы А и В называются перестановочными по отношению друг к другу.

2) Ассоциативность;

3) Дисрибутивность;

4) При умножении любой квадратной матрицы на единичную первоначальная матрица не меняется .
Вопрос №3

Перестановки. Расположение n элементов набора в произвольном порядке называется перестановка. Транспозицией называется перестановка двух каких либо элементов. Инверсией в перестановке называется наличие пары чисел, в которое большее число предшествует меньшему. Если число инверсий в перестановке честное, то она называется четной и наоборот.

Определитель произвольного порядка. Определителем квадратной матрицы n-го порядка, называется число равное алгебраической сумме n факториал слагаемых, каждый из которых является произведением n элементов матрицы взятых по одному из каждой строки и столбца, при этом каждое слагаемое умножается на (-1) в степени число инверсий в перестановке j если первые индексы взяты в порядке нарастания.

Вопрос №2

Определители 2-го и 3-го порядка и их свойства. Если квадратная матрица имеет определитель, отличный от нуля (Δ ≠ 0), то говорят, что матрица невырожденная, в противном случае — матрица вырожденная или особая.

Определителем квадратной матрицы 2-го порядка, называется число равное разности произведений элементов главной и побочной диагонали матрицы.

О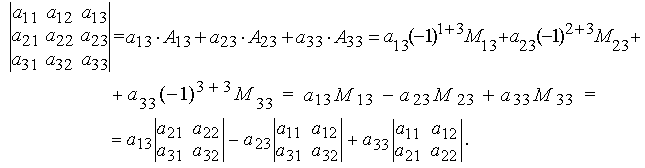пределителем квадратной матрицы 3-го порядка, называется число равное:

Таким образом, вычисление определителя третьего порядка сводится к вычислению определителей второго порядка.

Свойства определителей:

1) Если строка (столбец) матрицы состоит из 0, то ее определитель равен 0.

2) Если все элементы, какой либо строки (столбца) матрицы умножить на одно и тоже число, то и ее определитель умножится на это же число.

3) При транспонировании матрицы ее определитель не меняется.

4) При перестановки, каких либо двух строк (столбцов) матрицы знак матрицы меняется на противоположный. Доказательство вытекает из того, что при перестановке одной транспозиции четность инверсии меняется.

5) Если квадратная матрица содержит две одинаковые строки (столбца), то её определитель равен 0.

6) Сумма произведений элементов, какой либо строки (столбца) на алгебраические дополнения какой либо строки (столбца) равно 0.

7) Если элементы, какой либо строки (столбца) равны сумме двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы) кроме указанных, те же что и в исходном определителе, а рассматриваемая k-строка (столбец) в первом определителе содержит первые слагаемые, во втором вторые.

Определитель матрицы не изменится если к элементам какой либо строки (столбца) прибавить элемент какой либо строки (столбца) предварительно умноженные на одно и то же число.
Вопрос №4

Миноры и алгебраические дополнения. Минором элемента a_ij квадратной матрицы |A| n-ного порядка, называется определителем матрицы, полученной из матрицы |A| вычеркиванием i-той строки j-того столбца.

Алгебраическим дополнением A_ij элемента a_ij квадратной матрицы |A|, называется минор этого элемента, умноженный на (-1) в степени.

Вычисление определителей произвольного порядка (теорема Лапласа). Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения: (разложение по элементам i-й строки); (разложение по элементам j-го столбца).

Вопрос №5

Ранг матрицы, его нахождение. Рангом матрицы А (обозначается r(A)) называется наибольший порядок минора этой матрицы, отличного от нуля. Если все элементы матрицы равны нулю, то ранг такой матрицы принимают равным нулю.

Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы.

Ранг матрицы не изменится от следующих преобразований, называемых элементарными преобразованиями матрицы:

— замены строк столбцами, а столбцов соответствующими строками;

— перестановки строк матрицы;

— вычеркивания строки, все элементы которой равны нулю;

— умножения строки на число, отличное от нуля;

— прибавления к элементам строки соответствующих элементов другой строки, умноженной на одно и то же число.

Подчеркнем, что сама матрица при элементарных преобразованиях меняется, но ранг матрицы не изменится.

Пример. Определить ранг матрицы . Решение. Все миноры второго и третьего порядков данной матрицы равны нулю, т.к. элементы строк этих миноров пропорциональны. Миноры первого порядка (сами элементы матрицы) отличны от нуля. Следовательно, ранг матрицы равен единице.
Вопрос №6

Системы линейных уравнений. Уравнение называется линейным, если оно содержит неизвестные в первой степени и не содержит их произведений.

Запись в матричной форме.

— система линейных уравнений.

Обозначим, — матрица коэффициентов, — вектор неизвестных,

— вектор свободных членов. A_mn X_n1 + B_m1 = 0 — матричная запись системы уравнений.

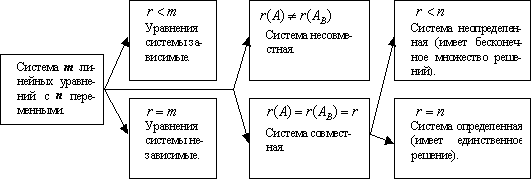
Если система уравнений имеет решение, она называется совместной, не имеет – несовместной. Совместная система, имеющая одно решение, называется определенной, если много – неопределенной. Две системы уравнений называются равносильными или эквивалентными, если каждое решение является решением уравнения системы или наоборот.
Вопрос №8

Решение систем линейных уравнений с помощью определителей (формулы Крамера). Пусть Δ = |A| определитель матричной системы n линейных уравнений с n неизвестных, а Δ_j определитель матрицы, полученный из матричной системы заменой j-того столбца на столбец правых частей. Тогда если Δ ≠ 0, то система имеет единственное решение, определенное по формулам x_j = Δ_j / Δ (j = 1,2,…n) – формула Крамера.

Вопрос №7

Обратная матрица. Матрицей, обратной матрице А, называется матрица A^-1 такая, что A^-1A = A A^-1 = E.

Обратная матрица может существовать только для квадратной матрицы. Причем сама является той же размерности, что и исходная матрица.

Можно показать, что для того, чтобы квадратная матрица имела обратную, она должна быть невырожденной (т.е. Δ ≠ 0 ). Это условие является и достаточным для существования A^-1 матрице А. Итак, всякая невырожденная матрица имеет обратную, и, притом, единственную.

Сформулируем правило нахождения обратной матрицы на примере матрицы А.

1. Находим определитель матрицы. Если Δ ≠ 0, то матрица A^-1 существует.

2. Составим матрицу В алгебраических дополнений элементов исходной матрицы А. Т.е. в матрице В элементом i — ой строки и j — го столбца будет алгебраическое дополнение A_ij элемента a_ij исходной матрицы.

3. Транспонируем матрицу В и получим B^T.

Теорема существования и единственности обратной матрицы. Для квадратной матрицы А существует и при том единственная обратная матрица А^-1 тогда и только тогда, когда эта матрица не вырождена.

Решение систем линейных уравнений с помощью обратной матрицы. Матричным методом могут быть решены только те системы, у которых число уравнений совпадает с числом неизвестных и определитель матрицы коэффициентов отличен от нуля (матрица А невырожденная). Из этих условий следует, что и, следовательно, система совместна и определена. Решение системы можно получить так: . Используя свойства произведения матриц и свойство обратной матрицы . Т.е., для получения столбца неизвестных нужно обратную матрицу матрицы коэффициентов системы умножить на столбец свободных членов.

Пример. Решить систему матричным методом. Решение. Найдем обратную матрицу для матрицы коэффициентов системы .

Вычислим определитель, раскладывая по первой строке: . Поскольку Δ ≠ 0, то A^-1 существует.

Обратная матрица найдена верно.

Найдем решение системы .

Следовательно, x₁ = 1, x₂ = 2, x₃ = 3.

Матричный метод годится для решения любых систем, у которых матрица А квадратная и невырожденная.
Вопрос №10

Теорема Кронекера-Капелли. Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы. RgA = RgA*.

Доказательство.

1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А* не изменяют ранга.

2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.

Исследование системы линейных уравнений.

Вопрос №9

Решение и исследование систем линейных уравнений методом Гаусса. Этот метод решения систем линейных уравнений пригоден для решения систем с любым числом уравнений и неизвестных.

Суть метода Гаусса заключается в преобразовании заданной системы уравнений с помощью элементарных преобразований в эквивалентную систему ступенчатого треугольного вида.

Полученная система содержит все неизвестные в первом уравнении. Во втором уравнении отсутствует первое неизвестное, в третьем уравнении отсутствуют первое и второе неизвестные и т. д.

Если система совместна и определена (единственное решение), то последнее уравнение содержит одно неизвестное. Найдя последнее неизвестное, из предыдущего уравнения находим еще одно — предпоследнее. Подставляя полученные величины неизвестных, мы последовательно найдем решение системы.

Элементарными преобразованиями системы линейных уравнений, используемыми для приведения системы к треугольному виду, являются следующие преобразования:

— перестановка местами двух уравнений;

— умножение обеих частей одного из уравнений на любое число, отличное от нуля;

— прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число.

Элементарные преобразования переводят данную систему линейных алгебраических уравнений в эквивалентную систему.

Две системы называются эквивалентными, если всякое решение первой системы является решением другой системы и наоборот.
Вопрос №11

Базис и размерность пространства решений однородной системы линейных уравнений. Базисом линейного пространства L называется такая конечная упорядоченная линейно независимая система векторов, что любой вектор пространства L является линейной комбинацией этих векторов. В отличие от трехмерного пространства векторов, в некоторых линейных пространствах базис не существует.

В линейном пространстве любые два базиса содержат одинаковое число векторов.

Линейное пространство L, в котором существует базис, состоящий из n векторов, называется — n мерным линейным или векторным пространством. Число n называется размерностью пространства и обозначается dimL. Линейное пространство, в котором не существует базис, называется бесконечномерным.

Общее решение неоднородной системы линейных уравнений. Систему неоднородных уравнений запишем в матричном виде Ax = b, где матрица A имеет размеры mxn.

[T] Система линейных уравнений Ax = b может иметь либо бесконечно много решений, либо одно решение, либо не иметь решений.

[D] Пусть система имеет решение x⁽⁰⁾ . Если однородная система Ax = 0 имеет только одно решение, то из формулы общего решения будет следовать, что x⁽⁰⁾ — единственное решение неоднородной системы. Если однородная система имеет хотя бы одно ненулевое решение, то ее фундаментальная система решений будет состоять не менее, чем из одного решения. В формуле общего решения неоднородной системы будет произвольный коэффициент С1 , и при различных его значениях мы будем получать различные решения неоднородной системы.

Вопрос №12

Векторы на плоскости и в пространстве. Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевой вектор, начало и конец которого совпадают.

Ортом вектора а называется вектор а⁰, который имеет единичную длину и то же направление, что и вектор а.

Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными.

Векторы, лежащие в одной плоскости или параллельные одной плоскости, называются компланарными.

Два вектора считаются равными, если они коллинеарные, одинаково направлены и равны по длине.

Пусть даны два вектора. Параллельным переносом приведем их к общему началу. Наименьший угол, на который надо повернуть один вектор до совпадения с другим, называется углом между векторами.

1) Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.

2) Базисом на плоскости называются любые 2 неколлинеарные векторы, взятые в определенном порядке.

3) Базисом на прямой называется любой ненулевой вектор.

Три вектора, a,b,c, называются линейно-независимыми, если они не лежат в одной плоскости.

Базисом в трехмерном пространстве R³ называется упорядоченная тройка любых линейно-независимых векторов.

Вопросы по курсу «Линейная
алгебра» 1 курс 1 семестр

1. Матрицы,
   определение, виды матриц

2. Операции
   над матрицами, свойства операций

3. Определители
   второго и третьего порядка. Способы
   вычисления.

4. Свойства
   определителей.

5. Обратная
   матрица. Существование, единственность.
   Нахождение обратной матрицы.

6. Ранг
   матрицы. Вычисление ранга различными
   способами

7. Системы
   линейных уравнений. Матричная запись
   системы.

8. Применение
   обратной матрицы к решению линейных
   систем.

9. Метод
   Крамера решения линейных систем.

10. Решение
    систем линейных уравнений методом
    Гаусса.

11. Теорема
    Кронекера–Капелли. Решение неопределенных
    систем линейных уравнений.

12. Решение
    систем линейных уравнений методом
    Жордана-Гаусса.

13. Математическая
    модель Леонтьева межотраслевого
    баланса.

14. Однородные
    системы линейных уравнений. Структура
    общего решения ЛОС

15. Фундаментальная
    система решений.

16. Векторы.
    Основные операции над векторами.

17. Скалярное
    произведение 2-х векторов и его свойства.

18. Векторное
    произведение векторов и его свойства.

19. Смешанное
    произведение векторов и его свойства

20. Простейшие
    задачи на плоскости.

21. Различные
    уравнения прямой.

22. Угол
    между прямыми. Условия перпендикулярности
    и параллельности прямых.

23. Общее
    уравнение кривой. Кривые второго
    порядка.

24. Эллипс.

25. Гипербола.

26. Парабола.

27. Уравнение
    плоскости.

28. Угол
    между плоскостями. Условия параллельности
    и перпендикулярности плоскостей

29. Уравнения
    прямой в пространстве.

30. Угол
    между прямыми. Условия параллельности
    и перпендикулярности прямых.

31. Угол
    между прямой и плоскостью. Условия
    параллельности и перпендикулярности
    прямой и плоскости

32. n
    –мерное векторное линейное пространство.
    Аксиомы. Примеры.

33. Линейно
    зависимые и линейно независимые системы
    векторов.

34. Базис
    линейного пространства. Разложение
    вектора по произвольному базису.

35. Линейные
    преобразования. Изменение матрицы
    линейного преобразования при изменении
    базиса.

36. Линейные
    операторы. Основные понятия. Действия
    над линейными операторами.

37. Собственные
    значение и собственные векторы матрицы.

38. Линейная
    модель торговли.

39. Квадратичные
    формы. Приведение квадратичной формы
    к каноническому виду

40. Канонический
    вид квадратичной формы. Метод Лагранжа.
    метод собственных векторов

41. Определение
    положительной и отрицательной
    квадратичной формы.

42. Понятие
    комплексного числа. Геометрическая
    интерпретация комплексного числа.

43. Алгебраическая
    и тригонометрическая форма записи
    комплексного числа.

44. Основные
    свойства комплексных чисел.

45. Возведение
    в степень извлечение из степени
    комплексного числа.

1. Матрицы, определение,
виды матриц

Матрица –
это таблица из m строк и n столбцов.
Произведение m×n называют размером
матрицы.

Виды:

• Квадратной
  матрицей называется матрица, у которой
  количество строк равно количеству
  столбцов (размера n×n), число n называется
  порядком матрицы.

• Нулевой
  матрицей называется матрица, все
  элементы которой равны нулю.

• Вектор-строкой
  называется матрица, состоящая из одной
  строки.

• Вектор-столбцом
  называется матрица, состоящая из одного
  столбца.

• Диагональной
  матрицей называется квадратная матрица,
  все элементы которой, стоящие вне
  главной диагонали, равны нулю.

• Единичной
  матрицей (E) называется
  диагональная матрица, диагональные
  элементы которой равны 1

• Верхней
  треугольной матрицей называется
  матрица, все элементы которой ниже
  главной диагонали равны нулю.

• Нижней
  треугольной матрицей называется
  матрица, все элементы которой выше
  главной диагонали равны нулю.

• Ступенчатой
  матрицей называется матрица,
  удовлетворяющая следующим условиям:

  • если
    матрица содержит нулевую строку, то
    все строки, расположенные под нею,
    также нулевые;

  • если
    первый ненулевой элемент некоторой
    строки расположен в столбце с номером
    i, и следующая строка не нулевая, то
    первый ненулевой элемент следующей
    строки должен находиться в столбце с
    номером большим, чем i.

2. Операции над матрицами,
свойства операций

Операции
над матрицами:

1. Сложение
   матриц.

2. Вычитание
   матриц.

3. Умножение
   матрицы на число.

4. Умножение
   матриц.

5. Транспонирование.

6. Элементарные
   преобразования:

• перестановка
  любых двух строк матрицы;

• умножение
  любой строки на произвольное, отличное
  от нуля, число;

• сложение
  любой строки с другой строкой ,
  умноженной на произвольное число;

Свойства
операции сложения.

1. Сочетательный:
   для матриц А, В и С одного порядка
   характерно свойство ассоциативности
   сложения А+(В+С)=(А+В)+С.

2. Для
   матриц данного порядка существует
   нейтральный элемент по сложению,
   которым является нулевая матрица. То
   есть, справедливо свойство А+О=А.

3. Для
   ненулевой матрицы А данного порядка
   существует матрица (–А), их суммой
   является нулевая матрица: А+(-А)=О.

4. Для
   матриц А и В данного порядка справедливо
   свойство коммутативности сложения
   А+В=В+А.

Свойства
операции умножения матрицы на число.

1. Для
   матриц одного порядка А и В,
   а также произвольного действительного
   (или комплексного) числа  справедливо
   свойство дистрибутивности умножения
   относительно сложения .

2. Для
   произвольной матрицы А и
   любых действительных (или комплексных)
   чисел и  справедливо
   свойство ассоциативности умножения .

3. Нейтральным
   числом по умножению на произвольную
   матрицу А является единица,
   то есть, .

4. 0 * A
   = 0

Свойства операции умножения
матриц.

1. Свойство ассоциативности
   умножения матриц .

2. Два свойства дистрибутивности 
   .

3. В общем случае операция
   умножения матриц некоммутативна .

4. Для произвольной
   матрицы А порядка p на n справедливо
   равенство ,
   а для произвольной матрицы А порядка n на p —
   равенство .

3. Определители второго и
третьего порядка. Способы вычисления.

Вычисление
определителя второго порядка.

Чтобы
вычислить определитель матрицы  второго
порядка, надо от произведения элементов
главной диагонали отнять
произведение элементов побочной
диагонали:

Вычисление
определителя третьего порядка.

1. Правило
   треугольника

Схематически это правило можно изобразить
следующим образом:

Произведение элементов в первом
определителе, которые соединены прямыми,
берется со знаком «плюс»; аналогично,
для второго определителя — соответствующие
произведения берутся со знаком «минус»,
т.е.

1. Правило
   Саррюса

Справа от определителя дописывают
первых два столбца и произведения
элементов на главной диагонали и на
диагоналях, ей параллельных, берут со
знаком «плюс»; а произведения
элементов побочной диагонали и
диагоналей, ей параллельных, со знаком
«минус»:

4. Свойства определителей.

1. Определитель
   транспонированной матрицы равен
   определителю исходной матрицы.

2. Умножение
   всех элементов строки или столбца
   определителя на некоторое число λ
   равносильно умножению определителя
   на это число.

3. Если
   в определителе переставить местами
   любые две строки или два столбца, то
   определитель изменяет свой знак на
   противоположный.

4. Если
   матрица содержит нулевую строку
   (столбец), то определитель этой матрицы
   равен нулю.

5. Если
   две строки (столбца) матрицы равны
   между собой, то определитель этой
   матрицы равен нулю.

6. Если
   две строки (столбца) матрицы пропорциональны
   друг другу, то определитель этой матрицы
   равен нулю.

7. Определитель
   матрицы треугольного вида равен
   произведению элементов, стоящих на
   главной диагонали.

8. Если
   все элементы k-ой строки (столбца)
   определителя представлены в виде сумм
   ak j + bk j, то определитель можно представить
   в виде суммы соответствующих
   определителей.

9. Определитель
   не изменится, если к элементам любой
   его строки (или столбца) прибавить
   соответствующие элементы другой строки
   (или соответствующего столбца),
   умноженные на одно и тоже число.

5. Обратная матрица.
Существование, единственность. Нахождение
обратной матрицы.

Комплексный сборник тестов с ответами по Высшей математике

Кривые второго порядка

Правильный ответ подчёркнут.

1. Кривой II порядка является

— эллипс, не вырожденный в окружность

— гипербола

— парабола

— окружность

2. Кривой II порядка является

— эллипс, не вырожденный в окружность

— гипербола

— парабола

— окружность

3. Кривой II порядка является

— эллипс, не вырожденный в окружность

— гипербола

— парабола

— окружность

4. Кривой II порядка является

— эллипс, не вырожденный в окружность

— гипербола

— парабола

— окружность

Прямые и плоскости в пространстве

Правильный ответ выделен и подчёркнут.

1. Уравнением плоскости, проходящей через точку и перпендикулярной прямой является

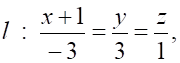
а.        б.       в.

2. Общее уравнение плоскости, содержащей точку и параллельной плоскости , имеет вид

а. 

б. 

в. 

г. 

3. Плоскость перпендикулярна плоскости

а. 

б. 

в. 

г. £

4. Прямая, проходящая через точки и , перпендикулярна плоскости

а. 

б. 

в. 

г. 

5. Даны три прямых на плоскости: , и Верным является утверждение

а.  и перпендикулярны

б.   и перпендикулярны

в.   и перпендикулярны

г.  перпендикулярных прямых нет

6. Уравнением плоскости, проходящей через точку и перпендикулярной прямой является

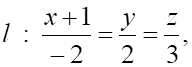
а. 

б. 

в. 

г. 

тест 7. Общее уравнение плоскости, содержащей точку и параллельной плоскости , имеет вид

а. 

б. 

в. 

г. 

8. Плоскость перпендикулярна плоскости

а. 

б. 

в. 

г. 

Прямые на плоскости

Правильный ответ выделен и подчёркнут.

1. Прямая, проходящая через точку и параллельная прямой имеет вид

а. 

б. 

в. 

г. 

2. Уравнением прямой, содержащей точку и параллельной прямой является

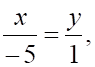
а. 

б. 

в. 

г.  

3. Общее уравнение прямой, содержащей точки и имеет вид

а. 

б. 

£

£

Треугольник на плоскости

Правильный ответ выделен и подчёркнут.

1. Длина стороны в треугольнике с вершинами , , равна

а.        б.          в.           г.  

2. Длина медианы в треугольнике с вершинами , , равна

а.          б.         в.           г.  

3. Угол в треугольнике с вершинами , и

а.  прямой     б. тупой        в. острый

4. В треугольнике , где , , , угол при вершине равен

а.          б.            в.            г. 

5. В треугольнике , где , , , угол

а. прямой         б. тупой         в. острый

Линейная алгебра. Алгебра матриц. Обратная матрица. Определители

Правильный ответ выделен и подчёркнут.

1тест. Обратной к матрице 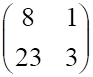является матрица

а.          б.             в.               г.  

2. Определитель матрицы 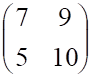равен

а.         б.          в.             г. 

3. Определитель матрицы 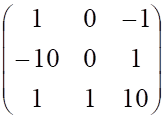равен

а.        б.          в.             г.  

4. Определитель матрицы 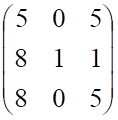равен

а.        б.          в.          г. 

5. Определитель матрицы 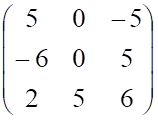равен

а.       б.       в.        г. 

6. Уравнение для нахождения собственных значений матрицы имеет вид

а. 

б. 

в. 

г. £

Сумма и произведение матриц

Правильный ответ выделен и подчёркнут.

1. Выражение эквивалентно

а.        б.        в.          г. 

2. Выражение эквивалентно

а.       б.        в.          г. 

3. Произведение матриц 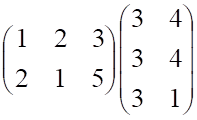равно

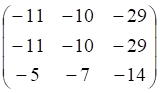
а.            б.                в.                 г. 

4. Заданы матрицы 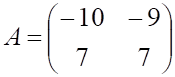и . Произведение равно

а.                б.                        в.                       г. 

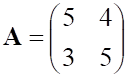
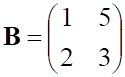
5. Заданы матрицы и . Произведение равно

а.             б.              в.                г. 

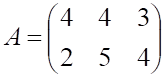
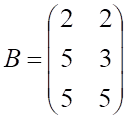
6. Заданы матрицы и . Сумма равна

а.            б.                 в.                    г. 

тест №7. Транспонированной к матрице 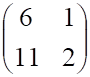является матрица

а.         б.          в.            г. 

Векторная алгебра

Правильный ответ выделен и подчёркнут.

1. Заданы векторы и . Выражение равно

а.       б.       в.        г. 

2. Заданы векторы и . Длина вектора равна

а.         б.          в.          г. 

3. Из векторов , и , ортогональными являются

а. и

б.  и

в.  и

г.  и , и

Комплексные числа

Правильный ответ выделен и подчёркнут.

1. Сумма если , , равна

а.         б.           в.           г. 

2. Произведение если , , равно

а.         б.        в.         г. 

Системы линейных уравнений

Правильный ответ выделен и подчёркнут.

1. Система линейных уравнений 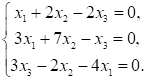имеет

а. одно нулевое решение

б. бесконечно много решений

в. одно ненулевое решение

г. нет решений

2. Частным решением системы линейных уравнений 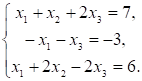является

а.         б.          в.            г. 

3. Система линейных уравнений 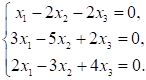имеет

а. одно решение£ два решения

б. бесконечно много решений

в. нет решений

4. Матричное уравнение с невырожденной квадратной матрицей А имеет решение

а.         б.           в.         г.

5. Матричное уравнение с невырожденной квадратной матрицей А имеет решение

а.            б.           в.            г. 

Математический анализ. Дифференциальное исчисление

Правильный ответ выделен и подчёркнут.

1 — тест. Производная функции равна

а. 

б. 

в.  

г. 

2. Производная функции равна

а. 

б. 

в. 

г. 

3. Производная функции 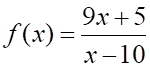равна

а.           б.            в.             г. 

4. Частной производной для функции является

а.           б.            в.           г. 

5. Производная функции равна

а.          б.         в.           г. 

6. Градиент функции равен

а. 

б. 

в. 

г. 

7. Смешанная производная для функции равна

а.            б.           в.           г. 

8. Достаточным условием выпуклости функции на интервале является

а.  на  

б.  на

в.  на

г.  на

9. Достаточным условием убывания функции на интервале является

а.  на

б.  на

в.  на

г.  на

10. Точкой локального экстремума функции является

а.       б.         в.         г.

11. Градиент функции равен

а. 

б. 

в. 

г. 

Дифференциальные уравнения

Правильный ответ выделен и подчёркнут.

тест — 1. Общим решением дифференциального уравнения является

а. 

б. 

в. 

г. 

Интегральное исчисление

Правильный ответ выделен и подчёркнут.

1. Определенный интеграл 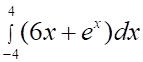равен

а.        б.        в.         г. 

2. Несобственный интеграл равен

а.       б.      в.        г. 

3. Несобственный интеграл 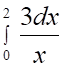равен

а.        б.      в.       г. 

4. Определенный интеграл 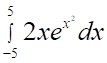равен

а.        б.       в.        г. 

5. Несобственный интеграл 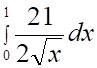равен

а.       б.         в. 

Последовательности

Правильный ответ выделен и подчёркнут.

1. Примером неограниченной последовательности является последовательность

а.      б.         в.      г. 

2. Примером сходящейся последовательности является последовательность

а.         б.          в.          г. 

3. Примером ограниченной последовательности является последовательность

а.       б.        в.         г. 

4. Примером бесконечно малой последовательности является последовательность

а.       б.        в.         г. 

5. Примером бесконечно большой последовательности является последовательность

а.        б.         в.        г. 

6. Примером ограниченной последовательности является последовательность

а.        б.        в.        г. 

7. Примером бесконечно малой последовательности является последовательность

а.        б.        в.          г. 

8. Примером бесконечно большой последовательности является последовательность

а.        б.         в.        г. 

9_тест. Примером ограниченной последовательности является последовательность

а.       б.       в.        г. 

Предел функции

Правильный ответ выделен и подчёркнут.

1. Предел 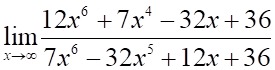равен

а.         б.           в.           г. 

2. Предел 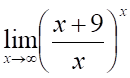равен

а.         б.        в.          г. 

3. Предел равен

а.        б.       в.          г. 

Ряды

Правильный ответ выделен и подчёркнут.

1. Радиус сходимости ряда 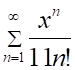равен

а.       б.        в.         г. 

2. Радиус сходимости ряда 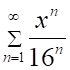равен

а.         б.         в.        г. 

3. Радиус сходимости ряда 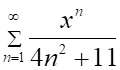равен

а.       б.        в.         г. 

Теория вероятностей

Правильный ответ выделен и подчёркнут.

1. Распределение дискретной случайной величины задано таблицей

Математическое ожидание равно

а.        б.       в.        г. 

2. Распределение дискретной случайной величины задано таблицей

Математическое ожидание равно

а.      б.      в.      г. 

3. Распределение дискретной случайной величины задано таблицей

Дисперсия равна

а.      б.       в.       г. 

тест_4. Распределение дискретной случайной величины задано таблицей

Дисперсия равна

а.        б.         в.        г. 

Классическая вероятность

Правильный ответ выделен и подчёркнут.

1. Вероятность, что кубик упадет на грань « «, при условии, что выпадет нечетная грань, равна

а.       б.       в.        г. 

2. В урне находится красных и черных шаров. Вероятность на удачу достать два красных шара равна

а.      б.      в.       г. 

3. Вероятность попадания в цель при одном выстреле равна Вероятность того, что из двух выстрелов попали оба раза, равна

а.       б.       в.         г. 

4. Урна содержит белых и черных шаров. Вероятность наудачу достать первым белый шар, а вторым черный, равна

а.        б.        в.         г. 

5. Количество способов, которыми можно выбрать экзаменационных билетa из , равно

а.      б.       в.        г.