Муниципальное бюджетное образовательное учреждение
дополнительного образования детей дом детского творчества
г. Зверева Ростовской области.
Муниципальное бюджетное образовательное учреждение
средняя образовательная школа №1
г.Зверева Ростовской области.
Билеты к устному экзамену по геометрии 8 класс
Работа педагога дополнительного
образования МБОУ ДОД ДДТ,
учителя математики МБОУ СОШ №1
Куца Фёдора Ивановича
г. Зверево
2014 г.
Билет №1.
1. Сформулируйте определение выпуклого многоугольника ( периметр, диагональ). Сформулируйте теорему о сумме углов выпуклого многоугольника.
2.Признаки подобия треугольников. Доказать один признак на выбор обучающегося.
3. В окружность вписан треугольник ABC так, что АВ — диаметр окружности. Найдите углы треугольника, если: дуга ВС=134°;
Билет №2.
1.Определение синуса, косинуса и тангенса острого угла прямоугольного треугольника.
2.Площадь прямоугольника (формулировка и доказательство).
3. Сумма двух противоположных сторон описанного четырехугольника равна 12 см. а радиус вписанной в него окружности равен 5 см. Найдите площадь четырехугольника
Билет №3
1.Параллелограмм. Определение. Свойства.
2.Теорема об окружности, вписанной в треугольник.
3. Стороны прямоугольника равны 3 см и 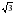
Билет № 4.
1.Четырехугольник. Сумма углов четырёхугольника.
2.Свойство касательной к окружности (формулировка и доказательство).
3. Докажите, что середины сторон произвольного четырехугольника являются вершинами параллелограмма.
Билет № 5.
1.Свойства площадей.
2.Теорема о средней линии треугольника (формулировка и доказательство).
3. Точка касания окружности, вписанной в равнобедренный треугольник, делит одну из боковых сторон на отрезки, равные 3 см и 4 см. считая от основания. Найдите периметр треугольника.
Билет № 6
1.Трапеция. Определение. Виды трапеций. Свойство равнобедренной трапеции.
2.Свойство отрезков касательных, проведенных из одной точки (формулировка и доказательство).
3. Подобны ли треугольники ABC и МКР если:
АВ=3 см, ВС=5 см, СА=7 см, МК=4,5 см, КР=7,5 см, РМ = 10,5 см.
Билет № 7
1.Прямоугольник. Свойства прямоугольника. Квадрат.
2.Теорема о вписанном угле (формулировка и доказательство).
3. Диагонали трапеции ABCD с основаниями АВ и CD пересекаются в точке О. Найдите: АВ, если ОВ=4 см, OD=10 см, DC=25 см.
Билет № 8
1.Ромб. Свойства ромба. Квадрат.
2.Свойство биссектрисы угла (формулировка и доказательство).
3. Площади двух подобных треугольников равны 75 и 300. Одна из сторон второго треугольника равна 9 . Найдите сходственную ей сторону первого треугольника.
Билет № 9
1.Квадрат. Свойства квадрата.
2.Свойство серединного перпендикуляра к отрезку (доказательство).
3. Найдите сторону и площадь ромба, если его диагонали равны 10 см и 24 см.
Билет № 10.
1.Подобные треугольники. Определение. Коэффициент подобия.
2.Свойства прямоугольника.
3. Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см. а больший угол равен 135°.
Билет № 11.
1.Медиана треугольника. Определение. Свойство точки пересечения медиан треугольника.
2.Площадь параллелограмма (формулировка и доказательство).
3. Две стороны треугольника равны 7,5 см и 3,2 см. Высота, проведенная к большей стороне, равна 2,4 см. Найдите высоту, проведенную к меньшей из данных сторон.
Билет № 12.
1.Пропорциональные отрезки в прямоугольном треугольнике.
2.Теорема об окружности, описанной около треугольника (формулировка и доказательство).
3. Найдите площадь прямоугольника, если одна из его сторон равна 5 см, а угол между диагоналями равен
Билет № 13.
1. Свойство описанного четырехугольника.
2.Свойства ромба (формулировка и доказательство).
3. Найдите углы выпуклого четырехугольника, если они пропорциональны числам 1,2,4,5.
Билет № 14.
1. Свойство вписанного четырехугольника.
2. Площадь треугольника (формулировка и доказательство).
3. Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см.
Билет № 15.
1. Центральный угол. Вписанный угол.
2.Площадь трапеции (формулировка и доказательство).
3. Найдите площадь равнобедренного треугольника, если его основание равно 10см, а боковая сторона
равна 13см.
Билет № 16.
1.Значения синуса, косинуса и тангенса для углов 30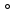
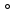
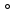
2.Теорема, обратная теореме Пифагора (формулировка и доказательство).
3.Катеты прямоугольного треугольника равны 6 и 8см., гипотенуза 10 см. Вычислите высоту, проведённую к гипотенузе.
Билет № 17
1.Описанная окружность. Центр окружности, описанной около треугольника.
2.Свойства параллелограмма (формулировка и доказательство).
3. Найдите площадь трапеции с основаниями AD и BC, если АD=12см, ВС=6см, СD=5см, АС=13см.
Билет № 18
1.Вписанная окружность. Центр окружности, вписанной в треугольник.
2. Теорема Пифагора (формулировка и доказательство). Пифагоровы треугольники.
3. Найдите площадь параллелограмма, если АD =12см, ВD=5см, АВ=13см.
.
Задачи для проведения промежуточного экзамена по геометрии .
1. Сумма трех углов параллелограмма равна 254⁰ .Найдите углы параллелограмма.
2. Найдите углы параллелограмма ,если его диагональ образует со сторонами углы 40⁰ и 35⁰ .
3. Дано: ВС АД , угол ВАС=ДСА
Доказать : АВСД -параллелограмма.
4.
В С Дано : АВСД- прямоугольник ,
угол АВД=48⁰
Найдите : угол СОД , угол САД.
А Д
5.Угол ромба равен 32⁰ . Найдите углы ,образующие его стороной с диагоналями.
6.Стороны параллелограмма равны 8см и 14см ,а один из углов равен 30⁰. Найдите площадь параллелограмма.
7.Найдите площадь треугольника ,если высота ,проведенная к одной из его сторон , равна 11см ,а средняя линия ,параллельная этой стороне , равна 10см.
В
М К
А С
Д
8.Найдите площадь равнобедренного прямоугольного треугольника ,если гипотенуза равна 2см.
9.Найдите площадь трапеции ,если ее основания 5см ,17см ,а боковые стороны соответственно равны 20см и 16см .
10.Докажите ,что треугольник со сторонами 9см ,40см ,41см является прямоугольным.
11. В прямоугольном треугольнике с острым углом 45⁰ гипотенуза равна 3√2 см. Найдите площадь этого треугольника.
12. Медиана ,проведенная к гипотенузе прямоугольного треугольника равна 13. найдите площадь треугольника , если один из его катетов равен 24.
13. У подобных треугольников сходственные стороны равны 7см и 35 см.Площадь первого треугольника равна 27см² .Найдите площадь второго треугольника.
14. Используя данные ,приведенные на рисунке ,найдите расстояние АВ от лодки А до берега b.
А
1м 10м В b
15.Средняя линия МК треугольника АВС отсекает от него треугольник МВК ,площадь которого равна 10 см² .Найдите площадь треугольника АВС.
16. Найдите сторону равностороннего треугольника ,если его высота равна 3.
17.В треугольнике АВС угол С равен 90⁰ ,синус угла А равен 12/13.Чему равен катет АС, если гипотенуза равна 13см?
18.Прямая КМ касается окружности радиуса 5см ( точка М- точка касания).Найдите КМ ,если КА=13см.
19.К окружности проведены две касательные СА и СВ из точки С. Найдите площадь четырехугольника
АСВО, если точка О-центр окружности ,ОС=25 ,а радиус равен 7.
20. Найдите угол α ,вписанный в окружность.
21.Точки Аи В делят окружность на две дуги ,длины которых относятся как 9:11.Найдите величину центрального угла, опирающегося на меньшую из дуг.
Устный экзамен по геометрии за курс 8 класса
Билет №1
1.Параллелограмм (определение и свойства).
2.Формула площади трапеции.
Билет №2
1.Признаки параллелограмма.
2.Определение тангенса острого угла прямоугольного треугольника.
Билет №3
1.Трапеция (определение и свойства).
2.Определение косинуса острого угла прямоугольного треугольника.
Билет №4
1.Ромб (определение и свойства).
2.Теорема о пересечении высот треугольника.
Билет №5
1.Прямоугольник (определение и свойства).
2.Определение синуса острого угла прямоугольного треугольника.
Билет №6
1.Квадрат (определение и свойства).
2.Теорема об отрезках пересекающихся хорд окружности.
Билет №7
1.Осевая симметрия (пример).
2.Свойство биссектрисы угла треугольника.
Билет №8
1.Центральная симметрия (пример).
2.Формула площади прямоугольника.
Билет №9
1.Теорема о касательной к окружности.
2.Формула площади ромба.
Билет №10
1.Теорема Пифагора.
2.Свойство биссектрисы угла.
Билет №11
1.Подобные треугольники (определение).
2.Формула площади квадрата.
Билет №12
1.Центральные и вписанные углы.
2.Отношение площадей подобных треугольников.
Билет №13
1.Признаки подобия треугольников.
2.Формула площади параллелограмма.
Билет №14
1.Средняя линия треугольника (определение и свойства).
2.Формула площади треугольника, прямоугольного треугольника.
Билет №15
1.Теорема о вписанной в треугольник окружности.
2.Синусы углов 30°, 45°,60°.
Билет №16
1.Теорема об окружности, описанной около треугольника.
2.Косинусы углов 30°, 45°, 60°.
Билет №17
1.Окружность, вписанная в четырехугольник.
2.Формула Герона.
Билет №18
1.Теорема об окружности, описанной около четырехугольника.
2.Тасгенсы углов 30°, 45°, 60°.
Билет №19
1.Четыре замечательные точки треугольника.
2.Теорема об отрезках касательных к окружности, проведенных из одной точки.
В данной работе представлен комплект билетов к устному экзамену по геометрии за курс восьмого класса ( к учебнику Атанасяна Л.С. «Геометрия. 7 — 9 классы».
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Билеты по геометрии для 8 класса (Атанасян) 2018 год
Билет №1.
-
Определение четырёхугольника. Виды четырёхугольников.
-
Доказать теорему Фалеса.
-
Задача.
Найти площадь ромба, если его высота 15 см, а острый угол 30°.
-
В треугольнике АВС
=90
,sinА=
, АС=4
Найдите АВ.
Билет №2.
-
Параллелограмм. Определение. Свойства параллелограмма.
-
Доказать теорему о средней линии треугольника.
-
Задача. В равнобокой трапеции боковая сторона 17 см, основания равны 10 см и 26 см. Найти площадь трапеции.
-
В треугольнике АВС
=90
,sinА=
, АС=5
Найдите АВ.
Билет №3.
-
Квадрат. Определение. Свойства.
-
Вписанная окружность. Доказать теорему об окружности, вписанной в треугольник.
-
Задача. В равнобедренном треугольнике основание равно 80 см, и угол при нём 45°. Найти площадь треугольника.
-
В треугольнике АВС
=90
,АВ=182, АС=70. Найдите tgА.
Билет №4.
-
Пропорциональность отрезков в прямоугольном треугольнике.
-
Прямоугольник. Доказательство теоремы о равенстве диагоналей прямоугольника.
-
Задача. Площадь равнобедренного треугольника равна 4800 см2, а его высота, проведённая к основанию, равна 80 см. Найти боковую сторону треугольника.
-
В треугольнике АВС
=90
,ВС=28, АВ=35. Найдите sinВ.
Билет №5.
-
Соотношения между сторонами и углами в прямоугольном треугольнике (определение синуса, косинуса и тангенса острого угла в прямоугольном треугольнике). Основное тригонометрическое тождество.
-
Ромб. Доказательство теоремы о диагоналях ромба.
-
Задача. В окружности проведены две пересекающиеся хорды. Одна из них делится на отрезки 3 см и 12 см, а другая – пополам. Найдите длину второй хорды.
-
В треугольнике АВС
=90
,cosВ=
, АВ=5
Найдите АС.
Билет № 6.
-
Касательная к окружности. Свойства.
-
Параллелограмм. Свойства параллелограмма. Доказательство одного из свойств параллелограмма (на выбор учащегося).
-
Задача. Определить площадь равнобедренного треугольника, если его основание 8 см и боковая сторона 5 см.
-
В треугольнике АВС
=90
,cosВ=
, АВ=45
Найдите АС.
Билет № 7.
-
Площадь четырехугольников: параллелограмма, трапеции
-
Значения синуса, косинуса и тангенса некоторых углов. Вывод нахождения значений синуса, косинуса и тангенса углов в 45°, 30° и 60°.
-
Задача. В равнобедренный треугольник с основанием 12 см и периметром 32 см вписана окружность. Найдите радиус этой окружности.
-
В треугольнике АВС
=90
,ВС=
21, АВ=5. Найдите sinВ.
Билет №8.
-
Вписанная и описанная окружности в треугольники и четырехугольники.
-
Докажите свойство противолежащих сторон и углов параллелограмма.
-
Задача. Периметр равнобедренного треугольника равен 50 см, а его боковая сторона на 11 см меньше основания. Найти высоту треугольника, опущенную на основание.
-
В треугольнике АВС
=90
,АВ=13, АС=5. Найдите tgА.
Билет №9.
-
Признаки параллельности прямых.
-
Докажите теорему об отношении площадей треугольников.
-
Задача. Меньшее основание трапеции относится к средней линии как 1:3, а большее основание равно 30 см. Найдите среднюю линию трапеции.
-
В треугольнике АВС
=90
,cosВ=
, АВ=25
Найдите АС.
Билет №10.
-
Вписанная и описанная окружности в треугольники и четырехугольники.
-
Площадь треугольника. Формулы для вычисления площади треугольника (общие и частные случаи).
-
Задача. Одна из сторон параллелограмма в 3 раза больше проведённой к ней высоты. Вычислите их, если площадь параллелограмма равна 48 см2.
-
В треугольнике АВС
=90
,АВ=15, АС=12. Найдите tgА.
Билет №11.
-
Вписанный и центральный углы, дуга окружности.
-
Признаки подобия треугольников. Докажите один из признаков подобия треугольников (по выбору учащегося).
-
Задача. Боковая сторона равнобокой трапеции образует с большим её основанием угол 45°. Вычислите площадь трапеции, если основания её равны 24 см и 60 см.
-
В треугольнике АВС
=90
,АВ=20, АС=12. Найдите sinА
Билет №12.
-
Признаки равенства треугольников.
-
Вписанный угол. Докажите теорему о вписанном угле.
-
Задача. Длины диагоналей ромба относятся, как 3 : 4. Площадь ромба равна 150 см2. Вычислить высоту ромба.
-
В треугольнике АВС
=90
,sinА=
, АС=4
Найдите АВ.
Билет № 13.
-
Понятие площади многоугольника. Свойства площадей.
-
Докажите теорему Пифагора.
-
Задача. В треугольник, углы которого относятся как 1:3:5, вписана окружность. Найдите углы между радиусами, проведёнными в точки касания.
-
В треугольнике АВС
=90
,sinА=
, АС=5
Найдите АВ.
Билет №14.
-
Формулы для вычисления площади параллелограмма.
-
Касательная к окружности. Докажите теорему о свойстве касательной к окружности.
-
Задача. В равнобокой трапеции, один из углов которой равен 45°, большее основание равно 70 см, высота равна 10 см. Вычислить площадь трапеции.
-
В треугольнике АВС
=90
,АВ=182, АС=70. Найдите tgА.
Билет №15.
-
Признаки равенства прямоугольных треугольников.
-
Вписанный угол. Докажите теорему о вписанном угле.
-
Задача. Боковая сторона равнобокой трапеции, равная 20 см, образует с меньшим её основанием угол 150°. Вычислите площадь трапеции, если её основания равны 12 см и 30 см.
-
В треугольнике АВС
=90
,ВС=28, АВ=35. Найдите sinВ.
Билет №16.
-
Треугольник. Свойства равнобедренного треугольника.
-
Описанная окружность. Докажите теорему об окружности, описанной около треугольника.
-
Задача. Площадь параллелограмма равна 24 см2, каждая из его сторон равна 6 см. Найти расстояние между противоположными сторонами.
-
В треугольнике АВС
=90
,cosВ=
, АВ=5
Найдите АС.
Вопросы, предлагаемые для устного экзамена по геометрии в 8 классах
1 часть
1.Определение четырёхугольника. Виды четырёхугольников.
2.Параллелограмм. Определение. Свойства параллелограмма.
3.Квадрат. Определение. Свойства.
4. Пропорциональность отрезков в прямоугольном треугольнике.
5. Соотношения между сторонами и углами в прямоугольном треугольнике (определение синуса, косинуса и тангенса острого угла в прямоугольном треугольнике). Основное тригонометрическое тождество.
6. Касательная к окружности. Свойства
7. Площадь четырехугольников: параллелограмма, трапеции
8. Вписанная и описанная окружности в треугольники и четырехугольники.
9. Признаки параллельности прямых
10. Вписанный и центральный углы, дуга окружности.
11. Признаки равенства треугольников.
12. Понятие площади многоугольника. Свойства площадей.
13. Формулы для вычисления площади параллелограмма
14. Признаки равенства прямоугольных треугольников.
15. Треугольник. Свойства равнобедренного треугольника.
2 часть.
1. Доказать теорему Фалеса.
2. Доказать теорему о средней линии треугольника.
3. Вписанная окружность. Доказать теорему об окружности, вписанной в треугольник.
4. Прямоугольник. Доказательство теоремы о равенстве диагоналей прямоугольника.
5. Ромб. Доказательство теоремы о диагоналях ромба.
6. Параллелограмм. Свойства параллелограмма. Доказательство одного из свойств параллелограмма (на выбор учащегося).
7. Значения синуса, косинуса и тангенса некоторых углов. Вывод нахождения значений синуса, косинуса и тангенса углов в 45°, 30° и 60°.
8. Докажите свойство противолежащих сторон и углов параллелограмма.
9. Докажите теорему об отношении площадей треугольников.
10. Площадь треугольника. Формулы для вычисления площади треугольника (общие и частные случаи).
11. Площадь треугольника. Формулы для вычисления площади треугольника (общие и частные случаи).
12. Признаки подобия треугольников. Докажите один из признаков подобия треугольников (по выбору учащегося).
13. Докажите теорему Пифагора.
14. Касательная к окружности. Докажите теорему о свойстве касательной к окружности.
15. Вписанный угол. Докажите теорему о вписанном угле.
16. Описанная окружность. Докажите теорему об окружности, описанной около треугольника.

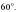
 =90
=90 ,
,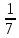 , АС=4
, АС=4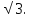 Найдите АВ.
Найдите АВ.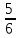 , АС=5
, АС=5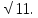 Найдите АВ.
Найдите АВ.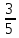 , АВ=5
, АВ=5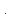 Найдите АС.
Найдите АС.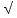 21, АВ=5. Найдите
21, АВ=5. Найдите 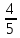 , АВ=25
, АВ=25