Вопросы по геометрии 7 класс для переводного экзамена - Помощь в подготовке к экзаменам и поступлению

Переводной экзамен по геометрии. 7 класс .

1 вариант.

Часть А

1. Через две любые точки А и В можно провести:

а) только две прямые б) только одну прямую

в) ни одной прямой г) множество прямых

2. На прямой отмечены точки: A,B,C,D. Какие из данных точек
принадлежат отрезку BD?

Ответ:____________

3. Точка А принадлежит отрезку CD. Длина CD=8см 9мм, CА=3см 6мм.
Найти длину отрезка АD.

Ответ:____________

4*. На прямой отмечены точки A,B,C, так, что AB=27см, AC=11см,
BC=16см. Какая из этих точек, может лежать между двумя другими?

Ответ:____________

5. Найти верное соответствие между рисунком и определением.

1. соответственные углы 2. односторонние углы

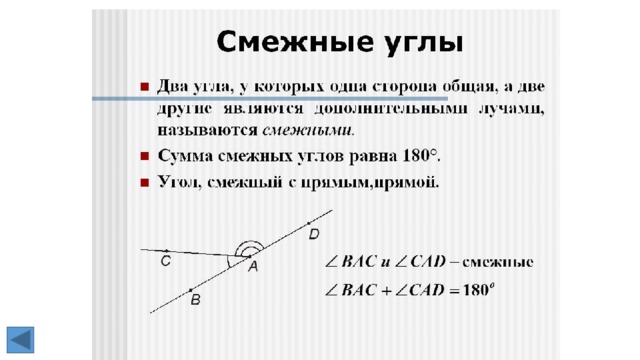
3. смежные углы 4. перпендикулярные прямые

6. Луч ОВ делит угол АОС на два угла. , на
15больше угла . Найти градусную меру углов

и .

Ответ: =_____ =______.

7*. Угол равный тремя лучами, исходящими из вершины угла,

разделили на четыре равные угла. Сколько углов равных при этом
получится?

Ответ:____________

8. Дано: , — смежные. =142. (рис.1)

Найти:

Ответ: =____________ рис.1

9*. Дано: , — смежные. :=7:2. (рис.1)

Найти: ,

Ответ: =____, =___.

10. На каком из рисунков прямые являются параллельными. Указать
только номер правильного рисунка.

рис.1 рис.2 рис.3 рис.4

Ответ:______________

11. Дано: прямая .

Найти:

12. Выберите верное утверждение из предложенных:

А) Угол — геометрическая фигура, состоящая из двух лучей,
исходящих из одной точки.

Б) Градусная мера прямого угла меньше .

В) Равные углы имеют равные градусные меры.

Г) Если два угла одного треугольника равны двум углам другого
треугольника, то такие треугольники равны.

13. Дано: , . 14. В треугольнике ,

Найти: , . Найти градусную меру каждого угла,
если известно, что они: ; ; .

Ответ: =___, =___. Ответ: =___, =___, =___

С какими из предложенных измерений сторон может существовать треугольник:

1) 5см, 3см, 4см 2) 7см, 7см, 3см

3) 6см, 3см, 2см 4) 3см, 3см, 8см.

Часть В

Отрезки АВ и CD пересекаются в точке О и

делятся в этой точке пополам. Докажите, что

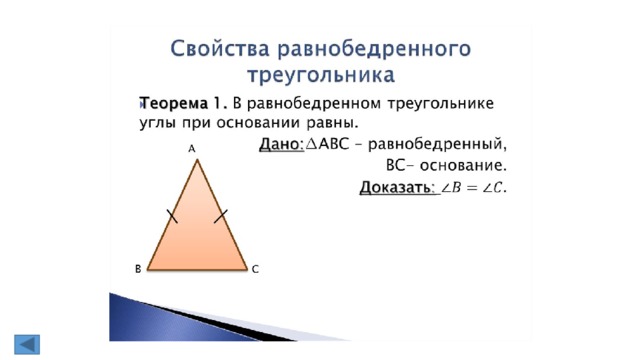
Периметр равнобедренного треугольника

равен 34см. Найти стороны треугольника, если

его основание на 2см меньше боковой стороны.

В равнобедренном треугольнике АВС, с основанием АС, проведена биссектриса AD. Докажите, что .

Используя предложенный рисунок доказать, что прямая .

Найти .

В треугольнике АВС, в 3 раза больше, чем, а на 25больше, чем. Найти углы в . Сравнить стороны этого треугольника.

6*. В равнобедренном треугольнике МОР проведена
высота ОН. Угол МОН равен 30. Боковая сторона

МО=8см. Найти периметр треугольника МОР.

Переводной экзамен по геометрии. 7 класс .

2 вариант.

Часть А

Каждая точка прямой делит ее на:

а) три луча б) два луча

в) число лучей нельзя определить г) не может разделить прямую.

На прямой отмечены точки:

Какие из данных точек принадлежат отрезку AD, но не
принадлежат отрезку CЕ?

Ответ:____________

3. Точка В принадлежит отрезку MN, отрезок MB=3см 4мм, отрезок
BN=5см 7 мм. Найти длину отрезка MN.

Ответ:____________

4*. На прямой отмечены точки A,B,C, так, что AB=7м, AC=21м,
BC=28м. Какая из этих точек, может лежать между двумя
другими?

Ответ:____________

Найти верное соответствие между рисунком и определением.

1. смежные углы 2. соответственные углы

3. вертикальные углы 4. накрест лежащие углы

6. Луч ОВ делит угол АОС на два угла. , в 4 раза
меньше угла . Найти градусную меру углов

и .

Ответ: =_____ =______.

7*. Угол равный разделили лучами, исходящими из вершины, на
пять равных углов. Сколько прямых углов при этом получилось?

Ответ:___________

8. Дано: =45.

Найти: , .

9*. Дано: +=286.

Найти: , , , .

10. На каком из рисунков прямые являются параллельными. Указать
только номер правильного рисунка.

рис.1 рис.2 рис.3 рис.4

Ответ:__________

11. Дано: прямая , =125.

Найти: .

12. Выберите верное утверждение из предложенных:

А) Фигуры называются равными, если они совпадают при наложении.

Б) Градусная мера острого угла больше .

В) При параллельных прямых и секущей накрест лежащие углы
равны.

Г) Два треугольника равны, если соответствующие углы равны.

13. Дано: , .

Найти: .

Ответ: ___, ___.

14. В треугольнике MNK, .

Найти длины сторон треугольника, если

Известно, что они имеют измерения 16см, 5см, 13см.

Ответ: MN=_____, NK=_____, MK=______.

15. С какими из предложенных измерений сторон может
существовать треугольник:

1) 4см, 2см, 6см 2) 3см, 5см, 5см

3) 2см, 4см, 7см 4) 6см, 7см, 8см.

Часть В

В четырехугольнике ABCD, AB=АD,

. Доказать, что .

Периметр равнобедренного треугольника равен

28см. Найти стороны треугольника, если основание треугольника

На 4см больше боковой стороны.

В равнобедренном треугольнике МОК с основанием МК проведена медиана ОР. Доказать, что .

Используя предложенный рисунок доказать, что прямая .

Найти .

В треугольнике АВС в 4 раза больше , на 12 меньше . Найти углы в треугольнике АВС. Сравнить стороны треугольника.

В равнобедренном треугольнике МОР проведена
высота ОН. Угол МОН равен 30. Отрезок

6*. МН = 3,5см. Найти периметр треугольника МОР.

Переводной экзамен по геометрии. 7 класс.

3 вариант.

Часть А

Через точку, не лежащую на прямой, можно провести:

а) две прямые, параллельные данной прямой;

б) только одну прямую, параллельную данной;

в) ни одной прямой, параллельной данной;

г) множество параллельных прямых.

Ответ:__________

2. На прямой отмечены точки: A,B,C,D. Какие из данных точек
принадлежат отрезку АС?

Ответ:____________

Точка А принадлежит отрезку CD. CD=10см 8мм, СА=4см 3мм. Найти длину отрезка АD.

Ответ:__________

4*. Дан отрезок АВ=16см. Точка М – середина отрезка АВ, точка К –
середина отрезка МВ. Найти длину отрезка АК.

Ответ:__________

5. Найти верное соответствие между рисунком и определением.

1. односторонние углы 2. смежные углы

3. вертикальные углы 4. соответственные углы

Луч, ОА делит угол ВОС на два угла.

, на 37 меньше . Найти

углы: и .

Ответ: =______, = _______.

7*. Угол равный 160 разделили тремя лучами, исходящими из
вершины угла на четыре равные части. Сколько углов равных
80при этом получилось?

8. Дано: , — смежные. =42. (рис.1)

Найти:

Ответ: =____________ рис.1

9*. Угол на 48 больше, чем (рис. 2).

Найти и

рис.2

10. На каком из рисунков прямые являются параллельными. Указать
только номер правильного рисунка.

рис.1 рис.2 рис.3 рис.4

Ответ:___________

11. Дано: прямая .

Найти:

12. Выберите верное утверждение из предложенных:

А) биссектриса делит угол пополам;

Б) градусная мера тупого угла больше 90, но меньше 180;

В) если две стороны и угол между ними одного треугольника,
соответственно равны двум сторонам и углу между ними другого
треугольника, то такие треугольники равны;

Г) в равнобедренном треугольнике углы равны.

Ответ:___________

13. Дано: , .

Найти:

14. В треугольнике MNK сторона

Определить для каждого угла градусную меру, если

Известно, что они 27, 99 и 54

15. С какими из предложенных измерений сторон может существовать
треугольник:

1) 5см, 8см, 7см 2) 5см, 15см, 5см

3) 3см, 4см, 2см 4) 3см, 8см, 5см.

Часть В

В четырехугольнике ABCD AB=CD, BC=AD.

Доказать, что .

Периметр равнобедренного треугольника равен 48см. Найти стороны треугольника, если его боковая сторона на 3см больше основания.

В равнобедренном треугольнике АВС, с основанием АС, проведена высота ВК. Найти углы треугольника, если .

Используя предложенный рисунок доказать, что прямая .

Найти и , если известно, что : = 12 : 6.

В треугольнике АВС в 2 раза больше, чем , на 22 больше, чем . Найти углы треугольника. Сравнить стороны треугольника.

6*. В прямоугольном треугольнике АВС , , длина
отрезка DC равна 3см, а . Найти длину гипотенузы
DC.

Переводной экзамен по геометрии. 7 класс .

4 вариант.

Часть А

Две фигуры называются равными, если:

А) они похожи по форме Б) они совпадают при наложении

В) имеют равные углы Г) отличаются только размером

2. На прямой отмечены точки:

Какие из данных точек принадлежат отрезку ВЕ, но не
принадлежат отрезку АC?

Ответ:____________

3. Точка В принадлежит отрезку MN, МВ=5см 8мм, BN=4см 6мм.
Найти длину отрезка MN.

Ответ:________________

4*. Точка М – середина отрезка АВ, точка К – середина отрезка МВ.
Найти длину отрезка АВ, если отрезок ВК=3см.

Ответ:_______________

5. Найти верное соответствие между рисунком и определением.

1. смежные 2. вертикальные

3. соответственные 4. накрест лежащие

Луч ОА делит угол ВОС на два угла.

, а в 3 раза меньше

. Найти углы: ,

7*. Угол равный разделили лучами, исходящими из вершины,

на пять равных углов. Сколько углов равных при этом
получилось?

Ответ:___________

8. Дано: (рис.1) рис.1

Найти: , .

9*. Дано: +=96 (рис.2).

Найти: , , , .

рис.2

10. На каком из рисунков прямые являются параллельными. Указать
только номер правильного рисунка.

рис.1 рис.2 рис.3 рис.4

11. Дано: прямая , =112.

Найти: .

12. Выберите верное утверждение из предложенных:

А) градусная мера развернутого угла равна 180;

Б) смежные углы равны;

В) в треугольнике может быть только один тупой угол;

Г) в прямоугольном треугольнике напротив угла в 30 градусов лежит
катет равный гипотенузе.

13. Дано: , .

Найти:

14. В треугольнике АВС . Указать

Стороны, если их длины равны 18см, 13см, 7см.

Ответ: АВ=______, АС=_____, ВС=______.

15. С какими из предложенных измерений сторон может существовать
треугольник:

1) 4см, 4см, 3см 2) 3см, 5см, 4см

3) 5см, 12см, 6см 4) 2см, 8см, 2см.

Часть В

В четырехугольнике ABCD

AB=CD,.

Доказать, что .

Периметр равнобедренного треугольника равен 21см. Найти стороны треугольника, если его боковая сторона на 3см меньше основания.

В равнобедренном треугольнике с основанием ОВ. Проведена медиана ОС. . Найти углы треугольника.

Используя предложенный рисунок доказать, что прямая .

Найти и , если известно, что : = 5 : 7.

5. В треугольнике АВС на 16меньше , в 5 раз больше,
чем . Найти углы треугольника АВС и сравнить стороны
треугольника.

6*. В прямоугольном треугольнике МОР , ,
отрезок . Найти длину отрезка МК, если длина
гипотенузы равна 18см.

Примерные задания переводного экзамена по геометрии. 7 класс

5 вариант

Часть А

1. Выберите верное утверждение из предложенных:

А) Две фигуры называются равными, если они совпадают при
наложении;

Б) В треугольнике может быть два тупых угла;

В) Градусная мера тупого угла больше 90, но меньше 180;

Г) Через точку, не лежащую на прямой, можно провести несколько
прямых, параллельных данной прямой.

2. На прямой отмечены точки:

Какие из данных точек принадлежат отрезку AL, но не
принадлежат отрезку BC?

Ответ:____________

3. Точка A принадлежит отрезку MN, МA=5см 8мм, MN=14см 2мм.
Найти длину отрезка aN.

Ответ:________________

4*. Точка М – середина отрезка АВ, точка К – середина отрезка МA.
Найти длину отрезка АВ, если отрезок MК=4см.

Ответ:_______________

5. Найти верное соответствие между рисунком и определением.

A) Б) В) Г)

1. смежные 2. вертикальные

3. соответственные 4. накрест лежащие

6. Луч ОА делит угол ВОС на два угла.

, а в 3 раза больше

. Найти углы: ,

Ответ: =____,

7*. Угол равный разделили лучами, исходящими из вершины,

на пять равных углов. Сколько углов равных при этом
получилось?

Ответ:___________

8. Дано: (рис.1) рис.1

Найти: , .

Ответ: =____, =_____.

9*. Угол на 18 меньше, чем (рис. 2).

Найти и

Ответ: =____, =_____.
рис.2

10. На каком из рисунков прямые являются параллельными. Указать
только номер правильного рисунка.

рис.1 рис.2 рис.3 рис.4

Ответ:___________

11. Дано: прямая .

Найти:

Ответ: =_____.

12. Выберите верное утверждение из предложенных:

А) смежные углы равны;

Б) если в треугольнике две стороны равны, то такой треугольник называется равнобедренным;

В) в равнобедренном треугольнике углы равны.

Г) Градусная мера острого угла меньше .

13. Дано: , .

Найти:

Ответ:

14. В треугольнике АВС . Указать

Стороны, если их длины равны 10см, 16см, 7см.

Ответ: АВ=______, АС=_____, ВС=______.

15. С какими из предложенных измерений сторон может существовать
треугольник:

1) 5см, 4см, 3см 2) 13см, 5см, 4см

3) 5см, 1см, 6см 4) 12см, 11см, 2см.

Часть В

В четырехугольнике ABCD AB=CD, ABD=BDC.

Доказать, что .

Периметр равнобедренного треугольника равен 21см. Найти стороны треугольника, если его боковая сторона на 3см больше основания.

В равнобедренном треугольнике АВС, с основанием АС, проведена высота ВК. Найти углы треугольника, если .

Используя предложенный рисунок доказать, что прямая .

Найти и , если известно, что : = 12 : 6.

5*. В равнобедренном треугольнике МОР проведена

медиана ОН = 4см. Найти периметр треугольника
МОР, если угол МОН равен 30, отрезок МН=3cм.

6. В треугольнике АВС на 15меньше , в 3 раз больше,
чем . Найти углы треугольника АВС и сравнить стороны
треугольника.

С)

В)

А)

102

114

148

106

Г)

В)

Б)

А)

103

118

112

127

А)

Б)

В)

Г)

107

105

107

142

Г)

В)

Б)

А)

144

122

117

144

122

125

122

Источник

ОБЩЕОБРАЗОВАТЕЛЬНАЯ АВТОНОМНАЯ НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ

«ШКОЛА ПРАВА И ЭКОНОМИКИ»

СОГЛАСОВАНО:

УТВЕРЖДЕНО:

На заседании Методического совета

Протокол № _____

от «__» ___________202__г.

Заместитель директора

по учебно-воспитательной работе

______________Маршинская Е.В.

«___» _________________ 202__ г.

Экзаменационный материал для переводного экзамена

по курсу «Геометрия» за 7 класс

Составители: Гельдимедова Ирина Рафиковна,

Пахолик Светлана Викторовна,

Юрченко Андрей Леонидович

Должность: учителя математики

Москва, 2021 г.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Экзаменационные билеты составлены в соответствии с содержанием программы на основе федерального компонента государственного образовательного стандарта основного общего образования по математике, примерной программы, рекомендованной Министерством образования и науки Российской Федерации и базисного учебного плана. В программе учтены основные идеи и положения федеральных образовательных стандартов общего образования третьего поколения, а также накопленный опыт преподавания математики в школе.

Вопросы составлены по основным темам, изучаемым в курсе геометрии 7 класса, включенным в УМК Атанасяна Л.С. и др.

Билеты представляют экзаменационный материал для устной формы экзамена. Каждый билет содержит 4 вопроса. В первом вопросе нужно сформулировать без доказательства определение или свойства некоторой геометрической фигуры или геометрической конструкции. Второй вопрос подразумевает доказательство одной из основных теорем курса. Третий и четвертый вопросы – задачи, причем задача из четвертого вопроса имеет более высокий уровень сложности. Рекомендуемое время для подготовки ответа экзаменуемого – 30 минут.

Требования к уровню подготовки обучающихся

Учащиеся к концу 7 класса должны обладать знаниями, соответствующими содержанию обучения, описанному в рабочей программе по предмету геометрия для 7 класса.

Экзаменуемые должны уметь:

распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры;
выполнять чертежи по условию задач;
осуществлять преобразования фигур;
вычислять значения геометрических величин (длин, углов, площадей);
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический аппарат;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования.

Содержание обучения

Начальные геометрические сведения.

Простейшие геометрические фигуры: прямая, точка, отрезок, луч, угол. Понятие равенства геометрических фигур. Сравнение отрезков и углов. Измерение отрезков, длина отрезков. Измерение углов, градусная мера угла. Смежные и вертикальные углы, их свойства. Перпендикулярные прямые.

Основная цель – систематизировать знания учащихся о простейших геометрических фигурах и их свойствах; ввести понятие равенства фигур. Определённое внимание должно уделяться практическим приложениям геометрических понятий.

Треугольники.

Треугольники. Признаки равенства треугольников. Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника. Равнобедренный треугольник и его свойства. Задачи на построение с помощью циркуля и линейки.

Основная цель – ввести понятие теоремы; выработать умение доказывать равенство треугольников с помощью изученных признаков; ввести новый класс задач – на построение с помощью циркуля и линейки.

Параллельные прямые.

Признаки параллельности прямых. Аксиома параллельности прямых. Свойства параллельных прямых.

Основная цель – ввести одно из важнейших понятий – понятие о параллельных прямых; дать первое представление об аксиомах и аксиоматическом методе в геометрии; ввести аксиому параллельных прямых.

Соотношение между сторонами и углами треугольника.

Сумма углов треугольника. Соотношение между сторонами и углами треугольника. Неравенство треугольника Прямоугольные треугольники, их свойства и признаки равенства. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Построение треугольника по трём элементам.

Основная цель – рассмотреть новые интересные и важные свойства треугольника.

Критерии оценки

Основой оценивания являются требования к знаниям и умениям, сформулированные в государственных стандартах базового уровня, а также указания по оцениванию заданий ГИА.

Ответ экзаменуемого оценивается с учетом:

полноты раскрытия содержания материала в объеме, предусмотренном программой и учебником;
изложения материала грамотным языком, точного использования математической терминологии и символики, в определенной логической последовательности;
правильного выполнения рисунков, чертежей, сопутствующих ответу;
умения иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
демонстрации знания теории ранее изученных сопутствующих тем, сформированности и устойчивости используемых при ответе умений и навыков;
самостоятельности, без наводящих вопросов учителя;
неточностей при освещении второстепенных вопросов или выкладок, которые ученик легко исправил после замечания учителя.

Рекомендации по оцениванию ответов

Экзаменационная оценка складывается следующим образом. За каждый вопрос начисляется определенное количество баллов:

Вопрос	№1	№2	№3	№4	Итого
Количество баллов	1	2	2	3	8

Отметка выставляется в соответствии с набранными баллами:

Набранные баллы	0 – 3	4 – 5	6	7 – 8
Отметка	2	3	4	5

Источник

Билеты по геометрии.

7 класс.

Выбери билет.

Конец!!!

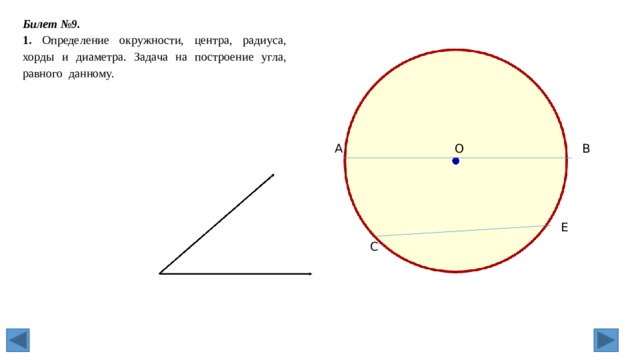
Билет №9.

1. Определение окружности, центра, радиуса, хорды и диаметра. Задача на построение угла, равного данному.

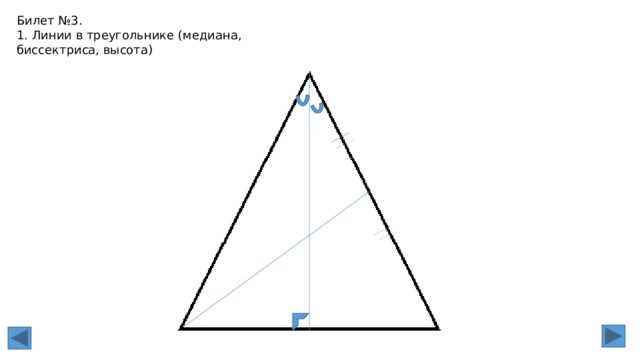
Билет №3.

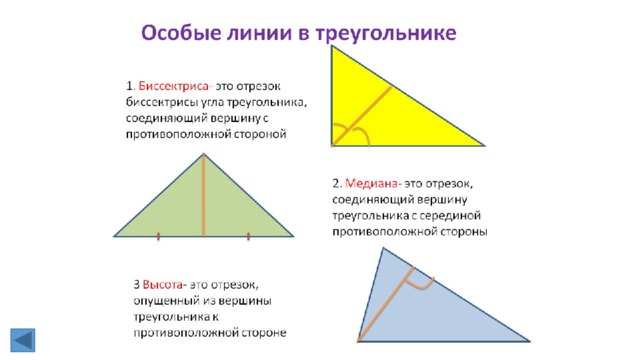
1. Линии в треугольнике (медиана, биссектриса, высота)

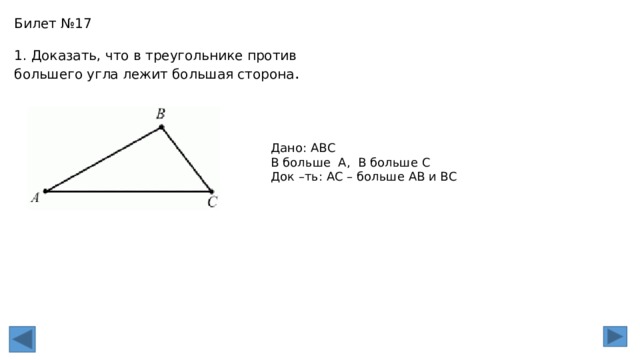
Билет №17

1. Доказать, что в треугольнике против большего угла лежит большая сторона .

Дано: АВС

В больше А, В больше С

Док –ть: АС – больше АВ и ВС

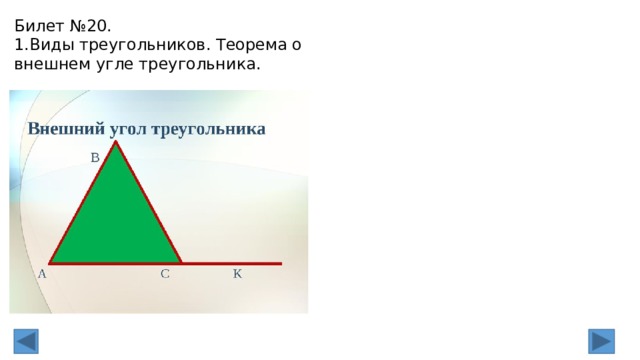
Билет №20.

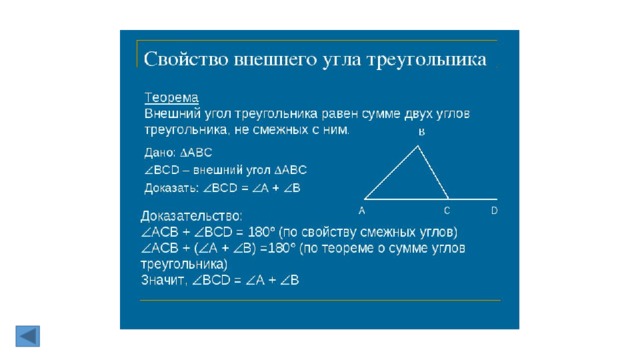
1.Виды треугольников. Теорема о внешнем угле треугольника.

Билет №6.

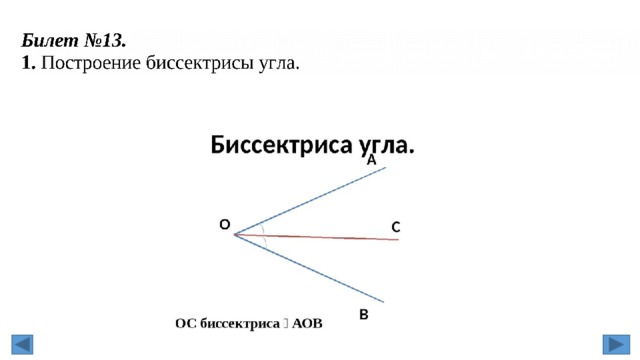
1.Свойство биссектрисы равнобедренного треугольника.

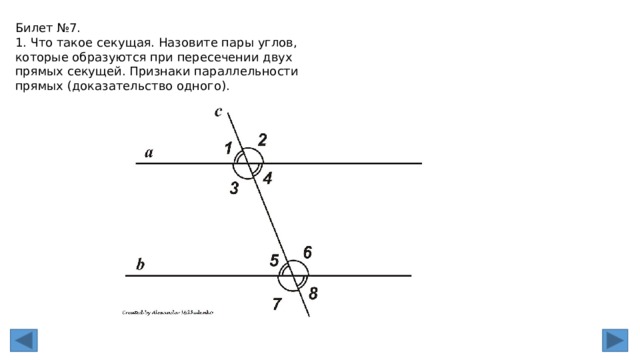
Билет №7.

1. Что такое секущая. Назовите пары углов, которые образуются при пересечении двух прямых секущей. Признаки параллельности прямых (доказательство одного).

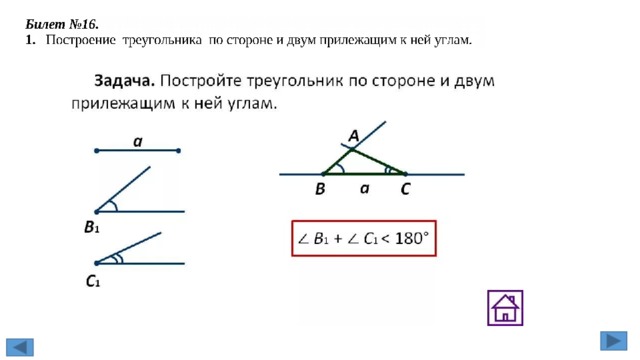
Билет №15.

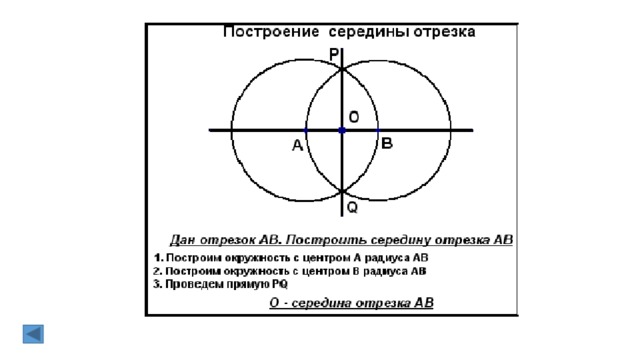
1.Построение середины отрезка.

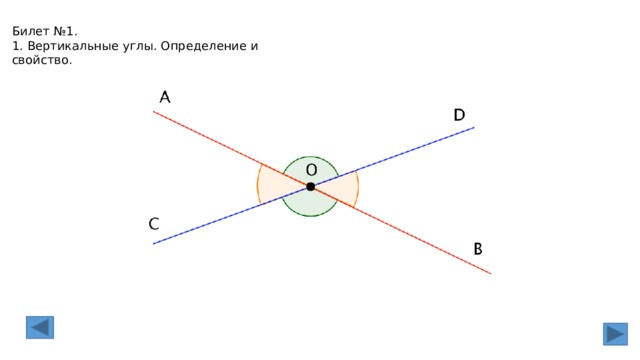
Билет №1.

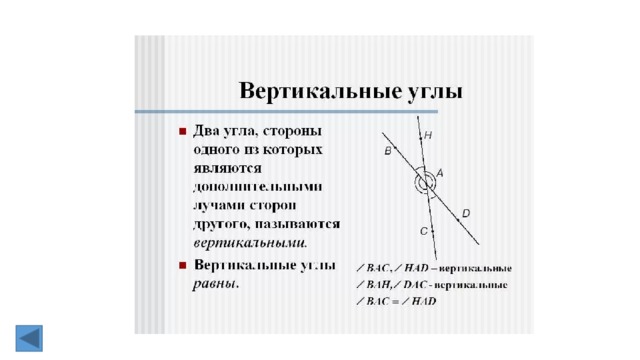
1. Вертикальные углы. Определение и свойство.

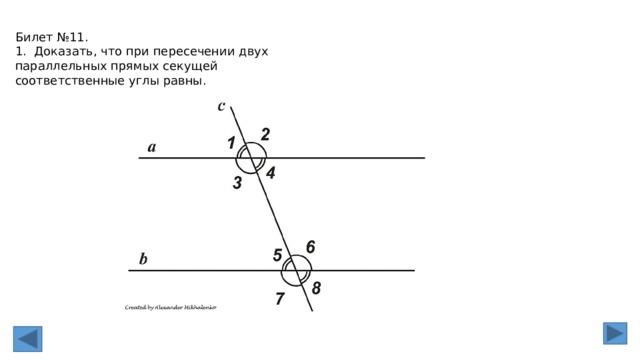
Билет №11.

1. Доказать, что при пересечении двух параллельных прямых секущей соответственные углы равны.

Билет №4.

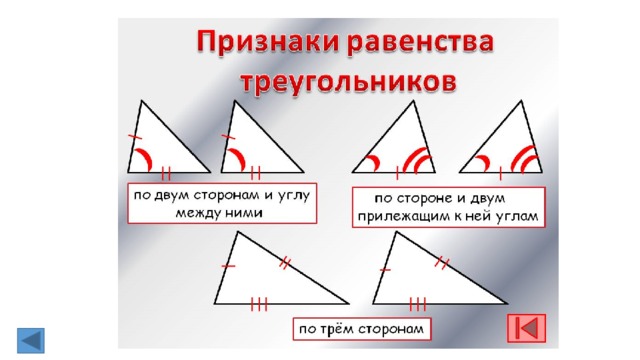
1.Признаки равенства треугольников(доказательство одного).

Билет №8.

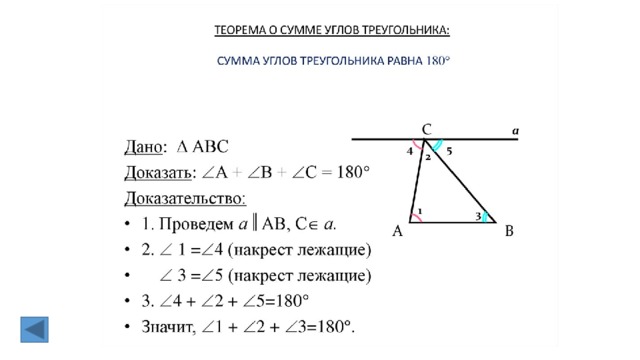
1. Теорема о сумме углов треугольника.

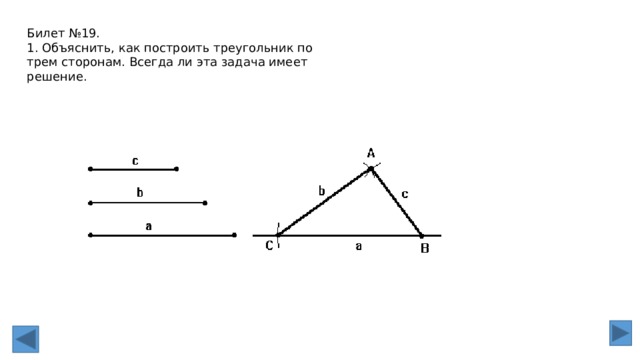
Билет №19.

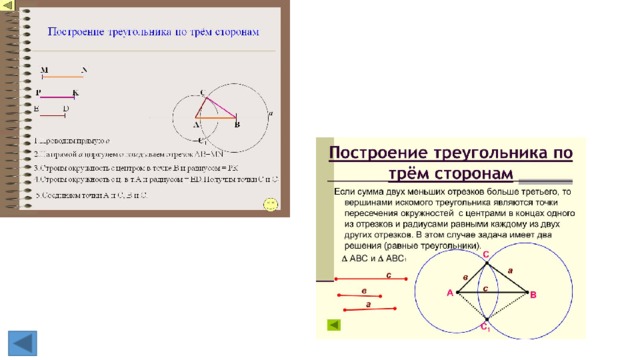
1. Объяснить, как построить треугольник по трем сторонам. Всегда ли эта задача имеет решение.

Билет №2.

1. Смежные углы. Определение и свойство.

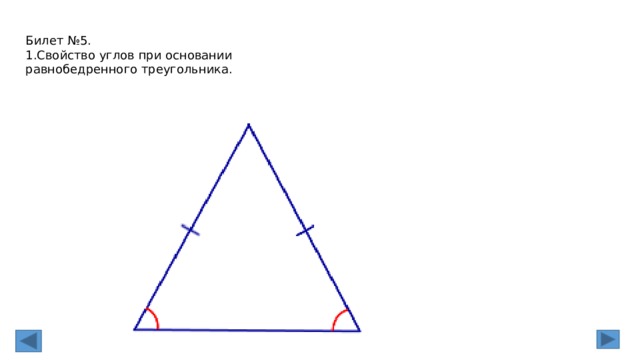
Билет №5.

1.Свойство углов при основании равнобедренного треугольника.

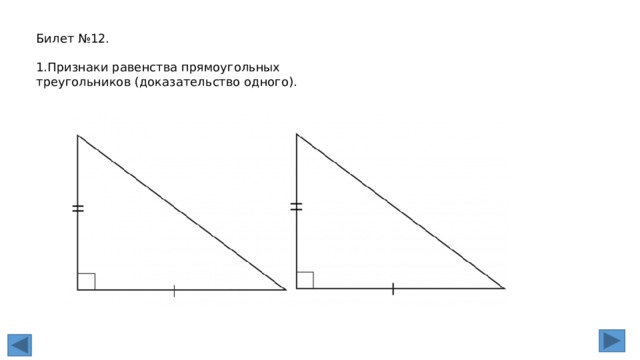
Билет №12.

1.Признаки равенства прямоугольных треугольников (доказательство одного).

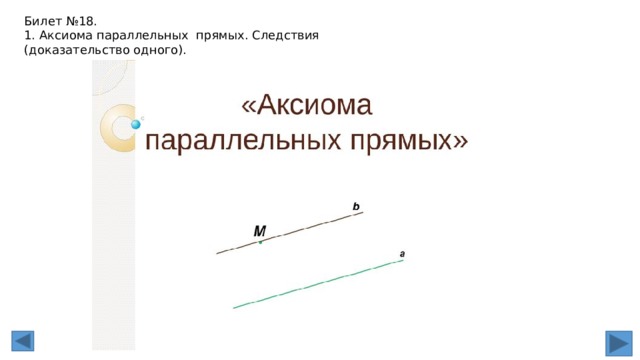
Билет №18.

1. Аксиома параллельных прямых. Следствия (доказательство одного).

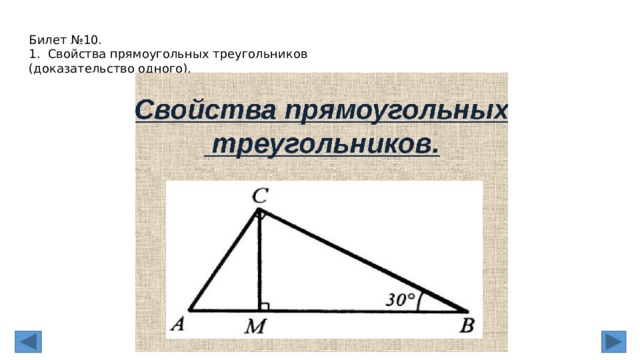
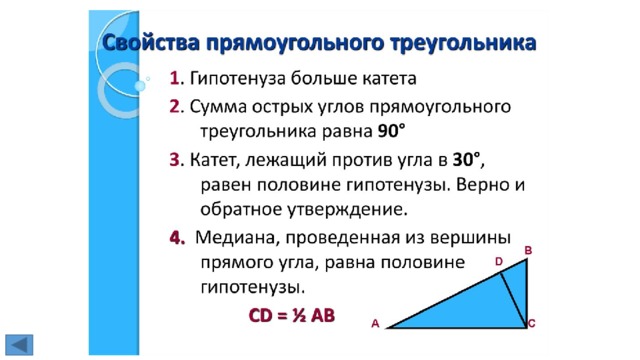
Билет №10.

1. Свойства прямоугольных треугольников (доказательство одного).

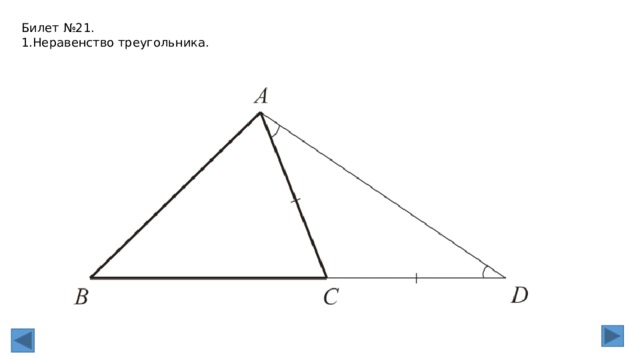
Билет №21.

1.Неравенство треугольника.

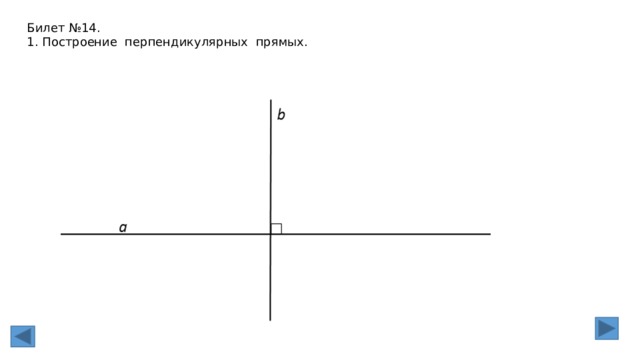
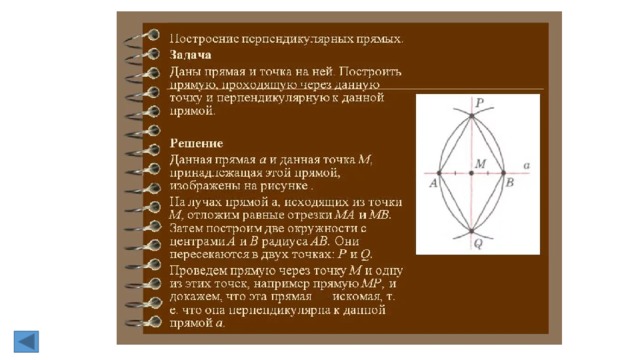
Билет №14.

1. Построение перпендикулярных прямых.

Источник

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №3»

_____________________________________________________________________________

БИЛЕТЫ ДЛЯ ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ

ПО ГЕОМЕТРИИ В УСТНОЙ ФОРМЕ ДЛЯ 7 КЛАССОВ

Пояснительная записка

Билеты для промежуточной аттестации по геометрии в устной форме за курс 7 класса составлены на основе федерального государственного стандарта основного общего образования, примерной программы основного общего образования по математике (Примерная программа по учебным предметам «Математика 5 – 9 класс: проект» – М.: Просвещение, 2011 г), Требований к результатам освоения основной образовательной программы основного общего образования, установленных в Федеральном государственном образовательном стандарте основного общего образования. Экзаменационные билеты ориентирована на содержание учебника Геометрия: 7 – 9 кл. / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – М.: Просвещение, 2014.

Промежуточная аттестация обеспечивает достижения следующих результатов освоения образовательной программы основного общего образования:

личностные:

умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
креативность мышления, инициативу, находчивость, активность при решении геометрических задач;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;

метапредметные:

регулятивные универсальные учебные действия:

умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
умение осуществлять контроль по результату и способу действия на уровне произвольного внимания и вносить необходимые коррективы;
умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;

познавательные универсальные учебные действия:

умение создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;
формирование и развитие учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
формирование первоначальных представлений об идеях и о методах математики как универсальном языке науки и техники, средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;

коммуникативные универсальные учебные действия:

умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, общие способы работы;
умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов;
слушать партнера;
формулировать, аргументировать и отстаивать свое мнение;

предметные:

овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях (геометрическая фигура, величина) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
умение работать с геометрическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;
овладение навыками устных письменных, инструментальных вычислений;
овладение геометрическим языком, умение использовать его для описания предметов окружающего мира, развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений;
усвоение систематических знаний о плоских фигурах и их свойствах, умение применять систематические знания о них для решения геометрических и практических задач;
умение измерять длины отрезков, величины углов;
умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочные материалы и технические средства.

Содержание заданий экзаменационных билетов разработано по основным темам курса геометрии для 7 класса. Содержание раздела «Начальные геометрические сведения» подразделяется на следующие темы: «Прямая и отрезок», «Точка, прямая, отрезок», «Луч и угол. Сравнение отрезков и углов», «Равенство геометрических фигур. Измерение отрезков и углов», «Длина отрезка. Градусная мера угла. Единицы измерения», «Виды углов. Вертикальные и смежные углы», «Биссектриса угла», «Перпендикулярные прямые». Раздел «Треугольники» имеет темы «Равнобедренные и равносторонние треугольники; свойства и признаки равнобедренного треугольника. Признаки равенства треугольников. Окружность. Дуга, хорда, радиус, диаметр. Построения с помощью циркуля и линейки. Основные задачи на построение: деление отрезка пополам; построение угла, равному данному; построение биссектрисы угла; построение перпендикулярных прямых. Раздел «Параллельные прямые» содержит темы «Параллельные и пересекающиеся прямые», «Теоремы о параллельности прямых», «Определение. Аксиомы и теоремы. Доказательство от противного. Теорема, обратная данной». Раздел «Соотношения между сторонами и углами треугольника» содержит темы «Сумма углов треугольника», «Внешние углы треугольника. Виды треугольников», «Теорема о соотношениях между сторонами и углами треугольника», «Неравенство треугольника», «Прямоугольные треугольники; свойства и признаки равенства прямоугольных треугольников», Расстояние от точки до прямой. Расстояние между параллельными прямыми», «Построения с помощью циркуля и линейки. Построение треугольника по трем элементам».

Комплект билетов по информатике имеет следующую структуру: каждый билет содержит две части — теоретическую и практическую. Теоретическая часть предполагает устный ответ учащихся с возможной демонстрацией необходимой для ответа иллюстративной части. Это может быть описание объектов изучения, их существенных признаков, свойств, связей между ними, т.е. раскрытие сущности изученного объекта. Практическая часть содержит задание, которое решает определённую геометрическую задачу.

Примерное время, отводимое на подготовку ученика к ответу – 15-20 минут.

Отметка «5» ставится, если ученик ответил на все теоретические вопросы и решил задачу.

Отметка «4» ставится, если ученик ответил:

— на все теоретические вопросы

— на первый теоретический вопрос и решил задачу.

Отметка «3» ставится, если ученик ответил:

— на первый теоретический вопрос;

— на второй теоретический вопрос и решил задачу;

— решил задачу.

В остальных случаях ставится отметка «2».

Экзаменационные билеты по геометрии с задачами. 7 класс.

Билет №1.

1. Точки. Прямые. Отрезки.

2. Сформулировать и доказать теорему, выражающую третий признак равенства треугольников.

3. Задача на тему «Смежные углы».

Найдите величины смежных углов, если один из них в 5 раз больше другого.

Билет №2.

1. Виды треугольников.

2. Доказать, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

3. Задача на тему «Признаки равенства треугольников».

Отрезки AC и BM пересекаются и точкой пересечения делятся пополам. Доказать, что треугольник ABC равен треугольнику CMA.

Билет №3.

1. Линии в треугольнике (медиана, биссектриса, высота).

2. Доказать, что если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны

3. Задача на тему «Окружность».

На окружности с центром О отмечены точки А и В так, что угол AOB прямой. Отрезок ВС — диаметр окружности. Докажите, что хорды AB и AC , равны.

Билет №4.

1. Наклонная, проведенная из данной точки к прямой, расстояние от точки до прямой.

2. Доказать, что если при пересечении двух прямых секущей сумма односторонних углов равна 180, то прямые параллельны.

3. Задача на тему «Внешний угол треугольника».

Два внешних угла треугольника при разных вершинах равны. Периметр треугольника равен 74 см, а одна из сторон равна 16 см. Найдите две другие стороны треугольника.

Билет №5.

1. Определение параллельных прямых, параллельные отрезки.

2. Сформулировать и доказать первый признак равенства треугольников.

3. Задача на тему «Треугольники».

В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найти медиану AM, если периметр треугольника ABC равен 32 см, а периметр треугольника ABM равен 24 см.

Билет №6.

1. Луч Угол. Виды углов.

2. Свойство углов при основании равнобедренного треугольника.

3. Задача на тему «Свойства параллельности двух прямых».

Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210. Найти эти углы.

Билет №7.

1. Что такое секущая. Назовите пары углов, которые образуются при пересечении двух прямых секущей.

2. Сформулировать и доказать теорему, выражающую второй признак равенства треугольников.

3. Задача на тему «Признаки параллельности двух прямых».

Отрезок АМ-биссектриса треугольника ABC. Через точку M проведена прямая, параллельная AC и пересекающая сторону AB в точке E. Доказать, что треугольник AME равнобедренный.

Билет №8.

1. Объясните, как построить треугольник по двум сторонам и углу между ними.

2. Теорема о сумме углов треугольника.

3. Задача на тему «Второй признак равенства треугольников».

На биссектрисе угла А взята точка E, а на сторонах этого угла точки В и С такие, что угол AEC равен углу AEB. Доказать, что BE равно CE.

Билет №9.

1. Определение окружности, центра, радиуса, хорды и диаметра.

2. Неравенство треугольника.

3. Задача на тему «Признаки параллельности двух прямых».

Отрезки AB и CM пересекаются в их общей середине. Доказать, что прямые AC и BM параллельны.

Билет №10.

1. Аксиомы геометрии. Аксиома параллельных прямых и свойства из нее вытекающие.

2. Свойства прямоугольных треугольников.

3. Задача на тему «Соотношения между сторонами и углами треугольника».

Доказать, что середины сторон равнобедренного треугольника являются вершинами другого равнобедренного треугольника.

Билет №11.

1. Какой треугольник называется прямоугольным. Стороны прямоугольного треугольника.

2. Доказать, что при пересечении двух параллельных прямых секущей соответственные углы равны.

3. Задача на тему «Смежные углы».

Найти смежные углы, если один из них на 45 больше другого.

Билет №12.

1. Смежные углы ( определение и свойства).

2. Доказать признак равенства прямоугольных треугольников по гипотенузе и катету.

3. Задача на тему «Свойства равнобедренного треугольника».

Докажите, что если биссектриса треугольника совпадает с его высотой, то треугольник равнобедренный.

Билет №13.

1. Вертикальные углы (определение и свойства).

2. Доказать признак равенства прямоугольных треугольников по гипотенузе и острому углу.

3. Задача на тему «Признаки равенства треугольников».

Отрезки AB и CE пересекаются в их общей середине О. На отрезках AC и BE отмечены точки К и M так, что AK равно BM. Доказать, что OK равно OM.

Билет №14.

1. Объяснить, как отложить на данном луче от его начала отрезок, равный данному.

2. Свойство биссектрисы угла равнобедренного треугольника, проведенной к основанию.

3. Задача на тему «Свойства прямоугольных треугольников».

Один из углов прямоугольного треугольника равен 60, а сумма гипотенузы и меньшего из катетов равна 26,4 см. Найти гипотенузу треугольника.

Билет №15.

1. Какая теорема называется обратной к данной теореме. Привести примеры.

2. Доказать, что если две прямые параллельны третьей, то они параллельны.

3. Задача на тему «Признаки параллельности двух прямых».

Разность двух односторонних углов при пересечении двух параллельных прямых секущей равна 50. Найти эти углы.

Билет №16.

1. Объясните, как построить треугольник по стороне и двум прилежащим к ней углам.

2. Свойство внешнего угла треугольника.

3. Задача на тему «Расстояние от точки до прямой».

Через середину отрезка проведена прямая. Доказать, что концы отрезка равноудалены от этой прямой.

Билет №17

1. Параллельные прямые. Расстояние между параллельными прямыми.

2. Доказать, что в треугольнике против большего угла лежит большая сторона.

3. Задача на тему «Признаки параллельности двух прямых».

В треугольнике ABC угол А равен 40, а угол ВСЕ, смежный с углом ACB, равен 80.Доказать, что биссектриса угла ВСЕ параллельна прямой AB.

Билет №18.

1. Признаки равенства прямоугольных треугольников.

2. Доказать свойство вертикальных углов.

3. Задача на тему «Расстояние от точки до прямой».

В равнобедренном треугольнике ABC с основанием АС = 37 см, внешний угол при вершине В равен 60. Найти расстояние от вершины С до прямой AB.

Билет №19.

1. Объяснить, как построить треугольник по трем сторонам. Всегда ли эта задача имеет решение.

2. Доказать, что против большей стороны в треугольнике лежит больший угол.

3. Задача на тему «Периметр треугольника».

Основание равнобедренного треугольника равно 8 см. Медиана, проведенная к боковой стороне, разбивает треугольник на два треугольника так, что периметр одного треугольника на 2 см больше периметра другого. Найти боковую сторону данного треугольника.

Билет №20.

1. Объясните, как построить биссектрису данного угла.

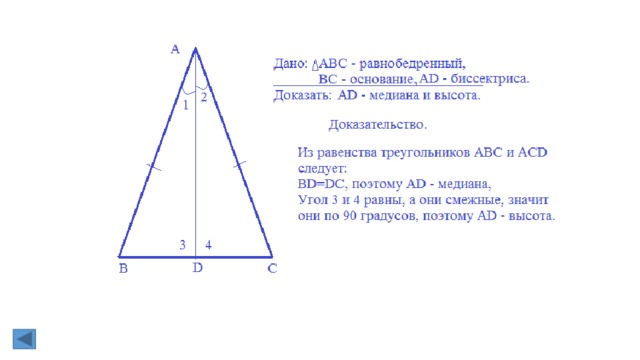
2. Доказать, что высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.

3. Задача на тему «Свойства прямоугольных треугольников».

В прямоугольном треугольнике ABC с прямым углом С внешний угол при вершине А равен 120, АС + АВ = 18 см. Найти AC и AB.

Билет №21.

1. Объясните, как найти середину отрезка.

2. Доказать, что если при пересечении двух прямых секущей, сумма односторонних углов равна 180, то прямые параллельны.

3. Задача на тему «Признаки равенства треугольников».

В треугольниках ABC и MKE отрезки СО и EH медианы, BC=KE, угол В равен углу К и угол С равен углу E. Доказать, что треугольник АСО равен треугольнику MEH.

Билет №22.

1. Определение окружности, центра, радиуса, хорды и диаметра.

2. Свойства прямоугольных треугольников.

3. Задача на тему «Признаки параллельности двух прямых».

Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них равен 42°

Билет №23.

1. Определение параллельных прямых, параллельные отрезки.

2. Доказать, что в треугольнике против большего угла лежит большая сторона.

3. Задача на тему «Свойства равнобедренного треугольника».

Найдите углы при основании MP равнобедренного треугольника МОР, если MK – его биссектриса и OKM = 96°.

Билет №24.

1. Виды треугольников.

2.Доказать, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

3. Задача на тему «Неравенство треугольника».

В равнобедренном треугольнике одна сторона равна 25см, а другая равна 10 см. Какая из них является основанием?

Билет №25.

1. Какой треугольник называется прямоугольным. Стороны прямоугольного треугольника.

2. Теорема о сумме углов треугольника.

3. Задача на тему «Вертикальные углы».

Прямые АВ и CD пересекаются в точке О. Угол АОС равен 58⁰. Найдите угол ВОD.

Экзаменационные билеты по геометрии. 7 класс.

Билет №1.

1. Точки. Прямые. Отрезки.

2. Сформулировать и доказать теорему, выражающую третий признак равенства треугольников.

3. Задача на тему «Смежные углы».

Билет №2.

1. Виды треугольников.

2. Доказать, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

3. Задача на тему «Признаки равенства треугольников».

Билет №3.

1. Линии в треугольнике (медиана, биссектриса, высота).

2. Доказать, что если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны

3. Задача на тему «Окружность».

Билет №4.

1. Наклонная, проведенная из данной точки к прямой, расстояние от точки до прямой.

3. Задача на тему «Внешний угол треугольника».

Билет №5.

1. Определение параллельных прямых, параллельные отрезки.

2. Сформулировать и доказать первый признак равенства треугольников.

3. Задача на тему «Треугольники».

Билет №6.

1. Луч Угол. Виды углов.

2. Свойство углов при основании равнобедренного треугольника.

3. Задача на тему «Свойства параллельности двух прямых».

Билет №7.

1. Что такое секущая. Назовите пары углов, которые образуются при пересечении двух прямых секущей.

2. Сформулировать и доказать теорему, выражающую второй признак равенства треугольников.

3. Задача на тему «Признаки параллельности двух прямых». .

Билет №8.

1. Объясните, как построить треугольник по двум сторонам и углу между ними.

2. Теорема о сумме углов треугольника.

3. Задача на тему «Второй признак равенства треугольников».

Билет №9.

1. Определение окружности, центра, радиуса, хорды и диаметра.

2. Неравенство треугольника.

3. Задача на тему «Признаки параллельности двух прямых».

Билет №10.

1. Аксиомы геометрии. Аксиома параллельных прямых и свойства из нее вытекающие.

2. Свойства прямоугольных треугольников.

3. Задача на тему «Соотношения между сторонами и углами треугольника».

Билет №11.

1. Какой треугольник называется прямоугольным. Стороны прямоугольного треугольника.

2. Доказать, что при пересечении двух параллельных прямых секущей соответственные углы равны.

3. Задача на тему «Смежные углы».

Билет №12.

1. Смежные углы (определение и свойства).

2. Доказать признак равенства прямоугольных треугольников по гипотенузе и катету.

3. Задача на тему «Свойства равнобедренного треугольника».

Билет №13.

1. Вертикальные углы (определение и свойства).

2. Доказать признак равенства прямоугольных треугольников по гипотенузе и острому углу.

3. Задача на тему «Признаки равенства треугольников».

Билет №14.

1. Объяснить, как отложить на данном луче от его начала отрезок, равный данному.

2. Свойство биссектрисы угла равнобедренного треугольника, проведенной к основанию.

3. Задача на тему «Свойства прямоугольных треугольников».

Билет №15.

1. Какая теорема называется обратной к данной теореме. Привести примеры.

2. Доказать, что если две прямые параллельны третьей, то они параллельны.

3. Задача на тему «Признаки параллельности двух прямых».

Билет №16.

1. Объясните, как построить треугольник по стороне и двум прилежащим к ней углам.

2. Свойство внешнего угла треугольника.

3. Задача на тему «Расстояние от точки до прямой».

Билет №17

1. Параллельные прямые. Расстояние между параллельными прямыми.

2. Доказать, что в треугольнике против большего угла лежит большая сторона.

3. Задача на тему «Признаки параллельности двух прямых».

Билет №18.

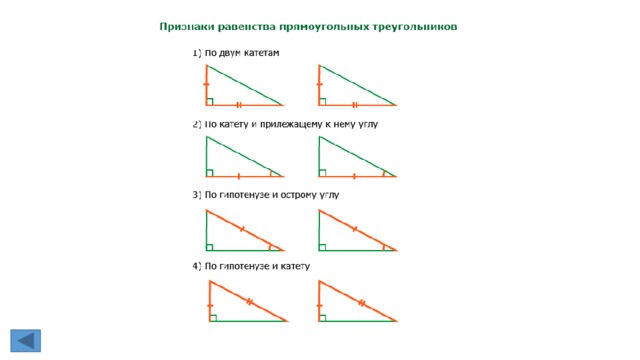
1. Признаки равенства прямоугольных треугольников.

2. Доказать свойство вертикальных углов.

3. Задача на тему «Расстояние от точки до прямой».

Билет №19.

1. Объяснить, как построить треугольник по трем сторонам. Всегда ли эта задача имеет решение.

2. Доказать, что против большей стороны в треугольнике лежит больший угол.

3. Задача на тему «Периметр треугольника».

Билет №20.

1. Объясните, как построить биссектрису данного угла.

3. Задача на тему «Свойства прямоугольных треугольников».

Билет №21.

1. Объясните, как найти середину отрезка.

3. Задача на тему «Признаки равенства треугольников».

Билет №22.

1. Определение окружности, центра, радиуса, хорды и диаметра.

2. Свойства прямоугольных треугольников.

3. Задача на тему «Признаки параллельности двух прямых».

Билет №23.

1. Определение параллельных прямых, параллельные отрезки.

2. Доказать, что в треугольнике против большего угла лежит большая сторона.

3. Задача на тему «Свойства равнобедренного треугольника».

Билет №24.

1. Виды треугольников.

2.Доказать, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

3. Задача на тему «Неравенство треугольника».

Билет №25.

1. Какой треугольник называется прямоугольным. Стороны прямоугольного треугольника.

2. Теорема о сумме углов треугольника.

3. Задача на тему «Вертикальные углы».

Источник

Введение

В данной работе я предлагаю вопросы для зачётов, задачи к этим зачётам и
билеты к экзамену за курс геометрии 7 класса. Практический материал на экзамене
можно предложить из задач к зачётам.

Надеюсь, что данная работа поможет преподавателю математики проверить знания
по данной дисциплине на начальной стадии её усвоения.

Для учащихся полезно будет по вопросам к зачётам готовить учебный материал
самостоятельно, решая задачи, усваивать теоретические знания на практике, тем
самым делая учебу интересной и успешной.

В 7 классе у наших детей появляется новый учебный предмет, который поначалу
может показаться простым и не очень серьезным. Но это далеко не так. В былые
годы наличие обязательного экзамена по геометрии с первых дней изучения новой
дисциплины настраивало на серьёзный лад. Сейчас наличие задач по геометрии в ГИА
и ЕГЭ по математике помогает убедить учащихся в насущности и значимости
предмета. Необходимость теоретических знаний понимается большинством учащихся
при решении задач, доказательстве теорем, везде, где не обойтись без
аргументированных объяснений. Задача учителя не только донести знания по
предмету, но и заставить овладеть ими. Готовясь к зачётам дети вынуждены
самостоятельно разбирать, заучивать учебный материал, а также консультироваться
у учителя, друг у друга, доказывая друзьям теоремы и решая задачи на
дополнительных занятиях и консультациях по математике. Этот процесс – объяснение
товарищу – очень нравится ребятам, они при этом повышают свою самооценку,
мотивацию к учебе, повышают качество собственных знаний. Учащиеся сначала
побаиваются зачетов, но в процессе подготовки и при проведении понимают их
необходимость, поэтому относятся более ответственно к данной технологии. Но как
любое полезное для детей мероприятие, подготовка зачёта и экзамена, требует
серьёзной и кропотливой работы со стороны взрослых, в данном случае – учителя
математики. Надеюсь своей работой облегчить на начальном этапе труд педагога при
подготовке к зачету по геометрии в 7 классе.

ЗАЧЕТ № 1

Основные геометрические фигуры на плоскости. Их изображение и
обозначение. Основные свойства принадлежности точек и прямых на плоскости.
Понятие «точка лежит между точками». Отрезок. Концы отрезка. Равные
отрезки. Основное свойство расположения точек на прямой.
Основное свойство измерения отрезков.
Основное свойство расположения точек относительно прямой.
Полупрямая. Начальная точка полупрямой. Дополнительные полупрямые.
Угол. Вершина угла. Стороны угла. Виды углов. Равные углы. Понятие «луч
проходит между сторонами угла». Основные свойства измерения углов.
Основные свойства откладывания отрезков и углов.
Треугольник. Вершины треугольника. Стороны треугольника. Угол
треугольника. Равные треугольники. Основное свойство существования
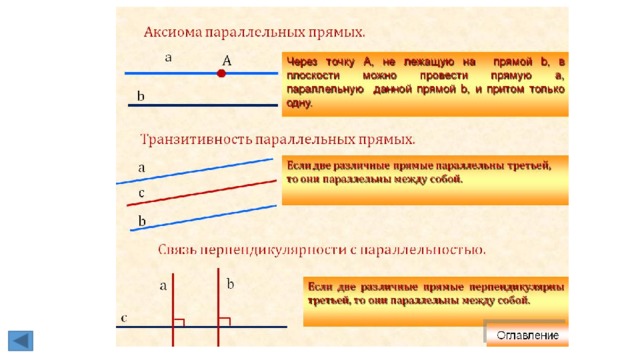
треугольника, равного данному.
Параллельные прямые. Изображение и обозначение. Основное свойство
параллельных прямых.

ЗАДАЧИ К ЗАЧЕТУ № 1

На отрезке AB длиной 23 см взята точка C так, что отрезок
AC на 7 см меньше отрезка CB.
Найдите длины отрезков BD, если AC и BC.
На отрезке AB длиной 17 см отмечена точка C так, что отрезок AC равен 9
см. Найдите длину отрезка BC.
На отрезке AB взяты точки C
и D. Найдите длину отрезка CD,
если AB= 22 см, AC= 13 см,
BD= 7см.
На отрезке AB взята точка C, а на отрезке CB –
точка D. Найдите длину отрезка BD, если AB= 17 см, CD=
8 см, AC= 7см.
На отрезке AB взяты точки C
и D. Известно, что AB= 22 см,
AC= 18 см, CD= 7см. Найдите
длину отрезка BD.
На отрезке AB длиной 28 см взята точка
K. Найдите длины отрезков AK и
BK, если AK больше
BK на 6 см.
На отрезке AB длиной 28 см взята точка K. Найдите длины отрезков AK и BK,
если AK меньше BK в 6 раз.
На отрезке AB длиной 56 см взята точка K. Найдите длины отрезков AK и BK,
если AK : BK=2:7.
Луч с проходит между сторонами угла (аb), равного
62?. Найдите угол ( ас), если угол (bс) равен 43?.
Луч с проходит между сторонами угла (аb), равного 62?. Найдите углы (ас)
и (bс), если угол (ac) на 27? больше угла (bc).
Луч ОС проходит между сторонами угла АОВ, равного 160?. Найдите углы АОС
и СОВ, если угол АОС меньше угла СОВ в 3 раза.
Луч ОС проходит между сторонами угла АОВ, равного 140?. Найдите углы АОС
и СОВ, если угол АОС на 50? больше угла СОВ.
Может ли луч с проходить между сторонами угла (ab),
если угол (ab) равен 45?, угол (aс) равен 130?, угол
(сb) равен 85??
Дано: угол АОВ равен 137?, угол AOD равен 28?, угол COB равен 34?
Найти: угол COD.
Треугольники АВС и MNK равны. Известно, что АВ=
17 см, АС= 11 см. Чему равны соответствующие стороны треугольника
MNK?
Треугольники АВС и MNK равны. Известно, что угол М равен 69?, угол
K равен 28?. Чему равны соответствующие углы
треугольника АВС?

ЗАЧЕТ № 2

Угол. Вершина угла. Стороны угла. Виды углов. Равные углы. Понятие «луч
проходит между сторонами угла». Основные свойства измерения углов.
Биссектриса угла.
Смежные углы. Теорема о смежных углах. Свойства из теоремы о смежных
углах.
Вертикальные углы. Теорема о вертикальных углах.
Перпендикулярные прямые. Изображение и обозначение. Теорема о
единственности перпендикуляра к прямой, проходящего через точку этой прямой.
Перпендикуляр к данной прямой.

ЗАДАЧИ К ЗАЧЕТУ № 2

Найдите углы смежные с углами 39?, 83?, 90?, 157?.
Найдите смежные углы, если один из них на 27? больше другого.
Найдите смежные углы, если один из в 2 раза меньше другого.
Смежные углы относятся как 3:2. Найдите эти смежные углы.
Один из смежных углов составляет 0,5 другого угла. Найдите эти смежные
углы.
Один из углов, образованных при пересечении двух прямых, равен 37?.
Найдите остальные углы.
Один из углов, образованных при пересечении двух прямых, в 3 раза больше
другого. Найдите все образовавшиеся при этом углы.
Один из углов, образованных при пересечении двух прямых, на 36? меньше
другого. Найдите все образовавшиеся при этом углы.
Сумма двух углов, которые получаются при пересечении двух прямых, равна
86?. Найдите все получившиеся при этом углы.
Сумма трех углов, образовавшихся при пересечении двух прямых, равна
235?. Найдите эти углы.

ЗАЧЕТ № 3

Треугольник. Вершины треугольника. Стороны треугольника. Угол
треугольника.Равные треугольники. Основное свойство существования
треугольника, равного данному.
Первый признак равенства треугольников.
Второй признак равенства треугольников.
Третий признак равенства треугольников.
Равнобедренный треугольник. Боковые стороны. Основание. Свойство углов
равнобедренного треугольника.
Равнобедренный треугольник. Высота, биссектриса, медиана треугольника.
Свойство медианы равнобедренного треугольника.
Равнобедренный треугольник. Признак равнобедренного треугольника.

ЗАДАЧИ К ЗАЧЕТУ № 3

Дано: ΔАВС и ΔСBD, AB=
CD, угол ABD равен углу
CBD. Докажите, что ΔАВС=ΔСBD.
Дано: ΔАВС и ΔАDС, угол ВAС равен углу DАС, угол ВСА равен углу
DCA. Докажите, что ΔАВС=ΔСBD.
Дано: ΔАВС и ΔСBD,
AB= CD, угол
ABD равен углу CBD. Докажите, что АD=СD.
Равные отрезки AB и CD точкой пересечения М делятся пополам. Докажите
равенство треугольников AMC и BMD.
Равные отрезки AB и CD
точкой пересечения М делятся пополам. Докажите равенство отрезков
AC и BD.
Отрезки AB и CD пересекаются в точке O. Отрезки CO и OD равны, угол ACO
равен 90?, угол BDO равен 90?. Докажите, что Δ AOС=ΔBOD.
Отрезки AB и CD
пересекаются в точке O. Отрезки CO
и OD равны, углы ACO и
BDO прямые. Докажите, что углы CAO
и DBO равны.
Треугольники MNK и MNR
равнобедренные с общим основанием MN. Докажите, что ΔMKR=Δ
NKR.
В равнобедренном треугольнике угол при основании равен 47?. Найдите угол
при вершине данного треугольника.
В равнобедренном треугольнике один из углов равен 91?. Найдите остальные
углы треугольника.
Периметр равнобедренного треугольника равен 34см, основание – 10см.
Найдите длины остальных сторон этого треугольника.
Периметр равнобедренного треугольника 39см. Основание на 6см меньше
боковой стороны. Найдите стороны треугольника.
Периметр равнобедренного треугольника равен 56см. Найдите стороны
треугольника, если его основание в 3 раза меньше боковой стороны.
В ΔCDF проведены медианы CA,
DB, FN. AF=6см,
BC=8см, DN=4см. Найдите
периметр ΔFCD.
Дано ΔABK, AB=
KB, точки M и
N принадлежат сторонам АВ и КВ, BM=BN,
BC – медиана треугольника. Докажите, что
MC=NC.

ЗАЧЕТ № 4

Параллельные прямые. Изображение и обозначение. Основное свойство
параллельных прямых. Теорема о параллельности двух прямых третьей.
Внутренние односторонние углы. Внутренние накрест лежащие углы.
Соответственные углы. Изображение и обозначение. Признак параллельности
прямых. Свойства из теоремы.
Треугольник. Вершины треугольника. Стороны треугольника. Угол
треугольника.. Сумма углов треугольника. Следствие из теоремы.
Треугольник. Вершины треугольника. Стороны треугольника. Угол
треугольника. Внешний угол треугольника. Теорема о внешнем угле
треугольника. Следствие из теоремы.
Прямоугольный треугольник. Признак равенства прямоугольных
треугольников.
Существование и единственность перпендикуляра к прямой. Расстояние от
точки до прямой.

ЗАДАЧИ К ЗАЧЕТУ № 4

Отрезки MN и PK
пересекаются в точке A и делятся ею пополам.
Докажите, что прямые MK ║ PN.
Угол MBA равен 69?, угол BAN
равен 111?. Параллельны ли прямые MB и
AN? Обоснуйте ответ.
Прямые AB и CD пересечены
секущей MN. Точка O– точка
пересечения АВ и MN, точка P –
точка пересечения прямых CD и MN.
Сумма углов AOP и DPN равна
180?. Докажите, что прямые AB и CD
параллельны.
Один из углов, которые получаются при пересечении двух параллельных
прямых секущей равен 49?. Найдите остальные углы.
Сумма двух внутренних накрест лежащих углов при двух параллельных прямых
и секущей равна 138?. Чему равны эти углы?
Найдите углы треугольника, если они пропорциональны числам 2, 3, 4.
Найдите угол между боковыми сторонами равнобедренного треугольника, если
угол при основании равен 53?.
Дано ΔABC, AB =
BC, внешний угол при вершине В равен 72?. Найдите
внутренние углы ΔАВС. Укажите тип данного треугольника.
Внутренние углы треугольника пропорциональны числам 8, 5, 2. Найдите
внешние углы этого треугольника.
Один из внутренних углов треугольника на 16? больше другого, а внешний
угол, смежный с третьим внутренним углом треугольника, равен 110?. Найдите
все внутренние углы треугольника.
Дано ΔMNR – равнобедренный с основанием
MR. Биссектрисы углов при основании пересекаются в
точке B. Угол MBR равен 102?.
Найдите угол MNR.
Дано ΔACB, угол C –
прямой, CD – высота ΔACB, угол DCB
равен 75?. Найти угол CAB.
Дано ΔABC, высоты AH и
CM пересекаются в точке D,
угол BAC равен 60?, угол BCA
равен 70?. Найти угол ADC.

ЗАЧЕТ № 5

Окружность. Центр, радиус, хорда, диаметр окружности. Описанная
окружность. Теорема о центре окружности описанной около треугольника.
Касательная к окружности. Виды касания окружностей. Окружность,
вписанная в треугольник. Теорема о центре окружности, вписанной в
треугольник.
Построение треугольника по трем сторонам.
Построение угла, равного данному.
Построение биссектрисы угла.
Деление отрезка пополам.
Построение перпендикулярной прямой.
Геометрическое место точек. Окружность как геометрическое место точек.
Теорема о точках равноудаленных от двух данных точек.

ЗАДАЧИ К ЗАЧЕТУ № 5

Дано: окружность с центром О. ОА – радиус, ВС – хорда, ОА и
ВС пересекаются в точке К, ОА перпендикулярен ВС. Докажите, что ВК = КС.
Дано: окружность с центром О, СА и СВ касательные. Докажите,
что СО – биссектриса угла АСВ.
Дано: окружность с центром О, АС – диаметр, ОВ – радиус,
градусная мера угла АОВ равна 42?. Найдите углы треугольника ВОС.
Дано: окружность с центром О, АВ – касательная, угол ОАВ
равен 36?. Найти углы ΔОАВ.
Найдите расстояние между центрами двух окружностей в случае
внешнего касания, если их радиусы 19см и 27см.
Найдите расстояние между центрами двух окружностей в случае
внутреннего касания, если их радиусы 23см и 17см.
Постройте треугольник АВС, если угол А равен 35?, угол В
равен 70?, АВ = 4,5см.
Постройте ΔCDF, если
CD = 5см, CF = 6см, угол DCF
равен 45?.
Постройте прямоугольный треугольник по гипотенузе и острому
углу.
Постройте прямоугольный треугольник по гипотенузе и катету.
Дана окружность с центром О и хорда АВ. На окружности
найдите точки, равноудаленные от точек А и В.
Постройте геометрическое место точек, равноудаленных от
точек А, В и С.

БИЛЕТЫ ПО ГЕОМЕТРИИ 7 КЛАСС

№ 1

Основные геометрические фигуры. Обозначение. Изображение. Основные
свойства, связанные с этими понятиями.
Смежные углы.
Задача.

№ 2

Отрезок. Обозначение. Изображение. Основные свойства, связанные с этим
понятием.
Вертикальные углы.
Задача.

№ 3

Измерение отрезков. Основные свойства, связанные с этим понятием.
Первый признак равенства треугольников.
Задача.

№ 4

Полуплоскость. Основные свойства, связанные с этим понятием.
Признак равнобедренного треугольника.
Задача.

№ 5

Полупрямая. Угол. Основные свойства, связанные с этими понятиями.
Свойство углов равнобедренного треугольника.
Задача.

№ 6

Откладывание отрезков и углов. Основные свойства, связанные с этими
понятиями.
Свойство медианы равнобедренного треугольника.
Задача.

№ 7

Треугольник. Основные свойства, связанные с этим понятием.
Признак параллельности прямых.
Задача.

№ 8

Равные треугольники. Основные свойства, связанные с этим понятием.
Теорема о двух прямых, параллельных третьей прямой.
Задача.

№ 9

Параллельные прямые. Основные свойства, связанные с этим понятием.
Сумма углов треугольника.
Задача.

№ 10

Перпендикулярные прямые.
Внешний угол треугольника.
Задача.

№ 11

Биссектриса треугольника.
Свойство углов, образованных при пересечении параллельных прямых
секущей.
Задача.

№ 12

Высота треугольника.
Существование и единственность перпендикуляра к прямой.
Задача.

№ 13

Медиана треугольника.
Теорема о центре окружности, описанной около треугольника.
Задача.

№ 14

Биссектриса треугольника.
Теорема о центре окружности, вписанной в треугольник.
Задача.

Источник

50 вопросов. 25 билетов.

Посмотреть онлайн файл: g7.pdf

1. Точки. Прямые. Отрезки.
2. Сформулировать и доказать теорему, выражающую третий признак равенства треугольников.
3. Виды треугольников.
4. Доказать, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
5. Линии в треугольнике (медиана, биссектриса, высота).
6. Доказать, что если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
7. Наклонная, проведенная из данной точки к прямой, расстояние от точки до прямой.
8. Доказать, что если при пересечении двух прямых секущей сумма односторонних углов равна 180, то прямые параллельны.
9. Определение параллельных прямых, параллельные отрезки.
10. Сформулировать и доказать первый признак равенства треугольников.
11. Луч Угол. Виды углов.
12. Свойство углов при основании равнобедренного треугольника.
13. Что такое секущая. Назовите пары углов, которые образуются при пересечении двух прямых секущей.
14. Сформулировать и доказать теорему, выражающую второй признак равенства треугольников.
15. Объясните, как построить треугольник по двум сторонам и углу между ними.
16. Теорема о сумме углов треугольника.
17. Определение окружности, центра, радиуса, хорды и диаметра.
18. Неравенство треугольника.
19. Аксиомы геометрии. Аксиома параллельных прямых и свойства из нее вытекающие.
20. Свойства прямоугольных треугольников.
21. Какой треугольник называется прямоугольным. Стороны прямоугольного треугольника.
22. Доказать, что при пересечении двух параллельных прямых секущей соответственные углы равны.
23. Смежные углы ( определение и свойства).
24. Доказать признак равенства прямоугольных треугольников по гипотенузе и катету.
25. Вертикальные углы (определение и свойства).
26. Доказать признак равенства прямоугольных треугольников по гипотенузе и острому углу.
27. Объяснить, как отложить на данном луче от его начала отрезок, равный данному.
28. Свойство биссектрисы угла равнобедренного треугольника, проведенной к основанию.
29. Какая теорема называется обратной к данной теореме. Привести примеры.
30. Доказать, что если две прямые параллельны третьей, то они параллельны.
31. Объясните, как построить треугольник по стороне и двум прилежащим к ней углам.
32. Свойство внешнего угла треугольника.
33. Параллельные прямые. Расстояние между параллельными прямыми.
34. Доказать, что в треугольнике против большего угла лежит большая сторона.
35. Признаки равенства прямоугольных треугольников.
36. Доказать свойство вертикальных углов.
37. Объяснить, как построить треугольник по трем сторонам. Всегда ли эта задача имеет решение.
38. Доказать, что против большей стороны в треугольнике лежит больший угол.
39. Объясните, как построить биссектрису данного угла.
40. Доказать, что высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
41. Объясните, как найти середину отрезка.
42. Доказать, что если при пересечении двух прямых секущей, сумма односторонних углов равна 180, то прямые параллельны.
43. Определение окружности, центра, радиуса, хорды и диаметра.
44. Свойства прямоугольных треугольников.
45. Определение параллельных прямых, параллельные отрезки.
46. Доказать, что в треугольнике против большего угла лежит большая сторона.
47. Виды треугольников.
48. Доказать, что если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
49. Какой треугольник называется прямоугольным. Стороны прямоугольного треугольника.
50. Теорема о сумме углов треугольника.

* Всероссийские работы СтатГрад
* Проверочные работы ВПР
* Олимпиады и конкурсы
* Итоговое сочинение
*

Итоговое собеседование

Источник