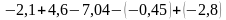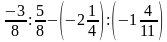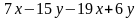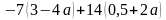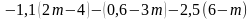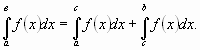Вопросы по устному экзамену по математике

Билет № 1

1. Решение неравенств с одной переменной
2. Параллелограмм. Определение. Свойства. Площадь параллелограмма.
3. Решите уравнение:        

Билет № 2

1. Неполные квадратные уравнения и их решения.  Привести примеры
2. Трапеция. Виды трапеций. Площадь трапеции.
3. Найдите площадь равнобедренного треугольника, если его основание равно 10см, а боковая сторона  равна 13см.

Билет № 3

1. Теорема  ВИЕТА
2. Треугольник. Средняя линия  треугольника.
3. Решите уравнение: х2-5х-1=0

Билет № 4

1. Что такое алгебраическая дробь? Область определения алгебраической дроби. Привести примеры
2. Ромб. Его свойства. Площадь ромба
3. В треугольнике АВС известно, что АС=38, ВМ — медиана, ВМ=17. Найдите АМ.

Билет № 5

1. Свойства  арифметического  квадратного  корня.
2.  Квадрат. Его свойства. Площадь квадрата
3. Сократите дробь:  

Билет № 6

1. Сбор и группировка статистических данных
2. Теорема Пифагора.
3. Катеты прямоугольного треугольника равны 6 и 8см, гипотенуза 10 см. Вычислите высоту, проведённую к гипотенузе

Билет № 7

1. Функция   у= ,  её  свойства  и  график.
2. Трапеция, средняя линия  трапеции.  
3. Упростите выражение:

Билет № 8

1. Квадратное  уравнение. Формулы  корней  квадратного  уравнения.
2. Параллелограмм. Признаки параллелограмма.
3. В окружность вписан треугольник ABC так, что АВ — диаметр окружности. Найдите углы треугольника, если: дуга ВС=134°

Билет № 9

1. Сложение и деление алгебраических дробей. Привести примеры
2. Прямоугольный треугольник. Площадь  прямоугольного  треугольника.
3. Упростите выражение:  

Билет № 10

      1.   Вычитание и умножение алгебраических дробей. Привести примеры.

      2. Теорема Пифагора.

      3. Найдите сторону и площадь ромба, если его диагонали равны 10см и 24см

Билет № 11

1. Вынесение  общего  множителя  из-под  знака  корня. Внесение множителя под знак корня
2. Многоугольники. Четырёхугольники. Сумма углов выпуклого многоугольника
3. Упростите выражение:

                               

Билет № 12.

1. Освобождение  дроби  от  иррациональности.
2. Прямоугольник. Его свойство, признак. Площадь прямоугольника.
3. Основания трапеции равны 3 и 11.  Найдите больший из отрезков, на которые делит среднюю линию этой трапеции

 одна из ее диагоналей.

Билет № 13.

1. Числовые промежутки

2.  Площадь  квадрата и  прямоугольника.

1. Решите систему уравнений:

Билет № 14.

1. Извлечение  квадратного  корня  из  произведения  нескольких  множителей
2. Средняя линия треугольника
3. Сторона треугольника равна 24, а высота, проведенная к этой стороне, равна 19. Найдите площадь треугольника.

Билет № 15.

1. Рациональные дроби и их свойства
2. Синус, косинус, тангенс, котангенс острого  угла  прямоугольного  треугольника.
3. Сократите дробь:  

Билет № 16.

1.  Свойства степени с целым показателем. Привести примеры.
2. Ромб.  Площадь  ромба.
3. Найдите величину острого угла параллелограмма ABCD,

если биссектриса угла А образует со стороной ВС угол,

равный 8°. Ответ дайте в градусах.

Билет № 17.

1. Дробные рациональные  уравнения.
2. Решение  прямоугольного  треугольника.
3. Решите неравенство: 8х-8>7х+6.

Билет № 18.

1. Функция y=  и ее график
2. Значения синуса, косинуса и тангенса для углов 300, 450 и 600
3. Один из острых углов прямоугольного треугольника равен 18°. Найдите его другой острый угол. Ответ дайте в градусах.

Билет № 19.

1   Определение  арифметического  квадратного  корня.

2.  Признаки подобия треугольников. Привести примеры.

3. Решите уравнение (х-2)(-2х-3)=0. Если уравнение имеет более одного   корня, в ответ запишите меньший из корней.

Билет № 20.

1.Стандартный вид числа

2.Трапеция.  Площадь  трапеции.

3. Периметр квадрата равен 32. Найдите площадь этого квадрата.

Билет № 21.

1. Числовые неравенства и их свойства.
2. Определение подобных треугольников.
3. Решите систему неравенств:    -35+5х <0,

                                                                6 — 3х > -18.

Билет № 22.

1. Сложение и умножение числовых неравенств

2. Касательная к окружности. Взаимное расположение прямой и окружности.

3. В треугольнике АВС известно, ∟ВАС=24°, а AD – биссектриса. Найдите ∟BAD. Ответ дайте в градусах.

Билет № 23

1. Окружность, круг, радиус, диаметр, хорда, вписанные углы, центральные  углы.
2. Приведённое  квадратное  уравнение.

1. Найдите значение выражение:

Билет № 24.

1.  Решение систем неравенств с одной переменной
2. Треугольник.  Площадь  треугольника. Формула  Герона
3. Два катета прямоугольного треугольника равны 16 и 4. Найдите его площадь.

Билет №25.

1.  Алгоритм решения дробного уравнения.
2. Вписанная и описанная окружности.

1. Найдите значение выражения  

Вопросы к промежуточной аттестации

по математике

в 6 классе

(по учебнику А.Г. Мерзляка)

Вопросы для устного экзамена по математике в 6 классе.

Каждый билет состоит из двух вопросов, первый – теория по курсу математики 5-6 классов, второй – практическое задание.

1. Определение натурального числа. Законы сложения и умножения: переместительный, сочетательный, распределительный (формулы и правила).

2. Обыкновенные дроби. Правильные и неправильные дроби. Сложение и вычитание дробей с одинаковым знаменателем. Смешанные числа. Перевод из неправильной дроби в смешанное число (выделить целую часть) и из смешанного числа в неправильную дробь.

3. Десятичные дроби. Представление десятичной дроби в виде обыкновенной и обыкновенной в виде десятичной. Сложение и вычитание десятичных дробей.

4. Умножение и деление десятичных дробей на 10, 100, 1000 и т.д. Умножение и деление десятичной дроби на десятичную дробь.

5. Делители и кратные. Признаки делимости на 2, 3, 5, 9, 10, 4, 8.

6. Простые и составные числа, взаимно простые числа. Разложение на простые множители. Нахождение НОД и НОК чисел.

7. Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю.

8. Правила сложения, вычитания, умножения и деления обыкновенных дробей.

9. Взаимно обратные числа. Правила нахождения дроби (процентов) от числа и числа по значению его дроби (процентов).

10. Преобразование обыкновенной дроби в десятичную дробь. Бесконечные периодические десятичные дроби (примеры). Рациональные числа.

11. Отношения и пропорция. Основное свойство пропорции.

12. Прямая и обратная пропорциональные зависимости. Случайные события и вероятность случайного события.

13. Окружность и круг (понятия радиуса, диаметра, хорды). Длина окружности и площадь круга (формулы). Площадь квадрата и прямоугольника (формулы). Объем куба и прямоугольного параллелепипеда (формулы).

14. Целые числа. Противоположные числа. Понятие модуля числа. Сравнение положительных и отрицательных чисел.

15. Правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.

16. Переместительное, сочетательное и распределительное свойства умножения рациональных чисел. Коэффициент. Правила раскрытия скобок, перед которыми стоит знак «плюс» или знак «минус».

17. Решение уравнений. Что значит «решить уравнение». Что такое «корень уравнения».

18. Прямая, отрезок, луч. Перпендикулярные и параллельные прямые. Свойство параллельных прямых.

19. Центральная и осевая симметрии (примеры).

20. Представление о координатной плоскости. Координаты точки на плоскости. График.

Практические задания к экзамену.

1. Задачи на проценты.

1. За контрольную работу по математике было поставлено 15% пятёрок. Сколько учеников писало контрольную работу, если пятёрки получили 6 человек?

(Ответ. 40 учеников)

1. Из 76 м² площади квартиры кухня занимает 12%. Найдите площадь кухни.

(Ответ. 9,12 м²)

1. Примеры на действия с положительными и отрицательными числами.

1. 

2. 

1. Задание на нахождение длины окружности и площади круга.

Найдите длину окружности и площадь круга, если диаметр круга равен 15 см. (Число 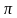округлите до сотых).

(Ответ. C = 47,1 см, S = 176,625 см²)

1. Задачи на масштаб.

а) На чертеже изображен прямоугольник, площадь которого 216 см². Найдите площадь этого прямоугольника в действительности, если чертеж выполнен в масштабе 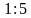. (Ответ. 1080 см²)

б) Расстояние между двумя городами равно 615 км. Каким будет это расстояние на карте, если масштаб карты 1:1500000? (Ответ. 41 см)

1. Координатная плоскость: построение точек с указанными координатами и нахождение координат указанных точек.

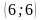
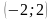
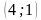
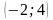
Отметьте на координатной плоскости точки M , N , K и P . Укажите в какой четверти лежит каждая точка. Проведите прямые MN и KP. Найдите координаты точки пересечения:

а) прямых MN и KP;

б) прямой MN с осью абсцисс;

в) прямой KP с осью ординат.

(Ответ. Точки K, M – 1 ч. и точки N, P – 2 ч.; а) (0;3); б) (-6;0); в) (0;3))

1. Задача на формулу объёма прямоугольного параллелепипеда.

Ширина прямоугольного параллелепипеда 12 дм, длина в 3 раза больше, а высота на 3 дм больше ширины. Найдите объем прямоугольного параллелепипеда. (Ответ. 6480 дм³).

1. Задание на понятие модуля числа.

Найдите значение выражения:

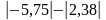
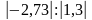
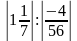
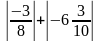
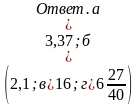
а) б) в) г)

1. Упростить выражения.

1. 

2. 

3. 

1. Текстовая задача на движение.

Из двух пунктов, расстояние между которыми 40 км, навстречу друг другу одновременно отправились пешеход и велосипедист. Скорость велосипедиста в 4 раза больше скорости пешехода. Найдите скорости пешехода и велосипедиста, если известно, что они встретились через 2,5 ч после своего выхода.

(Ответ. 3,2 км/ч и 12,8 км/ч)

1. Текстовая задача на составление уравнения.

На пришкольном участке было собрано 360 кг овощей. Картофеля было собрано в 5 раз больше, чем свёклы, а капусты – на 80 кг больше, чем свёклы. Сколько кг каждой культуры было собрано?

(Ответ. 40 кг свёклы, 200 кг картофеля, 120 кг капусты)

1. Задание на нахождение НОД и НОК чисел.

Найдите наименьшее общее кратное и наибольший общий делитель чисел:

а) 68 и 170;

б) 792 и 1188.

(Ответ. а) НОД = 34, НОК = 340; б) НОД = 396, НОК = 2376)

1. Примеры на действия с обыкновенными дробями.

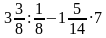
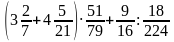
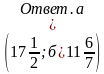
а) б)

1. Решение уравнений.

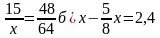
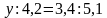
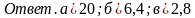
а) в)

( )

1. Задачи на пропорции.

1. 24 человека за 6 дней пропололи участок клубники. За сколько дней выполнят ту же работу 36 человек, если будут работать с такой же производительностью? (Ответ. 4 дня)

2. Для изготовления 14 деталей требуется 16,8 кг металла. Сколько металла пойдет на изготовление 27 таких деталей? (Ответ. 32,4 кг металла)

1. Примеры на действия с десятичными дробями.

а) ;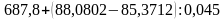

б)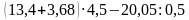

(Ответ. а) 748; б) 36,76)

1. Задания на сравнение чисел.

Сравните числа:

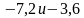
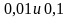
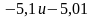
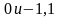
а) ; б) ; в) ; г) ;

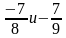
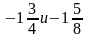
д) ; е) .

1. Примеры на действия с обыкновенными, десятичными дробями и квадрат, куб числа.

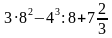
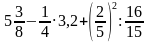
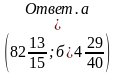
а) 1 ; б)

1. Задание на раскрытие скобок.

Раскройте скобки и найдите значение выражения:

а) ;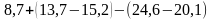

б) .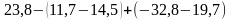

(Ответ. )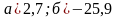

1. Решение уравнений.

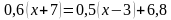
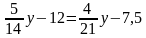
а) ; б)

(Ответ. )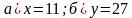

1. Задачи на нахождение дроби от числа и числа по его дроби.

1) Рабочие засадили пшеницей 0,6 часть участка, что составляет 132 га. Какова площадь всего участка, который нужно засадить? (Ответ. 220 га)

2) В магазине 1 кг конфет стоит 318 рублей. Сколько стоят 0,4 кг этих конфет? (Ответ. 127,2 р.)

1. Определение натурального числа. Законы арифметических действий: переместительный, сочетательный, распределительный.

1. Обыкновенные дроби. Правильные и неправильные дроби. Смешанные числа.

1. Определение десятичной дроби. Представление десятичной дроби в виде обыкновенной и обыкновенной в виде десятичной.

1. Арифметические действия с десятичными дробями (правила сложения, вычитания, умножения, деления).

1. Определения уравнения и корня уравнения. Перенос слагаемых из одной части уравнения в другую.

1. Проценты. Нахождение процента от величины, величины по её проценту.

1. Определение целого числа. Правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.

1. Определение простого и составного числа, взаимно простых чисел. НОД и НОК чисел.

2. Признаки делимости на 2, 3, 5, 9,10, 4, 8.

1. Правила сложения, вычитания, умножения и деления обыкновенных дробей.

1. Правила нахождения части от целого и целого по его части.

1. Представление об отношении и о пропорции. Основное свойство пропорции.

1. Понятие модуля числа. Противоположные числа.

1. Представление о координатной плоскости. Координаты точки.

1. Прямая, отрезок, луч как геометрические понятия. Перпендикулярные и параллельные прямые.

1. Определение угла. Виды углов. Биссектриса угла.

1. Треугольник. Виды треугольников. Сумма углов треугольника.

1. Окружность, круг как геометрические фигуры. Длина окружности и площадь круга.

1. Правила раскрытия скобок, перед которыми стоит знак «плюс» или знак «минус». Подобные слагаемые.

1. Прямоугольный параллелепипед и куб. Формулы объёма.

1. Задачи на проценты.

1) За контрольную работу по математике было поставлено 15% пятёрок. Сколько учеников писало контрольную работу, если пятёрки получили 6 человек?

2) Из 76 м² площади квартиры кухня занимает 12%. Найдите площадь кухни.

1. Примеры на действия с положительными и отрицательными числами.

1. 

2. 

1. Задание на нахождение длины окружности и площади круга.

Найдите длину окружности и площадь круга, если диаметр круга равен 15 см. (Число 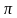округлите до сотых).

1. Задачи на масштаб.

а) На чертеже изображен прямоугольник, площадь которого 216 см². Найдите площадь этого прямоугольника в действительности, если чертеж выполнен в масштабе .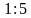

б) Расстояние между двумя городами равно 615 км. Каким будет это расстояние на карте, если масштаб карты 1:1500000?

1. Координатная плоскость: построение точек с указанными координатами и нахождение координат указанных точек.

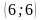
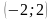
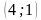
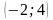
Отметьте на координатной плоскости точки M , N , K и P . Укажите в какой четверти лежит каждая точка. Проведите прямые MN и KP. Найдите координаты точки пересечения: а) прямых MN и KP; б) прямой MN с осью абсцисс; в) прямой KP с осью ординат.

1. Задача на формулу объёма прямоугольного параллелепипеда.

Ширина прямоугольного параллелепипеда 12 дм, длина в 3 раза больше, а высота на 3 дм больше ширины. Найдите объем прямоугольного параллелепипеда.

1. Задание на понятие модуля числа.

Найдите значение выражения:

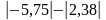
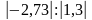
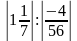
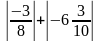
а) б) в) г)

1. Упростить выражения.

1. 

2. 

3. 

1. Текстовая задача на движение.

Из двух пунктов, расстояние между которыми 40 км, навстречу друг другу одновременно отправились пешеход и велосипедист. Скорость велосипедиста в 4 раза больше скорости пешехода. Найдите скорости пешехода и велосипедиста, если известно, что они встретились через 2,5 ч после своего выхода.

1. Текстовая задача на составление уравнения.

На пришкольном участке было собрано 360 кг овощей. Картофеля было собрано в 5 раз больше, чем свёклы, а капусты – на 80 кг больше, чем свёклы. Сколько кг каждой культуры было собрано?

1. Задание на нахождение НОД и НОК чисел.

Найдите наименьшее общее кратное и наибольший общий делитель чисел:

а) 68 и 170;

б) 792 и 1188.

1. Примеры на действия с обыкновенными дробями.

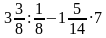
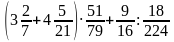
а) б)

1. Решение уравнений.

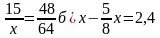
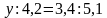
а) в)

1. Задачи на пропорцию.

1) 24 человека за 6 дней пропололи участок клубники. За сколько дней выполнят ту же работу 36 человек, если будут работать с такой же производительностью?

2) Для изготовления 14 деталей требуется 16,8 кг металла. Сколько металла пойдет на изготовление 27 таких деталей?

1. Примеры на действия с десятичными дробями.

а) ;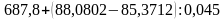

б)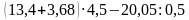

1. Задание на сравнение чисел.

Сравните числа:

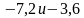
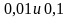
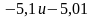
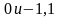
а) ; б) ; в) ; г) ;

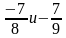
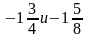
д) ; е) .

1. Примеры на действия с обыкновенными, десятичными дробями и квадрат, куб числа.

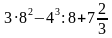
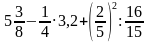
а) 1 ; б)

1. Задание на раскрытие скобок.

а) ;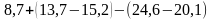

б) .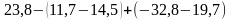

1. Решение уравнений.

а) ;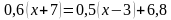

б)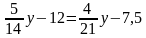

1. Задачи на нахождение части от целого и целого по его части.

1) Рабочие засадили пшеницей 0,6 часть участка, это составляет 132 га. Какова площадь всего участка, который нужно засадить?

2) В магазине килограмм конфет стоит 318 рублей. Сколько стоят 400 грамм этих конфет?

Название: Математика, ответы на вопросы. Устный экзамен, теория и практика.

Автор: Якушева Е.В., Попов А.В., Якушев А.Г.
1998

    В данном пособии даются ответы на вопросы, предлагаемые Министерством Образования РФ для выпускных экзаменов в школе по математике в 1998 году. Ответы подготовлены старшим научным сотрудником механико-математического факультета МГУ Якушевым А.Г., кандидатом физико-математических наук, доцентом механико-математического факультета МГУ Поповым А.В., преподавателем социологического факультета МГУ Якушевой Е.В. в соответствии с требованиями, предъявляемыми на вступительных экзаменах в ВУЗах Москвы. Предлагаемое издание адресовано выпускникам средних школ, профессионально-технических училищ, техникумов, собирающимся продолжить свое обучение в высших учебных заведениях.

ПРЕДИСЛОВИЕ

.
    Ежегодно миллионы юношей и девушек» получающих среднее образование, задаются вопросом: „Что дальше»? Основная дилемма, которую им предстоит разрешить, заключается в выборе между работой и дальнейшей учебой, но уже в высшем учебном заведении.

    Авторы не собираются утруждать себя доказательством прописных истин, как, например, та, что наиболее оплачиваемые категории работающих во всех сферах имеют высшее образование, или та, что разрыв в оплате труда, требующего специальных знаний, и труда малоквалифицированного, во всех развитых странах увеличивается год от года. Они намерены ограничиться лишь поздравлениями тем, кто решил после завершения среднего образования поступать в ВУЗ.
Помните, что зачисление в ВУЗ производится, как правило, на конкурсной основе, и успех на вступительных экзаменах зависит от того, насколько серьёзно Вы будете к ним готовы.

    Книга, которую Вы держите в руках, не является учебником в традиционном понимании. Она предназначена для самостоятельной подготовки к экзамену по математике, как выпускному за курс средней школы, так и вступительному в университеты, академии и институты. Она особенно полезна тем, кто по той или иной причине не имеет возможности заниматься на хороших подготовительных курсах или с опытным репетитором. Однако авторы предполагают, что читатель владеет материалом школьного учебника по математике.

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:

Скачать книгу Математика, ответы на вопросы. Устный экзамен, теория и практика. Якушева Е.В., Попов А.В., Якушев А.Г., 1998 — fileskachat.com, быстрое и бесплатное скачивание.

Скачать djvu
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу

Скачать книгу — Математика ответы на вопросы. Устный экзамен, теория и практика. Якушева Е.В., Попов А.В., Якушев А.Г., 1998

Дата публикации: 25.01.2012 05:01 UTC

Теги:

экзамены по математике :: ответы :: вопросы :: Якушева :: Попов :: Якушев

Классы с углубленным изучением математики в
нашей школе существуют с 1988 года. Показателями
продуктивности работы по этой программе можно
считать следующие: высокий процент поступления
выпускников этих классов в вузы, сдача устных и
письменных вступительных экзаменов по
математике абитуриентами в основном на
“хорошо” и “отлично”, значительное снижение
сопротивления материала при восприятии
студентами-первокурсниками математических
дисциплин в технических вузах.

Остановимся на системе преподавания алгебры и
математического анализа в старших классах.

Для успешного усвоения углубленного курса
математики необходимо ориентировать детей на
изучение его теоретических основ. Формировать
умения и отрабатывать навыки решения задач можно
лишь, опираясь на теоретические знания учащихся.
Одна из главных задач преподавателя –
организовать работу таким образом, чтобы к
выпускному письменному экзамену ученики были
способны самостоятельно выдвинуть идею при
решении конкретной задачи, наметить план этого
решения, грамотно обосновать свои действия,
найти способы оценки и проверки ответа. Для
получения подобного результата нужна серьезная
теоретическая подготовка.

Опыт работы подсказал необходимость
объединения в единую систему различных форм
обучения: устные опросы теории у доски,
изложенной на предыдущем уроке, письменные
теоретические опросы всего класса, проведение
контрольных работ и устных зачетов. По окончании
10 класса проводится переводной экзамен.

Эта система преподавания позволяет ученикам
выпускного класса успешно сдавать устный
экзамен по алгебре и математическому анализу
(экзамен по выбору).

Подробнее остановимся на содержании устных
зачетов и переводного экзамена в 10 классе. Темы
зачетов в 10 классе: “Тригонометрия”, “Пределы и
непрерывность”, “Производная и ее применение”;
в 11 классе – “Интеграл”, “Показательная,
логарифмическая и степенная функции”.

В 10 классе проводится устный переводной
экзамен. Необходимость именно устного экзамена
подсказала практика. Его цель – привести знания
учащихся в четкую систему, подвести их к
осознанному заучиванию формул и теорем. Устный
ответ учит грамотно оформлять свои мысли,
пользоваться математической терминологией. При
подготовке к зачетам и экзамену отрабатывается
логика изложения материала и структура ответа,
что позволяет успешно сдавать устные
вступительные экзамены по математике в высшие
учебные заведения.

Вопросы к зачетам в 10 классе составляют основу
экзаменационных билет ов. Зная это еще в начале
года, дети получают дополнительную мотивировку
при изучении зачетной программы.

Поскольку степень подготовки учащихся в классе
различна, я включаю в практическую часть зачетов
разноуровневые задачи. Это дает возможность с
одной стороны закрепить и проконтролировать
умения и навыки решения опорных задач по теме,
соответствующих базовому уровню, а с другой –
развивать творческую мысль ученика. При этом
уместно использовать задания письменных
выпускных экзаменов прошлых лет.

Широкий выбор специальной литературы позволит
каждому учителю составить практическую часть
зачетов, подобрать такие задачи, которые более
всего соответствуют уровню подготовки его
класса.

10 класс.

Зачет №1 по теме: “Тригонометрия”.

1. Функция синус, косинус, тангенс и котангенс
   числового аргумента. Табличные значения. Знаки
   этих функций, промежутки монотонности.
2. Графики функций y = sinx, y = ctgx. Свойства.
3. Графики функций y = cosx, y = tgx. Свойства.
4. Основное тригонометрическое тождество.
5. Формулы сложения.
6. Формулы приведения.
7. Тригонометрические функции двойного и тройного
   угла.
8. Тригонометрические функции половинного угла.
9. Преобразование суммы тригонометрических
   функций в произведение.
10. Преобразование произведения
    тригонометрических функций в сумму.
11. Арксинус, арккосинус. Тождества arcsin(-a) = …, arccos(-a)
    = …; решение уравнений sinx = a, cosx = a.
12. Арктангенс, арккотангенс. Тождества arctg(-a) = …,
    arcctg(-a) = …; решение уравнений tgx = a, ctgx = a.
13. Условие равенства синусов.
14. Условие равенства косинусов.
15. Условие равенства тангенсов.
16. Графики функций y = arcsinx, y = arccosx. Свойства.
    Основные тождества.
17. Графики функций y = arctgx, y = arcctgx. Свойства.
    Основные тождества.

Зачет №2 по теме: “Предел и
непрерывность”.

1. Определение бесконечно малой функции при ,
   примеры, операции над бесконечно малыми
   функциями, теорема о сравнении функции с
   бесконечно малой функцией при .
2. Операции над бесконечно малыми функциями при
    . Теорема о произведении двух бесконечно малых
   функций.
3. Операции над бесконечно малыми функциями при
     Теорема о сумме двух бесконечно малых
   функций.
4. Определение предела функции на бесконечности,
   примеры, свойства предела функции при Доказательство теоремы о
   единственности предела.
5. Предел функции на бесконечности. Теорема о
   пределе суммы двух функций.
6. Предел функции на бесконечности. Теорема о
   пределе произведения двух функций.
7. Определение бесконечно большой функции на
   бесконечности, примеры, свойства, доказательство
   одного из свойств.
8. Определение предела функции в точке и его
   свойства. Теорема о пределе многочлена Р(х) при,
   следствие из нее.
9. Бесконечно большие функции при
   Определение, примеры теорема о нахождении
   вертикальных асимптот.
10. Непрерывность функции в точке. Определение,
    примеры. Теорема о непрерывности суммы,
    произведения и частного непрерывных в точке а
    функций.
11. Непрерывность тригонометрических функций.
12. Первый замечательный предел.

Зачет №3 по теме: “Производная и ее
применение”.

1. Геометрический смысл производной. Касательная
   прямая к графику функции. Уравнение касательной.
2. Производная произведения двух функций.
3. Производная дроби.
4. Производная степенной функции с натуральным
   показателем.
5. Производная суммы двух функций.
6. Дифференцирование тригонометрических функций.
7. Необходимое условие экстремума функции.
   Теорема Ферма.
8. Достаточное условие экстремума функции.
9. Непрерывность дифференцируемой функции.
10. Производная степенной функции с целым
    показателем.
11. Признак возрастания и убывания функции.

Билет ы к экзамену по алгебре и математическому
анализу в 10 классе.

Билет 1.

1. Косинус и синус разности и суммы двух чисел.
2. Определение, физический смысл производной.
3. Задача по теме: “Предел функции”.

Билет 2.

1. Формулы приведения.
2. Теорема Безу и ее следствия.
3. Задача по теме: “Производная”.

Билет 3.

1. Тригонометрические функции двойного угла.
2. Касательная прямая к графику функции.
   Геометрический смысл производной. Уравнение
   касательной.
3. Задача по теме: “Предел функции”.

Билет 4.

1. Тригонометрические функции тройного угла.
2. Производная произведения двух функций.
3. Задача по теме: “Многочлены”.

Билет 5.

1. Тригонометрические функции половинного угла.
2. Производная дроби.
3. Задача по теме: “Производная”.

Билет 6.

1. Преобразование суммы тригонометрических
   функций в произведение.
2. Производная степенной функции с натуральным
   показателем.
3. Задача по теме: “Предел функции”.

Билет 7.

1. Преобразование произведения
   тригонометрических функций в сумму.
2. Производная суммы двух функций.
3. Задача по теме: “Предел функции”.

Билет 8.

1. Дифференцирование тригонометрических функций.
2. Бесконечно малые функции. Теорема о сравнении
   функции с бесконечно малой при
3. Задача по теме: “Тригонометрия”.

Билет 9.

1. Первый замечательный предел.
2. Необходимое условие экстремума функции.
3. Задача по теме: “Тригонометрия”.

Билет 10.

1. Решение уравнения sinx = а. Арксинус.
2. Достаточное условие экстремума функции.
3. Задача по теме: “Многочлены”.

Билет 11.

1. Решение уравнения cosx = а. Арккосинус.
2. Непрерывность дифференцируемой функции.
3. Задача по теме: “Предел функции”.

Билет 12.

1. Решение уравнений tgx =а, ctgx = а. Арктангенс,
   арккотангенс.
2. Предел функции в точке и его свойства.
3. Задача по теме: “Тригонометрия”.

Билет 13.

1. Тригонометрические уравнения, решаемые с
   помощью условия равенства синусов.
2. Бесконечно малые функции. Теорема о
   произведении бесконечно малых функций при
3. Задача по теме: “Производная”.

Билет 14.

1. Тригонометрические уравнения, решаемые с
   помощью условия равенства косинусов.
2. Бесконечно малые функции. Теорема о сумме двух
   бесконечно малых функций при
3. Задача по теме: “Производная”.

Билет 15.

1. Тригонометрические уравнения, решаемые с
   помощью условия равенства тангенсов.
2. Предел функции на бесконечности. Теорема о
   пределе суммы двух функций.
3. Задача по теме: “Производная”.

Билет 16.

1. Основные методы решения тригонометрических
   уравнений.
2. Предел функции на бесконечности. Теорема о
   пределе произведения двух функций.
3. Задача по теме: “Тригонометрия”.

Билет 17.

1. Решение тригонометрических неравенств вида sinx
   > а, sinx < а.
2. Теорема о пределе многочлена Р(х) при
3. Задача по теме: “Производная”.

Билет 18.

1. Решение тригонометрических неравенств вида cosx
   > а, cosx < а.
2. Непрерывные функции. Теорема о непрерывности
   суммы и произведения непрерывных в точке а
   функций.
3. Задача по теме: “Тригонометрия”.

Билет 19.

1. Решение тригонометрических неравенств вида tgx
   > а, tgx < а, ctgx > а, ctgx< а.
2. Производная степенной функции с целым
   показателем.
3. Задача по теме: “Предел функции”.

Билет 20.

1. Непрерывность тригонометрических функций.
2. Признак возрастания, убывания функции.
3. Задача по теме: “Многочлены”.

 11 класс.

Зачет №1 по теме: “Интеграл”.

1. Определение и теорема о первообразной функции.
2. Определение и свойства неопределенного
   интеграла. Доказать свойство об интеграле суммы
   двух функций.
3. Определение и свойства неопределенного
   интеграла. Доказать свойство о вынесении
   постоянного множителя за знак интеграла.
4. Определение и свойства неопределенного
   интеграла. Доказать свойство:
   Сформулировать теорему об интегрировании по
   частям.
5. Определение криволинейной трапеции. Теорема о
   площади криволинейной трапеции. Формула
   Ньютона-Лейбница.
6. Определение определенного интеграла. Показать,
   что неопределенный интеграл не зависит от выбора
   первообразной функции f . Физический и
   геометрический смысл определенного интеграла.
7. Определение и свойства определенного
   интеграла. Доказать свойство о перестановке
   пределов интегрирования и
8. Определение и свойства определенного
   интеграла. Доказать свойство об интеграле суммы
   двух функций на отрезке [ a,b] .
9. Вычисление площадей фигур, ограниченных
   графиками непрерывных на отрезке [ a,b] функций.
   Разобрать все случаи (с выводом некоторых).

Зачет №2 по теме:

“Показательная, логарифмическая и
степенная функции”.

1. Определение степенной функции, свойства и
   график степенной функции с отрицательным
   рациональным показателем. Доказательство одного
   из них.
2. Определение показательной функции. Свойства и
   график показательной функции с основанием
   0<а<1.
3. Определение логарифмической функции, свойства
   и график логарифмической функции с основанием
   а>1.
4. Логарифм произведения, степени и частного.
   Сформулировать теоремы и доказать одну из них.
5. Производные функций е^х и а^х. Вывод.
6. Производные функций lnx и log_ax. Вывод.
7. Свойства и график степенной функции с
   рациональным положительным показателем.
8. Вывод формулы перехода от одного основания
   логарифма к другому. Теоремы: log_ab = log_aⁿbⁿ;
   log_ab = 1/ log_na_.

Предлагаемые мной материалы, полученные в
результате восемнадцатилетней работы, могут
быть использованы при освоении программы
углубленного изучения математики, выборе форм
обучения и контроля. Естественно, индивидуальные
особенности класса потребуют от педагога
соответствующей адаптации материала и
корректировки заданий.