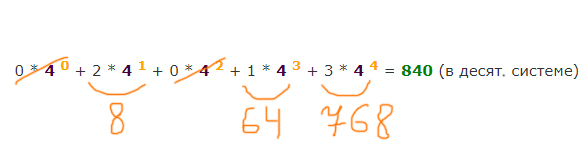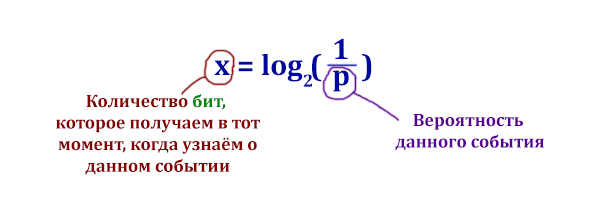На уроке рассматривается разбор 8 задания ЕГЭ по информатике про измерение количества информации
8-е задание: «Измерение количества информации»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 4 минуты.
Проверяемые элементы содержания: Знание о методах измерения количества информации
До ЕГЭ 2021 года — это было задание № 10 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«При использовании способа решения со системой счисления с основанием N следует помнить, что слова в списке нумеруются с единицы, поэтому числу 0 будет соответствовать первое слово»
ФГБНУ «Федеральный институт педагогических измерений»
Содержание:
- Объяснение темы
- Измерение количества информации
- Двоичное кодирование сообщений (равновероятностные события)
- Количество различных сообщений в алфавите разной мощности
- Количество сообщений при различном вхождении (встречаемости) букв
- Дополнительные формулы
- Тренировочные задания 8 ЕГЭ по информатике и их решение
- Сколько вариантов шифра или кодовых слов
- Перестановка букв в слове (каждая буква 1 раз)
- Сколько существует n-значных чисел, записанных в m-ной системе счисления
- Список в алфавитном порядке
- Вероятность событий
Объяснение темы
Рассмотрим кратко необходимые для решения 8 задания ЕГЭ понятия и формулы.
Измерение количества информации
- Кодирование — это представление информации в форме, удобной для её хранения, передачи и обработки. Правило преобразования информации к такому представлению называется кодом.
- 1 бит – это количество информации, которое можно передать с помощью одного знака в двоичном коде (0 или 1).
- Алфавит — это набор знаков, используемый в том или ином языке.
- Мощность алфавита — это количество используемых в алфавите знаков.
- Сообщение — это любая последовательность символов какого-либо алфавита.
1 байт (bytе) = 8 бит
1 Кб (килобайт) = 1024 байта
1 Мб (мегабайт) = 1024 Кб
1 Гб (гигабайт) = 1024 Мб
1 Тб (терабайт) = 1024 Гб
1 Пб (петабайт) = 1024 Тб
8 = 23
1024 = 210
Рассмотрим еще несколько определений:
Мощность алфавита
Для вычисления количества информации применяются несколько различных формул в зависимости от ситуации:
Двоичное кодирование сообщений (равновероятностные события)
При вычислении количества информации в сообщении для равновероятностных событий, общее количество которых равно N, используется формула:
N = 2L
* следует иметь в виду, что также приняты следующие обозначения: Q = 2k
Пример 2: Зашифруем буквы А, Б, В, Г при помощи двоичного кодирования равномерным кодом и посчитаем количество возможных сообщений:

Решение:
Таким образом, мы получили равномерный код, т.к. длина каждого кодового слова одинакова для всех кодовых слов (L = 2).
Количество сообщений длиной L битов:
N = 2L
Т.е. количество сообщений длиной 2 бита, как в примере с нашими буквами, будет равно N = 22 = 4
Ответ: 4
Количество различных сообщений в алфавите разной мощности
Рассмотрим вариант с 5 буквами (мощность алфавита = 5), которые надо разместить в сообщении длиной 2 символа:
Найдем формулу для нахождения количества различных сообщений в алфавите различной мощности:
Если мощность некоторого алфавита составляет N, то количество различных сообщений длиной L знаков:
- N – мощность алфавита
- L – длина сообщения
- Q – количество различных сообщений
Пример: Сколько существует всевозможных трехбуквенных слов в английском языке?
Решение:
В английском алфавите 26 букв. Значит, мощность алфавита = 26. Длина сообщения = 3. Найдем по формуле количество трехбуквенных слов:
Q = 263
или
26
*
26
*
26
= 17576
Ответ: 17576
N = n1 * n2 * … * nL
Количество сообщений при различном вхождении (встречаемости) букв
В таком случае можно использовать формулу для вычисления числа перестановок с повторениями; для двух разных символов она выглядит так:
[ P = frac{na+n*!}{na!n*!} ]
na – количество букв a n* — количество звёздочек или кол-во вариантов
Иногда в заданиях 8 можно использовать формулу комбинаторики для проверки полученных результатов перебора. Число сочетаний из n элементов по k элементов:
[ C{binom{k}{n}}= frac{n!}{k!(n-k)!} ]
n! = 1 * 2 * 3 * … * n
Пример: Сколько существует всевозможных четырехбуквенных слов в алфавите из 4 букв: А, Б, В, Г, если известно, что буква А встречается ровно два раза?
Решение:
- Длина сообщения = 4. Мощность алфавита = 4. Но мешает условие: буква А встречается ровно два раза.
- В таких заданиях можно использовать способ перебора всевозможных вариантов:
два раза буква А, на остальных местах - одна из трех оставшихся букв: А А 3 3 = 3 * 3 = 32 = 9 А 3 А 3 = 9 А 3 3 А = 9 3 А А 3 = 9 3 А 3 А = 9 3 3 А А = 9
Число сочетаний из n элементов по k элементов:
[ C{binom{k}{n}}= frac{n!}{k!(n-k)!} ]
[ C{binom{2}{4}}= frac{4!}{2!(4-2)!} = frac{24}{2*2} = 6 ]
* Факториал числа n! = 1 * 2 * 3 *..* n
6 * 9 = 54
Дополнительные формулы
Количество информации и равновероятные события
При определении количества информации для равновероятностных событий могут понадобиться две формулы:
x = log2(1/p)
p(A) = m / n
Количество информации и неравновероятные события
При использовании неравновероятного события, вероятность которого равна p, для вычисления количества информации используется формула:
i = -[log2p]
*квадратные скобки означают ближайшее целое, меньшее или равное значению выражения в скобках
Формула Хартли:
Формула Хартли
Алфавитный подход:
Информационный объем сообщения длиной L:
Алфавитный подход
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Сколько вариантов шифра или кодовых слов
Cartesian(n) — метод расширения последовательности, возвращающий декартову степень множества символов |
Когда применяется: Если требуется полный перебор вариантов букв для каждой позиции (каждая буква может встречаться в кодовом слове любое количество раз) |
||||||
|---|---|---|---|---|---|---|---|
| Пример: Сравним полный перебор букв слова «школа», размещенных на две позиции: |
|||||||
| Pascal | PascalABC.NET | ||||||
|
|
||||||
| Результат: | |||||||
|
[ш,ш] [ш,к] [ш,о] [ш,л] [ш,а] [к,ш] [к,к] [к,о] Итого 25 штук (5*5) |
[ш,ш] [ш,к] [ш,о] [ш,л] [ш,а] [к,ш] [к,к] [к,о] [к,л] [к,а] [о,ш] [о,к] [о,о] [о,л] [о,а] [л,ш] [л,к] [л,о] [л,л] [л,а] [а,ш] [а,к] [а,о] [а,л] [а,а] |
||||||
Permutations — метод возвращает все перестановки множества элементов, заданного массивом или последовательностью |
Когда применяется: Если требуется перестановка букв в слове. То есть количество каждой буквы в словах сохраняется, и каждая буква встречается только 1 раз |
||||||
| Пример: Сравним перестановку букв слова «мимикрия»: |
|||||||
| Pascal | PascalABC.NET | ||||||
|
|
|
||||||
| Результат: | |||||||
|
[М,И,М,И,К,Р,И,Я] [М,И,М,И,К,Р,Я,И] [М,И,М,И,К,И,Р,Я] [М,И,М,И,К,И,Я,Р] [М,И,М,И,К,Я,Р,И] [М,И,М,И,К,Я,И,Р] [М,И,М,И,Р,К,И,Я] [М,И,М,И,Р,К,Я,И] … |
Используются также следующие запросы и методы LINQ:
Фильтрация последовательностей (Where)
Метод Count([Type -> boolean]) Вычисление скаляра
Метод CountOf(s: Type) — Возвращает количество элементов, равных указанному значению
Метод First() — Возвращает первый элемент последовательности.
Метод Last() — Возвращает последний элемент последовательности.
Метод Pairwise(Self: sequence of T; func: (T,T)->Res) — Превращает последовательность в последовательность пар соседних элементов, применяет func к каждой паре полученных элементов и получает новую последовательность
8_1:
Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является цифрой от 1 до 6.
Сколько различных вариантов шифра можно задать, если известно, что цифра 1 должна встречаться в коде ровно 1 раз, а каждая из других допустимых цифр может встречаться в шифре любое количество раз или не встречаться совсем?
Типовые задания для тренировки
✍ Решение:
✎ Решение теоретическое:
- Формула нахождения количества различных сообщений:
- Итак, что у нас дано из этой формулы:
- Длина сообщения (L) = 5 символов
- Мощность алфавита (N) = 6 (цифры от 1 до 6).
- Но так как цифра 1 встречается по условию ровно один раз, а остальные 5 цифр — любое количество раз, то будем считать, что N = 5 (цифры от 2 до 6, исключая 1). Т.е. возьмем вариант, когда 1 стоит на первом месте, а остальные 5 цифр размещаем на 4 позиции:
Q = NL
1 5 5 5 5 - 1 * Q = 54 = 625
✎ 1 способ. Найдем количество вариантов методом перебора:
1 5 5 5 5 -1 * Q=54= 625 5 1 5 5 5 -1 * Q=54= 625 5 5 1 5 5 -1 * Q=54= 625 5 5 5 1 5 -1 * Q=54= 625 5 5 5 5 1 -1 * Q=54= 625
✎ 2 способ. Найдем количество вариантов при помощи формулы комбинаторики:
[ C{binom{4}{5}}= frac{5!}{4!(5-4)!} = 5 ]
625 * 5 = 3125
Результат: 3125
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
|
С++:
|
Детальный теоретический разбор задания 8 ЕГЭ по информатике предлагаем посмотреть в видеоуроке:
📹 YouTube здесьздесь (теоретическое решение)
8_2:
Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является либо буквой (A или B) или цифрой (1, 2 или 3).
Сколько различных вариантов шифра можно задать, если известно, что в коде присутствует ровно одна буква, а все другие символы являются цифрами?
✍ Решение:
-
✎ Решение теоретическое:
- Формула нахождения количества различных сообщений:
- Посчитаем количество возможных шифров для одного из вариантов (например, когда буквы находятся на первой позиции). Так как цифры (1, 2, 3) могут занимать 4 позиции из пяти, а две буквы (А и В) одну из позиций, значит:
Q = NL
Q = 2 * 34 = 162
AB 123 123 123 123 = 162
"2" означает одна из двух букв: А или B, "3" - одна из трех цифр: 2 3 3 3 3 -> Q = 2 * 34 = 162 3 2 3 3 3 -> Q = 2 * 34 = 162 3 3 2 3 3 -> Q = 2 * 34 = 162 3 3 3 2 3 -> Q = 2 * 34 = 162 3 3 3 3 2 -> Q = 2 * 34 = 162
5 * 162 = 810
Результат: 810
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(5) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 5-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
Подробное теоретическое решение данного задания предлагаем посмотреть на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_3:
Олег составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Олег использует 4-буквенные слова, в которых есть только буквы A, Б, В, Г, Д и Е, причём буква Г появляется ровно 1 раз и только на первом или последнем месте. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем.
Сколько различных кодовых слов может использовать Олег?
✍ Решение:
-
✎ Решение теоретическое:
- Вспомним формулу получения количества возможных вариантов слов:
- где n1 — количество вариантов выбора первой буквы, n2 — количество вариантов выбора второй буквы и т.п.
- Рассмотрим варианты, когда буква Г встречается на первом или последнем месте:
N = n1 * n2 * n3 * … * nL = nL
Г ? ? ? = 1 * 5 * 5 * 5 = 53 = 125 ? ? ? Г = 5 * 5 * 5 * 1 = 53 = 125
125 + 125 = 250
Результат: 250
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(4) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 4-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
Видеоразбор данного задания (теоретический способ):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_4:
Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является одной из букв X, Y или Z.
Сколько различных вариантов шифра можно задать, если известно, что буква X должна встречаться в коде ровно 2 раза, а каждая из других допустимых букв может встречаться в шифре любое количество раз или не встречаться совсем?
Типовые задания для тренировки
✍ Решение:
-
✎ Решение теоретическое:
- Формула нахождения количества различных сообщений:
- Итак, что у нас дано из этой формулы:
- Начальная мощность алфавита (N) = 3 (буквы X, Y, Z). Но так как буква X встречается ровно два раза, то мы ее рассмотрим отдельно, а остальные 2 буквы — встречаются любое количество раз, значит, будем считать, что:
Q = NL
N = 3 - 1 = 2 (Y и Z)
(L) = 5 - 2 = 3 символа (остальные два символа отведем на размещение X)
X X ? ? ? -> 12 * Q = 23 = 8
✎1 способ. Перебор всех вариантов:
X X ? ? ? - 12 * Q = 23 = 8 X ? X ? ? - 12 * Q = 23 = 8 X ? ? X ? - 12 * Q = 23 = 8 X ? ? ? X - 12 * Q = 23 = 8 ? X X ? ? - 12 * Q = 23 = 8 ? X ? X ? - 12 * Q = 23 = 8 ? X ? ? X - 12 * Q = 23 = 8 ? ? X X ? - 12 * Q = 23 = 8 ? ? X ? X - 12 * Q = 23 = 8 ? ? ? X X - 12 * Q = 23 = 8
✎ 2 способ. При помощи формулы поиска числа сочетаний:
[ C{binom{k}{n}}= frac{n!}{k!(n-k)!} ]
Число сочетаний из n элементов по k элементов:
[ C{binom{2}{5}}= frac{5!}{2!(5-2)!} = frac{120}{12} = 10 ]
* Факториал числа: n! = 1 * 2 * 3 * .. * n
8 * 10 = 80
* задание достаточно решить одним из способов!
Результат: 80
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(5) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 5-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
Детальный теоретический разбор задания 8 ЕГЭ по информатике теоретическим способом предлагаем посмотреть в видеоуроке:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_5:
Сколько слов длины 5, начинающихся с согласной буквы и заканчивающихся гласной буквой, можно составить из букв ОСЕНЬ? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
Типовые задания для тренировки
✍ Решение:
-
✎ Решение теоретическое:
- Из букв слова ОСЕНЬ имеем 2 гласных буквы (О, Е) и 2 согласных буквы (С, Н). Буква мягкий знак «нейтральна».
- Подсчитаем количество букв на каждой из 5 позиций:
2 5 5 5 2 СН все все все ОЕ
N = n1 * n2 * n3 * … * nL = nL
N = 2 * 5 * 5 * 5 * 2 = 500
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
Результат: 500
Разбор можно также посмотреть на видео (теоретическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_6:
Вася составляет 4-буквенные слова, в которых есть только буквы Л, Е, Т, О, причём буква Е используется в каждом слове хотя бы 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем.
✍ Решение:
-
✎ Решение теоретическое:
- Количество вариантов различных слов вычислим по формуле:
- n1 — количество вариантов выбора первой буквы и т.п.
- Рассмотрим все варианты расположения буквы Е:
✎ 1 способ:
N = n1 * n2 * n3 * …
где
1. Е ? ? ? или 2. ? Е ? ? или 3. ? ? Е ? или 4. ? ? ? Е Где вопросительный знак означает любую букву из Л, Е, Т, О.
Е ? ? ? = 1 * 4 * 4 * 4 = 64 т.е. на первой позиции - только 1 буква - Е, на каждой последующей - одна из четырех букв Л, Е, Т, О.
? Е ? ? = 3 * 1 * 4 * 4 = 48
? ? Е ? = 3 * 3 * 1 * 4 = 36
? ? ? Е = 3 * 3 * 3 * 1 = 27
64 + 48 + 36 + 27 = 175
Результат: 175
✎ 2 способ:
- Так как по условию буква Е встретится хотя бы 1 раз, значит, можно утверждать, что не может быть такого, чтобы буква Е не встретилась бы ни одного раза.
- Таким образом, рассчитаем случай, когда буква Е встречается все 4 раза (т.е. все случаи) и отнимем от результата невозможный случай: когда буква Е не встретится ни одного раза:
1. Буква Е используется 4 раза (т.е. на всех позициях): 4 * 4 * 4 * 4 = 256 2. Буква Е не используется совсем (т.е. только 3 буквы): 3 * 3 * 3 * 3 = 81
256 - 81 = 175
Результат: 175
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(4) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 4-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
Теоретическое решение задания 8 смотрите в видеоуроке:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_7:
Вася составляет 4-буквенные слова, в которых есть только буквы К, А, Т, Е, Р, причём буква Р используется в каждом слове хотя бы 2 раза. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем.
✍ Решение:
-
✎ Решение теоретическое:
- Количество возможных вариантов слов вычислим по формуле:
- где n1 — количество вариантов выбора первой буквы, n2 — количество вариантов выбора второй буквы и т.п.
- Сначала по формуле получим все варианты для всех пяти букв, включая букву Р:
N = n1 * n2 * n3 * … * nL = nL
5 * 5 * 5 * 5 = 54 = 625
4 * 4 * 4 * 4 = 44 = 256
р ? ? ? = 1 * 4 * 4 * 4 = 43 ? р ? ? = 4 * 1 * 4 * 4 = 43 ? ? р ? = 4 * 4 * 1 * 4 = 43 ? ? ? р = 4 * 4 * 4 * 1 = 43 Получим 43 * 4 = 256
625 - 256 - 256 = 113
✎ Решение с использованием программирования:
PascalABC.net (традиционный):
|
||
PascalABC.net (LINQ):
|
||
Python:
|
||
| С++: |
Результат: 113
Теоретическое решение 8 задания предлагаем посмотреть в видеоуроке:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_8:
Олег составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Олег использует 5-буквенные слова, в которых есть только буквы A, Б, В, и Г, причём буква Г появляется не более одного раза и только на последнем месте. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем.
Сколько различных кодовых слов может использовать Олег?
✍ Решение:
-
✎ Решение теоретическое:
- Вспомним формулу получения количества возможных вариантов слов:
- где n1 — количество вариантов выбора первой буквы,
- n2 — количество вариантов выбора второй буквы и т.п.
- Так как буква Г появляется не более одного раза и только на последнем месте, значит, она может либо появиться 1 раз на последнем месте, либо не появиться совсем.
- Рассмотрим варианты, когда буква Г встречается 1 раз на последнем месте и встречается 0 раз:
N = n1 * n2 * n3 * … * nL = nL
1 раз: ? ? ? ? Г = 3 * 3 * 3 * 3 * 1 = 34 = 81 0 раз: ? ? ? ? ? = 3 * 3 * 3 * 3 * 3 = 35 = 243
81 + 243 = 324
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(5) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 5-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Результат: 324
8_9:
Вася составляет 4-буквенные слова, в которых есть только буквы К, О, М, А, Р, причём буква А используется в них не более 3-х раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная.
✍ Решение:
-
✎ Решение теоретическое:
- Вспомним формулу получения количества возможных вариантов слов:
- где n1 — количество вариантов выбора первой буквы,
- n2 — количество вариантов выбора второй буквы и т.п.
- Так как буква А по условию используется не более 3-х раз, это значит, что она используется либо 3 раза, либо 2 раза, либо 1 раз, либо не используется совсем. Рассмотрим все эти варианты отдельно.
- 1. Буква А используется 3 раза:
N = n1 * n2 * n3 * … * nL = nL
А А А _ -> 1 * 1 * 1 * 4 = 4 А А _ А -> 1 * 1 * 4 * А = 4 А _ А А -> 1 * 4 * 1 * 1 = 4 _ А А А -> 4 * 1 * 1 * 1 = 4
_ может быть любая из 4 букв: К О М Р. Значит, имеем:4 * 4 = 16 вариантов
А А _ _ -> 1 * 1 * 4 * 4 = 16 А _ А _ -> 1 * 4 * 1 * 4 = 16 А _ _ А -> 1 * 4 * 4 * 1 = 16 _ А А _ -> 4 * 1 * 1 * 4 = 16 _ А _ А -> 4 * 1 * 4 * 1 = 16 _ _ А А -> 4 * 4 * 1 * 1 = 16
_ может быть любая из 4 букв: К О М Р. Значит имеем:16 * 6 = 96 вариантов
А _ _ _ -> 1 * 4 * 4 * 4 = 64 _ А _ _ -> = 64 _ _ А _ -> = 64 _ _ _ А -> = 64
64 * 4 = 256 вариантов
_ _ _ _ -> 44 = 256
16 + 96 + 256 + 256 = 624
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(4) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 4-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
Результат: 624
Теоретическое решение смотрите также на видео:
📹 YouTube здесьздесь (теоретическое решение)
8_10:
Сколько существует различных символьных последовательностей длины 3 в четырёхбуквенном алфавите {A,B,C,D}, если известно, что одним из соседей A обязательно является D, а буквы B и C никогда не соседствуют друг с другом?
✍ Решение:
✎ Решение теоретическое:
- Вспомним формулу получения количества возможных вариантов слов:
- где n1 — количество вариантов выбора первой буквы,
- n2 — количество вариантов выбора второй буквы и т.п.
- Будем рассматривать варианты, расставляя каждую букву последовательно по алфавиту, начиная с первой буквы. При этом будем учитывать указанные ограничения для букв А, B и С:
N = n1 * n2 * n3 * … * nL = nL
Начинаем с A: A D 4ABCD = 1 * 1 * 4 = 4 Начинаем с B: B A D, B B 2BD, B D 4ABCD = 7 Начинаем с C: C A D, C C 2CD, C D 4ABCD = 7 Начинаем с D: D A 3BCD, D B 2BD, D C 2CD, D D 4ABCD = 11
4 + 7 + 7 + 11 = 29
Результат: 29
Видеоурок демонстрирует подробное теоретическое решение задания:
📹 YouTube здесьздесь (теоретическое решение)
8_22:
Лена составляет 5-буквенные слова из букв Я, С, Н, О, В, И, Д, Е, Ц, причём слово должно начинаться с согласной и заканчиваться гласной. Первая и последняя буквы слова встречаются в нем только один раз; остальные буквы могут повторяться.
Сколько слов может составить Лена?
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
|
||
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
| Python: | ||
| С++: |
Результат: 6860
Использование метода Pairwise()
8_11:
Из букв С, Р, Е, Д, А составляются трехбуквенные комбинации по следующему правилу – в комбинации не может быть подряд идущих гласных и одинаковых букв.
Например, комбинации ААР или ЕСС не являются допустимыми.
Сколько всего комбинаций можно составить, используя это правило?
✍ Решение:
-
✎ Решение теоретическое:
- Рассмотрим два варианта: когда слово начинается с гласной буквы, и когда оно начинается с согласной.
1. С гласной:
1.1 2 3 2 = 2 * 3 * 2 = 12 гл с с 1.2 2 3 2 = 2 * 3 * 2 = 12 гл с гл
2. С согласной:
2.1 3 2 2 = 3 * 2 * 2 = 12 с с с 2.2 3 2 3 = 3 * 2 * 3 = 18 с гл с 2.3 3 2 2 = 3 * 2 * 2 = 12 с с гл
12 + 12 + 12 + 18 + 12 = 66
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
|
||
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
Python:
|
||
| С++: |
Результат: 66
Перестановка букв в слове (каждая буква 1 раз)
8_12:
Дано слово КОРАБЛИКИ. Таня решила составлять новые 5-буквенные слова из букв этого слова по следующим правилам:
1) слово начинается с гласной буквы;
2) гласные и согласные буквы в слове должны чередоваться;
3) буквы в слове не должны повторяться.
✍ Решение:
-
✎ Решение теоретическое:
- Учтем, что в слове КОРАБЛИКИ две буквы К и две И.
- Всего в слове 4 гласных, но поскольку две буквы
И, то необходимо считать только 3 гласных. - Всего в слове 5 согласных, однако две из них — буквы
К, поэтому считать следует 4 согласных. - Посчитаем количество согласных и гласных для каждой из 5 позиций слова, учитывая, что с каждой последующей буквой количество используемых гласных/согласных уменьшается. Под позициями приведем пример букв:
гл с гл с гл 3 4 2 3 1 оаи крбл оа крб и
3 * 4 * 2 * 3 * 1 = 72
Результат: 72
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
|
||
| Python: | ||
| С++: |
Результат: 72
8_21:
Ксюша составляет слова, меняя местами буквы в слове МИМИКРИЯ.
Сколько различных слов, включая исходное, может составить Ксюша?
✍ Решение:
-
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
Смысл решения в использовании типа множества ( |
||
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Ответ: 3360
Подробное решение программным способом смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (программное решение)
8_19:
Петя составляет шестибуквенные слова
перестановкой букв
слова АДЖИКА. При этом он избегает слов с двумя подряд одинаковыми буквами. Сколько всего различных слов может составить Петя?
Типовые задания для тренировки
✍ Решение:
-
✎ Решение теоретическое:
- Посчитаем количество слов без двух подряд одинаковых букв. Будем считать относительно буквы А, которых две в заданном слове АДЖИКА. Буквы не могут повторяться, поэтому их кол-во в каждом варианте будет уменьшается:
А*А*** = 4*3*2*1 = 24 слова с данным расположением буквы А. А**А** = 4*3*2*1 = 24 А***А* = 4*3*2*1 А****А = ... *А*А** *А**А* *А***А **А*А* **А**А ***А*А
10 * 24 = 240
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
Смысл решения в использовании типа — множества ( |
||
PascalABC.net (использование LINQ, быстрое решение):
|
||
| Python: | ||
| С++: |
Ответ: 240
8_20:
Маша составляет 7-буквенные коды из букв В, Е, Н, Т, И, Л, Ь. Каждую букву нужно использовать
ровно 1 раз
, при этом код буква Ь не может стоять на последнем месте и между гласными. Сколько различных кодов может составить Маша?
Типовые задания для тренировки
✍ Решение:
-
✎ Решение теоретическое:
- Выполним задание следующим образом: 1. посчитаем общее количество слов, не учитывая никакие ограничения. 2. Затем посчитаем случаи, которые необходимо исключить. 3. Вычтем из результата пункта 1 результат пункта 2.
- Общее количество независимо от ограничений (учтем, что буквы не должны повторяться):
7 6 5 4 3 2 1 - количество возможных вариантов букв на семи позициях ИТОГО: 7! = 5040 слов
6 5 4 3 2 1 Ь = 6! = 720
И Ь Е 4 3 2 1 = 24 варианта Так как буквы смещаются по всем позициям, то получим (4 И Ь Е 3 2 1, ...): 24 * 5 = 120 Е Ь И 4 3 2 1 = 24 варианта 24 * 5 = 120
5040 - 720 - 120 - 120 = 4080
✎ Решение с использованием программирования:
Стоит заметить, что теоретическое решение занимает меньше времени, чем программный способ!
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
|
||
| Python: | ||
| С++: |
Ответ: 4080
8_23:
Артур составляет 6-буквенные коды перестановкой букв слова ВОРОТА. При этом нельзя ставить рядом две гласные.
Сколько различных кодов может составить Артур?
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, спортивное прогр-е):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Ответ: 72
Сколько существует n-значных чисел, записанных в m-ной системе счисления
8_18: Объяснение 8 задания экзамена ЕГЭ 2020 г. (со слов учащегося):
Сколько существует восьмизначных чисел, записанных в восьмеричной системе счисления, в которых все цифры различны и рядом не могут стоять 2 чётные или 2 нечётные цифры?
Типовые задания для тренировки
✍ Решение:
-
✎ Решение теоретическое:
- Выпишем все четные и нечетные цифры, которые могут использоваться в 8-й с.с.:
четные: 0, 2, 4, 6 - итого 4 цифры нечетные: 1, 3, 5, 7 - итого 4 цифры
1) с четной цифры: 3 4 3 3 2 2 1 1 = 3*4*3*3*2*2*1*1 = 432 ч н ч н ч н ч н
Самый старший разряд не может быть равен 0 (поэтому 3 цифры из 4 возможных), так как разряд просто потеряется, и число станет семизначным). Каждый последующий разряд включает на одну цифру меньше, так как по заданию цифры не могут повторяться.
2) с нечетной цифры: 4 4 3 3 2 2 1 1 = 4*4*3*3*2*2*1*1 = 576 н ч н ч н ч н ч
Каждый последующий разряд включает на одну цифру меньше, так как по заданию цифры не могут повторяться.
432 + 576 = 1008
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Ответ: 1008
Список в алфавитном порядке
8_13:
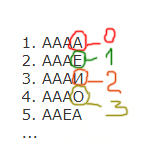
Все 5-буквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке. Ниже приведено начало списка:
1. ААААА
2. ААААО
3. ААААУ
4. АААОА
…
Запишите слово, которое стоит под номером 242 от начала списка.
✍ Решение:
-
✎ Решение теоретическое:
- Данное задание лучше решать следующим образом. Подставим вместо букв цифры (А -> 0, О -> 1, У -> 2):
1. 00000 2. 00001 3. 00002 4. 00010 ...
остатки 241 | 3 | 1 80 | 3 | 2 26 | 3 | 2 8 | 3 | 2 2 | |
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
Смотрим слова и находим по номеру нужное слово: … (241,[У,У,У,У,А]) (242,[У,У,У,У,О]) (243,[У,У,У,У,У])
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Результат: УУУУО
Подробное решение теоретическим способом смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_14: 8 задание. Демоверсия ЕГЭ 2018 информатика:
Все 4-буквенные слова, составленные из букв Д, Е, К, О, Р, записаны в алфавитном порядке и пронумерованы, начиная с 1.
Ниже приведено начало списка.
1. ДДДД 2. ДДДЕ 3. ДДДК 4. ДДДО 5. ДДДР 6. ДДЕД …
Под каким номером в списке идёт первое слово, которое начинается с буквы K?
✍ Решение:
-
✎ Решение теоретическое:
- Подставим вместо букв цифры (Д -> 0, Е -> 1, К -> 2, О -> 3, Р -> 4):
1. 0000 2. 0001 3. 0002 4. 0003 5. 0004 6. 0010 ...
K -> 2 -> 2000
По формуле разложения числа по степеням основания: 20005 = 2 * 53 + 0 * 22 + 0 + 0 = 2 * 125 = 25010
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Результат: 251
Подробное решение 8 (10) задания демоверсии ЕГЭ 2018 года смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_15:
Все 4-буквенные слова, составленные из букв П, Р, С, Т, записаны в алфавитном порядке.
Вот начало списка:
1. ПППП 2. ПППР 3. ПППС 4. ПППТ 5. ППРП ... ...
✍ Решение:
Результат: 65
Видеоразбор задания смотрите ниже:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_16:
Все четырёхбуквенные слова, составленные из букв В, Е, Г, А, Н записаны в алфавитном порядке и пронумерованы, начиная с 1. Начало списка выглядит так:
1. АААА 2. АААВ 3. АААГ 4. АААЕ 5. АААН 6. ААВА …
Под каким номером в списке идёт первое слово, в котором нет буквы А?
✍ Решение:
- ✎ Решение теоретическое:
- Пронумерованный список начинается со всех букв А. Представим, что А — 0, В — 1, Г — 2, Е — 3, Н — 4. Получим следующий список:
1. 0000 2. 0001 3. 0002 4. 0003 5. 0004 6. 0010
11115 = 1 * 53 + 1 * 52 + 1 * 51 + 1 * 50 = 156
156 + 1 = 157
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Результат: 157
Видеорешение задания (теоретическое):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
Вероятность событий
8_17:
За четверть Василий Пупкин получил 20 оценок. Сообщение о том, что он вчера получил четверку, несет 2 бита информации.
Сколько четверок получил Василий за четверть?
✍ Решение:
- Для решения данного задания необходимо вспомнить две формулы:
1. Формула Шеннона:
x = log2(1/p)
x - количество информации в сообщении о событии p - вероятность события
2. Формула вероятности случайного события:
p(A) = m/n
m - число случаев, способствующих событию А n - общее число равновозможных случаев
2 = log2(1/p);
=>
1/p = 4;
=>
p = 1/4
p = ?/20
1/4 = ?/20
? = 1/4 * 20 = 5
Результат: 5
Видеоразбор задания:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Сколько слов длины 5, начинающихся с гласной буквы, можно составить из букв Е, Г, Э? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
2
Сколько слов длины 6, начинающихся с согласной буквы, можно составить из букв Г, О, Д? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
3
Сколько слов длины 5, начинающихся с согласной буквы и заканчивающихся гласной буквой, можно составить из букв З, И, М, А? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
4
Вася составляет 5-буквенные слова, в которых есть только буквы С, Л, О, Н, причём буква С используется в каждом слове ровно 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Вася?
Источник: ЕГЭ 05.05.2015. Досрочная волна.
5
Сколько слов длины 6, начинающихся и заканчивающихся согласной буквой, можно составить из букв Г, О, Д? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
Пройти тестирование по этим заданиям
Сегодня будем решать 8 задание из ЕГЭ по информатике 2022 с помощью программирования.
Восьмое задание легко решается с помощью Python.
Приступим к практике решения задач.
Задача (Классическая)
Женя составляет 5-буквенные слова, в которых встречаются только буквы А, Б, В, Г, причём буква А появляется ровно 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Женя?
Решение:
Напишем программу на языке Python.
k=0 for x1 in 'АБВГ': for x2 in 'АБВГ': for x3 in 'АБВГ': for x4 in 'АБВГ': for x5 in 'АБВГ': s=x1+x2+x3+x4+x5 if s.count('А')==1: k=k+1 print(k)
Т.к. слова состоят из 5-ти символов, то мы формируем пять вложенных циклов! В каждом цикле перебираем все буквы, которые нам дали.
Внутри циклов мы составляем само слово в переменной s. Таким образом, в переменной s «прокрутятся» все возможные комбинации.
Но мы подсчитываем не все комбинации, а только те, где всего одна буква А.
Важно не перепутать русские и английские буквы.
Ответ: 405
Продолжим развивать навыки решения 8 задания из ЕГЭ по информатике 2022.
Задача (Каждую букву можно использовать один раз)
Артур составляет 5-буквенные коды из букв Е, С, А, У, Л. Каждую букву нужно использовать ровно один раз, при этом нельзя ставить рядом две гласные. Сколько различных кодов может составить Артур?
Источник задачи: https://kpolyakov.spb.ru/
Решение:
Запрограммируем решение этой задачи на Питоне.
k=0 for x1 in 'ЕСАУЛ': for x2 in 'ЕСАУЛ': for x3 in 'ЕСАУЛ': for x4 in 'ЕСАУЛ': for x5 in 'ЕСАУЛ': s=x1+x2+x3+x4+x5 if s.count(x1)==1 and s.count(x2)==1 and s.count(x3)==1 and s.count(x4)==1 and s.count(x5)==1: if s.count('ЕА')==0 and s.count('АЕ')==0 and s.count('ЕУ')==0 and s.count('УЕ')==0 and s.count('АУ')==0 and s.count('УА')==0: k=k+1 print(k)
В первом условии учли, что каждая буква встречается в слове только один раз. Второе условие говорит о том, что две гласные не стоят рядом (перебрали все возможные сочетания гласных).
Ответ: 12
Задача(Буквы составляют перестановкой)
Петя составляет шестибуквенные слова перестановкой букв слова КАБАЛА. При этом он избегает слов с двумя подряд одинаковыми буквами. Сколько всего различных слов может составить Петя?
Решение:
k=0 for x1 in 'КБЛА': for x2 in 'КБЛА': for x3 in 'КБЛА': for x4 in 'КБЛА': for x5 in 'КБЛА': for x6 in 'КБЛА': s=x1+x2+x3+x4+x5+x6 if s.count('К')==1 and s.count('А')==3 and s.count('Б')==1 and s.count('Л')==1: if s.count('АА')==0: k=k+1 print(k)
Повторяющиеся буквы в строке, из который берём символы в циклах, всегда убираем.
Слова составляются перестановкой, значит, можно представить, что просто собирают из кубиков КАБАЛА различные слова. Следовательно, в наших словах будет ровно одна буква «К», три буквы «А», одна буква «Б» и одна буква «Л». Это программируем с помощью условия и функции .count().
Т.к. повторятся может только буква «A», то мы прописываем условие, что две буквы «А» подряд не могут находится в наших комбинациях.
Если все условия будут пройдены, то мы подсчитываем такие комбинации.
Ответ: 24
В задании 8 из ЕГЭ по информатике часто нужно проанализировать первую или последнюю букву в слове. Узнаем, как это можно сделать с помощью питона.
Задача (Проверяем первую букву слова)
Сколько слов длины 5, начинающихся с гласной буквы, можно составить из букв Е, Г, Э? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
Источник задачи: https://kpolyakov.spb.ru/
Решение:
В этой тренировочной задаче из 8 задания ЕГЭ по информатике 2022 нужно держать на контроле первую букву в слове.
k=0 for x1 in 'ЕГЭ': for x2 in 'ЕГЭ': for x3 in 'ЕГЭ': for x4 in 'ЕГЭ': for x5 in 'ЕГЭ': s=x1+x2+x3+x4+x5 if x1=='Е' or x1=='Э': k=k+1 print(k)
Подсчитываем только те комбинации, которые начинаются с гласных букв.
Ответ: 162
Интересный пример, где можно ошибиться в 8 задании из ЕГЭ по информатике.
Задача (Важный пример)
Сергей составляет 6-буквенные коды из букв С, О, Л, О, В, Е, Й. Буква Й может использоваться в коде не более одного раза, при этом она не может стоять на первом месте, на последнем месте и рядом с буквой Е. Все остальные буквы могут встречаться произвольное количество раз или не встречаться совсем. Сколько различных кодов может составить Сергей?
Источник задачи: https://kpolyakov.spb.ru/
Решение:
Эта задача примечательная тем, что буква «О» в слове «СОЛОВЕЙ» повторяется. В этом случае мы должны убрать повторение буквы из перебора.
k=0 for x1 in 'СОЛВЕЙ': for x2 in 'СОЛВЕЙ': for x3 in 'СОЛВЕЙ': for x4 in 'СОЛВЕЙ': for x5 in 'СОЛВЕЙ': for x6 in 'СОЛВЕЙ': s=x1+x2+x3+x4+x5+x6 if s.count('Й')<=1 and x1!='Й' and x6!='Й' and s.count('ЕЙ')==0 and s.count('ЙЕ')==0: k=k+1 print(k)
Здесь также учитываем остальные условия.
Ответ: 23625
Задача (Количество гласных)
Василий составляет 4-буквенные коды из букв Г, А, Ф, Н, И, Й. Каждую букву можно использовать любое количество раз, при этом код не может начинаться с буквы Й и должен содержать хотя бы одну гласную. Сколько различных кодов может составить Василий?
Источник задачи: https://kpolyakov.spb.ru/
Решение:
Напишем программу.
k=0 for x1 in 'ГАФНИЙ': for x2 in 'ГАФНИЙ': for x3 in 'ГАФНИЙ': for x4 in 'ГАФНИЙ': s=x1+x2+x3+x4 if x1!='Й' and s.count('А') + s.count('И') >= 1: k=k+1 print(k)
Ответ: 888
Порешаем задачи из восьмого задания ЕГЭ по информатике на перебор чисел.
Задача (Перебор чисел)
Сколько существует чисел, восьмеричная запись которых содержит 7 цифр, причём все цифры различны и никакие две чётные и две нечётные цифры не стоят рядом.
Источник задачи: https://kpolyakov.spb.ru/
Решение:
k1=0 k2=0 for x1 in '1234567': for x2 in '01234567': for x3 in '01234567': for x4 in '01234567': for x5 in '01234567': for x6 in '01234567': for x7 in '01234567': s=x1+x2+x3+x4+x5+x6+x7 if s.count(x1)==1 and s.count(x2)==1 and s.count(x3)==1 and s.count(x4)==1 and s.count(x5)==1 and s.count(x6)==1 and s.count(x7)==1: if int(x1)%2==0 and int(x2)%2==1 and int(x3)%2==0 and int(x4)%2==1 and int(x5)%2==0 and int(x6)%2==1 and int(x7)%2==0: k1=k1+1 if int(x1)%2==1 and int(x2)%2==0 and int(x3)%2==1 and int(x4)%2==0 and int(x5)%2==1 and int(x6)%2==0 and int(x7)%2==1: k2=k2+1 print(k1+k2)
Число не может начинаться с нуля. Поэтому ноль был исключён из первого цикла.
Первое условие следит за тем, чтобы каждая цифра встречалась один раз в числе. Второе условие подсчитывает количество вариантов, когда первая цифра чётная. Второе условие следит за тем, чтобы чётность и нечётность цифр чередовалась. Третье условие, наоборот, подсчитывает варианты, когда первая цифра нечётная.
Операция % — остаток от деления. Если остаток от деления на 2 равен нулю, то число чётное. Если остаток от деления на 2 равен 1, то число нечётное.
Функция int() преобразует символ в число. Ведь мы работаем именно с символами, а не с реальными числами.
Ответ: 1008
Задача (Числа, Закрепление)
Сколько существует четырёхзначных чисел, записанных в восьмеричной системе счисления, в записи которых ровно две одинаковые цифры, причём стоящие рядом ?
Решение:
k=0 for x1 in '1234567': for x2 in '01234567': for x3 in '01234567': for x4 in '01234567': if (x1==x2 and x2!=x3 and x2!=x4 and x3!=x4) or (x2==x3 and x3!=x1 and x3!=x4 and x1!=x4) or (x3==x4 and x3!=x2 and x3!=x1 and x1!=x2): k=k+1 print(k)
Здесь следующий принцип составления условия. Два соседа должны быть равны. Берём одного соседа из пары, где цифры должны быть равны, и комбинируем его с другими цифрами. Пишем уже, чтобы цифры были не равны. Так же прописываем, чтобы две оставшиеся цифры также не были равны. Таким образом, перебираем все варианты.
Ответ: 882
Задача (Числа, важный приём)
Сколько существует различных трёхзначных чисел в шестнадцатиричной системе счисления, в записи которых цифры следуют слева направо в невозрастающем порядке?
Решение:
k=0 for x1 in '123456789ABCDEF': for x2 in '0123456789ABCDEF': for x3 in '0123456789ABCDEF': if x1 >= x2 >= x3: k=k+1 print(k)
Символы можно сравнивает знаками больше или меньше. Символы-цифры сравниваются, как обычные числа. Буквы сравниваются в алфавитном порядке.
Применяем этот приём и получаем ответ.
Ответ: 815
Задача(Две чётные и две нечётные цифры не стоят рядом)
Сколько существует чисел, делящихся на 5, десятичная запись которых содержит 7 цифр, причём все цифры различны и никакие две чётные и две нечётные цифры не стоят рядом.
Решение:
k=0 for x1 in '123456789': for x2 in '0123456789': for x3 in '0123456789': for x4 in '0123456789': for x5 in '0123456789': for x6 in '0123456789': for x7 in '05': s=x1+x2+x3+x4+x5+x6+x7 if s.count(x1)==1 and s.count(x2)==1 and s.count(x3)==1 and s.count(x4)==1 and s.count(x5)==1 and s.count(x6)==1 and s.count(x7)==1: if x1 in '02468' and x2 in '13579' and x3 in '02468' and x4 in '13579' and x5 in '02468' and x6 in '13579' and x7 in '02468': k=k+1 if x1 in '13579' and x2 in '02468' and x3 in '13579' and x4 in '02468' and x5 in '13579' and x6 in '02468' and x7 in '13579': k=k+1 print(k)
Перебираем 7 разрядов десятичного числа. С нуля число не может начинаться, поэтому из первого цикла удаляем ноль.
Число должно делиться на 5, значит, в последнем цикле оставляем только 0 и 5.
Все цифры различны, поэтому применяем условие, что символ x1 встречается 1 раз, символ x2 встречается 1 раз и т.д.
Фраза «две чётные и две нечётные цифры не стоят рядом» обозначает, что цифры должны чередоваться. Например, чётная, нечётная, чётная, нечётная и т.д. (или наоборот).
Направление задаёт именно первая цифра, остальные цифры выстраиваются по ней.
Проверить чётность/нечётность цифр просто, мы проверям существует ли конкретный символ с троке из чётных или нечётных цифр.
У нас два равноправных случая: когда первая цифра чётная, и когда первая цифра нечётная.
Ответ: 2880
Следующий тип задач из задания 8 ЕГЭ по информатике лучше решать без программирования.
Задача (Со списками, классическая)
Все 4-буквенные слова, составленные из букв А, Е, И, О записаны в алфавитном порядке и пронумерованы. Вот начало списка:
1. АААА
2. АААЕ
3. АААИ
4. АААО
5. ААЕА
…
Запишите слово, стоящее на 248-м месте от начала списка.
Источник задачи: https://inf-ege.sdamgia.ru/
Решение:
Обозначим условно А — 0, Е — 1, И — 2, О — 3.
Важно: Нужно буквам присваивать цифры именно в том порядке, в котором они идут в самом правом столбце, потому что буквы могут дать в «перепутанном порядке» (например Е, А, И, О), и тогда ничего не получится.
Теперь запишем список с помощью цифр.
1. 0000
2. 0001
3. 0002
4. 0003
5. 0010
…
Получился обычный счёт в четверичной системе!! (всего используются 4 цифры: 0, 1, 2, 3). А слева нумерация показывает соответствие нашей десятичной системе. Но все числа десятичной системы в этой таблице соответствия сдвинуты на 1, ведь мы должны были начать с нуля.
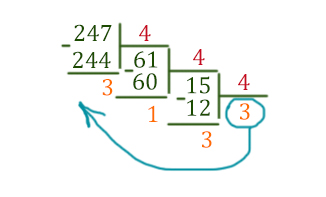
Нас просят записать слово стоящее на 248, т.е. если была обычная таблица соответствия чисел десятичной системы и четверичной системы, слово стоящее на 248 месте, находилось бы на 247 (248 — 1) месте. Значит, наше искомое четверичное число соответствует 247 в десятичной системе.
Переведём число 247 в четверичную систему!
Получилось число 33134 в четверичной системе. Сделаем обратное декодирование в буквы. Таким образом, ответ будет ООЕО.
Ответ: ООЕО
Ещё одна похожая задача 8 задания из примерных вариантов ЕГЭ по информатике 2022, но другой вариации.
Задача (Классика, Другая вариация)
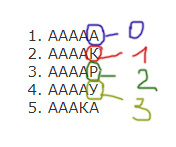
Все 5-буквенные слова, составленные из букв А, Р, У, К записаны в алфавитном порядке. Вот начало списка:
1. ААААА
2. ААААК
3. ААААР
4. ААААУ
5. АААКА
……
Укажите номер слова УКАРА
Источник задачи: https://inf-ege.sdamgia.ru/
Решение:
Закодируем буквы цифрами: А — 0, К — 1, Р — 2, У — 3. Здесь как раз буквы даны не в том порядке, как они идут в самом правом столбце. Но мы должны кодировать именно в том порядке, как буквы идут в самом правом столбце.
У нас получилось четыре цифры! Значит снова можно слова превратить в таблицу соответствия между десятичной системой и четверичной системой. Но десятичная система смещена на 1 позицию.
1. 00000
2. 00001
3. 00002
4. 00003
5. 00010
……
Выписываем данное нам слово и посмотрим, какое число в четверичной системе было бы, если бы у нас были в место слов числа в четверичной системе!
Получили число в четверичной системе 310204. Узнаем, какое число в десятичной системе соответствовало этому числу, если бы была обычная таблица соответствия. Для этого переведём число 310204 из четверичной системы в десятичную. Перевод делаем по аналогии перевода из двоичной системы в десятичную.
Но помним, что у нас нумерация идёт на 1 быстрее, нежели мы бы поставили десятичные числа, как в таблице соответствия, потому что нумерация начинается не с нуля, а с 1. Поэтому к числу 840 нужно прибавить 1, и в ответе будет 841
Ответ: 841
Задача (Демонстрационный вариант ЕГЭ по информатике, 2020)
Все 4-буквенные слова, в составе которых могут быть буквы Н, О, Т, К, И,
записаны в алфавитном порядке и пронумерованы, начиная с 1.
Ниже приведено начало списка.
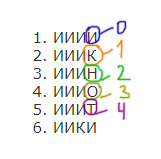
1. ИИИИ
2. ИИИК
3. ИИИН
4. ИИИО
5. ИИИТ
6. ИИКИ
…
Под каким номером в списке идёт первое слово, которое начинается
с буквы О?
Решение:
Закодируем буквы цифрами.
Получилось 5 цифр ( 0, 1, 2, 3, 4 ), значит, будем работать в пятеричной системе.
Нужно найти номер первого слова, которое начинается с буквы О. Если говорить на языке пятеричных чисел, то нужно найти номер числа 30005. Мы «забиваем нулями», чтобы число было четырёхразрядное, т.к. слова 4-х буквенные. Именно нулями, потому что нужно именно первое слово найти.
Теперь, как в предыдущей задаче, переведём число 30005 из пятеричной системы в десятичную.
0 * 5 0 + 0 * 5 1 + 0 * 5 2 +
3 * 5 3 = 375 (в десят. системе)
Но опять же должны прибавить 1 к числу 375, т.к. нумерация отличается от десятичных чисел на 1 в большую сторону.
Ответ: 376
Задача (Формула Шеннона)
В корзине лежат 8 черных шаров и 24 белых. Сколько бит информации несет сообщение о том, что достали черный шар?
Источник задачи: https://inf-ege.sdamgia.ru/
Решение:
Данную задачу нужно решать по формуле Шеннона
Найдём вероятность p того, что вытащили чёрный шарик.
p = (количество чёрных шаров) / (количество всех шаров) = 8 / (24 + 
p = 1 / 4
Применим формулу Шеннона.
x = log2(4)
2x = 4
x = 2 бита
Ответ: 2
Счастливых экзаменов!
Спасибо большое за отличный разбор. В задаче «Сколько существует различных трёхзначных чисел в шестнадцатЕричной системе счисления, в записи которых цифры следуют слева направо в невозрастающем порядке» можно немного упростить условие, так как строки сравниваются именно по их коду. Итак, условие ord(x1)>=ord(x2)>=ord(x3) заменяем на x1>=x2>=x3. И все работает также!!!
Здраствуйте пробовал решить задачу на pytone
Артур составляет 6-буквенные коды перестановкой букв слова КАБАЛА. При этом нельзя ставить рядом две гласные. Сколько различных кодов может составить Артур?
У вас я не было в примере такой задачи я посмотрел примеры у других блогеров.
Вот мой код выводит108 но правильный ответ 24 поясните пожалуйста где я ощибся?
letters = ‘КАБАЛА’
s=set()
for x1 in letters:
for x2 in letters:
for x3 in letters:
for x4 in letters:
for x5 in letters:
for x6 in letters:
word=x1+x2+x3+x4+x5+x6
if word.count(‘А’) ==3 and word.count(‘АА’)==0:
s.add(word)
print(len(s))
определите количество пятизначных чисел записанных в десятичной системе счисления в записи которых есть 1 при этом никакая четная цофра не считает рядом с фирой 1
Всем привет, Давыдову тоже.
Задание 8. Анализ программ. Циклы for и while. ЕГЭ 2023 по информатике
За это задание ты можешь получить 1 балл. На решение дается около 3 минут. Уровень сложности: базовый.
Средний процент выполнения: 85.3%
Ответом к заданию 8 по информатике может быть цифра (число) или слово.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
Саша составляет шестибуквенные слова, в которых есть только буквы А, М, О, К, Т и С, причём в каждом слове буква Т используется один или два раза и при этом может стоять только на первом или на втором местах, а буква О встречается в слове ровно 2 раза, на пятом и шестом месте. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная.
Сколько существует таких слов, которые может написать Саша?
Решение
Поскольку на двух последних позициях обязательно стоит буква О, там всегда ровно один вариант расстановки букв. Количество вариантов зависит только от первых 4-х символов. Дальше будем считать именно для 4-х символов.
Рассмотрим все варианты расстановки буквы Т:
1. Буква Т встречается ровно 2 раза на первом и втором месте. Тогда на 3 и 4 месте могут стоять только буквы А/М/К/С. 4·4 = 16 вариантов.
2. Буква Т встречается ровно 1 раз на первом месте. Тогда на 2, 3 и 4 месте могут стоять только буквы А/М/К/С. 4·4·4 = 64 варианта.
3. Буква Т встречается ровно 1 раз на втором месте. Тогда на 1, 3 и 4 месте могут стоять только буквы А/М/К/С. 4·4·4 = 64 варианта.
Всего вариантов: 64+64+16 = 144.
Ответ: 144
Ответ: 144
Задача 2
Саша составляет шестизначные числа, в которых есть только цифры 1, 2 и 3, причём цифра 1 используется в каждом числе не более двух раз и при этом может стоять только на первом или втором местах. Каждая из других допустимых цифр может встречаться в числе любое количество раз или не встречаться совсем. Сколько существует таких чисел, которые может написать Саша?
Решение
1) без цифры 1: 2*2*2*2*2*2=64
2) с одной 1 на первом месте: 1*2*2*2*2*2=32
3) с одной 1 на втором месте: 2*1*2*2*2*2=32
1) с двумя 1: 1*1*2*2*2*2=16
Итого: 64+32+32+16=144
Ответ: 144
Задача 3
Саша составляет пятибуквенные слова, в которых есть только буквы А, Б, В, Г, Д, Е, причём в каждом слове буква Г используется ровно 2 раза. Каждая из других допустимых букв может встречаться любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная.
Сколько существует таких слов, которые может написать Саша?
Решение
Количество перестановок букв Т на 5 позициях = 10. можно вычислить по формуле n!/(n-m)! где n — это количество позиций (в данном случае 5), а m — количество букв, которые необходимо расположить (в данном случае 2 буквы Т). по формуле получается 20, но у нас абсолютно одинаковые элементы (буквы Т) поэтому делим на факториал 2, чтобы не учитывать повторы.
На каждой из оставшихся трёх позиций в слове могут стоять по 5 букв — итого 125 комбинаций.
В итоге: для каждого из 10 вариантов расположения букв Т получается по 125 комбинаций оставшихся трёх букв: 10 * 125 = 1250.
Ответ: 1250
Задача 4
Аня составляет 5-буквенные слова, в которых встречаются только буквы А, Б, В. Причем буква A может встречаться только первой или последней (двух букв А в слове быть не может), но при этом должна присутствовать обязательно. Каждая из других допустимых букв может встречаться в слове на любом месте или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная.
Сколько существует таких слов, которые может написать Аня?
Решение
Поскольку буква А должна стоять либо на первом, либо на последнем месте (должна встретиться в слове, но не на обеих позициях), то получаем такие комбинации размещения букв:
A 2 2 2 2 = 16 слов
2 2 2 2 A = 16 слов
Итого: 16+16=32 слова
Ответ: 32
Задача 5
Все пятибуквенные слова, составленные из букв А, Л, Е, Т, Б записаны в алфавитном порядке и пронумерованы. Вот начало списка:
1. ААААА
2. ААААБ
3. ААААЕ
4. ААААЛ
5. ААААТ
6. АААБА
. . .
Под каким номером в списке идёт первое слово, которое начинается с буквы Л и заканчивается буквой Т?
Решение
Каждому слову поставим в соответствие пятизначное число в пятеричной системе счисления. Для этого каждой букве поставим в соответствие цифру в том порядке, в котором она появляетс в списке.
А — 0, Б — 1, Е — 2, Л — 3, Т — 4
Первое слово, которое начинается на Л — это слово ЛАААА и заканчивающееся на Т — то есть ЛАААТ. Этому слову соответствует число $30004_5$ = $1879_10$, которое стоит под номером 1880.
Ответ: 1880
Задача 6
Все шестибуквенные слова, составленные из букв Б, Л, О, Т записаны в алфавитном порядке и пронумерованы. Вот начало списка:
1. ББББББ
2. БББББЛ
3. БББББО
4. БББББТ
5. ББББЛБ
6. ББББЛЛ
. . .
Под каким номером стоит слово БОЛОТО?
Решение
Для составления слов используются 4 различных буквы. Поставим в соответствие каждой из букв цифры системы счисления с основанием 4 (с учётом порядка их следования в алфавите): Б — 0, Л — 1, О — 2, Т — 3.
Тогда упорядоченной по алфавиту последовательности слов
1. ББББББ
2. БББББЛ
3. БББББО
4. БББББТ
5. ББББЛБ
6. ББББЛЛ
. . .
будут соответствовать числа в системе счисления с основанием 4:
1. 0000004 = 010
2. 0000014 = 110
3. 0000024 = 210
4. 0000034 = 310
5. 0000104 = 410
5. 0000114 = 510
. . .
Слову БОЛОТО будет соответствовать число 0212324. Переведём это число из системы счисления с основанием 4 в десятичную.
0212324 = 0 · 45 + 2 · 44 + 1 · 43 + 2 · 42 + 3 · 41 + 2 · 40 = 62210.
Заметим, что соответствующая последовательность чисел, записанных в десятичной системе счисления, на 1 меньше номера строки, содержащей данное число. Значит, десятичное число 622 будет находиться на 623-м месте.
Ответ: 623
Задача 7
Саша составляет 6-значные числа, в которых есть только цифры 1, 2, 3 и 4 причём цифра 1 используется в каждом числе ровно 1 раз. Каждое из других допустимых цифр может встречаться в числе любое количество раз или не встречаться совсем. Сколько существует таких чисел, которые может написать Саша?
Решение
Пусть цифра 1 стоит в числе на первом месте. Тогда на оставшихся 5 местах может стоять одна из оставшихся цифр 2, 3 или 4. Причём каждая из этих цифр может встречаться в числе любое количество раз. Таким образом нам нужно определить количество 5-значных чисел, состоящих из трёх цифр.
Если M — количество символов в некотором алфавите (мощность алфавита), K — количество всех возможных «слов» (символьных цепочек) длиной N , то = MN.
Следовательно, количество пятизначных чисел, состоящих из трёх цифр, равно 35 = 243. А значит такое же количество 6-значных чисел, в которых на первом месте стоит цифра 1, а на остальных местах цифры 2, 3 или 4, возможно с повтором.
Рассуждая аналогичным образом, мы получим, что такое же количество чисел в 6-значных числах, в которых цифра 1 на втором, третьем, четвёртом, пятом и шестом местах.
То есть всего искомых чисел 6 · 243 = 1458.
Ответ: 1458
Задача 8
Саша составляет четырёхбуквенные слова, в которых есть только буквы Е, Д, О, Н и К, причём в каждом слове буква О используется ровно 2 раза. Каждое из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная.
Сколько существует таких слов, которые может написать Саша?
Задача 9
Саша составляет трёхбуквенные слова, в которых есть только буквы E, C, B, Н, К и У, причём в каждом слове буква К используется ровно 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная.
Сколько существует таких слов, которые может написать Саша?
Задача 10
Все шестибуквенные слова, составленные из букв М, Н, О, П, Р, записаны в алфавитном порядке и пронумерованы. Вот начало списка:
1. ММММММ
2. МММММН
3. МММММО
4. МММММП
5. МММММР
6. ММММНМ
. . .
Укажите слово, которое стоит под номером 267.
Задача 11
Все пятибуквенные слова, составленные из букв А, М, Н, Т, У, записаны в алфавитном порядке и пронумерованы. Вот начало списка:
1. ААААА
2. ААААМ
3. ААААН
4. ААААТ
5. ААААУ
6. АААМА
. . .
Под каким номером стоит слово ТУМАН?