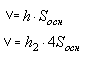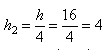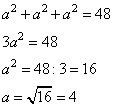Восьмое задание егэ математика как решать

7 января 2022

В закладки

Обсудить

Жалоба

Задания 8 профильного ЕГЭ по математике представляют собой текстовые задачи. В таких задачах нужно проинтерпретировать описанную в условии ситуацию, составить математическую модель и найти искомую величину. Как правило, решение задачи сводится к решению линейного или квадратного уравнения, или систем таких уравнений, однако некоторые из задач можно решить чисто арифметическими методами.

Сюжеты задач стандартны, но довольно разнообразны. Разберём основные типы сюжетов, возникающих на экзамене, и постараемся охватить как можно больше типов появляющихся уравнений и систем.

→ Задачи на движение.
→ Задачи на совместную работу.
→ Задачи на проценты.

8m-text.pdf

Источник: vk.com/alkaevalr

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Многие выпускники 11-х классов, которые выбирают ЕГЭ профильного уровня по математике в 2023 году, считают задание 9 трудным и опасаются его. И это несмотря на то, что с первого класса решали текстовые задачи на уроках математики.

На вопрос почему, отвечают так: нереально
научиться решать все текстовые задачи, поскольку их очень много и все они решаются по-разному.

Учащиеся, которые так думают, ошибаются.
Научиться решать все текстовые задачи вполне РЕАЛЬНО! Это только на первый взгляд задачи не похожи. Подходим к решению проблемы комплексно.

Первое, что нужно:

– знать, какие типы задач на экзамене,

– понимать, к какому типу относится задача, которую предстоит решить,

– владеть основными способами решения задач каждого типа.

Ниже на схеме представлены типы задач, которые встречаются в задании 9 ЕГЭ по математике.

Что нужно знать для того, чтобы успешно справиться с текстовой задачей 9 ЕГЭ по математике?

Движение	Работа	Смеси и сплавы	Проценты
S — путь (км), v -скорость (км/ч), t – время (ч) S =	A –работа, x -производительность t — время A=x t	m (кг) – масса раствора, содержащего n % вещества. кг вещества в растворе.	S – вклад в банк (руб.) под r % годовых. Через 1 год на вкладе S (1+ Через n лет — руб.

Что нужно уметь для того, чтобы успешно справиться с текстовой задачей?

1) Составлять математическую модель задачи, то есть перевести условие с русского языка на математический, например, составить уравнение (предварительно по данным текста можно составить таблицу или сделать рисунок).

2) Применять математические знания при реализации модели, чаще всего решать уравнение.

Приведём примеры задачи 9 ЕГЭ по математике профильного уровня на движение по прямой.

Задача 1
(движение в одном направлении).

Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам?

Решение. Через 1 час расстояние между пешеходами станет равным 1,5 км=1500 м, что в 5 раз больше 300 м, значит, расстояние между пешеходами станет 300 м через 1 ч. : 5 = 60 мин. : 5=12 мин.

Можно решить задачу иначе: пусть v км/час – скорость первого пешехода, а (v+1,5) км/ч, пусть через t часов расстояние между пешеходами станет равным 0,3 км. Тогда (v+1,5)t—vt=0,3, 1,5t =0,3, t=0,2 (час.)=12 (мин.).

Ответ. 12

Задача 2
(встречное движение).

По двум параллельным железнодорожным путям навстречу друг другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.

Решение. Пусть l м — длина скорого поезда.

Скорость сближения поездов равна 65+35=100 (км/ч) = (м/с). За 36 секунд скорый поезд прошёл путь, равный (l+700) м. Тогда , l=300 м.

Можно решить задачу иначе: пусть l м — длина скорого поезда. Если бы пассажирский поезд стоял, а скорый поезд проезжал мимо него со скоростью 100 км/ч, то время, за которое скорый поезд прошёл мимо пассажирского, то есть путь, равный (l+700) метров, было бы равно 36 секундам. Тогда м.

Ответ. 300.

Задача 3
(движение по воде).

Теплоход проходит по течению реки до пункта назначения 255 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 1 км/ч, стоянка длится 2 часа, а в пункт отправления теплоход возвращается через 34 часа после отплытия из него. Ответ дайте в км/ч.

Решение. Пусть x км/ч — скорость теплохода в неподвижной воде, тогда (x+1) км/ч и (x-1) км/ч скорость теплохода по течению и против течения соответственно.

Время на путь по течению равно а время на путь против течения — ч.

Так как в пути теплоход был 34-2=32 часа, то можно составить уравнение получим 32 16 , откуда x=16 км/ч.

Ответ. 16

Приведём примеры задач на проценты и смеси и сплавы.

Задача 4 (проценты)

В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?

Решение.

Первоначальная стоимость акций компании	n
Цена акций в понедельник после подорожания на x%	n (1+ )
Цена акций во вторник после падения цены на x%	n (1+ ) =0,96n

, , .

Ответ. 20%

Задача 5 (смеси и сплавы)

В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

Решение.

	Объём раствора	Процентное содержание вещества в растворе	Объём вещества в растворе
Первоначальный раствор	5л	12%	5
Раствор после добавления воды	5+7=12 л	?	0,6 л

Составим пропорцию 12 л — 100%

0,6 л — ?

Ответ. 5 %

---

Стереометрия

---

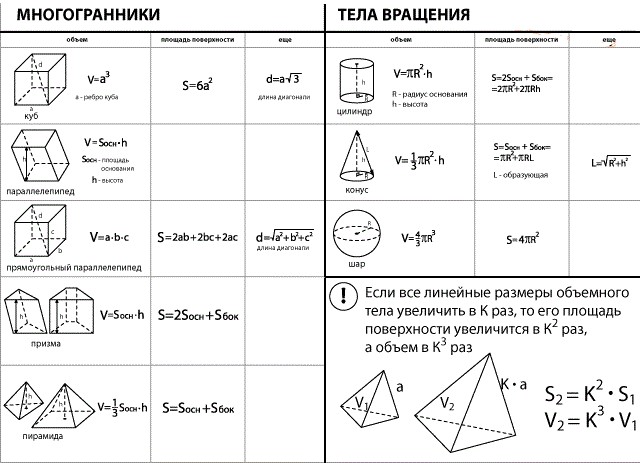
Задание №8 в профильном уровне ЕГЭ по математике проверяет базовые знания стереометрии. Задания в этом разделе простые, на базовые формулы – обычно на объемы простых стандартных фигур – цилиндра, куба, пирамиды, конуса.

---

Теория к заданию №8

---

Приведу формулы объема фигур, так данный материал довольно часто встречается.

---

Разбор типовых вариантов заданий №8 ЕГЭ по математике профильного уровня

---

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=”#defae6″]

В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 2 раза больше первого? Ответ выразите в см.

[/su_note]

Алгоритм решения:

1. Определяем площадь основания первого и второго сосудов.
2. Записываем формулы объемов и приравниваем их.
3. Убираем одинаковые величины. Делаем вывод.
4. Записываем ответ.

Решение:

1. Площадь основания первого сосуда определяется формулой

Диаметр второго сосуда в 2 раза больше. Значит площадь основания его равна

то есть в 4 раза больше:

2 Записываем формулы объема жидкости в каждом сосуде.

Так как объем жидкости остается постоянным, получаем уравнение:

Убираем одинаковые величины. Отсюда

Ответ: 4.

---

Второй вариант задания (из Ященко, №1)

[su_note note_color=”#defae6″]

Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 28. Найдите объём цилиндра.

[/su_note]

Алгоритм решения:

1. Записываем формулу объема конуса.
2. Записываем формулу объема цилиндра.
3. Сравниваем формулы, делаем вывод.
4. Вычисляем объем цилиндра.
5. Записываем ответ.

Решение:

1. Объем конуса определяем по формуле

где H – высота конуса; R – радиус основания конуса.

2. Объем цилиндра определяем по формуле

3. Сравниваем обе формулы. Легко видно, что объем цилиндра в 3 раза больше объема конуса.

4. Вычисляем объем цилиндра::

Ответ: 84.

---

Третий вариант задания (из Ященко)

[su_note note_color=”#defae6″]

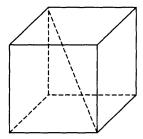
Диагональ куба равна . Найдите его объём.

[/su_note]

Алгоритм решения:

1. Выражаем диагональ куба, используя теорему Пифагора.
2. Решаем полученное уравнение.
3. Вычисляем объем.
4. Записываем ответ.

Решение:

1. По тереме Пифагора диагональ грани куба определяется формулой:

Тогда диагональ куба

2. Отсюда

3. Объем куба равен

Ответ: 64.

Даниил Романович | Просмотров: 28.5k

Для текстовых задач не существует единого алгоритма решения — в этом вся их сложность. Фактически, каждую задачу приходится решать «с нуля». Зубрить их тоже бесполезно, потому что текстовых задач слишком много.

Тем не менее, существуют типовые задачи, которые вполне стандартно решаются и постоянно встречаются на ЕГЭ по математике. Ими мы и займемся.

§ 1.

Вебинар по задачам B14: движение, работа, смеси и сплавы

Глава 1.

Классические задачи на движение

§ 1.

Особенности решения текстовых задач

§ 2.

Задача B14: движение навстречу

§ 3.

Движение вдогонку и сравнение времени

§ 4.

Тест по задачам B14: легкий уровень, 1 вариант

§ 5.

Тест по задачам B14: легкий уровень, 2 вариант

§ 6.

B14 и эскалаторы: считаем скорость

§ 7.

Задача B14 про эскалаторы: считаем ступеньки

Глава 2.

Работа и производительность труда

§ 1.

Производительность совместного труда

§ 2.

B14: количество вопросов в тесте

§ 3.

Трубы и резервуары: одинаковый объем

§ 4.

Трубы и резервуары: разный объем

§ 5.

Более сложные задачи на производительность

Глава 3.

Движение по воде

§ 1.

Решение задач на движение по воде

§ 2.

Тест по задачам B14: средний уровень, 1 вариант

§ 3.

Тест по задачам B14: средний уровень, 2 вариант

Глава 4.

Смеси и сплавы

§ 1.

Как решать задачи про смеси и сплавы

§ 2.

Простая задача B14 на смеси и сплавы

§ 3.

Сложная задача B14 на смеси и сплавы

§ 4.

Смеси и сплавы в задаче B14: неизвестна масса

Глава 5.

Проценты и нестандартные задачи

§ 1.

Задача B14: сложные проценты

§ 2.

Семья из трех человек (нестандартная задача)

§ 3.

Сложная задача B14: работа трех исполнителей

§ 4.

Изюм и виноград (смеси и сплавы)

Единый государственный экзамен по математике базового уровня состоит из 20 заданий. В задании 8 проверяются знания прикладной геометрии. Школьник должен уметь решать различные задачи на многоугольники. Здесь вы можете узнать, как решать задание 8 ЕГЭ по математике базового уровня, а также изучить примеры и способы решения на основе подробно разобранных заданий.