- Взрослым: Skillbox, Хекслет, Eduson, XYZ, GB, Яндекс, Otus, SkillFactory.
- 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- Английский: Инглекс, Puzzle, Novakid.
Формулы для заданий ЕГЭ по информатике
Кодирование текстовой информации
I = n * i
- n — количество символов
- i — количество бит на 1 символ (кодировка)
Формула для нахождения количества цветов в используемой палитре
i = log2N
- N — количество цветов
- i — глубина цвета
Формула объема памяти для хранения растрового изображения
I = M * N * i
- I — объем памяти, требуемый для хранения изображения
- M — ширина изображения в пикселях
- N — высота изображения в пикселях
- i — глубина кодирования цвета или разрешение
Или
I = N * i битов
- N – количество пикселей (M * N)
- i – глубина кодирования цвета (разрядность кодирования)
Для указания объема выделенной памяти встречаются разные обозначения (V или I).
Формула объема звукового файла
I = β * ƒ * t * S
- I — объем
- β — глубина кодирования
- ƒ — частота дискретизации
- t — время
- S — количество каналов (S=1 для моно, S=2 для стерео, S=4 для квадро)
Формула объема переданной информации
I = V * t
- I — объем информации
- v — пропускная способность канала связи (измеряется в битах в секунду и пр.)
- t — время передачи
Формула скорости передачи данных
V = I / t
- I — объем информации
- v — пропускная способность канала связи (измеряется в битах в секунду и пр.)
- t — время передачи
Формулы преобразования
- 1 Мбайт = 220 байт = 223 бит,
- 1 Кбайт = 210 байт = 213 бит
- Взрослым: Skillbox, Хекслет, Eduson, XYZ, GB, Яндекс, Otus, SkillFactory.
- 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- Английский: Инглекс, Puzzle, Novakid.
1.
1 задание. Демо ЕГЭ 2023 информатика, ФИПИ:
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|
| 1 | — | 39 | 3 | ||||
| 2 | 39 | — | 8 | 5 | |||
| 3 | 3 | — | 2 | ||||
| 4 | 8 | — | 53 | ||||
| 5 | 5 | — | 21 | 30 | |||
| 6 | 2 | 21 | — | 13 | |||
| 7 | 53 | 30 | 13 | — |
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе.
Определите, какова сумма протяжённостей дорог из пункта D в пункт B и из пункта F в пункт A.
В ответе запишите целое число.
Ответ: 58
🎦 Видео на RuTube
✍ Решение:
- Рядом с каждой вершиной проставим количество ребер вершины и в скобках — количество ребер у «соседей»:
- Выберем уникальные вершины, значения которых вместе с соседними вершинами отличаются от всех:
B = 2(3,3) A = 3(3,3,3)
B 2(3,3):Найдем строки в таблице с двумя вершинами:
№1: 39 и 3 = 2(3,2) , т.к. 1 сосед =(39,8,5) и 2 сосед=2(3,2). Данная строка не подходит, так как мы ищем 2(3,3)
№3: 3 и 2 = 3(2,2) не подходит
№4: 8 и 53 = 2(3,3) => B = №4
А 3(3,3,3):Найдем строки в таблице с двумя вершинами:
№2: 39 и 8 и 5 = 3(3,2,3) не подходит
№5: 5 и 21 и 30 = 3(3,3,3) => A = №5
B, и видим соседей — D(2,3,3) и F(2,2,3).№4=B пересекается с №2(2,2,3) и №7(2,3,3). Делаем вывод, что №2=F, №7=D.DB=53, FA=5 53+5 = 58
Ответ: 58
2.
2 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Миша заполнял таблицу истинности логической функции F
¬(y → x) ∨ (z → w) ∨ ¬z
но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | Функция |
| ??? | ??? | ??? | ??? | F |
| 0 | 0 | |||
| 0 | 1 | 0 | ||
| 1 | 0 | 0 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.).
Ответ: yxzw
Решение подобного задания (теоретическое):
🎦 RuTube
3.
3 задание. Демоверсия варианта ЕГЭ по информатике 2022, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
В файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц.
Таблица «Движение товаров» содержит записи о поставках товаров в магазины в течение первой декады июня 2021 г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок внесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня. Заголовок таблицы имеет следующий вид.
| ID операции | Дата | ID магазина | Артикул | Тип операции | Количество упаковок | Цена |
Таблица «Товар» содержит информацию об основных характеристиках каждого товара. Заголовок таблицы имеет следующий вид.
| Артикул | Отдел | Наименование | Единица измерения | Количество в упаковке | Производитель |
Таблица «Магазин» содержит информацию о местонахождении магазинов. Заголовок таблицы имеет следующий вид.
На рисунке приведена схема указанной базы данных.
Используя информацию из приведённой базы данных, определите общий вес (в кг) крахмала картофельного, поступившего в магазины Заречного района за период с 1 по 8 июня включительно.
В ответе запишите только число.
Ответ: 355
🎦 Видео на RuTube здесь
4.
4 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Н, Ч. Для передачи используется двоичный код, удовлетворяющий прямому условию Фано, согласно которому никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны:
Н – 1111 З – 110
Для трёх оставшихся букв А, К и Ч кодовые слова неизвестны.
Какое количество двоичных знаков потребуется для кодирования слова КАЗАЧКА, если известно, что оно закодировано минимально возможным количеством двоичных знаков?
Ответ: 14
🎦 Видео на RuTube здесь
5.
5 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1. Строится двоичная запись числа N.
2. Далее эта запись обрабатывается по следующему правилу:
а) если сумма цифр в двоичной записи числа чётная, то к этой записи справа дописывается 0, а затем два левых разряда заменяются на 10;
б) если сумма цифр в двоичной записи числа нечётная, то к этой записи справа дописывается 1, а затем два левых разряда заменяются на 11.
Полученная таким образом запись является двоичной записью искомого числа R.
Например, для исходного числа 610 = 1102 результатом является число 10002 = 810, а для исходного числа 410 = 1002 результатом является число 11012 = 1310.
Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число R, большее 40. В ответе это число запишите в десятичной системе счисления.
Ответ: 16
🎦 Видео на RuTube здесь (программирование Pascal)
🎦 Видео на RuTube здесь (аналитическое решение)
6.
6 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды:
Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова,
и Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке.
Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз.
1. Черепахе был дан для исполнения следующий алгоритм:
Повтори 7 [Вперёд 10 Направо 120].
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным
алгоритмом. Точки на линии учитывать не следует.
ИЛИ:
2. Черепахе был дан для исполнения следующий алгоритм:
Повтори 2 [Вперёд 10 Направо 90 Вперёд 20 Направо 90] Поднять хвост Вперёд 3 Направо 90 Вперёд 5 Налево 90 Опустить хвост Повтори 2 [Вперёд 70 Направо 90 Вперёд 80 Направо 90]
Определите, сколько точек с целочисленными координатами будут находиться внутри пересечения фигур, ограниченных заданными
алгоритмом линиями, включая точки на границах этого пересечения.
Ответ:1. 38 ИЛИ 2. 128
7.
7 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 28 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в 3,5 раза выше и частотой дискретизации в 2 раза меньше, чем в первый раз. Сжатие данных не производилось.
Укажите размер полученного при повторной записи файла в Мбайт. В ответе запишите только целое число, единицу измерения писать не нужно.
Ответ: 98
✍ Решение:
- Вспомним формулу объема звукового файла:
- Выпишем отдельно, все данные, касающиеся первого состояния файла, затем второго состояния — после преобразования:
I = β * ƒ * t * S
I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S -количество каналов
1 состояние: S = 1 канал I = 28 Мбайт 2 состояние: S = 2 канала β = в 3,5 раза выше ƒ = в 2 раза ниже I = ?
S), а стало два канала связи, то файл увеличился в 2 раза:I = I * 2
β) увеличилась в 3,5 раза, то и объем (I) увеличится в 3,5 раза (пропорциональная зависимость):I = I * 3,5
ƒ) уменьшилась в 2 раза, значит, объем (I) тоже уменьшится в 2 раза:I = I / 2
I = 28 Мбайт * 2 * 3,5 / 2 = 98 Мбайт
Ответ: 98
8.
8 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Ответ: 2961
Видео на RuTube здесь
9.
9 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия:
В ответе запишите только число.
Ответ: 2241
🎦 Видео на RuTube здесь (Excel)
10.
10 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
Текст произведения Льва Николаевича Толстого «Севастопольские рассказы» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз встречается в тексте отдельное слово «теперь» со строчной буквы. Другие формы этого слова учитывать не следует.
В ответе запишите только число.
Ответ: 45
11.
11 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 250 символов и содержащий только десятичные цифры и символы из 1650-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит.
Определите объём памяти (в Кбайт), необходимый для хранения 65 536 идентификаторов. В ответе запишите только целое число – количество Кбайт.
Ответ: 22016
✍ Решение:
- Основной формулой для решения данной задачи является:
- Чтобы найти количество бит, необходимое для хранения одного идентификатора, для начала нужно найти количество бит, необходимых для хранения 1 символа в идентификаторе. По формуле получаем:
Q = 2N
где Q — количество вариантов символов, которые можно закодировать с помощью N бит.
1650+10 = 2N -> N ~ 11 бит (т.к. 10 мало)
250 * 11 = 2750 бит всего на идентификатор
2750 бит / 8 =343,75 ~ 344 байт
344 * 65536 : 210 => выразим в степени двойки => 65536 =216 344 * 216 : 210 = 344*26 = 22016
Ответ: 22016
12.
12 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150.Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
Дана программа для Редактора:
НАЧАЛО ПОКА нашлось (>1) ИЛИ нашлось (>2) ИЛИ нашлось (>0) ЕСЛИ нашлось (>1) ТО заменить (>1, 22>) КОНЕЦ ЕСЛИ ЕСЛИ нашлось (>2) ТО заменить (>2, 2>) КОНЕЦ ЕСЛИ ЕСЛИ нашлось (>0) ТО заменить (>0, 1>) КОНЕЦ ЕСЛИ КОНЕЦ ПОКА КОНЕЦ
На вход приведённой выше программе поступает строка, начинающаяся с символа «>», а затем содержащая 39 цифр «0», n цифр «1» и 39 цифр «2», расположенных в произвольном порядке.
Определите наименьшее значение n, при котором сумма числовых значений цифр строки, получившейся в результате выполнения программы, является простым числом.
Ответ: 5
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.NET:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
begin for var n := 1 to 1000 do begin var s := '>' + 39 * '0' + n * '1' + 39 * '2'; while ('>1' in s) or ('>2' in s) or ('>0' in s) do begin if '>1' in s then s := s.Replace('>1', '22>', 1); if '>2' in s then s := s.Replace('>2', '2>', 1); if '>0' in s then s := s.Replace('>0', '1>', 1); end; var sum := s.CountOf('1') + s.CountOf('2') * 2; var isPrime := true; for var i := 2 to sum - 1 do begin if sum.Divs(i) then begin isPrime := false; break end; end; if isPrime then begin print(n); exit; end; end; end. |
🎦 Видео на RuTube здесь
13.
13 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Определите количество различных путей ненулевой длины, которые начинаются и заканчиваются в городе Е, не содержат этот город в качестве промежуточного пункта и проходят через промежуточные города не более одного раза.
Ответ: 21
14.
14 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Операнды арифметического выражения записаны в системе счисления с основанием 15.
123x515 + 1x23315
В записи чисел переменной x обозначена неизвестная цифра из алфавита 15-ричной системы счисления.
Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 14. Для найденного значения x вычислите частное от деления значения арифметического выражения на 14 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Ответ: 8767
🎦 Видео решения на Паскале (RuTube) здесь
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.NET:
uses school; begin foreach var x in '0123456789abcde' do begin var a := dec('123' + x + '5', 15); var b := dec('1' + x + '233', 15); var sum := a + b; if sum mod 14 = 0 then begin print(sum / 14); break; end end; end. |
|
Python:
|
| С++: |
15.
15 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого наименьшего натурального числа А формула
(ДЕЛ(x, 2) → ¬ДЕЛ(x, 3)) ∨ (x + A ≥ 100)
тождественно истинна (т.е. принимает значение 1) при любом натуральном значении переменной х?
Ответ: 94
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.NET:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
begin for var A := 1 to 500 do begin var ok := 1; for var x := 1 to 1000 do begin if (((x mod 2 = 0) <= (x mod 3 <> 0)) or (x + A >= 100)) =false then begin ok := 0; break; end; end; if (ok = 1) then print(A) end; end. |
Питон:
1 2 3 4 5 6 |
for A in range(1,1000): OK = 1 for x in range(1,1000): OK *= ((x % 2 == 0) <= (x % 3 != 0)) or (x + A >= 100) if OK: print( A ) |
C++:
16.
16 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1 при n = 1; F(n) = n × F(n − 1), если n > 1
Чему равно значение выражения F(2023) / F(2020)?
Ответ: 8266912626
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.NET:
Решается только с типом данных BigInteger!
1 2 3 4 5 6 7 8 9 10 11 |
function F(n: biginteger): biginteger; begin if n = 1 then F := 1 else if n > 1 then F := n * F(n - 1) end; begin print(F(2023)/F(2020)) end. |
Питон:
C++:
Ответ: 8266912626
17.
17 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите количество пар последовательности, в которых только одно число оканчивается на 3, а сумма квадратов элементов пары не меньше квадрата максимального элемента последовательности, оканчивающегося на 3. В ответе запишите два числа: сначала количество найденных пар, затем максимальную из сумм квадратов элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.
Ответ: 180 190360573
18.
18 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю.
Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота.
Определите максимальную и минимальную денежные суммы, которые может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N × N, каждая ячейка которой соответствует клетке квадрата. Внутренние и внешние стены обозначены утолщенными линиями.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
Ответ: 1099 1026
19.
19 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 129. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу из 129 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 128. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.
Ответ: 64
20.
20 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Для игры, описанной в задании 19, найдите два наименьших значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
Найденные значения запишите в ответе в порядке возрастания.
Ответ: 32 63
21.
21 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Для игры, описанной в задании 19, найдите минимальное значение S, при котором одновременно выполняются два условия:
Если найдено несколько значений S, в ответе запишите минимальное из них.
Ответ: 62
22.
22 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы – время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Типовой пример организации данных в файле:
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемого файла.
Ответ: 17
✍ Решение:
-
Откроем файл и проанализируем таблицу:
- В столбце
Суказаны номера процессов, после которых запускается процесс, указанный в столбцеА. - Если в столбце
Сдля некоторой строки указан0, значит процесс этой строки запускается сразу, не ожидая выполнения других процессов. То есть, процессы 1, 2, 9 и 10 запускаются одновременно и сразу после запуска системы процессов. При этом, процесс 1 будет выполняться 4 мс (столбецВ), а, к примеру, процесс 10 будет выполняться 8 мc. - Уменьшим ширину столбцов
D:V(примерный диапазон), и пронумеруем данные столбцы, начиная с 1, используя автозаполнение: - Далее, начиная с процессов, которые запускаются параллельно (цифра
0в столбцеС), выделяем вправо количество столбцов, равное количеству миллисекунд в столбцеВ. Заливаем их цветом: - Затем в столбце
Сищем те строки, в которых используются уже заполненные процессы. Так, процесс №3 запускается последовательно за процессом 1 и 2. Так как процесс №1 длится дольше — 4 мс, то заливаем цветом столбцы для процесса №3 вправо, после уровня залитых ячеек для процесса №1: - Теперь можно залить цветом данные о процессах 4 и 5, так как эти процессы следуют за процессом №3.
- Следуя той же логике, закрашиваем данные по всем процессам:
- Видим, что самая крайняя справа заполненная ячейка соответствует числу 17.
23.
23 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Исполнитель преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Программа для исполнителя – это последовательность команд.
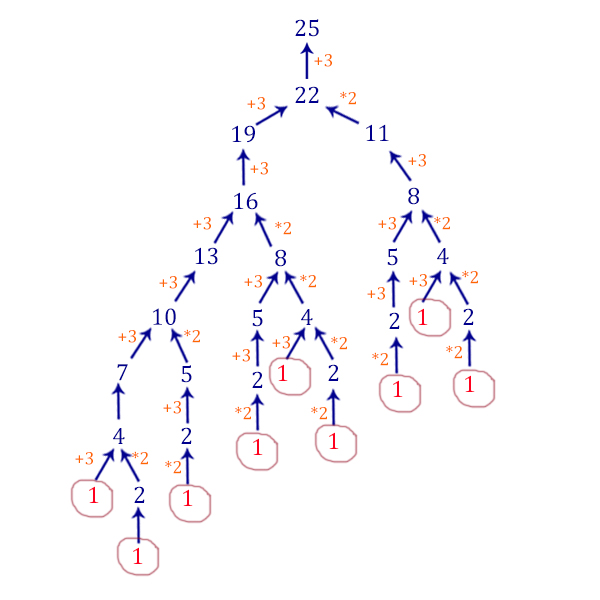
Сколько существует программ, для которых при исходном числе 1 результатом является число 35, при этом траектория вычислений содержит число 10 и не содержит 17?
Траектория вычислений программы – это последовательность результатов выполнения всех команд программы.
Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 16, 17.
Ответ: 98
24.
24 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
Текстовый файл состоит из символов A, C, D, F и O.
Определите максимальное количество идущих подряд пар символов вида
согласная + гласная
в прилагаемом файле.
Для выполнения этого задания следует написать программу.
Ответ: 95
25.
25 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Назовём маской числа последовательность цифр, в которой также могут встречаться следующие символы:
?» означает ровно одну произвольную цифру;*» означает любую последовательность цифр произвольной длины; в том числе «*» может задавать и пустую последовательность.Например, маске 123*4?5 соответствуют числа 123405 и 12300405.
Среди натуральных чисел, не превышающих 1010, найдите все числа, соответствующие маске 1?2139*4, делящиеся на 2023 без остатка.
В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, а во втором столбце – соответствующие им
результаты деления этих чисел на 2023.
Количество строк в таблице для ответа избыточно.
... ... ... ... ... ...
Ответ:
162139404 80148 1321399324 653188 1421396214 702618 1521393104 752048
26.
26 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрёшки – подарок упаковывается в одну из коробок, та в свою очередь в другую коробку и т.д.
Одну коробку можно поместить в другую, если длина её стороны хотя бы на 3 единицы меньше длины стороны другой коробки. Определите
наибольшее количество коробок, которое можно использовать для упаковки одного подарка, и максимально возможную длину стороны самой маленькой коробки, где будет находиться подарок. Размер подарка позволяет поместить его в самую маленькую коробку.
Входные данные
В первой строке входного файла находится число N – количество коробок в магазине (натуральное число, не превышающее 10 000). В следующих N строках находятся значения длин сторон коробок (все числа натуральные, не превышающие 10 000), каждое – в отдельной строке.
Запишите в ответе два целых числа: сначала наибольшее количество коробок, которое можно использовать для упаковки одного подарка, затем максимально возможную длину стороны самой маленькой коробки в таком наборе.
Типовой пример организации данных во входном файле
5 43 40 32 40 30
Пример входного файла приведён для пяти коробок и случая, когда минимальная допустимая разница между длинами сторон коробок, подходящих для упаковки «матрёшкой», составляет 3 единицы. При таких исходных данных условию задачи удовлетворяют наборы коробок с длинами сторон 30, 40 и 43 или 32, 40 и 43 соответственно, т.е. количество коробок равно 3, а длина стороны самой маленькой коробки равна 32.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.
Ответ: 2767 51
27.
27 задание. Демоверсия варианта ЕГЭ по информатике 2023, ФИПИ:
A
B
Задание выполняется с использованием прилагаемых файлов
У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера,
соответствующие расстоянию от нулевой отметки до конкретного пункта.
Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 36 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории.
Стоимость перевозки биоматериалов равна произведению расстояния от пункта до лаборатории на количество контейнеров с пробирками. Общая стоимость перевозки за день равна сумме стоимостей перевозок из каждого пункта в лабораторию. Лабораторию расположили в одном из пунктов приёма биоматериалов таким образом, что общая стоимость доставки биоматериалов из всех пунктов минимальна.
Определите минимальную общую стоимость доставки биоматериалов из всех пунктов приёма в лабораторию.
Входные данные
Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число N (1 ≤ N ≤ 10 000 000) – количество пунктов приёма биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает 1000).
Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки.
В ответе укажите два числа: сначала значение искомой величины для файла А, затем – для файла B.
6 1 100 2 200 5 4 7 3 8 2 10 190
При таких исходных данных и вместимости транспортировочного контейнера, составляющей 96 пробирок, компании выгодно открыть лабораторию в пункте 2. В этом случае сумма транспортных затрат составит: 1 · 2 + 3 · 1 + 5 · 1 + 6 · 1 + 8 · 2.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.
Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Ответ: 51063 5634689219329
ЕГЭ по информатике -> демоверсия ЕГЭ 2023
1. Кодирование
текста
2.
Анализ таблицы истинности
4. Бд и файловая система
6. Алгоритмы
Сколько 1, 0, целых A<X<B, вычислить, перевести (-а) в 2сс
Свойства чисел:
1.числа вида 2k записываются в двоичной системе как единица и k нулей, например:16 = 24 = 100002 (числа,
являющиеся степенями 2,3.. ( в любой СС!!)
2. числа вида 2k-1 записываются в двоичной системе k единиц, например: 15 = 24-1 = 11112 (числа
, предшествующие степеням «2»- состоят из «1» и на разряд меньше (в 3 из 2, 4
из 3 , т.е n-1))
3. Двоичное число (другая n CC), оканчивающееся — на 0 – четное(кратно n), — на 1- нечетное (и любое отличное от нуля число в той СС
говорит о том, что число не кратно n).
Отрицательное число =
1) а-1 2) (а-1)из10 перводим в 2сс 3) первая 1
сохраняется, все остальные цифры переворачиваем 1-0,0-1
|
10сс |
2сс |
8 сс |
триады |
16сс |
тетрады |
|
0 |
0 |
0 |
000 |
0 |
0000 |
|
1 |
1 |
1 |
001 |
1 |
0001 |
|
2 |
10 |
2 |
010 |
2 |
0010 |
|
3 |
11 |
3 |
011 |
3 |
0011 |
|
4 |
100 |
4 |
100 |
4 |
0100 |
|
5 |
101 |
5 |
101 |
5 |
0101 |
|
6 |
110 |
6 |
110 |
6 |
0110 |
|
7 |
111 |
7 |
111 |
7 |
0111 |
|
8 |
1000 |
10 |
8 |
1000 |
|
|
9 |
1001 |
11 |
9 |
1001 |
|
|
10 |
1010 |
12 |
A |
1010 |
|
|
11 |
1011 |
13 |
B |
1011 |
|
|
12 |
1100 |
14 |
C |
1100 |
|
|
13 |
1101 |
15 |
D |
1101 |
|
|
14 |
1110 |
16 |
E |
1110 |
|
|
15 |
1111 |
17 |
F |
1111 |
|
|
16 |
10000 |
20 |
10 |
10000 |
|
0+0=0 |
0-0=0 |
0*0=0 |
|
0+1=1 |
1-0=1 |
0*1=0 |
|
1+0=1 |
1-1=0 |
1*0=0 |
|
1+1=10 |
10-1=1 |
1*1=1 |

Сопоставлять
значений переменных с функциями (начинать с «одиночных»)
1. Отрицание
(НЕ,¬ , Ā) меняет знаки: < на >=,> на<=.<= на
>, >= на <
2.
Логическое умножение (И, •, ˄, &)
3.
Логическое сложение (ИЛИ, +, ˅, |)
Порядок
выполнения операций: ( ), не, и, или, →,º ….
|
А |
не(А) |
А |
В |
А ˄ В |
А |
В |
А ˅ В |
А |
В |
А→В |
А |
В |
АºВ |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
||
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1)внимательно читать задание
2)файловая система:?-точно 1 знак, *-произвольное количество или
их отсутствие
Автомат(10 СС):
1)определяем СС
2)записываем правило a+b, c+d или другое
3)определяем порядок записи , ¯
4) определяем максимально возможное числов этой СС и
максимальные суммы(!!!помнить о правилах сложения в разных СС)
5) помним о разрядах числа (десятки, сотни, единицы)
Автомат(2СС): четное оканчивается 0, нечетное на 1.
Обработка искаженных сообщений, Калькулятор и др.
5. Декодирование (условие Фано)
Условие Фано: ни одно кодовое слово
не является началом другого кодового слова (дерево 0-1): минимальный код,
короткое слово, сумма кодовых слов, только для конкретного слова и др.
Алгоритм Хаффмана
(оптимальный префиксный код): для самого частого- самый короткий код. Самое
частое повторение обычно 1 бит(0),самые малые повторения обычно 2-3 бита
(умножаем и складываем все ветви)
9.
Кодирование информации (+передача)
7. Анализ диаграмм и таблица Excel
8. Анализ программ (цикл while)
Звук: I=n*i*f*t (n-кол-во дорожек, i-бит на отсчет, f-частота дискретизации ,t-время)
1)
запись близка 2) секунды-минуты
3)
перезаписывают один и тот же файл — пропорция
1кГц=1000Гц, моно-1, стерео-2, квадро -4, …
Графика: I=k*i, N=2i(k –кол-во пикселей (200dpi= 200ppi=200*200)
i -инф. вес 1 пикселя, N-количество цветов)
1)определить кол-во цветов
2)не может превышать <
, >=, > , <=
3) перезаписывают один и тот же файл — пропорция
4) сохраняют каждые t сек(мин)
Передача информации: Iбит=Vбит/сек*tсек , V =I/t, t=I/V
I – размер файла, V – скорость , t – время передачи.
1)сравнение
способов передачи А и Б и на сколько
Наименьшая
единица информации 1 бит
1
байт = 8 бит = 23бит
1Кбайт(килобайт)
= 1024байт = 210байт
1Мбайт(мегабайт)
= 1024Кбайт = 210Кбайт
1Гбайт(гигабайт) = 1024Мбайт = 210Мбайт
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
|
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
210 |
211 |
|
N |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
2048 |
|
S передачи |
«Байт |
|
1 1 1 |
1 1 Кбайт/сек 1 Мбайт/сек |
!!!Важно в формулу подставлять значения в одинаковых единицах
измерения и переводить конечный результат в запрашиваемые в задаче единицы.
1)по формулам 2) по пропорции
1)геометрическая или арифметическая прогрессия
2)условие выполнения цикла (с предусловием)
1)вычисляем значения в ячейках по формулам какие можно
2) соотносим числовые величины и графические изображения
(подбираем число или формулу). Диапазон ячеек А1:D2 от первой ячейки до
последней. Весь круг соответствует сумме всех значений, по которым
строится диаграмма. Отдельные сектора пропорциональны доле одного значения в
общей сумм
В формулах * — умножение, / — деление, $ — абсолютная ссылка, при
копировании формулы значение не меняется
10. Перебор слов и СС
1)размещения(с повторениями, букву сколько угодно раз)Варианты =
2)перестановки (без повторов, букву 1 раз, буквы разные) Р=n!
2)перестановки (без повторов, букву 1 раз, есть одинаковые буквы
разные) Р=n!/n1! .n2!..
4) вероятности формула Шеннона.
5)Слова(определяем СС (= количество букв), переводим в ту СС, из
той в 10)
— На каком месте стоит слово +1
— Какое слово стоит под номером -1
3. Анализ информационной модели
15. Количество путей
Соотносим количество пересечений дорог и узлов вершин графа,
анализ начинаем с графа (вершин графа)
|
Город |
Откуда |
Кол-во путей |
|
А |
— |
1 |
|
Б |
А |
1 |
|
В |
АБ |
2 |
|
…… |
…. |
….. |
Потеря маршрутов, считая «вручную»
Траектория через А и
не через Б –внимательно!
22. Оператор ветвления
Строим дерево внимательно через те точки, которые указаны в
траектории
11.Рекурсия (функция возврата к самой себе)
14. Алгоритмы формальных исполнителей
1) Вызов функций F(n) или/и G(n) от предыдущих значений
2) Количество напечатанных
3) Сумма напечатанных
4) Какие выведет числа (!!!Важен порядок вызова (обращения к
рекурсии).
-если write
стоит в начале, то прямой последовательный обход.
— если write
стоит после какой-то первой функции, то выполняется вызов по этой ветке до
конца, по окончанию вызывается оставшаяся функция.
— если write
стоит после всех функций, аналогично предыдущему
Чертежник
Начал и вернулся туда же: (х,у)+…-…=(0,0)
Вернулся в другую точку: (х,у)+…-…=(х1,у1)
Повтори n
раз n*(3+2-4…)
Замена команды n*(а+2-4…)=0, n*(b+3-8….)=0
1)отдельно считаем смещение по x и по y;
2)внимательно читаем вопрос;
3)даём ответ на вопрос, поставленный в задаче.
Робот: клетка начала и конца
считается закрашенной, движение идет до упора и по условию.
Редактор: циклы считаем с НАЧАЛА!!!
17. Запросы интернета (Диаграммы Эйлера Венна)
23. Логические уравнения
19. Одномерные массивы
Знак
«&»-пересечение запросов (и) , а «|»-объединение запросов (или)
1) Обозначаем зоны запросов буквами a,b,c,d,e,f…..
2) !!! Два множества могут не пересекаться (просматриваем суммы
пересечений и объединений)
|
А ˄ В |
А ˅ В |
А→В |
АºВ |
А¹В |
|
1 и 1 |
1 и 1 |
1-1 |
1 и 1 |
0 и 1 |
|
0 и 1 |
0-0 |
0 и 0 |
1 и 0 |
|
|
1 и 0 |
0-1 |
1) замена переменных, если нужно
2) последовательное решение уравнений
Решение системы уравнений – это битовая цепочка (битовый вектор-
единичный объект)
3) уравнения–ограничения на битовый вектор (комбинации)
4) кол-во решений находиться по правилам комбинаторики (чаще
всего аn)
5) варианты комбинаций истинности и лжи для ˄,˅,→, º
Стратегия решения: трассировочная
таблица , узнать базовый алгоритм и проверить
а) алгоритм меняющий
элементы массива местами
б) массивы с индексами от 0
до 10 цикл for
в) цикл for или while в
нем ветвление (if)
г) двумерные
массивы(прямоугольная матрица A[i] , B[i]
Цикл for в цикле for
(выполняется первый внешний цикл, потом полностью выполняется внутренний цикл
for, далее 2 эл из 1, и все из
2го ) (прямоугольная матрица)
16. Уравнения в различных СС
26. Стратегия (теория игр)
13. Вычисление количества информации
21. Анализ программы с
подпрограммами
1)помнить,
что любое число в степени в соответвующей СС=
2)выражения
упрастить и определить СС, если сс 2,3,4,5,…..при вычитании 1 получается на
1 меньше чем СС.
3)
числа в конце переводим в нужную СС
4)
если произведение степени и числа, применяем правила арифменики в той СС
(арифметические операции выполняются в одной СС)
5) если
степень числа * на число, применяем арифметические правила той сс в которой
производиться *.
Важно!!!
Арифметика возможна только в одной и той же СС
Описывать стратегию для «выигравшего- выигрышную стратегию, для
проигравшего- все стратегии» (строим дерево игры)
1) камни (камни две кучи, 2 разных хода)
2) фишки (расстояние
3) карточки(таблички) с числами, убирать дубль, если нужно
укоротить, ставить дубль если нужно удлинить
4) слова (считаем количество букв в словах) Игрок 1- нечетные
ходы, Игрок 2- четные ходы
I=k*i, N=2i (N-алфавит, k–количество
символов в тексте, i–
инф. вес 1 символа:
КОИ-8(8 бит), ASCII(8 бит), Unicode (16
бит), др)
1) количество вариантов (кто прошел –это N из него находим i ( N=2i ), а I=k*i –это всего.
2) пароли и номера авто: доп. сведения + код+ пароль
!!!Внимательно читать условие (сведения могут быть в 2 коде или
другой СС)
1) Квадратичные
(биквадратные) уравнения:
Точки минимума =
,
=у(
или через F`(x)
Можно искать точки
(max, min), и
значения функций в точке (fmax, fmin). Оценивать
знаки , ¯ функции.
!!!Обязательно
проверять проверять значения на концах отрезков.
2) вызов функции k=10,64 и
т.п. min или max число
Если +1, то
интервал А £
х <В
Если ¯-1, то
интервал А < х £В
12. IP-адресация
20. Анализ алгоритма с циклами и ветвлениями
24. Поиск ошибки в программе
25. Обработка
массива
010=000000002 25510=111111112
маска-11111111.11111111.11111000.00000000 (1….потом 0)
1)мах количество 1 или 0 в маске
2)мах и min байт
маски
3) 2 байт маски, если 3 =0
4) сколько различных значений маски (сколько масок, варианты)
5)количество ПК в сети (2 в степени нулей маски )
6) номер ПК в сети (нули маски в проекции на ip-адрес)
7) два ip принадлежат
одной сети (однозначная маска для обоих)
Номер компьютера
Количество адресов в сети
1) Алгоритм Евклида (2 переменные и разность), НОД
прописан в условии, в условии смотреть какое х нужно вывести х>100, 150…
Выражаем L
через х, L кратно НОД, далее проверяем на числах.
Вычисление НОД(а,b)= НОД(а-b,b)= НОД(а,b—a)
Заменяем большее из двух чисел разностью большего и меньшего до
тех пор, пока они не станут равны. НОД(14,21)= НОД(14,7)= НОД(7,7)=7
Если разница велика и нужно определить количество шагов.
Заменяем большее остатком от деления на меньшее до тех пор, пока меньше не
станет равно нулю. НОД(21,28) (28mod21=7)= НОД(21,7) (21mod7=0)=НОД(0,7)=7
2) Обработка цифр в числе:
— на выводе отмечаем, какие числа выводит программа (указаны в
условии)
— ВАЖНО!!!определить СС в которой обрабатываются числа
x: = а div 10, x: = а div 2, x: = а div 3 , x: = а div 4 , x: = а div 5
ЗНАТЬ!!! числа входящие в конкретную СС (0- число четное!!!)
Перебор цифр в числе за счет цикла ( while x>0 ) пока оно не равно нулю.
— если определяют не просто число , а разрядное (трехзначное,
двузначное)- это дополнительное условие (первое двузначное-10n, трехзначное 100n и т.д конечная граница определяется переводом из 10 сс в нужную)
ЯЗЫК программирования Pascal не понимает другие СС, кроме 10!!
После решения задачи в какой-то СС , переводим полученное число
в 10СС
!!!Проверка на четность:
— в четных СС по последней цифре (0,2,4,6,8 СС)
— нечетных СС по сумме цифр в числе (1,3,5,7,9 СС)
Схема
решения задачи: прогнать задачу на требуемом числе или
на любом удобном Þ чаще всего можно сразу ответить на 1 и 3
вопрос задачи (найти ошибки) (прогнать и убедиться в правильности) Þ после
выполнить 2 задание задачи (найти число работающее правильно )
Решая
задачу делить ее на части:
1)
что выводит (writeln(…)) и
запрашивает readln(…))
2) проверять
инициализацию переменных s:=0, p:=1, k:=0
3)
проверяем условия циклов и условий (правила их работы) и сам алгоритм
Проверка
на степень: n=ak Þ , т.е if n=1.
Формулу для вычисления n-ого элемента арифметической прогрессии: аn=a1+d(n-1) формулу для вычисления суммы первых n членов арифметической прогрессии:,
где ai – i-ый
элемент последовательности,d – шаг (разность) последовательности
1) Организация ввода данных (уже есть)
2) Инициализация начальных значений некоторых переменных (требуется
задать!)
3)Обработка данных (требуется организовать!)
4) Вывод данных (требуется организовать!)
Обработка данных происходит в процессе циклической
обработки элементов ( может обрабатывается один, пара, тройка или
последовательность элементов, речь всегда идет о рядом стоящих элементах,
которые всегда можно обработать одним циклом) по некоторому комбинированному
условию, которое необходимо формализовать основе анализа условия задачи.
ВАЖНО!!! не писать программу полностью, а «дописать» её в рамках
уже организованного ввода, а также заданного количества переменных и их
типов: необходимо дописать инициализацию, организовать обработку и вывод.
Для проверки на кратность использовать —
a[i] mod
2 <> 0 (Кратность n)
18. Логические выражения
1) отрезки (преобразуем,
отделяем A (или Ā ) от отрезков, сумма должна
покрывать всю числовую прямую)
упростить А→В= Ā+В, А º В=А*В+Ā*, (см. табл задания№2)
2) неопределенный отрезок
(более чем 25 целых, т.е 26 чисел)преобразуем, пользуемся
распределительным законом)
Помнить два закона !А+В*С=(А+В)*(А+С)
и А*В+С=(А*В)+(А*С)
3) множества (отделяем
числа, отделяем А, делаем отрицание с числами и применяем закон де Моргана,
как с отрезками только на диаграммах Эйлера -Венна)
4) делители А=1,
остальное =0 (Ā=В, А= ) закон де Моргана
Если меду числами ˄-ищем
кратные, если ˅-делители
1. Если формула истинна (равна 1), и после упрощения A без
отрицания, то используется закон: Amin = ¬B
Если формула истинна (равна 1), и после
упрощения A с отрицанием, то используется закон:Amax =
B
2. Если формула ложна (равна 0), и после
упрощения A без отрицания, то используется закон: Amax =
¬B
Если формула ложна (равна 0), и 2. после
упрощения A с отрицанием, то используется закон: Amin =
B, где B — известная часть выражения
5)неравенства ( если А=1,
то остальное берется с отрицанием, если А=0 (отрицательно), то остальное не
меняем, оно положительно)
а)длина –это модуль от точки
до точки: (А..)→(….х ) ) ˄ ( (
….х) → (А..)) через
и
, если где-то парабола, то
модуль и отрезок значений параболы.
б) сколько существует
значений: кол-во чисел n+1
в) линейные неравенства
(графическим способом, как задача с параметром, определяем область и
пересечение графиков прямых линий, анализируем)
6) битовые операции
1) А→В= Ā+В
2) избавляемся от всех
отрицаний (закон де Моргана) и выстраиваем импликации
3) Упрощаем до выражений
следующего типа:
a) (Q•A) →P=1 , т.е Q+А=P
б) (Q•P) →А=1, т.е Q+ P = А
в) P→ (Q+A) =1, A→ (Q+P) =1,
г) (Q+Р) → (L+A) =1, т.е Q•А=A•L
(L•A) →(Q•Р) =1, т.е Q+А=A+L
д) побитовые операции равны числам
(переводим их в 2СС)
решаем как с делителями и отрезками А=1,
остальные =0, сначала находим маску х при =0 и варианты букв в маске х при ¹ 0) не решаем по общей схеме
4) применяем свойства 1)XP ˄XQ=XP or Q=P+Q
2) XP ˅ XQ=XP and Q=P•Q
- Треугольник
- Четырехугольники
- Окружность и круг
- Призма
- Пирамида
- Усеченная пирамида
- Цилиндр
- Конус
- Усеченный конус
- Сфера и шар
1. Формулы сокращённого умножения
Наверх
2. Модуль числа
Определение:
Основные свойства модуля:
Наверх
3. Степень с действительным показателем
Свойства степени с действительным показателем
Пусть Тогда верны следующие соотношения:
Наверх
4. Корень n-ой степени из числа
Корнем n-ой степени из числа a называется число, n-ая степень которого равна a.
Арифметическим корнем четной степени n из неотрицательного числа a называется неотрицательное число, n-ая степень которого равна a.
Основные свойства арифметического корня:
Наверх
5. Логарифмы
Определение логарифма:
Основное логарифмическое тождество:
Основные свойства логарифмов
Пусть
Тогда верны следующие соотношения:
Наверх
6. Арифметическая прогрессия
Формула n-го члена арифметической прогрессии:
Характеристическое свойство арифметической прогрессии:
Сумма n первых членов арифметической прогрессии:
При решении задач, связанных с арифметической прогрессией, могут оказаться полезными также следующие формулы:
Наверх
7. Геометрическая прогрессия
Формула n-го члена геометрической прогрессии:
Характеристическое свойство геометрической прогрессии:
Сумма n первых членов геометрической прогрессии:
При решении задач, связанных с геометрической прогрессией, могут оказаться полезными также следующие формулы:
Наверх
8. Бесконечно убывающая геометрическая прогрессия
Сумма бесконечно убывающей геометрической прогрессии:
Наверх
9. Основные формулы тригонометрии
Зависимость между тригонометрическими функциями одного аргумента:
Формулы сложения:
Формулы тригонометрических функций двойного аргумента:
Формулы понижения степени:
Формулы приведения
Все формулы приведения получаются из соответствующих формул сложения. Например:
Применение формул приведения укладывается в следующую схему:
— определяется координатная четверть, в которой лежит аргумент приводимой функции, считая, что ;
— определяется знак приводимой функции;
— определяется название приведенной функции по следующему правилу: если аргумент приводимой функции имеет вид или
, то функция меняется на сходственную функцию, если аргумент приводимой функции имеет вид
, то функция названия не меняет.
Например, получим формулу :
— — IV четверть;
— в IV четверти тангенс отрицательный;
— аргумент приводимой функции имеет вид , следовательно, название функции меняется. Таким образом,
Формулы преобразования суммы тригонометрических функций в произведение:
Формулы преобразования произведения тригонометрических функций в сумму:
Наверх
10. Производная и интеграл
Таблица производных некоторых элементарных функций
Правила дифференцирования:
1.
2.
3.
4.
5.
Уравнение касательной к графику функции в его точке
:
Таблица первообразных для некоторых элементарных функций
Правила нахождения первообразных
Пусть ― первообразные для функций
и
соответственно, a, b, k ― постоянные,
Тогда:
— ― первообразная для функции
— ― первообразная для функции
— ― первообразная для функции
— Формула Ньютона-Лейбница:
1. Треугольник
Пусть ― длины сторон BC, AC, AB треугольника ABC соответственно;
― полупериметр треугольника ABC; A, B, C ― величины углов BAC, ABC, ACB треугольника ABC соответственно;
― длины высот AA2, BB2, CC2 треугольника ABC соответственно; R ― радиус окружности, описанной около треугольника ABC; r — радиус окружности, вписанной в треугольник ABC;
― площадь треугольника ABC. Тогда имеют место следующие соотношения:
(теорема синусов);
(теорема косинусов);
Наверх
2. Четырёхугольники
Параллелограмм
Параллелограммом называется четырехугольник, противоположные стороны которого попарно параллельны.
Прямоугольником называется параллелограмм, у которого все углы прямые.
Ромбом называется параллелограмм, все стороны которого равны.
Квадратом называется прямоугольник, все стороны которого равны. Из определения следует, что квадрат является ромбом, следовательно, он обладает всеми свойствами прямоугольника и ромба.
Трапецией называется четырехугольник, две стороны которого параллельны, а две другие не параллельны.
Площадь четырехугольника
Площадь параллелограмма равна произведению его основания на высоту.
Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.
Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Площадь четырехугольника равна половине произведения его диагоналей на синус угла между ними.
Наверх
3. Окружность и круг
Соотношения между элементами окружности и круга
Пусть r — радиус окружности, d — ее диаметр, C — длина окружности, S — площадь круга, — длина дуги в
градусов,
— длина дуги в
радиан,
— площадь сектора, ограниченного дугой в n градусов,
— площадь сектора, ограниченного дугой в
радиан. Тогда имеют место следующие соотношения:
Вписанный угол
Вписанный угол измеряется половиной дуги, на которую он опирается.
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на полуокружность, — прямой.
Вписанная окружность
Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех сторон этого многоугольника, ― точка пересечения биссектрис углов этого многоугольника. Таким образом, в многоугольник можно вписать окружность, и притом только одну, тогда и только тогда, когда биссектрисы его углов пересекаются в одной точке.
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.
Описанная окружность
Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех вершин этого многоугольника, ― точка пересечения серединных перпендикуляров к сторонам этого многоугольника. Таким образом, около многоугольника можно описать окружность, и притом только одну, тогда и только тогда, когда серединные перпендикуляры к сторонам этого многоугольника пересекаются в одной точке.
Около четырехугольника можно описать окружность тогда и только тогда, когда суммы его противоположных углов равны
Наверх
4. Призма
Пусть H ― высота призмы, AA1 ― боковое ребро призмы, ― периметр основания призмы,
― площадь основания призмы,
― площадь боковой поверхности призмы,
― площадь полной поверхности призмы, V ― объем призмы,
― периметр перпендикулярного сечения призмы,
― площадь перпендикулярного сечения призмы. Тогда имеют место следующие соотношения:
Свойства параллелепипеда:
— противоположные грани параллелепипеда равны и параллельны;
— диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам;
— квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Наверх
5. Пирамида
Пусть H ― высота пирамиды, ― периметр основания пирамиды,
― площадь основания пирамиды,
― площадь боковой поверхности пирамиды,
― площадь полной поверхности пирамиды, V ― объем пирамиды. Тогда имеют место следующие соотношения:
;
.
Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны
, то
Наверх
6. Усечённая пирамида
Пусть H ― высота усеченной пирамиды, и
― периметры оснований усеченной пирамиды,
и
― площади оснований усеченной пирамиды,
― площадь боковой поверхности усеченной пирамиды,
― площадь полной поверхности усеченной пирамиды, V ― объем усеченной пирамиды.
Тогда имеют место следующие соотношения:
Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны
, то:
Наверх
7. Цилиндр
Пусть h ― высота цилиндра, r ― радиус цилиндра, ― площадь боковой поверхности цилиндра,
― площадь полной поверхности цилиндра, V ― объем цилиндра.
Тогда имеют место следующие соотношения:
Наверх
8. Конус
Пусть h ― высота конуса, r ― радиус основания конуса, l ― образующая конуса, ― площадь боковой поверхности конуса,
― площадь полной поверхности конуса, V ― объем конуса.
Тогда имеют место следующие соотношения:
Наверх
9. Усечённый конус
Пусть h ― высота усеченного конуса, r и ― радиусы основания усеченного конуса, l ― образующая усеченного конуса,
― площадь боковой поверхности усеченного конуса, V ― объем усеченного конуса. Тогда имеют место следующие соотношения:
Наверх
10. Сфера и шар
Пусть R ― радиус шара, D ― его диаметр, S ― площадь ограничивающей шар сферы, ― площадь сферической поверхности шарового сегмента (шарового слоя), высота которого равна h, V ― объем шара,
― объем сегмента, высота которого равна h,
― объем сектора, ограниченного сегментом, высота которого равна h. Тогда имеют место следующие соотношения:
Наверх
Шпаргалка ЕГЭ по информатике. Все необходимое
Скачать шпаргалку для подготовки к ЕГЭ по информатике. Содержимое:
— Логика
— Системы счисления
— Кодирование информации
— Программирование
— Теория игр
и другое
Похожие материалы
- 1
- 2
- 3
- 4
- 5
Оценка: 2.6 из 34
Комментарии
Всего комментариев: 0
Алгебра логики
Алгебра логики
Алгебра логики (англ. algebra of logic) — один из основных разделов математической логики, в котором методы алгебры используются в логических преобразованиях.
Основоположником алгебры логики является английский математик и логик Дж. Буль (1815–1864), положивший в основу своего логического учения аналогию между алгеброй и логикой. Любое высказывание он записывал с помощью символов разработанного им языка и получал «уравнения», истинность или ложность которых можно было доказать, исходя из определенных логических законов, таких как законы коммутативности, дистрибутивности, ассоциативности и др.
Современная алгебра логики является разделом математической логики и изучает логические операции над высказываниями с точки зрения их истинностного значения (истина, ложь). Высказывания могут быть истинными, ложными или содержать истину и ложь в разных соотношениях.
Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно или ложно.
Например, «3 умножить на 3 равно 9», «Архангельск севернее Вологды» — истинные высказывания, а «Пять меньше трех», «Марс — звезда» — ложные.
Очевидно, что не всякое предложение может быть логическим высказыванием, т. к. не всегда есть смысл говорить о его ложности или истинности. Например, высказывание «Информатика — интересный предмет» неопределенно и требует дополнительных сведений, а высказывание «Для ученика 10-А класса Иванова А. А. информатика — интересный предмет» в зависимости от интересов Иванова А. А. может принимать значение «истина» или «ложь».
Кроме двузначной алгебры высказываний, в которой принимаются только два значения — «истинно» и «ложно», существует многозначная алгебра высказываний. В такой алгебре, кроме значений «истинно» и «ложно», употребляются такие истинностные значения, как «вероятно», «возможно», «невозможно» и т. д.
В алгебре логики различаются простые (элементарные) высказывания, обозначаемые латинскими буквами (A, B, C, D, …), и сложные (составные), составленные из нескольких простых с помощью логических связок, например таких, как «не», «и», «или», «тогда и только тогда», «если … то». Истинность или ложность получаемых таким образом сложных высказываний определяется значением простых высказываний.
Обозначим как А высказывание «Алгебра логики успешно применяется в теории электрических схем», а через В — «Алгебра логики применяется при синтезе релейно-контактных схем».
Тогда составное высказывание «Алгебра логики успешно применяется в теории электрических цепей и при синтезе релейно-контактных схем» можно кратко записать как А и В; здесь «и» — логическая связка. Очевидно, что поскольку элементарные высказывания А и В истинны, то истинно и составное высказывание А и В.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение.
Логических значений всего два: истина (TRUE) и ложь (FALSE). Это соответствует цифровому представлению — 1 и 0. Результаты каждой логической операции можно записать в виде таблицы. Такие таблицы называют таблицами истинности.
Основные операции алгебры логики
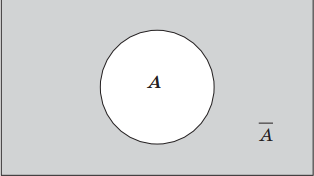
1. Логическое отрицание, инверсия (лат. inversion — переворачивание) — логическая операция, в результате которой из данного высказывания (например, А) получается новое высказывание (не А), которое называется отрицанием исходного высказывания, обозначается символически чертой сверху ($A↖{-}$) или такими условными обозначениями, как ¬, ‘not’, и читается: «не А», «А ложно», «неверно, что А», «отрицание А». Например, «Марс — планета Солнечной системы» (высказывание А); «Марс — не планета Солнечной системы» ($A↖{-}$); высказывание «10 — простое число» (высказывание В) ложно; высказывание «10 — не простое число» (высказывание B ) истинно.
Операция, используемая относительно одной величины, называется унарной. Таблица значений данной операции имеет вид
| A | ¬A |
| истина | ложь |
| ложь | истина |
или
Высказывание $A↖{-}$ ложно, когда А истинно, и истинно, когда А ложно.
Геометрически отрицание можно представить следующим образом: если А — это некоторое множество точек, то $A↖{-}$ — это дополнение множества А, т. е. все точки, которые не принадлежат множеству А.
2. Конъюнкция (лат. conjunctio — соединение) — логическое умножение, операция, требующая как минимум двух логических величин (операндов) и соединяющая два или более высказываний при помощи связки «и» (например, «А и В»), которая символически обозначается с помощью знака ∧ (А ∧ В) и читается: «А и В». Для обозначения конъюнкции применяются также следующие знаки: А ∙ В; А & В, А and В, а иногда между высказываниями не ставится никакого знака: АВ. Пример логического умножения: «Этот треугольник равнобедренный и прямоугольный». Данное высказывание может быть истинным только в том случае, если выполняются оба условия, в противном случае высказывание ложно.
Таблица истинности операции имеет вид
| A | B | A ∧ B |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | ложь |
| истина | истина | истина |
или
| A | B | A ∧ B |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∧ В истинно только тогда, когда оба высказывания — А и В истинны.
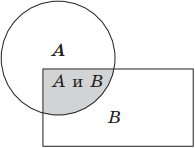
Геометрически конъюнкцию можно представить следующим образом: если А, В — это некоторые множества точек, то А ∧ В есть пересечение множеств А и В.
3. Дизъюнкция (лат. disjunction — разделение) — логическое сложение, операция, соединяющая два или более высказываний при помощи связки «или» (например, «А или В»), которая символически обозначается с помощью знака ∨ (А ∨ В) и читается: «А или В». Для обозначения дизъюнкции применяются также следующие знаки: А + В; А or В; А | B. Пример логического сложения: «Число x делится на 3 или на 5». Это высказывание будет истинным, если выполняются оба условия или хотя бы одно из условий.
Таблица истинности операции имеет вид
| A | B | A ∨ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | истина |
или
| A | B | A ∨ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∨ В ложно только тогда, когда оба высказывания — А и В ложны.
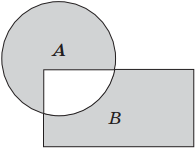
Геометрически логическое сложение можно представить следующим образом: если А, В — это некоторые множества точек, то А ∨ В — это объединение множеств А и В, т. е. фигура, объединяющая и квадрат, и круг.
4. Дизъюнкция строго-разделительная, сложение по модулю два — логическая операция, соединяющая два высказывания при помощи связки «или», употребленной в исключающем смысле, которая символически обозначается с помощью знаков ∨ ∨ или ⊕ (А ∨ ∨ В, А ⊕ В) и читается: «либо А, либо В». Пример сложения по модулю два — высказывание «Этот треугольник тупоугольный или остроугольный». Высказывание истинно, если выполняется какое-то одно из условий.
Таблица истинности операции имеет вид
| А | В | А ⊕ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | ложь |
или
| А | В | А ⊕ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
Высказывание А ⊕ В истинно только тогда, когда высказывания А и В имеют различные значения.
5. Импликация (лат. implisito — тесно связываю) — логическая операция, соединяющая два высказывания при помощи связки «если…, то» в сложное высказывание, которое символически обозначается с помощью знака → (А → В) и читается: «если А, то В», «А влечет В», «из А следует В», «А имплицирует В». Для обозначения импликации применяется также знак ⊃ (A ⊃ B). Пример импликации: «Если полученный четырехугольник квадрат, то около него можно описать окружность». Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием. Результат операции ложен только тогда, когда предпосылка есть истина, а следствие — ложь. Например, «Если 3 * 3 = 9 (А), то Солнце — планета (В)», результат импликации А → В — ложь.
Таблица истинности операции имеет вид
| А | В | А → В |
| истина | ложь | ложь |
| ложь | истина | истина |
| ложь | ложь | истина |
| истина | истина | истина |
или
| А | В | А → В |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Для операции импликации справедливо утверждение, что из лжи может следовать все что угодно, а из истины — только истина.
6. Эквивалентность, двойная импликация, равнозначность (лат. aequalis — равный и valentis — имеющий силу) — логическая операция, позволяющая из двух высказываний А и В получить новое высказывание А ≡ В, которое читается: «А эквивалентно B». Для обозначения эквивалентности применяются также следующие знаки: ⇔, ∼. Эта операция может быть выражена связками «тогда и только тогда», «необходимо и достаточно», «равносильно». Примером эквивалентности является высказывание: «Треугольник будет прямоугольным тогда и только тогда, когда один из углов равен 90 градусам».
Таблица истинности операции эквивалентности имеет вид
| А | В | А ∼ В |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | истина |
| истина | истина | истина |
или
| А | В | А ∼ В |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Операция эквивалентности противоположна сложению по модулю два и имеет результат «истина» тогда и только тогда, когда значения переменных совпадают.
Зная значения простых высказываний, можно на основании таблиц истинности определить значения сложных высказываний. При этом важно знать, что для представления любой функции алгебры логики достаточно трех операций: конъюнкции, дизъюнкции и отрицания.
| Сложение по модулю два | А ⊕ В | $(A↖{-} ∧B) ∧ (A ∧ B↖{-})$ |
| Импликация | А → В | $A↖{-} ∨ B$ |
| Эквивалентность | А ∼ В | $(A↖{-} ∧ B↖{-}) ∨ (A ∧ B)$ |
Приоритет выполнения логических операций следующий: отрицание («не») имеет самый высокий приоритет, затем выполняется конъюнкция («и»), после конъюнкции — дизъюнкция («или»).
С помощью логических переменных и логических операций любое логическое высказывание можно формализовать, т. е. заменить логической формулой. При этом элементарные высказывания, образующие составное высказывание, могут быть абсолютно не связаны по смыслу, но это не мешает определять истинность или ложность составного высказывания. Например, высказывание «Если пять больше двух (А), то вторник всегда наступает после понедельника (В)» — импликация А → В, и результат операции в данном случае — «истина». В логических операциях смысл высказываний не учитывается, рассматривается только их истинность или ложность.
Рассмотрим, например, построение составного высказывания из высказываний А и В, которое было бы ложно тогда и только тогда, когда оба высказывания истинны. В таблице истинности для операции сложения по модулю два находим: 1 ⊕ 1 = 0. А высказывание может быть, например, таким: «Этот мяч полностью красный или полностью синий». Следовательно, если утверждение А «Этот мяч полностью красный» — истина, и утверждение В «Этот мяч полностью синий» — истина, то составное утверждение — ложь, т. к. одновременно и красным, и синим мяч быть не может.
Примеры решения задач
Пример 1. Определить для указанных значений X значение логического высказывания ((X > 3) ∨ (X < 3)) → (X < 4) :
1) X = 1; 2) X = 12; 3) X = 3.
Решение. Последовательность выполнения операций следующая: сначала выполняются операции сравнения в скобках, затем дизъюнкция, и последней выполняется операция импликации. Операция дизъюнкции ∨ ложна тогда и только тогда, когда оба операнда ложны. Таблица истинности для импликации имеет вид
| A | B | A → B |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Отсюда получаем:
1) для X = 1:
((1 > 3) ∨ (1 < 3)) → (1 < 4) = ложь ∨ истина → истина = истина → истина = истина;
2) для X = 12:
((12 > 3) ∨ (12 < 3) → (12 < 4) = истина ∨ ложь → ложь = истина → ложь = ложь;
3) для X = 3:
((3 > 3) ∨ (3 < 3)) → (3<4) = ложь ∨ ложь → истина = ложь → истина = истина.
Пример 2. Указать множество целых значений X, для которых истинно выражение ¬((X > 2) → (X > 5)) .
Решение. Операция отрицания применена ко всему выражению ((X > 2) → (X > 5)) , следовательно, когда выражение ¬((X > 2) → (X > 5)) истинно, выражение ((X > 2) →(X > 5)) ложно. Поэтому необходимо определить, для каких значений X выражение ((X > 2) → (X > 5)) ложно. Операция импликации принимает значение «ложь» только в одном случае: когда из истины следует ложь. А это выполняется только для X = 3; X = 4; X = 5.
Пример 3. Для каких из приведенных слов ложно высказывание ¬(первая буква гласная ∧ третья буква гласная) ⇔ строка из 4 символов? 1) асса; 2) куку; 3) кукуруза; 4) ошибка; 5) силач.
Решение. Рассмотрим последовательно все предложенные слова:
1) для слова асса получим: ¬(1 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
2) для слова куку получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
3) для слова кукуруза получим: ¬ (0 ∧ 0) ⇔ 0, 1 ⇔ 0 — высказывание ложно;
4) для слова ошибка получим: ¬ (1 ∧ 1) ⇔ 0, 0 ⇔ 0 — высказывание истинно;
5) для слова силач получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 0 — высказывание ложно.
Логические выражения и их преобразование
Под логическим выражением следует понимать такую запись, которая может принимать логическое значение «истина» или «ложь». При таком определении среди логических выражений необходимо различать:
- выражения, которые используют операции сравнения («больше», «меньше», «равно», «не равно» и т. п.) и принимают логические значения (например, выражение а > b , где а = 5 и b = 7, равно значению «ложь»);
- непосредственные логические выражения, связанные с логическими величинами и логическими операциями (например, A ∨ В ∧ С, где А = истина, B = ложь и C = истина).
Логические выражения могут включать в себя функции, алгебраические операции, операции сравнения и логические операции. В этом случае приоритет выполнения действий следующий:
- вычисление существующих функциональных зависимостей;
- выполнение алгебраических операций (вначале умножение и деление, затем вычитание и сложение);
- выполнение операций сравнения (в произвольном порядке);
- выполнение логических операций (вначале операции отрицания, затем операции логического умножения, логического сложения, последними выполняются операции импликации и эквивалентности).
В логическом выражении могут использоваться скобки, которые изменяют порядок выполнения операций.
Пример. Найти значение выражения:
$1 ≤ a ∨ A ∨ sin(π/a — π/b) < 1 ∧ ¬B ∧ ¬(b^a + a^b > a + b ∨ A ∧ B)$ для а = 2, b = 3, A = истина, В = ложь.
Решение. Порядок подсчета значений:
1) ba + ab > a + b, после подстановки получим: 32 + 23 > 2 + 3, т. е. 17 > 2 + 3 = истина;
2) A ∧ B = истина ∧ ложь = ложь.
Следовательно, выражение в скобках равно (ba + ab > a + b ∨ A ∧ B) = истина ∨ ложь = истина;
3) 1≤ a = 1 ≤ 2 = истина;
4) sin(π/a — π/b) < 1 = sin(π/2 — π/3) < 1 = истина.
После этих вычислений окончательно получим: истина ∨ А ∧ истина ∧ ¬В ∧ ¬истина.
Теперь должны быть выполнены операции отрицания, затем логического умножения и сложения:
5) ¬В = ¬ложь = истина; ¬истина = ложь;
6) A ∧ истина ∧ истина ∧ ложь = истина ∧ истина ∧ истина ∧ ложь = ложь;
7) истина ∨ ложь = истина.
Таким образом, результат логического выражения при заданных значениях— «истина».
Примечание. Учитывая, что исходное выражение есть, в конечном итоге, сумма двух слагаемых, и значение одного из них 1 ≤ a = 1 ≤ 2 = истина, без дальнейших вычислений можно сказать, что результат для всего выражения тоже «истина».
Тождественные преобразования логических выражений
В алгебре логики выполняются основные законы, позволяющие производить тождественные преобразования логических выражений.
| Закон | Для ∨ | Для ∧ |
| Переместительный | A ∨ B = B ∨ A | A ∧ B = B ∧ A |
| Сочетательный | A ∨ (B ∨ C) = (B ∨ A) ∨ C | A ∧ (B ∧ C) = (A ∧ B) ∧ C |
| Распределительный | A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C) | A ∨ B ∧ C = (A ∨ B) ∧ (A ∨ C) |
| Правила де Моргана | ${A ∨ B}↖{-}$ = $A↖{-} ∧ B↖{-}$ | ${A ∧ B}↖{-}$ = $A↖{-} ∨ B↖{-}$ |
| Идемпотенции | A ∨ A = A | A ∧ A = A |
| Поглощения | A ∨ A ∧ B = A | A ∧ (A ∨ B) = A |
| Склеивания | (A ∧ B) ∨ (A↖{-} ∧ B) = B | (A ∨ B) ∧ (A↖{-} ∨ B) = B |
| Операция переменной с ее инверсией | $A ∨ A↖{-}$ = 1 | $A ∧ A↖{-}$ = 0 |
| Операция с константами | A ∨ 0 = A A ∨ 1 = 1 |
A ∧ 1 = A A ∧ 0 = 0 |
| Двойного отрицания | $A↖{=}$ = A |
Доказательства этих утверждений производят на основании построения таблиц истинности для соответствующих записей.
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определенному виду путем использования основных законов алгебры логики. Под упрощением формулы, не содержащей операций импликации и эквивалентности, понимают равносильное преобразование, приводящее к формуле, которая содержит либо меньшее по сравнению с исходной число операций, либо меньшее число переменных.
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т. п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Рассмотрим на примерах некоторые приемы и способы, применяемые при упрощении логических формул:
1) X1 ∧ X2 ∨ X1 ∧ X2 ∪ ¬X1 ∧ X2 = X1 ∧ X2 ∨ ¬X1 ∧ X2 = (X1 ∨ ¬X1) ∧ X2 = 1 ∧ X2 = X2 .
Для преобразования здесь можно применить закон идемпотенции, распределительный закон; операцию переменной с инверсией и операцию с константой.
2) X1 ∨ X1 ∧ X2 = X1 ∨ (1 ∨ 1 ∧ X2) = X1 ∨ (1 ∨ X2) = X1 .
Здесь для упрощения применяется закон поглощения.
3) ¬(X1 ∧ X2) ∨ X2 = (¬X1 ∨ ¬X2) ∨ X2 = ¬X1 ∨ ¬X2 ∨ X2 = ¬X1 ∨ 1 = 1 .
При преобразовании применяются правило де Моргана, операция переменной с ее инверсией, операция с константой
Примеры решения задач
Пример 1. Найти логическое выражение, равносильное выражению A ∧ ¬(¬B ∨ C) .
Решение. Применяем правило де Моргана для В и С: ¬(¬B ∨ C) = B ∧ ¬C .
Получаем выражение, равносильное исходному: A ∧ ¬(¬B ∨ C) = A ∧ B ∧ ¬C .
Ответ: A ∧ B ∧ ¬C.
Пример 2. Указать значение логических переменных А, В, С, для которых значение логического выражения (A ∨ B) → (B ∨ ¬C ∨ B) ложно.
Решение. Операция импликации ложна только в случае, когд а из истинной посылки следует ложь. Следовательно, для заданного выражения посылка A ∨ B должна принимать значение «истина», а следствие, т. е. выражение B ∨ ¬C ∨ B , — «ложь».
1) A ∨ B — результат дизъюнкции — «истина», если хотя бы один из операндов — «истина»;
2) B ∨ ¬C ∨ B — выражение ложно, если все слагаемые имеют значение «ложь», т. е. В — «ложь»; ¬C — «ложь», а следовательно, переменная С имеет значение «истина»;
3) если рассмотреть посылку и учесть, что В — «ложь», то получим, что значение А — «истина».
Ответ: А — истина, В — ложь, С — истина.
Пример 3. Каково наибольшее целое число X, при котором истинно высказывание (35 < X · X) → (X < (X — 3)) ?
Решение. Запишем таблицу истинности для операции импликации:
| A | B | A → B |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Выражение X < (X — 3) ложно при любых положительных значениях X. Следовательно, для того чтобы результатом импликации была «истина», необходимо и достаточно, чтобы выражение 35 < X · X также было ложно. Максимальное целое значение X, для которого 35 < X · X ложно, равно 5.
Ответ: X = 5.
Использование логических выражений для описания геометрических областей
Логические выражения могут быть использованы для описания геометрических областей. В этом случае задача формулируется так: записать для заданной геометрической области такое логическое выражение, которое принимает значение «истина» для значений x, y тогда и только тогда, когда любая точка с координатами (x; y) принадлежит геометрической области.
Рассмотрим описание геометрической области с помощью логического выражения на примерах.
Пример 1. Задано изображение геометрической области. Записать логическое выражение, описывающее множество точек, принадлежащих ей.
1) 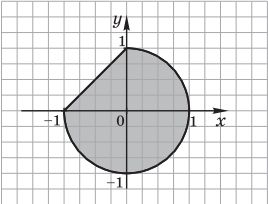
Решение. Заданную геометрическую область можно представить в виде набора следующих областей: первая область — D1 — полуплоскость ${x}/{-1} +{y}/{1} ≤ 1$, вторая — D2 — круг с центром в начале координат $x^2 + y^2 ≤ 1$. Их пересечение D1 $∩$ D2 представляет собой искомую область.
Результат: логическое выражение ${x}/{-1}+{y}/{1} ≤ 1 ∧ x^2 + y^2 ≤ 1$.
2)
Эту область можно записать так: |x| ≤ 1 ∧ y ≤ 0 ∧ y ≥ -1 .
Примечание. При построении логического выражения используются нестрогие неравенства, а это значит, что границы фигур также принадлежат заштрихованной области. Если использовать строгие неравенства, то границы учитываться не будут. Границы, не принадлежащие области, обычно изображаются пунктиром.
Можно решить обратную задачу, а именно: нарисовать область для заданного логического выражнения.
Пример 2. Нарисовать и заштриховать область, для точек которой выполняется логическое условие y ≥ x ∧ y + x ≥ 0 ∧ y < 2 .
Решение. Искомая область представляет собой пересечение трех полуплоскостей. Строим на плоскости (x, y) прямые y = x; y = –x; y = 2. Это границы области, причем последняя граница y = 2 не принадлежит области, поэтому ее наносим пунктирной линией. Для выполнения неравенства y ≥ x нужно, чтобы точки находились слева от прямой y = x, а неравенство y = –x выполняется для точек, которые находятся справа от прямой y = –x. Условие y < 2 выполняется для точек, лежащих ниже прямой y = 2. В результате получим область, которая изображена на рис.:
Использование логических функций для описания электрических схем
Логические функции очень удобны для описания работы электрических схем. Так, для схемы, представленной на рис., где значение переменной X — это состояние выключателя (если он включен, значение X — «истина», а если выключен — «ложь»), это значение Y — это состояние лампочки (если она горит — значение «истина», а если нет — «ложь»), логическая функция запишется так: Y = X . Функцию Y называют функцией проводимости.
Для схемы, представленной на рис., логическая функция Y имеет вид: Y = X1 ∪ X2, т. к. достаточно одного включенного выключателя, чтобы горела лампочка. В схеме на рис., для того чтобы горела лампочка, должны быть включены оба выключателя, следовательно, функция проводимости имеет вид: Y = X1 ∧ X2 .
Для более сложной схемы функция проводимости будет иметь вид: Y = (X11 ∨ (X12 ∧ X13)) ∧ X2 ∧ (X31 ∨ X32).
Схема также может содержать контакты на замыкание. В этом случае размыкаемый контакт как выключатель обеспечивает загорание лампочки, когда кнопка отпущена, а не нажата. Для таких схем размыкающий выключатель описывается отрицанием.
Две схемы называются равносильными, если через одну из них ток проходит тогда, когда он проходит и через другую. Из двух равносильных схем более простой считается схема, функция проводимости которой содержит меньшее число элементов. Задача нахождения наиболее простых схем среди равносильных очень важна.
Использование аппарата алгебры логики при проектировании логических схем
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера. Любая информация при обработке на компьютере представляется в двоичной форме, т. е. кодируется некоторой последовательностью 0 и 1. Обработку двоичных сигналов, соответствующих 0 и 1, выполняют в компьютере логические элементы. Логические элементы, которые выполняют основные логические операции И, ИЛИ, НЕ, представлены на рис.
Условные обозначения логических элементов являются стандартными и используются при составлении логических схем компьютера. С помощью этих схем можно реализовать любую логическую функцию, описывающую работу компьютера.
Технически компьютерный логический элемент реализуется в виде электрической схемы, которая представляет собой соединение различных деталей: диодов, транзисторов, резисторов, конденсаторов. На вход логического элемента, который называют также вентилем, поступают электрические сигналы высокого и низкого уровней напряжения, на выход выдается один выходной сигнал также либо высокого, либо низкого уровня. Эти уровни соответствуют одному из состояний двоичной системы: 1 — 0; ИСТИНА — ЛОЖЬ. Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем. Работу логических схем описывают с помощью таблиц истинности. Условное обозначение на схеме ИЛИ знак «1» — от устаревшего обозначения дизъюнкции как «>=1» (значение дизъюнкции равно 1, если сумма двух операндов больше или равна 1). Знак «&» на схеме И является сокращенной записью английского слова and.
Из логических элементов составляются электронные логические схемы, выполняющие более сложные логические операции. Набор логических элементов, состоящий из элементов НЕ, ИЛИ, И, с помощью которых можно построить логическую структуру любой сложности, называется функционально полным.
Построение таблиц истинности логических выражений
Для логической формулы всегда можно записать таблицу истинности, т. е. представить заданную логическую функцию в табличном виде. В этом случае таблица должна содержать все возможные комбинации аргументов функции (формулы) и соответствующие значения функции (результаты формулы на заданном наборе значений).
Удобной формой записи при нахождении значений функции является таблица, содержащая, кроме значений переменных и значений функции, также значения промежуточных вычислений. Рассмотрим пример построения таблицы истинности для формулы ${X1}↖{-} ∧ X2 ∨ {X1 ∨ X2}↖{-} ∨ X1$.
| X1 | X2 | ${X1}↖{-}$ | ${X1}↖{-}$ X2 | X1 ∧ X2 | ${X1 ∨ X2}↖{-}$ | ${X1}↖{-}$ ∧ X2 ∨ ${X1 ∨ X2}↖{-}$ | ${X1}↖{-}$ ∧ X2 ∨ ${X1 ∨ X2}↖{-}$ ∨ X1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
Если функция принимает значение 1 при всех наборах значений переменных, она является тождественно-истинной; если при всех наборах входных значений функция принимает значение 0, она является тождественно-ложной; если набор выходных значений содержит как 0, так и 1, функция называется выполнимой. Приведенный выше пример является примером тождественно-истинной функции.
Зная аналитическую форму логической функции, всегда можно перейти к табличной форме логических функций. С помощью заданной таблицы истинности можно решить обратную задачу, а именно: для заданной таблицы построить аналитическую формулу логической функции. Различают две формы построения аналитической зависимости логической функции по таблично заданной функции.
1. Дизъюнктивно нормальная форма (ДНФ) — сумма произведений, образованных из переменных и их отрицаний для ложных значений.
Алгоритм построения ДНФ следующий:
- в таблице истинности функции выбирают наборы аргументов, для которых логические формы равны 1 («истина»);
- все выбранные логические наборы как логические произведения аргументов записывают, последовательно соединив их между собой операцией логической суммы (дизъюнкции);
- для аргументов, которые являются ложными, в построенной записи проставляют операцию отрицания.
Пример. Построить функцию, определяющую, что первое число равно второму, используя метод ДНФ. Таблица истинности функции имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 1. Это первая и четвертая строки таблицы (строку заголовка при нумерации не учитываем).
Записываем логические произведения аргументов этих наборов, объединив их логической суммой: X1 ∧ X2 ∨ X1 ∧ X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих ложное значение (четвертая строка таблицы; второй набор в формуле; первый и второй элементы): X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ ${X2}↖{-}$.
Ответ: F(X1, X2) = X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ ${X2}↖{-}$.
2. Конъюнктивно нормальная форма (КНФ) — произведение сумм, образованных из переменных и их отрицаний для истинных значений.
Алгоритм построения КНФ следующий:
- в таблице истинности выбирают наборы аргументов, для которых логические формы равны 0 («ложь»);
- все выбранные логические наборы как логические суммы аргументов записывают последовательно, соединив их между собой операцией логического произведения (конъюнкции);
- для аргументов, которые являются истинными, в построенной записи проставляют операцию отрицания.
Примеры решения задач
Пример 1. Рассмотрим предыдущий пример, т. е. построим функцию, определяющую, что первое число равно второму, используя метод КНФ. Для заданной функции ее таблица истинности имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 0. Это вторая и третья строки (строку заголовка при нумерации не учитываем).
Записываем логические суммы аргументов этих наборов, объединив их логическим произведением: X1 ∨ X2 ∧ X1 ∨ X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих истинное значение (вторая строка таблицы, первый набор формулы, второй элемент; для третьей строки, а это второй набор формулы, первый элемент): X1 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ X2.
Таким образом, получена запись логической функции в КНФ.
Ответ: X1 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ X2.
Полученные двумя методами значения функций являются эквивалентными. Для доказательства этого утверждения используем правила логики: F(X1, X2) = X1 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ X2 = X1 ∧ ${X1}↖{-}$ ∨ X1 ∧ X2 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ ${X2}↖{-}$ ∧ X2 = 0 ∨ X1 ∨ X2 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ 0 = X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ ${X2}↖{-}$.
Пример 2. Построить логическую функцию для заданной таблицы истинности:
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Решение. Используем алгоритм ДНФ для построения исходной функции:
| X1 | X2 | F(X1, X2) | ||
| 1 | 1 | 1 | • | X1 ∧ X2 |
| 1 | 0 | 0 | ||
| 0 | 1 | 1 | • | ${X1}↖{-}$ ∧ X2 |
| 0 | 0 | 0 |
Искомая формула: X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ X2 .
Ее можно упростить: X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ X2 = X2 ∧ (X1 ∨ ${X1}↖{-}$) = X2 ∧ 1 = X2.
Пример 3. Для приведенной таблицы истинности построить логическую функцию, используя метод ДНФ.
| X1 | X2 | X3 | F(X1, X2, X3) | ||
| 1 | 1 | 1 | 1 | • | X1 ∧ X2 ∧ X3 |
| 1 | 0 | 1 | 0 | ||
| 0 | 1 | 1 | 1 | • | ${X1}↖{-}$ ∧ X2 ∧ X3 |
| 0 | 0 | 1 | 0 | ||
| 1 | 1 | 0 | 1 | • | X1 ∧ X2 ∧ ${X3}↖{-}$ |
| 1 | 0 | 0 | 1 | • | X1 ∧ ${X2}↖{-}$ ∧ ${X3}↖{-}$ |
| 0 | 1 | 0 | 0 | ||
| 0 | 0 | 0 | 0 |
Искомая формула: X1 ∧ X2 ∧ X ∨ ${X1}↖{-}$ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ ${X3}↖{-}$ ∪ X1 ∧ ${X2}↖{-}$ ∧ ${X3}↖{-}$.
Формула достаточно громоздка, и ее следует упростить:
X1 ∧ X2 ∧ X3 ∨ ${X1}↖{-}$ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ ${X3}↖{-}$ ∨ X1 ∧ ${X2}↖{-}$ ∧ ${X3}↖{-}$ = X2 ∧ X3 ∧ (X1 ∨ ${X1}↖{-}$) ∨ X1 ∧ ${X3}↖{-}$ ∧ (X2 ∨ ${X2}↖{-}$) = X2 ∧ X3 ∨ X1 ∧ ${X3}↖{-}$.
Таблицы истинности для решения логических задач
Составление таблиц истинности — один из способов решения логических задач. При использовании такого способа решения, условия, которые содержит задача, фиксируются с помощью специально составленных таблиц.
Примеры решения задач
Пример 1. Составить таблицу истинности для охранного устройства, которое использует три датчика и срабатывает при замыкании только двух из них.
Решение. Очевидно, что результатом решения будет таблица, в которой искомая функция Y(X1, X2, X3) будет иметь значение «истина», если какие-либо две переменные имеют значение «истина».
| X1 | X2 | X3 | Y(X1, X2, X3) |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
Пример 2. Составить расписание уроков на день, учитывая, что урок информатики может быть только первым или вторым, урок математики — первым или третьим, а физики — вторым или третьим. Возможно ли составить расписание, удовлетворив всем требованиям? Сколько существует вариантов расписания?
Решение. Задача легко решается, если составить соответствующую таблицу:
| 1-й урок | 2-й урок | 3-й урок | |
| Информатика | 1 | 1 | 0 |
| Математика | 1 | 0 | 1 |
| Физика | 0 | 1 | 1 |
Из таблицы видно, что существуют два варианта искомого расписания:
- математика, информатика, физика;
- информатика, физика, математика.
Пример 3. В спортивный лагерь приехали трое друзей — Петр, Борис и Алексей. Каждый из них увлекается двумя видами спорта. Известно, что таких видов спорта шесть: футбол, хоккей, лыжи, плавание, теннис, бадминтон. Также известно, что:
- Борис — самый старший;
- играющий в футбол младше играющего в хоккей;
- играющие в футбол и хоккей и Петр живут в одном доме;
- когда между лыжником и теннисистом возникает ссора, Борис мирит их;
- Петр не умеет играть ни в теннис, ни в бадминтон.
Какими видами спорта увлекается каждый из мальчиков?
Решение. Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание.
Так как видов спорта шесть, получается, что все мальчики увлекаются разными видами спорта.
Из условия 4 следует, что Борис не увлекается ни лыжами, ни теннисом, а из условий 3 и 5, что Петр не умеет играть в футбол, хоккей, теннис и бадминтон. Следовательно, любимые виды спорта Петра — лыжи и плавание. Занесем это в таблицу, а оставшиеся клетки столбцов «Лыжи» и «Плавание» заполним нулями.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | |||
| Алексей | 0 | 0 |
Из таблицы видно, что в теннис может играть только Алексей.
Из условий 1 и 2 следует, что Борис не футболист. Таким образом, в футбол играет Алексей. Продолжим заполнять таблицу. Внесем в пустые ячейки строки «Алексей» нули.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | 0 | ||
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Окончательно получаем, что Борис увлекается хоккеем и бадминтоном. Итоговая таблица будет выглядеть следующим образом:
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 1 | 0 | 0 | 1 | 0 |
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Ответ: Петр увлекается лыжами и плаванием, Борис играет в хоккей и бадминтон, а Алексей занимается футболом и теннисом.
Здравствуйте! Сегодня речь пойдёт о 23 задании из ЕГЭ по информатике 2023.
Двадцать третье задание является последним заданием из первой части ЕГЭ по информатике 2023.
Давайте познакомимся с примерными задачами 23 задания из ЕГЭ по информатике 2023.
Задача (классическая)
У исполнителя Удвоитель две команды, которым присвоены номера:
1. прибавить 3,
2. умножить на 2.
Первая из них увеличивает число на экране на 3, вторая — удваивает его.
Программа для Удвоителя — это последовательность команд.
Сколько есть программ, которые число 1 преобразуют в число 25 ?
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y: return 0 if x < y: return F(x+3, y) + F(x*2, y) print(F(1, 25))
Число x, это то число, с которым мы работаем. Число y — это куда нужно прийти.
Если число x достигло пункта назначения, то возвращаем 1. Если оно перескочило y, то возвращаем 0. А если ещё не дошло до y, то продолжаем вычисления с помощью рекурсии.
Ответ получается равен 9.
2 Способ (графический, для понимания)
Начинаем рассматривать задачку с конца. Если число нечётное, то оно может быть получено только с помощью первой команды. Если число чётное, то оно может быть получено с помощью двух команд.
Видим, что количество программ получается 9!
3 Способ (С помощью таблицы)
Некоторое число i можно получить только двумя способами: либо c помощью первой команды, либо с помощью второй команды. Тогда количество программ для некоторого числа i будет складываться из двух чисел: количества программ для числа i-3 и количества программ для числа i / 2 (Если i — чётное).
| Числа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| +3 | — | — | — | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| *2 | — | 1 | — | 2 | — | 3 | — | 4 | — | 5 |
| Кол. Прог. |
1 | 1 | 0 | 2 | 1 | 0 | 2 | 3 | 0 | 3 |
| Числа | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| +3 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| *2 | — | 6 | — | 7 | — | 8 | — | 9 | — | 10 | — | 11 | — | 12 | — |
| Кол. Прог. |
3 | 0 | 3 | 5 | 0 | 6 | 5 | 0 | 6 | 8 | 0 | 9 | 8 | 0 | 9 |
В первой строке пишутся числа от 1 до 25 (до того числа, которое нужно получить).
Во второй строке пишутся числа, которые в сумме с 3 (тройкой) дают числа, написанные в первой строке. (Прим. начиная с 4, числа идут по порядку.)
В третьей строке пишутся числа, которые при умножении на 2 дают числа, написанные в первой строке. (Прим. числа так же идут по порядку через одну пустую ячейку.)
В четвёртой строке для единицы ставим 1. Для остальных ячеек: смотрим, какие числа участвуют во второй и третьей строке для конкретной ячейки. Затем, эти числа ищем в первой строке и пишем сумму количеств программ для этих чисел (Т.е. пишем сумму уже известных значений из четвёртой строки для этих чисел).
Таким образом, основная идея 23 задания из ЕГЭ по информатике заключается в том, что результат каждого шага опирается на результаты предыдущих шагов!
Получаем ответ 9!
Ответ: 9
Задача (с избегаемым узлом)
Исполнитель НечетМ преобразует число на экране. У исполнителя НечетМ две команды, которым присвоены номера:
1. прибавь 1
2. сделай нечётное
Первая из этих команд увеличивает число x на экране на 1, вторая переводит число x в число 2x+1. Например, вторая команда переводит число 10 в число 21. Программа для исполнителя НечетМ — это последовательность команд. Сколько существует таких программ, которые число 1 преобразуют в число 25, причём траектория вычислений не содержит число 24? Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 17, 18.
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 18 января 2017 года Вариант ИН10304
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y or x==24: return 0 if x < y: return F(x+1, y) + F(x*2+1, y) print(F(1, 25))
Здесь на нельзя получать число 24, поэтому, если x будет равен 24, то мы возвращаем ноль.
Ответ получается равен 10.
2 способ (Решение с помощью таблицы).
Мы не может получать число 24! Значит, единственным способом добраться до числа 25 будет вторая команда.
Получается, что сначала нужно получить число 12, тогда 2 * 12 + 1 = 25 (2x+1). Это единственный путь!
Каждое число можем получить только 2 способами (Либо с помощью первой команды, либо с помощью второй команды). Поэтому количество программ для некоторого числа i будет равно сумме количеств команд для числа i-1 и для числа (i — 1) / 2 (Если число нечётное.) Если число i — чётное, то до числа i можно добраться единственным способом (с помощью первой команды).
Если записать с помощью массива:
A[i]=A[i-1] — если i — четное.
A[i]=A[i-1] + A[(i-1)/2] — если i нечетное;
| Числа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 2x+1 | — | — | 1 | — | 2 | — | 3 | — | 4 | — | 5 | — |
| +1 | — | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Кол. Прог. |
1 | 1 | 2 | 2 | 3 | 3 | 5 | 5 | 7 | 7 | 10 | 10 |
Ответ: 10
Задача (ЕГЭ по информатике, Москва, 2019)
У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 3
3. Прибавить 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 3, третья увеличивает его на 2.
Сколько существует программ, которые преобразуют исходное число 2 в число 12 и при этом траектория вычислений содержит число 9 и число 11?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 132 при исходном числе 7 траектория будет состоять из чисел 8, 10, 30.
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y: return 0 if x < y: return F(x+1, y) + F(x*3, y) + F(x+2, y) print(F(2, 9)*F(9, 11)*F(11, 12))
У нас числа 9 и 1 обязательные, поэтому разбиваем функцию следующим образом F(2, 9)*F(9, 11)*F(11, 12), через умножение. Это и будет ответ. Получается 50.
2 способ (с помощью таблицы).
От числа 11 до числа 12 можно добраться единственным путём (11 + 1 = 12).
От числа 9 до числа 11 можно добраться двумя способами (9 + 1 + 1 = 11, 9 + 2 = 11).
Найдём сколькими способами можно попасть от числа 2 до числа 9.
| Числа | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| +1 | — | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| *3 | — | — | — | — | 2 | — | — | 3 |
| +2 | — | — | 2 | 3 | 4 | 5 | 6 | 7 |
| Кол-во программ |
1 | 1 | 2 | 3 | 6 | 9 | 15 | 25 |
Учитывая, что от 9 до 11 двумя способами можно добраться, то 25 * 2 = 50 — это и будет ответ.
Ответ: 50
Задача ( ЕГЭ по информатике, Москва, 2020)
У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 3
3. Прибавить 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 3, третья увеличивает на 2.
Сколько существует программ, которые преобразуют исходное число 3 в число 14 и при этом траектория вычислений содержит число 9?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 132 при исходном числе 7 траектория будет состоять из чисел 8, 10, 30.
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y: return 0 if x < y: return F(x+1, y) + F(x*3, y) + F(x+2, y) print(F(3, 9)*F(9, 14))
Ответ получается 112.
2 способ (с помощью таблицы).
Последней командой для получении любого числа из траектории программы может быть одна из трёх выше указанных команд!
Значит, количество программ для некоторого числа будет складываться из количества программ для тех чисел, из которых это число может быть получено.
Получается, что мы будем использовать основной принцип 23 задания из ЕГЭ по информатике: результат для некоторого числа опирается на результаты предыдущих чисел. Т.к. траектория вычислений программ обязательно должна проходить через число 9, то при вычислении результата для чисел больших 9, мы не можем опираться на результаты для чисел меньших 9 (Иначе мы пропустим число 9).
| Числа | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| +1 | — | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| *3 | — | — | — | — | — | — | 3 | — | — | — | — | — |
| +2 | — | — | 3 | 4 | 5 | 6 | 7 | — | 9 | 10 | 11 | 12 |
| Кол-во программ |
1 | 1 | 2 | 3 | 5 | 8 | 14 | 14 | 28 | 42 | 70 | 112 |
Ответ: 112
Посмотрим следующую задачу из 23 задания ЕГЭ по информатике 2023
Задача (с обязательным узлом, закрепление)
Исполнитель Май17 преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 3
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 3. Программа для исполнителя Май17 — это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 17 и при этом траектория вычислений содержит число 9?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 12 при исходном числе 7 траектория будет состоять из чисел 8, 11, 12.
Решение:
1 способ (самый эффективный, на Python).
def F(x, y): if x == y: return 1 if x > y: return 0 if x < y: return F(x+1, y) + F(x+3, y) print(F(1, 9)*F(9, 17))
Ответ получается 169.
2 способ (с помощью таблицы).
Любое число может получится в результате двух команд! Тогда количество программ для числа i будет складываться из количеств команд для числа i — 1 и для числа i — 3.
Если написать на языке массива
A[i] := A[i-1] + A[i-3], при i > 3.
| Числа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| +1 | — | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| +3 | — | — | — | 1 | 2 | 3 | 4 | 5 | 6 | — | — | 9 | 10 | 11 | 12 | 13 | 14 |
| Кол-во программ |
1 | 1 | 1 | 2 | 3 | 4 | 6 | 9 | 13 | 13 | 13 | 26 | 39 | 52 | 78 | 117 | 169 |
При составлении значения для числа 10, мы не имеем право «заглядывать» за число 9, иначе число 9 будет пропущено! Поэтому для следующих трёх чисел (9, 9 + 1, 9 + 1 + 1), начиная с 9, будет 13 программ.
Для числа 17 получается ответ 169.
Ответ: 169