Все формулы геометрии для егэ профиль 2022 - Помощь в подготовке к экзаменам и поступлению

Алгебра — ЕГЭ Тригонометрия — ЕГЭ Геометрия — ЕГЭ Стереометрия — ЕГЭ Алгебра — ОГЭ Геометрия — ОГЭ

Шпаргалка по геометрии для ЕГЭ

Формулы по геометрии для ЕГЭ

Сборник формул по геометрии

Формулы для четырехугольников

Формулы для окружности

3621

На ЕГЭ по профильной математике с собой можно взять только черные гелевые ручки и линейку. На экзамене профильного уровня, в отличие от базового, не выдаются справочные материалы – выпускникам не предоставляются формулы, необходимые для решения задач. Исключение составляют лишь 5 формул по тригонометрии, но, естественно, они не помогут набрать максимальные баллы, если экзаменуемые не будут знать об остальных важных сведениях и математических свойствах.

Содержание

Формулы для ЕГЭ по профильной математике. Алгебра

Формулы сокращенного умножения

Квадрат суммы: (a + b)² = a² + 2ab + b²

Квадрат разности: (a – b)² = a² – 2ab + b²

Разность квадратов: a² – b² = (a + b)(a – b)

Сумма кубов: a³ + b³ = (a + b)(a² – ab + b²)

Разность кубов: a³ – b³ = (a – b)(a² + ab + b²)

Прогрессия

Арифметическая

Геометрическая

Таблица степеней

Свойства степеней

Таблица квадратов

Интенсивы по подготовке к региональному этапу ВсОШ

Все, что нужно знать
для победы, за 7 дней!

Свойства корней

Тригонометрия

Таблица значений тригонометрических функций

Тригонометрическая окружность

Тригонометрические формулы

Обратные тригонометрические функции

Преобразование суммы и разности в произведение

Регулярные курсы по подготовке к олимпиадам и ЕГЭ

Поступаем в вуз мечты без проблем!

Вероятность

Вероятность события А: m – благоприятные, n – общее число событий

P(A) = m/n

События А и В происходят одновременно: A · B

Независимые события: P(A · B) = P(A) · P(B)

Зависимые события: P(A · B) = P(A) · P(B | A)

Происходит или А, или В: A + B

Несовместные события: P(A + B) = P(A) + P(B)

Совместные события: P(A + B) = P(A) + P(B) – P(A · B)

Свойства модуля

Производные

Основные правила дифференцирования

Таблица производных

Первообразные

Логарифмы

Квадратные уравнения

Дискриминант

Теорема Виета

Разложение на множители

3528

Формулы для ЕГЭ по профильной математике. Геометрия

Планиметрия

Треугольник

Следствие из теоремы косинусов:

Длина биссектрисы (через угол):

Длина биссектрисы (через отрезки):

Прямоугольный треугольник

24 декабря – 20 января

5-11 классы

Онлайн-олимпиада Коалиции

Равносторонний треугольник

Аргументы для итогового сочинения

Подборка лучших аргументов

Равносторонний шестиугольник

Площадь внутреннего треугольника:

Площадь внутреннего прямоугольника:

Ромб

Трапеция

Произвольный четырёхугольник

Окружность

Стереометрия

Выводы

Не заучивайте формулы без осознания того, откуда берутся числа. Как можно чаще применяйте формулы при решении задач, тренируйте гибкость мышления, чтобы на ЕГЭ по профильной математике справиться со всеми заданиями.

А чтобы в разы повысить шансы на успех и разобраться в тонкостях непростой науки, можно обратиться за помощью к преподавателю онлайн-курса по подготовке к ЕГЭ.

Поделиться в социальных сетях

Какими формулами вам приходится пользоваться чаще всего?

Межтекстовые Отзывы

Посмотреть все комментарии

Все формулы по геометрии. Площади фигур

Чтобы решать задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.

Начнем с квадрата.

Площадь квадрата равна квадрату его стороны.

Площадь прямоугольника равна произведению его длины и ширины.

Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне. Она также равна произведению его сторон на синус угла между ними.

Для площади треугольника есть целых 5 формул. И все они применяются в задачах ЕГЭ.

1) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне: $S=displaystyle frac{1}{2}ah_a=displaystyle frac{1}{2}bh_b=displaystyle frac{1}{2}ch_c.$

2) Она также равна половине произведения его сторон на синус угла между ними:

$S=displaystyle frac{1}{2}ab{sin C=displaystyle frac{1}{2}ac{sin B= } }displaystyle frac{1}{2}bc{sin A }.$

3) По формуле Герона, где $p=displaystyle frac{1}{2}left(a+b+cright)$ полупериметр.

4) Также площадь треугольника равна произведению его полупериметра на радис вписанной окружности, S = pr.

5) Еще один способ. Площадь треугольника равна произведению его сторон, деленному на 4 радиуса описанной окружности, $S=displaystyle frac{abc}{4R}.$

Есть и другие формулы для площади треугольника. Но для решения заданий ЕГЭ, и первой, и второй части, достаточно этих пяти.

Площадь прямоугольного треугольника равна половине произведения его катетов. Она также равна половине произведения гипотенузы на высоту, проведенную к этой гипотенузе:

$S=displaystyle frac{1}{2}ab=displaystyle frac{1}{2}ch_{ }$

Площадь правильного треугольника равна квадрату его стороны, умноженному на sqrt{3} и деленному на 4:

Площадь трапеции равна произведению полусуммы оснований на высоту, $S=displaystyle frac{a+b}{2}cdot h.$

Также можно сказать, что площадь трапеции равна произведению ее средней линии на высоту,

Площадь произвольного четырехугольника равна половине произведения его диагоналей на синус угла между ними, $S=displaystyle frac{1}{2}ACcdot BDcdot {sin alpha }$

Площадь ромба равна произведению квадрата его стороны на синус угла ромба. Она также равна половине произведения диагоналей:

Площадь круга равна произведению числа и квадрата радиуса круга.

Ее также можно записать как произведение числа и квадрата диаметра круга, деленного на 4:

Вспомним важные свойства площадей фигур.

Равные фигуры имеют равные площади.
Иногда фигуры, имеющие равные площади, еще называют равновеликими.
Если фигура составлена из нескольких фигур, не имеющих общих внутренних точек, то ее площадь равна сумме площадей этих фигур.

Пример. Найдем площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1см times 1см.

Решение:

Найдем площадь фигуры на рисунке как сумму площадей нескольких фигур.

На рисунке это три треугольника и трапеция, указаны их площади. Тогда площадь фигуры равна 10 + 3,5 + 1,5 + 3 = 18.

Ответ: 18.

3. Отношение площадей подобных фигур равно квадрату коэффициента подобия.

Треугольники АВС и на рисунке называются подобными.

У треугольника все стороны в k раз длиннее, чем у треугольника АВС. Высота треугольника в k раз длиннее, чем высота треугольника АВС. Тогда площадь треугольника в k^2 раз больше, чем площадь треугольника АВС.

4. На рисунке показаны треугольники АВС и BCD, имеющие общую высоту. Отношение площадей этих треугольников равно отношению АС к CD:

$displaystyle frac{S_{ABC}}{S_{BCD}}=displaystyle frac{AC}{CD}$

5. Треугольники АВС и АЕС на рисунке имеют одинаковое основание и разные высоты.

Отношение площадей этих треугольников равно отношению их высот:

$displaystyle frac{S_{ABC}}{S_{AEC}}=displaystyle frac{BD}{EH}.$

6. Медиана треугольника делит его на два равновеликих, то есть равных по площади, треугольника.

На рисунке СМ — медиана треугольника АВС. Площади треугольников АСМ и ВСМ равны.

7. Три медианы треугольника делят его на шесть равных по площади треугольников.

На рисунке все 6 треугольников, из которых состоит треугольник АВС, имеют равные лощади.

Задачи ЕГЭ и ОГЭ по теме: Площади фигур.

Задача 1. Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен ${30}^circ.$

Решение:

Площадь треугольника равна половине произведения его сторон на синус угла между ними. Поэтому

$S=displaystyle frac{1}{2}cdot 8cdot 12cdot {sin 30{}^circ =displaystyle frac{1}{2}cdot 8cdot 12cdot displaystyle frac{1}{2}=24 }.$

Ответ: 24.

Задача 2. Площадь треугольника ABC равна 4, DE — средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE.

Решение:

Так как DE и АВ параллельны, треугольники CDE и САВ подобны с коэффициентом подобия $displaystyle frac{1}{2}.$ Площади подобных фигур относятся как квадрат коэффициента подобия. Тогда

$S=displaystyle frac{1}{4}cdot 4=1.$

Ответ: 1.

Задача 3. У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?

Решение:

Выразим площадь двумя способами:
$S_{ABC}=displaystyle frac{1}{2}CHcdot AB=displaystyle frac{1}{2}AKcdot CB.$

Тогда $AK=displaystyle frac{CHcdot AB}{CB}=displaystyle frac{4cdot 9}{6}=6.$

Ответ: 6.

Задача 4. Площадь треугольника ABC равна 10, DE — средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.

Решение:

Треугольник CDE подобен треугольнику CAB с коэффициентом $displaystyle frac{1}{2}.$ Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому

$S_{CDE}=displaystyle frac{1}{4}cdot 10=2.5.$

Следовательно, .

Ответ: 7,5.

Задача 5. В параллелограмме ABCD AB = 3, AD = 21, ${sin A=displaystyle frac{6}{7}}$ . Найдите большую высоту параллелограмма.

Решение:

Большая высота — это DH, потому что проведена к меньшей стороне. Из треугольника АDН:

$DH=AD{sin A=21cdot displaystyle frac{6}{7}=3cdot 6=18 }.$

Ответ: 18.

Задача 6. Найдите площадь квадрата, если его диагональ равна 1.

Решение:

Квадрат — это частный случай ромба. Площадь квадрата равна половине произведения его диагоналей. Поэтому она равна 0,5.

Ответ: 0,5.

Задача 7. Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2.

Решение:

Площадь прямоугольника равна произведению его длины на ширину. Периметр прямоугольника равен сумме длин всех сторон. Пусть одна из сторон прямоугольника равна a, тогда вторая равна 2a. Площадь прямоугольника равна тогда одна из сторон равна 3, а другая 6. Периметр P = 2 · 3 + 2 · 6 = 18.

Ответ: 18.

Задача 8. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

Решение:

Площадь параллелограмма равна произведению его сторон на синус угла между ними. Площадь прямоугольника равна произведению длины на ширину. Пусть одна сторона параллелограмма и прямоугольника равна вторая равна а острый угол параллелограмма равен alpha . Тогда площадь параллелограмма равна а площадь прямоугольника равна

По условию площадь прямоугольника вдвое больше:

${S_2=2S_1} .$ Следовательно, $acdot b=2acdot bcdot {sin alpha Leftrightarrow {sin alpha }=0,5 }Leftrightarrow alpha =30{}^circ.$

Ответ: 30.

Задача 9. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.

Решение:

Площадь параллелограмма равна произведению его основания на высоту, проведенную к этому основанию. Пусть высоты равны соответственно a и b. Тогда S = 5 · a = 10 · b = 40. Поэтому a = 8, b = 4. Большая высота равна 8.

Ответ: 8.

Задача 10. Найдите площадь ромба, если его высота равна 2, а острый угол 30 ${}^circ.$

Решение:

Площадь ромба равна произведению квадрата его стороны на синус угла ромба. С другой стороны, площадь ромба равна произведению его основания на высоту, проведенную к этому основанию. Пусть сторона ромба равна

Получим уравнение:

$a^2=a{sin alpha }.$

Корень уравнения a = 4, поэтому

Ответ: 8.

Задача 11. Найдите площадь ромба, если его диагонали равны 4 и 12.

Решение:

Площадь ромба равна половине произведения его диагоналей. $S=displaystyle frac{1}{2}cdot 4cdot 12=24.$

Ответ: 24.

Задача 12. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.

Решение:

Трапеция равнобедренная, значит,

$AH=displaystyle frac{AB-DC}{2}=6;$

$AD=displaystyle frac{P_{ABCD}-left(AB+DCright)}{2}=10.$

Тогда по теореме Пифагора из треугольника ADH:

$DH=sqrt{{AD}^2-{AH}^2}=8;$

$S=displaystyle frac{AB+CD}{2}cdot DH=20cdot 8=160.$

Ответ: 160.

Задача 13. Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45 ${}^circ.$

Решение:

Проведем высоту CH. Треугольник CHB — прямоугольный, в нем

$angle B=45{}^circ ,$ значит, он также равнобедренный, CH = HB = 4.
$S_{ABCD}=displaystyle frac{AB+CD}{2}cdot CH=4cdot 4=16.$

Ответ: 16.

Задача 14. Высота трапеции равна 5, площадь равна 75. Найдите среднюю линию трапеции.

Решение:

Средняя линия трапеции равна полусумме оснований. Выразим её из формулы площади трапеции:
$S=displaystyle frac{a+b}{2}cdot hLeftrightarrow displaystyle frac{a+b}{2}cdot 5=75Leftrightarrow displaystyle frac{a+b}{2}=15.$

Ответ: 15.

Задача 15. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту. Пусть высота равна h, тогда

$S=displaystyle frac{27+9}{2}cdot h=72.$

Из этого уравнения получим: h = 4.

Рассмотрим прямоугольный треугольник, гипотенузой которого является боковая сторона трапеции, равная 8, а катетом — высота трапеции. Длина катета равна половине гипотенузы, следовательно, он лежит напротив угла ${30}^circ.$

Ответ: 30.

Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Задача 16. Найдем площадь четырехугольника на рисунке.

Решение:

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным 5. Высоты этих треугольников равны 2 и 3. Тогда площадь четырёхугольника равна сумме площадей двух треугольников:

Ответ: 12,5.

В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Задача 17. Найдем площадь треугольника, изображенного на клетчатой бумаге.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной 5 и трёх прямоугольных треугольников. Видите их на рисунке? Получаем:

Ответ: 10,5.

Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.

Задача 18.

Найдите площадь сектора круга радиуса 1, длина дуги которого равна 2.

Решение:

На этом рисунке мы видим часть круга. Площадь всего круга равна так как R=1. Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R = 1), а длина дуги данного сектора равна 2, следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Ответ: 1.

Формула Пика

Покажем, как вычислять площадь фигуры, изображенной на координатной плоскости, с помощью формулы Пика.

Задача 19. Найдите площадь многоугольника АВСDE, изображенного на рисунке.

Первый способ:

Площадь многоугольника ABCDE равна сумме площадей треугольника BCD, трапеции BKDE и треугольника AKE.

Имеем:

$S_{vartriangle BCD}=displaystyle frac{1}{2}cdot 9cdot 2=9;$

$S_{BKDE}=displaystyle frac{1}{2}cdot (9+3)cdot 2=12;$

$S_{vartriangle AKE}=displaystyle frac{1}{2}cdot 3cdot 4=6;$

$S_{ABCDE}=9+12+6= 27.$

Второй способ — применить формулу Пика.

Назовем точку координатной плоскости целочисленной, если обе ее координаты — целые числа. На нашем рисунке это точки на пересечениях линий, разделяющих клетчатую бумагу на клетки.

Площадь многоугольника с целочисленными вершинами равна

Здесь В — количество целочисленных точек внутри многоугольника, Г — количество целочисленных точек на границе многоугольника.

Главное — аккуратно посчитать. На нашем рисунке

В = 24 (показаны зеленым),

Г = 8 (показаны красным),

S = 24 + $displaystyle frac{8}{2}$ — 1 = 27.

Ответ: 27.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Все формулы по геометрии. Площади фигур» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Формулы ЕГЭ по математике

27.09.2013

Полный сборник красиво оформленных школьных формул по алгебре и геометрии.

В пособии содержатся все разделы школьной математики, все формулы и даны подробные описания к каждому из них.

Смотреть в PDF:

Скачайте в pdf файле.

По разделам:

Комментарии

+30

#1
Плотников А.
04.06.2014 20:58

Класный сайт!

Цитировать

-4

#2
Гость
18.09.2014 11:22

Цитирую лоло:

школоло не осилило

Цитировать

+10

#6
Ann
10.04.2015 19:04

Благодарю за формулы

Цитировать

+6

#7
Мария
25.04.2015 08:05

Спасибо огромное за такой хороший сайт! ;-)

Цитировать

+1

#9
настюша
16.05.2015 10:03

не все формулы по заданиям :cry:

Цитировать

+20

#10
Алина
30.05.2015 10:52

Очень помогли формулы. Ребята, кто ссдает ЕГЭ, удачи нам!

Цитировать

+2

#12
Анон
02.08.2015 12:30

Спасибо.
Прошу выложить так же и в разрешении .jpg
Так удобнее просматривать и использовать на разных девайсах.

Цитировать

-2

#13
Анон
02.08.2015 12:32

Цитирую Анон:

Спасибо.
Прошу выложить так же и в разрешении .jpg
Так удобнее просматривать и использовать на разных девайсах.

Оказалось они под катом, я имел в виду весь pdf-файл в формате .jpg КАЖДУЮ картинку.
Спасибо.

Цитировать

+5

#15
Мария
30.09.2015 06:52

Здравствуйте! Спасибо за формулы и такое яркое цветное оформление — это помогает запомнить. Не могли бы вы еще дополнить свой список формул формулами, связанными с прогрессиями — это тоже очень важно.

Цитировать

+4

#16
Мария
30.09.2015 07:18

и еще нет формул поверхности, боковой и общей, у пирамиды.

Цитировать

0

#17
настя
01.03.2016 15:18

Цитирую galaxe:

спасиб большое

кто сдает гиа тому сюда

Цитировать

+4

#18
настя
01.03.2016 15:18

думаю мне пригодится для подготовки к гиа

Цитировать

-4

#21
а
03.03.2017 18:44

а это на профильный матан ил на базу?

Цитировать

+2

#23
Саша
28.01.2019 20:56

спасибо большое, очень помогли :roll: :roll:

Цитировать

+3

#24
Алексей Алексеевич
05.02.2019 14:23

Спасибо. А то нихера не помню а ЕГЭ уже скороо!!!!

Цитировать

-2

#25
Glebasta_Rhymes
13.05.2019 19:41

а где формулы призмы????????? ???????? :-?

Цитировать

0

#26
Татьяна
16.05.2019 04:06

А векторная часть? В 9 классе есть раздел векторов, координат векторов. Не нашла у вас этот раздел(((

Цитировать

+5

#27
Татьяна
16.05.2019 04:13

Не сказала вам огромное спасибо!!!! Работа проделана очень большая, поэтому благодарность вам за помощь :-) !!!

Цитировать

+1

#28
Мария
11.06.2019 12:07

Интересно ,мне эта информация поможет на экзамене по математике профиль?

Цитировать

0

#29
Нико
26.04.2022 06:55

Ещё бы среднюю линию, и было бы прекрасно

Цитировать

Добавить комментарий

Комментарии без регистрации. Несодержательные сообщения удаляются.

Источник

Геометрия

Планиметрия (2D)

Площади фигур:

Окружность:	`S=pir^2`
Треугольник:	`S=1/2ah`
Параллелограмм:	`S=ah`
Четырёхугольник:	`S=1/2d_1d_2sinvarphi`	У ромба `varphi=90^@`
Трапеция:	`S=(a+b)/2*h`

Стереометрия (3D)

Призма:	`V=S_(осн)h`
Пирамида:	`V=1/3S_(осн)h`
Конус:	`V=1/3S_(осн)h`
	`S_(бок)=pirl`
Цилиндр:	`V=pir^2h`	Формулы цилиндра нужно уметь выводить
	`S_(бок)=2pirh`
Шар:	`V=4/3pir^3`
	`S=4pir^2`

Все формулы для профильного ЕГЭ-2022 по математике

Все формулы для базового ЕГЭ-2022 по математике

ЕГЭ-2022 по математике, профильный и базовый уровни

Задачи, профильный:

Задача №7, производная
Задача №12, производная
Задача №13, тригонометрия, степени, логарифмы
Задача №15, неравенства
Задача №17, экономическая

Задачи, базовый:

Задача №14 (база), производная

ЕГЭ-2022 по физике

ОГЭ-2022 по математике

ОГЭ-2022 по физике

Поиск решения задачи:
Введите примерный текст задачи, и мы попробуем её найти вместе с Google

Google

Пользовательский поиск

: ЕГЭ по математике профиль

Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2022 из различных источников.

Тренировочные варианты ЕГЭ 2022 по математике (профиль)

Структура варианта КИМ ЕГЭ

Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и количеству заданий:

– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;

– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).

Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.

Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.

Связанные страницы:

Стартует 2021-2022 учебный год, а значит, самое время узнать, как будет осуществляться оценивание ОГЭ и ЕГЭ по математике в 2022 году и к каким результатам необходимо стремиться выпускникам.

ОГЭ по математике

В 2022 году на ОГЭ по математике выпускника предстоит выполнить 25 заданий, из которых 19 – с кратким ответом и 6 – с развернутым.

По уровню сложности задания будут разделены следующим образом:

базовый уровень – 19;
повышенный – 4;
высокий – 2.

Оценивание ОГЭ по математике в 2022 году не изменится – выпускнику будут начислять первичные баллы, которые после завершения проверки будут переведены в стандартную школьную оценку по такой таблице:

Оценка	Баллы
5	22-31
4	15-21
3	8-14
2 (не сдал)	0-7

Максимальный балл — 31. За модуль «Алгебра» – 20 баллов, за модуль «Геометрия» – 11 баллов.

Ориентиром при отборе в профильные классы могут быть показатели:

для естественнонаучного профиля: 18 баллов, из них не менее 6 по геометрии;
для экономического профиля: 18 баллов, из них не менее 5 по геометрии;
физико-математического профиля: 19 баллов, из них не менее 7 по геометрии.

Более подробно о том, как будет происходить оценивание ОГЭ по математике в 2022 году, рекомендует почитать в документации к демоверсии КИМов. Проект демон8страционного варианта, а также спецификаций и кодификатора уже доступен на официальном сайте ФИПИ.

ЕГЭ по базовой математике

Два года подряд экзамен по базовой математике был отменён в связи с эпидемией коронавируса, в 2022 году Рособрнадзор всё-таки планирует возобновить практику проведения ЕГЭ по математике в статусе обязательного экзамена с правом выбора уровня — базового или профильного.

Важно! Для получения школьного аттестата достаточно минимального балла по базовой математике. Для поступления в профильный вуз необходимо набрать проходной балл по профильной математике.

Прежде всего, надо сказать, что изменение заданий, анонсированные ФИПИ в перспективных моделях 2022 года, имеют общую тенденцию на усложнение. Средние баллы ЕГЭ по многим предметам ежегодно растут, поэтому принято решение избавиться от самых лёгких заданий и ввести в КИМы 2022 года новые форматы. Задания ЕГЭ по базовой математике изменились минимально: добавили текстовую задачу на составление уравнения или систем уравнений, внесли небольшие изменения в задачу «на клеточках», а также поменяли местами некоторые задания (не изменяя сути).

Базовый ЕГЭ по математике – единственный экзамен, для которого разработана шкала перевода баллов ЕГЭ 2022 в оценки привычной для школьников пятибальной системы.

В КИМе выпускникам будет предложено 20 заданий, каждое из которых оценивается в 1 балл. В результате максимально 11-классники могут набрать в 2022 году на ЕГЭ по математике 20 баллов (без деления на алгебру и геометрию).

Оценка	Баллы
5	17-20
4	12-16
3	7-11
2 (не сдал)	0-6

Для получения аттестата достаточно получить оценку «3» что эквивалентно 7 первичным баллам.

ЕГЭ по профильной математике

Выпускникам по-прежнему предстоит выбирать между базовой и профильной математикой. Последнюю выбирают ученики, которым она нужна для поступления в вуз — то есть те, кто намерен связать свою жизнь с точными науками.

Согласно новым проектам КИМов по профильной математике, из первой части пропали простые задания 1–3, зато появились задания на анализ функции и на сложную вероятность. Сменилась также логическая структура и нумерация.

В части с развернутым ответом изменены критерии оценивания заданий: за стереометрическую задачу №13 теперь можно получить 3 балла (критерии стали аналогичны планиметрической задаче), за экономическое задание теперь можно получить только 2 балла (ранее было 3). Максимальный первичный балл за всю работу — 31.

Как и ожидалось, экзамен поменялся достаточно сильно: были приняты почти все изменения, предложенные в перспективной модели, за исключением пары моментов. При этом задание, которое все боялись больше всего – на комплексные числа — так и не появилось. Больше нет заданий для простого набора баллов, которые может решить даже ученик младшей школы. Сейчас все задания в ЕГЭ потребуют более высокого уровня математической компетенции, которая формируется на уроках алгебры и геометрии.

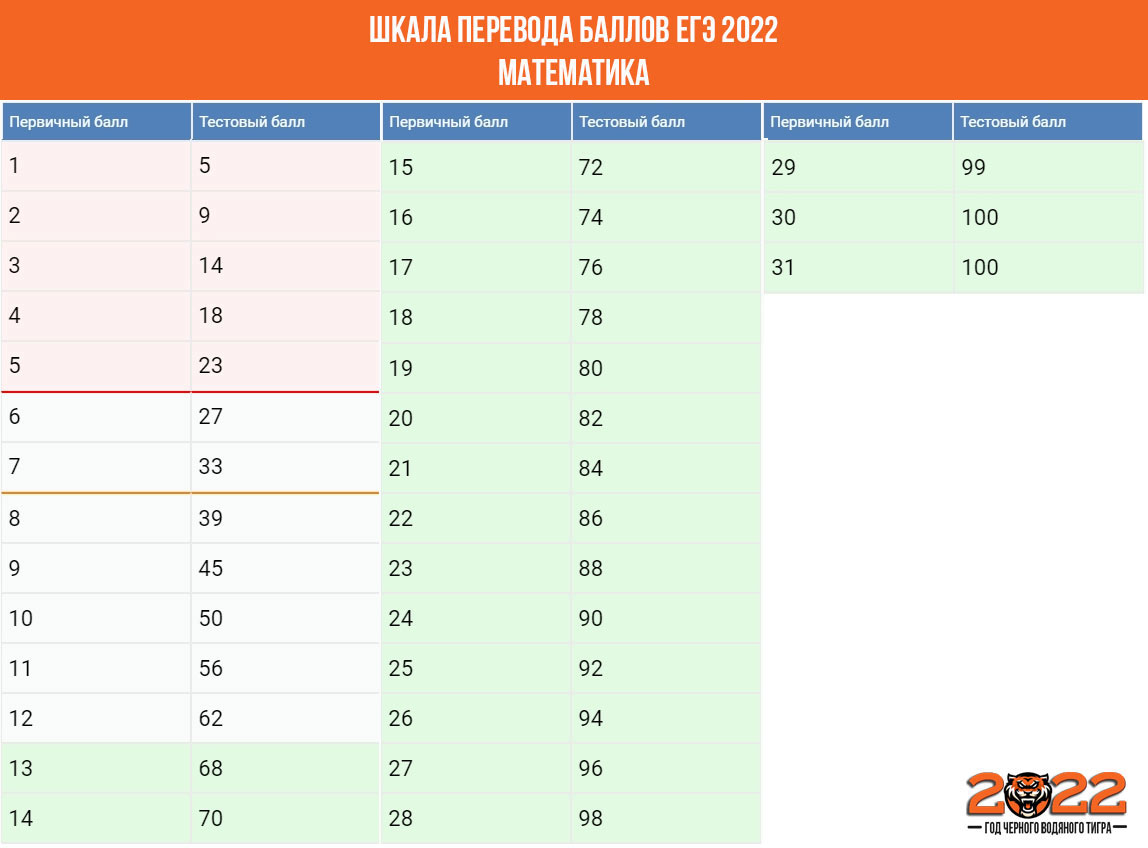
Оценивание результата на ЕГЭ-2022 по профильной математике будет происходит по такой рекомендованной ФИПИ таблице:

Возможные изменения

Обратите внимание, что материалы статьи написаны по предварительным вариантам демоверсий 2022 года. Возможно, в окончательной версии КИМов мы увидим слегка иную систему начисления баллов, но она точно не будет очень существенно отличаться от представленной. Окончательный вариант можно будет найти на страницах нашего сайта или на официальном сайте ФИПИ ближе к началу 2022 года.

Читайте также:

Олимпиады для школьников в 2022 году
Экзамены в 4 классе в 2022 году
Шкала перевода баллов ЕГЭ 2022 в оценки

— Окончил бакалавриат СПБГЭТУ «ЛЭТИ» с красным дипломом, сейчас учится в магистратуре

— Сдал ЕГЭ по профильной математике на 94 балла

— За 5 лет преподавания выпустил более 700 учеников со средним баллом — 82,6

— Прошел курсы повышения квалификации по геометрии в ЕГЭ и олимпиадах

Как выучить все формулы по математике к ЕГЭ

Чтобы сдать ЕГЭ по математике, необходимо знать математические формулы из школьного курса алгебры и геометрии.

Для того, чтобы запомнить формулы школьной математики, желательно держать в течение всего года на видном месте шпаргалку с красиво написанными формулами. Таким образом подключается зрительная память и формулы лучше запоминаются.

Проверяйте себя время от времени: попробуйте написать все важные математические формулы по памяти, а затем проверьте. На самом деле, формул, которые надо выучить наизусть, не так много. И целого учебного года вполне достаточно, чтобы все выучить.

Многие алгебраические, геометрические, тригонометрические формулы можно быстро вывести прямо на экзамене, если Вы их забыли. Но на это придется потратить какое-то время. Поэтому преимущество получают те школьники, которые выучили формулы.
Зная математические формулы наизусть, можно гораздо быстрей решить сложные задачи по алгебре, тригонометрии и геометрии на ЕГЭ.

Мы собрали самые важные формулы из школьного курса математики, которые надо выучить для успешной сдачи ЕГЭ.

Математические формулы школьного курса алгебры

Степени и корни

Формулы сокращенного умножения

Квадратный трехчлен: квадратное уравнение, формулы Виета, разложение на множители

Логарифмические формулы

Формулы тригонометрии

Основные формулы тригонометрии

Тригонометрические уравнения

Значения тригонометрических функций

Формулы приведения

Сумма и разность углов

Формулы двойного и тройного аргумента

Формулы половинного аргумента

Сумма и разность тригонометрических функций

Произведение тригонометрических функций

Формулы дифференциального исчисления

Формулы векторной алгебры из школьного курса математики

Формулы арифметической и геометрической прогрессии

Геометрические формулы школьного курса математики для ЕГЭ

Планиметрия

Стереометрия

Выучить формулы по математике – это еще не все, что надо для успешной сдачи ЕГЭ. Опыт решения задач, знания правил оформления заданий на экзамене не менее важны. Приглашаем всех школьников 11-х классов на курсы подготовки к ЕГЭ ПАРАГРАФ. С нами Вы подготовитесь к ЕГЭ наиболее продуктивно.

Учите формулы по математике и сдавайте ЕГЭ на максимальные баллы!

Источник