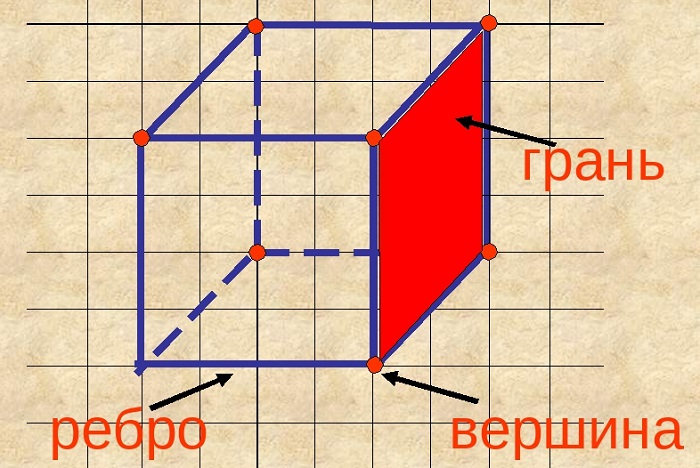
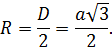Все про куб для егэ - Помощь в подготовке к экзаменам и поступлению

Куб – правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра куба равны.

Свойства куба:

1. В кубе $6$ граней и все они являются квадратами.

2. Противоположные грани попарно параллельны.

3. Все двугранные углы куба – прямые.

4. Диагонали равны.

5. Куб имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.

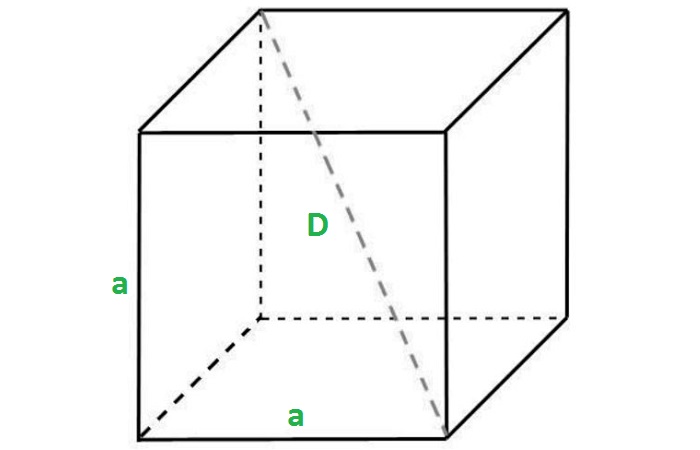
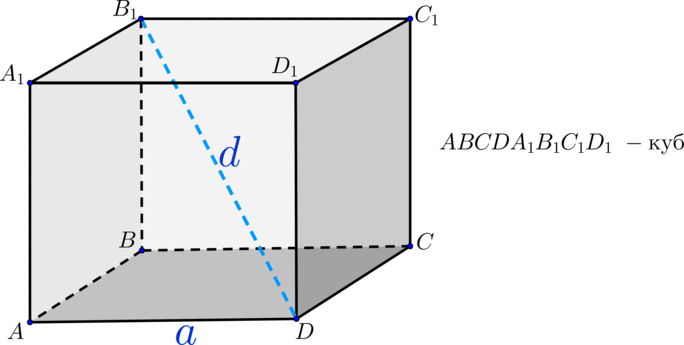
6. Диагональ куба в $√3$ раз больше его ребра

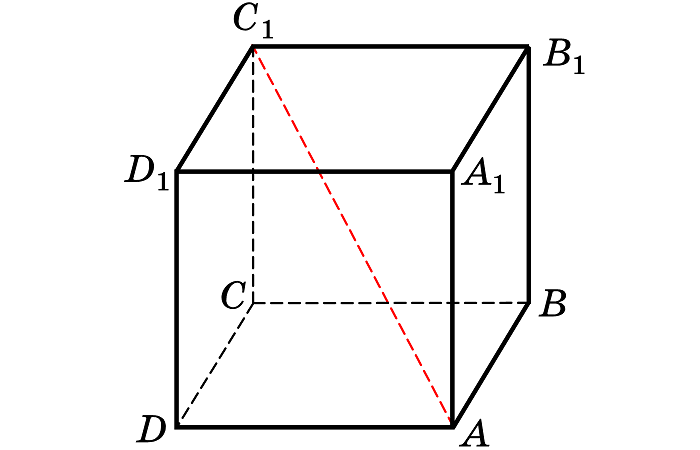
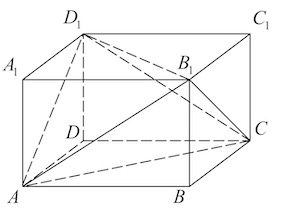
$B_1D=AB√3$

7. Диагональ грани куба в $√2$ раза больше длины ребра.

$DC_1=DC√2$

Пусть $а-$длина ребра куба, $d-$диагональ куба, тогда справедливы формулы:

Объем куба: $V=a^3={d^3}/{3√3}$.

Площадь полной поверхности: $S_{п.п}=6а^2=2d^2$

Радиус сферы, описанной около куба: $R={a√3}/{2}$

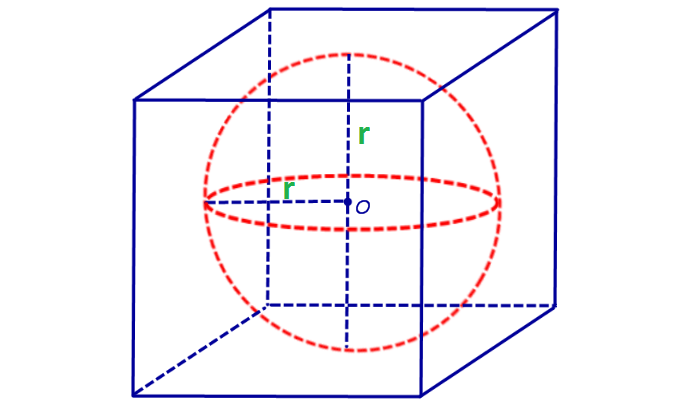
Радиус сферы, вписанной в куб: $r={a}/{2}$

При увеличении всех линейных размеров куба в $k$ раз, его объём увеличится в $k^3$ раз.

При увеличении всех линейных размеров куба в $k$ раз, площадь его поверхности увеличится в $k^2$ раз.

Прямоугольный параллелепипед

Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.

1. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

$B_1D^2=AD^2+DC^2+C_1C^2$

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.

Чтобы были понятны формулы, введем обозначения:

$а$-длина;

$b$-ширина;

$с$-высота(она же боковое ребро);

$P_{осн}$-периметр основания;

$S_{осн}$-площадь основания;

$S_{п.п}$-площадь полной поверхности;

$V$-объем.

$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.

$S_{п.п}=2(ab+bc+ac)$.

Пирамида

Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) — треугольники, имеющие общую вершину.

Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.

$SO$ — высота.

Формулы вычисления объема и площади поверхности правильной пирамиды.

$h_a$ — высота боковой грани (апофема)

$S_{бок}={P_{осн}·h_a}/{2}$

$S_{п.п}=S_{бок}+S_{осн}$

$V={1}/{3}S_{осн}·h$

В основании лежат правильные многоугольники, рассмотрим их площади:

Для равностороннего треугольника $S={a^{2}√3}/{4}$, где $а$ — длина стороны.
Квадрат $S=a^2$, где $а$ — сторона квадрата.

Задачи на нахождение объема составного многогранника:

Разделить составной многогранник на несколько параллелепипедов.
Найти объем каждого параллелепипеда.
Сложить объемы.

Задачи на нахождение площади поверхности составного многогранника.

— Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:

$S_{полн.пов.}=P_{осн}·h+2S_{осн}$

Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.

— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.

Источник

Куб. Формулы, признаки и свойства куба

Определение.

Куб (гексаедр) — это трехмерная фигура, которая состоит из шести динаковых квадратов так, что каждый квадрат полностью соприкасается своими четырьмя сторонами к сторонам остальных четырех квадратов под прямым углом. Куб является правильным многогранником, у которого грани образованы из квадратов. Также кубом можно назвать прямоугольный параллелепипед, у которого все ребра равны.

Определение. Грань куба — это часть плоскости, ограниченная сторонами квадрата.

— куб имеет шесть граней;

— каждая грань куба пересекается с четырьмя другими гранями под прямым углом и параллельная шестой грани;

— грани имеют одинаковую площадь, которую можно найти, используя формулы для вычисления площади квадрата.

Определение. Ребро куба — это отрезок, образованный пересечением двух граней куба.

— куб имеет двенадцать ребер;

— каждый конец ребра соединен с двумя соседними ребрами под прямым углом;

— ребра куба имеют одинаковую длину.

Определение. Вершина куба — это самая отдаленная от центра куба точка, которая лежит на пересечения трех граней куба.

— куб имеет восемь вершин;

— каждая вершина образована только тремя гранями и тремя ребрами.

Определение. Центр грани куба (O₁) — это равноудалена точка от всех ребер грани куба.

Определение. Центр куба (O) — это равноудалена точка от всех граней куба.

Определение. Ось куба (i) — это прямая, проходящая через центр куба и центры двух параллельных граней куба.

— куб имеет три оси;

— оси куба взаимно перпендикулярны.

Определение. Диагональ куба (d₁) — отрезок, который соединяет противоположные вершины куба и проходит через центр куба.

— куб имеет четыре диагонали;

— диагонали куба пересекаются и делятся пополам в центре куба;

— диагонали куба имеют одинаковую длину.

Формула. Диагональ куба d₁ через длину ребра a:

d₁ = a√3

Определение. Диагональ грани куба (d₂) -отрезок, который соединяет противоположные углы грани куба и проходит через центр грани куба.

Формула. Диагональ грани d₂ через длину ребра a:

d₂ = a√2

Определение. Объём куба — это совокупность всех точек в пространстве, ограниченные гранями куба.

Формула. Объём куба через длину ребра a:

V = a³

Формула. Объём куба через длину диагонали куба d₁:

Определение. Площадь поверхности куба — это совокупность плоскостей всех граней.

Формула. Площадь поверхности куба через длину ребра a:

S = 6a²

Определение. Периметр куба — это совокупность длин всех ребер куба.

Формула. Периметр куба P через длину ребра a:

P = 12a

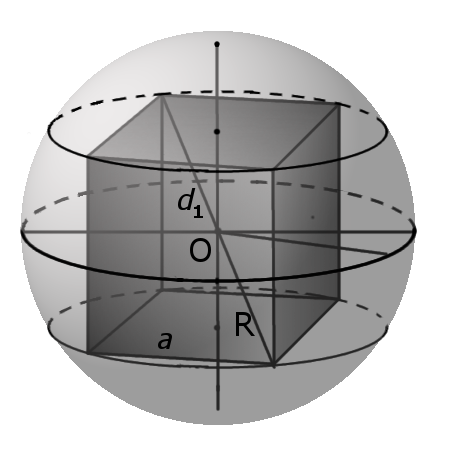
Определение. Сферой вписанной в куб называется сфера, центр которой совпадает с центром куба и которая касается центров граней куба.

— все шесть граней куба являются касательными плоскостями к вписанной сферы;

— радиус вписанной сферы равен половине длины ребра a.

Формула. Радиус вписанной сферы r через длину ребра a:

Формула. Объема вписанной сферы V через длину ребра a:

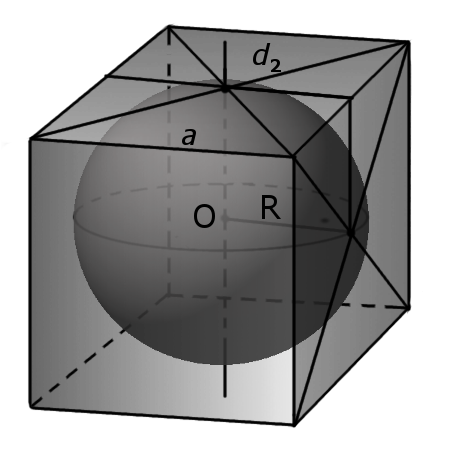
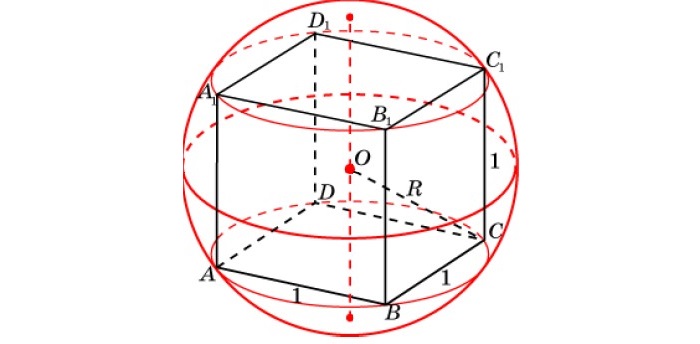
Определение. Сферой описанной вокруг куба называется сфера, центр которой совпадает с центром куба и которая соприкасается с восьмью вершинами куба.

— радиус описанной сферы равен половине длины диагонали (d₁) куба.

Формула. Радиус описанной сферы R через длину ребра a:

Формула. Объема сферы описанной вокруг куба V через длину ребра a:

Свойства куба

1. В куб можно вписать тетраэдр так, чтобы все четыре вершины тетраэдра лежали на четырех вершинах куба, а все шесть ребер тетраэдра будут лежать на шести гранях куба и ребра будут равны диагонали грани куба.

2. В куб можно вписать правильный шестиугольник так, что все шесть вершин лежат в центрах граней куба.

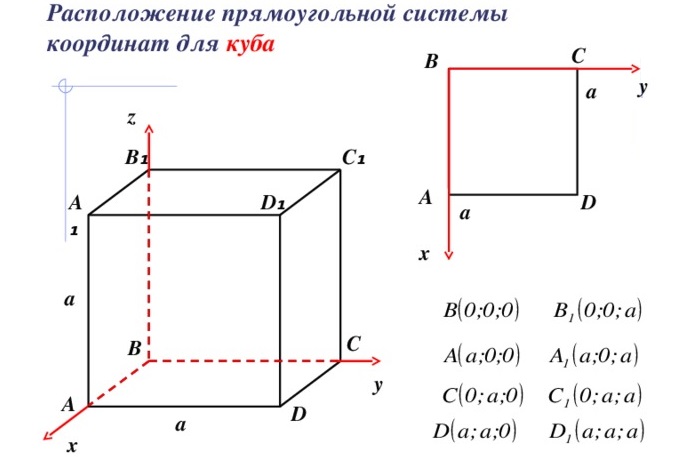
Координаты вершин куба

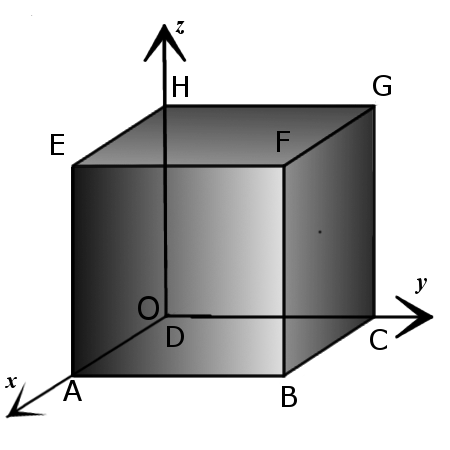
1. Координаты вершин куба со стороной a и вершиной D в начале декартовой системы координат так, что ребра этой вершины лежат на осях координат:

A(a, 0, 0),
B(a, a, 0),
C(0, a, 0),
D(0, 0, 0),
E(a, 0, a),
F(a, a, a),
G(0, a, a),
H(0, 0, a).

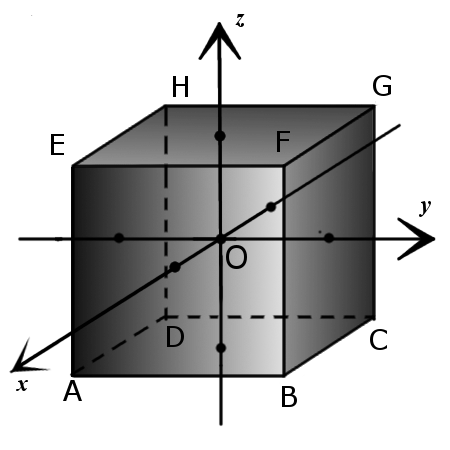
2. Координаты вершин куба с длиной стороны 2a, у которого центр куба находится в начале декартовой системы координат так, что ребра куба параллельны осям координат:

A(a, —a, —a),
B(a, a, —a),
C(-a, a, —a),
D(-a, —a, —a),
E(a, —a, a),
F(a, a, a),
G(-a, a, a),
H(-a, —a, a).

Определение. Единичный куб — это куб, у которого длина ребер равна единице.

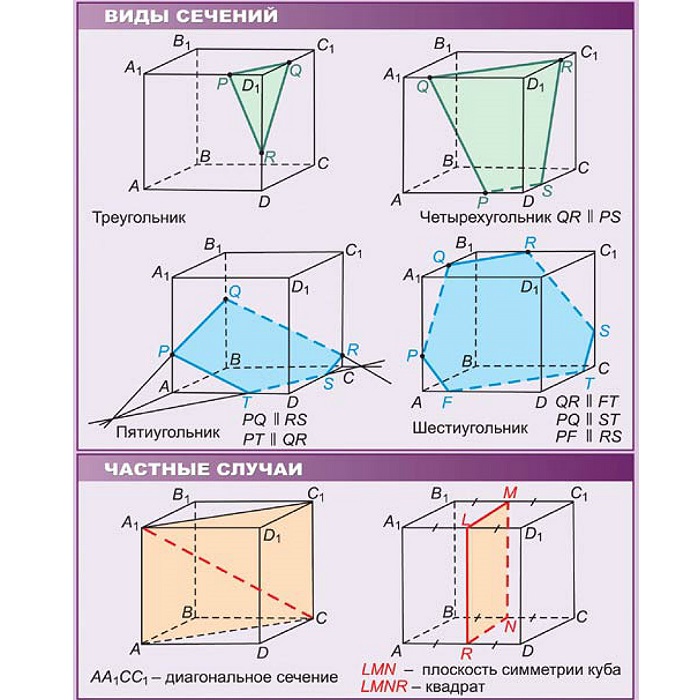
Пересечение куба плоскостью

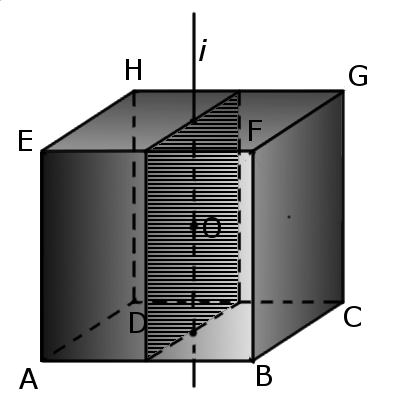
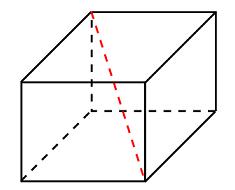
1. Если пересечь куб плоскостью, проходящей через центр куба и центры двух противоположных граней, то в сечении будет квадрат, длина стороны которого будет равна длине ребра куба. Эта плоскость делит куб два равных прямоугольных параллелепипеда.

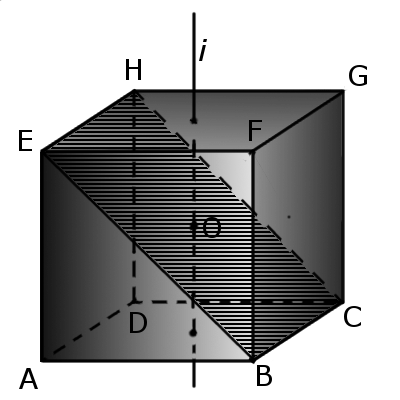
2. Если пересечь куб с ребром a плоскостью, проходящей через центр куба и два параллельных ребра, то в сечении будет прямоугольник со сторонами a и a√2, площадью сечения a²√2. Эта плоскость делит куб две равные призмы.

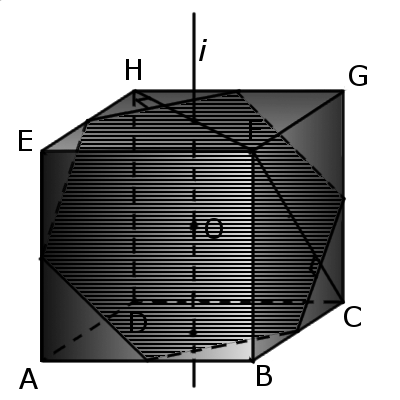
3. Если пересечь куб плоскостью, проходящей через центр и середины шести граней, то в сечении будет правильный шестиугольник со стороной a√2/2, площадью сечения a²(3√3)/4. У куба одна из диагоналей (FC) каждой грани, что пересекаются, перпендикулярна стороне шестиугольника.

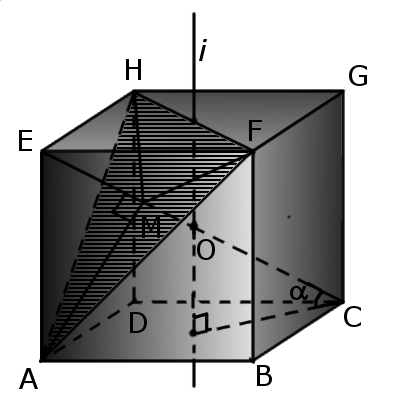
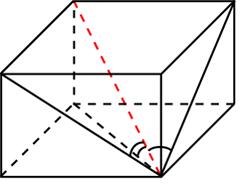
4. Если пересечь куб плоскостью, проходящей через три вершины куба, то в сечении будет правильный треугольник со стороной a√2, площадью сечения a²√3/2 и объемом большей части — 5a³/6 и меньшей — a³/6. Одна из диагоналей куба (EC) перпендикулярна к плоскости сечения и проходит через центр треугольника (M) и делится плоскостью в отношении MC:EМ = 2:1.

Источник

Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:

многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;
прямая призма, все грани которой есть квадраты;
прямоугольный параллелепипед, все рёбра которого равны.

Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.

Элементы куба

Основными элементами многогранника считаются грани, рёбра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.

Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.

Грани куба попарно перпендикулярны, являются квадратами, равны между собой.

Ребро

Линии пересечения сторон называются рёбрами.

Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.

Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.

Вершина

Точки пересечения рёбер называются вершинами. Их число равно восьми.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.

Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.

Центр куба

Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.

Это есть центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.

Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:

Формула доказывается с помощью дважды применённой теоремы Пифагора.

Диагональ куба — одна из осей симметрии.

Все диагонали куба равны между собой и точкой пересечения делятся пополам.

Диагональ грани куба

Длина диагонали грани в √2 раз больше ребра, то есть:

Эта формула доказывается также с помощью теоремы Пифагора.

Объем куба

Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:

Периметр куба

Сумма длин всех рёбер равна:

Площадь поверхности

Сумма площадей всех граней называется площадью поверхности куба. Она равна:

Сфера, вписанная в куб

Такая сфера имеет центр, совпадающий с центром куба.

Радиус равен половине ребра:

Сфера, описанная вокруг куба

Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:

106

Координаты вершин куба

В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.

Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:

Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).

Свойства куба

Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.

Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.

Прочие свойства:

у куба все грани равны, являются квадратами;
у куба все рёбра равны;
один центр и несколько осей симметрии.

Источник

Каталог заданий.
Куб

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 2 № 27055

Площадь поверхности куба равна 18. Найдите его диагональ.

Аналоги к заданию № 5041: 27055 72585 72539 72541 72543 72545 72547 72549 72551 72553 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.3.1 Призма, её основания, боковые рёбра, высота, боковая поверхность

Классификатор стереометрии: Площадь поверхности куба

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 2 № 27056

Объем куба равен 8. Найдите площадь его поверхности.

Аналоги к заданию № 27056: 5043 72587 72589 72591 72593 72595 72597 72599 Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.3.2 Параллелепипед; куб; симметрии в кубе, в параллелепипеде, 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы

Классификатор стереометрии: Площадь поверхности куба

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 2 № 27061

Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.

Аналоги к заданию № 27061: 5053 72865 520184 520203 27145 72823 72825 72827 72829 72831 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.3.2 Параллелепипед; куб; симметрии в кубе, в параллелепипеде

Классификатор стереометрии: Площадь поверхности куба

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 2 № 27081

Во сколько раз увеличится объем куба, если его ребра увеличить в три раза?

Аналоги к заданию № 27081: 73627 500957 73629 73631 73633 73635 73637 73639 Все

Классификатор планиметрии: Отношение длин, площадей, объемов подобных фигур

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 2 № 27098

Диагональ куба равна Найдите его объем.

Аналоги к заданию № 27098: 74417 74419 74429 505446 74421 74423 74425 74427 Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Источник

Факт 1.
(bullet) Куб – это прямоугольный параллелепипед, все грани которого – равные квадраты.
(bullet) Следовательно:

— ({color{red}{{small{объем куба}}}}) ищется по следующей формуле (где (a) – ребро куба): [{color{red}{{large{V=a^3}}}}] — ({color{red}{{small{диагональ куба}}}}) [{color{red}{{large{d^{,2}=3a^2}}}}] — ({color{red}{{small{площадь поверхности куба}}}}) равна сумме площадей шести одинаковых квадратов, т.е. [{color{red}{{large{S_{text{пов.куб}}=6a^2}}}}]

Факт 2.
(bullet) Если сфера вписана в куб (то есть касается всех его граней), то ее радиус равен (0,5a), где (a) – ребро куба.
(bullet) Если сфера описана около куба (то есть все вершины куба лежат на сфере), то ее радиус равен (0,5d), где (d) – диагональ куба.
(bullet) Центр сферы, вписанной в куб или описанной около куба, лежит в точке пересечения диагоналей куба.

Источник

В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).

Определение куба
Свойства куба
- Свойство 1
- Свойство 2
- Свойство 3
Формулы для куба
- Диагональ
- Диагональ грани
- Площадь полной поверхности
- Периметр ребер
- Объем
- Радиус описанного вокруг шара
- Радиус вписанного шара

Определение куба

Куб – это правильный многогранник, все грани которого являются квадратами.

Куб

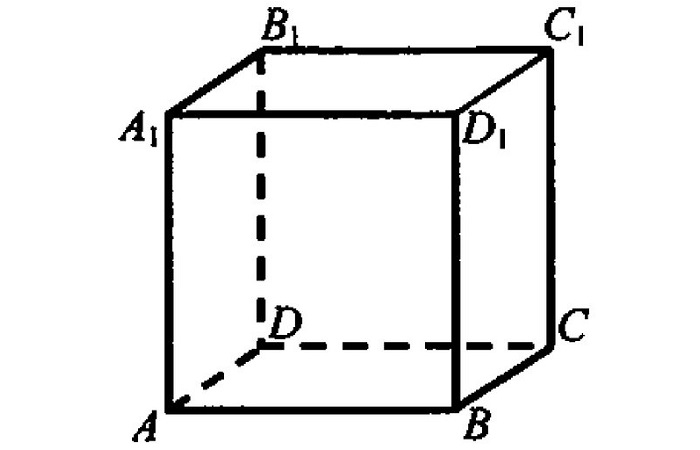
Вершины куба – это точки, являющиеся вершинами его граней.
Всего их 8: A, B, C, D, A₁, B₁, C₁ и D₁.
Ребра куба – это стороны его граней.
Всего их 12: AB, BC, CD, AD, AA₁, BB₁, CC₁, DD₁, A₁B₁, B₁C₁, C₁D₁ и A₁D₁.
Грани куба – это квадраты, из которого состоит фигура.
Всего их 6: ABCD, A₁B₁C₁D₁, AA₁B₁B, BB₁C₁C, CC₁D₁D и AA₁D₁D.

Примечание: куб является частным случаем параллелепипеда или призмы.

Свойства куба

Свойство 1

Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:

ABCD || A₁B₁C₁D₁
AA₁B₁B || CC₁D₁D
BB₁C₁C || AA₁D₁D

Свойство 2

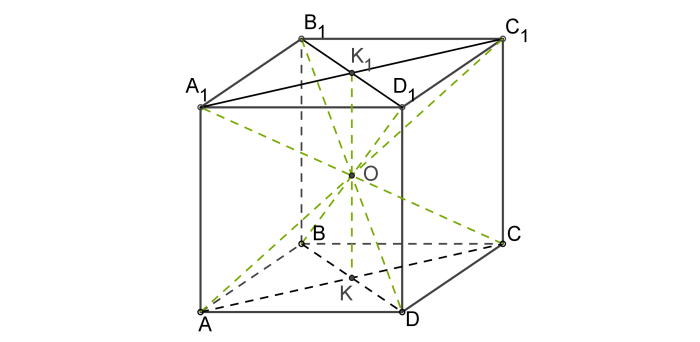
Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.

AC₁ = BD₁ = A₁C = B₁D (диагонали куба).
О – точка пересечения диагоналей:
AO = OC₁ = BO = OD₁ = A₁O = OC = B₁O = OD.

Свойство 3

Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.

Например, на рисунке выше угол между гранями ABCD и AA₁B₁B является прямым.

Формулы для куба

Примем следующие обозначения, которые будут использоваться далее:

a – ребро куба;
d – диагональ куба или его грани.

Диагональ

Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.

Диагональ грани

Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.

Площадь полной поверхности

Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.

Периметр ребер

Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.

Объем

Объем куба равен длине его ребра, возведенной в куб.

Радиус описанного вокруг шара

Радиус шара, описанного около куба, равняется половине его диагонали.

Радиус вписанного шара

Радиус вписанного в куб шара равен половине длины его ребра.

Источник

Задача 1. В прямоугольном параллелепипеде известно, что Найдите длину диагонали

Решение: + показать

Задача 2. Найдите угол прямоугольного параллелепипеда, для которого . Ответ дайте в градусах.

Решение: + показать

Задача 3. В прямоугольном параллелепипеде известны длины рёбер Найдите синус угла между прямыми и

Решение: + показать

Задача 4. Площадь поверхности куба равна Найдите его диагональ.

Решение: + показать

Задача 5. Объем куба равен Найдите площадь его поверхности.

Решение: + показать

Задача 6. Диагональ куба равна . Найдите его объем.

Решение: + показать

Задача 6. Объем куба равна . Найдите его диагональ.

Решение: + показать

Задача 7. Во сколько раз увеличится объем куба, если его ребра увеличить в десять раз?

Решение: + показать

Задача 8. Если каждое ребро куба увеличить на , то его площадь поверхности увеличится на Найдите ребро куба.

Решение: + показать

Задача 9. Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в раза?

Решение: + показать

Задача 10. Объем одного куба в раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

Решение: + показать

Задача 11. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны и Площадь поверхности этого параллелепипеда равна Найдите третье ребро, выходящее из той же вершины.

Решение: + показать

Задача 12. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны и Найдите ребро равновеликого ему куба.

Решение: + показать

Задача 13. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны и Диагональ параллелепипеда равна Найдите объем параллелепипеда.

Решение: + показать

Задача 14. Площадь грани прямоугольного параллелепипеда равна Ребро, перпендикулярное этой грани, равно Найдите объем параллелепипеда.

Решение: + показать

Задача 15. В прямоугольном параллелепипеде известны длины рёбер: Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки и

Решение: + показать

Задача 16. Диагональ прямоугольного параллелепипеда равна и образует углы $30^{circ}$ , $30^{circ}$ и $45^{circ}$ с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.

Решение: + показать

Задача 17. В прямоугольном параллелепипеде ребро , ребро , ребро . Точка — середина ребра Найдите площадь сечения, проходящего через точки .

Решение: + показать

Задача 18. Одна из граней прямоугольного параллелепипеда — квадрат. Диагональ параллелепипеда равна и образует с плоскостью этой грани угол °. Найдите объем параллелепипеда.