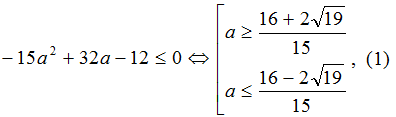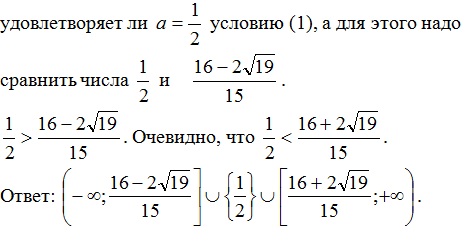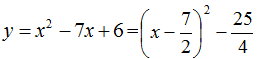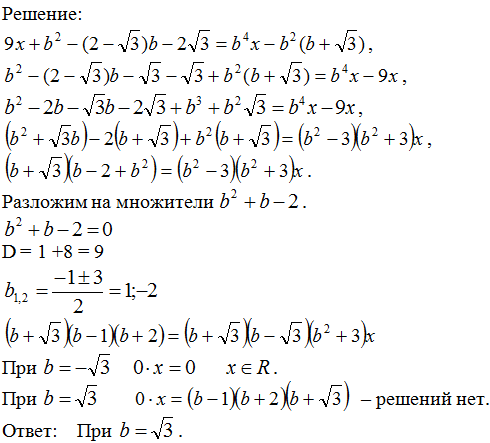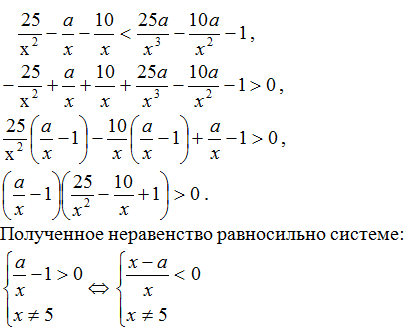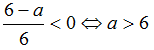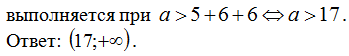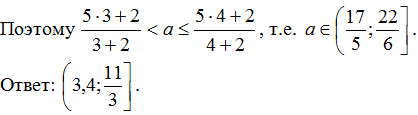Все способы решения параметров егэ

Задачи с параметрами на ЕГЭ по математике

Анна Малкова

Задача с параметрами – одна из самых сложных в ЕГЭ по математике Профильного уровня. Это задание №17.

И знать здесь действительно нужно много.

Лучше всего начать с темы «Элементарные функции и их графики».

Повторить, что такое функция, что такое четные и нечетные функции, периодические, взаимно обратные.

Научиться строить графики всех элементарных функций (и отличать по внешнему виду логарифм от корня квадратного, а экспоненту – от параболы).

Освоить преобразования графиков функций и приемы построения графиков.

И после этого – учимся решать сами задачи №17 Профильного ЕГЭ.

Вот основные типы задач с параметрами:

Что такое параметр? Простые задачи с параметрами

Базовые элементы для решения задач с параметрами

Графический способ решения задач с параметрами

Квадратичные уравнения и неравенства с параметрами

Использование четности функций в задачах с параметрами

Условия касания в задачах с параметрами

Метод оценки в задачах с параметрами 

Вот пример решения и оформления задачи с параметром

Еще одна задача с параметром – повышенного уровня сложности. Автор задачи – Анна Малкова

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 1, задача 18

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 5, задача 18

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 11, задача 18

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 26, задача 18

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 18

И несколько полезных советов тем, кто решает задачи с параметрами:

1. Есть два универсальных правила для решения задач с параметрами. Помогают всегда. Хорошо, в 99% случаев помогают. То есть почти всегда.

— Если в задаче с параметром можно сделать замену переменной – сделайте замену переменной.

— Если задачу с параметром можно решить нарисовать – рисуйте. То есть применяйте графический метод.

2. Новость для тех, кто решил заниматься только алгеброй и обойтись без геометрии (мы уже рассказывали о том, почему это невозможно). Многие задачи с параметрами быстрее и проще решаются именно геометрическим способом.

Эксперты ЕГЭ очень не любят слова «Из рисунка видно…» Ваш рисунок – только иллюстрация к решению. Вам нужно объяснить, на что смотреть, и обосновать свои выводы. Примеры оформления – здесь. Эксперты ЕГЭ также не любят слова «очевидно, что…» (когда ничего не очевидно) и «ёжику ясно…».

3. Сколько надо решить задач, чтобы освоить тему «Параметры на ЕГЭ по математике»? – Хотя бы 50, и самых разных. И в результате, посмотрев на задачу с параметром, вы уже поймете, что с ней делать.

4. Задачи с параметрами похожи на конструктор. Разобрав много таких задач, вы заметите, как решение «собирается» из знакомых элементов. Сможете разглядеть уравнение окружности или отрезка. Переформулировать условие, чтобы сделать его проще.

На нашем Онлайн-курсе теме «Параметры» посвящено не менее 12 двухчасовых занятий. Кстати, оценивается задача 17 Профильного ЕГЭ в 4 первичных балла, которые отлично пересчитываются в тестовые!

Задание № 18 варианта КИМ ЕГЭ по математике профильного уровня

Задача с параметром – для обычного школьника одна из самых сложных задач варианта КИМ ЕГЭ: в программах по математике для общеобразовательных школ (за исключением профильных и специализированных классов, школ и лицеев) таким задачам либо не уделяется должного внимания, либо они не рассматриваются вовсе. Несмотря на это, знание набора методов и подходов к решению таких задач и определенная практика их решения позволяют продвинуться в решении задачи с параметром достаточно далеко и если уж не решить ее полностью, то хотя бы получить за нее некоторое количество баллов на экзамене.

Ранее, до появления единого государственного экзамена, задачи с параметрами входили в варианты вступительных экзаменов по математике в ведущие вузы, а сегодня входят в вариант КИМ ЕГЭ профильного уровня. Дело в том, что эти задачи обладают высокой диагностической ценностью: они позволяют не только определить, насколько хорошо выпускник знает основные разделы школьного курса математики, но и проверить, насколько высок уровень его математического и логического мышления, насколько сильны первоначальные навыки математической исследовательской деятельности, а главное – насколько успешно он сможет овладеть курсом математики в вузе.

«Научите меня решать задачи с параметром», – такую просьбу я часто слышу от своих учеников. Что ж, эта задача потребует от выпускника немало интеллектуальных усилий. С чего начать изучение? С освоения методов решения задач с параметром. Собственно, если вы внимательно читали наши рекомендации, как подготовиться к решению сложных задач варианта КИМ ЕГЭ, то заметили, что это универсальный совет. Именно так построен наш курс «1С:Репетитор»: изучаем как можно более широкий спектр методов и приемов решения задач и тренируемся в применении этих методов на практике.

Чему нужно научиться, решая задачи с параметром

В первую очередь – правильно применять равносильные преобразования уравнений, неравенств и их систем. То есть понять, при каких ограничениях, накладываемых на параметр, можно выполнять то или иное преобразование. Лучше всего начать с заданий вида: «Для каждого значения параметра решить…» и рассмотреть по возможности все основные элементарные функции, встречающиеся в школьном курсе математики.

Если с несложными задачами такого вида школьник справляется неплохо, то можно переходить к изучению аналитических методов решения задач, содержательно усложняя и классифицируя задачи с точки зрения применения к ним этих методов исследования. Имеется в виду знакомство с подходами к решению задач, содержащих формулировки типа: «При каких значениях параметра уравнение (неравенство, система) имеет одно (два, три, бесконечно много и т.д.) решений», «При каких значениях параметра решением уравнения (неравенства, системы) является некоторое подмножество множества действительных чисел» и т.д.

Следующий шаг, который мы рекомендуем, – тщательно изучить схему исследования квадратичной функции. Поскольку квадратичная функция является одной из самых хорошо изученных в школьном курсе математики, на ее основе можно предложить большое количество исследовательских задач, разнообразных по форме и содержанию, чем и пользуются составители вариантов КИМ ЕГЭ.

Мы рекомендуем подойти к рассмотрению данных задач по следующей схеме:

задачи, основанные на свойствах дискриминанта и старшего коэффициента квадратного трехчлена;

применение теоремы Виета в задачах с параметром;

расположение корней квадратного трехчлена относительно заданных точек;

более сложные задачи, сводящиеся к исследованию квадратного трехчлена.

Следующая тема курса – графические методы решения задач с параметром

Существует два принципиально различных подхода – построение графиков функций или уравнений в плоскости (x; y) или в плоскости (x; a). Кроме того, для графического метода решения задач с параметром в плоскости (x; y) необходимо рассмотреть различные виды преобразования графиков – обычно это параллельный перенос, поворот прямой и гомотетия. Есть класс задач, решение которых основано на аналитических свойствах функций (области определения, области значений, четности, периодичности и т.д.), эти свойства и приемы их использования тоже нужно знать.

На этом перечень методов решения задач с параметрами, разумеется, не заканчивается, но анализ вариантов КИМ ЕГЭ профильного уровня и практика показывают, что в настоящее время этого достаточно для успешного решения задачи № 18 на экзамене.

В заключение отметим, что выстроить подобный курс самостоятельно, без преподавателя, обычный школьник не сможет, даже имея под рукой хорошие учебные пособия по методам решения задач с параметром. Здесь необходима помощь опытного наставника, который сможет подобрать нужные задачи и выстроить траекторию движения школьника по ним.

Заметим, кстати, что весьма эффективным инструментом для изучения именно методов решения задач с параметром являются интерактивные тренажеры с пошаговым разбором решения.

Работая с таким тренажером, школьник одновременно учится выстраивать логику решения задачи с параметром и контролирует правильность выполнения каждого шага решения. Это очень важное умение, так как одна из основных сложностей в решении задачи с параметром состоит в том, что необходимо на каждом шаге решения понимать, что означают уже полученные результаты и что (в зависимости от этих результатов) еще остается сделать, чтобы довести решение до конца.

Регулярно тренируйтесь в решении задач

Чтобы начать заниматься на портале «1С:Репетитор», достаточно Зарегистрироваться.
Вы можете:

• Начать заниматься бесплатно.
• 
  Купить доступ к этой задаче в составе
  экспресс-курса «Алгебра» и научиться решать задачи №13, №15, №17, №18 и №19 на максимальный балл.

Все курсы состоят из методически правильной последовательности теории и практики, необходимой для успешного решения задач. Включают теорию в форме текстов, слайдов и видео, задачи с решениями, интерактивные тренажеры, модели, и тесты.

Остались вопросы? Позвоните нам по телефону 8 800 551-50-78 или напишите в онлайн-чат.

Цель данной работы – изучение различных способов решения задач с параметрами.
Возможность и умение решать задачи с параметрами демонстрируют владение методами
решения уравнений и неравенств, осмысленное понимание теоретических сведений,
уровень логического мышления, стимулируют познавательную деятельность. Для
развития этих навыков необходимы длительнее усилия, именно поэтому в профильных
10-11 классах с углубленным изучением точных наук введен курс: “Математический
практикум”, частью которого является решение уравнений и неравенств с
параметрами. Курс входит в число дисциплин, включенных в компонент учебного
плана школы.

Успешному изучению методов решения задач с параметрами могут помочь
элективный или факультативный курсы, или компонент за сеткой по теме: “Задачи с
параметрами”.

Рассмотрим четыре больших класса задач с параметрами:

1. Уравнения, неравенства и их системы, которые необходимо решить для
   любого значения параметра, либо для значений параметра, принадлежащих
   определенному множеству.
2. Уравнения, неравенства и их системы, для которых требуется определить
   количество решений в зависимости от значения параметра.
3. Уравнения, неравенства и их системы, для которых требуется найти все те
   значения параметра, при которых указанные уравнения (системы, неравенства)
   имеют заданное число решений.
4. Уравнения, неравенства и их системы, для которых при искомых значениях
   параметра множество решений удовлетворяет заданным условиям в области
   определения.

Методы решений задач с параметрами.

1. Аналитический метод.

Это способ прямого решения, повторяющий стандартные процедуры нахождения
ответа в задачах без параметра.

Пример 1. Найдите все значения параметра
a, при которых уравнение:

(2a – 1)x² + ax + (2a – 3) =0  имеет не более
одного корня.

Решение:

При 2a
– 1 = 0 данное уравнение квадратным не является, поэтому случай
a =1/2 разбираем отдельно.

Если a = 1/2, то уравнение принимает вид
1/2x – 2 = 0, оно имеет один корень.

Если a ≠ 1/2,
то уравнение является квадратным; чтобы оно имело не более одного корня
необходимо и достаточно, чтобы дискриминант был неположителен:

D = a² – 4(2a – 1)(2a – 3) = -15a²
+ 32a  – 12;

Чтобы записать окончательный ответ, необходимо понять,

2. Графический метод.

В зависимости от задачи (с переменной x
и параметром a)
рассматриваются графики в координатной плоскости (x;y)
или в плоскости (x;a).

Пример 2. Для каждого значения параметра a
определите количество решений уравнения
.

Решение:

Заметим, что количество решений уравнения
 
равно количеству точек пересечения графиков функций

и y = a.

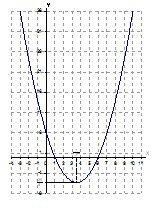
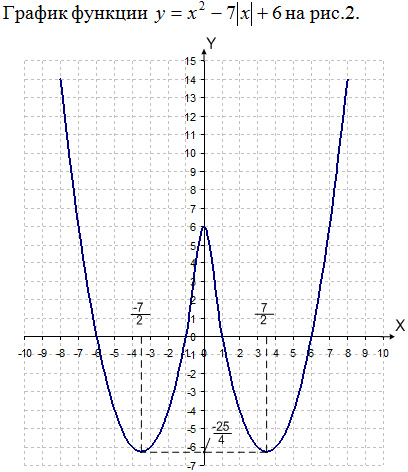
График функции

показан на рис.1.

Рис.1

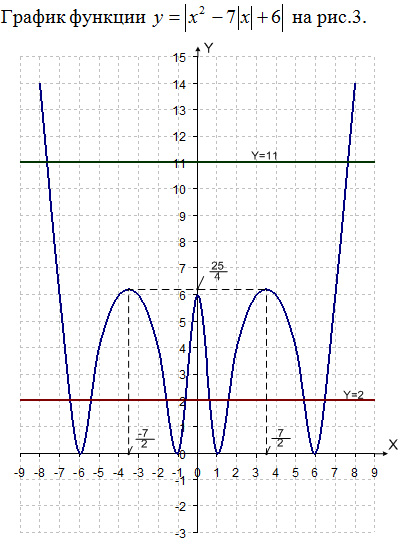
Рис. 2

Рис. 3

y = a – это горизонтальная прямая. По графику несложно
установить количество точек пересечения в зависимости от a
(например, при  a =
11 – две точки пересечения; при a
= 2 – восемь точек пересечения).

Ответ: при a < 0 – решений нет; при a
= 0 и a = 25/4  – четыре решения; при
0 < a < 6  – восемь решений; при a
= 6 – семь решений; при

6 < a < 25/4 – шесть решений; при a >
25/4 – два решения.

3. Метод решения относительно параметра.

При решении этим способом переменные х и а принимаются
равноправными, и выбирается та переменная, относительно которой аналитическое
решение становится более простым. После упрощений нужно вернуться к исходному
смыслу переменных х и а и закончить решение.

Пример 3. Найти все значения параметра а , при каждом из которых
уравнение

= —ax +3a +2  имеет единственное решение.

Решение:

Будем решать это уравнение заменой переменных. Пусть

= t , t ≥ 0
, тогда x = t² + 8  и
уравнение примет вид at² + t + 5a – 2 = 0
 . Теперь задача состоит в том, чтобы найти все а,
при которых уравнение at² + t + 5a – 2 =
0  имеет единственное неотрицательное решение. Это имеет
место в следующих случаях.

1) Если а = 0, то уравнение имеет единственное решение t
= 2.

Решение некоторых типов уравнений и неравенств с параметрами.

Задачи с параметрами помогают в формировании логического мышления, в
приобретении навыков исследовательской деятельности.

Решение каждой задачи своеобразно и требует к себе индивидуального,
нестандартного подхода, поскольку не существует единого способа решения таких
задач.

Ⅰ. Линейные уравнения.

Задача № 1.
При каких значениях параметра b
уравнение

не имеет корней?

Ⅱ. Степенные уравнения, неравенства и их системы.

Задача №2. Найти все значения параметра a,
при которых множество решений неравенства:

содержит число 6, а также содержит два отрезка длиной 6, не имеющие общих точек.

Решение:

.

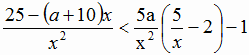
Преобразуем обе части неравенства.

Для того, чтобы множество решений неравенства содержало число 6, необходимо и
достаточно выполнение условия:

Рис.4

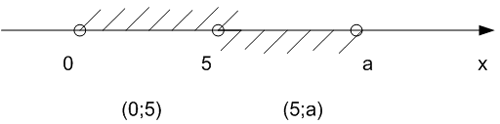
При a > 6 множество
решений неравенства:
.

Интервал (0;5) не может содержать ни одного отрезка
длины 6. Значит, два непересекающихся отрезка длины 6 должны содержаться в
интервале (5; a).

Это

Ⅲ. Показательные уравнения, неравенства и системы.

Задача № 3. В области определения функции
взяли
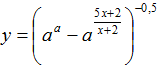
все целые положительные числа и сложили их. Найти все значения, при которых
такая сумма будет больше 5, но меньше 10.

Решение:

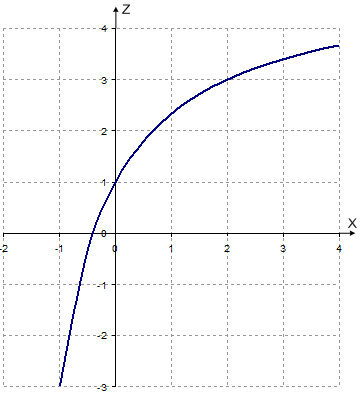
1) Графиком дробно-линейной функции
   
является гипербола. По условию x > 0. При
неограниченном возрастании х дробь

монотонно убывает и приближается к нулю, а значения функции z возрастают
и приближаются к 5. Кроме того, z(0) = 1.

Рис. 5

2) По определению степени область определения D(y)
состоит из решений неравенства
.
При a = 1 получаем неравенство, у которого решений
нет. Поэтому функция у нигде не определена.

3) При 0 < a < 1 показательная функция с
основанием а убывает и неравенство
 
равносильно неравенству

. Так как x > 0 , то z(x) >
z(0) = 1 . Значит, каждое положительное значение х
является решением неравенства

. Поэтому для таких а указанную в условии сумму нельзя найти.

4) При a > 1 показательная функция с основанием
а возрастает и неравенство
 
равносильно неравенству

. Если a  ≥ 5,
то любое положительное число является его решением, и указанную в условии сумму
нельзя найти. Если 1 < a < 5, то множество
положительных решений – это интервал (0;x₀)
, где a = z(x₀) .

5) Целые числа расположены в этом интервале подряд, начиная с 1. Вычислим
суммы последовательно идущих натуральных чисел, начиная с 1 : 1; 1+2 = 3; 1+2+3
= 6; 1+2+3+4 = 10;… Поэтому указанная сумма будет больше 5 и меньше 10, только
если число 3 лежит в интервале (0;x₀),
а число 4 не лежит в этом интервале. Значит, 3 < x₀
≤ 4 . Так как

 
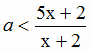
возрастает на
,
то z(3) < z(x₀)
≤ z(4) .

Решение иррациональных уравнений и неравенств, а также уравнений, неравенств
и систем, содержащих модули рассмотрены в Приложении 1.

Задачи с параметрами являются сложными потому, что не существует единого
алгоритма их решения. Спецификой подобных задач является то, что наряду с
неизвестными величинами в них фигурируют параметры, численные значения которых
не указаны конкретно, но считаются известными и заданными на некотором числовом
множестве. При этом значения параметров существенно влияют на логический и
технический ход решения задачи и форму ответа.

По статистике многие из выпускников не приступают к решению задач с
параметрами на ЕГЭ. По данным ФИПИ всего 10% выпускников приступают к решению
таких задач, и процент их верного решения невысок: 2–3%,
поэтому приобретение навыков решения трудных, нестандартных заданий, в том числе
задач с параметрами, учащимися школ по-прежнему остается актуальным.

Научно-образовательный форум школьников Республики Мордовия

Лицей федерального государственного бюджетного образовательного учреждения высшего образования «Национальный исследовательский Мордовский государственный университет им. Н.П. Огарёва»

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА

МЕТОДЫ РЕШЕНИЯ ЗАДАЧ С ПАРАМЕТРАМИ 

Секция: Математический калейдоскоп

Автор работы:	Ехлаков Д. Н.
	10 класс Лицей МГУ им. Н. П. Огарева
Руководитель работы:	Кубанцева А. В.
	учитель математики Лицей МГУ им Н. П. Огарева

Саранск

2021

СОДЕРЖАНИЕ

	Введение	3
1	Теоретическая часть	6
	1.1	Основные понятия	6
	1.2	Основные типы задач с параметром	7
	1.3	Методы решения задач с параметрами	9
2	Практическая часть
	2.1	Примеры решения задач с параметрами ЕГЭ по математике профильного уровня
	Заключение
	Список использованных источников

Введение

Задачи с параметрами являются одним из самых трудных разделов школьного курса математики, так как их решение связано с умением проводить сложные, разветвленные логические построения. В школе первые представления о параметре мы получаем при изучении прямой пропорциональности; линейной функции и линейного уравнения; при изучении квадратного уравнения и исследования количества его корней в зависимости от значений параметра.

Актуальность выбранной темы обусловлена тем, что затрагивает современную проблему, знакомую каждому выпускнику, а именно – решение задач единого государственного экзамена. Сдать ЕГЭ на высший балл – одно из самых актуальных желаний старшеклассников, так как это прямым образом влияет на шансы поступить в престижный ВУЗ и получение желаемой профессии. Добиться этого довольно непросто. Учебного времени не всегда хватает для углубленной подготовки к заданиям высокого уровня сложности, к одним из которых относятся уравнения и неравенства с параметрами.

Анализ предыдущих результатов ЕГЭ показывает, что школьники с большим трудом решают задания с параметром, а многие даже не приступают к ним. К решению задачи №18 из КИМ приступают лишь порядка 10% выпускников 11 классов. Причиной этого является отсутствие системы знаний по данной теме.

Статистика решения задачи №18 на ЕГЭ по профильной математике

Год	Проверяемые требования	Уровень сложности задания	Максимальный балл за выполнение задания	Средний процент выполнения
2017	Умение решать уравнения и неравенства, содержавшие параметр	Высокий уровень сложности	4	0,38
2018	1,2
2019	4,8
2020	2,4

В школьных учебниках по математике задач с параметрами недостаточно, к тому же, предлагаемые в них примеры слишком просты по сравнению с задачами из ЕГЭ. Поэтому исследование способов решения задач с параметрами является для меня одним из важных шагов в подготовке к единому государственному экзамену по математике профильного уровня. Рассматривая проблему решения 18-го задания по ЕГЭ, хочу определить самый рациональный способ, а точнее, наименее трудоемкий, менее время затратный и удобный метод решения задач с параметрами.

Цель работы заключается в исследование методов решения задач с параметрами и выявление наиболее рациональных, наименее трудоемких способов решения.

Для достижения поставленной цели необходимо решить следующие задачи:

1. познакомится с определением параметра и видами задач, содержащие параметры;
2. исследовать способы решения задач с параметрами и постараться выбрать из них для себя самые оптимальные;
3. приобрести опыт в решении задач, содержащиеся в ЕГЭ по профильной математике.

Гипотеза моего исследования заключается в том, что существуют общие методы решения заданий с параметрами, позволяющие решать задания разных видов.

Объект исследования: задания контрольно-измерительных материалов единого государственного экзамена по математике, содержащие параметр.

Предмет исследования: методы решения заданий с параметрами.

Методы исследования – теоретический анализ и синтез научной и учебной литературы по теме исследования, сравнение, систематизация информации, обобщение, вывод, подбор и решение задач.

Практическая значимость – возможность использования обобщенных данных при подготовке выпускников к сдаче единого государственного экзамена по математике профильного уровня, отработка решения задач, содержащих параметры.

1. Теоретическая часть

1. Основные понятия

Параметром называется независимая переменная, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.

Что означает «решить задачу с параметром»? Естественно, это зависит от вопроса в задаче. Если, например, требуется решить уравнение, неравенство, их систему или совокупность, то это означает предъявить обоснованный ответ либо для любого значения параметра, либо для значения параметра, принадлежащего заранее оговоренному множеству.

Если же требуется найти значения параметра, при которых множество решений уравнения, неравенства и т. д. удовлетворяет объявленному условию, то, очевидно, решение задачи и состоит в поиске указанных значений параметра.

Одним из способов решения задания №18 из ЕГЭ является графический способ, поэтому следует повторить что такое функция, виды функций и их свойства. Понятие функции – одно из ключевых в математике. Под функцией понимают некий закон, по которому одна переменная величина зависит от другой. Согласно определению, если каждому значению переменной х множества Х ставится в соответствие одно определенное значение переменной у множества Y, то такое соответствие называется функцией. Другое определение – однозначное соответствие двух переменных величин на множестве действительных чисел R называется функцией. Существует всего пять типов элементарных функций: степенные, показательные, тригонометрические, обратные тригонометрические.

1. Основные типы задач с параметрами

Выделяют основные 4 больших класса задач с параметрами:

• Уравнения, неравенства, их системы и совокупности, которые необходимо решить либо для любого значения параметра (параметров), либо для значений параметра, принадлежащих заранее оговоренному множеству.

Этот тип задач является базовым при овладении темой «Задачи с параметрами», поскольку вложенный труд предопределяет успехи при решении задач всех других основных типов.

• Уравнения, неравенства, их системы и совокупности, для которых требуется определить количество решений в зависимости от значения параметра (параметров).

При решении задач данного типа нет необходимости ни решать заданные уравнения, неравенства, их системы и совокупности и т. д., ни приводить эти решения; такая лишняя в большинстве случаев работа является тактической ошибкой, приводящей к неоправданным затратам времени. Однако не стоит абсолютизировать сказанное, так как иногда прямое решение в соответствии с типом 1 является единственным разумным путем получения ответа при решении задачи типа 2.

• Уравнения, неравенства, их системы и совокупности, для которых требуется найти все те значения параметра, при которых указанные уравнения, неравенства, их системы и совокупности имеют заданное число решений (в частности, не имеют или имеют бесконечное множество решений). Легко увидеть, что задачи типа 3 в каком-то смысле обратны задачам типа 2.
• Уравнения, неравенства, их системы и совокупности, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.

Например, найти значения параметра, при которых:

1) уравнение выполняется для любого значения переменной из заданного промежутка;

2) множество решений первого уравнения является подмножеством множества решений второго уравнения и т. д.

Наиболее массовый класс задач с параметром – задачи с одной неизвестной и одним параметром.

1.3 Методы решения задач с параметром

В пособиях, посвященных задачам с параметрами, выделяют три метода решений:

• Аналитический метод: это способ прямого решения, повторяющий стандартные процедуры нахождения ответа в задачах без параметра.
• Графический метод: в зависимости от задачи (с переменной x и параметром a) рассматриваются графики или в координатной плоскости (x; y), или в координатной плоскости (x; a).  
• Метод решения относительно параметра: при решении этим способом переменные х и а принимаются равноправными, и выбирается та переменная, относительно которой аналитическое решение становится более простым. После упрощений нужно вернуться к исходному смыслу переменных х и а и закончить решение.

Иногда также применяется так называемый метод оценки для уравнений и неравенств, где функции, стоящие в левой и правой части, могут быть равны друг другу только в определенной точке, причем одна из них принимает в этой точке наименьшее значение, а другая – наибольшее.

При рассмотрении данных методов я пришел к выводу, что самые распространенные и удобные способы – это аналитический и графический. Рассмотрим их более подробно.

Графический способ. В зависимости от того, какая роль параметру отведена в задаче, можно соответственно выделить два основных графических приёма:

• первый – построение графика на координатной плоскости (х;у),
• второй – построение графика на координатной плоскости на (х;а).

На плоскости (х;у) или (х;а)  функция y=f(x;a) задаёт семейство кривых, зависящих от параметра а. Понятно, что каждое семейство f обладает определёнными свойствами. Нас же в первую очередь будет интересовать с помощью какого преобразования плоскости (параллельный перенос, поворот и т.д.) можно перейти от одной прямой к какой-нибудь другой.

Разумеется, не всегда графический образ семейства y=f(x;a) описывается простым преобразованием. Графический метод — всего лишь одно из средств наглядности. Поэтому те случаи, когда результат «прочитан» с рисунка и вызывает сомнение, лучше подкрепить аналитически.

Алгоритм решения задачи с параметром графическим способом состоит из следующих шагов:

1. задачу с параметром будем рассматривать как функцию ; п
2. строим графический образ, т.е. Построим в одной системе координат графики обеих частей уравнения;
3. пересекаем полученное изображение прямыми, параллельными оси абсцисс;
4. считываем нужную информацию.

Если уравнение одной из фигур не зависит от изменяющегося параметра, то график этой фигуры неподвижен относительно системы координат. Если в уравнение другой фигуры входит параметр, то от его изменения зависит расположение и даже форма графика. Тогда суть решения уравнения состоит в определении числа точек пересечения графиков построенных уравнений, а значит в определении количества возможных решений в зависимости от конкретных числовых значений параметра.  Для усложнения заданий эти уравнения искусственно преобразуют, «камуфлируют». Понятно, что каждое семейство обладает определенными характерными свойствами, они-то и помогают решить задачу.  Приведем несколько примеров.  

Аналитический способ. Это способ прямого решения, повторяющий стандартные процедуры нахождения ответа в задачах без параметра.

Широкое распространение за последние годы в ходе государственной (итоговой) аттестации выпускников средней школы  в формате ЕГЭ и на вступительных экзаменах в вузы, предъявляющие повышенные требования к математической подготовке абитуриентов, получили задачи на расположения корней квадратного трехчлена на оси. Для данного типа задач свойствен аналитический метод решения.

Выделим два наиболее распространенных вида задач, связанных с применением графика квадратичной функции. Первый вид – задачи, в которых изучается расположение корней квадратного трехчлена относительно точки с абсциссой, равной m. Второй вид – задачи, в которых выясняется, как расположены корни квадратного трехчлена относительно отрезка.

Первый тип задач предусматривает три случая:

• оба корня меньше m;
• один корень меньше m, а другой больше;
• оба корня больше m.

Для каждого из этих случаев выполним соответствующий рисунок и запишем к нему систему неравенств при условии, что старший коэффициент квадратного трехчлена f (x) = ax2 + bx + c положительный.  В таблице приведена полная система случаев расположения корней уравнения в зависимости от значений выражений, зависящих от коэффициентов уравнения.

Расположение корней квадратного трехчлена относительно точки с абсциссой, равной  

	Один корень меньше m, а другой больше: Условие  обеспечивает положительный коэффициент перед  (направленность ветвей параболы вверх); Условие  обеспечивает: наличие корней квадратного трехчлена; расположение точки m между корнями.
	Оба корня больше m: Условие  обеспечивает положительный коэффициент перед ; Условие  обеспечивает расположение точки m вне отрезка между корнями; Условие  обеспечивает наличие корней уравнения; Условие   обеспечивает расположение точки m левее отрезка между корнями.
	Оба корня меньше m:  Условие  обеспечивает положительный коэффициент перед ; Условие  обеспечивает расположение точки m вне отрезка между корнями;   Условие  обеспечивает наличие корней уравнения; Условие  обеспечивает расположение точки m правее отрезка между корнями.

Рассмотрим расположение корней квадратного трёхчлена относительно отрезка. При этом возможны шесть случаев:

• корни квадратного трёхчлена находятся справа от отрезка;
• корни квадратного трёхчлена находятся слева от отрезка;
• больший корень находится внутри отрезка  
• меньший корень находится внутри отрезка;
• оба корня внутри отрезка;
• отрезок между корнями квадратного трехчлена

Изобразим геометрическую модель каждой из этих ситуаций и составим к каждой из них адекватную систему неравенств при условии, что старший коэффициент квадратичной функции y = ax2 + bx + c больше нуля.

Расположение корней квадратного трёхчлена относительно отрезка

	Корни квадратного трёхчлена находятся справа от отрезка: Условие  обеспечивает нахождение корней вне отрезка между корнями; Условие  обеспечивает наличие двух корней квадратного трёхчлена; Условие  обеспечивает расположение отрезка левее абсциссы вершины.
	Корни квадратного трёхчлена находятся слева от отрезка: Условие  обеспечивает расположение корней вне отрезка между корнями; Условие  обеспечивает наличие корней уравнения; Условие  обеспечивает расположение точки m правее отрезка между корнями.
	Больший корень находится внутри отрезка: Условие  обеспечивает расположение точки m внутри отрезка между корнями; Условие  обеспечивает расположение корней вне отрезка меду корнями.
	Меньший корень находится внутри отрезка:   Условие  обеспечивает расположение точки p внутри отрезка между корнями;   Условие  обеспечивает расположение точки m вне отрезка между корнями.
	Оба корня внутри отрезка: Условие  обеспечивает расположение точки m вне отрезка между корнями; Условие  обеспечивает расположение точки p вне отрезка между корнями; Условие  обеспечивает наличие корней уравнения; Условие  обеспечивает расположение вершины параболы между концами отрезка.
	Отрезок между корнями квадратного трехчлена:   Условие  обеспечивает расположение точки p внутри отрезка между корнями;   Условие  обеспечивает расположение точки m вне отрезка между корнями.

1. Практическая часть

2.1 Примеры решения задач с параметрами ЕГЭ по математике профильного уровня

В ходе исследования я понял, что наиболее универсальным и наглядными для меня оказались графический и аналитический способы решения задач с параметрами. Далее предлагаю провести разбор некоторых задач прошлых лет ЕГЭ по математике профильного уровня.

Пример №1.

Найдите все значения , при каждом из которых система неравенств  имеет хотя бы одно решение на отрезке [4; 5].

Преобразуем систему:  

Построим прямоугольную систему координат xOa. Изобразим множество точек, координаты которых удовлетворяют системе неравенств.

Гипербола  и график корня пересекаются в точке N(3; 2). Гипербола и прямая  пересекаются в точке M(5; 1). График корня и прямая пересекаются в точке K(6; 4). Множество точек, координаты которых удовлетворяют заданной системе состоит из точек криволинейного треугольника NMK, не включая границу, лежащую на прямой КМ.

Поскольку система должна иметь хотя бы одно решение на отрезке [4; 5], определим наименьшую и наибольшую ординаты проекции выделенного на рисунке четырехугольника на ось ординат.

Найдём координаты точки P:

 =>

 

Проекции точек P и M дают искомое множество: заданная система неравенств имеет хотя бы одно решение на отрезке [4; 5] при  (выделено штриховкой на рисунке).

Ответ: (1;

Пример №2.

Найдите все значения , при каждом из которых имеет ровно три различных решения система уравнений

Первое уравнение системы является уравнением окружности с центром в точке  и радиусом 3. График функции  получается параллельным переносом на вектор  графика функции  Поскольку график функции  представляет собой прямой угол с вершиной в точке  и сторонами лежащими на прямых  и  выше оси абсцисс, график функции  также представляет собой прямой угол, но с вершиной в точке  и сторонами, параллельными прямым  Заметим, что прямая  на которой лежит вершина угла, является касательной к окружности.

Ровно три общие точки фигуры имеют в следующих случаях:

1. Вершина прямого угла лежит в точке  касания окружности и прямой , а его стороны пересекают окружность в двух точках (первый случай). Это возможно, только если .

2. Одна из сторон прямого угла пересекает окружность в двух точках, а другая касается окружности в точке  (второй случай) или в точке (третий случай). Найдём значения параметра для этих двух случаев. Поскольку радиус окружности, проведённый в точку касания окружности и прямой, перпендикулярен прямой, четырёхугольник  является квадратом со стороной и диагональю . Тогда . Следовательно, для случая касания в точке  получаем  Для касания стороны угла и окружности в точке  аналогично получаем ещё одно значение параметра:  

При  или  прямой угол имеет не более двух общих точек с окружностью.

При  или  прямой угол имеет четыре общие точки с окружностью.

Ответ:

Пример №3.

Найдите все значения параметра  при каждом из которых уравнение  имеет хотя бы одно решение на интервале (0;

Обозначим в исходном уравнении  .

Пример №4.  

Найдите все значения , при каждом из которых уравнение меет ровно два различных корня на промежутке

Сделаем замену тогда получим: .

Выполним обратную замену:  =>  Дискриминант этого уравнения равенпоэтому оно при всех значениях  имеет ровно два различных корня. Положим  Так как  оба корня уравнения  принадлежат промежутку  тогда и только тогда, когда  и  то есть когда  и Значит, уравнение  имеет ровно два различных корня на промежутке  при

Ответ:

Пример №5.

Найдите все значения , при каждом из которых уравнение  имеет ровно один корень на отрезке

Преобразуем уравнение:  => Рассмотрим эти случаи:

Первый случай:  при условиях:

=>  

Число  лежит на отрезке  если  Тогда для первого случая получаем: .

Второй случай:  при условии :

 => =>

Число  лежит на отрезке , если  Тогда для второго случая получаем:

Корень  равен  если

Итак, исходное уравнение имеет ровно один корень на отрезке  при   

Ответ:   

Пример №6.

Найдите все значения , для каждого из которых уравнение  имеет единственное решение.

Аналитический способ решения:

;

Пусть   = t >0, тогда:  

(*)

Исходное уравнение будет иметь единственное решение:

1 случай: еcли уравнение (*) имеет единственное решение (D=0);

2 случай: если уравнение (*) имеет два корня (D>0), один из которых меньше нуля или равен нулю.

Пусть n=a+6, m=5+3|a|;

1 случай:

 =>  =>  =>  => ;

если a<0, то  => ; если a>0, то  => .

2 случай:

; ;

если n>m, то:

  ;

если n

; ;

 система не имеет решений, т.к. выражение 3|a|+5 всегда положительно.

 =>  =>

или  =>  =>

или  =>   => система не имеет решений.

Ответ:  ;  ; .

Графический способ:

Преобразуем исходное уравнение:

 =>
 =>   или .

Построим графики функций   на координатной плоскости xOa:

На чертеже заметим, что система имеет единственное решение при ,  и . Найдём  и :

Если a>0, то:  => => .

Если а<0, то: =>  => .

Ответ:  ;  ; .

Важно помнить:

• при использовании только графического метода, так же, как и только аналитического, может быть допущена ошибка, поэтому необходимо последовательно и внимательно указывать ход своего решения. При возможности выполнить проверку полученного результата, применяя другой способ решения;
• ответ, полученный только с помощью графика, может быть сомнителен, поэтому необходимо подкрепить его с помощью аналитического вывода, что в первую очередь подтвердит правоту выбранного пути решения и полученный ответ.

Заключение

Работая над своей темой исследования, я провел большую работу: изучил литературу по выбранной теме; разобрался, что такое параметр и задачи с параметрами; познакомился с методами их решения.

Выполняя практическую часть, было решено много уравнений, неравенств и их систем, я приобрел опыт и научился решать определённый круг задач и пришёл к некоторым выводам.

Решение каждого задания требует к себе индивидуального подхода, но при этом задачи с параметрами чем-то похожи на детский конструктор. Разобрав много таких примеров, можно заметить, как решение «собирается» из мелких деталей – хорошо знакомых нам фактов.

Для себя я выделил два основных способа решения №18 из ЕГЭ: аналитический и графический.

Графический способ является наиболее наглядным, простым и доступным способом решения задач с параметрами. Если задачу с параметром можно нарисовать – рисуем. То есть применяем графический метод. Размытость в решение уравнения, неравенства или их системы с помощью графика, можно подкрепить аналитическим выводом, что поможет подтвердить правоту выбранного решения и ответа.

Сочетание аналитического способа решения с графической интерпретацией полученных результатов позволяет сделать процесс решения уравнений с параметрами более осознанным, способствуя при этом формированию элементов исследовательской деятельности.

Думаю, что данная работа будет интересна моим сверстникам. Задачи с параметрами помогают в формировании логического мышления, в приобретении навыков исследовательской деятельности. Возможность и умение решать задачи с параметрами демонстрируют владение методами решения уравнений и неравенств, осмысленное понимание теоретических сведений, уровень логического мышления, стимулируют познавательную деятельность.

Список использованных источников