|
§3. Простой категорический силлогизм |
113 |
|
Правильность силлогизма не |
зависит от его содержания, |
|
а зависит только от его формы. |
Теперь мы можем дать уже более точное определение силлогизма:
Простым категорическим силлогизмом называется умозаключение, в котором от наличия некоторых отношений между терминами S и М и терминами Р и М, фиксируемых в посылках, приходят к заключению о наличии определенного отношения между терминами S и Р.
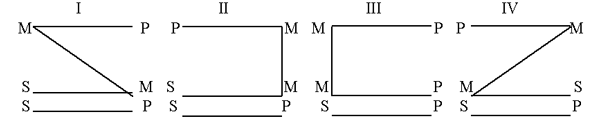
Все силлогизмы можно разделить по фигурам (рис. 28). Посылки обозначаются горизонтальными линиями, а наклонные и вертикаль-
|
ные линии соединяют средний термин в посылках: |
|||||||||||||
|
1-я фигура |
2-я фигура |
3-я фигура |
4-я фигура |
||||||||||
|
М |
Р P |
M M |
P |
P |
M |
||||||||
S M S M M S M S
Рис. 28
Фигурой называется множество силлогизмов, имеющих одну
иту же структуру, определяемую расположением среднего термина
впосылках.
Каждаяизэтихфигур, кромечетвертой, имеетсобственнуюпознавательную ценность.
По первой фигуре решают задачи, требующие подведения частного случая под общее правило.
Все преступления являются правонарушениями. Кража – преступление.
Кража является правонарушением.
Вторую фигуру используют для опровержения каких-либо выводов.
Все законопослушные граждане уважают чужие права. Воры и мошенники не уважают чужие права.
Воры и мошенники не являются законопослушными гражданами.

Третья фигура помогает обосновать частный случай или исключение из общих правил.
Клевета есть преступление против свободы, чести и достоинства личности.
Клевета есть правонарушение.
Некоторые правонарушения есть преступления против свободы, чести и достоинства личности.
Если в фигуре силлогизма указать тип суждений, стоящих на местах посылок и заключений, то получим разновидность данной фигуры, называемую модусом силлогизма.
Например, для 1-й фигуры это ААА, ЕАЕ, АII, EIO.
Всего их насчитывается 256 (по 64 модуса для каждой фигуры). Однако не все модусы представляют собой правильные умозаключения.
Правильных модусов всего лишь 24 (по 6 на каждую фигуру). Из них выделяется 19 сильных модусов.
Понятие модуса было разработано в Средние века. По-видимому, тогдажеимбылиданыназвания. Так, сильныемодусыпервойфигуры называются Barbara, Celarent, Darii, Ferio. Гласные буквы в этих названиях указывают на типы суждений, играющих соответственно роль большей посылки, меньшей посылки и заключения.
В наше время понятие модуса представляет чисто исторический интерес и не используется в анализе силлогизмов.
Для решения задачи отделения правильных силлогизмов от неправильных в логике сформулированы общие правила силлогизма. Нарушение хотя бы одного из этих правил приводит к неправильности силлогизма, соблюдение всех правил говорит о том, что силлогизм правильный.
Правила силлогизма делятся на правила терминов и правила посылок.
Правила терминов
1. Всиллогизмедолжнобытьтолькотритермина. Снарушением этого правила связана ошибка, называемая «учетверение термина». Она возникает тогда, когда один термин употребляется в разных смыслахиполучается, чтозаоднимсловомстоятдвапонятия. Напри-
|
§3. Простой категорический силлогизм |
115 |
мер, «Человек со временем полетит на Марс. Иванов – человек. Следовательно, Иванов со временем полетит на Марс». Слово «человек» употреблено в первой посылке в собирательном смысле, а во второй –
внесобирательном. Получается, что это два разных понятия.
2.Средний термин должен быть распределен по крайней мере
водной из посылок. Возьмем простой пример:
Некоторые змеи ядовиты. Уж – змея.
?
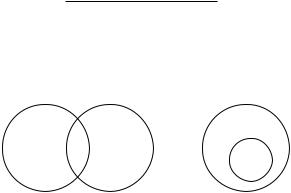
Следует ли из этих посылок, что уж ядовит? Очевидно, что такой выводбылбыложен. Покажемнакруговыхсхемах, какраспределены термины в посылках (рис. 29).
1-я посылка 2-я посылка
ЗМЕЯ
|
ЗМЕИ |
ЯДОВИТЫЕ |
|
|
СУЩЕСТВА |
УЖ |
|
Рис. 29
Термин «змея» не распределен ни в одной из посылок, и он никак не связывает два других понятия – «уж» и «ядовитые существа». На схемах наглядно видно, что объем понятия «уж» может как входить, так и не входить в объем понятия «ядовитые существа».
3. Если термин не распределен в посылках, то он не должен быть распределенвзаключении. Обэтомправилемыужеупоминаливсвязи с обращением. Его нарушение ведет к недопустимому расширению информации.
Правила посылок
1.Из двух отрицательных посылок нельзя вывести никакого заключения.
2.Если одна из посылок отрицательная, то и заключение должно быть отрицательным.
3.Из двух частных посылок нельзя вывести никакого заключения.
4.Если одна из посылок частная, то и заключение должно быть частным.

Кроме общих правил силлогизма существуют специальные правила фигур, которые носят вспомогательный характер.
Для 1-й фигуры: a) большая посылка должна быть общей;
b)меньшая посылка должна быть утвердительной.
Для 2-й фигуры: a) большая посылка должна быть общей;
b) однаизпосылокдолжнабытьотрицательной.
Для 3-й фигуры: a) меньшая посылка должна быть утвердительной;
b) заключение должно быть частным.
Для 4-й фигуры: a) если большая посылка – утвердительное суждение, то меньшая посылка должна быть общим суждением;
b)если одна из посылок – отрицательное суждение, то большая посылка должна быть общим суждением;
c)при утвердительной меньшей посылке заключение должно быть частным.
Четвертая фигура редко применяется в практике рассуждений.
Итак, для полного анализа силлогизма нам необходимо:
•записать посылки и заключение в виде стандартных категорических суждений;
•определить термины силлогизма;
•составить круговые схемы для посылок и заключения и определить по ним распределенность терминов;
•проверить силлогизм на соответствие правилам;
•сделать вывод (правильный силлогизм или нет).
Покажем это на примере.
Все, кто любит театр, ходят в театр часто. Мы ходим в театр часто.
Мы любим театр.
Меньший термин – «мы», больший – «те, кто любит театр», сред-
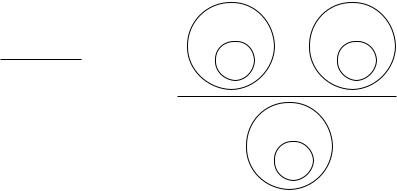
ний – «те, кто ходит в театр часто». Стандартнаясхемаданного силлогизма (рис. 30) такова:
|
§4. Сокращенные и сложные силлогизмы |
117 |
Все Р есть М.
|
М– |
М– |
|
Все S есть М. |
|
|
P+ |
S+ |
Все S есть Р .
P–
S+
Рис. 30
На круговых схемах мы можем видеть, что М – средний термин – не распределен ни в одной из посылок. Это свидетельствует о нарушении второго правила терминов. Следовательно, данный силлогизм является неправильным.
§4. СОКРАЩЕННЫЕ И СЛОЖНЫЕ СИЛЛОГИЗМЫ
В логике выделяют четыре вида сокращенных, сложных и сложносокращенных силлогизмов: энтимема, эпихейрема, полисиллогизм и сорит.
Энтимемы
На практике мы часто выражаем свои мысли не в виде полного силлогизма, а пропуская некоторые посылки (в силу их очевидности) или даже заключение.
Умозаключения, в которых пропущена одна из посылок или заключение, называются энтимема (от греч. en tyme – в уме).
Чтобы убедиться в логической правильности рассуждения, выраженного в форме энтимемы, нужно восстановить ее до полного силлогизмаипроверить, соответствуетлионаправилам. Восстановление проводится в несколько шагов:
1. Нужно определить, что пропущено: посылка или заключение. (Как правило, бывает пропущена одна из посылок).

2.Определив заключение, можно тем самым определить меньший
ибольший термины силлогизма.
3.На основе имеющихся терминов и одной посылки можно определить средний термин.
4.С помощью уже определенных терминов, используя правила фигур, можно построить пропущенную посылку. При этом надо помнить, что она должна быть истинным суждением.
5.Восстановить полный силлогизм и проверить его по правилам силлогизма.
Рассмотрим пример: «Петров – юрист, потому что он знает законы».
Предложение «Петров – юрист» является заключением, так как втораячастьэнтимемы«Он(Петров) знаетзаконы» служитобоснованием первой. Итак, у нас есть одна посылка и заключение:
Петров знает законы.
Петров – юрист.
Меньшим термином силлогизма является «Петров», большим – «юрист», средним – «человек, знающий законы». Пропущена большая посылка, куда должны войти термины «юрист» и «человек, знающий законы». Она может быть сформулирована в двух вариантах:
a) «Все юристы знают законы» – силлогизм будет строиться по второй фигуре, но при этом будут нарушены правила фигуры и правило распределенности среднего термина:
Все юристы знают законы. Петров знает законы.
Петров – юрист.
b) «Некоторые люди, знающие законы, – юристы» – силлогизм будет строиться по первой фигуре, что также приведет к нарушению правил фигуры и распределенности среднего термина.
Читателям предоставляется возможность убедиться самостоятельновтом, чтообасиллогизмабудутневерны. Следовательно, данная энтимема является неправильным умозаключением.
В энтимеме, как мы уже отмечали, может быть пропущено заключение.

|
§4. Сокращенные и сложные силлогизмы |
119 |
Пример: «Все радикалы опасны для общества, а он – радикал». Здесь пропущено заключение – «Он опасен для общества». Такие энтимемы, выполняярольнамека, иногдадалеконебезобидного, подводят слушателя к желательному для говорящего выводу.
Хотя энтимемы не предлагают какую-либо новую форму умозаключения, на практике очень важно уметь их распознавать.
Эпихейремы
Эпихейрема – это умозаключение, посылками которого высту-
пают энтимемы. Это сложносокращенное умозаключение. Например:
Все студенты сдают экзамены, так как они – учащиеся.
Этот молодой человек – студент, так как он учится на нашем факультете.
Этот молодой человек сдает экзамены.
В этом примере каждая из посылок является энтимемой с пропущеннойбольшейпосылкой, хотявозможныидругиеслучаи. Восстановим эти посылки и проверим, не нарушены ли тут правила логики для умозаключений этого вида. В итоге получаем два полных силлогизма (до которых восстанавливаются энтимемы):
Первый силлогизм:
Все учащиеся сдают экзамены. Все студенты – учащиеся.
Все студенты сдают экзамены.
Второй силлогизм:
Все учащиеся нашего факультета – студенты.
Этот молодой человек – учащийся нашего факультета.
Этот молодой человек – студент.

Вывод первой и вывод второй энтимем выступают посылками для третьего силлогизма (который и дает окончательный вывод эпихейремы):
Все студенты сдают экзамены. Этот молодой человек – студент.
Этот молодой человек сдает экзамены.
Таким образом, эпихейрему составляют не два, а три отдель-
ных силлогизма. В виде схемы эпихейрема записывается так:
Все А есть С, так как А есть В. Все D есть А, так как D есть Е.
Все D есть С.
В ходе сопоставления схемы и содержательного примера мы показали:
1)какой именно элемент был пропущен в эпихейреме;
2)восстановленные силлогизмы оказались правильно построенными.
(Проверку правильности полученных трех силлогизмов – в силу их простоты – предоставляем учащимся).
Связующим звеном в данной эпихейреме, средним термином между ее посылками-энтимемами выступает понятие, обозначенное символом А. В пропущенных же посылках устанавливается связь понятий, обозначенных на схеме символами В и Е.
Еще один пример эпихейремы предваряется силлогизмами, которые помогут внести ясность в ее построение.
Первый силлогизм:
Человек, твердо следующий своим убеждениям (B) – принципиальный человек (C).
Сохраняющий целостность характера (A) твердо следует убеждениям (B).
Сохраняющий целостность характера (A) – принципиальный человек (C).

|
§4. Сокращенные и сложные силлогизмы |
121 |
Второй силлогизм:
Не деградирует морально (E) лишь тот, кто сохраняет целостность характера (A).
Сильный духом (D) не подвержен моральной деградации (морально устойчив) (E).
Сильный духом (D) сохраняет целостность характера (A).
Третий силлогизм:
Сохраняющий целостность характера (A) – принципиальный человек (C).
Сильный духом (D) сохраняет целостность характера (A).
Сильный духом (D) – это принципиальный человек (C).
Эпихейрема:
Сохраняющий целостность характера (A) – принципиальный человек (C), поскольку твердо следует своим убеждениям (B).
Сильный духом (D) сохраняет целостность характера (A), поскольку не подвержен моральной деградации (E).
Сильный духом (D) – это принципиальный человек (C).
Однако далеко не всегда эпихейрема бывает правильно построена.
Проверьте с помощью следующего примера, заслуживает ли уважения труд юриста.
Благородный труд (А) заслуживает уважения (С), так как благородный труд (А) способствует социальному прогрессу (В).
Труд юриста (D) есть благородный труд (А), так как труд юриста (D) связан с решением важных общественных проблем (Е).
Труд юриста (D) заслуживает уважения (С).

Полисиллогизмы
Сложный силлогизм, или полисиллогизм − соединение двух
или нескольких простых категорических силлогизмов таким образом, что заключение одного силлогизма становится посылкой для другого силлогизма.
Сложный силлогизм похож на каскад или лестницу силлогизмов, в которых вывод предшествующего силлогизма (просиллогизма) становится посылкой следующего силлогизма (эписиллогизма). Если вывод просиллогизма становится большей посылкой эписиллогизма, то полисиллогизм называется прогрессивным; если же вывод просиллогизма становится меньшей посылкой эписиллогизма, то полисиллогизм называется регрессивным. Понятно, что эписиллогизм, в свою очередь, становится просиллогизмом для следующего за ним силлогизма и т. д.
Пример прогрессивного полисиллогизма:14
1. (Просиллогизм)
Все преступления общественно опасны. Все хищения – преступления.
Все хищения общественно опасны.
2. (Первый эписиллогизм)
Все хищения общественно опасны. Все кражи – хищения.
Все кражи – общественно опасны.
3. (Второй эписиллогизм)
Все кражи – общественно опасны.
Все тайные присвоения книг из библиотеки – кражи.
Все тайные присвоения книг из библиотеки общественно опасны.
14 Примеры полисиллогизмов приведены по: Брюшинкин В.Н. Практический курс логики для гуманитариев. – М., 1996.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
24.02.201622.34 Mб50Логика. Демина.pdf
- #
- #
- #
- #
Фигуры силлогизма – это его разновидности, различающиеся положением среднего термина (М) в посылках.
Правильные виды силлогизма (или модусы), распределённые по фигурам
| Фигура 1 | Фигура 2 | Фигура 3 | Фигура 4 |
| AAA | EAE | AAI | AAI |
| EAE | AEE | IAI | AEE |
| AII | EIO | AII | IAI |
| EIO | AOO | EAO | EAO |
| OAO | EIO | ||
| EIO |
Данные модусы необходимо знать наизусть. Для облегчения заучивания придумали следующее стихотворение, написанное гекзаметром:
Фигура 1: Barbara Celarent Darii Ferio
Фигура 2: Cesare Camestres Festino Baroco
Фигура 3: Darapti Disamis Datisi Felapton Bocardo Ferison
Фигура 4: Bramantip Camenes Dimaris Fesapo Fresison
Здесь каждое слово, напечатанное курсивным шрифтом, означает отдельный модус, посылки и заключение которого легко определить, если взять гласные буквы. Например,
- Barbara означает модус фигуры 1, в котором обе посылки и заключение суть ААА;
- Celarent означает модус ЕАЕ.
Посылки изображаются горизонтальными линиями, крайние точки которых обозначают термины, при этом соединяют линией средний термин в разных посылках.
Существует четыре фигуры силлогизма, каждая из которых имеет свои правила.
Во 2-й фигуре средний термин занимает место предиката в обеих посылках.
Например:
Все студенты юрфака (Р) сдают экзамен по логике (M).
Иванов (S) не сдает экзамен по логике (М).
_______________________________________________________________________________
Иванов (S) не является студентом юрфака (P).
Модусы второй фигуры
Cesare
Е Ни один справедливый человек не завистлив.
А Всякий честолюбивый завистлив.
___________________________________________________________
E Ни один честолюбивый человек не есть справедлив.
Camestres
А Преступники действуют из злого намерения.
Е N. не действовал из злого намерения.
__________________________________________________
Е N не есть преступник.
Festino
Е Ни один благоразумный человек не суеверен.
I Некоторые хорошо образованные люди суеверны.
_______________________________________________________________
О Некоторые хорошо образованные люди неблагоразумны.
Baroko
A Все истинно моральные действия совершаются из правильных мотивов.
O Некоторые действия, благодетельные для других, нe совершаются из таких мотивов.
___________________________________________________________________________
О Некоторые благодетельные для других действия не суть истинно моральные.
Правила 2-й фигуры простого категорического силлогизма
-
- Первая (большая) посылка должна быть общей.
- Одна из посылок должна быть отрицательной.
Второе правило фигуры выводится из 2-го правила терминов (средний термин должен быть распределен хотя бы в одной из посылок). Но так как средний термин занимает место предиката в обеих посылках, то одна из них должна быть отрицательным суждением, т.е. суждением с распределенным предикатом.
Если одна из посылок — отрицательное суждение, то и заключение должно быть отрицательным (суждение с распределенным предикатом). Но в этом случае предикат заключения (больший термин) должен быть распределен и в большей посылке, где он занимает место субъекта суждения. Такой посылкой должно быть общее суждение, в котором субъект распределен. Значит, большая посылка должна быть общим суждением.
Правила 2-й фигуры исключают сочетания посылок АА, IA, ОА, IE, AI, оставляя модусы ЕАЕ, AEE, ЕIO, АОО, которые показывают, что эта фигура дает только отрицательные заключения.
Например:
Все физики стремятся к истине.
Некоторые историки стремятся к истине.
______________________________________________________
Некоторые историки являются физиками?
Вывод ложный, поскольку нарушено правило второй фигуры – обе посылки утвердительные суждения.
Другой пример:
Некоторые люди могут быть отцами.
Ни одна женщина не может быть отцом.
___________________________________________________________
Некоторые женщины не могут быть людьми?
Вывод ложный, поскольку нарушено первое правило второй фигуры – первая посылка частное суждение.
Роль второй фигуры простого категорического силлогизма в познании
2-я фигура применяется, когда необходимо показать, что отдельный случай (конкретное лицо, факт, явление) не может быть подведен под общее положение. Этот случай исключается из числа предметов, о которых сказано в большей посылке.
В судебной практике 2-я фигура используется
-
- для заключений об отсутствии состава преступления в данном конкретном случае,
- для опровержения положений, противоречащих тому, о чем говорится в посылке, выражающей общее положение.
Например:
Подстрекателем (Р) признается лицо, склонившее другое лицо к совершению преступления (М).
H.(S) не признается лицом, склонившим другое лицо
к совершению преступления (М).
_____________________________________________________
H.(S) не является прдстрекателем (Р)
Задачи, решаемые при помощи силлогизмов:
1. Применение общих положений (аксиом, законов природы, правoвых норм) к частным случаям.
Эту задачу решают силлогизмы по первой фигуре.
Например:
Все студенты сдают экзамены.
Вы — студенты.
_________________________________________
Вы сдаете экзамены.
2. Опровержение неправильных дедукций или неправильных подчинений.
Данная задача противоположна первой задаче и силлогизмы, используемые для ее решения, часто используются для опровержения неправильных выводов, сделанных по первой фигуре, когда происходит исключение частного случая из общего правила (по второй фигуре).
Например:
Этот удар мог быть нанесен человеком большой физической силы.
Обвиняемый не обладает большой физической силой.
____________________________________________________________________
Обвиняемый не мог нанести этот удар.
3. Обоснование исключений из общих положений.
Эта ситуация часто встречается в споре. Предположим, ваш оппонент выдвигает какое-либо общее положение, а вам надо доказать исключение из него. Тогда можно прибегнуть к 3-й фигуре.
Например, надо доказать, что суждение «Все люди имеют преступные наклонности» является ложным. Для этого надо построить силлогизм по 3-й фигуре:
Ни один ребенок не имеет преступных наклонностей.
Каждый ребенок является человеком.
___________________________________________________________________
Следовательно, некоторые люди не имеют преступных наклонностей.
Определите фигуру простого категорического силлогизма, его модус и правильность сделанного вывода
1. Все деньги обесцениваются. Некоторые средства платежа есть деньги. Следовательно, некоторые средства платежа обесцениваются.
2. Граждане России имеют право на собственность, а я – гражданин России. Следовательно, я имею право на собственность.
3. Право автора охраняется государством. Право этого человека – право автора. Следовательно, право этого человека охраняется государством.
4. Все владельцы телефонов платят абонентскую плату, а ты – владелец телефона, значит, ты платишь абонентскую плату.
5. Все звезды светят собственным светом. Некоторые небесные тела не светят собственным светом. Следовательно, некоторые небесные тела не звезды.
6. Все металлы ковки. Железо – металл. Следовательно, железо ковко.
7. Все пацифисты являются сторонниками запрещения ядерного оружия, и каждый из них противник насилия. Следовательно, всякий противник насилия выступает за запрещение ядерного оружия.
8. Идеальное – отображение материального. Мой образ в зеркале – отображение материального. Значит, мой образ в зеркале идеален.
9. Некоторые студенты – отличники. Некоторые студенты участвуют в КВН. Следовательно, все отличники участвуют в КВН.
10. Ни один школьник не студент. Все студенты сдают экзамены. Следовательно, некоторые люди, сдающие экзамены, не являются школьниками.
Комментарий и примеры: В зависимости от положения среднего термина М различают четыре фигуры силлогизма.

субъектом в большей посылке и предикатом
в меньшей. Первая фигура дает выводы всех
S М основных видов суждений, т.е. А, Е, I, О.
1-ая фигура имеет следующие правильные модусы (буквы обозначают последовательно количество и качество большей посылки, меньшей посылки и заключения): ААА, ЕАЕ, АII, ЕIО.
Р М II фигура – средний термин может быть предикатом

получается только отрицательным (Е, О).
2-ая фигура имеет следующие правильные модусы:
|
Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм… |
Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени… |
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил… |
Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах… |
|
1 / 1 / 1 Регистрация: 23.01.2016 Сообщений: 153 |
|
|
1 |
|
Предложение на языке логики предикатов01.10.2016, 10:21. Показов 4468. Ответов 8
Добрый всем день! Прошу объяснить, почему в данном примере сначала идет A(x)&B(y), и почему нельзя просто написать Предложение по которому строится формула: Введем предикаты: A(x) = “x – студент”; B(y) = “y – экзамен”, C(x, y) = ”x сдал экзамен y”. “Некоторые студенты сдали все экзамены” Буду очень благодарен за ответ! Добавлено через 47 минут
__________________
0 |
|
4468 / 3262 / 1051 Регистрация: 01.09.2014 Сообщений: 9,064 |
|
|
01.10.2016, 17:02 |
2 |
|
Формулировка задачи подразумевает, что область интерпретации, в которой рассматриваются данные формулы, содержит студентов и экзамены. В этом случае при указанном значении предикатов формула
1 |
|
1 / 1 / 1 Регистрация: 23.01.2016 Сообщений: 153 |
|
|
01.10.2016, 19:55 [ТС] |
3 |
|
3D Homer, если не составит труда объясните пожалуйста почему вы взяли для примера С(х,х), ведь у нас же не только студент задействован тут, а так же экзамен. Или вы произвели замену переменной?
0 |
|
4468 / 3262 / 1051 Регистрация: 01.09.2014 Сообщений: 9,064 |
|
|
01.10.2016, 20:40 |
4 |
|
Решение Если Выбирать b = a было необязательно; достаточно в качестве b взять любого человека, а не экзамен. Это возможно, так как область интерпретации состоит из тех и других. Это, правда, если у вас логика односортная. Если логика многосортная, то областей интерпретации несколько (например, множество студентов и множество экзаменов) и каждая переменная пробегает по своей области. Но все это относится к делу, если у вас курсе присутствовала фраза «многосортная логика». Если нет, то верно то, что я сказал выше.
1 |
|
1 / 1 / 1 Регистрация: 23.01.2016 Сообщений: 153 |
|
|
01.10.2016, 20:49 [ТС] |
5 |
|
Понял, спасибо огромное за разъяснения!
0 |
|
4468 / 3262 / 1051 Регистрация: 01.09.2014 Сообщений: 9,064 |
|
|
01.10.2016, 21:03 |
6 |
|
Между прочим, правильная формула, говорящая «Некоторые студенты сдали все экзамены», есть Вообще стандартными комбинациями являются
1 |
|
1 / 1 / 1 Регистрация: 23.01.2016 Сообщений: 153 |
|
|
01.10.2016, 21:05 [ТС] |
7 |
|
Таким образом дали нам лекцию, и там именно такой пример, как я указал в первом сообщении
0 |
|
4468 / 3262 / 1051 Регистрация: 01.09.2014 Сообщений: 9,064 |
|
|
01.10.2016, 21:08 |
8 |
|
Одно из неформальных определений говорит, что доказательство — это рассуждение, которое убедило вас настолько, что вы можете убеждать других. Вам представляется возможность доказать лектору, что он неправ.
1 |
|
1 / 1 / 1 Регистрация: 23.01.2016 Сообщений: 153 |
|
|
01.10.2016, 21:14 [ТС] |
9 |
|
Постараюсь максимально разобраться в этой теме! Еще раз большое спасибо!
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
01.10.2016, 21:14 |
|
Помогаю со студенческими работами здесь
Записать на языке логики предикатов Записать на языке логики предикатов, №1 Записать на языке логики предикатов, №2 Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 9 |






 Сообщение было отмечено dune777 как решение
Сообщение было отмечено dune777 как решение
