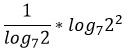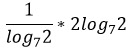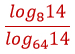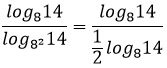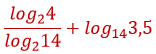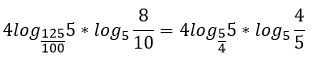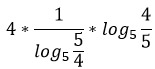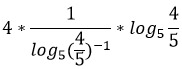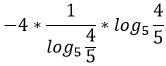Все свойства логарифмов для егэ по профильной математике - Помощь в подготовке к экзаменам и поступлению

Логарифмом положительного числа $b$ по основанию а, где $a>0$, $a≠1$, называется показатель степени, в которую надо возвести число $а$, чтобы получить $b$.

Пример:

$log_{2}8=3$, т.к. $2^{3}=8;$

$log_{3}{1}/{27}=-3$, т.к $3^{-3}={1}/{27}$

Особенно можно выделить три формулы:

$log_{a}a=1;$

$log_{a}1=0;$

$log_{a}a^b=b.$

Основное логарифмическое тождество:

$a^{log_{a}b}=b$

Это равенство справедливо при $b>0, a>0, a≠1$

Пример:

$4^{log_{4}5}=5;$

$3^{-2log_{3}5}={3^{log_{3}5^{-2}}}=5^{-2}={1}/{25}$

Десятичным логарифмом числа называют логарифм этого числа по основанию $10$ и пишут $lg⁡b$ вместо $log_{10}b$.

Пример:

$lg100000=lg10^5=5$

Ответ: $5$

Натуральным логарифмом числа называют логарифм этого числа по основанию $е$, где $е$ – иррациональное число, приближенно равное $2.7$. При этом пишут $lnb$, вместо $log_{e}b$

Свойства логарифмов.

Все свойства логарифмов мы будем рассматривать для $a>0, a≠1, b>0, c>0, m$ – любое действительное число.

1. Для любых действительных чисел $m$ и $n$ справедливы равенства:

$log{_а}b^m=mlog_{a}b;$

$log_{a^m}b={1}/{m}log_{a}b.$

$log_{a^n}b^m={m}/{n}log_{a}b$

Пример:

$log_{3}3^{10}=10log_{3}3=10;$

$log_{5^3}7={1}/{3}log_{5}7;$

$log_{3^7}4^5={5}/{7}log_{3}4;$

2. Логарифм произведения равен сумме логарифмов по тому же основанию от каждого множителя.

$log_{a}(bc)=log_{a}b+log_{a}c$

Пример:

Вычислить $log_{12}2+log_{12}72$

Применим второе свойство наоборот: сумма логарифмов по одинаковому основанию равна логарифму произведения подлогарифмических выражений

$log_{12}2+log_{12}72=log_{12}2·72=log_{12}144=2$

Ответ: $2$

3. Логарифм частного равен разности логарифмов от числителя и знаменателя по тему же основанию

$log_{a}{b}/{c}=log_{a}b-log_{a}c$

Пример:

Вычислить $log_{5}75-log_{5}3$

Решение:

Разность логарифмов с одинаковыми основаниями равна логарифму частного подлогарифмических выражений

$log_{5}75-log_{5}3=log_{5}{75}/{3}=log_{5}25=2$

Ответ: $2$

4. При умножении двух логарифмов можно поменять местами их основания

$log_{a}b·log_{c}d=log_{c}b·log_{a}d$, если $a$, $b$, $c$, $d>0$, $a≠1$, $b≠1.$

5. $c^{log_{a}b}=b^{log_{a}c}$, где $а, b, c>0, a≠1$

6. Формула перехода к новому основанию

$log_{a}b={log_{c}b}/{log_{c}a}$

7. В частности, если необходимо поменять местами основание и подлогарифмическое выражение

$log_{a}b={1}/{log_{b}a}$

Пример:

Найдите значение выражения: ${log_{2}∜{13}}/{log_{2}13}$

Решение:

В выражении видим, что был произведен переход к новому основанию $2$. Нам необходимо вернуться к старому основанию $13$.

${log_{2}∜{13}}/{log_{2}13}=log_{13}∜{13}$

Далее вычислим получившийся логарифм, для этого подлогарифмическое выражение необходимо представить в виде степени. Любой корень можно выразить в виде степени с дробным показателем, в знаменателе показателя будет находиться показатель корня

$∜{13}=13^{{1}/{4}}$

$log_{13}∜{13}=log_{13}13^{{1}/{4}}={1}/{4}=0.25$

Ответ: $0.25$

Источник

Что такое логарифм?

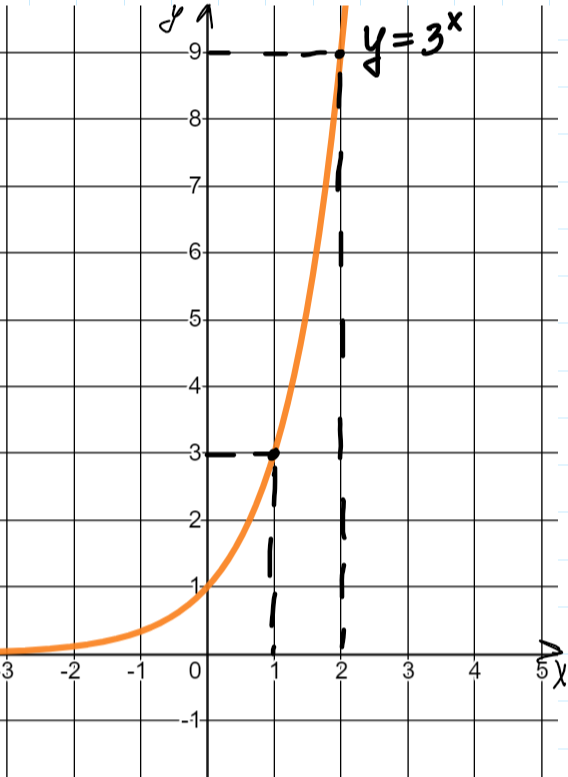
Нагляднее всего понять это с помощью графического решения уравнений. Начертим график

и с его помощью решим уравнения:

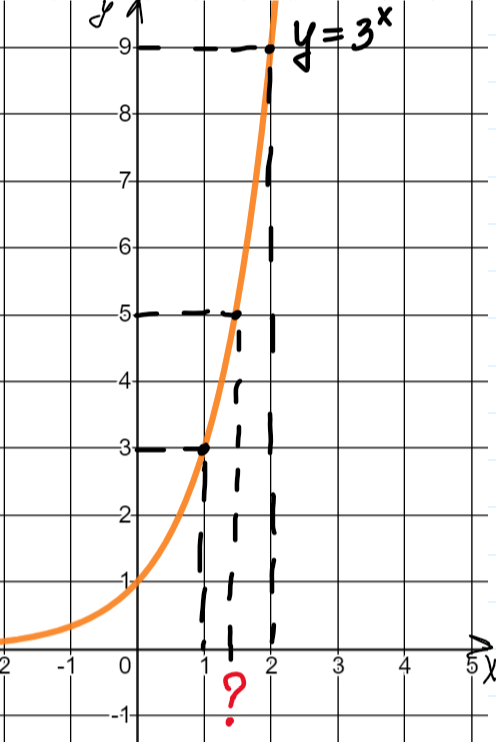
Отлично! А теперь решим уравнение

И в этом случае невозможно назвать точное значение, то есть мы понимаем, что корень больше одного и меньше двух, но более точных данных нет.

Вот такой корень и задается с помощью логарифма, а именно

(читается как «логарифм пяти по основанию три» или «логарифм по основанию три от пяти»).

Мы определили смысл — теперь перейдем к общему определению логарифма.

Логарифмом числа b по основанию a называют показатель степени с основанием a, равной b. То есть, попросту говоря, логарифм — это степень, в которую нужно возвести a для получения b. Однако у логарифма есть условия или ограничения, что основание а больше нуля и не равно единице, а также показатель b больше нуля.

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Как решать примеры с логарифмами?

Рассмотрим пример, как решить логарифм:

Задаем вопрос: в какую степень нужно возвести 7, чтобы получить 49?

Ответ: во вторую степень. Значит,

Какие бывают виды логарифмов?

Логарифм по основанию 10 называется десятичным логарифмом и обозначается как

. Пример десятичного логарифма:

Логарифм по основанию e называется натуральным логарифмом и обозначается как

. Пример натурального логарифма:

Свойства и формулы логарифмов

Эта формула называется основным логарифмическим тождеством.

Пример:

.
Пример:

.
Пример:

.
Логарифм степени находится по формуле:

.

Видно, что показатель степени выносим перед логарифмом.

Пример:

.
Показатель степени основания также выносим перед логарифмом, но в виде обратного числа, то есть, например, вместо 5 будет

.

Пример:

.
Если нужно перейти к другому основанию, то можно сделать это по формуле:

. Свойство называется формулой перехода к новому основанию.
А частным случаем предыдущей формулы является формула, которая позволяет менять местами основание и аргумент логарифма:

.

Конечно, это не все свойства логарифмов, а только самые главные. Комбинируя свойства выше, можно получать все новые и новые формулы для логарифмов. Например, соединив 4-ю и 5-ю формулы, получим

. Но запоминать ее нет смысла, важно знать лишь базовые свойства логарифмов.

Применение логарифмических свойств в примерах

Пример 1

Найдите значение выражения

, если

Если видите частное в показателе логарифма, то распишите по 3-й формуле:

Решение

У каждого логарифма в показателе стоит степень, значит, поможет 4-я формула:

Первый логарифм можно вычислить по определению. И обратите внимание на второй логарифм: у него в основании стоит а, а в условии задачи дан логарифм с основанием b, значит, нужно а как-то заменить на b. Возможно ли это? Конечно, 7-я формула в помощь!

Подставьте числовое значение из условия, и все готово:

Отличный пример! Мы использовали практически все свойства логарифмов. А теперь попрактикуйтесь еще, но помните, что задача с подвохом!

Пример 2

Вычислите:

Получился ответ 27? Если да, то поздравляю: вы попались на удочку самых популярных ошибок! Какое бы задание вам ни встретилось, действия с логарифмами нужно производить только по определениям и правилам. В примере вы видите деление двух логарифмов. А есть ли какая-то формула, в которой записано деление двух логарифмов?

Конечно, это формула перехода к новому основанию, которую мы привели в пункте 6 выше. Применим ее к этому случаю и вычислим логарифм по определению, задав вопрос: в какую степень нужно возвести основание, чтобы получился показатель?

И получается ответ 4, а не 27.

Практическое применение логарифмов

Помните, выше мы говорили, что логарифм объединяет задания на ЕГЭ, галактики и рога горных козлов? И если с баллами на ЕГЭ все понятно, то про галактики и рога — интереснее.

Все дело в том, что существует логарифмическая спираль, которая задается по формуле:

. По этой логарифмической спирали растут рога горных козлов, закручены многие галактики (и даже та, в которой мы живем), а также раковины некоторых морских животных, усики растений, ураганы, смерчи и многое другое.

Как видите, логарифмы имеют большое значение для нашей жизни — не только баллы на ЕГЭ!

Вопросы для самопроверки

Чтобы информация точно усвоилась, вспомните:

Что такое логарифм?
Какие ограничения есть у логарифма?
Какие логарифмические свойства вы знаете?
Какие бывают способы преобразования выражений с логарифмом?
В чем практическое применение логарифмов?

На курсах по математике в онлайн-школе Skysmart мы всегда показываем, зачем нужны математические правила и формулы в реальной жизни — ведь так учиться гораздо интереснее! И подтянуть знания перед ЕГЭ тоже поможем: приходите на бесплатный вводный урок и все увидите сами.

Источник

Логарифм и его свойства

Логарифм — это показатель степени, в которую надо возвести основание степени, чтобы получилось некоторое число.

Ничего не понятно! Будем разбираться на простых примерах.

Пусть дано уравнение: 2^х = 4 (2 — основание степени, х — неизвестный показатель степени, 4 — некоторое число).

Это показательное уравнение. Интуитивно понятно, что неизвестная переменная х равна 2, т.к. 2² = 4.

Модернизируем уравнение: 2^х = 5.

Хм… И как?

х = 2 — мало, а х = 3 много, т.е. х — это какое-то дробное число, скорее всего, даже иррациональное. В любом случае, точно подобрать не получится, разве что на калькуляторе и с округлением.

И поэтому для таких вот случаев ленивые математики придумали определение логарифма. В общем, корнем этого уравнения будет являться х = log₂5 (читается: логарифм числа 5 по основанию 2).

Естественно, что у логарифма есть ограничения, числа a и b должны быть положительными и а не должно быть равно 1 (Если пораскинуть мозгами, станет понятно почему).

Пришло время красиво записать полное определение логарифма на математическом языке, с помощью которого ты сможешь решать простейшие показательные уравнения (наподобие тех, что были выше).

Мы рассмотрели самый приятный вид логарифма. Есть еще два вида, десятичный и натуральный.

В десятичном логарифме основание равно 10, а в натуральном — е (е ≈ 2,718…).

Такие логарифмы пишутся немного по-другому:

log₁₀b = lgb;

log_eb = lnb.

Основные свойства логарифмов.

Свойства работают в обе стороны, при этом a, b, c — положительные и основания логарифмов не равны 1.

Прототипы заданий из ЕГЭ по математике (ФИПИ). Базовый и профильный уровни.

Задание 1.

Найдите корень уравнения

___________

Для решения этого уравнения используем определение логарифма. Продублирую его еще раз:

Наша задача основание логарифма 3 возвести в третью степень и приравнять выражению в скобках. Уравнение примет вид:

2х — 7 = 3³.

При этом важно не забыть, что (2х — 7) должно быть больше нуля. Это важно.

Решаем обычное линейное уравнение:

2х — 7 = 27;

2х = 34;

х = 17.

Надо убедится, что корень подходит области определения логарифма: 2 · 17 — 7 > 0. Неравенство верно.

Ответ: 17.

Задание 2.

Найдите корень уравнения

___________

Основания у логарифмов одинаковые, значит можно приравнять (5х — 23) и 17.

Снова получаем обычное линейное уравнение:

5х — 23 = 17;

5х = 40;

х = 8.

Удовлетворяет ли корень области определения логарифма? Да (5 · 8 — 23 > 0).

Ответ: 8.

Задание 3.

Найдите значение выражения

___________

Воспользуемся 8-м свойством: изменим основание первого логарифма на удобное нам. А еще представим 4 как 2 в квадрате.

Теперь преобразуем второй логарифм, используя свойство 4.

Одинаковые логарифмы сокращаются…

Ответ: 2.

Задание 4.

Найдите значение выражения

___________

Представим основание нижнего логарифма как 8² и по свойству 5 вынесем показатель степени вперед.

Логарифмы сокращаются, остается разделить 1 на ½.

Ответ: 2.

Задание 5.

Найдите значение выражения

___________

У логарифмов одинаковые основания, значит сработает свойство 2.

В какую степени надо возвести число 7, чтобы получилось 49? Правильно, 2.

Ответ: 2.

Задание 6.

Найдите значение выражения

___________

Для дроби используем свойство 7, только наоборот, а затем — свойство 2.

Ответ: 1.

Задание 7.

Найдите значение выражения

___________

Представим десятичные дроби в виде обыкновенных и сократим их.

Поменяем основание у первого логарифма, используя свойство 8.

Представим дробь 5/4 как 4/5 в минус первой степени.

По свойству 4 выносим -1 вперед.

Логарифмы равны и сокращаются.

Ответ: -4.

Источник

Свойства и графики логарифмических функций

1.
Область определения: D( y ): x ϵ (0; +∞).

2.
Множество значений: E( y ): y ϵ (-∞;+∞).

3.
Функция не является четной и не является нечетной.

4.
Нули функции: при x = 1 логарифмическая функция y = log a x
приобретает значение, равное 0.

5.
График пересекает ось O x в точке (1; 0).

6.
Интервалы монотонности: При a > 1 функция возрастает на
интервале (0; +∞). При 0 < a < 1 функция убывает на интервале (0; +∞)

7.
Интервалы выпуклости / вогнутости: При a > 1 график функции
выпуклый на интервале (0; +∞). При 0 < a < 1 график функции вогнутый на
интервале (0; +∞).

8.
Из равенства логарифмов двух чисел по одному и тому же основанию
следует равенство самих чисел: log a x = log a y => x = y , a > 0, a ≠ 1.

Примеры решения логарифмических уравнений

Краткий алгоритм решения логарифмических
уравнений:

1. Привести логарифмы в разных частях уравнения к одному
основанию, исключая коэффициенты перед ними с помощью свойства логарифмов.

2. Исключить логарифмы, прибегая к правилу потенцирования.

3. Решить стандартное уравнение.

4. Проверить результат.

5.Записать ответ.

Несколько схем решений логарифмических
уравнений

Схема выполнения равносильных преобразований
логарифмических неравенств (потенцирование неравенств)

Обобщенный метод интервалов

Схема:

1. Привести неравенство к такому виду, где в
левой части находится функция f(x), а в правой 0.

2. Найти область определения функции f(x).

3. Найти нули функции f(x), то есть – решить
уравнение f(x) = 0 (а решать уравнение обычно проще, чем решать неравенство)

4. Изобразить на числовой прямой область
определения и нули функции.

5. Определить знаки функции f(x) на полученных
интервалах.

6. Выбрать интервалы, где функция принимает
необходимые значения и записать ответ.

Запомни:
знаки расставляются только на области определения функции!

Метод рационализации

(метод
декомпозиции, метод замены множителей, метод замены функции, правило знаков)

Метод рационализации заключается в замене сложного выражения F(x)ü0 на более простое выражение G(x)ü0 равносильно неравенству F(x)ü0 в области определения выражения F(x).

Выделим некоторые выражения F и
соответствующие им рационализирующие выражения G, где f, g, h, p, q – выражения с переменной x (h>0; h≠1; f>0, g>0), a –
фиксированное число (a>0; a≠1)