Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов).
Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$
7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.
1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
В прямоугольном треугольнике $АВС$ для острого угла $В$:
$sinB={AC}/{AB};$
$cosB={BC}/{AB};$
$tgB={AC}/{BC};$
$ctgB={BC}/{AC}.$
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
$sin BOA=sin BOC;$
$cos BOA=-cos BOC;$
$tg BOA=-tg BOC;$
$ctg BOA=-ctg BOC.$
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Площадь прямоугольного треугольника равна половине произведения его катетов
$S={AC∙BC}/{2}$
Пример:
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√{91}$. Найдите косинус внешнего угла при вершине $В$.
Решение:
Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то
$cosABD=-cosABC$
Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:
$cosABC={ВС}/{АВ}$
Катет $ВС$ мы можем найти по теореме Пифагора:
$ВС=√{10^2-√{91}^2}=√{100-91}=√9=3$
Подставим найденное значение в формулу косинуса
$cos ABC = {3}/{10}=0,3$
$cos ABD = — 0,3$
Ответ: $-0,3$
Пример:
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sinA={4}/{5}, AC=9$. Найдите $АВ$.
Решение:
Распишем синус угла $А$ по определению:
$sinA={ВС}/{АВ}={4}/{5}$
Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.
Применим теорему Пифагора, чтобы отыскать $«х»$
$АС^2+ВС^2=АВ^2$
$9^2+(4х)^2=(5х)^2$
$81+16х^2=25х^2$
$81=25х^2-16х^2$
$81=9х^2$
$9=х^2$
$х=3$
Так как длина $АВ$ составляет пять частей, то $3∙5=15$
Ответ: $15$
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
$CD^2=DB∙AD$
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
$CB^2=AB∙DB$
$AC^2=AB∙AD$
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
$AC∙CB=AB∙CD$
31
Июл 2013
Категория: Справочные материалы
Прямоугольный треугольник
2013-07-31
2019-09-30
Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).
Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.
Стороны, прилежащие к прямому углу, называются катетами.
Признаки равенства прямоугольных треугольников
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны (по двум катетам).
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны (по катету и острому углу).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны (по гипотенузе и катету).
Свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна 90˚.
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.
3. Теорема Пифагора:
, где
– катеты,
– гипотенуза. Видеодоказательство
4. Площадь прямоугольного треугольника с катетами
:
5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты
и гипотенузу
следующим образом:
6. Центр описанной окружности – есть середина гипотенузы.
7. Радиус описанной окружности есть половина гипотенузы
:
8. Медиана, проведенная к гипотенузе, равна ее половине
9. Радиус вписанной окружности выражается через катеты
и гипотенузу
следующим образом:
Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.
И, думаю, будет полезна таблица формул для треугольника
Автор: egeMax |
комментария 3
Печать страницы
Сумма квадратов катетов равна квадрату гипотенузы.
В буквах это так:
- ( A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}})
или так:
- ( {{c}^{2}}={{a}^{2}}+{{b}^{2}})
Помнишь шутку: «Пифагоровы штаны на все стороны равны!»?
Давай нарисуем эти самые пифагоровы штаны и посмотрим на них.
Правда, похоже на какие-то шорты? Ну и на какие стороны и где они равны? Почему и откуда возникла шутка? М-да… Кажется, у людей в античности с юмором явно проблемы.
Вовсе нет! А шутка эта связана как раз с теоремой Пифагора, точнее с тем, как сам Пифагор формулировал свою теорему. А формулировал он её так:
«Сумма площадей квадратов, построенных на катетах, равна площади квадрата, построенного на гипотенузе».
Правда, немножко по-другому звучит? И вот, когда Пифагор нарисовал утверждение своей теоремы, как раз и получилась такая картинка.
На этой картинке сумма площадей маленьких квадратов равна площади большого квадрата. А чтобы дети лучше запоминали, что сумма квадратов катетов равна квадрату гипотенузы, кто-то остроумный и выдумал эту шутку про Пифагоровы штаны.
Почему же мы сейчас формулируем теорему Пифагора так:
( {{c}^{2}}={{a}^{2}}+{{b}^{2}}),
а Пифагор мучился и рассуждал про площади?
Понимаешь, в древние времена не было… алгебры! Не было никаких обозначений ( displaystyle a,text{ }b,text{ }c,text{ }x) и так далее. Не было надписей ( displaystyle {{a}^{2}},text{ }{{b}^{2}},text{ }{{c}^{2}}).
Представляешь, как бедным древним ученикам было ужасно запоминать всё словами?! А мы можем радоваться, что у нас есть простая формулировка теоремы Пифагора 
Давай её ещё раз повторим, чтобы лучше запомнить:
( A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}})
или
( {{c}^{2}}={{a}^{2}}+{{b}^{2}})
Теперь уже должно быть легко:
Квадрат гипотенузы равен сумме квадратов катетов.
Ну вот, самую главную теорему о прямоугольном треугольнике обсудили. Если тебе интересно, как она доказывается, то… сейчас мы ее докажем)
Нарисуем квадрат со стороной ( a+b).
Видишь, как хитро мы поделили его стороны на отрезки длин ( a) и ( b)!
А теперь соединим отмеченные точки:
Тут мы, правда, ещё кое что отметили, но ты сам посмотри на рисунок и подумай, почему так.
Чему же равна площадь большего квадрата?
Правильно, ( {{left( a+b right)}^{2}}).
А площадь меньшего?
Конечно, ( c^2).
Осталась суммарная площадь четырех уголков. Представь, что мы взяли их по два и прислонили друг к другу гипотенузами.
Что получилось? Два прямоугольника. Значит, площадь «обрезков» равна ( displaystyle 2ab).
Давай теперь соберем всё вместе.
( displaystyle underbrace{{{left( a+b right)}^{2}}}_{{{S}_{большого квадрата}}}=underbrace{2ab}_{{{S}_{“обрезков”}}}+underbrace{{{c}^{2}}}_{{{S}_{малого квадрата}} })
Преобразуем: ( {{a}^{2}}+2ab+{{b}^{2}}=2ab+{{c}^{2}})
то есть ( {{a}^{2}}+{{b}^{2}}={{c}^{2}})
Вот и побывали мы Пифагором – доказали его теорему древним способом 
Можем обрадовать: для решения задач про прямоугольный треугольник можно просто заполнить следующие простые вещи:
- ( sin angle A=frac{a}{c});
- ( cos angle A=frac{b}{c});
- ( tg~angle A=frac{a}{b});
- ( ctg~angle A=frac{b}{a}).
А почему же всё только про угол ( A)? Где же угол ( B)?
Для того, чтобы в этом разобраться, нужно знать, как утверждения 1 – 4 записываются словами.
Смотри, понимай и запоминай!
- ( displaystyle sin angle A=frac{a}{c})
Вообще-то звучит это так:
Синус острого угла в прямоугольном треугольнике равен отношению противоположного катета к гипотенузе.
А что же угол ( displaystyle B)?
Есть ли катет, который находится напротив угла ( displaystyle B), то есть противолежащий (для угла ( displaystyle B)) катет?
Конечно, есть! Это катет ( displaystyle b)!
- Значит, ( displaystyle sin angle B=frac{b}{c})
Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе.
( displaystyle cos angle A=frac{b}{c})
Значит, ( displaystyle sin angle B=frac{b}{c})
А как же угол ( displaystyle B)?
Посмотри внимательно. Какой катет прилегает к углу ( displaystyle B)? Конечно же, катет ( displaystyle a).
Значит, для угла ( displaystyle B) катет ( displaystyle a) – прилежащий, и
- ( displaystyle cos angle B=frac{a}{c}).
А теперь, внимание! Посмотри, что у нас получилось:
( displaystyle begin{array}{l}sin angle A=frac{a}{c} sin angle B=frac{b}{c} \cos angle A=frac{b}{c} cos angle B=frac{a}{c}end{array})
Видишь, как здорово:
( displaystyle sin angle A=cos angle B) и ( displaystyle sin angle B=cos angle A)
Это очень удобно – если тебе дан в задаче синус одного угла прямоугольного треугольника, то ты знаешь и косинус другого!
Итак, запомни очень твёрдо:
В прямоугольном треугольнике синус одного острого угла равен косинусу другого и наоборот.
Теперь перейдём к тангенсу и котангенсу.
- ( displaystyle tg~angle A=frac{a}{b})
Как это теперь записать словами?
Катет ( displaystyle a) каким является по отношению к углу ( displaystyle A)? Противолежащим, конечно – он «лежит» напротив угла ( displaystyle A).
А катет ( displaystyle b)? Прилегает к углу ( displaystyle A).
Значит, что у нас получилось?
Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему.
- ( displaystyle ctg~angle A=frac{b}{a})
Видишь, числитель и знаменатель поменялись местами?
Котангенс острого угла в прямоугольном треугольнике равен отношению прилежащего катета к противолежащему.
Вспомним теперь про угол ( displaystyle angle B). Что будет для него? Правильно:
- ( displaystyle tg~angle B=frac{b}{a})( displaystyle ctg~angle B=frac{a}{b})
И теперь снова углы ( displaystyle A) и ( displaystyle B) совершили обмен:
( displaystyle begin{array}{l}tg~angle A=frac{a}{b} tg~angle B=frac{b}{a}\ctg~angle A=frac{b}{a} ctg~angle B=frac{a}{b}end{array})
В прямоугольном треугольнике тангенс одного острого угла равен котангенсу другого.
Давай вкратце запишем всё, что мы узнали.
Признаки равенства прямоугольных треугольников:
I. По двум катетам
Прямоугольные треугольники равны, если два катета одного треугольника соответственно равны двум катетам другого треугольника.
II. По катету и гипотенузе
Прямоугольные треугольники равны, если катет и гипотенуза одного треугольника соответственно равны катету и гипотенузе другого.
III. По гипотенузе и острому углу
Прямоугольные треугольники равны, если гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого.
IV. По катету и острому углу
Прямоугольные треугольники равны, если катет и острый угол одного треугольника соответственно равны катету и острому углу другого треугольника.
Внимание! Здесь очень важно, чтобы катеты были «соответствующие». Например, если будет так:
То треугольники не равны, несмотря на то, что имеют по одному одинаковому острому углу.
Нужно, чтобы в обоих треугольниках катет был прилежащим, или в обоих – противолежащим.
Ты заметил, чем отличаются признаки равенства прямоугольных треугольников от обычных признаков равенства треугольников?
Загляни в тему «Треугольник» и обрати внимание на то, что для равенства «рядовых» треугольников нужно равенство трех их элементов: две стороны и угол между ними, два угла и сторона между ними или три стороны.
А вот для равенства прямоугольных треугольников достаточно всего двух соответственных элементов. Здорово, правда?
Примерно такая же ситуация и с признаками подобия прямоугольных треугольников.
Почему это так?
Рассмотрим вместо прямоугольного треугольника целый прямоугольник.
Что видим?
Треугольник ( displaystyle ABC) – половина прямоугольника.
Проведём диагональ ( displaystyle CD) и рассмотрим точку ( displaystyle O) – точку пересечения диагоналей. Что известно про диагонали прямоугольника?
- Точкой пересечения диагонали делятся пополам
- Диагонали равны
И что из этого следует?
- Точкой пересечения диагонали делятся пополам
Запомни этот факт! Очень помогает!
А что ещё более удивительно, так это то, что верно и обратное утверждение.
Если медиана, проведенная к какой-нибудь стороне треугольника, оказалась равна половине этой стороны, то треугольник – прямоугольный.
Что же хорошего можно получить из того, что медиана, проведенная к гипотенузе, равна половине гипотенузы?
А давай посмотрим на картинку.
Здесь( displaystyle CO) – медиана и равна( frac{AB}{2}).
Что же это получилось за точка ( displaystyle O)?
Посмотри внимательно. У нас есть: ( OA=OB=OC), то есть расстояния от точки ( displaystyle O) до всех трёх вершин треугольника оказались равны. Но в треугольнике есть всего одна точка, расстояния от которой о всех трёх вершин треугольника равны, и это – ЦЕНТР ОПИСАННОЙ ОКРУЖНОСТИ. Значит, что получилось?
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.
Посмотрим на ( Delta ABC) и ( Delta ACH).
У них общий ( angle A), и они оба – прямоугольные. Значит (вспоминаем только что прочитанные признаки подобия прямоугольных треугольников) – они подобны!
Еще раз. ( displaystyle begin{array}{l}Delta ABC, Delta ACH:\left{ begin{array}{l}angle CAB=angle CAH\angle C=90{}^circ ; angle H=90{}^circ end{array} right.Rightarrow \Rightarrow Delta ABCsim Delta ACHend{array})
Но у подобных треугольников все углы равны!
( angle HCA=angle CBA) (Посмотри на рисунок)
То же самое можно сказать и про ( Delta CBH) и ( Delta ABC)
А теперь нарисуем это вместе:
( displaystyle begin{array}{l}Delta ABC, Delta CBH:\left{ begin{array}{l}angle ABC=angle CBH\angle C=90{}^circ ; angle H=90{}^circ end{array} right.Rightarrow \Rightarrow Delta ABCsim Delta CBHRightarrow \Rightarrow angle BAC=angle BCHend{array})
Что видим?
У ( Delta BCH) и ( Delta CHA) одинаковые острые углы!( displaystyle Rightarrow Delta BCHsim Delta CHA)
Какую же пользу можно извлечь из этого «тройственного» подобия.
Ну, например – две формулы для высоты прямоугольного треугольника.
Чтобы писать меньше букв, обозначим:
( displaystyle AC=b);
( displaystyle BC=a );
( displaystyle AB=c);
( displaystyle CH=h) (посмотри на рисунке).
Применяем подобие:( Delta ABCsim Delta ACH).
Запишем отношения соответствующих сторон:
Для нахождения высоты решаем пропорцию и получаем первую формулу “Высота в прямоугольном треугольнике”:
( displaystyle h=frac{ab}{c})
Как же получить вторую?
А теперь применим подобие треугольников ( BCH) и ( CAH).
Но сначала обозначим ( BH={{c}_{a}}) и ( CH={{c}_{b}}) ( смотри на рисунок)
Итак, применим подобие: ( displaystyle Delta BCHsim Delta CAH).
Значит,
Что теперь получится?
Опять решаем пропорцию и получаем вторую формулу “Высота в прямоугольном треугольнике”:
( displaystyle {{h}^{2}}={{c}_{a}}{{c}_{b}}) ,то есть ( displaystyle h=sqrt{{{c}_{a}}{{c}_{b}}})
Обе эти формулы нужно очень хорошо помнить и применять ту, которую удобнее.
Запишем их ещё раз:
( displaystyle h=frac{ab}{c})
( displaystyle h=sqrt{{{c}_{a}}{{c}_{b}}})
Ну вот, теперь, применяя и комбинируя эти знания с другими, ты решишь любую задачу с прямоугольным треугольником!
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Прямоугольный треугольник. Теорема Пифагора
Прямоугольный треугольник – это треугольник, один из углов которого равен (90^circ) (прямой).
Сторона, лежащая напротив прямого угла, называется гипотенузой ((AB)), а две другие стороны — катетами ((AC) и (BC)).
(bullet) Катет, лежащий против угла (30^circ), равен половине гипотенузы.
Следовательно, если, например, (angle A=30^circ), то (BC=dfrac12AB).
(bullet) Сумма острых углов прямоугольного треугольника равна (90^circ): (angle A+angle B=90^circ).
Следовательно, если в прямоугольном треугольнике один из острых углов равен (45^circ), то такой треугольник является равнобедренным.
(bullet) Если в прямоугольном треугольнике (ABC) провести высоту (CH) из прямого угла, то (angle BAC=angle BCH) и (angle
ABC=angle
ACH):
(bullet) Теорема Пифагора: квадрат длины гипотенузы равен сумме квадратов длин катетов: [AB^2=AC^2+BC^2]
(bullet) (triangle ABCsim triangle AHCsim triangle BHC)
(bullet) Высота, проведенная из вершины прямого угла, есть среднее геометрическое (среднее пропорциональное) отрезков, на которые делится гипотенуза этой высотой: [CH=sqrt{AHcdot HB}]
Задание
1
#3770
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C) равен (90^circ), угол (A) равен (30^circ), (AB=2sqrt3). Найдите высоту (CH).
Так как катет, лежащий против угла (30^circ), равен половине гипотенузы, то (BC=0,5AB=sqrt3).
По свойству прямоугольного треугольника (angle BCH=angle
A=30^circ), следовательно, из (triangle BCH): (HB=0,5
BC=sqrt3:2).
Тогда по теореме Пифагора из (triangle BCH): [CH=sqrt{BC^2-BH^2}=sqrt{dfrac94}=1,5]
Ответ: 1,5
Задание
2
#3771
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C) равен (90^circ), (CH) – высота, угол (A) равен (30^circ). Найдите (AH), если (AB=2).
Так как катет, лежащий против угла (30^circ), равен половине гипотенузы, то (BC=0,5AB=1).
Тогда по теореме Пифагора из (triangle ABC): [AC=sqrt{AB^2-BC^2}=sqrt3] Из прямоугольного (triangle AHC): (HC=0,5AC=sqrt3:2). Тогда по теореме Пифагора [AH=sqrt{AC^2-HC^2}=1,5]
Ответ: 1,5
Задание
3
#3772
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C) равен (90^circ), (CH) – высота, угол (A) равен (30^circ). Найдите (BH), если (AB=4).
Так как катет, лежащий против угла (30^circ), равен половине гипотенузы, то (BC=0,5AB=2).
По свойству прямоугольного треугольника (angle BCH=angle
A=30^circ), следовательно, из (triangle BCH): (HB=0,5
BC=1).
Ответ: 1
Задание
4
#3773
Уровень задания: Равен ЕГЭ
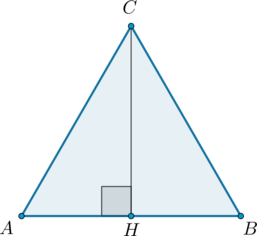
В треугольнике (ABC) ( AB=BC=AC=2sqrt3). Найдите высоту (CH).
Так как (AC=BC), то (CH) также является медианой, следовательно, (AH=0,5 AB=sqrt3). Тогда по теореме Пифагора из (triangle ACH): [CH=sqrt{AC^2-AH^2}=3]
Ответ: 3
Задание
5
#3774
Уровень задания: Равен ЕГЭ
В равностороннем треугольнике (ABC) высота (CH) равна (2sqrt3). Найдите (AB).
Так как (AC=BC), то (CH) также является медианой. Следовательно, если (AH=a), то (AB=AC=2a). Тогда по теореме Пифагора из (triangle
ACH): [AC^2=AH^2+CH^2quadRightarrowquad 4a^2=a^2+12quadRightarrowquad
a=2quadRightarrowquad AB=2a=4]
Ответ: 4
Задание
6
#3775
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) (AC=BC=4), (angle C=30^circ). Найдите высоту (AH).
Рассмотрим прямоугольный (triangle ACH). Катет, лежащий против угла (30^circ), равен половине гипотенузы, следовательно, (AH=0,5AC=2).
Заметим, что условие (BC=4) в данной задаче является лишним.
Ответ: 2
Задание
7
#3776
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) (AC=BC), высота (AH) равна (4), угол (C) равен (30^circ). Найдите (BC).
Рассмотрим прямоугольный (triangle ACH). Катет, лежащий против угла (30^circ), равен половине гипотенузы, следовательно, (4=AH=0,5AC), откуда (8=AC=BC).
Ответ: 8

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ