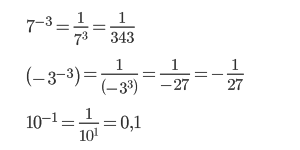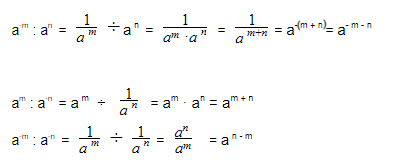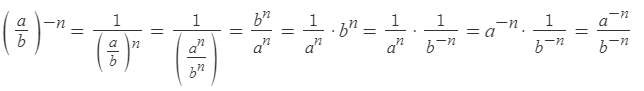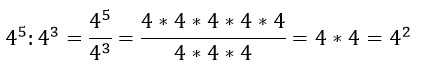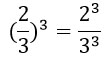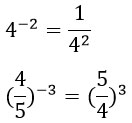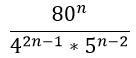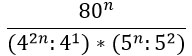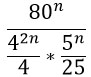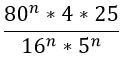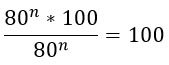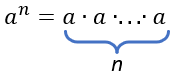Все свойства степеней для егэ - Помощь в подготовке к экзаменам и поступлению

Возведение в степень – это такая же математическая операция, как сложение, вычитание, умножение или деление.

Сейчас объясню все человеческим языком на очень простых примерах. Будь внимателен. Примеры элементарные, но объясняющий важные вещи. Начнем со сложения.

Сложение

( 2+2+2+2+2+2+2+2=16 )

Объяснять тут нечего. Ты и так все знаешь: нас восемь человек. У каждого по две бутылки колы. Сколько всего колы? Правильно – 16 бутылок. Теперь умножение.

Умножение

Тот же самый пример с колой можно записать по-другому: (displaystyle 2cdot 8=16).

Математики – люди хитрые и ленивые. Они сначала замечают какие-то закономерности, а потом придумывают способ как быстрее их «считать».

В нашем случае они заметили, что у каждого из восьми человек одинаковое количество бутылок колы и придумали прием, который называется умножением.

Согласись, (displaystyle 2cdot 8=16) считается легче и быстрее, чем (displaystyle 2+2+2+2+2+2+2+2=16).

И еще одна важная деталь. Ошибок при таком счете делается гораздо меньше. Математики из Стэнфорда, кстати, считают, что человек, знающий приемы счета, делает это в два раза легче и быстрее и совершает в два раза меньше ошибок. Работы меньше, а результат лучше.

Круто, да?

Итак, чтобы считать быстрее, легче и без ошибок, нужно всего лишь запомнить таблицу умножения. Ты, конечно, можешь делать все медленнее, труднее и с ошибками, но лучше ее запомнить! Вот таблица умножения. Выучи ее наизусть.

И другая таблица, красивее:

А какие еще хитрые приемы счета придумали ленивые математики? Правильно – возведение числа в степень.

Возведение числа в степень

Если тебе нужно умножить число само на себя пять раз, то математики говорят, что тебе нужно возвести это число в пятую степень.

Например, (displaystyle 2cdot 2cdot 2cdot 2cdot 2={{2}^{5}}). Математики помнят, что два в пятой степени – это (displaystyle 32).

И решают такие задачки в уме – быстрее, легче и без ошибок.

Для этого нужно всего лишь запомнить то, что выделено цветом в таблице степеней чисел. Поверь, это сильно облегчит тебе жизнь.

Кстати, почему вторую степень называют квадратом числа, а третью – кубом? Что это значит? Очень хороший вопрос. Сейчас будут тебе и квадраты, и кубы.

Примеры из жизни

Далее, почему говорят «степень числа с натуральным показателем»?

Ты уже наверное, догадался: потому что показатель степени – это натуральное число. Да, но что такое натуральное число? Элементарно! Натуральные это те числа, которые используются в счете при перечислении предметов: один, два, три… Мы же когда считаем предметы не говорим: «минус пять», «минус шесть», «минус семь». Мы так же не говорим: «одна третья», или «ноль целых, пять десятых». Это не натуральные числа. А какие это числа как ты думаешь?

Числа типа «минус пять», «минус шесть», «минус семь» относятся к целым числам.

Вообще, к целым числам относятся все натуральные числа, числа противоположные натуральным (то есть взятые со знаком минус), и число ( displaystyle 0) . Ноль понять легко – это когда ничего нет.

А что означают отрицательные («минусовые») числа? А вот их придумали в первую очередь для обозначения долгов: если у тебя баланс на телефоне ( displaystyle -100) рублей, это значит, что ты должен оператору ( displaystyle 100) рублей.

Всякие дроби – это рациональные числа. Как они возникли, как думаешь? Очень просто. Несколько тысяч лет назад наши предки обнаружили, что им не хватает натуральных чисел для измерения длинны, веса, площади и т.п. И они придумали рациональные числа… Интересно, правда ведь?

Есть еще иррациональные числа. Что это за числа? Если коротко, то бесконечная десятичная дробь. Например, если длину окружности разделить на ее диаметр, то в получится иррациональное число ( displaystyle 3,141592…).

Итак…

Откуда взялись, например, первые два свойства? Сейчас покажу.

1. ( displaystyle {{a}^{n}}cdot {{a}^{m}}={{a}^{n+m}})

Посмотрим: что такое ( displaystyle {{a}^{n}}) и ( displaystyle {{a}^{m}}) ?

По определению:

( displaystyle left. begin{array}{l}{{a}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}\{{a}^{m}}=underbrace{acdot acdot …cdot a}_{mtext{ множителей}}text{ }end{array} right|Rightarrow text{ }{{a}^{n}}cdot {{a}^{m}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}cdot underbrace{acdot acdot …cdot a}_{mtext{ множителей}}text{ }leftarrow )

Сколько здесь множителей всего?

Очень просто: к ( displaystyle n) множителям мы дописали ( displaystyle m) множителей, итого получилось ( displaystyle n+m) множителей.

Итак, в правой части этого выражения получается такое произведение:

( displaystyle {{a}^{n}}cdot {{a}^{m}}=underbrace{acdot acdot …cdot a}_{n+mtext{ множителей}})

Но по определению это степень числа ( displaystyle a) с показателем ( displaystyle n+m) , то есть: ( displaystyle {{a}^{n}}cdot {{a}^{m}}={{a}^{n+m}}) , что и требовалось доказать.

Пример: Упростите выражение ( displaystyle {{5}^{4}}cdot {{5}^{7}}cdot {{5}^{9}}) .

Решение: ( displaystyle {{5}^{4}}cdot {{5}^{7}}cdot {{5}^{9}}={{5}^{4+7+9}}={{5}^{20}})

Пример: Упростите выражение ( displaystyle {{3}^{5}}cdot {{3}^{8}}cdot {{5}^{7}}) .

Решение:

Важно заметить, что в нашем правиле обязательно должны быть одинаковые основания!

Поэтому степени с основанием ( displaystyle 3) мы объединяем, а ( displaystyle {{5}^{7}}) остается отдельным множителем:

( displaystyle {{3}^{5}}cdot {{3}^{8}}cdot {{5}^{7}}={{3}^{5+8}}cdot {{5}^{7}}={{3}^{13}}cdot {{5}^{7}})

Еще одно важное замечание: это правило – только для произведения степеней!

Ни в коем случае нельзя написать, что ( displaystyle {{2}^{4}}+{{2}^{6}}={{2}^{10}}).

2. ( displaystyle n) -ая степень числа ( displaystyle {{a}^{n}}cdot {{b}^{n}}={{left( acdot b right)}^{n}})

Так же, как и с предыдущим свойством, обратимся к определению степени:

( displaystyle left. begin{array}{l}{{a}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}\{{b}^{n}}=underbrace{bcdot bcdot …cdot b}_{ntext{ множителей}}end{array} right|Rightarrow text{ }{{a}^{n}}cdot {{b}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}cdot underbrace{bcdot bcdot …cdot b}_{ntext{ множителей}})

Перегруппируем это произведение так:

( displaystyle {{a}^{n}}cdot {{b}^{n}}=underbrace{acdot acdot …cdot a}_{n множителей}cdot underbrace{bcdot bcdot …cdot b}_{ntext{ множителей}}=underbrace{left( acdot b right)cdot left( acdot b right)cdot …cdot left( acdot b right)}_{ntext{ множителей}})

Получается, что выражение ( displaystyle left( acdot b right)) умножается само на себя ( displaystyle n) раз, то есть, согласно определению, это и есть ( displaystyle n) -ая степень числа ( displaystyle left( acdot b right)):

( displaystyle {{a}^{n}}cdot {{b}^{n}}={{left( acdot b right)}^{n}}), ч.т.д.

По сути это можно назвать «вынесением показателя за скобки». Но никогда нельзя этого делать в сумме:

( displaystyle {{2}^{4}}+{{3}^{4}}ne {{left( 2+3 right)}^{4}})!

Вспомним формулы сокращенного умножения: сколько раз нам хотелось написать ( displaystyle {{left( a+b right)}^{2}}={{a}^{2}}+{{b}^{2}}) ?

Но это неверно, ведь ( displaystyle {{left( a+b right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}).

Давайте подумаем, какие знаки («( displaystyle +)» или «( displaystyle –)») будут иметь степени положительных и отрицательных чисел?

Например, положительным или отрицательным будет число ( displaystyle {{3}^{5}})? А ( displaystyle {{left( -3 right)}^{5}}) ? ( displaystyle {{left( -3 right)}^{4}})?

С первым все понятно: сколько бы положительных чисел мы друг на друга не умножали, результат будет положительным.

Но с отрицательными немного интереснее. Мы ведь помним простое правило из 6 класса: «минус на минус дает плюс». То есть ( displaystyle left( -3 right)cdot left( -3 right)=+9) или ( displaystyle {{left( -3 right)}^{2}}=9). Но если мы ( displaystyle 9) умножим на ( displaystyle left( -3 right)), получится ( displaystyle -27).

И так до бесконечности: при каждом следующем умножении знак будет меняться. Можно сформулировать такие простые правила:

Определи знак:

1) ( displaystyle {{left( 0,6 right)}^{5}})	2) ( displaystyle {{left( -4 right)}^{5}})	3) ( displaystyle -{{left( -sqrt{3} right)}^{6}})
4) ( displaystyle {{left( -frac{2}{5} right)}^{4}})	5) ( displaystyle {{left( 2-sqrt{5} right)}^{8}})	6) ( displaystyle {{left( sqrt{5}-3 right)}^{7}})

Справился?

Вот ответы: В первых четырех примерах, надеюсь, все понятно? Просто смотрим на основание и показатель степени, и применяем соответствующее правило.

1) ( displaystyle +);	2) ( displaystyle –);	3) ( displaystyle –);
4) ( displaystyle +);	5) ( displaystyle +);	6) ( displaystyle –).

В примере 5) все тоже не так страшно, как кажется: ведь неважно, чему равно основание – степень четная, а значит, результат всегда будет положительным.

Ну, за исключением случая, когда основание равно нулю. Основание ведь не равно ( displaystyle 0) ? Очевидно нет, так как ( displaystyle 2ne sqrt{5}) (потому что ( displaystyle 2=sqrt{4}) ).

Пример 6) уже не так прост!

Тут нужно узнать, что меньше: ( displaystyle sqrt{5}) или ( displaystyle 3) ?

Если вспомнить, что ( displaystyle 3=sqrt{9}) , становится ясно, что ( displaystyle sqrt{5}<3) , а значит, основание меньше нуля.

То есть, применяем правило II: результат будет отрицательным.

Начнем с показателя, равного ( displaystyle 0) .

Любое число в нулевой степени равно единице:

( displaystyle {{a}^{0}}=1, ane 0)

Как всегда, зададимся вопросом: почему это так?

Рассмотрим какую-нибудь степень с основанием ( displaystyle 3). Возьмем, например ( displaystyle {{3}^{5}}), и домножим на ( displaystyle {{3}^{0}}):

( displaystyle {{3}^{5}}cdot {{3}^{0}}underset{text{по правилу умножения}}{mathop{=}},{{3}^{5+0}}={{3}^{5}})

Итак, мы умножили число ( displaystyle {{3}^{5}}) на ( displaystyle {{3}^{0}}) и получили то же, что и было – ( displaystyle {{3}^{5}}). А на какое число надо умножить, чтобы ничего не изменилось? Правильно, на ( displaystyle 1) . Значит ( displaystyle {{3}^{0}}=1) .

Можем проделать то же самое уже с произвольным числом ( displaystyle a):

( displaystyle {{a}^{n}}cdot {{a}^{0}}underset{по правилу умножения}{mathop{=}},{{a}^{n+0}}={{a}^{n}}={{a}^{n}}cdot 1text{ }Rightarrow text{ }{{a}^{0}}=1)

Повторим правило:

Любое число в нулевой степени равно единице.

Но из многих правил есть исключения. И здесь оно тоже есть – это число ( displaystyle 0) (в качестве основания).

С одной стороны, ( displaystyle 0) в любой степени должен равняться ( displaystyle 0) – сколько ноль сам на себя ни умножай, все-равно получишь ноль, это ясно. Но с другой стороны, ( displaystyle {{0}^{0}}) , как и любое число в нулевой степени, должен равняться ( displaystyle 1) . Так что из этого правда? Математики решили не связываться и отказались возводить ноль в нулевую степень.

То есть теперь нам нельзя не только делить на ноль, но и возводить его в нулевую степень.

Поехали дальше. Кроме натуральных чисел и числа ( displaystyle 0) к целым относятся отрицательные числа.

Чтобы понять, что такое отрицательная степень, поступим как в прошлый раз: домножим какое-нибудь нормальное число на такое же в отрицательной степени:

( displaystyle {{3}^{5}}cdot {{3}^{-5}}underset{text{по правилу умножения}}{mathop{=}},{{3}^{5+left( -5 right)}}={{3}^{5-5}}={{3}^{0}}=1)

Отсюда уже несложно выразить искомое ( displaystyle {{3}^{-5}}) :

( displaystyle {{3}^{5}}cdot {{3}^{-5}}=1text{ }Rightarrow text{ }{{3}^{-5}}=frac{1}{{{3}^{5}}})

Теперь распространим полученное правило на произвольную степень:

( displaystyle {{a}^{n}}cdot {{a}^{-n}}={{a}^{n+left( -n right)}}={{a}^{0}}=1text{ }Rightarrow text{ }{{a}^{-n}}=frac{1}{{{a}^{n}}})

Итак, сформулируем правило:

Число в отрицательной степени обратно такому же числу в положительной степени. Но при этом основание не может быть нулевым: ( displaystyle ane 0) (т.к. на ( displaystyle 0) делить нельзя).

( displaystyle {{a}^{-n}}=frac{1}{{{a}^{n}}}, ane 0)

Подведем итоги:

I. Выражение ( {{0}^{k}}) не определено в случае ( kle 0) . Если ( k>0) , то ( {{0}^{k}}=0) .

II. Любое число в нулевой степени равно единице: ( displaystyle {{a}^{0}}=1, ane 0) .

III. Число, не равное нулю, в отрицательной степени обратно такому же числу в положительной степени: ( displaystyle {{a}^{-n}}=frac{1}{{{a}^{n}}}, ane 0).

( displaystyle {{6}^{-1}}=frac{1}{6})

( displaystyle {{left( frac{3}{2} right)}^{-2}}=frac{4}{9})

Чтобы понять, что такое «дробная степень», рассмотрим дробь ( displaystyle frac{1}{n}) :

пусть ( displaystyle {{3}^{frac{1}{n}}}=x) .

Возведем обе части уравнения в степень ( displaystyle n) :

( displaystyle {{left( {{3}^{frac{1}{n}}} right)}^{n}}={{x}^{n}})

Теперь вспомним правило про «степень в степени»:

( displaystyle {{x}^{n}}={{left( {{3}^{frac{1}{n}}} right)}^{n}}={{3}^{frac{1}{n}cdot n}}={{3}^{1}}=3)

Какое число надо возвести в степень ( displaystyle n) , чтобы получить ( displaystyle 3) ?

Эта формулировка – определение корня ( displaystyle n) -ой степени.

Напомню: корнем ( displaystyle n) -ой степени числа ( displaystyle a) (( displaystyle sqrt[n]{a}) ) называется число, которое при возведении в степень ( displaystyle n) равно ( displaystyle a) .

То есть, корень ( displaystyle n) -ой степени – это операция, обратная возведению в ( displaystyle n) степень: ( displaystyle sqrt[n]{a}=btext{ }Leftrightarrow text{ }a={{b}^{n}}) .

Получается, что ( displaystyle x={{3}^{frac{1}{n}}}=sqrt[n]{3}) . Очевидно, этот частный случай можно расширить: ( displaystyle {{a}^{frac{1}{n}}}=sqrt[n]{a}) .

Теперь добавляем числитель: что такое ( displaystyle {{a}^{frac{m}{n}}}) ? Ответ легко получить с помощью правила «степень в степени»:

( displaystyle {{a}^{frac{m}{n}}}={{a}^{frac{1}{n}cdot m}}={{left( {{a}^{frac{1}{n}}} right)}^{m}}={{left( sqrt[n]{a} right)}^{m}}) или ( displaystyle sqrt[n]{{{a}^{m}}}) .

Но может ли основание ( displaystyle a) быть любым числом? Ведь корень можно извлекать не из всех чисел.

Например, можно ли посчитать число ( displaystyle sqrt[4]{-16}) ? То есть, какое число нужно возвести в ( displaystyle 4) степень, чтобы получить ( displaystyle -16) ?

Никакое!

Вспоминаем правило: любое число, возведенное в четную степень – число положительное. То есть, извлекать корни четной степени из отрицательных чисел нельзя!

А это значит, что нельзя такие числа возводить в дробную степень с четным знаменателем, то есть выражение ( displaystyle {{left( -1 right)}^{frac{1}{2}}}) не имеет смысла.

А что насчет выражения ( displaystyle {{left( -1 right)}^{frac{1}{3}}}) ?

Его уже вроде бы можно посчитать: это ( displaystyle sqrt[3]{-1}=-1) .

Но тут возникает проблема.

Число ( displaystyle frac{1}{3}) можно представить в виде дргих, сократимых дробей, например, ( displaystyle frac{2}{6}) или ( displaystyle frac{4}{12}) .

И получается, что ( displaystyle {{left( -1 right)}^{frac{1}{3}}}) существует, но ( displaystyle {{left( -1 right)}^{frac{2}{6}}}) не существует, а ведь это просто две разные записи одного и того же числа.

Или другой пример: раз ( displaystyle sqrt[3]{-8}=-2) , то можно записать ( displaystyle {{left( -8 right)}^{frac{1}{3}}}=-2) . Но стоит нам по-другому записать показатель, и снова получим неприятность: ( displaystyle {{left( -8 right)}^{frac{1}{3}}}={{left( -8 right)}^{frac{2}{6}}}=sqrt[6]{{{left( -8 right)}^{2}}}=sqrt[6]{64}=2) (то есть, получили совсем другой результат!).

Чтобы избежать подобных парадоксов, рассматриваем только положительное основание степени с дробным показателем.

Итак, если:

( a>0);
( m) – натуральное число;
( n) – целое число;

Тогда:

( {{a}^{frac{n}{m}}}=sqrt[m]{a^n})

Примеры:

( {{a}^{frac{1}{2}}}=sqrt{a})

( {{a}^{frac{1}{5}}}=sqrt[5]{a})

( {{a}^{-frac{3}{4}}}=frac{1}{sqrt[4]{a^3}})

( displaystyle frac{{{5}^{-frac{1}{2}}}cdot {{left( {{5}^{frac{5}{6}}} right)}^{frac{3}{10}}}cdot {{3}^{-frac{5}{4}}}}{{{3}^{-frac{3}{2}}}}={{5}^{-frac{1}{2}}}cdot {{5}^{frac{5}{6}cdot frac{3}{10}}}cdot {{3}^{left( -frac{5}{4}+frac{3}{2} right)}}=)

( displaystyle={{5}^{left( -frac{1}{2}+frac{1}{4} right)}}cdot {{3}^{frac{1}{4}}}={{5}^{-frac{1}{4}}}cdot {{3}^{frac{1}{4}}}={{left( frac{3}{5} right)}^{frac{1}{4}}}=sqrt[4]{frac{3}{5}})

Степени с рациональным показателем очень полезны для преобразования выражений с корнями, например:

( displaystyle frac{sqrt[9]{6}cdot sqrt[18]{6}}{sqrt[6]{6}}=frac{{{6}^{frac{1}{9}}}cdot {{6}^{frac{1}{18}}}}{{{6}^{frac{1}{6}}}}={{6}^{frac{1}{9}+frac{1}{18}-frac{1}{6}}}={{6}^{frac{2+1-3}{18}}}={{6}^{0}}=1)

При изучении степеней с натуральным, целым и рациональным показателем, мы каждый раз составляли некий «образ», «аналогию», или описание в более привычных терминах.

Например, степень с натуральным показателем – это число, несколько раз умноженное само на себя; число в нулевой степени – это как-бы число, умноженное само на себя ( 0) раз, то есть его еще не начали умножать, значит, само число еще даже не появилось – поэтому результатом является только некая «заготовка числа», а именно число ( 1) ; степень с целым отрицательным показателем – это как будто произошел некий «обратный процесс», то есть число не умножали само на себя, а делили.

Вообразить степень с иррациональным показателем крайне сложно (так же, как сложно представить 4-мерное пространство). Это, скорее, чисто математический объект, который математики создали, чтобы расширить понятие степени на все пространство чисел.

Между прочим, в науке часто используется степень с комплексным показателем, то есть показатель – это даже не действительное число. Но в школе мы о таких сложностях не думаем, постичь эти новые понятия тебе представится возможность в институте.

Итак, что мы делаем, если видим иррациональный показатель степени? Всеми силами пытаемся от него избавиться!:)

Например: ( {{3}^{sqrt{2}}}cdot {{3}^{1-sqrt{2}}}={{3}^{sqrt{2}+1-sqrt{2}}}=3)

Или: ( frac{{{2}^{3sqrt{3}}}}{{{8}^{sqrt{3}-1}}}=frac{{{2}^{3sqrt{3}}}}{{{2}^{3left( sqrt{3}-1 right)}}}={{2}^{3sqrt{3}-3sqrt{3}+3}}=8)

И еще: ( {{left( {{5}^{sqrt[3]{4}}} right)}^{sqrt[3]{2}}}={{5}^{sqrt[3]{8}}}={{5}^{2}}=25).

Определение степени

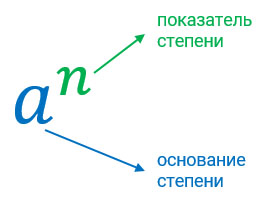
Степенью называется выражение вида: ( {{a}^{b}}), где ( a) – основание степени и ( b) – показатель степени.

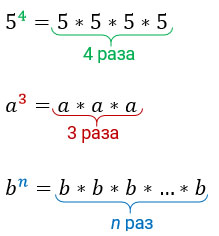
Степень с натуральным показателем {n = 1, 2, 3,…}

( {{a}^{1}}=a)
( {{a}^{2}}=acdot a)
( {{a}^{3}}=acdot acdot a)

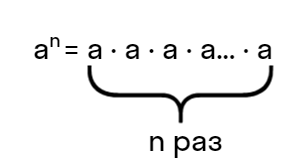
Возвести число в натуральную степень n — значит умножить число само на себя ( n) раз:

( {{a}^{n}}=underbrace{acdot acdot acdot …a}_{n})

Степень с целым показателем {0, ±1, ±2,…}

Если показателем степени является целое положительное число:

( {{a}^{n}}={{a}^{n}}, n>0)

Возведение в нулевую степень:

( {{a}^{0}}=1, ane 0) . ( {{0}^{0}}) – выражение неопределенное, т.к., с одной стороны, ( 0) в любой степени – это ( 0) , а с другой – любое число в ( 0) -ой степени – это ( 1) .

Если показателем степени является целое отрицательное число:

( {{a}^{-n}}=frac{1}{{{a}^{n}}}, ane 0) (т.к. на ( 0) делить нельзя).

Еще раз о нулях: выражение ( {{0}^{k}}) не определено в случае ( kle 0). Если ( k>0) , то ( {{0}^{k}}=0) .

Примеры:

( {{6}^{-1}}=frac{1}{6})

( {{left( frac{3}{2} right)}^{-2}}=frac{4}{9})

Степень с рациональным показателем

Если,

( a>0);
( m) – натуральное число;
( n) – целое число;

Тогда:

( {{a}^{frac{n}{m}}}=sqrt[m]{{{a}^{n}}})

Примеры:

( {{a}^{frac{1}{2}}}=sqrt{a})

( {{a}^{frac{1}{5}}}=sqrt[5]{a})

( {{a}^{-frac{3}{4}}}=frac{1}{sqrt[4]{{{a}^{3}}}})

Свойства степеней

Произведение степеней	( {{a}^{n}}cdot {{a}^{m}}={{a}^{n+m}}) ( {{a}^{n}}cdot {{b}^{n}}={{left( acdot b right)}^{n}})
Деление степеней	( frac{{{a}^{n}}}{{{a}^{m}}}={{a}^{n-m}}) ( frac{{{a}^{n}}}{{{b}^{n}}}={{left( frac{a}{b} right)}^{n}})
Возведение степени в степень	( {{left( {{a}^{m}} right)}^{n}}={{a}^{mcdot n}})

Чтобы проще было решать задачи, попробуем понять: откуда эти свойства взялись? Докажем их.

Доказательства свойств степени

1. ( displaystyle {{a}^{n}}cdot {{a}^{m}}={{a}^{n+m}})

Посмотрим: что такое ( displaystyle {{a}^{n}}) и ( displaystyle {{a}^{m}}) ?

По определению:

Сколько здесь множителей всего? Очень просто: к ( displaystyle n) множителям мы дописали ( displaystyle m) множителей, итого получилось ( displaystyle n+m) множителей.

Итак, в правой части этого выражения получается такое произведение:

( displaystyle {{a}^{n}}cdot {{a}^{m}}=underbrace{acdot acdot …cdot a}_{n+mtext{ множителей}})

Но по определению это степень числа ( displaystyle mathbf{a}) с показателем ( displaystyle mathbf{n}+mathbf{m}), то есть:

( displaystyle {{a}^{n}}cdot {{a}^{m}}={{a}^{n+m}}) , что и требовалось доказать.

Пример: Упростите выражение ( displaystyle {{5}^{4}}cdot {{5}^{7}}cdot {{5}^{9}}) .

Решение: ( displaystyle {{5}^{4}}cdot {{5}^{7}}cdot {{5}^{9}}={{5}^{4+7+9}}={{5}^{20}}) .

Пример: Упростите выражение ( displaystyle {{3}^{5}}cdot {{3}^{8}}cdot {{5}^{7}}) .

Решение: Важно заметить, что в нашем правиле обязательно должны быть одинаковые основания. Поэтому степени с основанием ( displaystyle 3) мы объединяем, а ( displaystyle {{5}^{7}}) остается отдельным множителем:

( displaystyle {{3}^{5}}cdot {{3}^{8}}cdot {{5}^{7}}={{3}^{5+8}}cdot {{5}^{7}}={{3}^{13}}cdot {{5}^{7}}) .

Еще одно важное замечание: это правило – только для произведения степеней!

Ни в коем случае нелья написать, что ( displaystyle {{2}^{4}}+{{2}^{6}}={{2}^{10}}) .

2. ( displaystyle {{a}^{n}}cdot {{b}^{n}}={{left( acdot b right)}^{n}})

Так же, как и с предыдущим свойством, обратимся к определению степени:

Перегруппируем это произведение так:

( displaystyle {{a}^{n}}cdot {{b}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}cdot underbrace{bcdot bcdot …cdot b}_{ntext{ множителей}}=underbrace{left( acdot b right)cdot left( acdot b right)cdot …cdot left( acdot b right)}_{ntext{ множителей}}).

Получается, что выражение ( displaystyle acdot b) умножается само на себя ( displaystyle n) раз, то есть, согласно определению, это и есть ( displaystyle n) -я степень числа ( displaystyle acdot b) :

( displaystyle {{a}^{n}}cdot {{b}^{n}}={{left( acdot b right)}^{n}}), ч.т.д.

По сути это можно назвать «вынесением показателя за скобки». Но никогда нельзя этого делать в сумме: ( displaystyle {{2}^{4}}+{{3}^{4}}ne {{left( 2+3 right)}^{4}}) !

Вспомним формулы сокращенного умножения: сколько раз нам хотелось написать ( displaystyle {{left( a+b right)}^{2}}={{a}^{2}}+{{b}^{2}}) ? Но это неверно, ведь ( displaystyle {{left( a+b right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}) .

3. ( displaystyle frac{{{a}^{n}}}{{{a}^{m}}}={{a}^{n-m}})

И снова используем определение степени:

( displaystyle left. begin{array}{l}{{a}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}\{{a}^{m}}=underbrace{acdot acdot …cdot a}_{mtext{ множителей}}text{ }end{array} right|Rightarrow text{ }frac{{{a}^{n}}}{{{a}^{m}}}=frac{underbrace{acdot acdot …cdot a}_{ntext{ множителей}}}{underbrace{acdot acdot …cdot a}_{mtext{ множителей}}})

Здесь, очевидно, можем сократить. Но с одной оговоркой: чтобы степень получилась натуральная, нам придется предположить, что ( displaystyle n>m) (то есть, в числителе множителей должно быть больше, чем в знаменателе). Тогда ( displaystyle m) множителей числителя сокращаются со всеми ( displaystyle m) множителями знаменателя. Таким образом множители остаются только в числителе, причем в количестве ( displaystyle n-m) штук:

( displaystyle frac{{{a}^{n}}}{{{a}^{m}}}=frac{underbrace{acdot acdot …cdot a}_{ntext{ множителей}}}{underbrace{acdot acdot …cdot a}_{mtext{ множителей}}}=frac{underbrace{acdot acdot …cdot a}_{n-mtext{ множителей}}}{1}={{a}^{n-m}}) , ч.т.д.

4. ( displaystyle frac{{{a}^{n}}}{{{b}^{n}}}={{left( frac{a}{b} right)}^{n}})

Все как обычно – записываем определение степеней ( displaystyle {{a}^{n}}) и ( displaystyle {{b}^{n}}) , делим их друг на друга, разбиваем на пары ( displaystyle frac{a}{b}) и получаем:

( displaystyle left. begin{array}{l}{{a}^{n}}=underbrace{acdot acdot …cdot a}_{ntext{ множителей}}\{{b}^{n}}=underbrace{bcdot bcdot …cdot b}_{ntext{ множителей}}end{array} right|Rightarrow text{ }frac{{{a}^{n}}}{{{b}^{n}}}=frac{underbrace{acdot acdot …cdot a}_{ntext{ множителей}}}{underbrace{bcdot bcdot …cdot b}_{ntext{ множителей}}}=underbrace{frac{a}{b}cdot frac{a}{b}cdot …cdot frac{a}{b}}_{ntext{ множителей}}={{left( frac{a}{b} right)}^{n}}) , ч.т.д.

Прежде чем разобрать последнее правило, решим несколько примеров.

Источник

Что такое степень числа

В учебниках по математике можно встретить такое определение:

«Степенью n числа а является произведение множителей величиной а n раз подряд»

aⁿ — степень,

где:

a — основание степени;

n — показатель степени.

Соответственно:

Читается такое выражение, как a в степени n

Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) само на себя.

А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:

2³ = 2·2·2, где:

2 — основание степени;

3 — показатель степени.

Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.

Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.

Задачка про миллион: представьте, что у вас есть миллион рублей. За один год вы заработали на нем еще два. Еще через год каждый миллион принес еще два и т. д. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.

Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:

3·3·3·3 = 81. То есть получается, что три в степени четыре равно 81.

Математики заскучали и решили все упростить:

3⁴ = 81

Ответ: через четыре года у вас будет 81 миллион.

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Таблица степеней

Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени 2) и куб (показатель степени 3).

Число	Вторая степень	Третья степень
1	1	1
2	4	8
3	9	27
4	16	64
5	25	125
6	36	216
7	49	343
8	64	512
9	81	729
10	100	1000

Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.

Свойства степеней

В математике степень с натуральным показателем имеет несколько важных свойств, которые позволяют упрощать вычисления. Всего их пять штук — ниже мы их рассмотрим.

Мы будем употреблять такие понятия, как натуральные числа, целые числа, рациональные числа, иррациональные числа. Чтобы не запутаться, дадим им определение:

Натуральные числа — это числа, которые мы используем, чтобы считать предметы: один банан, два банана.

Целые числа — это все натуральные числа, все противоположные натуральным числам и число 0.
Рациональными называют числа, которые можно представить в виде обыкновенной дроби. Например: 1/2; −5/3; 8/4.
Иррациональные числа — это бесконечная десятичная дробь. Например, число пи как раз такое — 3,141592…

Все, теперь мы точно готовы разбираться со свойствами степеней. Поехали!

Свойство 1: произведение степеней

При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:

aⁿ · a^m = a^m+n

a — основание степени

m, n — показатели степени, любые натуральные числа.

Свойство 2: частное степеней

Когда мы делим степени с одинаковыми основаниями, основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.

частное степеней

a — любое число, не равное нулю

m, n — любые натуральные числа такие, что m > n

Свойство 3: возведение степени в степень

Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.

(aⁿ)^m = a^{n· m}

a — основание степени

m, n — показатели степени, натуральное число

Свойство 4: возведение в степень произведения

При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.

(a · b)ⁿ = aⁿ · bⁿ

a, b — основание степени

n — показатели степени, натуральное число

Свойство 5: возведение в степень частного

Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.

(a : b)ⁿ = aⁿ : bⁿ

a, b — основание степени, b ≠ 0,

n — показатель степени, натуральное число

Сложение и вычитание степеней

Как складывать числа со степенями и как вычитать степени — очень просто. Основной принцип такой: выполняется сначала возведение в степень, а уже потом действия сложения и вычитания.

2³+ 3⁴= 8 + 81= 89

6³— 3³= 216 — 27 = 189

И еще парочка правил

Если есть скобки — начинать вычисления нужно внутри них
Только потом возводим этот результат из скобок в степень
Затем выполняем остальные действия: сначала умножение и деление по порядку (слева направо), а в конце — сложение и вычитание по порядку (слева направо)

Давай потренируемся

Реши примеры со степенями:

2³ + 2⁴ =
3⁴ + 5⁴ =
6³ − 3³ =
7⁴ − 3² =

В конце статьи ты найдешь правильные ответы.

Примеры умножения и деления степеней

Умножение степеней с одинаковыми показателями

Чтобы произвести умножение степеней с одинаковыми показателями, можно перемножить основания и возвести произведение в степень, показатель которой останется прежним:

aⁿ · bⁿ = (a · b)ⁿ , где

a, b — основание степени (не равное нулю)

n — показатели степени, натуральное число

a⁵ · b⁵ = (a·a·a·a·a) ·(b·b·b·b·b) = (ab)·(ab)·(ab)·(ab)·(ab) = (ab)⁵
3⁵ · 4⁵ = (3·4)⁵ = 12⁵ = 248 832
16a² = 4²·a² = (4a)²

Умножение степеней с одинаковыми основаниями

Степени с одинаковыми основаниями умножаются путём сложения показателей степеней:

a^m · aⁿ= a^m+n, где

a — основание степени

m, n — показатели степени, любые натуральные числа

3⁵ · 3² = 3^{5 + 2} = 3⁷ = 2 187
2⁸ · 8¹= 2⁸ · 2³ = 2^{8 + 3} = 2¹¹ = 2048

Умножение степеней с разными основаниями и показателями

Если разные и показатели, и основания, и одна из степеней не преобразуется в число с тем же основанием, как у другой степени (как здесь: 2⁸ · 8¹= 2⁸ · 2³ = 2¹¹ = 2048), то производим возведение в степень каждого числа и лишь затем умножаем:

3³ · 5² = 27·25 = 675

Деление степеней с одинаковыми основаниями и одинаковыми показателями

Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным. формула деления степеней с разными основаниями

a — любое число, не равное нулю

m, n — любые натуральные числа такие, что m > n

Деление чисел с одинаковыми показателями степени

При делении степеней с одинаковыми показателями результат частного этих чисел возводится в степень:

aⁿ : bⁿ = (a : b)ⁿ , где

a, b — основание степени, b ≠ 0,

n — показатель степени, натуральное число

Пример:

5³ : 2³ = (5 : 2)³ = 2,5³ = 15,625

Деление степеней с разными основаниями и показателями

Если разные и показатели, и основания, то возводим в степень каждое число и только потом делим:

3³ ÷5² = 27÷25 = 1,08

Степень с отрицательным показателем и её свойства

Число с отрицательным показателем степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:

Степень с отрицательным показателем

Примеры

Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.

Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.

напоминание формулы частного степеней

Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:

a³÷a⁶=a^{3 — 6} = a^-3

Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:

запись деления в виде дроби

Умножение отрицательных степеней

При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются, так же как и при умножении положительных степеней:

a^m · aⁿ = a^m+n

Примеры

примеры умножения отрицательных степеней

Деление отрицательных степеней

При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя, так же как и при делении положительных степеней:

формула второго свойства степеней

Примеры

Возведение дроби в отрицательную степень

Возведение произведения в отрицательную степень

формула возведения произведения в отрицательную степень

Как представить число в виде степени

Чтобы представить число в виде степени, нужно разложить его на простые множители. Если в произведении встречаются несколько одинаковых сомножителей, то это произведение записывается в виде степени.

Например, представим в виде степени число 243:

243 = 3 × 3 × 3 × 3 × 3 = 3⁵

Ответы на вопросы для самопроверки

24
706
189
2392

Источник

Степени и их свойства

Данная тема очень легкая, если выучить все свойства степеней. Они, кстати, достаточно просты для запоминания.

Перед тем, как перейти в свойствам степеней, разберемся, что такое степень.

Степень — это произведение одинаковых множителей, состоящая из основания и показателя. Наглядно это можно рассмотреть на рисунке ниже.

Показатель степени показывает (масло масляное) сколько раз мы умножаем основание на себя. Это очень хорошо проглядывается на следующих примерах:

Вроде бы ничего сложного нет, правда?

Что ж, время перейти к свойствам.

Свойства степеней.

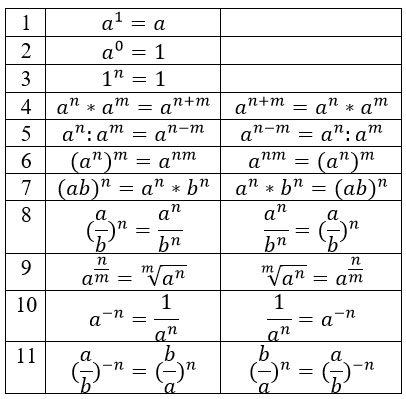
1. Любое число в первой степени равно самому себе: a¹ = a.

Сразу рассмотрим примеры.

2¹ = 2;

(-10)¹ = -10;

0¹ = 0.

2. Любое число в нулевой степени равно 1: а⁰ = 1.

Примеры:

2⁰ = 1;

(-3)⁰ = 1;

0⁰ = 1.

3. Единица в любой степени равна 1: 1ⁿ = 1.

4. При умножении степеней с одинаковыми основаниями показатели складываются: aⁿ · a^m = a^{n + m}.

Почему так?

Это свойство легко доказать на числовом примере.

2³ · 2² = 2 · 2 · 2 · 2 · 2 = 2⁵.

Конечно, так никто не расписывает, а сразу пользуется готовой формулой. Вот еще несколько примеров:

3⁴ · 3⁹ · 3¹⁵ = 3^{4 + 9 + 15} = 3²⁸;

(-2)³ · (-2)⁴ = (-2)^{3 + 4} = (-2)⁷.

5. При делении степеней с одинаковыми основаниями показатели вычитаются: aⁿ : a^m = a^{n — m}(a ≠ 0).

Доказывается эта формула тоже очень просто с помощью числового примера: три четверки из числителя сокращаем с тремя четверками из знаменателя и остаются две четверки в числителе, т.е. 4².

Еще парочка примеров:

15¹⁰ : 15³ : 15⁵ = 15^{10 — 3 — 5} = 10²;

(-3)¹¹ : (-3)⁵ = (-3)^{11 — 5} = (-3)⁶.

6. При возведении степени в степень показатели умножаются: (аⁿ)^m= a^nm.

Примеры:

(2²)³ = 2^{2 · 3} = 2⁶;

(5³)¹⁰ = 5^{3 · 10} = 5³⁰.

7. При возведении произведения в степень каждый множитель возводится в эту степень: (ab)ⁿ = aⁿbⁿ.

Примеры:

(5 · 4)² = 5² · 4²;

(2 · 3 · 4 · 5)^а= 2^а · 3^а · 4^а ·5^а.

8. Чтобы возвести дробь в степень надо и числитель, и знаменатель возвести в эту степень:.

Пример:

9. Степень с дробным показателем можно представить в виде корня некоторой степени по формуле (а > 0, n ≥ 2).

Пример:

10. Чтобы возвести число, отличное от нуля, в степень с отрицательным показателем надо взять число, обратное данному, и возвести его в ту же степень, только без минуса: (a ≠ 0).

Это же правило работает и для дробей: (a ≠ 0, b ≠ 0).

Примеры:

Все эти свойства срабатывают как в одну сторону, так и в другую. Соберем их в аккуратную табличку.

Напоследок, разберем пример, который может встретиться во второй части ОГЭ по математике. Он, конечно, не охватывает сразу все формулы — только несколько из них.

Нам нужно сократить такую дробь:

Преобразуем знаменатель дроби, дважды использовав формулу по номером 5 из второго столбика таблицы.

Получившиеся частные в знаменателе запишем в виде дробей.

Получилась трехярусная дробь (можно произведение дробей в знаменателе переписать под одну черту). Нижний ярус этой дроби перейдет в верхний. Это не магия вне Хогвартса, но описывать эти преобразования текстом очень грустно. Если коротенько, то при делении на дробь мы ее переворачиваем и получается, что знаменатель заползает наверх

К тому же здесь можно воспользоваться свойством 6 из второго столбика и 4²ⁿпревратится в 16ⁿ.

Переходим к финалу. Преобразуем знаменатель по свойству 7 из второго столбика таблицы (снова) и, наконец-таки, сокращаем дробь!

Успехов в учебе!

С уважением, Васильева Анна.

Источник

20
Фев 2013

Категория: Справочные материалы

Степень числа. Корень

Елена Репина
2013-02-20
2021-06-17

Автор: egeMax |

комментариев 10
| Метки: Степень, шпаргалки-таблицы

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Печать страницы

Материалы для подготовки к ЕГЭ
Рубрики
- 01 Геометрия (13)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (78)
- 13 (С2) Стереометр. задачи (94)
- 14 (С3) Неравенства (89)
- 15 (С4) Практич. задачи (71)
- 16 (С5) Планиметр. задачи (86)
- 17 (С6) Параметры* (79)
- 18 (С7) Числа, их свойства (38)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (60)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина
ЕгэТренер – О. Себедаш
Математика?Легко!
Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы

Источник

Корни и степени

Степень с натуральным показателем
Степень с целым показателем
Кубический корень
Корень -ной степени
Сравнение арифметических корней
Как избавиться от иррациональности в знаменателе
Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения

Степенью называется выражение вида a^c .

Здесь — основание степени, — показатель степени.

к оглавлению ▴

Степень с натуральным показателем

Проще всего определяется степень с натуральным (то есть целым положительным) показателем.

По определению, a^1=a .

Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.

Возвести число в куб — значит умножить его само на себя три раза.

Возвести число в натуральную степень — значит умножить его само на себя раз:

a^n= $underbrace{a cdot a cdot a cdot a cdot ldots cdot a}_{displaystyle n}.$

к оглавлению ▴

Степень с целым показателем

Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.

По определению,

a^0=1 .

Это верно для aneq 0 . Выражение 0⁰ не определено.

Определим также, что такое степень с целым отрицательным показателем.

$a^{-1}=genfrac{}{}{}{0}{1}{a};$

$a^{-2}=genfrac{}{}{}{0}{1}{a^2};$

$a^{-n}=genfrac{}{}{}{0}{1}{a^n}.$

Конечно, все это верно для aneq 0 , поскольку на ноль делить нельзя.

Например,

$5^{-2}=genfrac{}{}{}{0}{1}{5^2};$

$left( genfrac{}{}{}{0}{1}{2} right)^{-1}=2;$

$left( genfrac{}{}{}{0}{2}{7} right)^{-1}=genfrac{}{}{}{0}{7}{2}.$

Заметим, что при возведении в минус первую степень дробь переворачивается.

$left( genfrac{}{}{}{0}{5}{3} right)^{-2}=1 : left( genfrac{}{}{}{0}{5}{3} right)^{2}=left( genfrac{}{}{}{0}{3}{5} right)^{2}=genfrac{}{}{}{0}{9}{25}.$

Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби $genfrac{}{}{}{0}{p}{q}$ , где — целое, — натуральное.

Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.

Определение.

Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен .

Согласно определению, $left (sqrt{a} right )^2=a; , , sqrt{a}geq 0; , , ageq 0.$

В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение sqrt{a} для нас сейчас имеет смысл только при ageq 0 .

Выражение sqrt{a} всегда неотрицательно, т.е. . Например, .

Свойства арифметического квадратного корня:

$sqrt{ab}=sqrt{a} cdot sqrt{b}, ; sqrt{a^2}=left|aright| , ; sqrt{a^{2n}}={left|aright|}^n;$

$sqrt{genfrac{}{}{}{0}{a}{b}}=genfrac{}{}{}{0}{sqrt{a}}{sqrt{b}}.$

Запомним важное правило: $sqrt{a^2}=left|aright| .$

По определению, .

к оглавлению ▴

Кубический корень

Аналогично, кубический корень из — это такое число, которое при возведении в третью степень дает число .

$left( sqrt[leftroot{3}scriptstyle 3]{a} right) ^3 = sqrt[leftroot{3}scriptstyle 3]{a} cdot sqrt[leftroot{3}scriptstyle 3]{a} cdot sqrt[leftroot{3}scriptstyle 3]{a}.$

Например, , так как ;

, так как ;

$sqrt[leftroot{3}scriptstyle 3]{-genfrac{}{}{}{0}{1}{125}} = -genfrac{}{}{}{0}{1}{5}$ , так как $left( -genfrac{}{}{}{0}{1}{5} right) ^3 = -genfrac{}{}{}{0}{1}{125}$ .

Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.

Теперь мы можем дать определение корня -ной степени для любого целого .

к оглавлению ▴

Корень -ной степени

Корень -ной степени из числа — это такое число, при возведении которого в -ную степень получается число .

Например,

Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.

Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.

Итак, — такое число, что $left( sqrt[leftroot{3}scriptstyle n]{a} right) ^n = a$ . Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.

По определению,

$a^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 2}} = sqrt{a},$

$a^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 3}} = sqrt[leftroot{3}scriptstyle 3]{a},$

в общем случае $a^{frac{1}{n}} = sqrt[leftroot{3}scriptstyle n]{a}.$ .

Сразу договоримся, что основание степени больше 0.

Например,

$25^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 2}} = 5;$

$8^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 3}} = 2;$

$81^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 4}} = 3;$

$100000^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 5}} = 10;$

$0,001^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 3}} = 0,1.$

Выражение $a^{genfrac{}{}{}{3}{scriptstyle m}{scriptstyle n}}$ по определению равно $sqrt[leftroot{3}scriptstyle n]{a^m}$ .

При этом также выполняется условие, что больше 0.

$a^{genfrac{}{}{}{3}{scriptstyle m}{scriptstyle n}} = sqrt[leftroot{3}scriptstyle n]{a^m} = left( sqrt[leftroot{3}scriptstyle n]{a} right) ^m.$

Например,

$8^{genfrac{}{}{}{3}{scriptstyle 4}{scriptstyle 3}} = left( sqrt[leftroot{3} scriptstyle 3]{8} right) ^4 = 2^4 = 16;$

$a^{genfrac{}{}{}{3}{scriptstyle 3}{scriptstyle 5}} = sqrt[leftroot{3} scriptstyle 5]{a^3} = left( sqrt[leftroot{3} scriptstyle n]{a} right) ^m;$

$b^{-genfrac{}{}{}{3}{scriptstyle 2}{scriptstyle 3}} = genfrac{}{}{}{0}{1}{sqrt[leftroot{3} scriptstyle 3]{b^2}}.$

Запомним правила действий со степенями:

$a^ma^n = a^{m+n}$ — при перемножении степеней показатели складываются;

$genfrac{}{}{}{0}{a^m}{a^n} = a^{m-n}$ — при делении степени на степень показатели вычитаются;

$left( a^m right) ^n = left( a^n right) ^m = a^{mn}$ — при возведении степени в степень показатели перемножаются;

$genfrac{}{}{}{0}{a^n}{b^n} = left( genfrac{}{}{}{0}{a}{b} right) ^n.$

Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:

1. $genfrac{}{}{}{0}{sqrt{ mathstrut 2,8} cdot sqrt{ mathstrut 4,2}}{sqrt{ mathstrut 0,24}}= sqrt{ mathstrut genfrac{}{}{}{0}{2,8 cdot 4,2}{0,24}} = sqrt{ mathstrut genfrac{}{}{}{0}{28 cdot 42}{24}}=sqrt{ mathstrut genfrac{}{}{}{0}{7 cdot 4 cdot 7 cdot 6}{4 cdot 6}} =$

Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.

2. $genfrac{}{}{}{0}{left( 2 sqrt{7} right) ^2}{14}= genfrac{}{}{}{0}{ 2^2 cdot left( sqrt{7} right) ^2}{14} = genfrac{}{}{}{0}{4 cdot 7}{14} = 2.$

3. $genfrac{}{}{}{0}{ sqrt[leftroot{3} scriptstyle 9]{7} cdot sqrt[leftroot{3} scriptstyle 18]{7}}{sqrt[leftroot{3} scriptstyle 6]{7}}=genfrac{}{}{}{0}{7^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 9}} cdot 7^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 18}}}{7^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 6}}}=7^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 9} + genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 18}- genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 6}}= 7^{genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 6} - genfrac{}{}{}{3}{scriptstyle 1}{scriptstyle 6}}=7^0=1.$

Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.
4. Найдите значение выражения $displaystyle frac{11a^6b^3-{left(3a^2bright)}^3}{4a^6b^6}$ при b = 2.

Решение:

$displaystyle frac{11a^6b^3-{left(3a^2bright)}^3}{4a^6b^6}=displaystyle frac{11a^6b^3-{27a^6b}^3}{4a^6b^6}=displaystyle frac{-16a^6b^3}{4a^6b^6}=-displaystyle frac{4}{b^3}.$

При b = 2 получим $-displaystyle frac{4}{2^3}=-displaystyle frac{4}{8}=-0,5 .$

Ответ: -0,5.

5. Найдите значение выражения $displaystyle frac{a^{3,21} cdot a^{7,36}}{a^{8,57}}$ при a=12 .

Решение:

$displaystyle frac{a^{3,21} cdot a^{7,36}}{a^{8,57}}=displaystyle frac{a^{3,21+7,36}}{a^{8,57}}=displaystyle frac{a^{10,57}}{a^{8,57}}=a^{10,57-8,57}=a^2.$

При a = 12 получим ${12}^2=144.$

Мы воспользовались свойствами степеней.

Ответ: 144.

6. Найдите значение выражения $displaystyle frac{{left(b^{sqrt{3}}right)}^{2sqrt{3}}}{b^4}$ при b = — 5.

Решение: $displaystyle frac{{left(b^{sqrt{3}}right)}^{2sqrt{3}}}{b^3}=displaystyle frac{b^{sqrt{3} cdot 2sqrt{3}}}{b^3}=displaystyle frac{b^6}{b^3}=b^3 .$

При b = — 5 получим: ${(-5)}^3=-125 .$

Ответ: -125.

7. Расположите в порядке возрастания: ${left(displaystyle frac{7}{8}right)}^{-3};$ $displaystyle frac{7}{8};$ ${left(displaystyle frac{8}{7}right)}^{-3}.$

Решение:

Запишем выражения как степени с положительным показателем и сравним.

$left(displaystyle frac{7}{8}right)^-3=left(displaystyle frac{8}{7}right)^3.$ Так как $displaystyle frac{8}{7} textgreater 1,$ то $left(displaystyle frac{8}{7}right)^3 textgreater 1.$

$left(displaystyle frac{8}{7}right)^-3=left(displaystyle frac{7}{8}right)^3.$ Так как $displaystyle frac{7}{8} textless 1,$ то $left(displaystyle frac{7}{8}right)^3 textless 1.$

Сравним $displaystyle frac{7}{8}$ и ${left(displaystyle frac{7}{8}right)}^3,$ для этого оценим их разность:

$displaystyle frac{7}{8} - {left(displaystyle frac{7}{8}right)}^3=displaystyle frac{7}{8} - displaystyle frac{7^3}{8^3}=displaystyle frac{7 cdot 8^2-7^3}{8^3}=displaystyle frac{7(8^2-7^2)}{8^3}=displaystyle frac{7(64-49)}{8^3} textgreater 0 ,$ значит $displaystyle frac{7}{8} textgreater {left(displaystyle frac{7}{8}right)}^3 .$

Получим : ${left(displaystyle frac{7}{8}right)}^3 textless displaystyle frac{7}{8} textless {left(displaystyle frac{8}{7}right)}^3 ,$ поэтому ${left(displaystyle frac{8}{7}right)}^{-3} ; displaystyle frac{7}{8} ; {left(displaystyle frac{7}{8}right)}^{-3} .$

Ответ: ${left(displaystyle frac{8}{7}right)}^{-3}; displaystyle frac{7}{8} ; {left(displaystyle frac{7}{8}right)}^{-3}.$

8. Представьте выражение в виде степени: $displaystyle frac{x^{-6}+x^{-4}+x^{-2}}{x^2+x^4+x^6}.$

Решение:

Вынесем за скобку степень с меньшим показателем:

$displaystyle frac{x^{-6}+x^{-4}+x^{-2}}{x^2+x^4+x^6}=displaystyle frac{x^{-6}(1+x^2+x^4)}{x^2(1+x^2+x^4)}=displaystyle frac{x^{-6}}{x^2}=x^{-6-2}=x^{-8}.$

Ответ: $x^{-8} .$

9. Упростите выражение: $displaystyle frac{2^{2n-1} cdot 3^{n+1}}{6 cdot {12}^n} .$

Решение:

Приведем основания 6 и 12 к основаниям 2 и 3:

$displaystyle frac{2^{2n-1} cdot 3^{n+1}}{6 cdot {12}^n}=displaystyle frac{2^{2n-1} cdot 3^{n+1}}{2 cdot 3 cdot {(2^2 cdot 3 )}^n}= displaystyle frac{2^{2n-1} cdot 3^{n+1}}{2^1cdot 3^1cdot 2^{2n} cdot 3^n} =$

(выполним деление степеней с одинаковыми основаниями)

$= 2^{2n-1-1-2n}cdot 3^{n+1-1-n}=2^{-2}cdot 3^0=displaystyle frac{1}{2^2}cdot 1=displaystyle frac{1}{4} = 0,25.$

Ответ: 0,25.

10. Чему равно значение выражения $displaystyle frac{a^{-4}cdot { a}^{-3}}{a^{-5}}$ при $a=displaystyle frac{1}{3}$ ?

Решение:

$displaystyle frac{a^{-4}cdot { a}^{-3}}{a^{-5}}=a^{-4+left(-3right)-(-5)}=a^{-2}.$

При $a=displaystyle frac{1}{3},$ получим ${left(displaystyle frac{1}{3}right)}^{-2}=3^2=9.$

Ответ: 9.

к оглавлению ▴

Сравнение арифметических корней

11. Какое из чисел больше: или ?

Решение:

Возведем в квадрат оба числа (числа положительные):

${left(sqrt{5}+sqrt{6}right)}^2= 5 + 2sqrt{5cdot 6}+6=11+2sqrt{30};$

${left(2+7right)}^2={left(sqrt{4}+sqrt{7}right)}^2= 4 + 2sqrt{4cdot 7}+7=11+2sqrt{28}.$

Найдем разность полученных результатов:

так как

Значит, первое число больше второго.

Ответ:

к оглавлению ▴

Как избавиться от иррациональности в знаменателе

Если дана дробь вида $displaystyle frac{a}{sqrt{b}},$ то нужно умножить числитель и знаменатель дроби на sqrt{b} :

$displaystyle frac{a}{sqrt{b}} = displaystyle frac{a cdot sqrt{b}}{sqrt{b}cdot sqrt{b}} = displaystyle frac{a cdot sqrt{b}}{sqrt{b}^2} = displaystyle frac{a cdot sqrt{b}}{b}.$

Тогда знаменатель станет рациональным.

Если дана дробь вида $displaystyle frac{c}{ a pm sqrt{b}}$ или $displaystyle frac{c}{ sqrt{a} pm sqrt{b}},$ то нужно умножить числитель и знаменатель дроби на сопряженное выражение, чтобы получить в знаменателе разность квадратов.

Сопряженные выражения — это выражения, отличающиеся только знаками. Например,

и и — сопряженные выражения.

Пример:

$displaystyle frac{c}{sqrt{a}-sqrt{b}}=displaystyle frac{c (sqrt{a}+ sqrt{b})}{ (sqrt{a}- sqrt{b})(sqrt{a}+ sqrt{b})}=$

$=displaystyle frac{c (sqrt{a}+sqrt{b})}{{ left(sqrt{a}right)}^2-{left(sqrt{b}right)}^2 }=displaystyle frac{c(sqrt{a}+ sqrt{b})}{a-b } .$

12. Вот несколько примеров — как избавиться от иррациональности в знаменателе:

Пример 1.

$displaystyle frac{2}{sqrt{27}}= displaystyle frac{2 cdot sqrt{3}}{sqrt{3^3} cdot sqrt{3}}=displaystyle frac{2 sqrt{3}}{sqrt{3^4} }=displaystyle frac{2 sqrt{3}}{9}.$

Пример 2.

$displaystyle frac{6}{1+sqrt{3}} = displaystyle frac{6(sqrt{3}-1)}{(sqrt{3}+1)(sqrt{3}-1)}=displaystyle frac{6(sqrt{3}-1)}{3-1}=$

$=displaystyle frac{6(sqrt{3}-1)}{2}=3(sqrt{3}-1).$

Пример 3.

$displaystyle frac{33}{7-3sqrt{3}} = displaystyle frac{33(7+3sqrt{3})}{(7-3sqrt{3})(7+3sqrt{3})}= displaystyle frac{33(7+3sqrt{3})}{49 -9 cdot 3}=$

$displaystyle frac{33(7+3sqrt{3})}{22}=displaystyle frac{3(7+3sqrt{3})}{2}.$

Пример 4.

$displaystyle frac{12}{sqrt{3}+sqrt{6}}=displaystyle frac{12(sqrt{6}-sqrt{3})}{(sqrt{3}+sqrt{6})(sqrt{6}-sqrt{3})}=displaystyle frac{12(sqrt{6}-sqrt{3})}{6-3}=$

$=displaystyle frac{12(sqrt{6}-sqrt{3})}{3}=4(sqrt{6}-sqrt{3}).$

Совет. Если в знаменателе дана сумма двух корней, то в разности первым числом пишите то, которое больше, и тогда разность квадратов корней будет положительным числом.

Пример 5.

$displaystyle frac{5+3sqrt{3}}{sqrt{3}+2}= displaystyle frac{(5+3sqrt{3})(2-sqrt{3})}{(sqrt{3}+2)(2-sqrt{3})}=$

$=displaystyle frac{10+6sqrt{3}-5sqrt{3}-9}{2^2-{(sqrt{3} )}^2}=displaystyle frac{1+sqrt{3}}{4-3}= 1+sqrt{3}.$

13. Сравните и $displaystyle frac{1}{7+4sqrt{3}}+displaystyle frac{1}{7-4sqrt{3}}.$

1) $displaystyle frac{1}{7+4sqrt{3}}+displaystyle frac{1}{7-4sqrt{3}}=displaystyle frac{7-4sqrt{3}+7+4sqrt{3}}{(7+4sqrt{3})(7-4sqrt{3})}=displaystyle frac{14}{7^2-{(4sqrt{3})}^2}=$

$=displaystyle frac{14}{49-48}=14.$

2) Сравним и 14.

$14 = sqrt{{14}^2}=sqrt{196},$ то и а значит,

$sqrt{140} textless displaystyle frac{1}{7+4sqrt{3}}+displaystyle frac{1}{7-4sqrt{3}} .$

Ответ: меньше.

к оглавлению ▴

Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения

Покажем несколько примеров.

14. Упростите: выражения:

Пример 5.

$sqrt{3-2sqrt{2}}=sqrt{2+1-2sqrt{2}}=sqrt{{left(sqrt{2}right)}^2-2cdot 1cdot sqrt{2}+1}=$

$=sqrt{{left(sqrt{2}-1right)}^2} = left|sqrt{2}-1right| = sqrt{2}-1,$ т.к.

Пример 6.

$sqrt{7+4sqrt{3}} = sqrt{4+3+4sqrt{3 }}=sqrt{2^2+2cdot 2cdot sqrt{3 }+{(sqrt{3 })}^2} =$

$= sqrt{{(2+sqrt{3})}^2} = 2+sqrt{3}.$

Пример 7.

$sqrt{19-8sqrt{3}} = sqrt{16+3-8sqrt{3 }}=sqrt{4^2-2cdot 4cdot sqrt{3 }+{(sqrt{3 })}^2} =$

$=sqrt{{(4-sqrt{3})}^2} = 4-sqrt{3},$

так как

Следующие несколько задач решаются с помощью формулы:

$sqrt{a^2}=left|aright|.$

Решение:

$sqrt{{(5-2x)}^2}=left|5-2xright|.$

Получим уравнение

Ответ:

19. Вычислите значение выражения: $sqrt{{(sqrt{3}-1)}^2}+sqrt{{(sqrt{3}-2)}^2}.$

Решение:

$sqrt{(sqrt{3}-1)^2}+sqrt{(sqrt{3}-2)^2}=|sqrt{3}-1|+|sqrt{3}-2|=$

Ответ: 1.

20. Вычислите значение выражения: $sqrt{{(2-sqrt{5})}^2}+sqrt{{(3-sqrt{5})}^2}.$

Решение: $sqrt{{(2-sqrt{5})}^2}+sqrt{{(3-sqrt{5})}^2}= left|2-sqrt{5}right|+left|3-sqrt{5}right|=$

Ответ: 1.

21. Вычислите значение выражения: $(x - 3) sqrt{displaystyle frac{1}{x^2-6x+9}},$ если

Решение. $(x - 3) sqrt{displaystyle frac{1}{x^2-6x+9}}=left(x - 3right)sqrt{displaystyle frac{1}{{left(x-3right)}^2}}=displaystyle frac{x-3}{left|x-3right|}=$

$=displaystyle frac{x-3}{3-x}=-1.$

Если то следовательно

Ответ: — 1.

22. Вычислите:

Решение: $left(sqrt{3}-2right)left(sqrt{7+4sqrt{3}}right) = sqrt{{left(sqrt{3}-2right)}^2(7+4sqrt{3}})=$

$=sqrt{left(3-4sqrt{3}+4right)left(7+4sqrt{3}right)}=sqrt{left(7-4sqrt{3}right)left(7+4sqrt{3}right)}=sqrt{7^2-{left(4sqrt{3}right)}^2}=$

Ответ: 1.

Рассмотрим уравнение вида где

Это равенство выполняется, только если

Подробно об таких уравнениях — в статье «Показательные уравнения».

При решении уравнений такого вида мы пользуемся монотонностью показательной функции.

23. Решите уравнение:

а) $2^{3-x}=16;$

б) ${27}^{displaystyle frac{1}{3}x-1}-3=0;$

в) ${left(displaystyle frac{1}{sqrt{3}}right)}^{2x+1}={left(3sqrt{3}right)}^x.$

Решение.

23. Решите уравнение: $2^{3-x}=16.$

Решение:

$2^{3-x}=2^4,$ тогда

Ответ: -1.

24. Решите уравнение:

${27}^{displaystyle frac{1}{3}x-1}-3=0.$

Решение:

${left(3^3right)}^{left(displaystyle frac{1}{3}x-1right)}=3 , ; 3^{3left(displaystyle frac{1}{3}x-1right)}=3^1;$

$3left(displaystyle frac{1}{3}x-1right)=1, ; x - 3 = 1, ; x = 4.$

Ответ: 4.

25. Решите уравнение: ${left(displaystyle frac{1}{sqrt{3}}right)}^{2x+1}={left(3sqrt{3}right)}^x.$

Решение:

${left(3^{- displaystyle frac{1}{2}}right)}^{2x+1}={left(3^{1+ displaystyle frac{1}{2}}right)}^x ,; ; 3^{-displaystyle frac{1}{2} cdot (2x+1)}=3^{displaystyle frac{3}{2}x}.$

Значит, $-displaystyle frac{1}{2} cdot left(2x+1right)=displaystyle frac{3}{2}x,$ $x = -displaystyle frac{1}{5}.$

Ответ: -0,2.

Если вы хотите разобрать большее количество примеров — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Корни и степени» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Свойства степеней

Для того, чтобы возвести число в степень с натуральным показателем n , нужно умножить число само на себя (n) раз:

где a – основание, n – показатель степень.

Для проведения вычислений удобно использовать формулы преобразования выражений со степенями. Они универсальны и работают для любых показателей (целых, рациональных или иррациональных):

Любое число в нулевой степени равно единице.

(a^{0} = 1)

Любое число в первой степени равно самому себе.

(a^{1} = a)

Единица в любой степени равна единице.

(1^{n} = 1)

При перемножении степеней с одинаковыми основаниями их степени складываются. А основание не меняется.

(a^{n} bullet a^{m} = a^{n + m})

При делении степеней с одинаковыми основаниями из показателя делимого вычитается показатель делителя, а основание не меняется.

(frac{a^{n}}{a^{m}} = a^{n – m})

При возведении степени в степень показатели перемножаются, а основание не меняется.

({{(a}^{n})}^{m} = a^{n bullet m})

Степень произведения равна произведению степеней

(left( text{ab} right)^{n} = a^{n} bullet b^{n})

Степень частного равна частному степеней.

(left( frac{a}{b} right)^{n} = frac{a^{n}}{b^{n}})

При возведении в отрицательную степень основание «переворачивается», а знак показателя степени меняется на противоположный.

(a^{– n} = left( frac{1}{a} right)^{n})

Применим эти правила для решения следующих задач.

Пример №1:

(frac{3^{5}}{3^{3}} = 3^{5 – 3} = 3^{2} = 9)

Воспользуемся формулой для частного степеней с одинаковыми основаниями (п.5).

Пример №2:

(frac{20^{3}}{10^{3}} = left( frac{20}{10} right)^{3} = 2^{3} =

Так как степень частного равна частному степеней, занесем всю дробь под одну степень (п.8).

Пример №3:

(frac{1}{2^{–2}} = frac{1^{–2}}{2^{–2}} = left( frac{1}{2} right)^{–2} = 2^{2} = 4)

Для удобства представим (1 = 1^{- 2}) (п.3) и занесем всю дробь под одну степень (п.9).

Пример №4:

(frac{a^{2} cdot left( a^{frac{5}{2}} right)^{2}}{a^{7}} = frac{a^{2} cdot a^{frac{5}{2} cdot 2}}{a^{7}} = a^{2 + 5 — 7} = a^{0} = 1 )

Возведем степень в степень, перемножая показатели (п.6). Так как все основания одинаковые, то заменим произведение степеней на сумму показателей (п.4), а частное – на разность (п.5). Основание при этом не меняем. Любое число в нулевой степени равно единице (п.1).

Источник

Примеры из жизни

Определение степени

Степень с натуральным показателем {n = 1, 2, 3,…}

Степень с целым показателем {0, ±1, ±2,…}

Степень с рациональным показателем

Доказательства свойств степени

Что такое степень числа

Таблица степеней

Свойства степеней

Свойство 1: произведение степеней

Свойство 2: частное степеней

Свойство 3: возведение степени в степень

Свойство 4: возведение в степень произведения

Свойство 5: возведение в степень частного

Сложение и вычитание степеней

Давай потренируемся

Примеры умножения и деления степеней

Умножение степеней с одинаковыми показателями

Умножение степеней с одинаковыми основаниями

Умножение степеней с разными основаниями и показателями

Деление степеней с одинаковыми основаниями и одинаковыми показателями

Деление чисел с одинаковыми показателями степени

Деление степеней с разными основаниями и показателями

Степень с отрицательным показателем и её свойства

Умножение отрицательных степеней

Деление отрицательных степеней

Возведение дроби в отрицательную степень

Возведение произведения в отрицательную степень

Как представить число в виде степени

Ответы на вопросы для самопроверки

Степени и их свойства

Степень числа. Корень

Корни и степени

Степень с натуральным показателем

Степень с целым показателем

Кубический корень

Корень <img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://l.wordpress.com/latex.php?latex=n&amp;bg=FFFFFF&amp;fg=000000&amp;s=1" title="n" alt="n" />-ной степени

Сравнение арифметических корней

Как избавиться от иррациональности в знаменателе

Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения

Свойства степеней

Корень -ной степени