Все теоремы для егэ по математике профильный уровень

Профильный ЕГЭ по математике сдают не все. Это вариант для тех, кто намерен поступить в технический Вуз или освоить профессию, связанную с экономикой или математикой. Чтобы сдать данный экзамен, вам нужно будет показать глубокие знания предмета.

Основные требования

Во время сдачи базового госэкзамена вам понадобятся познания, которые были получены из школьного курса алгебры и геометрии. Вы должны уметь решать разнообразные неравенства и уравнения, а также знать терминологию и алгоритмы решения разных задач. А вот чтобы выполнить тесты высокой сложности, вы должны знать:

• планиметрию;
• стереометрию;
• прогрессию.

Помимо этого от учащегося потребуется знание финансовой математики и умение работать с параметрическими системами, уравнениями, неравенствами, процентами.

Во время подготовки вам придется повторить теорию. При этом вы должны совмещать ее с практикой, чтобы уметь применять все выученные правила, теоремы, аксиомы.

Принципы подготовительного процесса

С самого начала года необходимо готовиться к ЕГЭ. Благодаря этому можно качественно усвоить весь необходимый материал.

Желательно повторять вслух все прочитанное, чтобы запомнить правила.

Некоторые аксиомы и теоремы нужно будет просто выучить. А после этого применять их при работе с тренировочными упражнениями.

Если вы готовитесь вместе с одноклассниками, контролируйте друг друга. Так материал быстрее усвоится.

Анализируйте ошибки во время решения задач. Благодаря этому вы значительно продвинетесь в подготовке.

Не забывайте про решение практических заданий. Во время сдачи тестирования этот навык вам очень пригодится.

Геометрия

• Треугольник
• Четырехугольники
• Окружность и круг
• Призма
• Пирамида
• Усеченная пирамида
• Цилиндр
• Конус
• Усеченный конус
• Сфера и шар

1. Формулы сокращённого умножения

Наверх

2. Модуль числа

Определение:

Основные свойства модуля:

Наверх

3. Степень с действительным показателем

Свойства степени с действительным показателем

Пусть Тогда верны следующие соотношения:

Наверх

4. Корень n-ой степени из числа

Корнем n-ой степени из числа a называется число, n-ая степень которого равна a.
Арифметическим корнем четной степени n из неотрицательного числа a называется неотрицательное число, n-ая степень которого равна a.

Основные свойства арифметического корня:

Наверх

5. Логарифмы

Определение логарифма:

Основное логарифмическое тождество:

Основные свойства логарифмов

Пусть Тогда верны следующие соотношения:

Наверх

6. Арифметическая прогрессия

Формула n-го члена арифметической прогрессии:

Характеристическое свойство арифметической прогрессии:

Сумма n первых членов арифметической прогрессии:

При решении задач, связанных с арифметической прогрессией, могут оказаться полезными также следующие формулы:

Наверх

7. Геометрическая прогрессия

Формула n-го члена геометрической прогрессии:

Характеристическое свойство геометрической прогрессии:

Сумма n первых членов геометрической прогрессии:

При решении задач, связанных с геометрической прогрессией, могут оказаться полезными также следующие формулы:

Наверх

8. Бесконечно убывающая геометрическая прогрессия

Сумма бесконечно убывающей геометрической прогрессии:

Наверх

9. Основные формулы тригонометрии

Зависимость между тригонометрическими функциями одного аргумента:

Формулы сложения:

Формулы тригонометрических функций двойного аргумента:

Формулы понижения степени:

Формулы приведения

Все формулы приведения получаются из соответствующих формул сложения. Например:

Применение формул приведения укладывается в следующую схему:

— определяется координатная четверть, в которой лежит аргумент приводимой функции, считая, что ;

— определяется знак приводимой функции;

— определяется название приведенной функции по следующему правилу: если аргумент приводимой функции имеет вид или , то функция меняется на сходственную функцию, если аргумент приводимой функции имеет вид , то функция названия не меняет.

Например, получим формулу :

— — IV четверть;

— в IV четверти тангенс отрицательный;

— аргумент приводимой функции имеет вид , следовательно, название функции меняется. Таким образом,

Формулы преобразования суммы тригонометрических функций в произведение:

Формулы преобразования произведения тригонометрических функций в сумму:

Наверх

10. Производная и интеграл

Таблица производных некоторых элементарных функций

Правила дифференцирования:

1.

2.

3.

4.

5.

Уравнение касательной к графику функции в его точке :

Таблица первообразных для некоторых элементарных функций

Правила нахождения первообразных

Пусть ― первообразные для функций и соответственно, a, b, k ― постоянные, Тогда:

— ― первообразная для функции

— ― первообразная для функции

— ― первообразная для функции

— Формула Ньютона-Лейбница:

1. Треугольник

Пусть ― длины сторон BC, AC, AB треугольника ABC соответственно; ― полупериметр треугольника ABC; A, B, C ― величины углов BAC, ABC, ACB треугольника ABC соответственно; ― длины высот AA₂, BB₂, CC₂ треугольника ABC соответственно; R ― радиус окружности, описанной около треугольника ABC; r — радиус окружности, вписанной в треугольник ABC; ― площадь треугольника ABC. Тогда имеют место следующие соотношения:

(теорема синусов);

(теорема косинусов);

Наверх
2. Четырёхугольники

Параллелограмм

Параллелограммом называется четырехугольник, противоположные стороны которого попарно параллельны.

Прямоугольником называется параллелограмм, у которого все углы прямые.

Ромбом называется параллелограмм, все стороны которого равны.

Квадратом называется прямоугольник, все стороны которого равны. Из определения следует, что квадрат является ромбом, следовательно, он обладает всеми свойствами прямоугольника и ромба.

Трапецией называется четырехугольник, две стороны которого параллельны, а две другие не параллельны.

Площадь четырехугольника

Площадь параллелограмма равна произведению его основания на высоту.

Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.

Площадь трапеции равна произведению полусуммы ее оснований на высоту.

Площадь четырехугольника равна половине произведения его диагоналей на синус угла между ними.

Наверх

3. Окружность и круг

Соотношения между элементами окружности и круга

Пусть r — радиус окружности, d — ее диаметр, C — длина окружности, S — площадь круга,  — длина дуги в градусов,  — длина дуги в радиан,  — площадь сектора, ограниченного дугой в n градусов,  — площадь сектора, ограниченного дугой в радиан. Тогда имеют место следующие соотношения:

Вписанный угол

Вписанный угол измеряется половиной дуги, на которую он опирается.

Вписанные углы, опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на полуокружность, — прямой.

Вписанная окружность

Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех сторон этого многоугольника, ― точка пересечения биссектрис углов этого многоугольника. Таким образом, в многоугольник можно вписать окружность, и притом только одну, тогда и только тогда, когда биссектрисы его углов пересекаются в одной точке.

В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.

Описанная окружность

Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех вершин этого многоугольника, ― точка пересечения серединных перпендикуляров к сторонам этого многоугольника. Таким образом, около многоугольника можно описать окружность, и притом только одну, тогда и только тогда, когда серединные перпендикуляры к сторонам этого многоугольника пересекаются в одной точке.

Около четырехугольника можно описать окружность тогда и только тогда, когда суммы его противоположных углов равны

Наверх

4. Призма

Пусть H ― высота призмы, AA₁ ― боковое ребро призмы,  ― периметр основания призмы,  ― площадь основания призмы,  ― площадь боковой поверхности призмы,  ― площадь полной поверхности призмы, V ― объем призмы,  ― периметр перпендикулярного сечения призмы,  ― площадь перпендикулярного сечения призмы. Тогда имеют место следующие соотношения:

Свойства параллелепипеда:

— противоположные грани параллелепипеда равны и параллельны;

— диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам;

— квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

Наверх

5. Пирамида

Пусть H ― высота пирамиды,  ― периметр основания пирамиды,  ― площадь основания пирамиды,  ― площадь боковой поверхности пирамиды,  ― площадь полной поверхности пирамиды, V ― объем пирамиды. Тогда имеют место следующие соотношения:

;

.

Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны , то

Наверх

6. Усечённая пирамида

Пусть H ― высота усеченной пирамиды, и  ― периметры оснований усеченной пирамиды, и  ― площади оснований усеченной пирамиды,  ― площадь боковой поверхности усеченной пирамиды,  ― площадь полной поверхности усеченной пирамиды, V ― объем усеченной пирамиды.

Тогда имеют место следующие соотношения:

Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны , то:

Наверх

7. Цилиндр

Пусть h ― высота цилиндра, r ― радиус цилиндра,  ― площадь боковой поверхности цилиндра,  ― площадь полной поверхности цилиндра, V ― объем цилиндра.

Тогда имеют место следующие соотношения:

Наверх

8. Конус

Пусть h ― высота конуса, r ― радиус основания конуса, l ― образующая конуса,  ― площадь боковой поверхности конуса,  ― площадь полной поверхности конуса, V ― объем конуса.

Тогда имеют место следующие соотношения:

Наверх

9. Усечённый конус

Пусть h ― высота усеченного конуса, r и  ― радиусы основания усеченного конуса, l ― образующая усеченного конуса,  ― площадь боковой поверхности усеченного конуса, V ― объем усеченного конуса. Тогда имеют место следующие соотношения:

Наверх

10. Сфера и шар

Пусть R ― радиус шара, D ― его диаметр, S ― площадь ограничивающей шар сферы,  ― площадь сферической поверхности шарового сегмента (шарового слоя), высота которого равна h, V ― объем шара,  ― объем сегмента, высота которого равна h,  ― объем сектора, ограниченного сегментом, высота которого равна h. Тогда имеют место следующие соотношения:

Наверх

Материалы, выдаваемые на экзамене, смотрите здесь

• Полный краткий справочник
  • Формулы сокращенного умножения
  • Модуль числа, модуль выражения
  • Степень с действительным показателем
  • Корень n-ой степени из числа
  • Логарифмы
  • Арифметическая прогрессия
  • Геометрическая прогрессия
  • Бесконечно убывающая геометрическая прогрессия
  • Основные формулы тригонометрии
  • Производная и интеграл
  • Треугольник
  • Четырехугольники
  • Окружность и круг
  • Призма
  • Пирамида
  • Усеченная пирамида
  • Цилиндр
  • Конус
  • Усеченный конус
  • Сфера и шар
  • Векторы и координаты
• Особенности экзаменационных заданий профильной математики
  • Задания 1: округление величин, проценты
    • Особенности экзаменационных заданий на округление
    • Округление величин с избытком и недостатком
    • Проценты
    • Особенности экзаменационных заданий на проценты
  • Задания 2: анализ графических зависимостей
    • Анализ графических зависимостей
    • Особенности экзаменационных заданий на чтение графиков и диаграмм
  • Задания 3 и 6: планиметрия
    • Треугольник
      • Равносторонний треугольник
      • Равнобедренный треугольник
      • Прямоугольный треугольник
      • Тригонометрические функции дополнительных углов
      • Основное тригонометрическое тождество и следствия из него
      • Смежные углы
      • Средняя линия треугольника
      • Медиана треугольника
      • Биссектриса треугольника
      • Высота треугольника
      • Серединный перпендикуляр
      • Теорема косинусов
    • Параллелограмм
      • Прямоугольник
      • Ромб
      • Параллелограмм Вариньона
      • Трапеция
    • Правильный шестиугольник
    • Теоремы о площадях многоугольников
    • Окружность
      • Вписанный угол
      • Хорда
      • Касательная к окружности
      • Секущая
      • Круг и его элементы
      • Соотношения между элементами окружности и круга
      • Вписанная окружность
      • Описанная окружность
    • Вектор
      • Сумма и разность векторов
      • Координаты вектора
      • Скалярное произведение векторов
      • Расстояния от точки до координатных осей
      • Расстояние между точками
  • Задания 4: вероятности событий
    • Определение вероятности
    • Теоремы о вероятностях событий
    • Особенности экзаменационных заданий на начала теории вероятности
  • Задания 5: простейшие уравнения
    • Простейшие уравнения
    • Линейные уравнения
    • Квадратные уравнения
    • Рациональные уравнения
    • Иррациональные уравнения
    • Показательные уравнения
    • Логарифмические уравнения
    • Особенности решения экзаменационных заданий на простейшие уравнения
  • Задания 7: производные, первообразные
    • Правила дифференцирования
    • Производная числа, линейной и степенной функции
    • Производная многочлена
    • Уравнение прямой
    • Уравнение касательной
    • Физический смысл производной
    • Монотонность и экстремумы функции
    • Первообразная
    • Криволинейная трапеция и ее площадь
  • Задания 8: стереометрия
    • Особенности экзаменационных заданий по стереометрии
    • Куб
    • Призма. Прямоугольный параллелепипед
      • Прямая призма
      • Прямоугольный параллелепипед и его свойства
      • Особенности правильной шестиугольной призмы
    • Пирамида
    • Сечения
    • Цилиндр и его соотношения
    • Конус и его соотношения
    • Сфера и шар
      • Комбинации круглых тел. Вписанные сферы
      • Комбинации круглых тел. Описанные сферы
      • Комбинации конуса и цилиндра
      • Комбинации многогранников и круглых тел. Описанные сферы
      • Комбинации многогранников и круглых тел. Вписанные сферы
      • Комбинации конуса, цилиндра и многогранников
  • Задания 9: тождественные преобразования выражений
    • Действия с дробями
    • Формулы сокращенного умножения
    • Степень и её свойства
      • Свойства степени
      • Степень с дробным показателем
    • Арифметический корень
      • Свойства арифметического корня
    • Определение логарифма и его свойства
    • Основные тригонометрические формулы
    • Правило для запоминания формул приведения
    • Свойства четности и нечетности функций
  • Задания 10: задачи с прикладным содержанием
    • Задачи с прикладным содержанием
  • Задания 11: текстовые задачи
    • Определение процента
    • Правило креста для решения задач на смеси
    • Движение по прямой
    • Движение по окружности
    • Алгоритм решения задач на совместную работу
  • Задания 12: исследование функций при помощи производной
    • Производная некоторых элементарных функций
    • Правила дифференцирования
    • Монотонность и экстремумы функции
    • Наибольшее и наименьшее значение функции

Математика — теория ЕГЭ

• 
  23.02.2020

  Критерии оценивания ЕГЭ по математике 2020

  
  (37509)
  

• 
  07.01.2020

  Теория вероятностней ЕГЭ по математике

  
  (39453)
  

• 
  11.03.2019

  Критерии оценивания ЕГЭ 2019 по математике (профиль)

  
  (59994)
  

• 
  08.10.2018

  Задание 1 ЕГЭ 2021 по математике, теория

  
  (166663)
  

• 
  08.10.2018

  Задание 2 ЕГЭ 2021 по математике, теория

  
  (51378)
  

• 
  08.10.2018

  Задание 3 ЕГЭ 2021 по математике, теория

  
  (176341)
  

• 
  08.10.2018

  Задание 4 ЕГЭ 2021 по математике, теория

  
  (94146)
  

• 
  08.10.2018

  Задание 5 ЕГЭ 2021 по математике, теория

  
  (95483)
  

• 
  08.10.2018

  Задание 6 ЕГЭ 2021 по математике, теория

  
  (163107)
  

• 
  08.10.2018

  Задание 7 ЕГЭ 2021 по математике, теория

  
  (102801)
  

• 
  08.10.2018

  Задание 8 ЕГЭ 2021 по математике, теория

  
  (136733)
  

• 
  08.10.2018

  Задание 9 ЕГЭ 2021 по математике, теория

  
  (98512)
  

• 
  08.10.2018

  Задание 10 ЕГЭ 2021 по математике, теория

  
  (55218)
  

• 
  08.10.2018

  Задание 11 ЕГЭ 2021 по математике, теория

  
  (83083)
  

• 
  08.10.2018

  Задание 12 ЕГЭ 2021 по математике, теория

  
  (118439)
  

• 
  08.10.2018

  Задание 13 ЕГЭ 2021 по математике, теория

  
  (98217)
  

• 
  08.10.2018

  Задание 14 ЕГЭ 2021 по математике, теория

  
  (70812)
  

• 
  08.10.2018

  Задание 15 ЕГЭ 2021 по математике, теория

  
  (68311)
  

• 
  08.10.2018

  Задание 16 ЕГЭ 2021 по математике, теория

  
  (58595)
  

• 
  08.10.2018

  Задание 17 ЕГЭ 2021 по математике, теория

  
  (119892)
  

• 
  08.10.2018

  Задание 18 ЕГЭ 2021 по математике, теория

  
  (66311)
  

• 
  08.10.2018

  Задание 19 ЕГЭ 2021 по математике, теория

  
  (65681)
  

• 
  12.08.2018

  Популярные ошибки в ЕГЭ по математике

  
  (22794)
  

• 
  20.03.2018

  Критерии оценивания ЕГЭ 2019 по математике

  
  (124279)
  

• 
  19.01.2018

  Задания ЕГЭ по стереометрии: как научиться решать

  
  (20753)
  

• 
  22.12.2017

  Векторы, подготовка к ЕГЭ по математике

  
  (7920)
  

• 
  22.12.2017

  Координаты, подготовка к ЕГЭ по математике

  
  (5217)
  

• 
  22.12.2017

  Комбинации, подготовка к ЕГЭ по математике

  
  (5640)
  

• 
  22.12.2017

  Площади, подготовка к ЕГЭ по математике

  
  (10406)
  

• 
  22.12.2017

  Углы, подготовка к ЕГЭ по математике

  
  (6786)
  

• 
  22.12.2017

  Шар и сфера, подготовка к ЕГЭ по математике

  
  (7788)
  

• 
  22.12.2017

  Конус, подготовка к ЕГЭ по математике

  
  (6864)
  

• 
  22.12.2017

  Цилиндр, подготовка к ЕГЭ по математике

  
  (6974)
  

• 
  22.12.2017

  Правильные многогранники, подготовка к ЕГЭ по математике

  
  (4579)
  

• 
  22.12.2017

  Пирамида, подготовка к ЕГЭ по математике

  
  (7477)
  

• 
  22.12.2017

  Параллелепипед, подготовка к ЕГЭ по математике

  
  (4485)
  

• 
  22.12.2017

  Призма, подготовка к ЕГЭ по математике

  
  (5996)
  

• 
  22.12.2017

  Многоугольник, подготовка к ЕГЭ по математике

  
  (6145)
  

• 
  22.12.2017

  Окружность и круг, подготовка к ЕГЭ по математике

  
  (8735)
  

• 
  22.12.2017

  Трапеция, подготовка к ЕГЭ по математике

  
  (6488)
  

• 
  22.12.2017

  Параллелограмм, прямоугольник, подготовка к ЕГЭ по математике

  
  (4497)
  

• 
  22.12.2017

  Треугольник, подготовка к ЕГЭ по математике

  
  (9982)
  

• 
  10.12.2017

  Методы решения задач по геометрии ЕГЭ по математике

  
  (13252)
  

• 
  03.10.2017

  Формулы объема

  
  (7434)
  

• 
  03.10.2017

  Скрещивающиеся прямые

  
  (4017)
  

• 
  03.10.2017

  Аксиомы стереометрии

  
  (5433)
  

• 
  03.10.2017

  Справочные материалы к ЕГЭ по математике (профиль)

  
  (181896)
  

• 
  06.09.2017

  Основные свойства трапеции

  
  (4797)
  

• 
  06.09.2017

  Окружность, вписанная в треугольник

  
  (4033)
  

• 
  06.09.2017

  Окружность и четырехугольник

  
  (3648)
  

• 
  06.09.2017

  Окружность и треугольник

  
  (3400)
  

• 
  18.08.2017

  Решение задач со сложными процентами ЕГЭ по математике

  
  (8445)
  

• 
  14.06.2017

  Критерии оценивания реального ЕГЭ 2017 по математике

  
  (31003)
  

• 
  15.05.2017

  Как решать задачи на работу

  
  (5918)
  

• 
  15.05.2017

  Как решать задачи на числовые зависимости

  
  (4568)
  

• 
  15.05.2017

  Как решать задачи на прогрессии

  
  (4897)
  

• 
  15.05.2017

  Как решать задачи на проценты

  
  (7238)
  

• 
  15.05.2017

  Как решать задачи на движение с дополнительной скоростью

  
  (3880)
  

• 
  15.05.2017

  Как решать задачи на движение по прямой

  
  (5839)
  

• 
  15.05.2017

  Как решать задачи на движение по окружности

  
  (7956)
  

• 
  29.04.2017

  Неравенства с модулем: как решать

  
  (16180)
  

• 
  29.04.2017

  Неравенства с параметром: как решать

  
  (5822)
  

• 
  29.04.2017

  Иррациональные неравенства: как решать

  
  (8350)
  

• 
  29.04.2017

  Тригонометрические неравенства: как решать

  
  (11300)
  

• 
  29.04.2017

  Логарифмические неравенства: как решать

  
  (9734)
  

• 
  29.04.2017

  Показательные неравенства: как решать

  
  (6211)
  

• 
  28.03.2017

  Методы решения уравнений, содержащих модуль

  
  (4803)
  

• 
  28.03.2017

  Методы решения тригонометрических уравнений

  
  (6397)
  

• 
  28.03.2017

  Методы решения уравнений высших степеней

  
  (4730)
  

• 
  28.03.2017

  Методы решения показательных уравнений

  
  (4394)
  

• 
  28.03.2017

  Методы решения показательно-степенных уравнений

  
  (3658)
  

• 
  28.03.2017

  Методы решения неравенств, содержащих модуль

  
  (3733)
  

• 
  28.03.2017

  Методы решения логарифмических неравенств

  
  (4402)
  

• 
  28.03.2017

  Методы решения иррациональных уравнений

  
  (3993)
  

• 
  28.03.2017

  Методы решения иррациональных неравенств

  
  (3435)
  

• 
  20.03.2017

  Разбор экономических задач по математике

  
  (26459)
  

• 
  20.03.2017

  Разбор задач на работу по математике

  
  (3493)
  

• 
  20.03.2017

  Алгоритм решения задач на растворы по математике

  
  (5510)
  

• 
  20.03.2017

  Разбор задач на движение по математике

  
  (3495)
  

• 
  21.02.2017

  Разбор ключевых задач по стереометрии из ЕГЭ по математике

  
  (5237)
  

• 
  21.02.2017

  Теория к заданию 14 ЕГЭ по математике (профильный уровень)

  
  (25988)
  

• 
  03.02.2017

  Методика решения задач с параметрами

  
  (10993)
  

• 
  22.12.2016

  Теория по математике на тему «Задачи на составление уравнений»

  
  (3761)
  

• 
  22.12.2016

  Теория по математике на тему «Средние пропорциональные отрезки в прямоугольном треугольнике, окружности»

  
  (3475)
  

• 
  22.12.2016

  Теория по математике на тему «Призма»

  
  (4189)
  

• 
  22.12.2016

  Теория по математике на тему «Логарифмы». Часть 2

  
  (4693)
  

• 
  22.12.2016

  Теория по математике на тему «Логарифмические уравнения»

  
  (4348)
  

• 
  22.12.2016

  Теория по математике на тему «Функции и их графики»

  
  (5496)
  

• 
  22.12.2016

  Теория по математике на тему «Декартовы координаты»

  
  (2993)
  

• 
  10.11.2016

  Теория по математике на тему «Формулы стереометрии»

  
  (9522)
  

• 
  10.11.2016

  Теория по математике на тему «Формулы двойного и тройного угла в тригонометрии»

  
  (3231)
  

• 
  10.11.2016

  Теория по математике на тему «Конус, цилиндр, пирамида»

  
  (4378)
  

• 
  24.09.2016

  Теория по математике на тему «Степенные и иррациональные функции»

  
  (3473)
  

• 
  24.09.2016

  Теория по математике на тему «Производная»

  
  (8820)
  

• 
  24.09.2016

  Теория по математике на тему «Параметры»

  
  (10685)
  

• 
  24.09.2016

  Теория по математике на тему «Графики функций»

  
  (8646)
  

• 
  24.09.2016

  Теория по математике на тему «Формулы сокращенного умножения»

  
  (3455)
  

• 
  15.09.2016

  Теория по математике на тему «Окружность»

  
  (6583)
  

• 
  15.09.2016

  Теория по математике на тему «МЗМ для логарифмических неравенств»

  
  (5955)
  

• 
  15.09.2016

  Теория по математике на тему «Задачи на работу»

  
  (3932)
  

ЕГЭ по математике профильного уровня — один из самых сложных экзаменов. Планируете сдавать его, но не знаете, с чего начать? Этот экзамен не покажется вам таким трудным, если вы узнаете про него побольше и грамотно подготовитесь. В этой статье обсудим, что нужно знать про ЕГЭ по математике 2023, из каких разделов он состоит и как к нему подготовиться.

Какие темы важно знать для ЕГЭ по математике 2023?

В математике, как и в любом предмете, есть опорные темы. Если вы их выучите, будет легче справиться с экзаменом.

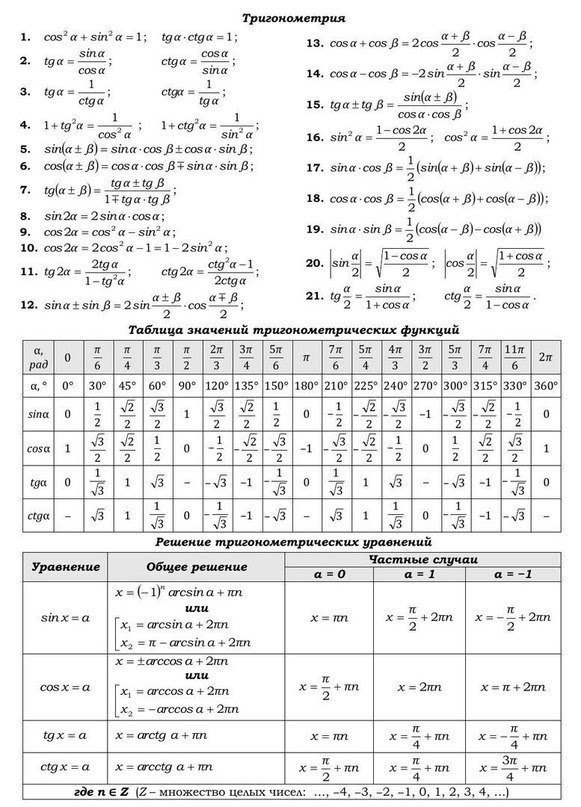
Формулы тригонометрии

Очень важно знать формулы тригонометрии и уметь применять их. Хорошая новость: в справочных материалах можно найти несколько тригонометрических формул.

Но формул гораздо больше. Я советую не зубрить их, а научиться выводить: приходить к формулам шаг за шагом, опираясь на тождества. Кстати, мы учим выводить формулы на курсах подготовки к ЕГЭ: это полезно, чтобы оказаться на экзамене во всеоружии и ничего не перепутать.

Квадратные уравнения

Эти уравнения мы учимся решать еще в 7 классе. Они встречаются в ЕГЭ по математике постоянно: и как самостоятельные задания, и внутри более сложных уравнений или неравенств. Квадратные уравнения могут встретиться в математических моделях № 9 и № 15, в задачах на геометрию и стереометрию, в задании № 17 с параметром.

Самое главное — хорошо знать универсальные методы решения. Первый — через формулу дискриминанта, второй — через теорему Виета, которая может сэкономить время на экзамене.

Треугольники

Эта замечательная тема, которую проходят в 7 классе — основа основ всей геометрии. Она нужна и для решения стереометрии, и для простейших планиметрических задач. Еще треугольники необходимы, чтобы освоить огромное количество теорем. Выучите все, что с ними связано! Особое внимание обратите на прямоугольные треугольники, которые встречаются чаще остальных — тогда геометрические задачи сразу станут проще.

Проценты

Самая нелюбимая тема моих учеников после тригонометрии, которую необходимо хорошо знать. Проценты нужны для реальной математики — это № 9 (с кратким ответом) и № 15 (с развернутым ответом). Понимание этой темы может принести вам 3 первичных балла.

План успешной подготовки к ЕГЭ по математике 2023

Если вы хотите получить больше 80 баллов на ЕГЭ, нужно идеально решать часть с кратким ответом, а также справляться с большинством заданий с развернутым ответом.

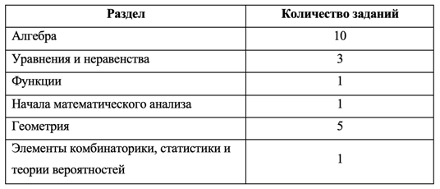
Чтобы постепенно прорабатывать материал, воспользуйтесь кодификатором. В нем обратите внимание на таблицу 2, а именно на блоки:

• Алгебра
• Уравнения и неравенства
• Элементы комбинаторики, статистики и теории вероятностей
• Функции
• Начала математического анализа
• Геометрия

Ориентируйтесь на указанную последовательность, но геометрию изучайте параллельно с остальными блоками — на нее нужно больше времени.

Самое главное — ни в коем случае не ограничивайтесь теорией. Ее у вас не спросят на экзамене, а вот задания решать придется. Поэтому тренируйте практические навыки: актуальные задания вы сможете найти в открытом банке заданий на сайте ФИПИ или в нашем тренажере «Решутест».

Как решать часть с кратким ответом

Ни в коем случае не пренебрегайте частью с кратким ответом! Иначе будет обидно: например, вы наберете за экономическую задачу № 15 полные 2 балла, но потеряете их в двух заданиях первой части. Это актуально для всех ЕГЭ: подробнее о том, как идеально справляться с первой частью экзамена, читайте здесь.

Еще одно заблуждение: «часть с кратким ответом простая, к ней можно не готовиться». Даже в первой части иногда встречаются такие задания, которые ученики даже не решают, потому что не готовились к ним.

Как я уже говорила, часть с кратким ответом содержит 11 заданий. Начинать подготовку необходимо именно с заданий базового уровня сложности, потому что это та основа, на которую потом накладывается более сложная теория.

Что касается задач повышенного уровня сложности, то среди каждого номера есть лайфхаки, например, в этой статье я уже рассказывала про № 11, в котором нужно работать с производной.

Задания с развернутым ответом: немного статистики

Многие думают, что эта часть ЕГЭ по математике очень сложная. Поэтому ребята, которые не рассчитывают на высокие баллы, даже не приступают к ней. И очень зря! С помощью этих заданий можно заработать дополнительные баллы и побороться за высокое место в рейтинге.

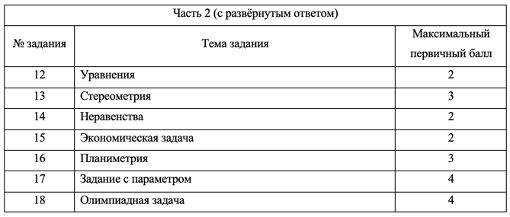
Сейчас будет немного статистики. В среднем около 35% учеников получают полные 2 балла за решение № 12, а вот неравенство № 14 дается хуже, только около 12% с ним справляются на полный балл. Геометрия даётся ещё хуже: стереометрию № 13 полностью решают 2% выпускников, планиметрию (№ 16) менее 5%. А вот с экономической задачей (№ 15) справляются около 20%, а это целых 2 балла! Что касается № 17 и 18, то они даются ещё хуже, но на то они и самые сложные, хотя 1 балл за № 18 по статистике получают около 25% сдающих — там нужно просто привести пример.

Особенности уровней ЕГЭ по математике

В 2015 году ЕГЭ по математике разделили на базовый и профильный уровни. Это упростило жизнь выпускникам, которые не планируют поступать на специальности, связанные с математикой. Если ЕГЭ по математике нужен только для получения аттестата, можно сдать его облегченную версию, оставив время и силы для профильных экзаменов.

Базовый уровень ЕГЭ по математике

Как устроен базовый ЕГЭ по математике? Экзамен идет 180 минут, он состоит из 21 задания, за каждое из которых можно получить 1 балл. Этот экзамен единственный, который переводится не в 100-бальную систему, а в оценки.

В ЕГЭ по математике базового уровня 6 тематических блоков:

Также обратите внимание, что базовый ЕГЭ по математике не поменялся с точки зрения наполнения, изменился лишь порядок заданий. Вот что пишут ФИПИ:

Подробнее про базовый ЕГЭ по математике, включая разбор всех заданий, читайте здесь, а мы перейдём к профильному.

Профильный уровень ЕГЭ по математике

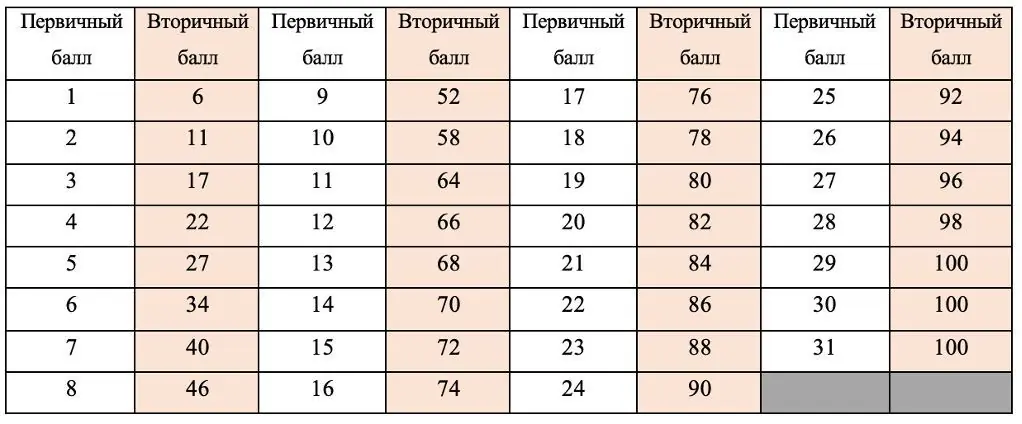
Данный экзамен, как и остальные ЕГЭ, переводится в 100-бальную систему:

Экзамен состоит из двух частей: Часть 1 с кратким ответом, а Часть 2 — с развернутым. Длится он 235 минут. Всего есть 18 заданий, которые разделены на 3 блока: алгебра, геометрия и реальная математика. Максимальное количество первичных баллов — 31.

Структура ЕГЭ по математике 2023

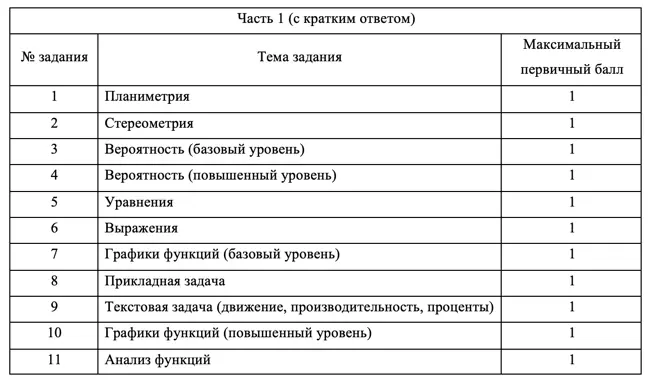
Часть 1:

• Приносит 11 баллов, то есть 35% всего экзамена
• 11 заданий с кратким ответом

Часть 2:

• Приносит 20 баллов, то есть 65% всего экзамена
• 7 заданий с развернутым ответом

Внимание! Вся нумерация заданий в статье соответствует ЕГЭ 2023 года.

В заданиях с кратким ответом нужно лишь записать верное число в бланк. Заданий с развернутым ответом 7, в них нужно подробно расписать решение, которое должно соответствовать критериям оценивания.

ЕГЭ — стандартизированный экзамен, поэтому каждое задание всегда соответствует определенной теме.

Обратите внимание, что по сравнению с 2022 годом, в части 1 изменился только порядок заданий. Сами сотрудники ФИПИ говорят следующее:

Задания с кратким ответом принесут вам до 11 первичных баллов (64 вторичных). Если не понимаете, что это за баллы и откуда они берутся, почитайте эту статью. Самая популярная цель на ЕГЭ по математике — набрать 80 баллов, для этого раньше было необходимо 19 первичных баллов. Ранее многие ученики пользовались рабочей стратегией — решить всю часть с кратким ответом, а также № 12, 14 и 15. Если хорошо разбирались в геометрии, выбирали № 13 и 16 — или использовали их как запасные задания. Сейчас стратегия должна быть другая, так как № 13 (стереометрия) стал стоить дороже — 3 балла вместо 2, а № 15 (экономическая задача) — подешевел с 3 баллов до 2. Изменилась также шкала перевода баллов, поэтому подумайте, какими заданиями вы сможете набрать необходимое количество первичных баллов.

Разделы ЕГЭ по математике

• Алгебра и начала анализа — 8 заданий, 13 первичных баллов
• Геометрия — 4 задания, 8 первичных баллов
• Реальная математика — 6 заданий, 10 первичных баллов

Какие задания входят в ЕГЭ по математике?

Здесь вам на помощь приходят документы с официального сайта ФИПИ: кодификатор, демоверсия и спецификация.

• Кодификатор — это краткий перечень всех блоков и тем, которые включены в экзамен.

  Сейчас кодификатор общий для обоих уровней экзамена, как базового, так и профильного. Он снова представляет собой единый документ, так что не запутаетесь.

• Демоверсия — типовой вариант ЕГЭ. Он показывает уровень экзамена и ориентировочную сложность заданий.
• Спецификация — это документ, описывающий структуру экзамена и разбалловку.

Что в итоге

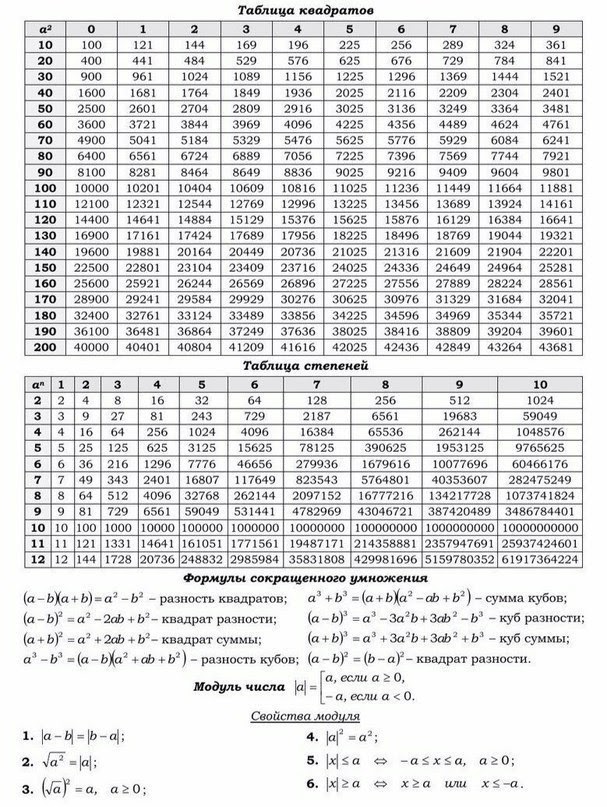
Боитесь экзамена по профильной математике? Неудивительно, ведь это один из самых сложных предметов. Его нельзя сдать, просто выучив основную теорию математики, ведь каждое задание представляет собой решение задачи или примера. Но не переживайте — уделив достаточно времени подготовке к ЕГЭ, вы обязательно получите высокие баллы! А мы хотим вам в этом помощь. Сохраняйте себе таблицы с некоторой теорией по математике. В них вы найдете основы тригонометрии, производные и логарифмы, свойства корня и степени, формулы сокращенного умножения и таблицу квадратов, а также принцип решения уравнений и неравенств.