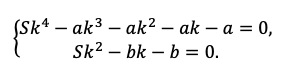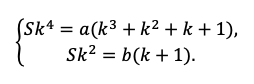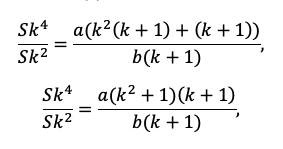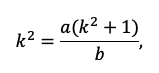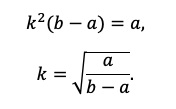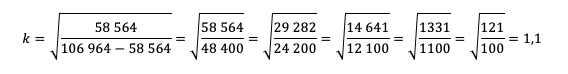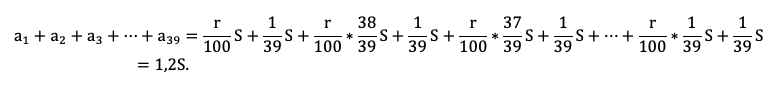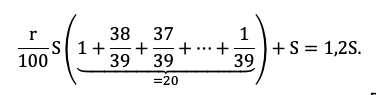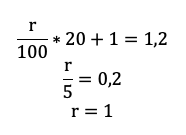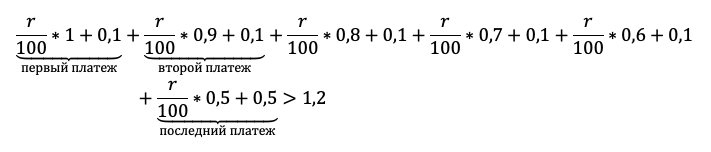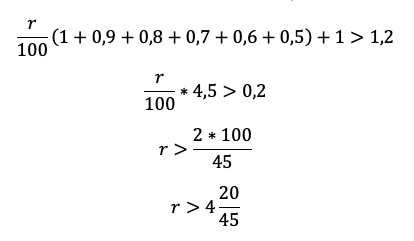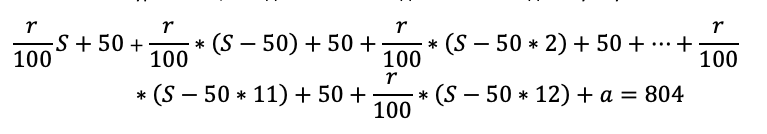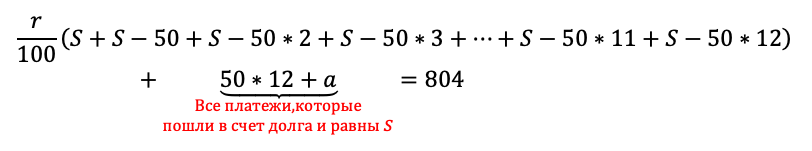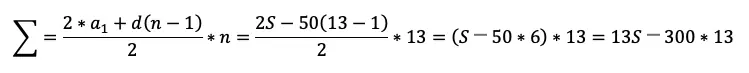В части с развернутым ответом в ЕГЭ по профильной математике есть уникальный номер, к которому школьник почти готов сразу после освоения материала для первых 12-ти заданий. Речь об экономической задаче под номером 17 в ЕГЭ по математике. Конечно, поготовиться придется, но, если повезет с прототипом, баллы можно урвать почти даром!
Прототипы для 17-го номера делятся на три большие группы:
- банковские задачи,
- на ценные бумаги,
- задачи на оптимальный выбор.
В этой статье мы расскажем, как научить ученика структурировать условие любой банковской задачи, как составить по этим данным математическую модель и найти решение. Расскажем, на что обратить внимание ученика, чтобы школьник не потерял баллы из-за неверного оформления.
Главная трудность — школьник плохо понимает условие, ведь с кредитами и вкладами он пока не сталкивался.
- Как работает процент по кредиту?
- На какую сумму начисляется?
- Из каких частей состоит платеж?
- Как уменьшается долг?
На все эти вопросы вам придется ответить. Это отличная возможность показать пользу уроков математики, ведь 17-ый номер — едва ли не самая прикладная задача за весь школьный курс!
Например, можно рассказать о том, какие бывают образовательные кредиты. Вы в курсе, что их дают с 14 лет, а платеж первые годы может быть ничтожным? Школьник об этом точно не знает.
С чего начать разбор экономической (банковской) задачи в ЕГЭ по математике
Экзамен немного утрирует реальную ситуацию, в жизни кредит работает сложнее. Однако грустно упускать возможность рассказать школьнику что-то из реальности! Если у вас есть опыт с кредитованием, самое время им поделиться. Если нет, то воспользуйтесь нашим:
- Например, расскажите, что клиенту придется сверх купить страховку на случай потери работоспособности, ведь банк не хочет терять прибыль даже если на заемщика кирпич упадет. Ваши ученики знают, как работает страховка?
- Расскажите о механизме аннуитетного платежа: как часть денег банк забирает себе в качестве дохода, то есть на погашение процентов за пользование кредитом; а на вторую часть уменьшает ваш долг. В реальности это разделение считается по специальной формуле, и совсем не в пользу заемщика.
- Например, по нашему опыту, в ипотеке на 10 лет из 20 тысяч ежемесячного платежа на первых порах всего 5 000 рублей идет в счет уменьшения долга, а 15 000 — забирает себе банк! Но каждый раз платеж чуть ребалансируется, и в счет долга идет чуть больше. Так в последних платежах через 10 лет в счет процентов идет буквально пара сотен, а все остальное гасит долг.
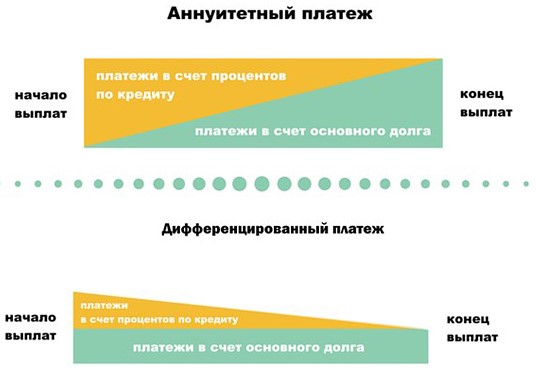
Хорошая новость в том, что в экзаменационных задачах подобной вакханалии не бывает. Долг и проценты или гасятся равномерно, или по заранее известному алгоритму, достаточно просто внимательно прочитать условие.
Еще одно частое упрощение в ЕГЭ — процент там обычно не годовой, а ежемесячный! То есть своим платежом заемщик гасит набежавший за этот месяц процент и уменьшает долг на заданную величину. Удобно.
Мы предлагаем научить школьника упорядочивать данные банковской задачи в ЕГЭ по математике с помощью таблицы. Табличка — не единственный способ решить 17-ый номер, кто-то использует последовательности, кто-то — считает прикладным методом как заправский бухгалтер. Однако наш метод универсален, а значит вы дадите школьнику один алгоритм на все типы банковских задач. Согласитесь, работать с одним алгоритмом проще, чем подбирать разные по ситуации.
Тип 1. Равные платежи
Особенность этого типа заданий в том, что заемщик всегда вносит одинаковые суммы.
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r.
Очевидно, что эта схема должна оказаться у школьника в тетради. Ведь вы же знаете: того, чего нет в тетради, и на уроке-то не было!
Заполняем всю табличку. Учитываем обе ситуации из условия. Для наглядности каждую выделим жирной рамкой.
Теперь остался еще один непростой шаг — перейти от структурированных данных к математической модели. Дайте ученику возможность увидеть, что уже почти составил ее.
Мы получили два уравнения, которые подсветили в табличке оранжевым. Объединим их в систему и решим!
Напомните выпускнику о культуре вычислений! Порой эти задачи составлены так, что неудачная последовательность действий сделает их нерешаемыми без калькулятора. Потому не надо спешить делать первое попавшееся действие, пусть школьник тренируется думать на пару ходов вперед.
Например, разделим одно уравнение на другое, ведь так мы избавимся от одной неизвестной S:
Наше решение не зависит от суммы кредита, S сокращается.
По сути, мы получили уравнение с одной неизвестной, ведь платежи a и b знаем из условия. Выразим k:
Пожалуй, все, проще уже некуда. Подставляем значения!
Тут можно обратить внимание ученика на то, как составители экзамена на самом деле заботятся о нем! Ведь будь задачка хоть чуть-чуть другой, посчитать без калькулятора было бы невозможно.
Вспоминаем, что k=1+r/100, а найти нам надо r.
Ответ: 10%.
Не забудьте после решения расставить акценты в задаче:
Чтобы решить задачу и получить 3 балла, мы:
— Воспользовались простым алгоритмом упорядочивания данных,
— Составили математическую модель,
— Нашли удобный способ решить ее, ВСЕ!
Это и есть алгоритм решения банковской задачи.
Тип 2. Равномерно убывающий долг
В прошлой задаче заемщик платил одинаковую сумму каждый месяц. Тут ему нужно уменьшать долг на одну и ту же величину. То есть за месяц пользования деньгами банк начислил на них процент, клиент теперь должен чуть больше. Своим платежом он оплатит банку проценты, чтобы заем стал таким, как ДО их начисления. А сверху внесет сумму, которая как раз и пойдет на то самое РАВНОМЕРНОЕ уменьшение долга.
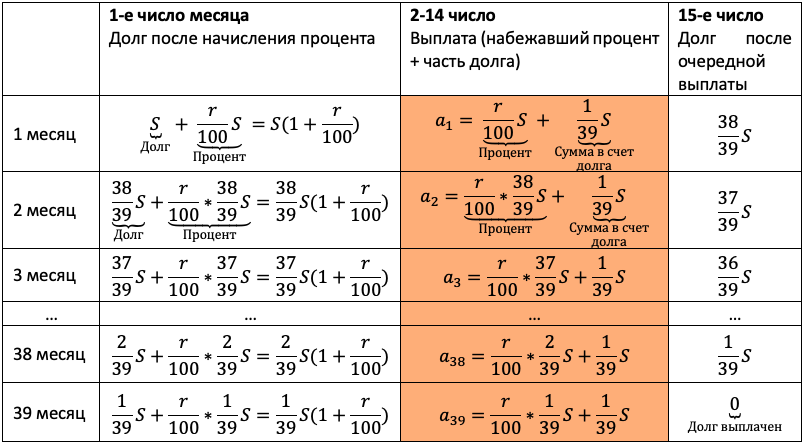
15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
(Считайте, что округления при вычислении платежей не производятся.)
Тут главный элемент в задаче — равномерно убывающий долг. Если мы взяли сумму S на 39 месяцев, и каждый месяц долг должен быть меньше на одинаковую величину, то что это за величина? Пусть правильный ответ 1/39 S даст ученик.
Проиллюстрируйте школьнику, как здорово работает наш алгоритм. Пусть выпускник проговаривает пункты вслух, а вы их выполняйте. Следите, чтобы каждый шаг подопечный фиксировал в тетради:
Продолжаем заполнять табличку. Пусть дальше пробует выпускник, ведь пока сам не попробуешь, не научишься:
Осталось увязать добытую информацию в уравнение или неравенство. Обратите внимание подопечного на то, что ненужных подробностей в задачах ЕГЭ не бывает! Единственная информация в задаче, которую мы до сих пор не использовали — общая сумма выплат. По условию она на 20% больше суммы кредита, то есть равна 1,2S:
Приведем подобные, вынесем общий множитель за скобку:
Решение в итоге снова не зависит от того, какую сумму взяли в долг. Разделим обе части на S и упростим выражение:
Ответ: 1%.
И снова все по нашему алгоритму, ничего нового, кроме него, мы не используем! Не забудьте излучать восторг, иначе школьник не проникнется мощью вашего метода решения.
Тип 3. Долг, убывающий согласно табличке
Задача похожа на прошлую. Разница лишь в том, что кроме процентов нам каждый месяц придется гасить не равную долю долга, а долю согласно таблице.
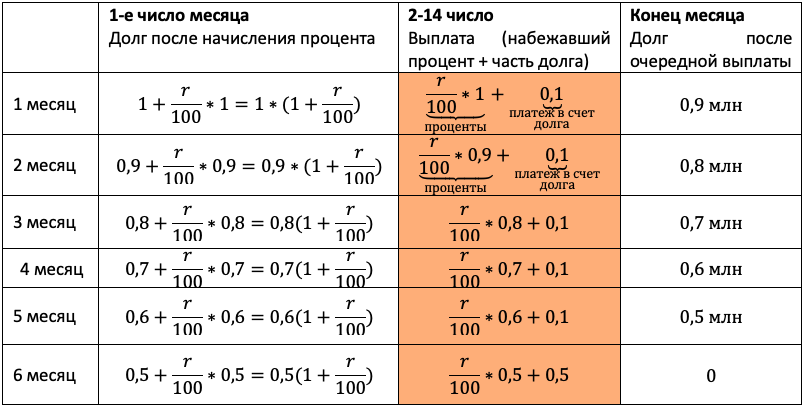
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг(в млн рублей) | 1 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0 |
Найдите наименьшее значение r, при котором общая сумма выплат будет больше 1,2 млн рублей.
Протестируем нашу универсальную табличку в третий раз, доверьте это непростое занятие школьнику. Пусть процессом командует он! По ответам будет ясно, ловит ли он суть.
Отличие от прошлого типа будет лишь в том, что в третий столбец мы будем записывать не равномерно убывающий долг, а перенесем остаток долга из таблицы условия. Чтобы не таскать по решению нули, считать будем в миллионах:
Чтобы долг убывал согласно табличке, нам снова каждый раз придется гасить набежавшие проценты и первые 5 месяцев добавлять сверху 0,1 млн. После останется погасить весь остаток.
Акцентируйте внимание на механизме погашения, для школьника он не всегда очевиден.
«По условию нам снова дана общая сумма выплат, значит достаточно просуммировать оранжевый столбец, и уравнение готово», — вероятно, подумает школьник. Подловите его! Уравнение в этой задаче — прямой путь потерять балл! Сумма выплат должна быть БОЛЬШЕ 1,2 млн. Отразим это в модели с помощью неравенства:
Подопечный должен быть уверен в каждом символе в бланке ответа. Даже не пригодившиеся промежуточные вычисления с ошибкой приведут к катастрофе.
Приведем подобные и вынесем общие множители за скобку:
Последний шаг – не забыть, что по условию процент должен быть целым и округлить в верную сторону.
Ответ: 5%.
Правильная математическая модель — это суперважно! К ней проверяющие обязательно придерутся.
Тип 4. Погашение кредита в два этапа.
По сути, это та же прошлая задача, но месяцев больше
В 2017-2018 учебном году составителей экзамена посетило вдохновение, на свет родился вот этот тип банковских задач. Школьники были в шоке, и от страха завалили 17-ый номер. Хотя всего-то нужно было догадаться воспользоваться знаниями об арифметической прогрессии и достать из условия одно немного неочевидное дано!
15-го декабря планируется взять кредит в банке на 13 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 12-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 13-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 804 тысячи рублей?
И снова пусть по возможности командует школьник. По крайней мере он уже точно в курсе, что происходит первые 13 месяцев.
Последовательно начисляем процент на остаток долга – считаем выплату – фиксируем остаток долга после выплаты. Сумму кредита возьмем за S.
Научите школьника не спешить с вычислениями. Например, вместо того чтобы написать S-600, мы пишем S-50*12, потому что так удобнее: нам сразу ясно, что речь идет о двенадцатом месяце. Да и потом вычисления будут проще, если мы оставим маленькие числа.
Осталось составить уравнение, и модель готова. В задаче нам снова дали сумму всех выплат:
Как обычно, сгруппируем отдельно слагаемые с r/100, отдельно слагаемые без них:
Вот именно последняя группировка всех платежей в счет долга и оказалась неочевидной. Без нее в задаче остается одна лишняя неизвестная величина, которая рушит все решение.
Осталось привести уравнение к решаемому виду. Для этого надо просуммировать то, что получилось в скобках. Если внимательно приглядеться, то видно, что это сумма арифметической прогрессии:
Посчитаем эту сумму:
Подставляем выражение для суммы в уравнение, заметим, что по условию r=2:

Мы сокращали дробь, пока это было возможно, и в итоге довольно просто получили ответ даже без калькулятора. Ваш подопечный должен научиться также!
Ответ: 700 тысяч.
Зачем использовать формулу суммы прогрессии, если можно посчитать вручную? Все верно, можно. Но это только в данном случае кредит взяли всего на 13 месяцев. А бывают прототипы, когда срок – 21 и больше месяцев. В какой-то момент считать вручную станет совсем долго и неудобно, потому воспользоваться формулой суммы – более универсальный метод.
Чем закончить разбор экономической (банковской) задачи № 17 в ЕГЭ по математике
Чтобы у ученика окончательно сложилась картинка занятия, пробегитесь еще раз по основным выводам:
- Повторите алгоритм заполнения таблицы и решения задачи (да, пятый раз);
- Повторите типы задач и механизм распределения платежа на проценты и долг;
- Напомните, как важно считать культурно и быть уверенным в каждой циферке в бланке;
- Проговорите, что математическая модель должна точно отражать условие задачи.
Как показывает практика, чем больше повторяешь, тем больше шансов, что в голове выпускника останется хоть что-то.
За что дают баллы?
Знание критериев оценивания экономической (банковской) задачи № 17 в ЕГЭ по математике поможетученику чувствовать себя увереннее, ведь выставление баллов — это не какая-то магия и не вредность экспертов. Все правила игры прописаны в нормативных документах.
17-ый номер стоит 3 балла. Чтобы узнать, как их присуждают, мы залезли в методические рекомендации для членов предметных комиссий.
Согласно пояснениям из документа, для получения одного балла мало просто обоснованно составить математическую модель по задаче, надо предложить правильный метод ее анализа.
Два балла получит школьник, который ошибся в вычислениях или не обосновал появление математической модели в решении. Например, согласно методическим рекомендациям, решение на 2 балла выглядит так:
А вот отсутствие промежуточных вычислений хоть и усложняет проверку, но баллы не снимает.
Идеально выполненная первая часть ЕГЭ по профильной математике принесет школьнику всего 62 тестовых балла. Добавим сюда пару ошибок по невнимательности, и останутся совсем крохи — баллов 50, не больше. Для поступления на бюджет мало, а значит необходимо планировать делать вторую часть! Чем раньше школьник это осознает, тем проще будет с ним работать. А банковская задача поможет получить дополнительные баллы с минимальными усилиями.
Однако кредиты – не единственный прототип 17-го номера, и в следующий раз мы расскажем, как научить школьника решать задачи на оптимальный выбор и ценные бумаги.
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Антон взял кредит в банке на срок 6 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на одно и то же число процентов (месячную процентную ставку), а затем уменьшается на сумму, уплаченную Антоном. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Общая сумма выплат превысила сумму кредита на 63%. Найдите месячную процентную ставку.
Источник: Интеллект-центр. Репетиционные варианты ЕГЭ 2015.
2
Жанна взяла в банке в кредит 1,2 млн рублей на срок 24 месяца. По договору Жанна должна вносить в банк часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 2%, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна выплатит банку в течение первого года кредитования?
3
1 марта 2010 года Аркадий взял в банке кредит под 10% годовых. Схема выплаты кредита следующая: 1 марта каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Аркадий переводит в банк платеж. Весь долг Аркадий выплатил за 3 платежа, причем второй платеж оказался в два раза больше первого, а третий – в три раза больше первого. Сколько рублей взял в кредит Аркадий, если за три года он выплатил банку 2 395 800 рублей?
Источник: А. Ларин: Тренировочный вариант № 122.
4
В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг возрастает на 31% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга, равную 69 690 821 рубль.
Сколько рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами ( то есть за три года)?
Источник: А. Ларин: Тренировочный вариант № 131.
5
Анатолий решил взять кредит в банке 331000 рублей на 3 месяца под 10% в месяц. Существуют две схемы выплаты кредита.
По первой схеме банк в конце каждого месяца начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Анатолий переводит в банк фиксированную сумму и в результате выплачивает весь долг тремя равными платежами (аннуитетные платежи).
По второй схеме тоже сумма долга в конце каждого месяца увеличивается на 10%, а затем уменьшается на сумму, уплаченную Анатолием. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину (дифференцированные платежи). Какую схему выгоднее выбрать Анатолию? Сколько рублей будет составлять эта выгода?
Источник: А. Ларин: Тренировочный вариант № 137.
Пройти тестирование по этим заданиям
Муниципальное бюджетное
общеобразовательное учреждение
«Средняя
общеобразовательная школа № 2»
Cпособы решения
банковских задач при подготовке к ЕГЭ
Исследовательская работа
Выполнила: И.В. Лужных,
учитель
математики МБОУ «СОШ № 2»,
г. Ленинск-Кузнецкий
______________
(подпись)
Ленинск-Кузнецкий
2021
Оглавление
Введение…………………………………………………………………………..3
1.
Обоснование
выбора описываемого в данной работе решения ……….4
2.
Основные
виды банковских заданий ……………..……………………..5
2.1.
Банковские
задачи направленные на уменьшение суммы основного долга на одну и ту же сумму ………………………………………….5
2.2.
Банковские
задачи направленные на уменьшение суммы основного долга, когда сумма выплат
одинаковая или разная …………………9
2.3.
Банковские
задачи, направленные на вклад …………………………12
Заключение……………………………………………………………………….15
Литература……………………………………………………………………….16
Приложения……………………………………………………………………….17
Введение
Во второй части ЕГЭ может присутствовать
банковская задача, которую решить по силам даже десятикласснику, если изучить
удобный и доступный способ решения. Методы решения задач данного типа,
представленные в сети Интернет часто не являются универсальными, простыми,
достаточно обоснованными. Поэтому необходимы способы, которые отвечали бы
данным критериям.
Таким образом, изучение этих способов
является актуальным уже в 10 классе.
Объект исследования: банковские задачи на ЕГЭ.
Предмет исследования: основные
типы банковских задач и способы их решения.
Гипотеза – существуют простые и удобные методы решения
банковских задач, представленных в ЕГЭ, овладеть которыми могут учащиеся
десятых классов общеобразовательных школ.
Цель: изучение наиболее рационального способа решения
банковских задач
Задачи:
1.Рассмотреть типы банковских заданий на ЕГЭ и изучить
их возможные способы решения.
2.Выбрать наиболее рациональный способ.
3.Применить способ для решения разных типов заданий
4.Создать сборник задач по данной теме.
Практическая значимость работы – составление задачника
с распределением задач по способам решения.
Обоснование
выбора описываемого в данной работе решения.
При выборе метода по
решению банковских заданий мной предъявлялись следующие требования:
-полнота, обоснованность;
-простота применения;
-наглядность;
-универсальность;
-доступность для решения
задачи десятыми классами.
Больше всего этим
критериям соответствует решение с помощью таблиц. Также в решении удобно
применять коэффициент, на который умножается основная сумма долга или вклада, b = 1 + , где r — месячная или
годовая ставка.[2]
2.Основные виды банковских заданий и
способы их решения.
2.1.
Банковские задачи направленные на уменьшение
суммы основного долга на одну и ту же сумму.
Для
решения данного типа задач можно воспользоваться следующим алгоритмом.
1. Обозначаем
основную сумму долга за n×S,
где n – количество месяцев или
лет, месячную процентную ставку, коэффициент умножения суммы долга.
2. Строим
таблицу, в первой колонке – месяц или год, во второй – основная сумма долга, в
третьей — сумма долга с процентами, в следующих – сумма платежа и сумма
оставшегося долга.
3.
Пользуемся
таблицей и находим нужные величины, решая уравнение или составляя пропорцию.
Примеры.
Рисунок 1.Задание
1[1]
Решение.
Пусть 6S – сумма,
взятая Антоном в кредит
r % — месячная процентная ставка
b
= 1 + – коэффициент, на который умножается
основная сумма долга
|
Месяц |
Основная сумма долга |
Сумма долга с процентами |
Сумма платежа |
Сумма оставшегося долга |
|
1 |
6S |
6Sb |
6Sb-5S |
5S |
|
2 |
5S |
5Sb |
5Sb -4S |
4S |
|
3 |
4S |
4Sb |
4Sb — 3S |
3S |
|
4 |
3S |
3Sb |
3Sb — 2S |
2S |
|
5 |
2S |
2Sb |
2Sb — S |
S |
|
6 |
S |
Sb |
Sb |
0 |
Сумма всех выплат
равна 21Sb –
15 S
Обозначим
изначальную сумму долга за 100 процентов, а сумму всех выплат за 163 процента,
тогда
6S
– 100%
21Sb
— 15S ̶ 163%
Решая пропорцию,
получаем:
2100Sb
– 1500S = 978 S
2100b
= 2478
b
= = 1,18
Так как b = 1 + ,
Откуда r
= 18%
Ответ: 18%.
Рисунок
2.
Задание 2 [4]
Решение.
Пусть
24S – сумма, взятая Жанной в
кредит
r
% — месячная процентная ставка
b = 1 + – коэффициент, на который умножается
основная сумма долга
b = 1,02
|
Месяц |
Основная сумма долга |
Сумма долга с процентами |
Сумма платежа |
Сумма оставшегося долга |
|
1 |
24S |
24Sb |
24Sb — 23S |
23S |
|
2 |
23S |
23Sb |
23Sb — 22S |
22S |
|
3 |
22S |
22Sb |
22Sb — 21S |
21S |
|
4 |
21S |
21Sb |
21Sb — 20S |
20S |
|
5 |
20S |
20Sb |
20Sb -19S |
19S |
|
6 |
19S |
19Sb |
19Sb — 18S |
18S |
|
7 |
18S |
18Sb |
18Sb — 17S |
17S |
|
8 |
17S |
17Sb |
17Sb -16S |
16S |
|
9 |
16S |
16Sb |
16Sb -15S |
15S |
|
10 |
15S |
15Sb |
15Sb -14S |
14S |
|
11 |
14S |
14Sb |
14Sb — 13S |
13S |
|
12 |
13S |
13Sb |
13Sb — 12S |
12S |
|
13 |
12S |
12Sb |
12Sb — 11s |
11S |
|
14 |
11S |
11Sb |
11Sb — 10S |
10S |
|
15 |
10S |
10Sb |
10Sb — 9S |
9S |
|
16 |
9S |
9Sb |
9Sb — 8S |
8S |
|
17 |
8S |
8Sb |
8Sb — 7S |
7S |
|
18 |
7S |
7Sb |
7Sb -6S |
6S |
|
19 |
6S |
6Sb |
6Sb — 5S |
5S |
|
20 |
5S |
5Sb |
5Sb — 4S |
4S |
|
21 |
4S |
4Sb |
4Sb — 3S |
3S |
|
22 |
3S |
3Sb |
3Sb — 2S |
2S |
|
23 |
2S |
2Sb |
2Sb -s |
S |
|
24 |
S |
Sb |
Sb |
0 |
Сумма всех выплат
за первый год кредитования равна
37Sb*6
– 35S*6 = 222Sb –210S= 222*0,05*1,02 – 210*0,05= 0,822 млн рублей=
= 822000 руб.
Ответ: 822000 руб.
2.2
Банковские
задачи направленные на уменьшение суммы основного долга, когда сумма выплат
одинаковая или разная
Для решения данного типа задач воспользуемся следующим алгоритмом.
1. Обозначим
сумму, взятую в кредит за S,
месячную процентную ставку, коэффициент умножения суммы долга, платеж.
2. Строим
таблицу, в первой колонке – месяц или год, во второй – основная сумма долга, в
третьей- сумма долга с процентами, в следующих – сумма платежа и сумма
оставшегося долга.
3. Пользуемся
таблицей и находим нужные величины, решая уравнение или составляя пропорцию.
Примеры.
Рисунок
3. Задание 3[3]
Решение.
Пусть
S руб. – сумма, взятая в
кредит
r =
10% — ежегодная процентная ставка
b = 1 + – коэффициент, на
который умножается основная сумма долга
b
= 1,1
x руб.
– сумма платежа в первый год
2x
руб.
– сумма платежа во второй год
3x
руб.
– сумма платежа в третий год
|
Год |
Основная сумма долга |
Сумма долга с процентами |
Сумма платежа |
Сумма оставшегося долга |
|
1 |
S |
Sb |
x |
Sb -x |
|
2 |
Sb -x |
Sb² — bx |
2x |
Sb² -bx — 2x |
|
3 |
Sb² -bx — 2x |
Sb³ -b²x — 2bx |
3x |
Sb³ -b²x — 2bx — 3x |
x +2x
+ 3x =2395800
x = 399300
Так как долг погашен,
Sb³ -b²x — 2bx — 3x = 0
Sb³ = b²x + 2bx+ 3x
Sb³ = x(b² + 2b+ 3)
S
=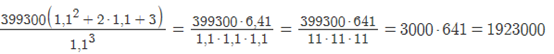
Ответ: 1923000
руб.
Рисунок 4. Задание 4[3]
Решение.
Пусть
S руб. – сумма, взятая в
кредит
r
= 31% — ежегодная процентная ставка
b = 1 + – коэффициент, на
который умножается основная сумма долга
b
= 1,31
x
= 69690821 руб. – сумма ежегодного платежа
|
Год |
Основная сумма долга |
Сумма долга с процентами |
Сумма платежа |
Сумма оставшегося долга |
|
1 |
S |
Sb |
x |
Sb — x |
|
2 |
Sb — x |
Sb² — bx |
x |
Sb² — bx |
|
3 |
Sb² — bx |
Sb³ — b²x |
x |
Sb ³- |
Так
как долг погашен,
Sb³
—
b²x
— bx – x = 0
Sb³ — b²x — bx — x = 0
Sb³ = b²x + bx+ x
Sb³ = x(b² + b+ 1)
S = 124809100 рублей
Ответ: 124809100 руб.
2.3. Банковские задачи, направленные на вклад.
Для решения данного типа задач воспользуемся следующим алгоритмом.
1. Обозначим
сумму вклада за S, месячную процентную
ставку, коэффициент умножения суммы долга, платеж.
2. Строим
таблицу, в первой колонке – месяц или год, во второй – основная сумма вклада, в
третьей — сумма вклада с процентами, в следующих (если необходимо) — сумма
платежа и сумма остатка.
3. Пользуемся
таблицей и находим нужные величины, решая уравнение или составляя пропорцию
Примеры.
Рисунок
5. Задание 5[1]
Решение.
Пусть S руб. –
изначальная сумма вклада
r = 10% — ежегодная процентная ставка
b = 1 + – коэффициент, на
который умножается основная сумма вклада
b
= 1,1
x = 2000 руб.– сумма, которая снимается со
вклада
Для запланированной суммы
|
Год |
Вклад |
Вклад с процентами |
|
1 |
S |
Sb |
|
2 |
Sb |
Sb² |
|
3 |
Sb² |
Sb³ |
Для фактической суммы
|
Год |
Вклад |
Вклад с процентами |
Остаток |
|
1 |
S |
Sb |
Sb — x |
|
2 |
Sb — x |
Sb² — bx |
Sb² — bx +x |
|
3 |
Sb² — bx +x |
Sb³ — b²x +bx |
Разница между запланированной и фактической суммой
равна
Sb³ — (Sb³
— b²x
+bx) = b²x
— bx = 1,1²×2000 – 1,1×2000= 220 руб.
То есть, вкладчик получит на 220 руб. меньше
запланированной суммы
Ответ: 220 руб.
Рисунок
6. Задание 6[5]
Решение.
Пусть S = 400000 руб. –
изначальная сумма вклада
r = 12,5% — ежегодная процентная ставка
b = 1 + – коэффициент, на
который умножается основная сумма вклада
b
= 1,125
m – сумма, на которую пополняется вклад
|
Год |
Основная сумма вклада |
Платеж |
Сумма вклада с |
|
1 |
S |
— |
Sb |
|
2 |
Sb |
— |
Sb² |
|
3 |
Sb² |
m |
Sb³+mb |
|
4 |
Sb³+mb |
m |
Sb⁴+mb²+mb |
Так как сумма на вкладе к четвертому году должна быть
не меньше должна быть не меньше 7000000 руб.,
Sb⁴+mb²+mb >700000
m(b²+b)>700000 — Sb⁴
m >
m > 24795,751633…руб.
Так как m –
целое число, m минимальное
равно 25 тысяч рублей
Ответ: 25
тысяч руб.
Заключение
Был выбран наиболее
рациональный и соответствующий критериям способ решения банковских задач. Этот
метод был успешно применен для решения задач из разных сборников для подготовки
к ЕГЭ. Была доказана его простота, доступность для учащихся десятых классов.
Для успешной подготовки
учащихся к ЕГЭ был составлен задачник, помогающий в изучении данного способа
решения банковских задач, который разбит на главы по типам заданий и содержит
как задания с готовым решением, так и задачи для самостоятельного решения с
ответами для самопроверки.
Данный задачник был предложен ученикам десятого класса
школы №2 в качестве вспомогательного пособия для подготовки к ЕГЭ.
Работая над темой данной работы, можно сделать вывод,
что несмотря на кажущуюся сложность и многообразие банковских задач на ЕГЭ, начинать
готовиться к их успешному выполнению можно уже в десятом классе
общеобразовательных школ, что становиться возможным, используя предложенный в
данной работе способ.
Литература.
1. Математика.
Подготовка к ЕГЭ 2020. Профильный уровень. 40 тренировочных вариантов по
демоверсии 2020 года : учебно-методическое пособие / под редакцией Ф.Ф.
Лысенко, С.Ю. Кулабухова.- Ростов-на-Дону: Легион, 2019. – 416с. – (ЕГЭ)
2. Алгебра
: 9 класс : учебник для учащихся общеобразовательных организаций / А.Г.
Мерзляк, В.Б. Полонский, М.С. Якир.- М. : Вентана-Граф, 2018. – 304 с. : ил.
3. ЕГЭ.
Математика. Профильный уровень : типовые экзаменационные варианты : 36
вариантов / под редакцией И.В. Ященко. – М. : Издательство «Национальное
образование», 2019. – 256с. – (ЕГЭ. ФКР – школе)
4. Решу
ЕГЭ Дмитрий Гущин.
https://math-ege.sdamgia.ru/test?theme=221
5. ЕГЭ.
Математика. Профильный уровень : типовые экзаменационные варианты : 36
вариантов / под редакцией И.В. Ященко. – М. : Издательство «Национальное
образование», 2020. – 256с. – (ЕГЭ. ФКР – школе)
Приложения.
Задачник
Муниципальное
бюджетное общеобразовательное учреждение
«Средняя
общеобразовательная школа № 2»
НОУ
«Эрудит»
Cпособы решения
банковских задач при подготовке к ЕГЭ
Задачник
с рекомендациями
Ленинск-Кузнецкий
2021
Содержание
Введение………………………………………………………………………..….3
§1. Банковские
задачи направленные на уменьшение суммы основного долга на одну и ту же сумму ………………………………………………..…………..4
§2. Банковские
задачи направленные на уменьшение суммы основного долга, когда сумма выплат
одинаковая или разная …………………………..……….10
§3. Банковские задачи,
направленные на вклад …………………….……..…..16
Ответы…………………………………………………………………………….19
Литература………………………………………………………………….……20
Введение
Данное
пособие предназначено для подготовки к ЕГЭ по математике профильного уровня.
Банковские задачи относятся к заданиям, готовиться к которым можно с успехом
уже в десятом классе. Существует много методов решения задач этого типа, но в
этом задачнике рассмотрен рациональный способ, отвечающий всем критериям к
решению. В данном задачнике представлены основные способы решения,
проработанные примеры и задания для самостоятельного решения.
§1.
Банковские
задачи направленные на уменьшение суммы основного долга на одну и ту же сумму.
Для решения данного типа задач можно воспользоваться
следующим алгоритмом.
1. Обозначаем
основную сумму долга за n×S,
где n – количество месяцев или
лет, месячную процентную ставку, коэффициент умножения суммы долга.
2. Строим
таблицу, в первой колонке – месяц или год, во второй – основная сумма долга, в
третьей- сумма долга с процентами, в следующих – сумма платежа и сумма
оставшегося долга.
3. Пользуемся
таблицей и находим нужные величины, решая уравнение или составляя пропорцию.
Примеры.
Решение.
Пусть 6S – сумма,
взятая Антоном в кредит
r % — месячная процентная ставка
b
= 1 + – коэффициент, на который умножается
основная сумма долга
|
Месяц |
Основная сумма долга |
Сумма долга с процентами |
Сумма платежа |
Сумма оставшегося долга |
|
1 |
6S |
6Sb |
6Sb-5S |
5S |
|
2 |
5S |
5Sb |
5Sb -4S |
4S |
|
3 |
4S |
4Sb |
4Sb — 3S |
3S |
|
4 |
3S |
3Sb |
3Sb — 2S |
2S |
|
5 |
2S |
2Sb |
2Sb — S |
S |
|
6 |
S |
Sb |
Sb |
0 |
Сумма всех выплат
равна 21Sb –
15 S
Обозначим
изначальную сумму долга за 100 процентов, а сумму всех выплат за 163 процента,
тогда
6S
– 100%
21Sb
— 15S ̶ 163%
Решая пропорцию,
получаем:
2100Sb
– 1500S = 978 S
2100b
= 2478
b
= = 1,18
Так как b = 1 + ,
Откуда r
= 18%
Ответ: 18%.
Решение.
Пусть
24S – сумма, взятая Жанной в
кредит
r
% — месячная процентная ставка
b = 1 + – коэффициент, на который умножается
основная сумма долга
b = 1,02
|
Месяц |
Основная сумма долга |
Сумма долга с процентами |
Сумма платежа |
Сумма оставшегося долга |
|
1 |
24S |
24Sb |
24Sb — 23S |
23S |
|
2 |
23S |
23Sb |
23Sb — 22S |
22S |
|
3 |
22S |
22Sb |
22Sb — 21S |
21S |
|
4 |
21S |
21Sb |
21Sb — 20S |
20S |
|
5 |
20S |
20Sb |
20Sb -19S |
19S |
|
6 |
19S |
19Sb |
19Sb — 18S |
18S |
|
7 |
18S |
18Sb |
18Sb — 17S |
17S |
|
8 |
17S |
17Sb |
17Sb -16S |
16S |
|
9 |
16S |
16Sb |
16Sb -15S |
15S |
|
10 |
15S |
15Sb |
15Sb -14S |
14S |
|
11 |
14S |
14Sb |
14Sb — 13S |
13S |
|
12 |
13S |
13Sb |
13Sb — 12S |
12S |
|
13 |
12S |
12Sb |
12Sb — 11s |
11S |
|
14 |
11S |
11Sb |
11Sb — 10S |
10S |
|
15 |
10S |
10Sb |
10Sb — 9S |
9S |
|
16 |
9S |
9Sb |
9Sb — 8S |
8S |
|
17 |
8S |
8Sb |
8Sb — 7S |
7S |
|
18 |
7S |
7Sb |
7Sb -6S |
6S |
|
19 |
6S |
6Sb |
6Sb — 5S |
5S |
|
20 |
5S |
5Sb |
5Sb — 4S |
4S |
|
21 |
4S |
4Sb |
4Sb — 3S |
3S |
|
22 |
3S |
3Sb |
3Sb — 2S |
2S |
|
23 |
2S |
2Sb |
2Sb -s |
S |
|
24 |
S |
Sb |
Sb |
0 |
Сумма всех выплат
за первый год кредитования равна
37Sb*6
– 35S*6 = 222Sb –210S= 222*0,05*1,02 – 210*0,05= 0,822 млн рублей=
= 822000 руб.
Ответ:
822000
руб.
Решение.
Пусть 9S – сумма, взятая Антоном в кредит
r = 12% — месячная процентная ставка
b = 1 +
– коэффициент, на который умножается
основная сумма долга
b = 1,12
|
Месяц |
Основная сумма долга |
Сумма долга с процентами |
Сумма платежа |
Сумма оставшегося долга |
|
1 |
9S |
9Sb |
9Sb — 8S |
8S |
|
2 |
8S |
8Sb |
8Sb — 7S |
7S |
|
3 |
7S |
7Sb |
7Sb -6S |
6S |
|
4 |
6S |
6Sb |
6Sb — 5S |
5S |
|
5 |
5S |
5Sb |
5Sb — 4S |
4S |
|
6 |
4S |
4Sb |
4Sb — 3S |
3S |
|
7 |
3S |
3Sb |
3Sb — 2S |
2S |
|
8 |
2S |
2Sb |
2Sb -s |
S |
|
9 |
1S |
1Sb |
Sb |
0 |
Сумма всех выплат равна
10Sb *4 + 5Sb – 9S*4= 45Sb
– 36S
Пусть сумма всех выплат – z%,
а изначальная сумма кредита – 100%
45Sb – 36S
—z%
9S — 100%
4500Sb – 3600S = 9 Sz
9z = 1440
z = 160% cумма,
выплаченная банку
160% — 100% = 60% составляет плата сверх кредита
Ответ: 60%.
Задания для самостоятельного решения
1. 1
января 2015 года Павел Витальевич взял в банке 1 млн рублей в кредит. Схема
выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет 1
процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Павел
Витальевич переводит в банк платёж. На какое минимальное количество месяцев
Павел Витальевич может взять кредит, чтобы ежемесячные выплаты были не более
125 тыс. рублей?
2. 31
декабря 2014 года Алексей взял в банке 6 902 000 рублей в кредит под 12,5%
годовых. Схема выплат кредита следующая — 31 декабря каждого следующего года
банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на
12,5%), затем Алексей переводит в банк x рублей. Какой должна быть сумма x,
чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре
года)?
3. 31
декабря 2014 года Тимофей взял в банке 7 007 000 рублей в кредит под 20%
годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года
банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на
20%), затем Тимофей переводит в банк платёж. Весь долг Тимофей выплатил за 3
равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог
выплатить долг за 2 равных платежа?
§2. Банковские
задачи направленные на уменьшение суммы основного долга, когда сумма выплат
одинаковая или разная
Для
решения данного типа задач воспользуемся следующим алгоритмом.
1. Обозначим
сумму, взятую в кредит за S,
месячную процентную ставку, коэффициент умножения суммы долга, платеж.
2. Строим
таблицу, в первой колонке – месяц или год, во второй – основная сумма долга, в
третьей- сумма долга с процентами, в следующих – сумма платежа и сумма
оставшегося долга.
3. Пользуемся
таблицей и находим нужные величины, решая уравнение или составляя пропорцию.
Примеры.
Решение.
Пусть
S руб. – сумма, взятая в
кредит
r =
10% — ежегодная процентная ставка
b = 1 + – коэффициент, на
который умножается основная сумма долга
b
= 1,1
x руб.
– сумма платежа в первый год
2x
руб.
– сумма платежа во второй год
3x
руб.
– сумма платежа в третий год
|
Год |
Основная сумма долга |
Сумма долга с процентами |
Сумма платежа |
Сумма оставшегося долга |
|
1 |
S |
Sb |
x |
Sb -x |
|
2 |
Sb -x |
Sb² — bx |
2x |
Sb² -bx — 2x |
|
3 |
Sb² -bx — 2x |
Sb³ -b²x — 2bx |
3x |
Sb³ -b²x — 2bx — 3x |
x +2x
+ 3x =2395800
x = 399300
Так как долг погашен,
Sb³ -b²x — 2bx — 3x = 0
Sb³ = b²x + 2bx+ 3x
Sb³ = x(b² + 2b+ 3)
S
=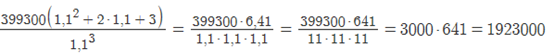
Ответ: 1923000
руб.
Решение.
Пусть
S руб. – сумма, взятая в
кредит
r =
31% — ежегодная процентная ставка
b = 1 + – коэффициент, на
который умножается основная сумма долга
b
= 1,31
x
= 69690821 руб. – сумма ежегодного платежа
|
Год |
Основная сумма долга |
Сумма долга с процентами |
Сумма платежа |
Сумма оставшегося долга |
|
1 |
S |
Sb |
x |
Sb -x |
|
2 |
Sb -x |
Sb² — bx |
x |
Sb² -bx — x |
|
3 |
Sb² -bx — x |
Sb³ -b²x — bx |
x |
Sb³ -b²x-bx–x=0 |
Так
как долг погашен,
Sb³
-b²x — bx – x = 0
Sb³ -b²x — bx — x = 0
Sb³ = b²x + bx+ x
Sb³ = x(b² + b+ 1)
S = 124809100 рублей
Ответ: 124809100
руб.
Решение.
Пусть
S = 2180000 руб. – сумма,
взятая в кредит
r =
40% — ежегодная процентная ставка
b = 1 + – коэффициент, на
который умножается основная сумма долга
b
= 1,4
x руб.
– сумма ежегодного платежа
|
Год |
Основная сумма долга |
Сумма долга с процентами |
Сумма платежа |
Сумма оставшегося долга |
|
1 |
S |
Sb |
x |
Sb -x |
|
2 |
Sb -x |
Sb² — bx |
x |
Sb² -bx — x |
|
3 |
Sb² -bx — x |
Sb³ -b²x — bx |
x |
Sb³ -b²x-bx–x=0 |
Так
как долг погашен,
Sb³
-b²x — bx – x = 0
Sb³ -b²x — bx — x = 0
Sb³ = b²x + bx+ x
Sb³ = x(b² + b+ 1)
x = 1372000 руб.
Сумма
всех выплат равна 3x
Сумма
переплат равна 3x –
S = 1 936 000 руб.
Ответ: 124809100
руб.
Решение.
Пусть
S руб. – сумма, взятая в
кредит
r =
5% — ежегодная процентная ставка
b = 1 + – коэффициент, на
который умножается основная сумма долга
b = 1,05
|
Год |
Основная |
Сумма |
Сумма |
|
1 |
S |
Sb |
Sb |
|
2 |
0,9S |
9Sb |
0,9Sb |
|
3 |
0,7S |
8Sb |
0,8Sb |
|
4 |
0,8S |
7Sb |
0,7Sb |
|
5 |
0,6S |
6Sb |
0,6Sb |
|
6 |
0,5S |
5Sb |
0,5Sb |
Сумма всех выплат равна
4,5Sb – 3,5 S = 1, 225S
1, 225S – z%
S – 100%
z =
z = 122,5%
Сумма выплат сверх суммы основного кредита равна
122,5% — 100% = 22, 5%
Ответ: 22,5 %.
Задания для
самостоятельного решения
1. Фермер
получил кредит в банке под определенный процент годовых. Через год фермер в
счет погашения кредита вернул в банк от всей суммы, которую он должен банку к
этому времени, а еще через год в счет полного погашения кредита он внес в банк
сумму, на 21% превышающую величину полученного кредита. Каков процент годовых
по кредиту в данном банке?
2. 15-го
января планируется взять кредит в банке на 19 месяцев. Условия его возврата
таковы:
—
1-го числа каждого месяца долг возрастёт на r% по сравнению с концом
предыдущего месяца;
—
со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
—
15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга
на 15-е число предыдущего месяца. Известно, что общая сумма выплат после
полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r.
3.
В
июле 2016 года планируется взять кредит в размере 6,6 млн. руб. Условия
возврата таковы:
—
каждый январь долг возрастает на r% по сравнению с концом предыдущего года.
—
с февраля по июнь необходимо выплатить часть долга.
—
в июле 2017, 2018 и 2019 годов долг остается равным 6,6 млн. руб.
—
суммы выплат 2020 и 2021 годов равны.
Найдите
r, если в 2021 году долг будет выплачен полностью и общие выплаты составят 12,6
млн. рублей.
3. Банковские задачи,
направленные на вклад.
Для решения данного типа задач воспользуемся следующим алгоритмом.
1. Обозначим
сумму вклада за S, месячную процентную
ставку, коэффициент умножения суммы долга, платеж.
2. Строим
таблицу, в первой колонке – месяц или год, во второй – основная сумма вклада, в
третьей- сумма вклада с процентами, в следующих (если необходимо) — сумма
платежа и сумма остатка.
3. Пользуемся
таблицей и находим нужные величины, решая уравнение или составляя пропорцию
Примеры.
Решение.
Пусть S руб. –
изначальная сумма вклада
r = 10% — ежегодная процентная ставка
b = 1 + – коэффициент, на
который умножается основная сумма вклада
b
= 1,1
x= 2000 руб.– сумма, которая снимается со вклада
Для запланированной суммы
|
Год |
Вклад |
Вклад с процентами |
|
1 |
S |
Sb |
|
2 |
Sb |
Sb² |
|
3 |
Sb² |
Sb³ |
Для фактической суммы
|
Год |
Вклад |
Вклад с процентами |
Остаток |
|
1 |
S |
Sb |
Sb — x |
|
2 |
Sb — x |
Sb² — bx |
Sb² — bx +x |
|
3 |
Sb² — bx +x |
Sb³ — b²x +bx |
Разница между запланированной и фактической суммой
равна
Sb³ — (Sb³
— b²x
+bx) = b²x
— bx = 1,1²×2000 – 1,1×2000= 220 руб.
То есть, вкладчик получит на 220 руб. меньше
запланированной суммы
Ответ: 220 руб.
Решение.
Пусть S = 400000 руб. –
изначальная сумма вклада
r = 12,5% — ежегодная процентная ставка
b = 1 + – коэффициент, на
который умножается основная сумма вклада
b
= 1,125
m – сумма, на которую пополняется вклад
|
Год |
Основная сумма вклада |
Платеж |
Сумма вклада с |
|
1 |
S |
— |
Sb |
|
2 |
Sb |
— |
Sb² |
|
3 |
Sb² |
m |
Sb³+mb |
|
4 |
Sb³+mb |
m |
Sb⁴+mb²+mb |
Так как сумма на вкладе к четвертому году должна быть
не меньше должна быть не меньше 7000000 руб.,
Sb⁴+mb²+mb >700000
m(b²+b)>700000 — Sb⁴
m >
m > 24795,751633…руб.
Так как m –
целое число, m минимальное
равно 25 тысяч рублей
Ответ: 25
тысяч руб.
Задания для самостоятельного решения
1. Миша
и Маша положили в один и тот же банк одинаковые суммы под 10% годовых. Через
год сразу после начисления процентов Миша снял со своего счета 5000 рублей, а
еще через год снова внес 5000 рублей. Маша, наоборот, через год доложила на
свой счет 5000 рублей, а еще через год сразу после начисления процентов сняла
со счета 5000 рублей. Кто через три года со времени первоначального вложения
получит большую сумму и на сколько рублей?
2. Близнецы
Саша и Паша положили в банк по 50 000 рублей на три года под 10% годовых Однако
через год и Саша, и Паша сняли со своих счетов соответственно 10% и 20%
имеющихся денег. Еще через год каждый из них снял со своего счета
соответственно 20 000 рублей и 15 000 рублей. У кого из братьев к концу
третьего года на счету окажется большая сумма денег? На сколько рублей?
3. Владимир
поместил в банк 3600 тысяч рублей под 10% годовых. В конце каждого из первых
двух лет хранения после начисления процентов он дополнительно вносил на счет
одну и ту же фиксированную сумму. К концу третьего года после начисления
процентов оказалось, что размер вклада увеличился по сравнению с первоначальным
на 48,5%. Какую сумму Владимир ежегодно добавлял к вкладу?
Ответы.
§ 1.
1. на 9 месяцев.
2. 2 296 350 руб.
3. 806400
руб.
§ 2.
1. 120 %.
2. 3%.
3.20%.
§ 3.
1. Маша, на 1100 рублей.
2. у Саши, на 1155
рублей.
3. 240 тыс. рублей.
Литература
1. Математика.
Подготовка к ЕГЭ 2020. Профильный уровень. 40 тренировочных вариантов по
демоверсии 2020 года : учебно-методическое пособие / под редакцией Ф.Ф.
Лысенко, С.Ю. Кулабухова.- Ростов-на-Дону: Легион, 2019. – 416с. – (ЕГЭ)
2. Алгебра
: 9 класс : учебник для учащихся общеобразовательных организаций / А.Г.
Мерзляк, В.Б. Полонский, М.С. Якир.- М. : Вентана-Граф, 2018. – 304 с. : ил.
3. ЕГЭ.
Математика. Профильный уровень : типовые экзаменационные варианты : 36
вариантов / под редакцией И.В. Ященко. – М. : Издательство «Национальное
образование», 2019. – 256с. – (ЕГЭ. ФКР – школе)
4. Решу
ЕГЭ Дмитрий Гущин.
https://math-ege.sdamgia.ru/test?theme=221
5. ЕГЭ.
Математика. Профильный уровень : типовые экзаменационные варианты : 36
вариантов / под редакцией И.В. Ященко. – М. : Издательство «Национальное
образование», 2020. – 256с. – (ЕГЭ. ФКР – школе)
Скачано с www.znanio.ru
МКОУ «Калиновская средняя общеобразовательная школа»
Хомутовского района Курской области
Региональная «Неделя математики — 2017»
п. Хомутовка
19 октября 2017 года
Целевая аудитория: педагоги школ района, области.
Материалы и оборудование: ноутбук, проектор, презентация, тексты задач.
План мастер-класса:
- Актуальность обучения решению задач экономического содержания.
- Критерии оценивания задачи №17.
- Метод математического моделирования.
- Классификация банковских задач.
- Решение типовых задач (практическая работа).
Добрый день, уважаемые коллеги! Меня зовут Дрюкова Оксана Михайловна, я учитель математики Калиновской средней школы. В последние годы большую социальную значимость набирает финансовая и экономическая грамотность молодёжи. Это и организованный Центральным банком Российской Федерации проект «Онлайн уроки финансовой грамотности», и Всероссийский экономический диктант «Сильная экономика – процветающая Россия!», организованный Вольным экономическим обществом России, в котором мои ученики приняли участие 12 октября. Кроме того, Концепция математического образования призывает нас обеспечивать необходимое стране число выпускников, математическая подготовка которых достаточна для продолжения образования в различных направлениях и для практической деятельности, включая преподавание математики, математические исследования, работу в сфере информационных технологий и др.
Именно поэтому одной из особенностей вариантов ЕГЭ по математике профильного уровня с 2015 году является включение практико-ориентированной задачи. Эта задача направлена на применение методов математики при решении содержательных и прикладных задач, в том числе социально-экономического содержания. У учащихся при этом проверяется умение выполнять действия с целыми числами, действий со степенями с натуральным показателем, знаний и умений обращаться с процентами, в том числе и сложными «банковскими» процентами.
Использование задач на проценты раньше также практиковалось в проведении итоговой аттестации. Их достаточно часто включали в варианты как школьных выпускных экзаменов, так и вступительных экзаменов в различные вузы страны. И вот по истечении многих лет задачи на проценты вновь входят в состав заданий ЕГЭ по математике.
Сегодня я остановлюсь на вопросах методики обучения учащихся умению решать задачи с социально-экономическим содержанием при подготовке к ЕГЭ по математике, а именно — решению банковских задач. Выбор темы выпал не случайно, поскольку, на мой взгляд, такие задачи чаще встречаются на экзаменах, к тому же я сама имею образование по специальности «финансы и кредит».
В первую очередь знакомимся с критериями оценивания задачи №17.
|
Содержание критерия |
Баллы |
|
Обоснованно получен верный ответ |
3 |
|
Верно построена математическая модель, решение сведено к исследованию этой модели и получен результат: — неверный ответ из-за вычислительной ошибки; — верный ответ, но решение недостаточно обосновано |
2 |
|
Верно построена математическая модель, решение сведено к исследованию этой модели, при этом решение может быть не завершено |
1 |
|
Решение не соответствует ни одному из критериев, перечисленных выше |
0 |
|
Максимальный балл |
3 |
При обучении решению задач с социально экономическим содержанием передо мной стояла методическая задача – обучить учащихся использованию математического моделирования». Необходимо учащимся подчеркнуть, что процесс решения задачи представляет собой такую систему преобразований условий задачи, при которых достигается требуемое искомое.
Метод математического моделирования содержит следующие этапы:
1) построение математической модели объекта (явления, процесса);
2)исследование полученной модели, т.е. решение полученной математической задачи средствами математики;
3) интерпретация полученного решения с точки зрения исходной ситуации.
Среди задач с социально-экономическим содержанием важное место занимают так называемые «банковские задачи», так как при ее решении можно столкнуться с различными банковскими операциями (вкладами, ссудами). Такие задачи вызывают у учащихся большие трудности. Это объясняется тем, что в учебниках по математике не рассматриваются такие понятия, как простые и сложные проценты, и не вводятся формулы их вычисления. Предполагается, что учащиеся должны решать эти задачи, опираясь не на формулы, а на понимание понятия процента и умения решать основные три вида задач на проценты.
Итак, для начала выводим основную формулу.
Вспомним, как увеличить число на некоторое количество a%: А (1 + ).
Если этот процесс повторяется, то А (1 + )n.
Итак, пусть А- сумма кредита, а %- процент по кредиту, р=1 + это коэффициент, на который умножается остаток долга или коэффициент приращения, S – ежегодная выплата (транш) банку.
Остаток банку через 1 год: Ар- S.
Остаток банку через 2 года: (Ар- S)р – S= Ар2 – S (p+1).
Остаток банку через 3 года: (Ар2 — Sр-S)р – S= Ар3 – S (p2+p+1).
Остаток банку через 4 года: Ар4 – S (p3 + p2+p+1)= Ар4 – S (p+1)(p2+1).
Остаток банку через n лет: Арn – S (pn-1 + p n- 2+…+ p+1)= Арn – S , где (pn-1 + p n- 2+…+ p+1) можно преобразовать по формуле суммы геометрической прогрессии: b1=1, q=p.
Понятие этой схемы помогает учащимся решать задачи.
Банковские задачи можно классифицировать на следующие типы:
|
№ |
Годы выплаты |
Сумма кредита (долга) |
Транш (выплата) |
Проценты |
|
1 тип |
? |
+ |
+ |
+ |
|
2 тип |
+ |
+ |
? |
+ |
|
3 тип |
+ |
? |
+ |
+ |
|
4 тип |
+ |
+ |
+ |
? |
Итак, предлагаю рассмотреть 4 типа задач на проценты:
- Нахождение ежегодного платежа.
- Нахождение суммы кредита.
- Вычисление процентной ставки по кредиту.
- Нахождение количества лет выплаты кредита.
Поскольку мы живем в сельской местности, где развиваются фермерские хозяйства, то предлагаю тексты задач соответствующей тематике, близкой к реальности. Предлагаю вам выступить в роли моих учеников и , используя тексты задач, решить четыре задачи.
Нахождение количества лет выплаты кредита.
Фермерское хозяйство «Сапфир» планирует купить культиватор, взяв кредит в банке 1,5 миллиона рублей. Погашение кредита происходит раз год равными платежами (кроме, может быть, последней) после зачисления процентов. Процентная ставка, предлагаемая банком – 10 % годовых. На какое минимально количество лет фермерское хозяйство может взять кредит, чтобы ежегодные выплаты были не более 350 тысяч рублей?
Данная задача относится к первому типу, т.е. необходимо найти, за сколько периодов N кредит будет выплачен полностью.
Решение:
Итак, имеем А=1500 000 руб, а = 10%, р= 1+0,01*а=1,1.
N≥0, S≤ 350 000 руб,
В конце первого года долг составит: 1500 000 *1,1 – 350 000=1300 000 руб.
В конце второго года долг составит:1300 000 *1,1 – 350 000=1080 000 руб.
В конце третьего года долг составит: 1080 000 *1,1 – 350 000=838 000 руб.
В конце четвертого года долг составит: 838 000 *1,1 – 350 000=571800 руб.
В конце пятого года долг составит:571 800 *1,1 – 350 000=278980 руб.
В конце шестого года долг составит:278900 *1,1 =306878 руб.
Полученная сумма меньше 350 000 руб.
Ответ: кредит будет погашен за 6 лет.
Нахождение ежегодного платежа.
Фермерское хозяйство «Колос» для покупки комбайна берёт 15 960 000 рублей в кредит под 30% годовых. По истечении каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 30%), затем фермерское хозяйство переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы клиент выплатил долг тремя равными ежегодными платежами?
Решение:
Итак, имеем А=15960000 руб, а = 30%, р= 1+0,01*а=1,3.
Пусть искомый ежегодный платёж составляет Х рублей.
Тогда в конце первого года клиент будет должен
1,3 * 15 960 000 − x = (20 748 000 − x) рублей.
Аналогично, в конце второго года его долг составит
(1,3 *(20 748 000 − x) − x) = 26 972 400 − 2,3x рублей,
а к концу третьего : 1,3 * (26 972 400 − 2,3x) − x = 35 064 120 − 3,99x рублей.
Однако по условию клиент должен выплатить кредит тремя равными платежами, то есть в конце третьего года его долг должен составить 0 рублей.
35 064 120 − 3,99x = 0, x = 8 788 000.
Ответ: 8 788 000 рублей.
Нахождение суммы кредита.
31декабря 2018 года фермерское хозяйство «Хуторок» планируется взять кредит в банке для покупки животноводческой фермы под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга, затем фермерское хозяйство переводит в банк 2928200 рублей. Какую сумму может взять фермерское хозяйство в банке, чтобы выплатить долг четырьмя равными платежами, то есть за 4 года?
Решение:
Пусть сумма кредита Х, а сумма ежегодного платежа S = 2928200 руб., а = 10%, р= 1+0,01*а=1,1, тогда распишем сумму долга для каждого года:
1 год: 1,1х–S.
2 год :(1,1х – S) 1,1 – S.
3 год : (1,1 2 х –1,1 S – S) 1,1 – S
4 год : 1,1 4 х – S (1,1+1)(1,12 +1) .
После последней выплаты сумма долга стала равна нулю.
Составим и решим уравнение: 1,1 4 х – S (1,1+1)(1,12 +1)
1, 4641х — 4,641S = 0
1, 4641х = 4,641* 2928200
х = 9282000
Ответ: 9282000 рублей.
Нахождение процентной ставки по кредиту.
31 декабря 2014 года фермер, занимающийся разведением цветов в теплицах, взял в банке 1000000 рублей в кредит на приобретение удобрений. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга, затем фермер переводит в банк очередной транш. Фермер выплатил кредит за 2 транша. В первый раз он перевел в банк 660000 рублей, во второй – 484000 рублей. Под какой процент банк выдал кредит фермеру?
Решение:
Пусть А=1000000 рублей , первый транш S1=660 000 рублей, второй транш S2=484 000 рублей. Необходимо найти а, если р=1+0,01а.
Сумма долга после выплаты первого транша будет равна:
100000(1+0,01 а ) – 660000=340000+10000а.
Сумма долга после выплаты первого транша будет равна:
(340000+10000а) (1+0,01 а ) – 484000.
После выплаты второго транша сумма долга стала равна нулю.
Составим и решим уравнение:
(340000+10000а) (1+0,01 а ) – 484000= 0
100а2 +13400а -144000 = 0/ :100
а2 +134а – 1440 = 0
D = 23716 = 1542 , а1 = 10, а2 = -144 — не удовлетворяет условию задачи.
Ответ: 10%
Спасибо за работу! На мой взгляд, такой подход к решению доступен любому ученику. А рациональное включение экономического материала в текст задачи возможно при изучении практически любой темы школьного курса математики. Даже если учащимся неизвестно точное значение того или иного экономического понятия, они понимают его на житейском (бытовом) уровне. В процессе решения соответствующей задачи смысл экономического понятия уточняется. Хотя, не скрою, большую пользу приносят уроки обществознания и занятия элективного курса «Основы финансовой грамотности».
Для закрепления учащимся можно предложить составить аналогичную задачу и решить ее. Опыт показывает, что учащиеся с большим интересом решают такие задачи, с удовольствием составляют их самостоятельно. Материал для уроков можно найти и в открытом банке заданий ЕГЭ, а также в системе СтатГрад, в которой мы работаем, проводя тренировочные и диагностические работы при подготовке к экзамену.
Таким образом, считаю, что предлагаемая методика обучения решению задач является эффективным способом обучения решению задач с социально- экономическим содержанием при подготовке выпускников к ЕГЭ по математике профильного уровня.
23
Апр 2016
Категория: 15 (С4) Практич. задачи
Сборник банковских задачи для подготовки к ЕГЭ
Елена Репина
2016-04-23
2019-08-06
Автор: egeMax |
Нет комментариев
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Печать страницы
Добавить комментарий
- Материалы для подготовки к ЕГЭ
-
- Рубрики
- 01 Геометрия (13)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (78)
- 13 (С2) Стереометр. задачи (94)
- 14 (С3) Неравенства (89)
- 15 (С4) Практич. задачи (71)
- 16 (С5) Планиметр. задачи (86)
- 17 (С6) Параметры* (79)
- 18 (С7) Числа, их свойства (38)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
- II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (60)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
- Дружественные сайты
Сайт А. Ларина
ЕгэТренер – О. Себедаш
Математика?Легко!
Егэ? Ок! – И. Фельдман
- Свежие записи
- Тест «Гиперболы»
- Тест. Графики функций. Комбинированные задачи
- 10. Графики функций. Комбинированные задачи
- Тест. Тригонометрические функции
- 10. Тригонометрическая функция
- Тест. Кусочно-линейная функция
- 10. Кусочно-линейная функция
- Архивы Архивы
Как решать банковские задачи ЕГЭ по математике
- 24.01.2016
Представляем вам обновлённое издание Джендубаева Эдуарда по решению нового типа задач в ЕГЭ по математике — банковские задачи.
В 2019 году в ЕГЭ по математике банковские задачи размещаются под номером 17.
Немного истории. В 2015 году эти задачи были под номером 19. В 2016 году эти задачи будут под номером 17 и по сей день за ними сохранилась такая нумерация.
В методичке приводятся конкретные принципы решения банковских задач, а так же приводятся примеры с решениями и ответами.
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.