Все типы неравенств егэ - Помощь в подготовке к экзаменам и поступлению

При решении неравенств вы должны свободно владеть понятием числового неравенства, знать, что такое решение неравенства, что значит решить неравенство, помнить свойства неравенств. То же относится и к системам числовых неравенств. Все эти сведения вы можете найти в любом пособии для поступающих в вузы.
 Напомним свойства числовых неравенств.
 1. Если а > b , то b < а; наоборот, если а < b, то b > а.
 2. Если а > b и b > c, то а > c. Точно так же, если а b, то а + c > b+ c (и а – c > b – c). Если же а < b, то а + c < b+ c (и а – c b и c > d, то а + c > b + d; точно так же, если а < b и c < d, то а + c < b + d, т. е. два неравенства одинакового смысла можно почленно складывать.

Замечание.

Два неравенства одинакового смысла нельзя почленно вычитать друг из друга, так как результат может быть верным, но может быть и неверным. Например, если из неравенства 11 > 9 почленно вычесть неравенство 3 > 2, то получим верное неравенство 8 > 7. Если из неравенства 11 > 9 почленно вычесть неравенство 7 > 2, то полученное неравенство будет неверным.
 5. Если а > b и c < d, то а – c > b – d; если а d, то а – c b и m – положительное число, то m а > m b и , т.е. обе части неравенства можно умножить или разделить на одно и то же положительное число ( знак неравенства остаётся тем же ).
 Если же а > b и n – отрицательное число, то n а < n b и , т.е. обе части неравенства можно умножить или разделить на одно и то же отрицательное число, но при этом знак неравенства нужно переменить на противоположный.
 7. Если а > b и c > d , где а, b, c, d > 0, то а c > b d и если а 0, то аc < bd, т.е. неравенства одного смысла на множестве положительных чисел можно почленно перемножать.
Следствие. Если а > b, где а, b > 0, то а² > b², и если а < b, то а² < b², т.е. на множестве положительных чисел обе части неравенства можно возводить в квадрат.

8. Если а > b, где а, b > 0, то и если а < b , то .

Виды неравенств и способы их решения

1. Линейные неравенства и системы неравенств

Пример 1. Решить неравенство .
 Решение:
 .
 Ответ: х < – 2.

Пример 2. Решить систему неравенств
    Решение:
         .
    Ответ: (– 2; 0].

Пример 3. Найти наименьшее целое решение системы неравенств

    Решение:

    Ответ:

2. Квадратные неравенства

Пример 4. Решить неравенство х² > 4.
    Решение:
        х² > 4   (х – 2)∙(х + 2) > 0.
        Решаем методом интервалов.

Ответ:

3. Неравенства высших степеней

Пример 5. Решить неравенство (х + 3)∙(х² – 2х + 1) > 0.
    Решение:

    Ответ: .

Пример 6. Найти середину отрезка, который является решением неравенства 4х² – 24х + 24 < 4у², где .
 Решение:
 Область определения неравенства: .
 С учётом области определения 4х² – 24х + 24 < 4у² будет равносильно неравенству

Решаем методом интервалов.

        Решение неравенства: .
        Середина отрезка: .
    Ответ: .

4. Рациональные неравенства

Пример 7. Найти все целые решения, удовлетворяющие неравенству .
    Решение:

Методом интервалов:

        Решение неравенства: .
        Целые числа, принадлежащие полученным полуинтервалам: – 6; – 5; – 4; 1.
    Ответ: – 6; – 5; – 4; 1.

5. Иррациональные неравенства

Помните! Начинать решение иррациональных неравенств нужно с нахождения области определения.

Пример 8. Решить неравенство .
    Решение:
        Область определения: .
        Так как арифметический корень не может быть отрицательным числом, то .
    Ответ: .

Пример 9. Найти все целые решения неравенства .

Решение:

Область определения .

– быть отрицательным не может, следовательно, чтобы произведение было неотрицательным достаточно потребовать выполнения неравенства , при этом учитывая область определения. Т.е. исходное неравенство равносильно системе .

Целыми числами из этого отрезка будут 2; 3; 4.

Ответ: 2; 3; 4.

Пример 10. Решить неравенство .

Решение:

Область определения:

Преобразуем неравенство: . С учётом области определения видим, что обе части неравенства — положительные числа. Возведём обе части в квадрат и получим неравенство, равносильное исходному.

т.е. , и этот числовой отрезок включён в область определения.

Ответ: .

Пример 11. Решить неравенство .

Решение:

Раскрываем знак модуля.

Объединим решения систем 1) и 2): .

Ответ: .

6. Показательные, логарифмические неравенства и системы неравенств

Пример 12. Решите неравенство .

Решение:

Ответ: .

Пример 13. Решите неравенство .

Решение:

Ответ: .

Пример 14. Решите неравенство .

Решение:

Ответ: .

Пример 15. Решите неравенство .

Решение:

Ответ: .

Задания для самостоятельного решения

Базовый уровень

Целые неравенства и системы неравенств

1) Решите неравенство 2х – 5 ≤ 3 + х.

2) Решите неравенство – 5х > 0,25.

3) Решите неравенство .

4) Решите неравенство 2 – 5х ≥ – 3х.

5) Решите неравенство х + 2 < 5x – 2(x – 3).

6) Решите неравенство
.

7) Решите неравенство (х – 3) (х + 2) > 0.

Решить систему неравенств

9) Найдите целочисленные решения системы неравенств .

10) Решить систему неравенств .

11) Решить систему неравенств

12) Найти наименьшее целое решение неравенства

13) Решите неравенство .

14) Решите неравенство .

15) Решите неравенство .

16) Решите неравенство .

17) Найдите решение неравенства , принадлежащие промежутку .

18) Решить систему неравенств

19) Найти все целые решения системы

Рациональные неравенства и системы неравенств

20) Решите неравенство .

21) Решите неравенство .

22) Определите число целых решений неравенства .

23) Определите число целых решений неравенства .

24) Решите неравенство .

25) Решите неравенство 2^x<16 .

26) Решите неравенство .

27) Решите неравенство .

28) Решите неравенство .

29) Найдите сумму целых решений неравенства на отрезке [– 7, 7].

30) Решите неравенство .

31) Решите неравенство .

Иррациональные неравенства

32) Решите неравенство .

33) Решите неравенство

34) Решите неравенство .

Показательные, логарифмические неравенства и системы неравенств

35) Решите неравенство .

36) Решите неравенство .

37) Решите неравенство .

38) Решите неравенство .

39) Решите неравенство .

40) Решите неравенство 49∙7^х < 7^{3х + 3}.

41) Найдите все целые решения неравенства .

42) Решите неравенство .

43) Решите неравенство .

44) Решите неравенство 7^x+1-7^x<42 .

45) Решите неравенство log₃(2x²+x-1)>log₃2 .

46) Решите неравенство log_0,5(2x+3)>0 .

47) Решите неравенство .

48) Решите неравенство .

49) Решите неравенство .

50) Решите неравенство log_x+112>log_x+12 .

51) Решите неравенство log_x9<2.

52) Решите неравенство .

Повышенный уровень

53) Решите неравенство |x-3|>2x.

54) Решите неравенство 2│х + 1| > х + 4.

55) Найдите наибольшее целое решение неравенства .

56) Решить систему неравенств

57) Решить систему неравенств .

58) Решите неравенство .

59) Решите неравенство 25•2^x-10^x+5^x>25 .

60) Решите неравенство .

Ответы

1) х ≤ 8; 2) х < – 0,05; 3) х ≥ 5; 4) х ≤ 1; 5) х > –2; 6) х < 11; 7) ; (-2;0]; 9) – 1; 10) х ≥ 7,5; 11); 12) 1; 13); 14) х ≤ – 0,9; 15) х < – 1; 16) х < 24; 17); 18) ; 19) 3, 4, 5;

20) (0; 2); 21) (0; 1,5); 22) 3; 23) 6; 24) (–1; 1,5); 25) х < 4; 26); 27) (– 3; 17); 28)

; 29) – 10; 30) (0; + ∞); 31); 32) [1;17); 33) x > 17; 34) х ≥ 2; 35); 36) х < 2; 37) х > 0; 38) х ≤ 3; 39) х > – 3,5; 40) х > – 0,5; 41) 0, 1, 2, 3, 4, 5; 42) х < 3; 43) ; 44) х < 1; 45) ; 46) (– 1,5; – 1); 47) х < 0; 48); 49) ; 50) х > 0; 51) ; 52) ; 53) х < 1; 54); 55) – 1; 56) ; 57) [3,5; 10]; 58) (0, 1); 59) (0; 2); 60)

Источник

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Решение неравенств

Задание
1

#2500

Уровень задания: Легче ЕГЭ

Решите неравенство [x+10<3x^2]

Перенесем слагаемые в левую часть: [-3x^2+x+10<0] Разложим на множители выражение (-3x^2+x+10): [-3x^2+x+10=0 quad Rightarrow quad x_1=2quadtext{и}quad x_2=-dfrac53] Следовательно, (-3x^2+x+10=-3(x-2)left(x-frac53right)=-(x-2)(3x+5)).
Тогда неравенство примет вид [-(x-2)(3x+5)< 0quad Rightarrow
quad (x-2)(3x+5)>0] Решим его методом интервалов:

Таким образом, подходят (xin
left(-infty;-frac53right)cup(2;+infty)).

Ответ:

(left(-infty;-frac53right)cup(2;+infty))

Задание
2

#2501

Уровень задания: Легче ЕГЭ

Решите неравенство [x^2+34x+289>0]

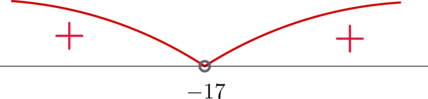
Заметим, что по формуле квадрата суммы (x^2+34x+289=(x+17)^2), следовательно, неравенство принимает вид: [(x+17)^2>0] Решим его методом интервалов:

Таким образом, нам подходят (xin(-infty;-17)cup(-17;+infty)).

Ответ:

((-infty;-17)cup(-17;+infty))

Задание
3

#2502

Уровень задания: Легче ЕГЭ

Решите неравенство [x^2-4x+4leqslant 0]

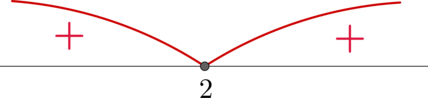
Заметим, что по формуле квадрата разности (x^2-4x+4=(x-2)^2), следовательно, неравенство принимает вид: [(x-2)^2leqslant 0] Решим его методом интервалов:

Таким образом, нам подходят (xin{2}).

Ответ:

({2})

Задание
4

#2503

Уровень задания: Легче ЕГЭ

Решите неравенство [x^2+3x+3geqslant 0]

Разложим на множители выражение (x^2+3x+3), для этого решим уравнение (x^2+3x+3=0). Оно имеет отрицательный дискриминант, следовательно, не разлагается на множители и принимает значения одного знака: либо положительно, либо отрицательно при всех (x). Проверить его знак можно, подставив вместо (x) любое число, например, (x=0): получим (3), следовательно, выражение всегда (>0).

Таким образом, нам подходят (xin mathbb{R}).

Ответ:

(mathbb{R})

Задание
5

#2412

Уровень задания: Легче ЕГЭ

Решите неравенство

[begin{aligned}
dfrac{(x — 1)(x + 2)}{(x — 3)(x + 4)}leqslant 0
end{aligned}]

ОДЗ:

[begin{aligned}
(x — 3)(x + 4)neq 0
end{aligned}]

Решим исходное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.

1) Нули числителя находятся из уравнения [(x — 1)(x + 2) = 0] Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя: [x = 1,qquadqquad x = -2]

2) Найдём нули знаменателя: [(x — 3)(x + 4) = 0qquadLeftrightarrowqquad
left[
begin{gathered}
x = 3\
x = -4
end{gathered}
right.]

По методу интервалов:

откуда [xin(-4; -2]cup[1; 3),.] В этом ответе ОДЗ уже учтено (мы учли его, когда выкололи на числовой прямой нули знаменателя).

Ответ:

((-4; -2]cup[1; 3))

Задание
6

#3762

Уровень задания: Легче ЕГЭ

Решить неравенство [dfrac 6{xsqrt3-3}+dfrac{xsqrt3-6}{xsqrt3-9}geqslant 2]

(Задача от подписчиков)

Пусть (xsqrt3-3=t). Тогда [dfrac 6t+dfrac{t-3}{t-6}geqslant 2quadLeftrightarrowquad
dfrac{t^2-15t+36}{t(t-6)}leqslant 0quadLeftrightarrowquad
dfrac{(t-3)(t-12)}{t(t-6)}leqslant 0] Решая данное неравенство методом интервалов, получим (0<tleqslant 3) или (6<tleqslant 12). Следовательно, [left[begin{gathered}begin{aligned}
&0<xsqrt3-3leqslant 3\
&6<xsqrt3-3leqslant
12end{aligned}end{gathered}right.quadLeftrightarrowquad
left[begin{gathered}begin{aligned}
&sqrt3<xleqslant 2sqrt3\
&3sqrt3<xleqslant 5sqrt3
end{aligned}end{gathered}right.]

Ответ:

((sqrt3;2sqrt3]cup(3sqrt3;5sqrt3])

Задание
7

#2413

Уровень задания: Легче ЕГЭ

Решите неравенство

[begin{aligned}
dfrac{(x + 1)(x — 2)}{(x + 3)(x^2 + 4)}leqslant 0
end{aligned}]

ОДЗ:

[begin{aligned}
(x — 3)(x^2 + 4)neq 0
end{aligned}]

Решим исходное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.

1) Нули числителя находятся из уравнения [(x + 1)(x — 2) = 0] Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя: [x = -1,qquadqquad x = 2]

2) Найдём нули знаменателя: [(x + 3)(x^2 + 4) = 0] так как (x^2geqslant 0), то (x^2 + 4geqslant 4), следовательно, нули знаменателя: [x = -3]

По методу интервалов:

откуда [xin(-infty; -3)cup[-1; 2],.] В этом ответе ОДЗ уже учтено (мы учли его, когда выкололи на числовой прямой нули знаменателя).

Ответ:

((-infty; -3)cup[-1; 2])

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

14 задача ЕГЭ – это всегда неравенство. На реальных ЕГЭ бывают 3 вида неравенств: показательные, логарифмические и смешанные.

Что нужно знать?

Метод интервалов
Как решаются дробно-рациональные неравенства
Как делается замена и обратная замена в неравенствах
Как решаются показательные неравенства
Свойства логарифмов
Как решаются логарифмические неравенства
Метод рационализации

Задачи, которые были на экзамене за последние 7 лет с решениями на полный балл

2022:

Решение

2021:

Решение

2020:

Решение

2019:

Решение

2018:

Решение

2017:

Решение

2016:

Решение

2015:

Решение

Процент выполнения

А вот данные сколько процентов пишущих экзамен решили задачу на неравенство в разные годы:

Сколько процентов из тех, кто решал экзамен в 2021 году*, набрал в задаче хотя бы 1 балл:

* так как в 2022 году ЕГЭ был сильно скорректирован, то некоторые задачи изменили свой номер, какие-то исчезли совсем, а другие добавились. В таблице приведены данные 2021 года, приведенные к формату экзамена 2022 (поэтому, например, в задачах 9 и 10 стоят прочерки – это новые задачи)

Типичные ошибки

1. Ошибки по невнимательности

Если вы будете готовиться к 14 задаче ЕГЭ, то практически наверняка одной из главных проблем станут ошибки по невнимательности. Из всех задач профильного ЕГЭ эта задача, пожалуй, самая опасная в плане мелких ошибок. Как научиться не допускать их написано в этой статье.

Примеры таких ошибок по невнимательности выделены желтым

2. Неправильно использовать метод интервалов

Метод интервалов – это база для 14 задачи ЕГЭ. Поэтому если вы хотите научиться решать неравенства на ЕГЭ – первым делом освойте метод интервалов, чтоб ошибок не было. Вот как «косячат» в нем школьники на реальном экзамене.

3. Умножить/делить на выражение с переменной

Почему в общем случае неравенство нельзя умножать или делить на выражение с переменной? Все дело в том, что если мы неравенство умножаем (делим) на положительное число, то должны оставить знак сравнения тем же, а если на отрицательное – перевернуть его.

(2x>4) (-2x>4)
(x>2) (x<-2)

Но чаще всего мы не знаем положительно или отрицательно выражение, на которое собрались умножать (делить), потому что при разных значениях переменной знак выражения может меняться. То есть, возникает неясность — переворачивать знак сравнения или оставить тем же? Поэтому в неравенствах так не делают. В уравнении можно, в неравенстве нет.

Уравнение (можно и нужно умножать на икс)	Неравенство (нужно приводить к общему знаменателю)
(frac{1}{x}=1) \|(·x)	(frac{1}{x}>1)
(1=x)	(frac{1}{x}-1>0)
(x=1)	(frac{1-x}{x}>0) (\|·(-1))
	(frac{x-1}{x}<0)
	(x∈(0;1))

Хотя бывают исключения, когда знак выражения с иксом определен. Например, на (2^x) умножить или разделить неравенство можно, потому что (2^x) положительно всегда, независимо от значения (x).

(frac{2^x-1}{2^x} ≥0) (|cdot2^x)
(2^x-1≥0)

Также бывает, что выражение положительно не всегда, но мы знаем, что в данном конкретном неравенстве это так, поскольку, например, таковы требования ОДЗ.

(log_2⁡x+log_2⁡frac{1}{x^2}≥0)
(log_2⁡x frac{1}{x^2} ≥log_2⁡1)
(frac{1}{x}≥ 1) (|cdot x)
(1≥x)
(x≤1)

Огр. (begin{cases} x>0 \ frac{1}{x^2} >0 end{cases})

Несколько примеров с ошибками:

4. Неправильно привести к общему знаменателю

Чаще всего такую ошибку допускают те ученики, которые ленятся написать лишнюю строчку, делают два, а то и три действия за один ход: сразу и домножаем, и раскрываем скобки, и тут же в уме приводим подобные слагаемые. Вот, например, в примере внизу пропущен шаг домножения дробей на недостающие множители и раскрытие скобок. Подозреваю, что из-за этого и возникла ошибка.

Сравните с этим бланком, где выпускник все сделал постепенно, по шагам и закономерно получил верный ответ.

5. Не сделать обратную замену

Это вообще классика – сделать замену и забыть вернуться к исходной переменной. Вот пример.

6. Неправильно снять квадрат

Такая ошибка редко совершается на самом ЕГЭ, потому что так обычно ошибаются те, кто только начал проходить неравенства. Но зато в начале пути ее делают практически все, поэтому я внесла её в список.

Источник

Решите неравенство

!!! Смотрите также подборку задач С3 (с ответами) для подготовки к ЕГЭ !!!

Список всех неравенств (С3), разобранных на сайте:

-11. (Реальный ЕГЭ, 2021) Решите неравенство:

$(9^x-3^{x+1})^2+8cdot 3^{x+1}<8cdot 9^x+20.$

Ответ: Решение

-10. (Реальный ЕГЭ, 2021) Решите неравенство: $16^{frac{1}{x}-1}-4^{frac{1}{x}-1}-2geq 0.$

Ответ: $(0;frac{2}{3}].$ Решение

-9. (Демо ЕГЭ, 2020) Решите неравенство

$log_{11}(8x^2+7)-log_{11}(x^2+x+1)geq log_{11}(frac{x}{x+5}+7).$

Ответ: $(-infty;-12]cup (-frac{35}{8};0].$ Видеорешение New*

-8. (Реальный ЕГЭ, 2019) Решите неравенство

$log_{frac{1}{3}}(18-9x)<log_{frac{1}{3}}(x^2-6x+5)+ log_{frac{1}{3}}(x+2).$

Ответ: Решение Видеорешение New*

-7. (Реальный ЕГЭ, 2019) Решите неравенство

Ответ: Решение

-6. (Реальный ЕГЭ, 2018) Решите неравенство

$log_7(2x^2+12)-log_7(x^2-x+12)geq log_7(2-frac{1}{x}).$

Ответ: $(frac{1}{2};frac{4}{3}]cup [3;+infty).$ Решение Видеорешение New*

-5. (Досрочный резервный ЕГЭ, 2018) Решите неравенство $frac{6^x-4cdot 3^x}{xcdot 2^x-5cdot 2^x-4x+20}leq frac{1}{x-5}.$

Ответ: Решение Видеорешение New*

-4. (Досрочный ЕГЭ, 2018) Решите неравенство $3^{x^2}cdot 5^{x-1}geq 3.$

Ответ: Решение Видеорешение New*

-3. (Резервный ЕГЭ, 2017) Решите неравенство $frac{1}{3^x-1}+frac{9^{x+frac{1}{2}}-3^{x+3}+3}{3^x-9}geq 3^{x+1}.$

Ответ: Решение

-2. (Резервный ЕГЭ, 2017) Решить неравенство $9^{4x-x^2-1}-36cdot 3^{4x-x^2-1}+243geq 0.$

Ответ: {} Решение Видеорешение New*

-1. (Реальный ЕГЭ, 2017) Решить неравенство $frac{log_2(4x^2)+35}{log_2^2x-36}geq -1.$

Ответ: $(0;frac{1}{64})cup$ { $frac{1}{2}$ } Решение

0. (Реальный ЕГЭ, 2017) Решить неравенство $frac{log_4(64x)}{log_4x-3}+frac{log_4x-3}{log_4(64x)}geq frac{log_4x^4+16}{log_4^2x-9}.$

Ответ: $(0;frac{1}{64})cup$ {} Решение

1. (Досрочн. ЕГЭ, 2017) Решите неравенство

Ответ: Решение Видеорешение New*

2. (Резервн. ЕГЭ, 2016) Решите неравенство

$frac{9^x-3^{x+1}-19}{3^x-6}+frac{9^{x+1}-3^{x+4}+2}{3^x-9}leq 10cdot 3^x+3.$

Ответ: Решение Видеорешение New*

3. (ЕГЭ, 2016) Решите неравенство

$frac{25^x-5^{x+2}+26}{5^x-1}+frac{25^x-7cdot 5^{x}+1}{5^x-7}leq 2cdot 5^x-24.$

Ответ: Решение

4. (Т/Р, 2016) Решите неравенство

$2^{frac{x}{x+1}}-2^{frac{5x+3}{x+1}}+8leq 2^{frac{2x}{x+1}}.$

Ответ: Решение

5. (Досрочн. ЕГЭ, 2016) Решите неравенство

$(5x-13)log_{2x-5}(x^2-6x+10)geq 0.$

Ответ: . Решение Видеорешение New*

6. (ЕГЭ, 2015) Решите неравенство

$frac{3}{(2^{2-x^2}-1)^2}-frac{4}{2^{2-x^2}-1}+1geq 0.$

Ответ: {} Решение

7. (Т/Р 2013) Решите систему неравенств

$begin{cases} 9^x-5cdot 3^x+4geq 0,;(1)& &log_{frac{3x^2+4x+1}{4x+1}}|frac{x}{2}|leq 0;;(2) end{cases}$

Ответ: $(-frac{1}{3};0)cup[log_53;1].$ Решение

8. (Т/Р 2013) Решите систему неравенств

$begin{cases} 1-frac{2}{|x|}leq frac{23}{x^2},;(1)& & frac{2-(x-5)^{-1}}{2(x-5)^{-1}-1}leq -0,5;;(2) end{cases}$

Ответ: Решение

9. (Т/Р 2013) Решите систему неравенств

$begin{cases} log_{6x^2-x-1}(2x^2-5x+3)geq 0,& & frac{12x^2-31x+14}{4x^2+3x-1}leq 0; end{cases}$

Ответ: $(-2;-1)cup [frac{1}{10};frac{1}{6})cup$ { $frac{3}{2}$ }. Решение

10. (ДЕМО 2014) Решите систему неравенств

$begin{cases} 4^xle9cdot 2^x+22,& & log_3(x^2-x-2)le1+log_3frac{x+1}{x-2}; end{cases}$

Ответ: Решение

11. (ЕГЭ 2013) Решите систему неравенств

$begin{cases}log_{6-x}frac{x+5}{(x-6)^{12}}ge - 12,& & x^3+7x^2+frac{30x^2+7x-42}{x-6}le 7;& end{cases}$

Ответ: {} Решение

12. (Т/Р А. Ларина) Решите неравенство

$log_4(x^2-4)^2+log_2(frac{x-1}{x^2-4})>0.$

Ответ: Решение

13. (Т/Р А. Ларина) Решите неравенство

$log_5(2+x)(x-5)>log_{25}(x-5)^2.$

Ответ: Решение

14. (Т/Р А. Ларина) Решите неравенство

$sqrt{7-log_2x^2}+log_2x^4>4.$

Ответ: Решение

15. (Т/Р А. Ларина) Решите неравенство

$frac{1}{2}log_{x-1}(x^2-8x+16)+log_{4-x}(-x^2+5x-4)>3.$

Ответ: Решение Видеорешение

16. (Т/Р А. Ларина) Решите неравенство

$log_2(5-x)log_2(x+1)leq log_2frac{(x^2-4x-5)^2}{16}.$

Ответ: Решение

17. (Т/Р А. Ларина) Решите неравенство

$frac{x^4-2x^2+1}{2x^2-x-6}geq frac{1-2x^2+x^4}{2x^2-7x+6}.$

Ответ: {} Решение

18. (Т/Р А. Ларина) Решите неравенство

$frac{(3^x-3)^3}{2cdot 3^x-4}leq frac{27^x-2cdot 3^{2x+1}+3^{x+2}}{3^x-9^x+2}.$

Ответ: $[frac{1}{2};log_32)cup$ {}. Решение

19. (Т/Р А. Ларина) Решите неравенство

Ответ: Решение

20. (Т/Р А. Ларина) Решите неравенство

$frac{4^{x^2-2x}-16cdot 2^{(x-1)^2}+35}{1-2^{(x-1)^2}}leq 4^xcdot 2^{(x-2)^2}.$

Ответ: Решение

21. (Т/Р А. Ларина) Решите неравенство

$frac{log_{x+0,5}(4^x-3cdot 2^{x+1}+8)}{log_{sqrt{x+0,5}}2}leq x.$

Ответ: Решение

22. (Т/Р А. Ларина) Решите неравенство

$sqrt{1+x^2}-xleq frac{5}{2sqrt{1+x^2}}.$

Ответ: $[-frac{3}{4};+infty).$ Решение

23. (Т/Р А. Ларина) Решите неравенство

$frac{1}{2}log_{134+tg^2(frac{x}{2})}(21x+16)<log_{134+tg^2(frac{x}{2})}(20+sqrt{x-4}).$

Ответ: Решение

24. (Т/Р А. Ларина) Решите неравенство

Ответ: Решение

25. (Т/Р А. Ларина) Решите неравенство

$frac{x^3-18x^2+89x-132}{(sqrt x-2)(5^x-25)(|x|-1)}leq 0.$

Ответ: Решение

26. (Т/Р А. Ларина) Решите неравенство

$2sqrt{x+131}-frac{5}{sqrt{x+131}-3}leq 15.$

Ответ: Решение

27. (Т/Р А. Ларина) Решите неравенство

$x^2+xsqrt{3-3x^2}geq 0,5+x.$

Ответ: $[-1;-sinfrac{5pi}{18}]cup [frac{1}{2};sinfrac{7pi}{18}].$ Решение

28. (Т/Р А. Ларина) Решите неравенство

$log_{x+1}2leq log_{3-x}2.$

Ответ: Решение

29. (Т/Р А. Ларина) Решите неравенство

$frac{2x^2}{x+3}+frac{x+3}{x^2}leq 3.$

Ответ: $(-infty;-3)cup [frac{1-sqrt{13}}{2};-1]cup [frac{3}{2};frac{1+sqrt{13}}{2}].$ Решение

30. (Т/Р А. Ларина) Решите неравенство

$log_{2x}(x+4)cdot log_x(2-x)leq 0.$

Ответ: Решение

31. (Т/Р А. Ларина) Решите неравенство

$log_{(x-2)^2}frac{5-x}{4-x}leq 1+log_{(2-x)^2}frac{1}{x^2-9x+20}.$

Ответ: Решение

33. (Т/Р А. Ларина) Решите неравенство

$frac{2sqrt{x+3}}{x+1}leq frac{3sqrt{x+3}}{x+2}$ .

Ответ: {} Решение

34. (Т/Р А. Ларина) Решите неравенство

$log_{9x}27leq frac{1}{log_3x}.$

Ответ: $(0;frac{1}{9})cup(1;3].$ Решение

35. (Т/Р А. Ларина) Решите неравенство

$frac{7-71cdot 3^{-x}}{3^x+10cdot 3^{-x}-11}leq 1$ .

Ответ: {} Решение

36. (Т/Р А. Ларина) Решите неравенство

$log_x512leq log_2frac{64}{x}.$

Ответ: {}. Решение

37. (Т/Р А. Ларина) Решите неравенство

$xsqrt x+2sqrt x+3leq frac{6}{2-sqrt x}.$

Ответ: {} Решение

38. (Т/Р А. Ларина) Решите неравенство

$log_x(11x-2x^2)+log_{11-2x}x^4leq 5.$

Ответ: {} Решение

39. (Т/Р А. Ларина) Решите неравенство

$frac{log_{(-36x)}6^{x+2}}{log_{36}6^{x+2}}leq log_{x^2}36.$

Ответ: $[-36;-2)cup (-2;-1)cup (-frac{1}{36};0).$ Решение

40. (Т/Р А. Ларина) Решите неравенство

$log^2_2frac{x-5}{x+2}-log_2(x-5)^2cdot log_{(x-5)^2}frac{x-5}{x+2}geq 0$ .

Ответ: Решение

41. (Т/Р А. Ларина) Решите неравенство

$log_x(1-2x)leq 3-log_{(frac{1}{x}-2)}x.$

Ответ: $(0;frac{1}{3})cup$ {}. Решение

42. (Т/Р А. Ларина) Решите неравенство

$log_3(x+1,5)-log_{sqrt2}(3,5-x)+log_{x+1,5}3cdot log_2^2(3,5-x)leq 0.$

Ответ: {}. Решение

43. (Т/Р А. Ларина) Решите неравенство

$frac{log_{3-x}sqrt x}{1-log_{x^2}(3-x)}leq 1.$

Ответ: $(0;1)cup (1;frac{sqrt{13}-1}{2})cup$ {} Решение

44. (Т/Р А. Ларина) Решите неравенство

Ответ: $(-1;-frac{5}{6}]cup$ {}. Решение

45. (Т/Р А. Ларина) Решите неравенство

$(x+3)(x+1)+3(x+3)sqrt{frac{x+1}{x+3}}+2leq 0.$

Ответ: Решение

46. (Т/Р А. Ларина) Решите неравенство

$log_{5-x}(5+9x-2x^2)+log_{1+2x}(x^2-10x+25)^2leq 5.$

Ответ: {} Решение

47. (Т/Р А. Ларина) Решите неравенство

$log_2(x^2-8x+6)geq 2+frac{1}{2}log_2(2x-1).$

Ответ: $(frac{1}{2};2-sqrt2]cup [6+sqrt{10};+infty).$ Решение

48. (Т/Р А. Ларина) Решите неравенство

$frac{sqrt{2x-1}+sqrt{x-3}-3x+10}{sqrt{2x^2-7x+3}}>2$ .

Ответ: Решение

49. (Т/Р А. Ларина) Решите неравенство

$frac{6-3x+sqrt{2x^2-5x+2}}{3x-sqrt{2x^2-5x+2}}geq frac{1-x}{x}.$

Ответ: $[-1;0)cup (frac{2}{7};frac{1}{2}]cup [2;+infty).$ Решение

50. (Т/Р А. Ларина) Решите неравенство

$log_{4x}2x-log_{2x^2}4x^2geq -frac{3}{2}.$

Ответ: $(0;frac{1}{4})cup [frac{1}{sqrt8};frac{1}{sqrt2})cup [1;+infty).$ Решение

51. (Т/Р А. Ларина) Решите неравенство

$frac{log_2(2cdot 4^x-11cdot 2^x+9)}{x+3}leq 1.$

Ответ: Решение

52. (Т/Р А. Ларина) Решите неравенство

Ответ: Решение

53. (Т/Р А. Ларина) Решите неравенство

$frac{sqrt{6+x-x^2}}{log_2(5-2x)}leq frac{sqrt{6+x-x^2}}{log_2(x+4)}.$

Ответ: $[-2;frac{1}{3}]cup (2;2,5).$ Решение

54. (Т/Р А. Ларина) Решите неравенство

$log_3(x^2-4x+5)leq frac{2x}{log_{x^2-4x+5}(9^x+3^x-12)}.$

Ответ: $(log_3frac{-1+sqrt{53}}{2};2)cup (2;log_312].$ Решение

55. (Т/Р А. Ларина) Решите неравенство

$log_x(frac{100}{x})leq sqrt{log_x(100x^5)}$ .

Ответ: $(0;frac{1}{sqrt[5]100}]cup [sqrt{10};+infty).$ Решение

56. (Т/Р А. Ларина) Решите неравенство

$log_{2x^2-x}(3x-1)cdot log_{2x-x^2}(3-2x)geq 0.$

Ответ: $[frac{2}{3};1)cup (1;1,5).$ Решение

57. (Т/Р А. Ларина) Решите неравенство

$log_{2x}(x-4)log_{x-1}(6-x)<0.$

Ответ: Решение

58. (Т/Р А. Ларина) Решите неравенство

$log_3(x+6)leq (1-log_{9x}(6-x))cdot log_3(9x).$

Ответ: Решение

59. (Т/Р А. Ларина) Решите неравенство

$sqrt{1-log_5(x^2-2x+2)}<frac{1}{2}log_{sqrt5}(5x^2-10x+10).$

Ответ: Решение

60. (Т/Р А. Ларина) Решите неравенство

$log_xlog_2(3-4^{x-1})leq 1.$

Ответ: Решение

61. (Т/Р А. Ларина) Решите неравенство

$frac{log_5(x^2-4x-11)^2-log_{11}(x^2-4x-11)^3}{2-5x-3x^2}geq 0.$

Ответ: Решение

62. (Т/Р А. Ларина) Решите неравенство

$frac{log_{2^{x+3}}4}{log_{2^{x+3}}(-4x)}leq frac{1}{log_2(log_{frac{1}{2}}2^x)}.$

Ответ: $[-4;-3)cup (-3;-1)cup (-frac{1}{4};0).$ Решение

63. (Т/Р А. Ларина) Решите неравенство

$log_x(1-2x)leq 3-log _{frac{1}{x}-2}x.$

Ответ: $(0;frac{1}{3})cup$ {}. Решение

64. (Т/Р А. Ларина) Решите неравенство

$log_2(5-x)cdot log_{x+1}frac{1}{8}geq -6.$

Ответ: Решение

65. (Т/Р А. Ларина) Решите неравенство

$frac{log_712}{log_7(x^2-9)}geq frac{log_5(x^2+8x+12)}{log_5(x^2-9)}.$

Ответ: Решение

66. (Т/Р А. Ларина) Решите неравенство

$4log_2x+log_2frac{x^2}{8(x-1)}leq 4-log_2(x-1)-log^2_2x.$

Ответ: (]. Решение

67. (Т/Р А. Ларина) Решите неравенство

$sqrt{1-log_5(x^2-2x+2)}<log_5(5x^2-10x+10).$

Ответ: [)(]. Решение

68. (Т/Р А. Ларина) Решите неравенство

$log_{frac{x^2-18x+91}{90}}(5x-frac{3}{10})leq0.$

Ответ: [ $frac{13}{50};9+4sqrt5$ ). Решение

69. (Т/Р А. Ларина) Решите неравенство

$log_{cosx^2}(frac{3}{x}-2x)<log_{cosx^2}(2x-1).$

Ответ: $(frac{1}{2};1).$ Решение

70. (Т/Р А. Ларина) Решите систему неравенств

$begin{cases} log_2(5-x)(2-x)>log_4(x-2)^2,& &frac{2^x-2^{2-x}-3}{2^x-2}geq 0; end{cases}$

Ответ: Решение

71. (Т/Р А. Ларина) Решите систему неравенств

$begin{cases} 4^{x+1}-33cdot 2^x+8leq 0,& & 2log_2frac{x-1}{x+1,3}+log_2(x+1,3)^2geq 2. end{cases}$

Ответ:

Показать скрытое содержание

{

}

Решение

72. (Т/Р А. Ларина) Решите систему неравенств

$begin{cases} frac{|x-5|-1}{2|x-6|-4}leq 1,& & frac{1}{4}log_2(x-2)-frac{1}{2}leq log_{frac{1}{4}}sqrt{x-5}. end{cases}$

Ответ: Решение

73. (Т/Р А. Ларина) Решите неравенство

$frac{x^2-x+1}{x-1}+frac{x^2-3x-1}{x-3}leq 2x+2.$

Ответ: {} Решение

74. (Т/Р А. Ларина) Решите неравенство

$frac{2^{cosx}-1}{3cdot 2^{cosx}-1}leq 2^{1+cosx}-2.$

Ответ: $[-frac{pi}{2}+2pi n;frac{pi}{2}+2pi n]cup$ {}, Решение

75. (Т/Р А. Ларина) Решите неравенство

$frac{5(x-6sqrt x+8)}{x-16}leq sqrt x-2.$

Ответ: Решение

76. (Т/Р А. Ларина) Решите неравенство

$frac{2^{x+1}sqrt{2^{x+1}-1}}{2^x-15}leq frac{sqrt{2^{x+1}-1}}{2^x-8}.$

Ответ: {} Решение

77. (Т/Р А. Ларина) Решите неравенство

$frac{4^{x}-3cdot 2^x+3}{2^x-2}+frac{4^{x}-5cdot 2^x+3}{2^x-4}leq 2^{x+1}.$

Ответ: {} Решение

78. (Т/Р А. Ларина) Решите неравенство

$log_{6x-x^2-8}(5-x)geq log_{6x-x^2-8}(4x^2-17x+20).$

Ответ: Решение

79. (Т/Р А. Ларина) Найдите область определения функции $y=sqrt{1-frac{2^{x+1}-14}{4^x-2^{x+2}-5}}.$

Ответ: {} Решение

80. (Т/Р А. Ларина) Решите неравенство $|3^{x+1}-9^x|+|9^x-5cdot 3^x+6|leq 6-2cdot 3^x.$

Ответ: {}. Решение

81. (Т/Р А. Ларина) Решите неравенство $frac{9}{3+log_3xcdot log_3frac{9}{x}}leq log_3^2x-log_3frac{x^2}{27}.$

Ответ: $(0;frac{1}{3})cup$ {} Решение

82. (Т/Р А. Ларина) Решите неравенство $frac{8^x-3cdot 2^{2x+1}+2^{x+3}+1}{4^x-3cdot 2^{x+1}+8}geq 2^x-1.$

Ответ: {} Решение

83. (Т/Р А. Ларина) Решите неравенство $frac{(2^x-2)^3}{2^{x+2}-12}geq frac{8^x-4^{x+1}+2^{x+2}}{9-4^x}.$

Ответ: {} Решение

84. (Т/Р А. Ларина) Решите неравенство $sqrt{4sqrt3 sinfrac{pi x}{3}-4sin^2frac{pi x}{3}-3}cdot (log_{frac{2}{3}}frac{3x+22}{14-x})leq 0.$

Ответ: {}. Решение

85. (Т/Р, 2017) Решите неравенство $3^{|x|}-8-frac{3^{|x|}+9}{9^{|x|}-4cdot 3^{|x|}+3}leq frac{5}{3^{|x|}-1}.$

Ответ: Решение

86. (Т/Р А. Ларина) Решите неравенство

$frac{sqrt{(x-1)(x-2)log_{x^2}frac{2}{x^2}}}{|x+2|}>frac{x^2-3x+1+log_{|x|}sqrt2}{x+2}.$

Ответ: Решение

87. (Т/Р А. Ларина) Решите неравенство

$3sqrt{x^2+6x+9}-(sqrt{3x+7})^2-2|x-1|leq 0.$

Ответ: $[-frac{7}{3};0]cup[2;+infty).$ Решение

88. (Т/Р А. Ларина) Решите неравенство

$2^{1+2x-x^2}-3geq frac{3}{2^{2x-x^2}-2}.$

Ответ: Решение

89. (Т/Р А. Ларина) Решите неравенство

$frac{log_2(|x|-1)log_2(frac{|x|-1}{16})+3}{sqrt{log_2(7-|x+4|)}}geq 0.$

Ответ: Решение

90. (Т/Р А. Ларина) Решите неравенство

$frac{4^{sqrt{x-1}}-5cdot 2^{sqrt{x-1}}+4}{log^2_2(7-x)}}geq 0.$

Ответ: {} Решение

91. (Т/Р А. Ларина) Решите неравенство

$frac{2^{x+1}-7}{4^x-2^{x+1}-3}leq 1.$

Ответ: {} Решение

92. (Т/Р А. Ларина) Решите неравенство

$frac{5-7log_x3}{log_3x-log_x3}geq 1.$

Ответ: $(frac{1}{3};1)cup(1;3)cup [9;27].$ Решение

93. (Т/Р А. Ларина) Решите неравенство

$frac{x+6sqrt x+28}{120}leq frac{2-sqrt x}{x-6sqrt x+8}.$

Ответ: Решение

94. (Т/Р А. Ларина) Решите неравенство

$frac{9}{log_2(4x)}leq 4-log_2x.$

Ответ: Решение

95. (Т/Р А. Ларина) Решите неравенство

$frac{1}{log_3(2x-1)cdot log_{x-1}9}< frac{log_3sqrt{2x-1}}{log_3(x-1)}.$

Ответ: Решение

96. (Т/Р А. Ларина) Решите неравенство

$log_{frac{5-x}{4}}(x-2)cdot log_{x-2}(6x-x^2)geq log_{frac{5-x}{4}}(3x^2-10x+15).$

Ответ: Решение

97. (Т/Р А. Ларина) Решите неравенство

$log_3(2^x+1)+log_{2^x+1}3geq 2,5.$

Ответ: Решение

98. (Т/Р А. Ларина) Решите неравенство

$frac{83-17cdot 2^{x+1}}{4^x-2^{x+2}+3}leq 4^x+3cdot 2^{x+1}+17.$

Ответ: Решение

99. (Т/Р А. Ларина) Решите неравенство

$xlog_2frac{x}{2}+log_x4leq 2.$

Ответ: {}. Решение

100. (Т/Р А. Ларина) Решите неравенство

$(3^x-2^x)(6^{x+1}+1)+6^xgeq 3^{2x+1}-2^{2x+1}.$

Ответ: {} Решение

101. (Т/Р А. Ларина) Решите неравенство

$2sqrt{sin^2x-sinx-1}geq cos^2x+sinx+3.$

Ответ: $-frac{pi}{2}+2pi n,nin Z.$ Решение

102. (Т/Р А. Ларина) Решите неравенство

$frac{log_8x}{log_2(1+2x)}leq frac{log_2sqrt[3]{1+2x}}{log_2x}.$

Ответ: Решение

103. (Т/Р А. Ларина) Решите неравенство

$-3log_{(x-1)}frac{1}{3}+log_{frac{1}{3}}(x-1)>2|log_{frac{1}{3}}(x-1)|.$

Ответ: Решение

104. (Т/Р 283 А. Ларина) Решите неравенство

$log_{sqrt3-1}(9^{|x|}-2cdot 3^{|x|})leq log_{sqrt3-1}(2cdot 3^{|x|-3).$

Ответ: Видеорешение

Источник