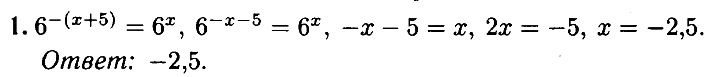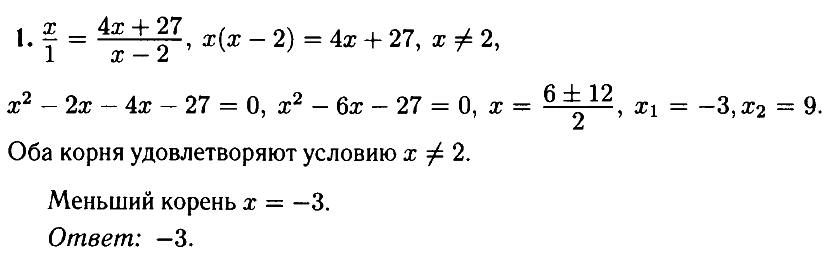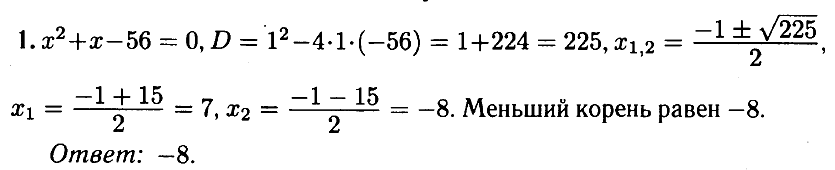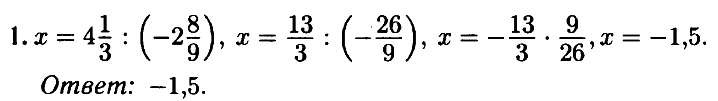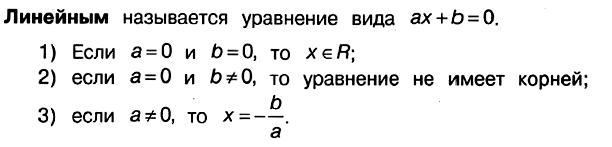Все уравнения егэ профиль математика

Каталог заданий.
Линейные, квадратные, кубические уравнения


Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

1

Тип 5 № 26662

Найдите корень уравнения: дробь: числитель: 4, знаменатель: 7 конец дроби x= целая часть: 7, дробная часть: числитель: 3, знаменатель: 7 .

Аналоги к заданию № 26662: 10149 9653 9659 9667 9669 9673 9677 9679 9691 9693 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.2 Рациональные уравнения

Решение

·

·

Курс Д. Д. Гущина

·

Сообщить об ошибке · Помощь

2

Тип 5 № 26663

Найдите корень уравнения: минус дробь: числитель: 2, знаменатель: 9 конец дроби x= целая часть: 1, дробная часть: числитель: 1, знаменатель: 9 .

Аналоги к заданию № 26663: 9655 10135 9657 9661 9663 9665 9671 9675 9681 9683 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.2 Рациональные уравнения

Решение

·

·

Курс Д. Д. Гущина

·

Сообщить об ошибке · Помощь

3

Тип 5 № 77368

Решите уравнение левая круглая скобка 2x плюс 7 правая круглая скобка в квадрате = левая круглая скобка 2x минус 1 правая круглая скобка в квадрате .

Аналоги к заданию № 77368: 100259 100757 509597 509988 510118 513336 513357 100261 100263 100265 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 1.4.2 Преобразования выражений, включающих операцию возведения в степень, 2.1.2 Рациональные уравнения

Решение

·

·

Курс Д. Д. Гущина

·

Сообщить об ошибке · Помощь

4

Тип 5 № 77369

Решите уравнение левая круглая скобка x минус 6 правая круглая скобка в квадрате = минус 24x.

Аналоги к заданию № 77369: 100759 100787 100761 100763 100765 100767 100769 100771 100773 100775 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 1.4.2 Преобразования выражений, включающих операцию возведения в степень, 2.1.2 Рациональные уравнения

Решение

·

·

Курс Д. Д. Гущина

·

2 комментария · Сообщить об ошибке · Помощь

5

Тип 5 № 77371

Найдите корень уравнения дробь: числитель: 1, знаменатель: 3 конец дроби x в квадрате = целая часть: 16, дробная часть: числитель: 1, знаменатель: 3 . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Аналоги к заданию № 77371: 100881 101379 524042 624069 624103 100883 100885 100887 100889 100891 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.1 Квадратные уравнения, 2.1.2 Рациональные уравнения

Решение

·

·

Курс Д. Д. Гущина

·

3 комментария · Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Источник

Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.

Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.

Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.

Задачи из сборников Ященко, 2021 год

Квадратные уравнения

Показательные уравнения

Логарифмические уравнения

Модуль числа

Уравнения с модулем

Тригонометрический круг

Формулы тригонометрии

Формулы приведения

Простейшие тригонометрические уравнения 1

Простейшие тригонометрические уравнения 2

Тригонометрические уравнения

Что необходимо помнить при решении уравнений?

1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть tg x — помним, что он существует, только если {cos xne 0}.

2) Стараемся записывать решение в виде цепочки равносильных переходов.

3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.

4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.

5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам -4 pi , -2 pi , 0, 2 pi , 4 pi dots Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений x=frac{pi}{3}+2pi n , где n — целое, а найти надо корни на отрезке left [frac{5 pi}{2};frac{9 pi}{2} right ]. На указанном промежутке лежит точка 4 pi. От нее и будем отсчитывать. Получим: x=4 pi +frac{pi}{3}=frac{13 pi}{3}.

6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!

Давайте потренируемся.

а) Решите уравнение 2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}

б) Найдите все корни этого уравнения, принадлежащие промежутку left[-3pi right.;left.-frac{3pi }{2}right]

2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}

Упростим левую часть по формуле приведения.

2{{cos}^2 x+sqrt{3}{cos x}=0}

Вынесем {cos x} за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

б) Отметим на тригонометрическом круге найденные серии решений и отрезок left[-3pi right.;left.-frac{3pi }{2}right].

Видим, что указанному отрезку принадлежат решения -frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.

Ответ: -frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.

Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам -4 pi , -2 pi , 0, 2 pi , 4 pi dots Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений x=frac{pi }{3}+2pi n, где n — целое, а найти надо корни на отрезке [frac{5pi }{2};frac{9pi }{2}]. На указанном промежутке лежит точка 4 pi. От нее и отсчитываем.

Получим: x=4pi +frac{pi }{3}=frac{13pi }{3}.

2. а) Решите уравнение {({27}^{{cos x}})}^{{sin x}}=3^{frac{3{cos x}}{2}}

б) Найдите все корни этого уравнения, принадлежащие отрезку left[-pi ;frac{pi }{2}right].

Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.

а) 3^{3{cos x{sin x}}}=3^{frac{3{cos x}}{2}}

Степени равны, их основания равны. Значит, равны и показатели.

3{cos x{sin x}}=frac{3{cos x}}{2}

2{cos x{sin x-{cos x=0}}}

{cos x({sin x-frac{1}{2})=0}}

Это ответ в пункте (а).

б) Отберем корни, принадлежащие отрезку left[-pi ;frac{pi }{2}right].

Отметим на тригонометрическом круге отрезок left[-pi ;frac{pi }{2}right] и найденные серии решений.

Видим, что указанному отрезку принадлежат точки x=-frac{pi }{2} и x=frac{pi }{2} из серии x=frac{pi }{2}+pi n,nin z.

Точки серии x=frac{5pi }{6}+2pi n,nin z не входят в указанный отрезок.

А из серии x=frac{pi }{6}+2pi n,nin z в указанный отрезок входит точка x=frac{pi }{6}.

Ответ в пункте (б): -frac{pi }{2},frac{pi }{6} , frac{pi }{2}.

3. а) Решите уравнение {cos 2x}+{{sin}^2 x=0,5}

б) Найдите все корни этого уравнения, принадлежащие отрезку left[-frac{7pi }{2}right.;left.-2pi right].

а)
{cos 2x}+{{sin}^2 x=0,5}

Применим формулу косинуса двойного угла: boldsymbol{cos2alpha =1-{2sin}^2alpha }

1-2{{sin}^2 x}+{{sin}^2 x}=0,5

{{-sin}^2 x=-0,5}

{{sin}^2 x=0,5}

Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.

Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.

б) Для разнообразия отберем корни на отрезке left[-frac{7pi }{2}right.;left.-2pi right] с помощью двойного неравенства.

Сначала серия x=frac{pi }{4}+pi n,nin Z.

-frac{7pi }{2}le frac{pi }{4}+pi nle -2pi

-frac{7}{2}le frac{1}{4}+nle -2

-3,75le nle -2,25

n=-3, x_1=frac{pi }{4}-3pi =-frac{11pi }{4}

Теперь серия x=-frac{pi }{4}+pi n,nin Z

-frac{7pi }{2}le -frac{pi }{4}+pi nle -2pi

-frac{7}{2}le -frac{1}{4}+nle -2

-3,25le nle -1,75

n=-3, x_2=-frac{pi }{4}-3pi =-frac{13pi }{4}

n=-2, x_3=-frac{pi }{4}-2pi =-frac{9pi }{4}

Ответ: -frac{13pi }{4};-frac{11pi }{4};-frac{9pi }{4} .

Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».

Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.

Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии x=-frac{pi }{4}+2pi n,nin Z на отрезке left[-frac{pi }{2}right.;left.20pi right]. Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.

4. а) Решите уравнение left({tg}^2x-3right)sqrt{11{cos x}}=0.

б) Найдите все корни этого уравнения, принадлежащие отрезку left[-frac{5pi }{2};-pi right].

Самое сложное здесь — область допустимых значений (ОДЗ). Условие {11cos x}ge 0 заметно сразу. А условие {cos x}ne 0 появляется, поскольку в уравнении есть {tg x=frac{{sin x}}{{cos x}}}.

ОДЗ:

Уравнение равносильно системе:

Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси Y.

Ответ в пункте а) x=pm frac{pi }{3}+2pi n, nin z

б) Отметим на тригонометрическом круге найденные серии решений и отрезок left[-frac{5pi }{2};-pi right].

Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки

x=frac{pi }{3}-2pi =-frac{5pi }{3} и x=-frac{pi }{3}-2pi =-frac{7pi }{3}.

5. а) Решите уравнение sqrt{{cos x+{sin x}}}({{cos}^2 x-frac{1}{2})=0}

б) Найдите корни, принадлежащие отрезку [-pi ;4pi ].

Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

Это значит, что уравнение равносильно системе:

Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых {cos x}=frac{sqrt{2}}{2} или {cos x}=-frac{sqrt{2}}{2}. Заметим, что среди них находятся и углы, для которых tgx=-1.

Числа серии x=-frac{3pi }{4}+2pi n не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие {cos x+{sin x}}ge 0. Остальные серии решений нас устраивают.

Тогда в ответ в пункте (а) войдут серии решений:

б) Отберем корни, принадлежащие отрезку [-pi ;4pi ] любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.

На отрезке left[-pi ;0right] нам подходит корень x =-frac{pi }{4}.

На отрезке left[0;2pi right] нам подходят корни x=frac{pi }{4};frac{3pi }{4};frac{7pi }{4}.

На отрезке left[2pi ;4pi right] — корни x= frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.

Ответ в пункте б): -frac{pi }{4};frac{3pi }{4};frac{7pi }{4};frac{pi }{4};frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание №12. Уравнения u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник
ЕГЭ по математике профиль

Прототипы задания №12 ЕГЭ по математике профильного уровня — уравнения. Практический материал для подготовки к экзамену в 11 классе.

Для успешного выполнения задания №12 необходимо уметь решать уравнения и неравенства.

Практика

Коды проверяемых элементов содержания (по кодификатору) — 2.1, 2.2

Уровень сложности задания — повышенный.

Максимальный балл за выполнение задания — 2

Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне (в мин.) — 10

Связанные страницы:

Источник
Skip to content

ЕГЭ Профиль №13. Показательные уравнения

ЕГЭ Профиль №13. Показательные уравненияadmin2018-09-29T19:55:18+03:00

Используйте LaTeX для набора формулы
Источник

ЕГЭ по математике Профиль. Задание 1: Уметь решать уравнения. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».

ЕГЭ Профиль. Задание № 1.

АЛГОРИТМ ВЫПОЛНЕНИЯ

Задание № 1 рассчитано на умение решать простейшие уравнения. Такие уравнения содержат одну переменную и не требуют значительных алгебраических преобразований. Прежде чем приступить к решению, важно определить тип уравнения — линейное, квадратное, показательное, логарифмическое и т. д. Это позволит выбрать правильный метод решения. В ответе надо записать целое или дробное число. Если в результате получилась обыкновенная дробь, её нужно перевести в десятичную.

План выполнения:

  1. Внимательно прочитайте условие задания.
  2. Решите уравнение.
  3. Проверьте, все ли корни уравнения удовлетворяют области определения.
  4. Запишите полученное число в поле ответа КИМ и бланк ответов № 1.

Пример задания № 1. Найдите корень уравнения (х – 2)2 = (3 + х)2.

Решение:
ЕГЭ по математике Профиль. Задание 1

Ответ: –0,5.

АНАЛИЗ ТИПИЧНЫХ ОШИБОК

  • При решении уравнений определенного вида следует пользоваться формулами сокращённого умножения.
  • Часто учащиеся опускают чётную степень, что приводит к неправильному решению.
  • Учащиеся иногда неправильно возводят двучлен в квадрат, забывая удвоенное произведение.
  • Кубические уравнения всегда имеют действительные корни.
  • Иногда учащиеся неправильно извлекают кубический корень из числа.

Тренировочные задания с самопроверкой

№ 1.1. Найдите корень уравнения (1/6)x+5 = 6х.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 1

№ 1.2. Найдите корень уравнения x = (4x + 27)/(x – 2). Если уравнение имеет более одного корня, в ответе запишите меньший из них.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 1

№ 1.3. Решите уравнение х2 + х – 56 = 0. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 1

№ 1.4. Найдите корень уравнения log8(5x – 7) = log8(x + 11).

Открыть ОТВЕТ

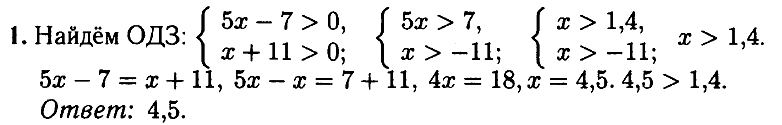
ЕГЭ по математике Профиль. Задание 1

№ 1.5. Найдите корень уравнения –2 8/9 • х = 4 1/3.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 1

СПРАВОЧНЫЙ МАТЕРИАЛ

Равенство с одной или несколькими переменными называется уравнением. Значение переменной, при котором получается верное решение, называется корнем уравнения. Решить уравнение — значит найти все его корни или доказать, что уравнение не имеет корней.

При решении задания необходимо определить тип уравнения — линейное, квадратное, показательное, логарифмическое и т. д. Это позволит выбрать правильный метод решения.

1. Линейные уравнения

ЕГЭ по математике Профиль. Задание 1

2. Квадратные уравнения

ЕГЭ по математике Профиль. Задание 1

3. Рациональные уравнения

Задачи такого типа содержат уравнения, в знаменателе которых находится выражение, содержащее переменную.ЕГЭ по математике Профиль. Задание 1

4. Иррациональные уравнения

Задачи этого задания решаются методом возведения обеих частей уравнения в степень, соответствующую степени корня.ЕГЭ по математике Профиль. Задание 1

5. Показательные уравнения

Задание состоит из простейшего показательного уравнения. Ответом к заданию является целое или дробное число.ЕГЭ по математике Профиль. Задание 1

6. Логарифмические уравнения

Уравнения этого типа решаются по определению логарифма, а также с использованием свойств логарифма. Ответом является целое или дробное число. При решении логарифмических уравнений обязательно учитывается область определения логарифма.ЕГЭ по математике Профиль. Задание 1

Методы решения логарифмических уравнений:

ЕГЭ по математике Профиль. Задание 1

Вы смотрели: ЕГЭ по математике Профиль. Задание 1: Уметь решать уравнения. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».


Просмотров:
10 786

Источник

Часть 1. УРАВНЕНИЯ

1. Целые рациональные уравнения

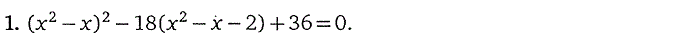
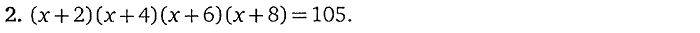
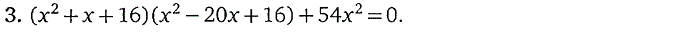
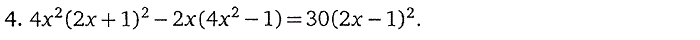
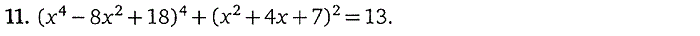
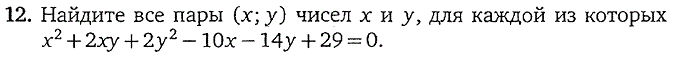
2. Уравнения, содержащие переменную
под знаком абсолютной величины (модуля)

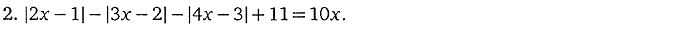
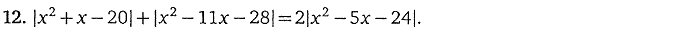
3. Дробно-рациональные уравнения

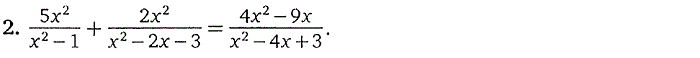
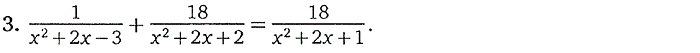
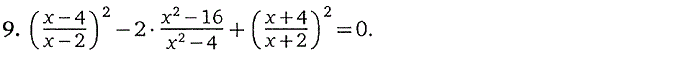
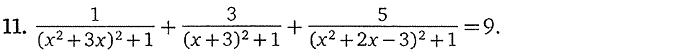
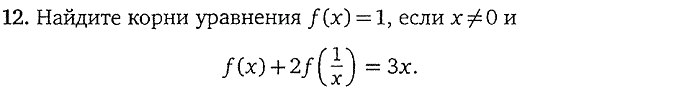
4. Иррациональные уравнения

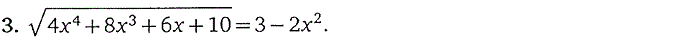
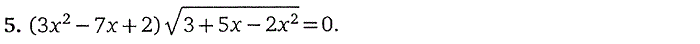
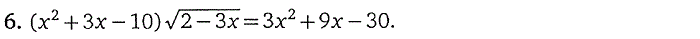
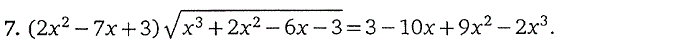
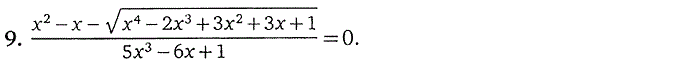
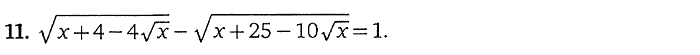
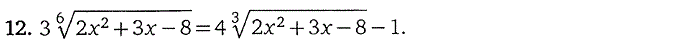
5. Тригонометрические уравнения

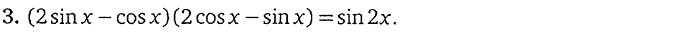
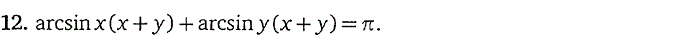
6. Показательные уравнения

7. Логарифмические уравнения

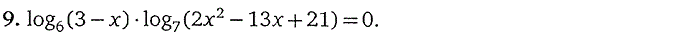
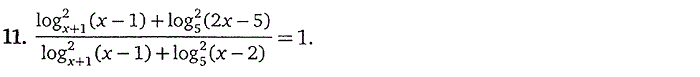
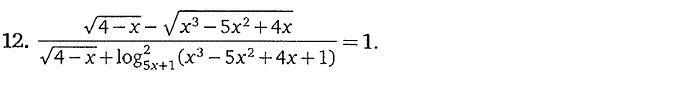
Часть 2. СИСТЕМЫ УРАВНЕНИЙ

1. Системы целых алгебраических уравнений

2. Системы, содержащие
дробно-рациональные уравнения

3. Системы, содержащие
иррациональные уравнения

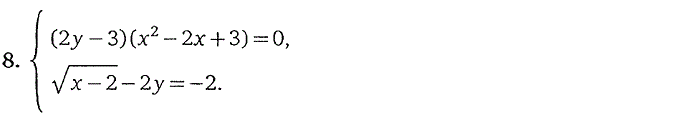
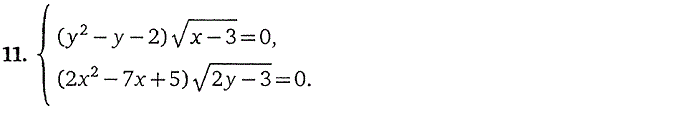
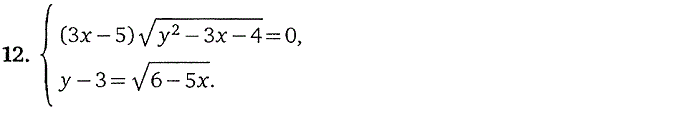
4. Системы, содержащие
тригонометрические уравнения

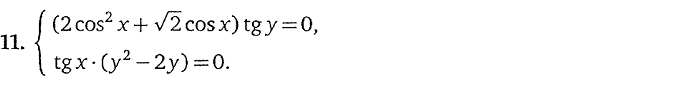
5. Системы, содержащие
показательные уравнения

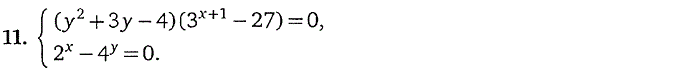
6. Системы, содержащие
логарифмические уравнения

Источник

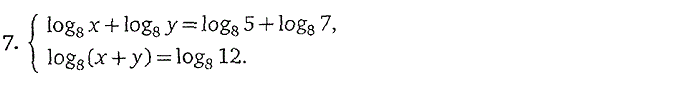
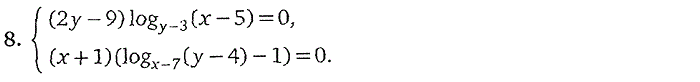
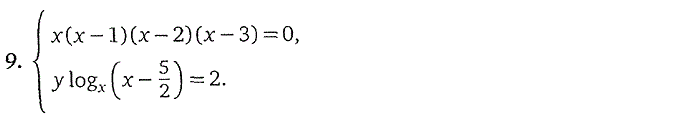
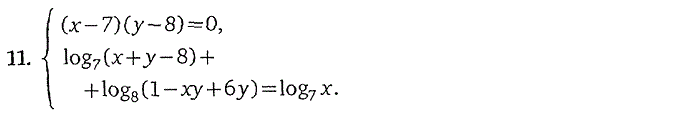
Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Простейшие уравнения»

Открытый банк заданий по теме простейшие уравнения. Задания B5 из ЕГЭ по математике (профильный уровень)

Геометрические фигуры на плоскости: вычисление величин с использованием углов

Задание №887

Условие

Найдите корень уравнения 5^{log_{25}(10x-8)}=8.

Показать решение

Решение

Найдем ОДЗ: 10x-8>0.

5^{log_{25}(10x-8)}=5^{log_58},

log_{25}(10x-8)=log_58,

log_{5^2}(10x-8)=log_58,

frac12log_5(10x-8)=log_58,

log_5(10x-8)=2log_58,

log_5(10x-8)=log_58^2,

10x-8=64, значит, условие 10x-8>0 выполняется.

10x=72,

x=7,2.

Ответ

7,2

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №886

Условие

Найдите корни уравнения cosfrac{pi(x+5)}{6}=0,5. В ответе напишите наибольший отрицательный корень.

Показать решение

Решение

frac{pi(x+5)}{6}=pmfrac{pi}{3}+2pi k, kin mathbb{Z}.

а) frac{pi(x+5)}{6}=frac{pi}{3}+2pi k, frac{x+5}{6}=frac13+2k, x+5=2+12k, x=-3+12k.

Наибольший отрицательный корень данного вида x=-3.

б) frac{pi(x+5)}{6}=-frac{pi}{3}+2pi k , frac{x+5}{6}=-frac13+2k, x+5=-2+12k, x=-7+12k.

Наибольший отрицательный корень данного вида x=-7.

Значит, наибольший отрицательный корень уравнения x=-3.

Ответ

-3

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №885

Условие

Найдите корень уравнения log_3(28+4x)=log_3(18-x).

Показать решение

Решение

28+4x=18-x,

5x=-10,

x=-2.

Сделаем проверку.

log_3(28+4cdot(-2))=log_3(18-(-2)),

log_3 20=log_3 20. Верно, значит, x=-2 — корень уравнения.

Ответ

-2

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №884

Условие

Найдите корень уравнения 4^{4-x}=0,8cdot5^{4-x}.

Показать решение

Решение

4^{4-x}=frac45cdot5^{4-x},

frac{4^{4-x}}{5^{4-x}}=frac45,

left ( frac45 right )^{4-x}=frac45,

4-x=1,

x=3.

Ответ

3

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №883

Условие

Найдите корень уравнения x=frac{3x-8}{x+9}. Если уравнение имеет более одного корня, в ответе укажите больший из них.

Показать решение

Решение

frac{x}{1}=frac{3x-8}{x+9}, при xneq-9 получим x(x+9)=3x-8,

x^2+6x+8=0,

x_{1,2}=-3pm1,

x_1=-4,;x_2=-2.

Больший из корней −2.

Ответ

-2

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №882

Условие

Найдите корень уравнения 2^{48-5x}=128.

Показать решение

Решение

2^{48-5x}=2^7,

48-5x=7,

-5x=-41,

x=8,2.

Ответ

8,2

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №881

Условие

Найдите корень уравнения sqrt{-19x+20}=x. Если уравнение имеет более одного корня, запишите меньший из корней.

Показать решение

Решение

(sqrt{-19x+20})^2=x^2,

-19x+20=x^2,

x^2+19x-20=0,

x_{1,2}=frac{-19pmsqrt{19^2-4cdot(-20)}}{2},

x_1=1,

x_2=-20.

Делаем проверку.

sqrt{-19cdot1+20}=1, это верно, значит, x=1 — корень уравнения.

sqrt{-19cdot(-20)+20}=-20, это неверно, значит, x=-20 — не является корнем уравнения.

Ответ

1

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №880

Условие

Найдите корень уравнения frac{16}{x^2-48}=1. Если уравнение имеет более одного корня, запишите меньший из корней.

Показать решение

Решение

Уравнения frac{16}{x^2-48}=1 и x^2-48=16 равносильны x^2-48neq0. Из последнего уравнения x^2=64,

x_1=-8, x_2=8. Меньший из корней равен −8.

Ответ

-8

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №879

Условие

Найдите корень уравнения x^2-19x+90=0.

Если уравнение имеет более одного корня, укажите меньший из них.

Показать решение

Решение

x_{1,2}=frac{19pmsqrt{19^2-4cdot90}}{2},

x_1=9,

x_2=10.

Меньший из корней равен 9.

Ответ

9

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №878

Условие

Найдите корень уравнения frac{5}{11}x=11frac{4}{11}.

Показать решение

Решение

frac{5}{11}x=frac{125}{11},

x=frac{125}{11}:frac{5}{11},

x=frac{125}{5},

x=25.

Ответ

25

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Источник

Понравилась статья? Поделить с друзьями:
  • Все уже узнано за две недели после возвращения в родную деревню сочинение егэ
  • Все ударения по русскому языку егэ фипи
  • Все ударения которые нужно знать на егэ по русскому
  • Все ударения егэ тест
  • Все ударения егэ 2022 список фипи