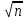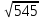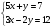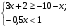Вступительный экзамен по математике в техникум

Тесты 1 вариант

1) В течении июля цены на картофель дважды увеличивались на 10 % . Цены на картофель в течении июля увеличились:

а) на 19 % в) на 21% с) на 20 д) на 25% е) на 18 %

2) В магазин привезли 14 т капусты, 30 % всей капусты продали. Сколько капусты осталось?

а) 9,8 т в) 10,2 т с) 4,2 т д) 8,3 т е) 5 т

3) Первый член геометрической прогрессии b₁ = 4, а знаменатель q =3. Найдите сумму первых пяти членов прогрессии.

а) 160 в) 484 с) 324 д) 380 е) 424

4) Разложите многочлен на множители: 15 ах + 20 ау

а) 5а (3х+4у) в) 5 (3ах+4ау) с) 5 (3х+4у) д) 5а (3х-4у) е) 5 (3ах-4ау)

5) Четырехугольник АВСD является ромбом, у которого сторона АВ равна 17 см, диагональ ВD равна 30 см. Найдите длину диагонали АС.

а) 8 см в) 16 см с) 17 см д) 14 см е) 20 см

6) Найдите tg х, если cos х= — 0,6 и х- угол третьей четверти.

а) 1/4 в) -3/4 с) -4/3 д) 4/3 е) -1

7) Найдите площадь треугольника, если ВС = 7 см, АС= 14 см. Угол С равен 30 градусов.

а) 31 см² в) 28,3 см² с) 40,1 см² д) 24,5 см² е) 12,5 см²

Средняя линия трапеции равна 7 см. Одно из её оснований больше другого на 4 см. Найдите основания трапеции.

а) 10 см и 4 см в) 8 см и 6 см с) 5 см и 9 см д) 11 см и 3 см е) 2 см и 12 см

9) Большая сторона параллелограмма равна 5 см. Найдите вторую сторону параллелограмма, если периметр равен 18 см.

а) 12 в) 4 с) 7,5 д) 3 е) 5,5

10) Решите неравенство: х² -8х +12

а) (- ∞; 2) в) (-2; 6) с) (- ∞; -2) д) (6; ∞) е) (2; 6)

11) Из 0,3 т свежих яблок получается 57 кг сушеных. Сколько сушеных яблок получится из 4,5 т свежих?

а) 855 в) 85,5 с) 8,55 д) 38 е) 3,8

12) На сколько процентов изменилась величина, если она увеличилась в 2 раза?

а) на 50 % в) на 100 % с) на 150 % д) на 200 % е) на 25 %

13) Вычислите 2,929 * 8,356 + 2,929 * 1,646.

а) 29,29 в) 2,929 с) 0,2929 д) 2929 е) 292,9

14) Решите уравнение 2,9х + 7,4 = х+ 1,7

а) -3 в) 3 с) -0,3 д) 0,3 е) -0,03

15) Автомобиль на 56,8 км пути затратил 4,26 л бензина. Сколько литров бензина потребуется ему, чтобы проехать 160 км?

а) 6 л в) 11,59 л с) 12 л д) 12,4 л е) 12,12л

16) Для 3 лошадей на 60 дней запасли 900 кг сена. Сколько сена надо запасти для 5 лошадей на 120 дней?

а) 30 000 кг в) 3 т с) 3 000 кг д) 30 т е) 0,3 т

17) В течении января цена на яблоки выросла на 30 %, а в течении февраля- на 20 %. На сколько процентов поднялась цена за 2 месяца?

а) на 56 % в) на 55 % с) на 54 % д) на 58 % е) на 60 %.

18) Найдите наименьшее целое х, удовлетворяющее неравенству -4х

а) 5 в) 4 с) 3 д) -4 е) -3

19) Решите неравенство: 30+ 5х

а) (-1; 1) в) (-1; ∞ ) с) (- ∞; -1) д) (-1; ∞) е) (-∞; -1)

20) С помощью числа π составьте выражение в радианах для дуги 30⁰ .

а) π/6 в) π/3 с) нельзя составить д) 5π/ 6 е) 2π/3

21) Угол 24⁰ выразите в радианах.

а) π/15 в) 2π/15 с) 3π/15 д) 4π/15 е) π/3

22) Найдите Х₈ , если Х_n = —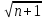

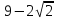
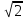
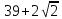
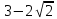
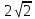
а) в) 2 -3 с) д) е) — 9.

23) Найдите 5-й член арифметической прогрессии: 19; 15; 11; …

а) -1 в) -3 с) 0 д) 1 е) 3

24) Определите радиус описанной около прямоугольного треугольника окружности, если катет равный 10 см. лежит против угла 45 градусов.

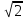
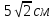
а) 20 см в) 10 см с) 10 см д) е) 5 см.

25) Определите длину вектора АВ. Если известны координаты точек А (-5; 4) и В (3; -2).

а) 2 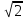в) 2 с) 10 д) е) 12

Тесты 2 вариант.

1) Найдите сумму первых двадцати членов арифметической прогрессии: 2; 5; ….

а) -590 в) 610 с) 640 д) 625 е) -610

2) В течении сентября цены на картофель дважды уменьшились на 10 %. Цены на картофель в течение сентября снизились

а) на 19 % в) на 21 % с) на 20 % д) на 15 % е) другой ответ

3) Сторона ромба равна 17 см, а одна из диагоналей 16 см. Найдите вторую диагональ.

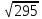
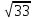
а) 15 см в) 30 см с) д) е)

4) В равнобокой трапеции большее основание равно 2,7 м, боковая сторона равна 1 м, угол между ними 60 градусов. Найдите меньшее основание.

а) 1,5 м в) 1,3 м с) 1,7 м д) 1,8 м е) 2 м.

5) Учитель проверил 18 тетрадей, что составляет 2/5 всех тетрадей. Сколько всего тетрадей?

а) 40 в) 24 с) 45 д) 38 е) 30

6) Углы, образованные стороной ромба с его диагоналями относятся как 5:4. Определить углы ромба (в градусах).

а) 70 и 110 в) 60 и 120 с) 50 и 130 д) 80 и 100 е) 40 и 140

7) Один из углов, получившихся при пересечении двух прямых, равен 110 градусов. Чему равны остальные углы (в градусах)?

а) 100 и 80 в) 110 и 70 с) 120 и 60 д) 90 и 90 е) 130 и 50

В саду 9 фруктовых деревьев, что составляет 45 % всех деревьев. Сколько всего в саду деревьев?

а) 50 в) 28 с) 46 д) 20 е) 15

9) Решите уравнение: 2х + 5 = 2 (х+1) + 11

а) 4,5 в) 4 с) -4,5 д) нет решений е) – 2.

10) MNPQ – прямоугольник, NP = 5 cм, MP = 12 см, О- точка пересечения диагоналей. Найдите периметр треугольника NОP.

а) 16 см в) 23 см с) 17 см д) 7 см е) 29 см

11) Один из корней квадратного уравнения равен 2. Найдите второй корень уравнения

х² + 17х -38 =0.

а) 19 в) -19 с) 15 д) -15 е) 16

12) Один из смежных углов в 5 раз меньше другого. Найдите разность между этими углами.

а) 120⁰ в) 110⁰ с) 100⁰ д) 90⁰ е) 80⁰

13) Сколько человек было в кино, если 1 % всех зрителей составляет 7 человек.

а) 300 в) 700 с) 400 д) 500 е) 600

14) После увеличения цены на товара на 50 %, она стала равна 12 000 тенге. Первоначальная цена товара составляла:

а) 6 000 в) 4 000 с) 8 000 д) 10 000 е) 9 000

15) Упростите выражение: С+С+2+С-19

а) С+ 21 в) С³ -17 с) С-17 д) 3С-17 е) 3С+21

16) Основания трапеции 7 см и 15 см, а высота- 8 см. Найдите площадь трапеции.

а) 176 см² в) 840 см² с) 88 см² д) 16 см² е) 60 см²

17) Упростите выражение: 14,7а (-5b)0,4.

а) 39аb в) -39аb с) -28,4аb д) -29,4аb е) 29,4аb

18) Найдите среднее арифметическое чисел: 5,9; 6,4; 5,7.

а) 6,3 в) 6 с) 6,1 д) 5,8 е) 6,2.

19) Решите неравенство: (х+5) (3-х) ˂ 0

a) (-5; 3) в) (- ∞; -3) U(5; +∞) с) (-3; 5) д) (- ∞; -5) U(3; +∞) е) (-3; 5]

20) Выполните действия: 728:1 +1(272- 0:272).

а) 728 в) 729 с) 990 д) 900 е) 1000

21) Упростите: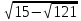

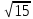
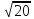
а) 2 в) -11 с) -2; 2 д) е) -2

22) Решите уравнение: 3х² -5х+2 = 0

а) -1; -2/3 в) -2/3; 2/3 с) 1; -2/3 д) 2/3; 1 е) 0; -1

23) Упростите выражение: 2cos² х- 1+ sin² х.

а) cos² х в) 2(1- sin² х) с) 3 cos² х д) sin² х е) -2sin² х.

24) Решите уравнение: 23- 4(3х +8) = 1-17х

а) -0,4 в) 25 с) -2,5 д) 2 е) 0,4

25) Под дождевой трубой поставили бочку вместимостью 180 л. Вода с крыши стекает в бочку через трубу по 8 л за одну минуту. Но в то же время через щель в бочке вытекает за одну минуту 3 л воды. Через сколько минут наполнится бочка?

а) 38 мин в) 36 мин с) 32 мини д) 30 мин е) 34 мин

Код ответов:

1 вариант

1В 2А 3В 4А 5В 6Д 7Д 8С 9В 10Е 11А 12В 13А 14А 15С 16С 17А 18А 19Е 20А 21В 22Д 23Е 24Д 25С

2 вариант

1В 2А 3В 4С 5С 6Д 7В 8Д 9Д 10С 11В 12А 13В 14С 15Д 16С 17Д 18В 19Д 20Е 21А 22Д 23А 24Д 25В

Copyright testserver.pro 2013-2021

Тесты по математике.

1- вариант.

1. Решите уравнение: x²-7x+12=0

A) 1;2; B) 0;1; C) 3;4; D) 4;3; E) -4;-3;

2. Решите неравенство: x²-3x-100

A) x6; B) -2xC) xx5; D) нет решений; E) 0x

3.Решите систему уравнений :

A) (2;3); B) (2;-3); C) (1;-3); D) (0;1); E) (1;-1);

4. Упростите выражение 3х – 2х* ( х² – 2х + 1,5)

A) – 2х³ – 4х² ; B) -2х³ + 4х² ; C) х³ – х² + 6х; D) x²-6; E) 0

5. Выполните деление многочленов: (6х³+19х²+19х+6): (3х+2).

A) 2х²-5х+3; B) 2х²+5х+3; C) х²-5х+2; D) 2х²+5х-3. E) 2х²+5х-2

6. Решите уравнение: 2хּּּ (5+3х) – хּּ (6х – 2 ) = 2 х– 4

A) – 1,5 B) 1,5 C) – 0,4 D) 7 E) -8.2

7. Решением системы уравнений:

является пара чисел

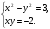
A) (1;2); B) (2;-1) C)(-1;2); D) (-1;-2) E) (-1;-3).

8. Упростите выражение: — 2(3а – 4) – 3(1+2а) + 2а

A) -10а – 11 B) 2а + 5 C) 5 – 10а D) a +8 E) -10a

9. Найдите произведение корней уравнения: х(х+2)(х-0,5)(х- 4,5)(х+5) = 0.

A) 4,5; B) 0; C) 22,5; D)-22,5. E)3

10. Выполните деление многочленов: (6х³-х²-20х+12): (2х- 3).

A) 3х²+4х — 4; B) 3х²+2х — 4; C) 3х²+х — 4; D) 3х²— 4х — 4; E) 3х²-4х -+4

11. Стороны треугольника не превосходят соот­ветственно 0,7м; 1,2м; 1,8м. Оцените периметр Р (м) данного треугольника.

A) РР 3,7 C) Р =3,7 D)Р 3,7 E) P -3,7

12. Какие из чисел -2,5, 1,4, 1 и 2,5 являются решением неравенства: -2х + 3

A) -1; 1 B) 1; 2,5 C) 2,5 D) -2,5. E) 1,4

13. Округлите до сотых: 0,53748.

A) 0,5; B) 0,54; C) 0,53; D) 0,537; E)0,2

14. Решите систему неравенств:

A) x-2; B) -2x3; C) x≥ -3; D) x≥ 3 E) не имеет решения.

15. Вычислите: .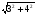

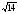
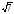
A) 7; B) ; C) 5; D) . E)3;

16. Найдите значение выражения — 4х² – 2х + 5 при х = — 1,5

A) 1 B) – 1 C) 17 D) 2 E) 3.5

17. Представьте 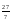в виде смешанного числа:

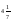
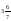
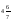
A) ; B); C) ; D) свой ответ. E)3

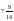
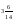
18. Значение выражения — равно:

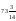
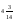
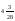
A) ; B); C); D) свой ответ. E)4

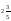
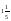
19. Турист проехал на автобусе часа, потом на попутной машине часа. Сколько часов турист был в пути?

A) 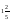; B); C); D) свой ответ. E)4

20.Из точек А(0,4) и В(0,6) лежит левее на координатном (числовом) луче:

A) А; B) В; C) нет ответа; D) свой ответ. E) AB

21.Между числами 2,3 и 3,1 заключено натуральное число:

A) 2,4; C) 2;

B) 3; D) свой ответ. E)4

22. При увеличении числа 2495,189 на 56,82 получим:

A) 8177,189; C) 2551,271;

B) 2552,009; D) свой ответ.

23. Вычислите .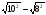

A) 2; B)6; C) 4; D). E)-4

24. Внесите множитель под знак корня .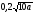

A) ; B); C); D). E)

25.Вынесите множитель из-под знака корня .

A) 3; B) 9; C) 3; D). E) 2

2- вариант.

1. Вычислите: .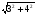

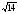
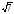
A) 7; B) ; C) 5; D) . E)3;

2. Найдите значение выражения — 4х² – 2х + 5 при х = — 1,5

A) 1 B) – 1 C) 17 D) 2 E) 3.5

3. Представьте 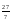в виде смешанного числа:

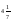
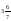
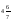
A) ; B); C) ; D) свой ответ. E)3

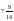
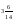
4. Значение выражения — равно:

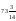
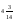
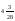
A) ; B); C); D) свой ответ. E)4

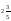
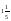
5. Турист проехал на автобусе часа, потом на попутной машине часа. Сколько часов турист был в пути?

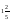
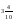
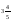
A) ; B); C); D) свой ответ. E)4

6.Из точек А(0,4) и В(0,6) лежит левее на координатном (числовом) луче:

A) А; B) В; C) не знаю; D) свой ответ. E) AB

7.Между числами 2,3 и 3,1 заключено натуральное число:

A) 2,4; C) 2;

B) 3; D) свой ответ. E)4

8. При увеличении числа 2495,189 на 56,82 получим:

A) 8177,189; C) 2551,271;

B) 2552,009; D) свой ответ. E) нет ответа

9. Вычислите .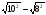

A) 2; B)6; C) 4; D). E)-4

10. Внесите множитель под знак корня .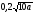

A) ; B); C); D). E)

11.Вынесите множитель из-под знака корня .

A) 3; B) 9; C) 3; D). E) 2

12. Решите уравнение: x²-7x+12=0

A) 1;2; B) 0;1; C) 3;4; D) 4;3; E) -4;-3;

13. Решите неравенство: x²-3x-100

A) x6; B) -2xC) xx5; D) нет решений; E) 0x

14.Решите систему уравнений :

A) (2;3); B) (2;-3); C) (1;-3); D) (0;1); E) (1;-1);

15. Упростите выражение 3х – 2х* ( х² – 2х + 1,5)

A) – 2х³ – 4х² ; B) -2х³ + 4х² ; C) х³ – х² + 6х; D) x²-6; E) 0

16. Выполните деление многочленов: (6х³+19х²+19х+6): (3х+2).

A) 2х²-5х+3; B) 2х²+5х+3; C) х²-5х+3+2; D) 2х²+5х-3. E) 2х²+5х-2

17. Решите уравнение: 2х (5+3х) – х (6х – 2 ) = 2х– 4

A) – 1,5 B) 1,5 C) – 0,4 D) 7 E) -8.2

18. Решением системы уравнений:

является пара чисел

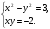
A) (1;2); B) (2;-1) C)(-1;2); D) (-1;-2). E) (-1;-3).

19. Упростите выражение: — 2(3а – 4) – 3(1+2а) + 2а

A) -10а – 11 B) 2а + 5 C) 5 – 10а D) a +8 E) -10a

20. Найдите произведение корней уравнения: х(х+2)(х-0,5)(х- 4,5)(х+5) = 0.

A) 4,5; B) 0; C) 22,5; D)-22,5. E)3

21. Выполните деление многочленов: (6х³-х²-20х+12): (2х- 3).

A) 3х²+4х — 4; B) 3х²+2х — 4; C) 3х²+х — 4; D) 3х²— 4х — 4; E) 3х²-4х -+4

22. Стороны треугольника не превосходят соот­ветственно 0,7м; 1,2м; 1,8м. Оцените периметр Р (м) данного треугольника.

A) РР 3,7 C) Р =3,7 D)Р 3,7 E) P -3,7

23. Какие из чисел -2,5, 1,4, 1 и 2,5 являются решением неравенства: -2х + 3

A) -1; 1 B) 1; 2,5 C) 2,5 D) -2,5. E) 1,4

24. Округлите до сотых: 0,53748.

A) 0,5; B) 0,54; C) 0,53; D) 0,537; E)0,2

25. Решите систему неравенств:

A) x-2; B) -2x3; C) x≥ -3; D) x≥ 3 E) не имеет решения.

3- вариант.

1. Выполните деление многочленов: (6х³-х²-20х+12): (2х- 3).

A) 3х²+4х — 4; B) 3х²+2х — 4; C) 3х²+х — 4; D) 3х²— 4х — 4; E) 3х²-4х -+4

2. Стороны треугольника не превосходят соот­ветственно 0,7м; 1,2м; 1,8м. Оцените периметр Р (м) данного треугольника.

A) РР 3,7 C) Р =3,7 D)Р 3,7 E) P -3,7

3. Какие из чисел -2,5, 1, 4, 1 и 2,5 являются решением неравенства: -2х + 3

A) -1; 1 B) 1; 2,5 C) 2,5 D) -2,5. E) 1,4

4. Округлите до сотых: 0,53748.

A) 0,5; B) 0,54; C) 0,53; D) 0,537; E)0,2

5. Решите систему неравенств:

A) x-2; B) -2x3; C) x≥ -3; D) x≥ 3 E) не имеет решения.

6. Вычислите: .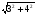

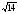
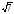
A) 7; B) ; C) 5; D) . E)3;

7. Найдите значение выражения — 4х² – 2х + 5 при х = — 1,5

A) 1 B) – 1 C) 17 D) 2 E) 3.5

8. Представьте 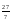в виде смешанного числа:

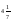
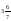
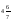
A) ; B); C) ; D) свой ответ. E)3

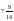
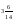
9. Значение выражения — равно:

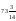
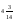
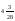
A) ; B); C); D) свой ответ. E)4

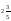
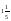
10. Турист проехал на автобусе часа, потом на попутной машине часа. Сколько часов турист был в пути?

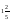
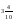
A) ; B); C); D) свой ответ. E)4

11.Из точек А(0,4) и В(0,6) лежит левее на координатном (числовом) луче:

A) А; B) В; C) не знаю; D) свой ответ. E) AB

12. Решите уравнение: x²-7x+12=0

A) 1;2; B) 0;1; C) 3;4; D) 4;3; E) -4;-3;

13. Решите неравенство: x²-3x-100

A) x6; B) -2xC) xx5; D) нет решений; E) 0x

14.Решите систему уравнений :

A) (2;3); B) (2;-3); C) (1;-3); D) (0;1); E) (1;-1);

15. Упростите выражение 3х – 2х* ( х² – 2х + 1,5)

A) – 2х³ – 4х² ; B) -2х³ + 4х² ; C) х³ – х² + 6х; D) x²-6; E) 0

16. Выполните деление многочленов: (6х³+19х²+19х+6): (3х+2).

A) 2х²-5х+3; B) 2х²+5х+3; C) х²-5х+3+2; D) 2х²+5х-3. E) 2х²+5х-2

17. Решите уравнение: 2х (5+3х) – х (6х – 2 ) = 2х– 4

A) – 1,5 B) 1,5 C) – 0,4 D) 7 E) -8.2

18. Решением системы уравнений:

является пара чисел

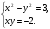
A) (1;2); B) (2;-1) C)(-1;2); D) (-1;-2). E) (-1;-3).

19. Упростите выражение: — 2(3а – 4) – 3(1+2а) + 2а

A) -10а – 11 B) 2а + 5 C) 5 – 10а D) a +8 E) -10a

20. Найдите произведение корней уравнения: х(х+2)(х-0,5)(х- 4,5)(х+5) = 0.

A) 4,5; B) 0; C) 22,5; D)-22,5. E)3

21.Между числами 2,3 и 3,1 заключено натуральное число:

A) 2,4; C) 2;

B) 3; D) свой ответ. E)4

22. При увеличении числа 2495,189 на 56,82 получим:

A) 8177,189; C) 2551,271;

B) 2552,009; D) свой ответ. E) нет ответа

23. Вычислите .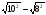

A) 2; B)6; C) 4; D). E)-4

24. Внесите множитель под знак корня .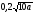

A) ; B); C); D). E)

25.Вынесите множитель из-под знака корня .

A) 3; B) 9; C) 3; D). E) 2

1- нұсқа.

1. Теңдеуді шеш: x²-7x+12=0

A) 1;2; B) 0;1; C) 3;4; D) 4;3; E) -4;-3;

2. Теңсіздікті шеш: x²-3x-100

A) x6; B) -2xC) xx5; D) жауабы жоқ; E) 0x

3.Теңдеулер жүйесін шеш :

A) (2;3); B) (2;-3); C) (1;-3); D) (0;1); E) (1;-1);

4. Ықшамда: 3х – 2х* ( х² – 2х + 1,5)

A) – 2х³ – 4х² ; B) -2х³ + 4х² ; C) х³ – х² + 6х; D) x²-6; E) 0

5. Көпмүшенің бөлінуі: (6х³+19х²+19х+6) : (3х+2).

A) 2х²-5х+3; B) 2х²+5х+3; C) х²-5х+3+2; D) 2х²+5х-3. E) 2х²+5х-2

6. Теңдеуді шеш: 2х (5+3х) – х (6х – 2 ) = 2х– 4

A) – 1,5 B) 1,5 C) – 0,4 D) 7 E) -8.2

7. Теңдеулер жүйесін шеш:

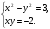
A) (1;2); B) (2;-1) C)(-1;2); D) (-1;-2). E) (-1;-3).

8. Ықшамда: — 2(3а – 4) – 3(1+2а) + 2а

A) -10а – 11 B) 2а + 5 C) 5 – 10а D) a +8 E) -10a

9.Түбірлердің көбейтіндісін тап: х(х+2)(х-0,5)(х- 4,5)(х+5) = 0.

A) 4,5; B) 0; C) 22,5; D)-22,5. E)3

10. Көпмүшенің бөлінуі: (6х³-х²-20х+12): (2х- 3).

A) 3х²+4х — 4; B) 3х²+2х — 4; C) 3х²+х — 4; D) 3х²— 4х — 4; E) 3х²-4х -+4

11. Үшбұрыштың қабырғалары: 0,7м; 1,2м; 1,8м. Периметрін тап Р (м) .

A) РР 3,7 C) Р 3,7 D)Р 3,7 E) P -3,7

12. Қай сандар -2,5, -1, 1 и 2,5 теңсіздіктің шешімі болады: -2х + 3

A) -1; 1 B) 1; 2,5 C) 2,5 D) -2,5 E) 3

13. Жүздікке дейін дөнгелет: 0,53748.

A) 0,5; B) 0,54; C) 0,53; D) 0,537; E)0,2

14. Теңдеулер жүйесін шеш:

A) x-2; B) -2x3; C) x≥ -3; D) x≥ 3 E) шешімі жоқ.

15.Есепте: .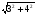

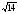
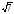
A) 7; B) ; C) 5; D) . E)3;

16. Есептін мәнін тап: — 4х² – 2х + 5 х = — 1,5

A) 1 B) – 1 C) 17 D) 2 E) 3.5

17. Аралас бөлшекке айналдыр :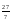

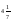
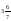
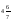
A) ; B); C) ; D) өз жауабын; E)3

18. Есепте — :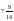

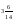
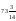
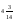
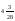
A) ; B); C); D) өз жауабы; E)4

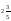
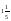
19. Жолаушы автобуспен сағат және көлікпен сағат жүрді. Барлығы қанша сағат жолда болды?

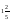
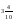
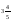
A) ; B); C); D) өз жауабы E)4

20.Қай нүкте А(0,4) және В(0,6) координатаның сол жағында орналасқан:

A) А; B) В; C) жауабы жоқ; D) өз жауабы E) AB

21.Екі санның арасында 2,3 және 3,1 қандай натурал сан орналасқан:

A) 2,4; C) 2;

B) 3; D) өз жауабы E)4

22. 2495,189 және 56,82 қосындысы неге тең :

A) 8177,189; C) 2551,271;

B) 2552,009; D) өз жауабы E) жауабы жоқ

23. Есепте:.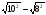

A) 2; B)6; C) 4; D). E)-4

24. Санды түбірдің ішіне еңгіз: .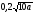

A) ; B); C); D). E)

25.Ықшамда: .

A) 3; B) 9; C) 3; D). E) 2

2- нұсқа.

1. Есепте: .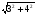

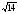
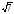
A) 7; B) ; C) 5; D) . E)3;

2. Есепте: — 4х² – 2х + 5 егер х = — 1,5

A) 1 B) – 1 C) 17 D) 2 E) 3.5

3. Аралас бөлшекке айналдыр :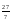

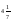
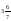
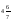
A) ; B); C) ; D) өз жауабын E)3

4. Есепте: —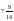

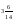
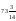
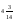
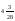
A) ; B); C); D) өз жауабын E)4

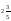
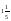
5. Жолаушы автобуспен сағат және көлікпен сағат жүрді. Барлығы қанша сағат жолда болды?

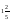
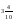
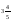
A) ; B); C); D) өз жауабын E)4

6. Қай нүкте А(0,4) және В(0,6) координатаның сол жағында орналасқан:

A) А; B) В; C)жауабы жоқ; D) өз жауабын E) AB

7. Екі санның арасында 2,3 және 3,1 қандай натурал сан орналасқан:

A) 2,4; C) 2;

B) 3; D) өз жауабын E)4

8. 2495,189 және 56,82 қосындысы неге тең:

A) 8177,189; C) 2551,271;

B) 2552,009; D) өз жауабын E) жауабы жоқ

9. Есепте:.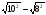

A) 2; B)6; C) 4; D). E)-4

10. Санды түбірдің ішіне еңгіз .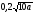

A) ; B); C); D) E)

11. Ықшамда .

A) 3; B) 9; C) 3; D) E) 2

12. Теңдеуді шеш: x²-7x+12=0

A) 1;2; B) 0;1; C) 3;4; D) 4;3; E) -4;-3;

13. Теңсіздікті шеш: x²-3x-100

A) x6; B) -2xC) xx5; D) жауабы жоқ ; E) 0x

14. Теңдеулер жүйесін шеш: :

A) (2;3); B) (2;-3); C) (1;-3); D) (0;1); E) (1;-1);

15. Ықшамда: 3х – 2х* ( х² – 2х + 1,5)

A) – 2х³ – 4х² ; B) -2х³ + 4х² ; C) х³ – х² + 6х; D) x²-6; E) 0

16. Көпмүшенің бөлінуі: (6х³+19х²+19х+6): (3х+2).

A) 2х²-5х+3; B) 2х²+5х+3; C) х²-5х+3+2; D) 2х²+5х-3. E) 2х²+5х-2

17. Теңдеуді шеш: 2х (5+3х) – х (6х – 2 ) = 2х– 4

A) – 1,5 B) 1,5 C) – 0,4 D) 7 E) -8.2

18. Теңдеулер жүйесін шеш:

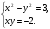
A) (1;2); B) (2;-1) C)(-1;2); D) (-1;-2). E) (-1;-3).

19. Ықшамда: — 2(3а – 4) – 3(1+2а) + 2а

A) -10а – 11 B) 2а + 5 C) 5 – 10а D) a +8 E) -10a

20. Түбірлердің көбейтіндісін тап: х(х+2)(х-0,5)(х- 4,5)(х+5) = 0.

A) 4,5; B) 0; C) 22,5; D)-22,5. E)3

21. Көпмүшенің бөлінуі: (6х³-х²-20х+12): (2х- 3).

A) 3х²+4х — 4; B) 3х²+2х — 4; C) 3х²+х — 4; D) 3х²— 4х — 4; E) 3х²-4х -+4

22. Үшбұрыштың қабырғалары: 0,7м; 1,2м; 1,8м. Периметрін тап Р (м) .

A) РB) Р 3,7 C) Р 3,7 D)Р 3,7 E) P -3,7

23. Қай сандар -2,5, -1, 1 и 2,5 теңсіздіктің шешімі болады: -2х + 3

A) -1; 1 B) 1; 2,5 C) 2,5 D) -2,5. E) 3

24. Жүздікке дейін дөнгелет 0,53748.

A) 0,5; B) 0,54; C) 0,53; D) 0,537; E)0,2

25. Теңдеулер жүйесін шеш:

A) x-2; B) -2x3; C) x≥ -3; D) x≥ 3 E) жауабы жоқ

3- нұсқа.

1. Көпмүшенің бөлінуі: (6х³-х²-20х+12): (2х- 3).

A) 3х²+4х — 4; B) 3х²+2х — 4; C) 3х²+х — 4; D) 3х²— 4х — 4; E) 3х²-4х -+4

2. Үшбұрыштың қабырғалары: 0,7м; 1,2м; 1,8м. Периметрін тап Р (м) .

A) РB) Р 3,7 C) Р 3,7 D)Р 3,7 E) P -3,7

3. Қай сандар -2,5, -1, 1 и 2,5 теңсіздіктің шешімі болады: -2х + 3

A) -1; 1 B) 1; 2,5 C) 2,5 D) -2,5. E) 3

4. Жүздікке дейін дөнгелет 0,53748.

A) 0,5; B) 0,54; C) 0,53; D) 0,537; E)0,2

5. Теңдеулер жүйесін шеш:

A) x-2; B) -2x3; C) x≥ -3; D) x≥ 3 E) жауабы жоқ.

6. Есепте: .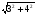

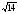
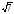
A) 7; B) ; C) 5; D) . E)3;

7. Есепте: — 4х² – 2х + 5 егер х = — 1,5

A) 1 B) – 1 C) 17 D) 2 E) 3.5

8. Аралас бөлшекке айналдыр :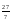

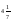
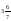
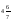
A) ; B); C) ; D) өз жауабын E)3

9. Есепте: —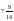

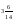
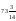
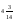
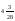
A) ; B); C); D) өз жауабын E)4

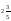
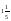
10. Жолаушы автобуспен сағат және көлікпен сағат жүрді. Барлығы қанша сағат жолда болды?

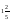
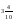
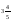
A) ; B); C); D) өз жауабын E)4

11. Қай нүкте А(0,4) және В(0,6) координатаның сол жағында орналасқан:

A) А; B) В; C) жауабы жоқ; D) өз жауабын E) AB

12. Теңдеуді шеш: x²-7x+12=0

A) 1;2; B) 0;1; C) 3;4; D) 4;3; E) -4;-3;

13.Теңсіздікті шеш: x²-3x-100

A) x6; B) -2xC) xx5; D) жауабы жоқ E) 0x

14. Теңдеулер жүйесін шеш:

A) (2;3); B) (2;-3); C) (1;-3); D) (0;1); E) (1;-1);

15. Ықшамда: 3х – 2х* ( х² – 2х + 1,5)

A) – 2х³ – 4х² ; B) -2х³ + 4х² ; C) х³ – х² + 6х; D) x²-6; E) 0

16. Көпмүшенің бөлінуі: (6х³+19х²+19х+6): (3х+2).

A) 2х²-5х+3; B) 2х²+5х+3; C) х²-5х+3+2; D) 2х²+5х-3. E) 2х²+5х-2

17. Теңдеуді шеш: 2х (5+3х) – х (6х – 2 ) = 2х– 4

A) – 1,5 B) 1,5 C) – 0,4 D) 7 E) -8.2

18. Теңдеулер жүйесін шеш:

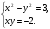
A) (1;2); B) (2;-1) C)(-1;2); D) (-1;-2). E) (-1;-3).

19. Ықшамда: — 2(3а – 4) – 3(1+2а) + 2а

A) -10а – 11 B) 2а + 5 C) 5 – 10а D) a +8 E) -10a

20. Түбірлердің көбейтіндісін тап: х(х+2)(х-0,5)(х- 4,5)(х+5) = 0.

A) 4,5; B) 0; C) 22,5; D)-22,5. E)3

21. Екі санның арасында 2,3 және 3,1 қандай натурал сан орналасқан:

A) 2,4; C) 2;

B) 3; D) өз жауабын E)4

22. 2495,189 және 56,82 қосындысы неге тең::

A) 8177,189; C) 2551,271;

B) 2552,009; D) өз жауабын

23. Есепте: .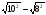

A) 2; B)6; C) 4; D). E)-4

24. Санды түбірдің ішіне еңгіз: .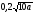

A) ; B); C); D). E)

25. Ықшамда: .

A) 3; B) 9; C) 3; D). E) 2

Ответы.

№

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

1

D

B

B

B

A

C

A

C

B

E

C

E

B

C

C

B

B

B

C

A

B

B

A

C

A

2

C

B

B

B

C

A

B

B

A

C

A

D

B

B

B

A

C

A

C

B

E

C

E

B

C

3

E

C

E

B

C

C

B

B

B

C

A

D

B

B

B

A

C

A

C

B

B

B

A

C

A

Государственное бюджетное образовательное учреждение

среднего профессионального образования

«Раменский политехнический техникум» МО

Программа

вступительного экзамена по математике

для поступающих

в ГБОУ СПО «Раменский политехнический техникум» МО

на базе основного общего образования

Раменское,

2012 г.

 Пояснительная записка

Программа вступительного  экзамена по математике предназначена для абитуриентов ГБОУ СПО «Раменский политехнический техникум» МО, поступающих на дневную форму обучения на базе основного общего образования и не имеющих результатов ГИА.

Тест является основной формой проверки знаний абитуриента за курс основной школы.

Объем теста – 15 заданий.

Продолжительность проведения экзамена – 5 часов.

 Программа вступительного экзамена по математике

    Для успешной подготовки к вступительному экзамену по математике в 2012 году поступающим в ГБОУ СПО «Раменский политехнический техникум» МО следует обратить особое внимание на повторение тем, согласно стандарта.

1. Алгебраические выражения:

Формулы сокращенного умножения. Алгебраическая дробь. Сокращение дробей. Действия с алгебраическими дробями. Степени.

1. Измерения, приближения, оценки:

Проценты. Нахождение отношения в процентах. Пропорция. Пропорциональная и обратно пропорциональная зависимость.

1. Уравнения и неравенства.

Уравнения с одной переменной. Корень уравнения. Квадратные уравнения. Решение рациональных уравнений. Система уравнений, решение систем. Неравенства с одной переменной.

1. Планиметрия:

Длина отрезка. Периметр фигуры. Равнобедренный треугольник. Прямоугольный треугольник. Теорема Пифагора.

5. Тригонометрия:

Основные тригонометрические формулы. Знаки тригонометрических функций в разных координатных четвертях.

 Критерии оценки контрольной работы

1 задание:

Вычисление длины отрезка – 3 балла

2 задание:

Сумма углов треугольника. Пропорция – 9 баллов

3 задание:

Свойство сторон равнобедренного треугольника, его периметр – 6 баллов

4 задание:

Свойство углов равнобедренного треугольника – 6 баллов

5 задание:

Теорема Пифагора – 5 баллов

6 задание:

Периметр прямоугольника – 3 балла

7 задание:

Формулы сокращенного умножения, сокращение дробей – 7 баллов

8 задание:

Свойства степени – 5 баллов

9 задание:

Решение линейного уравнения с одной неизвестной – 6 баллов

10 задание:

Решение неполного квадратного уравнения – 7 баллов

11 задание:

Решение полного квадратного уравнения – 7 баллов

12 задание:

Решение линейного неравенства с одной переменной – 7 баллов

13 задание:

Решение квадратного неравенства – 10 баллов

14 задание:

Формула тригонометрической единицы, знаки тригонометрических функций – 10 баллов

15 задание:

Решение системы линейных неравенств с одной переменной – 9 баллов

Рекомендации для проверки (проведения) экзаменационного теста.

Тест состоит из 15 заданий:

Задания содержат по 4 варианта ответов, причем каждый вопрос имеет только один вариант правильного ответа. Выберите нужный вариант и поставьте соответствующую цифру в таблицу ответов.

Максимальный балл за тест – 100.

Граница оценок будет зависеть от того сколько баллов наберут поступающие на вступительном экзамене.

Бланк ответов вступительного теста

по математике

Ф.И.О.___________________________________________________

___ вариант.

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

1 вариант

1. Точка С принадлежит отрезку АВ. Найдите длину отрезка АВ, если АС=10см, СВ=8см.

1. 6см     2) 18см     3) 2см     4) 10см

2) Найдите углы треугольника, если они пропорциональны числам 2; 3 и 7.

      1)300;450;1050      2)150;600;1050      3)200;300;700          4)700;700;400

3) Периметр равнобедренного треугольника 35см. Его основание больше боковой                                    стороны в 1,5 раза. Найдите длину основания треугольника.

      1) 15см     2) 3,5см    3) 10см      4) 30см

4) Найдите угол при основании равнобедренного треугольника, если угол между боковыми сторонами равен 800 .

      1) 1000         2) 800         3) 400         4) 500

5) У прямоугольного треугольника гипотенуза равна 5см, а один из катетов – 3см. Найдите длину второго катета.

      1) 16см      2) 9см      3) 4см        4) 25см

6) Стороны прямоугольника равны 7см и 3см. Найдите его периметр.

      1) 21см      2) 10см      3) 20см      4) 4см

7) Упростите выражение

      1)           2)         3)           4)

8) Представьте в виде степени выражение

      1)        2)            3)            4)

9) Решите уравнение  4х — 5,5 = 5х — 3(2х — 1,5)

      1) 3,5         2) 2               3) 0,8           4) 0,9

10) Решите уравнение  25 — 100 = 0

         1)        2) 0,5          3)         4)

11) Решите уравнение   х(х + 2) = 3

         1) -3;1      2) -1;3         3)          4) 1;3

12) Решите неравенство    3(3х – 1)  2(5х – 7)

1. )    2) (11;+  3) 4) (-11;+)

13) Решите неравенство  х2 – 2х  3

        2) (-1;3)          3);1)          4) (-

14) Найдите cos,если sin = — и 18002700

1)  2)3) —4)

15) Решите систему неравенств

2 вариант

1. Точка А принадлежит отрезку КС. Найдите длину отрезка АС, если КС=20см, КА=7см.

1)27см     2) 14см     3) 13см     4) 23см

1. Найдите углы треугольника, если они пропорциональны числам 6; 8 и 16.

      1)360;480;960      2)300;400;1100      3)300;400;800          4)600;300;900

3) Периметр равнобедренного треугольника 49 м. Его основание больше боковой                                    стороны на 1м. Найдите длину основания треугольника.

      1) 16м     2) 17м    3) 40м      4) 15м

4) Найдите угол между боковыми сторонами равнобедренного треугольника, если угол при основании равен 400 .

      1) 1000         2) 400         3) 600         4) 1400

5) У прямоугольного треугольника катеты равны 3см и 4см. Найдите длину гипотенузы этого треугольника.

      1) 5см      2) 7см      3) 25см        4) 16см

6) Стороны прямоугольника равны 6см и 8см. Найдите его периметр.

      1) 14см      2) 28см      3) 48см      4) 2см

7) Упростите выражение

1.           2)         3)          4)

 Представьте в виде степени выражение

      1)        2)            3)            4)

9) Решите уравнение  4 – 5(3х + 2,5) = 3х + 9,5

      1) 1          2) 1,5               3)            4) -1

10) Решите уравнение  4 — 36 = 0

         1)        2)           3)         4) 3

11) Решите уравнение   х(х + 3) = 4

         1) -1;4      2) -4;1         3) 1;4         4) 1

12) Решите неравенство    5(х + 4)  2(4х – 5)

     2)      3)    4) (-;

13) Решите неравенство  х2 + х  6

          1)        2)           3) (-3 ; 2)          4)

14) Найдите sin,если cos = и  27000

1)  — 2)3)  4)

15) Решите систему неравенств  

Ответы

1 вариант

№  задания	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Ответ	2	1	1	4	3	3	3	2	2	3	1	1	1	3	4

2 вариант

№ задания	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Ответ	3	1	2	1	1	2	4	2	4	1	2	2	2	1	1

9
сынып негізінде оқуға түсушілерге арналған математика пәнінен тест сұрақтары

Тесты
по математике для поступающих на базе 9 класса

1
– нұсқа/ 1 – вариант

1. Есепте: Вычислить:   54164:44

А) 0,88          
В)
50                 С)
0,61                     Д)
                Е)

2. Есептеп шығар: Вычислить:  

А) 2,5            
В)
12,9               С) -2,5                   
Д)
13,9            Е) -12,9

3. Көбейткіштерге жікте: Разложить на
простые множители: 3а+3+na+n

A) 3n (a+1)      B) (a -3)(n-1)                 C) (a
-1)(3-n)              D) (a+3) (n+1)            E) (a+1) (3+n)

4. Есептеп
шығар: Вычислить:  3 — 2

А) 19              
В)
18                    С)
9                      Д)
12                  Е)
24

5. Теңдеуді шеш: Решить уравнение: 3х²
– 27 = 0

А) 30             
В)
-3;3                  С)
3                       Д) 
24                 Е)
9; -9

6.  х² – 18х + 17 =
0 теңдеуін шешіп/решить уравнение: х₁+х₂ – х₁
· х₂ мәнін тап/найти значение.

А) -3              
В)
1                     С)
-1                       Д)
35                   Е)
-35

7. Квадрат  үшмүшені көбейткіштерге
жікте/Разложить квадратный трехчлен на множители:

— х² – 8х + 9

А) –(х-1)(х-9)         
В)
–(х+1)(х+9)             С)
–(х-1)(х+9)            Д)
–(х-2)(х-9)             Е)
(х-1)(х+9)

8. Ромбының
диагональдары 8 және 7 см. Ауданын тап/Диагонали ромба 8 и 7см. Найти площадь.

А)27                  В)26  
                       С)29  
                 D)25 
                    E)28

9.  теңсіздіктер жүйесінің
шеш / Решить систему неравенств :

А)                В)
                 С)
           Д)
                  Е)

10. Өрнектің мәнің тап/Найти значение
выражения:  + а + 5   егер / если а =
 8

А) 13                 В)
14                    С)
13                     Д)
14              Е)
13

11. Үшбұрыштың қабырғалары 12 және 9
см, арасындағы бұрыш 30⁰. Ауданын табыңыз/ Стороны треугольника 12
и 9 см, угол между ними 30⁰. Найти площадь треугольника.

А)30                    В)40  
                      С)27   
                     Д)50    
              E)51

12. 0,76 санын пайыз түрінде
көрсет/Записать в процентах десятичную дробь 0,76

А) 760%            
B)
7.6%                 C) 76%                 
Д)
0.76%                  E) 0.076%

13. Пропорцияның белгісіз мүшесін тап/
найти неизвестный член пропорции:  : 1 =
5 :
х

А) 19                  В)
11                     С)
17                      Д)
20                     Е)
18

14. Ықшамда/Упростите:

А) -2а                  
В)
                     С)
2а                         Д)
                         
Е)
а

15. 2-(х-1)(х+1) өрнегін ықшамдап, х=
-3 болғандағы мәнін есепте/ Упростить выражение и найти
его значение при  х= -3

А) -6                    
В)
6                    С)
12                          Д)
5                         Е)
-9

16. Өрнекті ықшамда/Упростить выражение:

А)                   В)
а – с                 С)
                        Д)
а + с                  Е)

17. Есепте/ Вычислить: 36^-1

А) 6                    
В)
216                 С)
36                         Д)
36^-1                       Е)
1

18. Иррационалдықтан арыл/
Избавиться от иррациональности:

А) 9-2             В)
9+2              С)
9(3+2)             
Д)
2                 Е)
9(3-2)

19. 5х -2(х+1)
= 13 теңдеудің түбірлерін тап/Найти корни уравнения:

А) 0                  
В)
5                         С)
2                         Д)
-5                  Е)
13

20.
Өрнектің 
мәнін  табыңдар/ Найти значение выражения: 

A)
2,5         B)
1,5             C)
0             D)
-1,5           E)
3

21.
(b_n)  тізбегі b_n = n² – n формуласымен
берілген b₅₀ мүшесін тап. / Последовательность  (b_n)  задана
формулой b_n = n² – n. Найти b₅₀

А)
1540           В) 2450                 С) 3210                 Д)
9040                          Е) 2540

22.
Егер a₁=-2;
d=3 болса,онда  арифметикалық прогрессиянның бесінші мүшесін табыңдар/ Если a₁=-2;
d=3 то найти пятый член последовательности.

A) -5;-3;-1;0;2     B)
-2;-5;-8;-11;-14     C) -2;1;4;7;10     D) -2;0;2;4;6        E) -2;-1;0;1;2

23.
{b_n}-
геометриялық 
прогрессия, егер  b₁=-9;
g=2
Табыңдар S₆ / В геометрической
прогрессии b₁=-9;
g=2. Найти
S₆

A)     155;          B)
311;       C) 529;          D) -567;          E) 534

24. Теңсіздікті
шеш/ Решить неравенство:  х² – 4х – 21 0

А)
           В)                 С)              Д)                    Е) 

25. Өрнекті ықшамдаңдар/
Упростить выражение:

A)            B)           C)             D)            E)

26. Қандай бірдей екі санның
қосындысы -3,6-ға тен?/Сумма каких двух чисел равна -3,6?

А) 1,8 ;
-1,8              В) -3,2; -6,8             С) -1,8; -1,8             Д)
-8,6;5                Е) 1,8;1,8

27. Теңсіздікті
интервалдар әдісімен шеш/Решить неравенство методом интервала:

(2х-6)(4+х)(1-х)0

А)              В)
         С)
          Д)
         Е)

28. Параллелограммның
қабырғалары 6 және 10 см, ал кіші қабырғасына түсірілген биіктік 8
см. Екінші биіктігін тап/Стороны параллелограмма 6 и 10см, высота проведенная
на меньшую сторону равна 8см. Найти вторую высоту.

A)4          B)5              C)4.8                D)4.7
                E)6

29. Бөлшекті
қысқарт/ Сократите дробь:

A.
            B.  
                   C.
— — 1               D.
                 E.    
3         

30. Теңдеуді шеш/ Решить
уравнение:  5х⁴ + 3х²  — 2 = 0

        A. 
x
= 5           B.   X  2                   C. 
X
= — 0,4              D. 
X
=                 E. 
             

2
– нұсқа/ 2 — вариант

1. Есепте/Вычислить:
205 * 26 + 27

A.
5357            B. 
5600                    C. 
5603              D. 
41357                E.  6337      

2. Бөлуді орында/
Выполнить деление:

               A.  
                    B. 
3                    C.  3                        D.  
4                         E.    
          3.
Ромбының диоганальдары 5 және 12 см. Ауданын табыңыз.

            А)29  В)30  С)31  D)39  E)38

  4. x_n
=  2n  + 1  формуласымен берілген тізбектің 15-ші мүшесін тап/ Найти 15-й член
последовательности заданной формулой x_n
=  2n 
+ 1:

A. 
33           B.  34                    C.  
32             D. 
31                E.   30      

5. Өрнекті
ықшамда/Упростить выражение:   

A)         B)       C)          D)            E)

6. Амалдарды орында Выполнить действия:  
— 63( 7 – 11 )

A.  
254          B.  -252                  
C.252              
D. 
-254                E.  25      

7. Квадраттың диагоналы 10
см, қабырғасын тап/ Диагональ квадрата 10см. Найти сторону:

       A)6   B)5   C)5   D)7   E)3

8. Ықшамда: ( x + 6y ) — (8x — 7)

A.
6y — 7x + 7            B.  –7x          C. 6y — 7x — 7               D.
6xy                 E.  6y + 7x     

  9. Көпмүшені көпмүшеге көбейту/Умножить
многочлен на многочлен: ( 2a — b)( 3a + 2b)

A. 6a² + ab –
2b            B. 6a² + ab – 2b²            C. 6ab –
1        D. 6a – ab² – 3        E. -6a² + ab + 2b²    

10 Көпмүшеге
түрлендір/ Запишите в виде многочлена:  ( x + 2)³

A. x³ —
6x² + 12x +8    B. x³ + 6x² + 12x
+8       C. x³ — 6x² + 12x +7    D. x³ — 6x²
+ 12x -8   

 E.  x³ + 6x² + 12x -8

11. Ортақ
көбейткішті жақшаның сыртына шығар/ Вынести общий множитель за скобки:

3a³b  —
6a³b²

A. a²b(3a-6b)            
B. 3a²b(a-2b)                     C. 3a³b(1-2b)              
D. 3a²(a²-2b²)    E. a²b(3-6b)        

 12. Теңдеуді шеш/ Решить
уравнение:   — 9 = 0

A.  
9          B. 4                      C. 
81              D.
3                 E.  -81            

13. Теңдеуді шеш/ Решить
уравнение:  x² = 6

            A.
-3            B. Түбірі
жоқ /нет корня             
C. 
–3;3              D.  —                 E. 
—;            

      14. Теңсіздікті
шеш/ решить неравенство:  x
– 6 < 8

A. (
— 14 ;  )            
B. ( — ;
-14)            C. [ — 14;   )              
D.   [ 14 ;  )              
E.  (- ;          

       15. Өрнекті
ықшамда/Упростить выражение: xxx

A.   x          B.   x^-1                 
C.   x                        D.   –
x               
E.  
1           

    16. Иррационалдықтан
құтыл/Избавиться от иррациональности: 

      A.  
3 + 2          B.
19(3 + 2 )      C. 
27 + 18      D. 
3 — 2        E. 
27 — 18             

   17. Бөлшекті
қысқарт/ Сократите дробь:

A.
            B.  
                   C.
— — 1               D.
                 E.    
3         

   18. Теңдеуді
шеш/ Решить уравнение:

A.  
10          B.   11                   C.   
12            D. 
13                E.    14          

   19. Теңдеуді
шеш/ Решить уравнение:  5х⁴ + 3х²  — 2 = 0

        A. 
x
= 5           B.   X  2                   C. 
X
= — 0,4              D. 
X
=                 E. 
             

  20. Бөлшекті
қысқарт/ Сократите дробь:

A.  
          B.   
2( m
+ 2)                  C.                D.
2( m
— 2)         E.               

   21.Өрнекті
ықшамда/Упрость выражение:     

A.   
         B.
                     C.
               D.
                  E.   
2x
+ 1

    22. Трапеция
табандарының ұзындықтарының қатынасы  2:3 болса, биіктігі 6
см, ал ауданы 60 см².-ге тең. Табандарын табыңыз/Основания трапеции
относятся как 2:3. Высота 6см а площадь 60 см². Найти основания
трапеции.

A)8;12   B)9;10   C)4;6   D)9;11  E)6;9

23. Функцияның
анықталу облысын тап/ Найти область определения функции: y =

      A.
( —  ; — 3)             B.
басқа
жауап/другой ответ       C.  
( — 3 ; 0)  (0 ; 3)       D.
( — 3 ; 3)

    E. (— ; 3 ) ( 3 ; +  )

24.
Өрнектің мәнін  табыңдар.

A)
0;                B) 2,5;         C)
3;            D) 4;       E)
-2,5

25.  2x² +5x –3 = 0 теңдеу шеш, 
x₁²  + x₂²  мәнін есептеңіз/ Решить
уравнение 2x² +5x –3 = 0

и найти x₁²  + x₂²
:

A. 
9,25           B.  9,75                    C.  16             D.  –
9,75                E.    -34          

26. Теңсіздікті
шеш/ Решить неравенство: 9x² – x + 9  3x²
+ 18x – 6

      A. [ -1 ; 0
]            B. ( — ;
 ] [ 1 ; + )      C.  
шешімі жоқ/нет решения

             D. [;1  ]     E.      ( — ; 1]        

27. Арифметикалық
прогрессияның бірінші мүшесін тап, егер/В арифметической прогрессии найти
первый член если:    a₃ = 10    a₁ + a₄ = 16

        A.  —
4          B.    2                  C.    1            D.  5                E. 
4            

28. Геометриалық
прогрессияның еселігі 2-ге тең, ал оның алғашқы жеті мүшесінің қосындысы 635-ке
тең. Осы прогрессияның алтыншы мүшесін тап/ В геометрической прогрессии
знаменатель равен 2, а сумма первых семи членов равна 635. Найти шестой член
этой последовательности:

A. 
160           B. 16                    C.  360              D.
633                 E.   1600           

29. Теңсіздікті
шеш/ Решить неравенство:  

        A. ( — ; — 1)   (- ; 2)          B. 
( -1; — )  [2;6]                 
C.  ( — ;
+ )      

D. (- ; 2)  (6 ; + )             E. 
( — ;
-1  )    (
-1; — )  ( 6; + )          

30. Теңдеулер
жүйесін шеш/ Решить систему неравенства:      x² + y² =
26

                                                       
                                           xy – 5 = 0

        A. ( -9; 0
) ;( 6; 4 ); (-5;0 ); ( 0;2 )            B. ( 5; 1) ; ( 1; 5 ) ; (-5 ;
-1 ) ; (- 1 ; -5)  

        C. ( 0; 5)
; ( 6; 8 ) ; ( 1;5 ); (-1;-5)     D. ( 2; — 1 ) ; ( 6 ; — 8 ) ; ( — 2 ; 1 ) ; (
— 6 ;       

        E.   ( — 3
; 4 ) ; ( 4 ; 5 ) ; (- 4 ; 5

11
сынып негізінде оқуға түсушілерге арналған математика пәнінен тест сұрақтары

Тесты
по математике для поступающих на базе 11 класса

1
– нұсқа/ 1 – вариант

1.
Екі санның көбейтіндісі 144 ал бір көбейткіші 8,
екінші көбейткішті тап/Если произведение двух
чисел равно 144 и один из множителей равен 8, то другой множитель равен:

      A)
136                   B)
36                          C)
72               D)
18                          E)
12

2.
Өрнекті ықшамда/Упростите
выражение: (х – у)(х + у)(х² + у²)

      A)
x⁴ – y⁴                 B) (x² – y²)²        
       C) x² – y²        D) (x²
+ y²)²                 E) x⁴ + y⁴

3.
Өрнектін мәнін тап/Найдите
числовое значение выражения 3sin

      A)
2,5                    B)
-0,5+             
  C)
6,5              D)
1                            E)
1,5

4.
Үшмұшені көбейткіштерге жікте/Разложите
на множители: 16у² – 24у + 9

      A)
(4у(у+3))²       B)
(3у – 4)²                   C)
(4у – 3)²                D)
4у – 3        E)
– (4у – 3)(4у + 3)

5.
Параллелограмнің
периметрі 36см. Бір қабырғасы 12см болса екінші қабырғасын тап/
Периметр
параллелограмма равен 36 см. Одна из его сторон равна 12
см. Найти длину соседней с ней стороны

      A)
6 см                 B)
4 см                       C)
12 см                     D)
9 см                       E)
18 см

6.
Теңдеуді шеш/Решите
уравнение:

      A)
          B)
                 C)

      D)
                    E)

7.
Теңдеулер жүйесін шеш/Решите
систему уравнений:

      A)
(-1; -3)             B)
(-7; -4)              C)
(5; -2)            D)
(11; -1)                  E)
(-13; -5)

8.
Есепте/ Вычислите:

      A)
-30^о                   B)
145^о                            C)
30^о                                D)
60^о             E)
-45^о

9.
 Функцияның туындысын тап/
Найти производную функции: f(x)
= 3

      A) 21          B)           C) 21                 D)                   E) 21

10.
у(х) = tgx функцияның
туындысын тап, егер /Найдите
значение производной функции: у(х) = tgx
при

      A)
                   B)
4                 C)
-4               D)
                E)

11.
Тікбұрышты
үшбұрыштың гипотенузасы 18см. Гипотенузаға түсірілген медиананың ұзындығын тап/Гипотенуза
прямоугольного треугольника равна 18 см. Чему равна медиана, проведенная к
гипотенузе?

      A)
8 см                 B)
11 см         C)
12 см         D)
10 см         E)
9 см

12.
Тікбұрышты
үшбұрыштың катеты 5см, гипотенуза 13см. Тікбұрышты үшбұрыштың ауданың тап/ Катет
прямоугольного треугольника равен 5 см, гипотенуза – 13
см. Найти площадь треугольника

      A)
12 см²                B)
65 см²        C)
24 см²        D)
30 см²        E)
60 см²

13.
Қабырғасы
5см болатын тең қабырғалы үшбұрыштың биіктігін тап/ Найти
высоту равностороннего треугольника со стороной 5
см

      A)
см              B)
см          C)
см          D)
см        E)
см

14.
Цилиндрдің
табан радиусы 5см, биіктігі 6см. Цилиндрдің бүйір ауданың тап/Радиус
основания цилиндра 5 см, высота 6 см. Найдите площадь боковой поверхности
цилиндра

      A)
 см²          B)
 см²   
C)
 см²                 D)
 см²    
           E)
 см²

15.
Теңдеуді
шеш/ Решите уравнение: (x
– 5)(x
+ 2)= 0

      A) x
= 3                B) x₁ = 5, x₂ = -2, x₃
= 7                    C) x = 5          D) x₁ = 7, x₂
= -2        E) x = 7

16.
Теңдеуде
шеш/Решите уравнение:

      A)
4                       B)
2                 C)
6                D)
9                 E)
1

17.
(x)
= .  Функция берілген.
мәнін тап/ Дана
функция f(x)
= . Найдите

      A)
5                       B)
-3               C)
1    
           D)
6          
      E)
0

18.
Функцияның
анықталу облысын тап/Найдите область определения функции:
у =

      A)
(-5; -2)(3; +)       B)
[-5; -2)       C)
[-5; -2)[3; )          D)
(-5; 3)            E)
(; -2)

19.
Геометриялық
прогрессияның еселегін тап/Найдите знаменатель
геометрической прогрессии, если b₃
+ b₄
= 2(b₄
+ b₅)

      A)
                     B)
-1,               C)
—, 1                   D)
-1                 E)
1

20.
Ықшамда/
Упростите:

      A)
2m² – 5n²                         B) 10mn          C)
25m²n²                      D) 5mn           E)
2m² + 5n²

21.
Теңсіздіктер
жүйесін шеш/Решите систему неравенств:

      A)
(-4; -2]             B)
(-; -2]                 C)
(-; -4)                 D)
(-4; +)                E)
(-2; 4)

22.
 Функцияның
туындысын тап/ Найдите производную функции:
f(x)
= (3 + 4x)(4x
– 3)

      A)
16x      
            B)
32x²                
            C)
8x²                   
            D)
16   
           E)
32x

23.
Есепте/
Вычислите:

      A)
         B)
               C)
4                D)
1                 E)

24.
Үшбұрышты
тік призманің қабырғалары .
Көлемін тап/ Все ребра прямой треугольной призмы равны . Найдите объем призмы

      A)
17                     B)
19               C)
20              D)
21                          E)
18

25.
 А (1;2)  В(7;10) АВ
кесіндісін 1:3 қатынасында бөлетін нүктенінің координатасын тап/Найти
координаты точки которая делит отрезок АВ в отношении 1:3.

      A)
(2;4)     
           B)
(2,5;4)       
            C)
(3;4)          
            D)
(4;4)          
           E)
(5;4)

26.
Теңдеуді
шеш/ Решите уравнение: (x²
– 6x)²
– 2(x
– 3)² = 81

      A)
11                     B)
-9; 11                     C)
3                            D)
3      
           E)
3; 3

27.
Теңсіздікті
шеш/ Решите неравенство:

      A)
           B)
             C)

      D)
           E)

28.
Теңдеулер
жүйесінің   ху мәнің тап/Дана система уравненией:  Найдите xy

      A)
                       B)
                         C)
                            D)
                           E)

29.
Решите уравнение:

      A)
8                      B)
3                             C)
6                            D)
9                            E)
5

30.
m –нің
мәнің тап/Найти значение m,
при котором точка С(0; m) равноудалена от
точек А(-3; 5) и В(6; 4)

      A)
-9

      B)
-10

      C)
10

      D)
9

      E)
8

2
– нұсқа/ 2 — вариант

1.
Өрнектін мәнін тап/Найдите
значение выражения: , егер
/если

      A)
                   B)
               C)
1               D)
                        E)

2.
12,5% от числа составляет 10. Чему равно это число

      A)
70                     B)
100             C)
80              D)
85               E)
75

3. Ықшамда/
Упрости выражение:   

 А)              В)
           С)
          Д)
          Е)

4.
 мәнін
тап/ Найдите числовое значение выражения:

      A)
1,5                    B)
4                 C)
                         D)
3                E)

5.
Параллелограммның бұрыштарын тап, егер бір бұрышы екіншісінен
50⁰ артық болса./ Найдите углы
параллелограмма, если один из них больше другого на 50^о

      A)
65^о и 115^о            B)
125^о и 55^о                  C)
75^о и 105^о                  D)
50^о и 130^о               E)
60^о и 120^о

6. Теңдеуді
шеш/ Решите уравнение:
 

А) 0,5                  В)
-4                  С) 12                Д)
2                         Е)
түбірі жоқ/нет корней

7.
Теңдеуді шеш/ Решите
уравнение:

      A)
               B)
                             C)

      D)
                  E)

8.
10х – 5у – 7 = 0 теңдеудің у
айнымалысын х арқылы өрнектеңдер/

Выразите
у через х из уравнения 10х – 5у – 7 = 0

      A)
у = 2х – 7                    B)
у = 2х + 1,4                       C)
у = 2х – 1,4                       D)
у = 2х + 7

      E)
у = –2х – 1,4

9.
Функцияның туындысын тап/Найдите
производную функции: f
(x)
=

      A)
x                       B) 3x⁴                   C)
11x⁴                D) 7x⁴                   E)
x⁴ – 7

10.
Функцияның
туындысын тап/ Найдите производную функции:
f
(х) = 8^х + е^х

      A)
8^xln e               B) 8^xln 8 + e^x              
    C) xln 8                      D) 8^xln 8                   
E) 8^xln x + e

11.
Үшбұрыштың
қабырғалары 5 см,
12 см и 13 см,  13см қарама қарсы бұрыштың градус өлшемін
тап/ Чему равен угол треугольника со сторонами 5
см, 12 см и 13 см, противолежащий стороне 13
см?

      A)
30^о                        B)
90^о                  C)
45^о                                D)
25^о                                 E)
60^о

12.
АВС үшбұрышта АВ = ВС ВС
қабырғасын АК биіктіктігі ВК = 24
см және  КС = 1 см
кесінділерге боледі. Үшбұрыштың ауданың тап/ В
треугольнике АВС АВ = ВС. Высота АК делит сторону ВС на отрезки ВК = 24
см и КС = 1 см. Найдите площадь треугольника АВС

      A)
87,5 см²              B)
25 см²           C)
875 см²                        D)
175 см²                        E)
276 см²

13.
АВС
үшбұрыш берілген. АВ = 4, =30^о, =
45^о. табу керек
АС/

 Дан
треугольник АВС. АВ = 4, =30^о, = 45^о   
Найти АС.

      A)
                  B)
           C)
                          D)
                         E)

14.
Қиық
конустың табан радиустары  10см және 4см, биіктігі 8см. Жасаушысын тап/Радиусы
оснований усеченного конуса 10 см, 4 см, высота 8см. Найдите образующую

      A)
20 см               B)
5 см           C)
100 см                   D)
10 см                     E)
6 см

15.
х² + 7х + 1 = 0 теңдеудің түбірлердің
қосындысын тап/Дано уравнение х² + 7х + 1 = 0.
Найти сумму квадратов его корней

      A)
49                     B)
65                C)
47                         D)
25                          E)
51

16. Өрнекті
ықшамда/ Упростить выражение:   

А)                В)
а-х+3                С)
х+4                      Д)
2-5х              Е) а-5

17.
Теңсіздікті
шеш/Решите неравенство:

      A)
(5; 4)                B)
(1; -5)                 C)
(6; 1)              D)
(-1; -3)                   E)
(-2; 3)

18.
Арифметикалық
прогрессияда S₄
= 42 және S₈
= 132. а₁ және
d
– ны тап/

В
арифметической прогрессии S₄
= 42 и S₈
= 132. Найдите а₁ и
d

      A)
a₁ = -6; d = 2               B) a₁ = 6; d = 3                  
    C) a₁ = 6; d = 2

      D)
a₁
= 3; d
= -6               E)
a₁
= 3; d
= 6

19.
Көбейткіштерге
жікте/Разложите на множители: 5ax²
– 10ax
– bx
+ 2b
– x
+ 2

      A)
(x – 2)(5ax – b – 1)                 B) (x – 2)(ax – 5b – 1)           C)
(x – 2)(5ax + b + 1)

      D)
(x + 2)(5ax – b – 1)                 E)
(x
+ 2)(5ax
– 1)

20.
Өрнекті
ықшамда/Упростите выражение:

      A)
          B)
1 – x²
+ x³      
         C)
x³
– 19x²            
       D)
6 – x²
– 7x   
         E)
5x²
– x³

21.
Теңдеулер
жүйесін шеш/Решить систему уравнений:

      A)
(4; 0)       
        B)
(0;               
       C)
(0; -4)           
        D)
(-4; 2)            
       E)
(8; -2)

22.
Теңсіздіктер
жүйесін шеш/Решите систему неравенств:

      A)
(-1; -1)             B)
(5; -2)                    C)
(-1; 2)                   D)
(-3; -1)                   E)
(1; -3)

23. Есепте/
Вычислить:   

А) 840                       В)
8400                        С)
84                           Д)
8,4                       Е)
0,84

24.
Функцияның
алғашқы функциясын тап/Найдите первообразную функции f(x)
= 2(2x
+ 5)⁴

      A)
4(2x
+ 5)³ + C                         B)
8(2x
+ 5)³ + C                        C)
 

D)
                               E)

25.
Теңсіздіктің
бүтін шешімін тап/Найти наибольшее целое решение
неравенства:

(x²
– x
– 6)

      A)
0          
            B)
-1               
           C)
2                
           D)
5                       
    E)
3

26.
Теңдеулер
жүйесін шеш/Решить систему уравнений

      A)
(0; 0), (;
)                    B)
(0; -1), (;
0)                 C)
(1; 1), (0; )

      D)
(2; 2), (;
)                     E)
(1; 1), (-;
—)

27. Сөйлемді
аяқтаңыз: «синус пен косинус функцияларының мәндерінің облысы…»/Закончи
предложение «Область значения синуса и косинуча является промежуток…»

А)               В)                   С)
                 Д)
                    Е)

28.
Есепте/Вычислите:

      A)
1          
            B)
0,97            
          C)
0,99            
          D)
0,96               
       E)
0,98

29.
Табу
керек/Найти , егер/если
 = 11,  = 23,
и  = 30

      A)
20                     B)
19                          C)
22                          D)
18                          E)
21

30. Егер
дұрыс үшбұрышқа іштей сызылған шеңбер радиусы 5см-ге тең болса, онда үшбұрыш
ауданын табыңыз/Около равностороннего треугольника описана окружность радиусом
5см. Найти площадь треугольника. 

А)   

В)  

 С)  

 Д)    

Е)

Предисловие

По сравнению с 2018 годом выбор вопросов с заполнением пропусков добавляет 1 математическую культуру и 1 вероятность; сокращает количество модулей с тремя представлениями, линейным программированием, блок-схемой, перестановками и комбинациями и модулями биномиальных теорем;

1. Вопросы с несколькими вариантами ответов

Пример 1 【Документ для вступительных экзаменов в колледж 2019 г. Вопрос 1】

анализ:

Анализ:

Отражение после решения:

Ссылки по теме:

Пример 2 [Новый стандарт естественной учебной программы для вступительных экзаменов в колледж 2019 Ⅱ Вопрос 2]

анализ:

Анализ:

Отражение после решения:

Ссылки по теме:

Пример 3 【Контрольная работа для вступительных экзаменов в колледж 2019 г. New Вопрос 3】

анализ:

Анализ:

Отражение после решения:

Ссылки по теме:

Пример 4 [Вопрос 4 нового стандарта естественной учебной программы Ⅱ контрольной работы по математике для вступительных экзаменов в колледж в 2019 году] Оригинальное название,

Без учета фона физических знаний в реальных вопросах вступительного экзамена в колледж, следующие математические вопросы даются с высокой степенью абстракции:

Известная формула:(cfrac{M_1}{(R+r)^2}+cfrac{M_2}{r^2}=(R+r)cfrac{M_1}{R^3})И известный(alpha=cfrac{r}{R})，(cfrac{3alpha^3+3alpha^4+alpha^5}{(1+alpha)^2}approx 3alpha^3),проверять(M_1)，(M_2)，(R)Означает(r)Приблизительная стоимость

$A.sqrt{cfrac{M_2}{M_1}}cdot R$ $B.sqrt{cfrac{M_2}{2M_1}}cdot R$ $C.sqrt[3]{cfrac{3M_2}{M_1}}cdot R$ $D.sqrt[3]{cfrac{M_2}{3M_1}}cdot R$

Анализ: Что касается ответов на вопросы по математике на вступительных экзаменах в этом году, то первое, что нужно сделать, это понимание смысла вопросов. Общий смысл состоит в том, что, учитывая уравнение, вы должны изменить то(r)Она решена, но, поскольку она рассчитывается вручную, для уменьшения сложности приводится приблизительная справочная формула.Вы должны использовать эту приближенную формулу расчета, чтобы решить проблему плавно. После понимания смысла вопроса возникает другой вопрос, а именно, как пользоваться примерной формулой расчета. Как указано в примерном расчете(alpha=cfrac{r}{R}), Итак, нам нужно, чтобы уравнение появилось первым(alpha), используйте(cfrac{r}{R}=alpha)Заменить, решить до конца, а затем использовать(alpha=cfrac{r}{R}), Пусть появится выражение(r), Просто посчитайте.

Анализ: умножьте обе части уравнения на(R^2), Получаем $ cfrac {R cdot M_1} {(R + r) ^ 2} + cfrac {R cdot M_2} ​​{r ^ 2} = (R + r) cfrac {R cdot M_1} {R ^ 3} $,

который(cfrac{M_1}{frac{(R+r)^2}{R^2}}+cfrac{M_2}{frac{r^2}{R^2}}=(R+r)cfrac{M_1}{frac{R^3}{R^2}}), Деформированный,

(cfrac{M_1}{(1+alpha)^2}+cfrac{M_2}{alpha^2}=(R+r)cfrac{M_1}{R}), который(cfrac{M_1}{(1+alpha)^2}+cfrac{M_2}{alpha^2}=(1+alpha)M_1)，

Затем отсортируйте точки и получите,(alpha^2M_1+(1+alpha)^2M_2=(1+alpha)^3cdot alpha^2M_1)，

Тогда есть((1+alpha)^2M_2=alpha^2M_1+(3alpha^3+3alpha^4+alpha^5)M_1-alpha^2M_1)，

который((1+alpha)^2M_2=(3alpha^3+3alpha^4+alpha^5)M_1),тогда(cfrac{M_2}{M_1}=cfrac{3alpha^3+3alpha^4+alpha^5}{(1+alpha)^2})，

который(cfrac{M_2}{M_1}approx 3alpha^3),тогда(alpha^3approx cfrac{M_2}{3M_1})，

Следовательно(alphaapprox sqrt[3]{cfrac{M_2}{3M_1}}), который(cfrac{r}{R}approx sqrt[3]{cfrac{M_2}{3M_1}}),тогда(rapprox sqrt[3]{cfrac{M_2}{3M_1}}cdot R), Так что выберите(D)。

[Размышление после решения]

• 1. Как вы можете укрепить свои способности к пониманию прочитанного, не так уж и много; процесс анализа приблизительного расчета должен быть ясным; навыки расчета должны быть прочными и на месте.

• 2、((1+alpha)^3=1+3alpha+3alpha^2+alpha^3)；((apm b)^3=a^3mp 3a^2bpm 3ab^2-b^3)；

• 3. Идея использования метода подстановки во всем процессе решения:

(cfrac{M_1}{(R+r)^2}+cfrac{M_2}{r^2}=(R+r)cfrac{M_1}{R^3}) ( xlongequal [то же умножение на R ^ 2, деформация] {для того, чтобы ввести alpha, что удобно для приближенного вычисления} )

(stackrel{frac{r}{R}=>alpha}{Longrightarrow} cfrac{M_1}{(1+alpha)^2}+cfrac{M_2}{alpha^2}=(1+alpha)M_1)，

Разберите деформацию и получите(alphaapprox sqrt[3]{cfrac{M_2}{3M_1}})， (stackrel{alpha=>frac{r}{R}}{Longrightarrow} cfrac{r}{R}approx sqrt[3]{cfrac{M_2}{3M_1}})，

Получить,(rapprox sqrt[3]{cfrac{M_2}{3M_1}}cdot R), Так что выберите(D)。

• 4. Это вопрос по математике или по физике?

Когда вы удалите все знания физики в этой теме, абстрагируйте ее как «известную формулу:(cfrac{M_1}{(R+r)^2}+cfrac{M_2}{r^2}=(R+r)cfrac{M_1}{R^3})И известный(alpha=cfrac{r}{R})，(cfrac{3alpha^3+3alpha^4+alpha^5}{(1+alpha)^2}approx 3alpha^3),проверять(M_1)，(M_2)，(R)Означает(r)«Приблизительное значение», тогда тема в настоящее время является чисто математической. Когда добавляются знания физики, ее можно рассматривать либо как физическую проблему, либо как математическую проблему. Из этого мы все еще можем понять, что предмет математики должен Это инструментальная дисциплина физики, химии, биологии и др. Когда задачи в других конкретных дисциплинах трансформируются и устанавливаются математические модели, оставшиеся решения остаются чистыми математическими знаниями.

Наша проблема: я не знаю направление упрощения и метод упрощения.

• Ссылки по теме:Общее математическое упрощение

Пример 5 【Контрольная работа для вступительных экзаменов в колледж 2019 г. New Вопрос 5】

анализ:

Анализ:

Отражение после решения:

Ссылки по теме:
Пример 6 【Контрольная работа для вступительных экзаменов в колледж 2019 г. New Вопрос 6】

Анализ: метод 1, метод неравенства свойств, метод 2, метод присваивания;

• Ссылки по теме:Сравнение размеров [коучинг для начинающих и среднего продвинутого]

Пример 7 [Документ для вступительных экзаменов в колледж, новая учебная программа по естествознанию, 2019 Вопрос 7]

• Ссылки по теме:Необходимые и достаточные условия

Пример 8 【Документ для вступительных экзаменов в колледж 2019 г. Вопрос 8】

анализ:

Анализ:

Отражение после решения:

Ссылки по теме:

Пример 9 【Контрольная работа для вступительных экзаменов в колледж 2019 г. Вопрос 9】

анализ:

Анализ:

Отражение после решения:

Ссылки по теме:

Пример 10 【Контрольная работа для вступительных экзаменов в колледж 2019 г. Вопрос 10】

анализ:

Анализ:

Отражение после решения:

Ссылки по теме:

Пример 11 【Документ для вступительных экзаменов в колледж 2019 г. Новая учебная программа по естествознанию Ⅱ Вопрос 11】 Дизайн(F)Гиперболический(cfrac{x^2}{a^2}+cfrac{y^2}{b^2}=1(a>0，b>0))Правый фокус,(O)Начало координат, с(OF)Круг и круг(x^2+y^2=a^2)Сдать(P)，(Q)Два балла, если(|PQ|=|OF|),тогда(C)Эксцентриситет []

$A.sqrt{2}$ $B.sqrt{3}$ $C.2$ $D.sqrt{5}$

Анализ: в основном подумайте, как получить(a)против(b)、(c)Отношения между;

Анализ: Как показано на рисунке,

Метод 1: по(left{begin{array}{l}{(x-cfrac{c}{2})^2+y^2=cfrac{c^2}{4}}\{x^2+y^2=a^2}end{array}right.), Ликвидировать(y), Решения должны(x=cfrac{a^2}{c})，

Замена(y^2=a^2-x^2=a^2-cfrac{a^4}{c^2}=cfrac{a^2(c^2-a^2)}{c^2})，

Снова(|PQ|=|OF|), который(2|y|=c),тогда(4y^2=c^2)，

Разобрались(4a^2(c^2-a^2)=c^4), который(c^4-4a^2c^2+4a^2=0),тогда((c^2-2a^2)=0)，

который(c^2=2a^2),тогда(e^2=cfrac{c^2}{a^2}=2), Следовательно(e=sqrt{2}), выбрано(A)；

Метод 2: из-за(|PQ|=|OF|), Ты можешь видеть(B)Это центр круга, поэтому укажите(B)Абсцисса(x=cfrac{c}{2})，

от(left{begin{array}{l}{x=cfrac{c}{2}}\{x^2+y^2=a^2}end{array}right.), Решения должны(y=sqrt{a^2-cfrac{c^2}{4}})，

Тогда мы можем увидеть(|PQ|=2sqrt{a^2-cfrac{c^2}{4}}),также(|PQ|=|OF|=c)，

Следовательно(2sqrt{a^2-cfrac{c^2}{4}}=c), Упрощено и разобрано(c^2=2a^2), Решения должны(e=sqrt{2}), выбрано(A)；

Переосмысление после решения: 1. Очевидно, что действие метода 2 проще, чем метода 1, потому что сложность решения системы уравнений, состоящей из двух квадратных уравнений, обязательно больше, чем сложность решения системы первичных и одного квадратного уравнений;

2. Хорда с одинаковым диаметром в круге должна быть диаметром окружности, а пересечение двух диаметров должно быть центром окружности. Необходимо закрепить знания по геометрии плоскости в младших классах средней школы.

• Ссылки по теме:Обзор теорем о плоской геометрии

3. Обратите внимание на уравнение(c^4-4a^2c^2+4a^2=0)Решение, или преобразованное в((c^2-2a^2)=0), Или преобразован в(cfrac{c^4}{a^4}-4cfrac{c^2}{a^2}+4=0), который(e^4-4e^2+4=0)；

Пример 12 [Документ для вступительных экзаменов в колледж 2019 г. New Вопрос 12] Настройка функции(f(x))Определяется как(R), Удовлетворительно(f(x+1)=2f(x)), И когда(xin (0，1])Время,(f(x)=x(x-1)), Если для любого(xin (-infty，m]), И то и другое(f(x)geqslant -cfrac{8}{9}),тогда(m)Диапазон значений: 【】

$A.(-infty，cfrac{9}{4}]$ $B.(-infty，cfrac{7}{3}]$ $C.(-infty，cfrac{5}{2}]$ $D.(-infty，cfrac{8}{3}]$

Анализ: Чтобы понять, как решить этот тип проблемы, лучше всего понять цель условий, указанных в задаче.

Данные условия »(f(x+1)=2f(x))«Используется для решения аналитической формулы на других интервалах, для решения или построения графика;

Данные условия »(xin (0，1])Время,(f(x)=x(x-1))«Является ли основой для построения графиков или поиска аналитических формул на других интервалах; следовательно, нам нужно сначала найти аналитическую формулу функции;

Данные условия »(xin (-infty，m]), И то и другое(f(x)geqslant -cfrac{8}{9})«Это для нас, чтобы сделать функцию(y=f(x))Изображение и(y=-cfrac{8}{9})Изображение, судя по изображению, в функции(y=f(x))Какой абзац какой удовлетворяет(f(x))Изображение всегда по прямой(y=-cfrac{8}{9})Выше.

Анализ: Пусть(x+1=t),тогда(x=t-1), Данное условие(f(x+1)=2f(x))Превратился в(f(t)=2f(t-1))，

который(f(x)=2f(x-1)star), Это важное выражение, которое мы будем использовать для преобразования вниз;

из-за(xin (0，1])Время,(f(x)=x(x-1))①，

Чжэ Данг(xin (1，2])Время,(x-1in (0，1]), От(star)И ① получить, а именно(f(x)=2f(x-1)=2(x-1)(x-2))②；

когда(xin (2，3])Время,(x-1in (1，2]), От(star)И ② получить, а именно(f(x)=2f(x-1)=2times 2[(x-1)-1][(x-2)-1]=4(x-2)(x-3))③；

Аналитическая формула для следующего интервала бесполезна, но давайте посмотрим.

когда(xin (3，4])Время,(x-1in (2，3]), От(star)И получается, в это время(f(x)=2f(x-1)=2times 4[(x-1)-2][(x-1)-3]=8(x-3)(x-4))④；

Таким же образом мы можем найти(xin (-1，0])Аналитическая формула времени;

Чжэ Данг(xin (-1，0])Время,(x+1in (0，1]), От(f(x+1)=2f(x))Получить, то есть(f(x)=cfrac{1}{2}f(x+1)=cfrac{1}{2}x(x+1))⑤；

Произвести кусочную функцию в системе координат в интервале((-1，3])Изображение и прямая линия(y=-cfrac{8}{9})，

По изображению мы можем решить уравнение(4(x-2)(x-3)=-cfrac{8}{9}), Решения должны(x=cfrac{7}{3})или же(x=cfrac{8}{3})(В сочетании с изображением для удаления)

который(m=cfrac{7}{3}), Так что выберите(B)。

Размышления после решения: 1. В этой теме задействовано множество точек знаний: кусочная функция, поиск аналитической формулы, метод подстановки, квадратичная функция, комбинация числа и формы и т.д .;

2. Парное выражение(f(x)=2f(x-1))Понимая, это две трансформации, такие как трансформация перевода(f(x)=f(x-1))И преобразование амплитуды(f(x)=2f(A))После понимания этой темы, если мы столкнемся с подобными темами в будущем, мы можем знать, что это понимание.(f(x-1))Означает базовое изображение(y=x(x-1))Сдвиньте вправо на одну единицу, затем умножьте на(2), Что означает, что на основе исходного переведенного изображения(y)Осевое расширение(2)Раз, изображение намного быстрее.

3. Мы также можем написать аналитическую формулу непосредственно с использованием изображений вместо того, чтобы подробно решать аналитические формулы для каждого интервала. Например, после однократного сдвига вправо мы знаем, что изображение функции проходит через точку((1，0))с участием((2，0)), Тогда аналитическая формула(y=a(x-1)(x-2)), И знайте, что самая низкая точка((cfrac{1}{2}，-cfrac{1}{2})), Мы можем увидеть(a=2), который(xin (1，2])Время,(f(x)=2(x-1)(x-2))；

4. Можно ли использовать напрямую без трансформации(f(x+1)=2f(x))А как насчет аналитической формулы? Да, но вы всегда должны следить за независимыми переменными(x)Держись за ценность

такие как(xin (0，1])Время,(f(x)=x(x-1)),от(f(x+1)=2f(x)), Получите это первым(f(x+1)=2x(x-1)), Обратил внимание(x+1in (1，2]), Запросить решение(xin (1，2])Приведенную выше аналитическую формулу необходимо обменять на юань, поэтому(x+1=tin (1，2]),тогда(x=t-1), Замена(f(x+1)=2x(x-1)), Деформированный, чтобы получить(f(t)=2(t-1)(t-2))，(tin (1，2]), который(f(x)=2(x-1)(x-2))，(xin (1，2]).

5. Обратите внимание на написание и понимание аналитического выражения функции.

Форма 1:(f(x)=left{begin{array}{l}{x(x-1)，xin(0，1]}\{2(x-1)(x-2)，xin(1，2]}\{4(x-2)(x-3)，xin(2，3]}\{8(x-3)(x-4)，xin(3，4]}\{cdots，cdots}end{array}right.)

Форма вторая:(f(x)=left{begin{array}{l}{x(x-1)，xin(0，1]}\{2f(x-1)，x>1}end{array}right.)

• Ссылки по теме:Метод рисования некоторых специальных изображений кусочных функций

2. Заполните пустые поля.

Пример 13 [Новый учебный план естественных наук для вступительных экзаменов в колледж 2019 г. Ⅱ Вопрос 13] высокоскоростные железные дороги моей страны быстро развиваются, и технологии передаются. По статистике среди скоростных поездов, которые останавливаются на определенной станции, есть(10)Пунктуальность каждого поезда(0.97),Есть(20)Пунктуальность каждого поезда(0.98),Есть(10)Пунктуальность каждого поезда(0.99), Тогда ориентировочная средняя пунктуальность всех поездов высокоскоростной железной дороги на этой станции составляет ____________.

Анализ: Из вопроса видно, что все поезда высокоскоростного поезда на этой станции(40)Среднее число может быть решено с помощью формулы расчета средневзвешенного числа.

Анализ:(bar{x}=cfrac{10}{40}times 0.97+cfrac{20}{40}times 0.98+cfrac{10}{40}times 0.99=0.98).

Переосмысление после понимания: прислушиваясь к отзывам студентов, которые говорят, что название было неправильно понято, он не знал уровень пунктуальности.(0.98)из(20)В этой поездке есть начало(10)Количество поездов явно не включается, поэтому очень важно правильно и точно понимать смысл вопроса.

Пример 14 [Контрольная работа для вступительных экзаменов в колледж, стандарт II, вопрос 14], известная(f(x))Странная функция, и когда(x<0)Время,(f(x)=-e^{ax})Если(f(ln2)=8),тогда(a)=___________。

Анализ: Используйте четность функции, чтобы найти значение параметра.

Анализ: по(f(ln2)=8)И странная функция,(f(-ln2)=-8)，

тогда(f(-ln2)=-e^{a(-ln2)}=-e^{-aln2}=-8), который((e^{ln2})^{-a}=8),тогда(2^{-a}=8=2^3), Следовательно(-a=3),тогда(a=-3)。

Размышления после решения: глубокое понимание природы и законов экспонент и логарифмов.

• Ссылки по теме:Экспоненциальный логарифм

Пример 15 【Контрольная работа для вступительных экзаменов в колледж 2019 г. Вопрос 15】(triangle ABC)Внутренний угол(A)，(B)，(C)Противоположные стороны(a)，(b)，(c)Если(b=6)，(a=2c)，(B=cfrac{pi}{3}),тогда(triangle ABC)Площадь __________.

Анализ: используйте синус и косинус, чтобы понимать треугольники.

Анализ: Сделайте соответствующие графики самостоятельно, стремясь(b)Используя закон косинусов, получаем

(b^2=a^2+c^2-2accosB), который(36=c^2+4c^2-2cdot ccdot 2ccdot coscfrac{pi}{3})

Решения должны,(c=2sqrt{3}),тогда(a=4sqrt{3})，

тогда(S_{triangle ABC}=cfrac{1}{2}accosB=cfrac{1}{2}times 2sqrt{3}times 4sqrt{3}times cfrac{sqrt{3}}{2}=6sqrt{3})。

• Ссылки по теме:Понимание треугольников

Пример 16 [Новый учебный план естественных наук для вступительных экзаменов в колледж 2019 г. China Вопрос 16] Китай имеет долгую историю культуры цзиньши, и тюлень является одним из представителей культуры цзиньши. Форма печати в основном кубовидная, кубическая или цилиндрическая, но форма печати официального письма дугу Северной и Южной династий представляет собой «полуправильный многогранник». Полуправильный многогранник — это многогранник, окруженный двумя или более правильных многоугольников. Многогранник олицетворяет симметричную красоту математики. На рисунке 2 показано число ребер(48)Полуправильный многогранник, все его вершины лежат на поверхности того же куба, а длина ребра этого куба равна(1), Полуправильный многогранник имеет __________ граней, а длина его ребра _____________.

Анализ: Процесс изготовления полуправильного многогранника показан на рисунке ниже;

Анализ: если рассматривать его как три слоя, каждый слой имеет(8)Одна сторона плюс две следующие стороны, так что есть(3times 8+2=26)Лапша.

Как показано на рисунке, пусть длина кромки будет(x), который(MN=NE=x),от(triangle EHN)Равнобедренный прямоугольный треугольник,

от(NE=x), Ты можешь видеть(NH=cfrac{sqrt{2}}{2}x),также(MN+2NH=1)，

тогда(x+2times cfrac{sqrt{2}}{2}x=1), который((sqrt{2}+1)x=1), Решения должны(x=sqrt{2}-1).

Таким образом, этот полуправильный многогранник имеет(26)Грань, длина кромки(sqrt{2}-1)。

[Размышление после решения]

1. Найдите площадь его поверхности;

2. Найдите его объем;

3. Найдите радиус вписанной сферы;

Анализ: Из этой анимации видно, что полуправильный многогранник не имеет вписанной сферы.

4. Найдите радиус описанной сферы;

Радиус описываемой сферы можно определить с помощью рисунка ниже.

5、Подсчет геометрии в классических вероятностях