Вся стереометрия для егэ профиль математика - Помощь в подготовке к экзаменам и поступлению

На этой странице – все необходимое для освоения стереометрии и решения задач ЕГЭ.

Для того чтобы справиться с задачей 2 из первой части Профильного ЕГЭ, вам нужно знать формулы объемов и площадей поверхности. Объем конуса, площадь боковой поверхности призмы, длина диагонали куба – все это вы найдете здесь:

Многогранники: формулы объема и площади поверхности

Тела вращения: формулы объема и площади поверхности

Не ждите, когда конус или сферу будут «проходить» в школе. Начинайте решать задачи по стереометрии из первой части ЕГЭ. Это задание №2 .

Вам помогут наши методические материалы:

Задачи по стереометрии часть 1: Просто применяем формулы

Стереометрия на ЕГЭ. Приемы и секреты

Для решения задачи №13 из второй части Профильного ЕГЭ по математике надо повторить весь курс стереометрии. Нет, не обязательно перечитывать весь учебник. Полный курс стереометрии – здесь:

Задача 13 (часть 2 ЕГЭ по математике). Программа по стереометрии

Плоскость в пространстве. Взаимное расположение плоскостей

Прямые в пространстве. Пересекающиеся, параллельные, скрещивающиеся прямые

Параллельность прямой и плоскости

Угол между прямой и плоскостью. Перпендикулярность прямой и плоскости

Параллельность плоскостей

Угол между плоскостями. Перпендикулярность плоскостей

Угол и расстояние между скрещивающимися прямыми. Расстояние от точки до плоскости –

Метод объемов

Теорема о трёх перпендикулярах

Теорема о прямой и параллельной ей плоскости

Параллельное проецирование

Как строить чертежи в задачах по стереометрии

Построение сечений в задачах по стереометрии

Можно ли, посмотрев на задачу, сразу понять, что с ней делать и каким методом решать? Да, можно! Для вас — наш новый уникальный материал:

Стереометрия, задача 13 Профильного ЕГЭ по математике. Классификация задач и методы их решения

Обратите внимание на координатный метод. Если вы в 10-м классе – у вас есть время освоить оба способа решения задач по стереометрии, классический и векторно-координатный.

Векторы и метод координат. Задача 13, часть 2 на ЕГЭ по математике

Для старшеклассников и учителей – дополнительные материалы, автор В.М. Мамаева.

«Перпендикулярность. Книга для учащихся»

«Перпендикулярность. Книга для учителя»

«Тела вращения. Книга для учащихся»

«Тела вращения. Книга для учителя»

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 6, задача 13

Несколько полезных советов тем, кто решает задачи по стереометрии

1. Учитесь строить чертежи. Изучите правила построения чертежей. Хороший чертеж – это половина решения. И если чертеж вам не нравится, бросайте его и рисуйте другой.

2. Выучите теорему о прямой и параллельной ей плоскости. Ее очень трудно найти в учебнике. Однако множество задач решаются с помощью этой теоремы.

3. Запомните формулу для площади прямоугольной проекции фигуры. И посмотрите, как решаются с ее помощью задачи на нахождение угла между плоскостями.

4. Учитесь правильно оформлять решения. Часто старшеклассники говорят: «Сделаем параллельный перенос и перенесем прямую АВ так, чтобы она проходила через точку М». Однако, если вы решили ввести параллельный перенос, вам надо его описать. В каком направлении, на какое расстояние. И зачем вам лишние сложности? Намного проще сказать: «Проведем через точку М прямую, параллельную АВ».

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Стереометрия» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Параллельность в пространстве

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек.
Если две прямые на плоскости перпендикулярны к третьей прямой, то они параллельны.
Если две прямые в трехмерном пространстве перпендикулярны к одной плоскости, то они параллельны.
Если прямая a, не лежащая в плоскости $α$, параллельна некоторой прямой $b$, которая лежит в плоскости $α$, то прямая a параллельна плоскости $α$.
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым, лежащим в другой плоскости, то такие плоскости параллельны.

Перпендикулярность в пространстве

Две прямые называются перпендикулярными, если угол между ними равен $90°$.
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.
Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то заданные плоскости перпендикулярны.
Теорема о трех перпендикулярах: если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна и самой наклонной.
Если из одной точки проведены к плоскости перпендикуляр и наклонные, то:

Перпендикуляр короче наклонных.
Равные наклонные имеют равные проекции на плоскости.
Большей наклонной соответствует большая проекция на плоскости.

Скрещивающиеся прямые

Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются.
Через две скрещивающиеся прямые проходит единственная пара параллельных плоскостей.
Расстояние между скрещивающимися прямыми – это расстояние от некоторой точки одной из скрещивающихся прямых до плоскости, проходящей через другую прямую параллельно первой прямой.
Угол между скрещивающимися прямыми – это острый угол между двумя пересекающимися прямыми, которые соответственно параллельны заданным скрещивающимся прямым.

Многогранники

Введем общие обозначения

$P_{осн}$ — периметр основания;

$S_{осн}$ — площадь основания;

$S_{бок}$ — площадь боковой поверхности;

$S_{п.п}$ — площадь полной поверхности;

$V$ — объем фигуры.

Название	Определение и свойства фигуры	Обозначения и формулы объема, площади
Прямоугольный параллелепипед	1. Все двугранные углы прямоугольного параллелепипеда – прямые. 2. Противоположные грани попарно равны и параллельны. 3. Диагонали прямоугольного параллелепипеда равны. 4. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты). $B_1D^2=AD^2+DC^2+C_1C^2$	$V=a·b·c$, где $a, b$ и $с$ – длина, ширина и высота. $S_{бок}=P_{осн}·c=2(a+b)·c$ $S_{п.п}=2(ab+bc+ac)$.
Куб	1. Противоположные грани попарно параллельны. 2. Все двугранные углы куба – прямые. 3. Диагональ куба в $√3$ раз больше его ребра. $B_1 D=АВ√3$ 4. Диагональ грани куба в $√2$ раза больше длины ребра. $DС1=DC√2$	Пусть $а$ — длина ребра куба, $d$ — диагональ куба, тогда справедливы формулы: $V=a^3={d^3}/{3√3}$. $S_{п.п}=6а^2=2d^2$ $R={a√3}/{2}$, где $R$ — радиус сферы, описанной около куба. $r={a}/{2}$, где $r$ — радиус сферы, вписанной в куб.
Призма	Призма – это многогранник, состоящий из двух равных многоугольников, расположенных в параллельных плоскостях, и $n$-го количества параллелограммов. Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру. Прямая призма называется правильной, если ее основания – правильные многоугольники. В правильной четырехугольной призме диагонали точкой пересечения делятся пополам.	$S_{бок}=P_{осн}·h$ $S_{п.п}=S_{бок}+2S_{осн}$ $V=S_{осн}·h$
Пирамида	У треугольной пирамиды есть еще одно название – тетраэдр (четырехгранник). Пирамида называется правильной, если в ее основании лежит правильный многоугольник, а ее высота приходит в центр основания (в центр описанной окружности). Все боковые ребра правильной пирамиды равны, следовательно, все боковые грани являются равнобедренными треугольниками.	Формулы вычисления объема и площади поверхности правильной пирамиды. $h_a$ — высота боковой грани (апофема) $S_{бок}={P_{осн}·h_a}/{2}$ $S_{п.п}=S_{бок}+S_{осн}$ $V={1}/{3} S_{осн}·h$
Усеченная пирамида	Усеченной пирамидой называется многогранник, заключенный между пирамидой и секущей плоскостью, параллельной. Правильная усечённая пирамида получается при сечении правильной пирамиды плоскостью, параллельной основанию. У правильной усеченной пирамиды апофемы равны	$V={h(F+f+√{Ff})}/{3}$ Где $F,f$ — площади оснований; $h$ — высота (расстояние между основаниями); Для правильной ус. пирамиды $S_{бок}={(P+p)·a}/{2}$, где $P$ и $p$ – периметры оснований; $а$ – апофема.
Цилиндр	Осевое сечение цилиндра — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра. Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра. Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра. Если в цилиндр вписана сфера, то радиус сферы равен радиусу цилиндра и равен половине высоты цилиндра. $R_{сферы}=R_{цилиндра}={h_{цилиндра}}/{2}$	$S_{бок.пов.}=2πR·h$ $S_{полной.пов.}=2πR(R+h)$ $V=πR^2·h$
Конус	Осевым сечением конуса является равнобедренный треугольник, основание которого равно двум радиусам, а боковые стороны равны образующим конуса. Если боковая поверхность конуса – полукруг, то осевым сечением является равносторонний треугольник, угол при вершине равен $60°$. Если радиус или диаметр конуса увеличить в $n$ раз, то его объем увеличится в $n^2$ раз. Если высоту конуса увеличить в m раз, то объем конуса увеличится в то же количество раз.	$S_{бок.пов.}=πR·l$ $S_{полной.пов.}=πR^2+πR·l=πR(R+l)$ $V={πR^2·h}/{3}$
Усеченный конус	Усеченным конусом называется часть конуса, заключенная между основанием и секущей плоскостью, параллельной основанию. Осевым сечением усеченного конуса является равнобедренная трапеция.	$S_{бок}=πl(R+r)$ $S_{п.п.}=π(R^2+r^2+l(R+r))$ $V={πH(R^2+r^2+Rr)}/{3}$ Где $R$ и $r$ – радиусы оснований; $Н$ — высота усеченного конуса.
Сфера, шар	Тело, ограниченное сферой, называется шаром. Осевое сечение шара это круг, радиус которого равен радиусу шара. Осевым сечением является самый большой круг шара. Если радиус или диаметр шара увеличить в $n$ раз, то площадь поверхности увеличится в $n^2$ раз, а объем в $n^3$ раз.	$S_{п.п}=4π·R^2=π·d^2$, где $R$ — радиус сферы, $d$ — диаметр сферы $V={4π·R^3}/{3}={π·d^3}/{6}$, где $R$ — радиус шара, $d$ — диаметр шара.

Тетраэдр

Радиус описанной сферы тетраэдра.

Вокруг тетраэдра можно описать сферу, радиус которой находим по формуле, где $R$ — радиус описанной сферы, $a$ — ребро тетраэдра.

$R={a√6}/{4}$

Радиус вписанной в тетраэдр сферы.

В тетраэдр можно вписать сферу, радиус вписанной сферы находим по формуле, приведенной ниже.

Где $r$ — радиус вписанной в тетраэдр сферы,

$a$ — ребро тетраэдра.

$r={a√6}/{12}$

Составные многогранники

Задачи на нахождение объема составного многогранника:

Разделить составной многогранник на несколько параллелепипедов.
Найти объем каждого параллелепипеда.
Сложить объемы.

Задачи на нахождение площади поверхности составного многогранника.

— Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:

$S_{полн.пов.}=P_{осн}·h+2S_{осн}$

Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.

— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.

Пример:

Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).

Представим данный многогранник как прямую призму с высотой равной $12$.

$S_{полн.пов.}=P_{осн}·h+2S_{осн}$

$P_{осн}=8+6+6+2+2+4=28$

Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:

$S_1=6·6=36$

$S_2=2·4=8$

$S_осн=36+8=44$

Далее подставим все данные в формулу и найдем площадь поверхности многогранника

$S_{полн.пов.}=28·12+2·44=336+88=424$

Ответ: $424$

Задачи на нахождение расстояния между точками составного многогранника.

В данных задачах приведены составные многогранники, у которых двугранные углы прямые. Надо соединить расстояние между заданными точками и достроить его до прямоугольного треугольника. Далее остается воспользоваться теоремой Пифагора для нахождения нужной стороны.

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$АС^2+ВС^2=АВ^2$

Задачи на нахождение угла или значения одной из тригонометрических функций обозначенного в условии угла составного многогранника.

Так как в данных задачах приведены составные многогранники, у которых все двугранные углы прямые, то достроим угол до прямоугольного треугольника и найдем его значение по тригонометрическим значениям.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$:

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	${1}/{2}$	${√2}/{2}$	${√3}/{2}$
$cosα$	${√3}/{2}$	${√2}/{2}$	${1}/{2}$
$tgα$	${√3}/{3}$	$1$	$√3$
$ctgα$	$√3$	$1$	${√3}/{3}$

Связь между сторонами правильного n-угольника и радиусами описанной и вписанной окружностей

$АВ=a_n$ — сторона правильного многоугольника

$R$ — радиус описанной окружности

$r$ — радиус вписанной окружности

$n$ — количество сторон и углов

$a_n=2·R·sin{180°}/{n}$;

$r=R·cos{180°}/{n}$;

$a_n=2·r·tg{180°}/{n}$.

Формула нахождения градусной меры угла в правильном многоугольнике:

$α={(n-2)·180°}/{n}$

Формулы площадей треугольников и многоугольников, которые могут находиться в основании многогранников

В основании лежит треугольник

1. $S={a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне а

2. $S={a·b·sin⁡α}/{2}$, где $a, b$ — соседние стороны, $α$ — угол между этими соседними сторонами.

3. $S=p·r$, где $r$ — радиус вписанной окружности

4. $S={a·b·c}/{4R}$, где $R$ — радиус описанной окружности

5. Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ — катеты прямоугольного треугольника.

В основании лежит четырехугольник

Прямоугольник

$S=a·b$, где $а$ и $b$ — смежные стороны.

Ромб

$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба

$S=a^2·sin⁡α$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.

Трапеция

$S={(a+b)·h}/{2}$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.

Площади правильных многоугольников:

1. Для равностороннего треугольника $S={a^{2}√3}/{4}$, где $а$ — длина стороны.

2. Квадрат

$S=a^2$, где $а$ — сторона квадрата.

3. Правильный шестиугольник

Шестиугольник разделим на шесть правильных треугольников и найдем площадь как:

$S=6·S_{треугольника}={6·a^{2}√3}/{4}={3·a^{2}√3}/{2}$, где $а$ — сторона правильного шестиугольника.

Источник

Справочник с основными фактами стереометрии

2. Вникай в доказательства

Готовиться с нами — ЛЕГКО!

Эффективное решение существует!

Вы ищете теорию и формулы для ЕГЭ по математике? Образовательный проект «Школково» предлагает вам заглянуть в раздел «Теоретическая справка». Здесь представлено пособие по подготовке к ЕГЭ по математике, которое фактически является авторским. Оно разработано в соответствии с программой школьного курса и включает такие разделы, как арифметика, алгебра, начала анализа и геометрия (планиметрия и стереометрия). Каждое теоретическое положение, содержащееся в пособии по подготовке к ЕГЭ по математике, сопровождается методически подобранными задачами с подробными разъяснениями.

Таким образом, вы не только приобретете определенные знания. Полный справочник для ЕГЭ по математике поможет вам научиться логически и нестандартно мыслить, выполнять самые разнообразные задачи и грамотно объяснять свои решения. А это уже половина успеха при сдаче единого государственного экзамена.

После того, как вы нашли необходимые формулы и теорию для ЕГЭ по математике, рекомендуем вам перейти в раздел «Каталоги» и закрепить полученные знания на практике. Для этого достаточно выбрать задачу по данной теме и решить ее. Кроме того, справочные материалы по математике для ЕГЭ пригодятся вам и для других естественнонаучных дисциплин, таких как физика, химия и т. д.

({color{red}{textbf{Факт 1. Про параллельность прямых}}})
(bullet) Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.
(bullet) Через две параллельные прямые проходит плоскость, и притом только одна.
(bullet) Если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость.
(bullet) Если прямая (a) параллельна прямой (b), а та в свою очередь параллельна прямой (c), то (aparallel c).
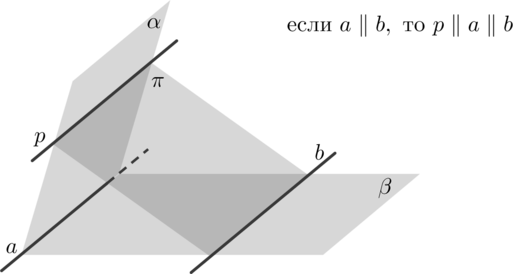
(bullet) Пусть плоскость (alpha) и (beta) пересекаются по прямой (a), плоскости (beta) и (pi) пересекаются по прямой (b), плоскости (pi) и (alpha) пересекаются по прямой (p). Тогда если (aparallel
b), то (pparallel a) (или (pparallel b)):

({color{red}{textbf{Факт 2. Про параллельность прямой и плоскости}}})
(bullet) Существует три вида взаимного расположения прямой и плоскости:
1. прямая имеет с плоскостью две общие точки (то есть лежит в плоскости);
2. прямая имеет с плоскостью ровно одну общую точку (то есть пересекает плоскость);
3. прямая не имеет с плоскостью общих точек (то есть параллельна плоскости).
(bullet) Если прямая (a), не лежащая в плоскости (pi), параллельна некоторой прямой (p), лежащей в плоскости (pi), то она параллельна данной плоскости.

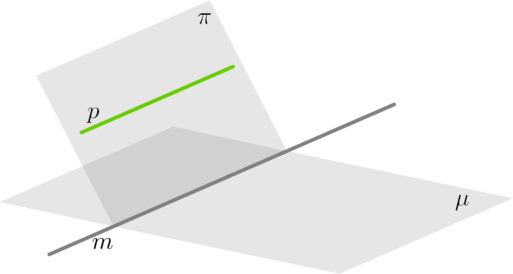
(bullet) Пусть прямая (p) параллельна плоскости (mu). Если плоскость (pi) проходит через прямую (p) и пересекает плоскость (mu), то линия пересечения плоскостей (pi) и (mu) — прямая (m) — параллельна прямой (p).

({color{red}{textbf{Факт 3. Про параллельность плоскостей}}})
(bullet) Если две плоскости не имеют общих точек, то они называются параллельными плоскостями.
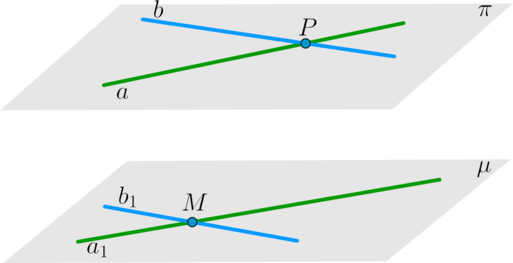
(bullet) Если две пересекающиеся прямые из одной плоскости соответственно параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.

(bullet) Если две параллельные плоскости (alpha) и (beta) пересечены третьей плоскостью (gamma), то линии пересечения плоскостей также параллельны: [alphaparallel beta, alphacap gamma=a,
betacapgamma=b Longrightarrow aparallel b]

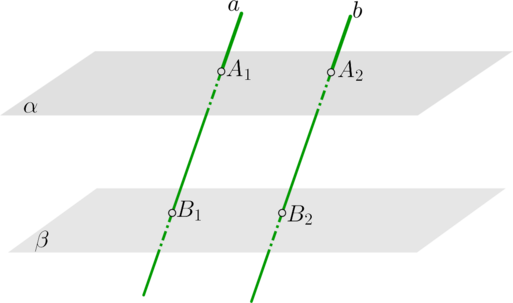
(bullet) Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны: [alphaparallel beta, aparallel b Longrightarrow
A_1B_1=A_2B_2]

({color{red}{textbf{Факт 4. Про скрещивающиеся прямые}}})
(bullet) Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости.
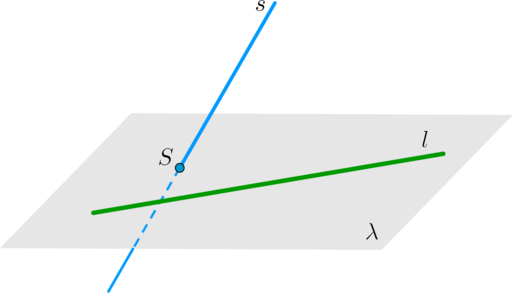
(bullet) Признак:
Пусть прямая (l) лежит в плоскости (lambda). Если прямая (s) пересекает плоскость (lambda) в точке (S), не лежащей на прямой (l), то прямые (l) и (s) скрещиваются.

(bullet) алгоритм нахождения угла между скрещивающимися прямыми (a) и (b):
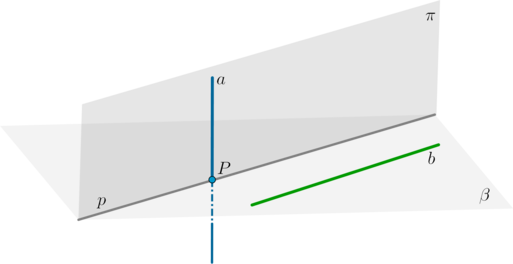
Шаг 1. Через одну из двух скрещивающихся прямых (a) провести плоскость (pi) параллельно другой прямой (b). Как это сделать: проведем плоскость (beta) через прямую (b) так, чтобы она пересекала прямую (a) в точке (P); через точку (P) проведем прямую (pparallel b); тогда плоскость, проходящая через (a) и (p), и есть плоскость (pi).
Шаг 2. В плоскости (pi) найти угол между прямыми (a) и (p) ((pparallel b)). Угол между ними будет равен углу между скрещивающимися прямыми (a) и (b).

({color{red}{textbf{Факт 5. Про перпендикулярность прямой и плоскости}}})
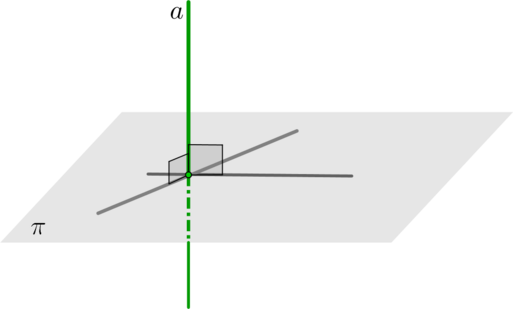
(bullet) Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
(bullet) Если две прямые перпендикулярны плоскости, то они параллельны.
(bullet) Признак: если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.

({color{red}{textbf{Факт 6. Про расстояния}}})
(bullet) Для того, чтобы найти расстояние между параллельными прямыми, нужно из любой точки одной прямой опустить перпендикуляр на другую прямую. Длина перпендикуляра и есть расстояние между этими прямыми.
(bullet) Для того, чтобы найти расстояние между плоскостью и параллельной ей прямой, нужно из любой точки прямой опустить перпендикуляр на эту плоскость. Длина перпендикуляра и есть расстояние между этими прямой и плоскостью.
(bullet) Для того, чтобы найти расстояние между параллельными плоскостями, нужно из любой точки одной плоскости опустить перпендикуляр к другой плоскости. Длина этого перпендикуляра и есть расстояние между параллельными плоскостями.
(bullet) алгоритм нахождения расстояния между скрещивающимися прямыми (a) и (b):
Шаг 1. Через одну из двух скрещивающихся прямых (a) провести плоскость (pi) параллельно другой прямой (b). Как это сделать: проведем плоскость (beta) через прямую (b) так, чтобы она пересекала прямую (a) в точке (P); через точку (P) проведем прямую (pparallel b); тогда плоскость, проходящая через (a) и (p), и есть плоскость (pi).
Шаг 2. Найдите расстояние от любой точки прямой (b) до плоскости (pi). Это расстояние и есть расстояние между скрещивающимися прямыми (a) и (b).

({color{red}{textbf{Факт 7. Про теорему о трех перпендикулярах (ТТП)}}})
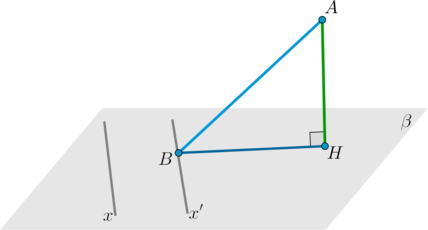
(bullet) Пусть (AH) – перпендикуляр к плоскости (beta). Пусть (AB, BH) – наклонная и ее проекция на плоскость (beta). Тогда прямая (x) в плоскости (beta) будет перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции: [begin{aligned}
&1. AHperp beta, ABperp xquad Rightarrowquad BHperp x\[2ex]
&2. AHperp beta, BHperp xquadRightarrowquad ABperp
xend{aligned}]

Заметим, что прямая (x) необязательно должна проходить через точку (B). Если она не проходит через точку (B), то строится прямая (x’), проходящая через точку (B) и параллельная (x). Если, например, (x’perp BH), то и (xperp BH).

({color{red}{textbf{Факт 8. Про угол между прямой и плоскостью,
а также угол между плоскостями}}})
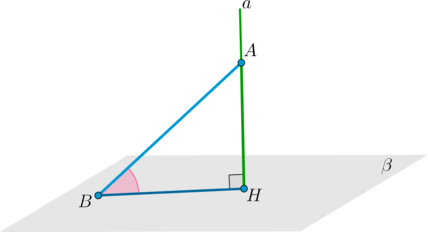
(bullet) Угол между наклонной прямой и плоскостью — это угол между этой прямой и ее проекцией на данную плоскость. Таким образом, данный угол принимает значения из промежутка ((0^circ;90^circ)).
Если прямая лежит в плоскости, то угол между ними считается равным (0^circ). Если прямая перпендикулярна плоскости, то, исходя из определения, угол между ними равен (90^circ).
(bullet) Чтобы найти угол между наклонной прямой и плоскостью, необходимо отметить некоторую точку (A) на этой прямой и провести перпендикуляр (AH) к плоскости. Если (B) – точка пересечения прямой с плоскостью, то (angle ABH) и есть искомый угол.

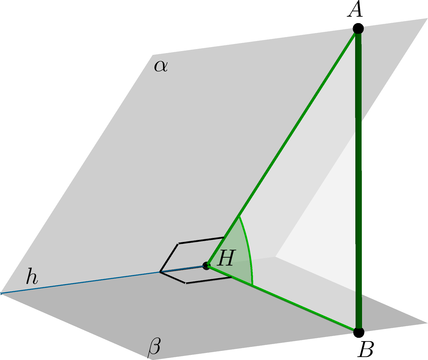
(bullet) Для того, чтобы найти угол между плоскостями (alpha) и (beta), можно действовать по следующему алгоритму:
Отметить произвольную точку (A) в плоскости (alpha).
Провести (AHperp h), где (h) — линия пересечения плоскостей.
Провести (AB) перпендикулярно плоскости (beta).
Тогда (AB) – перпендикуляр к плоскости (beta), (AH) – наклонная, следовательно, (HB) – проекция. Тогда по ТТП (HBperp h).
Следовательно, (angle AHB) — линейный угол двугранного угла между плоскостями. Градусная мера этого угла и есть градусная мера угла между плоскостями.

Заметим, что мы получили прямоугольный треугольник (triangle AHB) ((angle B=90^circ)). Как правило, находить (angle AHB) удобно из него.

({color{red}{textbf{Факт 9. Про перпендикулярность плоскостей}}})
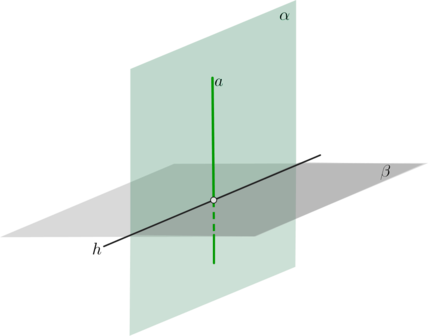
(bullet) Признак: если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости. [aperp beta, ain alphaquadRightarrowquad alphaperp beta]

(bullet) Заметим, что так как через прямую (a) можно провести бесконечное множество плоскостей, то существует бесконечное множество плоскостей, перпендикулярных (beta) (и проходящих через (a)).

Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, — на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете.

Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?

Потому что это расширяет кругозор. Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир.
Потому что это развивает интеллект. Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы.

Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Площадь поверхности – это суммарная площадь всех поверхностей, которые составляют объемную фигуру.

Призма

1. Призма — это многогранник, у которого две грани (основания) — равные (n)-угольники, лежащие в параллельных плоскостях, остальные (n) граней (боковые) — параллелограммы. Призмы подразделяются на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон основания.
Высотой призмы называется перпендикуляр, опущенный из точки верхнего основания на плоскость нижнего.

2. Призма, у которой боковое ребро перпендикулярно основанию, называется прямой. Ее боковые грани — прямоугольники, и высота равна боковому ребру.
Прямая призма, в основании которой лежит правильный многоугольник, называется правильной. Ее боковые грани, равные прямоугольники.

3. Площадь боковой поверхности призмы равна сумме площадей ее боковых граней: (S_{бок}= S_1+ S_2+…+ S_n).
Площадь поверхности призмы равна сумме площади боковой поверхности и двух площадей оснований: (S_{полн} = S_{бок}+ 2S_{осн}).

4. Объем произвольной призмы равен произведению площади основания на высоту: (V_{призмы}=S_{осн}cdot h).

Параллелепипед

5. Параллелепипедом называется призма, в основании которой лежит параллелограмм. Противоположные боковые грани параллелепипеда равны.
Прямой параллелепипед — это параллелепипед, у которого боковое ребро перпендикулярно основанию.
Прямоугольный параллелепипед — это прямой параллелепипед, у которого в основании лежит прямоугольник.
Диагональ прямоугольного параллелепипеда выражается через его измерения (ширину, длину и высоту) формулой (d^2=a^2+b^2+c^2).
Куб — параллелепипед, у которого все грани квадраты. Диагональ куба с ребром (a): (d=asqrt{3}).

Пирамида

6. Пирамидой называется многогранник, у которого одна грань (основание) — (n)—угольник, а остальные (n) граней (боковые) — треугольники с общей вершиной. Пирамиды подразделяются на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон основания.
Тетраэдер – другое название треугольной пирамиды.
Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на основание.

7. Пирамида называется правильной, если ее боковые ребра равны, а в основании лежит правильный многоугольник.
Основание высоты правильной пирамиды совпадает с центром ее основания, углы наклона боковых ребер к основанию равны, двугранные углы при основании равны, все боковые грани — равные равнобедренные треугольники.
Апофема – высота боковой грани правильной пирамиды, проведенная из её вершины к ребру основания.

8. Площадь боковой поверхности пирамиды равна сумме площадей ее боковых граней: (S_{бок}= S_1+ S_2+…+ S_n).
Площадь полной поверхности пирамиды равна сумме площади боковой поверхности и площади основания: (S_{полн} = S_{бок}+ S_{осн}).

9. Объем произвольной пирамиды равен произведению одной трети площади основания на высоту: (V=frac{1}{3} S_{осн}cdot h).

Сфера и шар

10. Сфера — это множество всех точек пространства, равноудаленных от данной точки, называемой центром сферы.
Радиусом сферы называется отрезок, соединяющий центр сферы с точкой на сфере, или длина этого отрезка.
Хордой сферы называется отрезок, соединяющий две точки на сфере.
Диаметр сферы — это хорда, которая проходит через центр сферы. Диаметр сферы равен двум радиусам сферы.

11. Площадь сферы находится по формуле: (S_{сф}=4πR^2).

12. Шаром называется часть пространства, ограниченная сферой, вместе с самой сферой и ее центром. Данная сфера называется поверхностью шара.
Сечение шара с радиусом (R) плоскостью, проходящей через центр шара, называется большим кругом шара. Радиус, хорда, диаметр шара те же, что и его сферы.

13. Объем шара находится по формуле (V_{шара}=frac{4}{3} πR^2).

Цилиндр

14. Цилиндром называется тело, полученное при вращении прямоугольника вокруг прямой, проходящей через одну из его сторон.
Прямая вращения называется осью цилиндра.
Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.Осевое сечение цилиндра — прямоугольник со сторонами (2r) и (l), где (r) — радиус основания цилиндра, (l) — его образующая.
Образующая цилиндра — отрезок (обозначается (l) или (L)), перпендикулярный основаниям цилиндра и соединяющий точку окружности верхнего основания с точкой окружности нижнего основания.
Высотой цилиндра называется расстояние между плоскостями оснований (обозначается (h) или (H)).

15. Площадь боковой поверхности цилиндра: (S_{бок}=2πrh); (S_{полн} = S_{бок}+ 2S_{осн}=2πrh+2πr^2).

16. Объем цилиндра (V_{цил}=S_{осн} h=πr^2 h).

Конус

17. Конусом называется тело, полученное при вращении прямоугольного треугольника вокруг прямой, проходящей через один из его катетов.
Прямая вращения называется осью конуса.
Сечение конуса, проходящее через ось, называется осевым сечением. Осевое сечение конуса — равнобедренный треугольник со стороной основания (2r) боковой стороной (l), где (r) — радиус основания конуса, (l) — его образующая.
Вершина осевого сечения является вершиной конуса.
Образующая конуса (обозначается (l) или (L)) — отрезок, соединяющий вершину конуса и точку окружности основания.
Высотой конуса называется расстояние от вершины конуса до плоскости основания (обозначается (h) или (H)). Высота конуса равна высоте осевого сечения, опущенной на основание.

18. Площадь боковой поверхности конуса: (S_{бок кон}=πrl), (S_{кон}=S_{бок}+S_{осн}=πrl+2πr^2).

19. Объем конуса: (V_{кон}=frac{1}{3}S_{осн}h=frac{1}{3}πr^2 h).

Источник