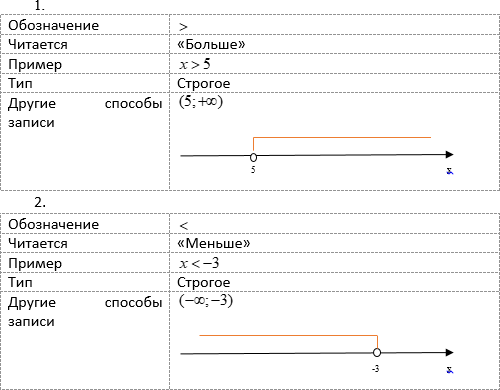
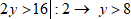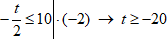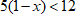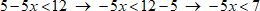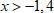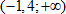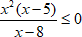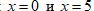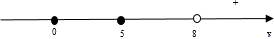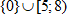Если в выражении с переменными вы увидели знак = , то это уравнение.
Если знак < или ˃ или ≤ или ≥ — то это, конечно, неравенство.
Как правило, неравенства решаются сложнее, чем аналогичные им уравнения. И знать надо больше – чтобы не наделать ошибок
В этом разделе – все основные способы и приемы решения неравенств на ЕГЭ по математике. Повторите их. Даже такие неравенства, как квадратичные или дробно-рациональные, содержат немало ловушек для неопытного школьника. И тем более — показательные и логарифмические. А иррациональные неравенства и неравенства с модулями вообще считаются одними из самых сложных тем школьного курса алгебры.
Здесь рассказано также о методе замены множителя (еще он называется методом рационализации неравенства). В учебнике вы его не найдете. И еще – об основных ошибках и полезных лайфхаках для решения неравенств.
New
Решаем задачи из сборника И. В. Ященко, 2021
Квадратичные неравенства
Метод интервалов
Иррациональные неравенства
Задача 15 Репетиционного ЕГЭ онлайн, май 2020, Анна Малкова
Неравенства с модулем
Показательные неравенства
Логарифмические неравенства
Метод замены множителя (рационализации)
Решение неравенств: основные ошибки и полезные лайфхаки
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 15
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 32, задача 15
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 15
Логарифмические неравенства повышенной сложности
Еще раз повторим основные правила:
— Равносильными называются неравенства, множества решений которых совпадают.
— Если обе части неравенства умножить на отрицательное число, знак неравенства поменяется на противоположный. А если на положительное число – знак неравенства останется тем же.
— Возводить обе части неравенства в квадрат можно только если они неотрицательны.
— Извлекать корень из неравенства нельзя. Нет такого действия!
— Если в неравенстве можно сделать замену переменной – сделайте замену переменной. А потом аккуратно вернитесь к той переменной, которая была вначале.
— Если вы решаете простейшее показательное или логарифмическое неравенство – не забудьте сравнить основание степени (или логарифма) с единицей.
— Если в неравенстве есть дроби, корни четной степени или логарифмы – там обязательно будет область допустимых значений.
— Решение неравенства лучше всего записывать в виде цепочки равносильных переходов.
— Если вы воспользовались методом рационализации (замены множителя) – соответствующие формулы лучше доказать.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Решение неравенств» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.03.2023
Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Неравенства
Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:
> больше,
≥ больше или равно,
< меньше,
≤ меньше или равно,
то получится неравенство.
Линейные неравенства
Линейные неравенства – это неравенства вида:
a x < b a x ≤ b a x > b a x ≥ b
где a и b – любые числа, причем a ≠ 0, x – переменная.
Примеры линейных неравенств:
3 x < 5 x − 2 ≥ 0 7 − 5 x < 1 x ≤ 0
Решить линейное неравенство – получить выражение вида:
x < c x ≤ c x > c x ≥ c
где c – некоторое число.
Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.
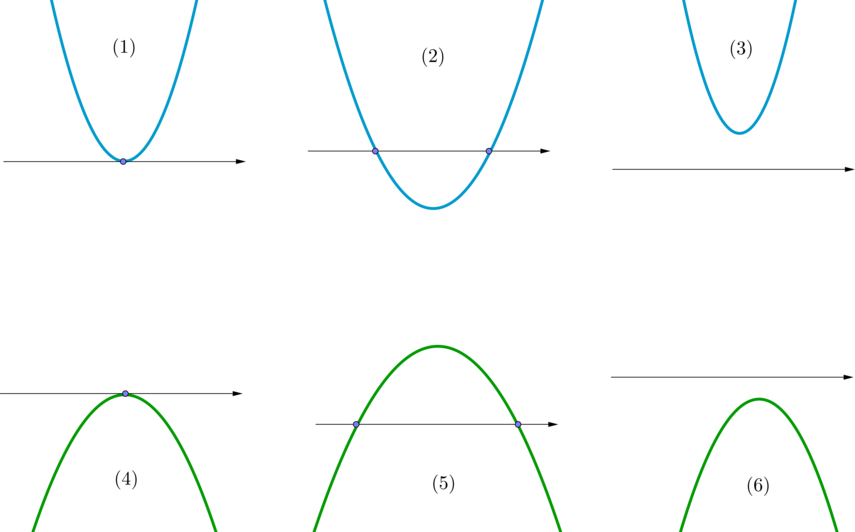
- Если знак неравенства строгий > , < , точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой.
Смысл выколотой точки в том, что сама точка в ответ не входит.
- Если знак неравенства нестрогий ≥ , ≤ , точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной.
Смысл жирной точки в том, что сама точка входит в ответ.
- Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.
Таблица числовых промежутков
| Неравенство | Графическое решение | Форма записи ответа |
|---|---|---|
| x < c |
|
x ∈ ( − ∞ ; c ) |
| x ≤ c |
|
x ∈ ( − ∞ ; c ] |
| x > c |
|
x ∈ ( c ; + ∞ ) |
| x ≥ c |
|
x ∈ [ c ; + ∞ ) |
Алгоритм решения линейного неравенства
- Раскрыть скобки (если они есть), перенести иксы в левую часть, числа в правую и привести подобные слагаемые. Должно получиться неравенство одного из следующих видов:
a x < b a x ≤ b a x > b a x ≥ b
- Пусть получилось неравенство вида a x ≤ b. Для того, чтобы его решить, необходимо поделить левую и правую часть неравенства на коэффициент a.
- Если a > 0 то неравенство приобретает вид x ≤ b a .
- Если a < 0 , то знак неравенства меняется на противоположный, неравенство приобретает вид x ≥ b a .
- Записываем ответ в соответствии с правилами, указанными в таблице числовых промежутков.
Примеры решения линейных неравенств:
№1. Решить неравенство 3 ( 2 − x ) > 18.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 − 3 x > 18
− 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 )
Делим обе части неравенства на (-3) – коэффициент, который стоит перед x. Так как − 3 < 0 , знак неравенства поменяется на противоположный. x < 12 − 3 ⇒ x < − 4 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x ∈ ( − ∞ ; − 4 )
№2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 x + 4 ≥ 3 x + 3 − 14
6 x − 3 x ≥ 3 − 14 − 4
3 x ≥ − 15 | ÷ 3 Делим обе части неравенства на (3) – коэффициент, который стоит перед x. Так как 3 > 0, знак неравенства после деления меняться не будет.
x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x ∈ [ − 5 ; + ∞ )
Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).
Примеры:
№1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 x − 1 ≤ 6 x − 1
6 x − 6 x ≤ − 1 + 1
0 ≤ 0
Получили верное неравенство, которое не зависит от переменной x. Возникает вопрос, какие значения может принимать переменная x, чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа.
Ответ:
- x – любое число
- x ∈ ( − ∞ ; + ∞ )
- x ∈ ℝ
№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
x + 6 − 9 x > − 8 x + 48
− 8 x + 8 x > 48 − 6
0 > 42
Получили неверное равенство, которое не зависит от переменной x. Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ.
Ответ: x ∈ ∅
Квадратные неравенства
Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c < 0 a x 2 + b x + c ≤ 0 где a, b, c — некоторые числа, причем a ≠ 0, x — переменная.
Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.
Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).
Алгоритм решения квадратного неравенства методом интервалов
- Решить уравнение a x 2 + b x + c = 0 и найти корни x 1 и x 2 .
- Отметить на числовой прямой корни трехчлена.
Если знак неравенства строгий > , < , точки будут выколотые.
Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный).
- Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A) и подставить её значение в выражение a x 2 + b x + c вместо x.
Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
- Выбрать подходящие интервалы (или интервал).
Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.
Если знак неравенства < или ≤ в ответ выбираем интервалы со знаком -.
- Записать ответ.
Примеры решения квадратных неравенств:
№1. Решить неравенство x 2 ≥ x + 12.
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
x 2 ≥ x + 12
x 2 − x − 12 ≥ 0
x 2 − x − 12 = 0
a = 1, b = − 1, c = − 12
D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6. Подставляем эту точку в исходное выражение:
x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0
Это значит, что знак на интервале, в котором лежит точка 6 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪ .
Точки -3 и 4 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ )
№2. Решить неравенство − 3 x − 2 ≥ x 2 .
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
− 3 x − 2 ≥ x 2
− x 2 − 3 x − 2 ≥ 0
− x 2 − 3 x − 2 = 0
a = − 1, b = − 3, c = − 2
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1
x 1 = − 2, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение:
− x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 < 0
Это значит, что знак на интервале, в котором лежит точка 0 будет − .
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥ , выбираем в ответ интервал со знаком +.
Точки -2 и -1 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ [ − 2 ; − 1 ]
№3. Решить неравенство 4 < x 2 + 3 x .
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
4 < x 2 + 3 x
− x 2 − 3 x + 4 < 0
− x 2 − 3 x + 4 = 0
a = − 1, b = − 3, c = 4
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1
x 1 = − 4, x 2 = 1
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение:
− x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 < 0
Это значит, что знак на интервале, в котором лежит точка 2, будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервалы со знаком − .
Точки -4 и 1 будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ )
№4. Решить неравенство x 2 − 5 x < 6.
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
x 2 − 5 x < 6
x 2 − 5 x − 6 < 0
x 2 − 5 x − 6 = 0
a = 1, b = − 5, c = − 6
D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1
x 1 = 6, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение:
x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0
Это значит, что знак на интервале, в котором лежит точка 10 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервал со знаком -.
Точки -1 и 6 будут в круглых скобках, так как они выколотые
Ответ: x ∈ ( − 1 ; 6 )
№5. Решить неравенство x 2 < 4.
Решение:
Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.
x 2 < 4
x 2 − 4 < 0
x 2 − 4 = 0
( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2
x 1 = 2, x 2 = − 2
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3. Подставляем эту точку в исходное выражение:
x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0
Это значит, что знак на интервале, в котором лежит точка 3 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервал со знаком − .
Точки -2 и 2 будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − 2 ; 2 )
№6. Решить неравенство x 2 + x ≥ 0.
Решение:
Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0.
x 2 + x ≥ 0
x 2 + x = 0
x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1
x 1 = 0, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1. Подставляем эту точку в исходное выражение:
x 2 + x = 1 2 + 1 = 2 > 0
Это значит, что знак на интервале, в котором лежит точка 1 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥ , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ )
Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.
Дробно рациональные неравенства
Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:
f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).
Примеры дробно рациональных неравенств:
x − 1 x + 3 < 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3
Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.
Алгоритм решения дробно рациональных неравенств:
- Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве):
f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
- Приравнять числитель дроби к нулю f ( x ) = 0. Найти нули числителя.
- Приравнять знаменатель дроби к нулю g ( x ) = 0. Найти нули знаменателя.
В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.
- Нанести нули числителя и нули знаменателя на ось x.
Вне зависимости от знака неравенства
при нанесении на ось x нули знаменателя всегда выколотые.
Если знак неравенства строгий,
при нанесении на ось x нули числителя выколотые.
Если знак неравенства нестрогий,
при нанесении на ось x нули числителя жирные.
- Расставить знаки на интервалах.
- Выбрать подходящие интервалы и записать ответ.
Примеры решения дробно рациональных неравенств:
№1. Решить неравенство x − 1 x + 3 > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравниваем числитель к нулю f ( x ) = 0.
x − 1 = 0
x = 1 — это ноль числителя. Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.
- Приравниваем знаменатель к нулю g ( x ) = 0.
x + 3 = 0
x = − 3 — это ноль знаменателя. При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x − 1 x + 3 = 2 − 1 2 + 3 = 1 5 > 0,
Это значит, что знак на интервале, в котором лежит точка 2 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые.
Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )
№2. Решить неравенство 3 ( x + 8 ) ≤ 5.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Привести неравенство к виду f ( x ) g ( x ) ≤ 0.
3 ( x + 8 ) ≤ 5
3 ( x + 8 ) − 5 x + 8 ≤ 0
3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 x − 40 x + 8 ≤ 0
− 5 x − 37 x + 8 ≤ 0
- Приравнять числитель к нулю f ( x ) = 0.
− 5 x − 37 = 0
− 5 x = 37
x = − 37 5 = − 37 5 = − 7,4
x = − 7,4 — ноль числителя. Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.
- Приравнять знаменатель к нулю g ( x ) = 0.
x + 8 = 0
x = − 8 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
− 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 < 0
Это значит, что знак на интервале, в котором лежит точка 0 будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства ≤ , выбираем в ответ интервалы со знаком -.
В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная.
Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ )
№3. Решить неравенство x 2 − 1 x > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравнять числитель к нулю f ( x ) = 0.
x 2 − 1 = 0
( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1
x 1 = 1, x 2 = − 1 — нули числителя. Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.
- Приравнять знаменатель к нулю g ( x ) = 0.
x = 0 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ )
Системы неравенств
Сперва давайте разберёмся, чем отличается знак { системы от знака [ совокупности. Система неравенств ищет пересечение решений, то есть те точки, которые являются решением и для первого неравенства системы, и для второго. Проще говоря, решить систему неравенств — это найти пересечение решений всех неравенств этой системы друг с другом. Совокупность неравенств ищет объединение решений, то есть те точки, которые являются решением либо для первого неравенства, либо для второго, либо одновременно и для первого неравенства, и для второго. Решить совокупность неравенств означает объединить решения обоих неравенств этой совокупности. Более подробно об этом смотрите короткий видео-урок.
Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.
Пример системы неравенств:
{ x + 4 > 0 2 x + 3 ≤ x 2
Алгоритм решения системы неравенств
- Решить первое неравенство системы, изобразить его графически на оси x.
- Решить второе неравенство системы, изобразить его графически на оси x.
- Нанести решения первого и второго неравенств на ось x.
- Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.
Примеры решений систем неравенств:
№1. Решить систему неравенств { 2 x − 3 ≤ 5 7 − 3 x ≤ 1
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2 x − 3 ≤ 5
2 x ≤ 8 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x ≤ 4 ;
Графическая интерпретация:
Точка 4 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
7 − 3 x ≤ 1
− 3 x ≤ 1 − 7
− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 < 0, знак неравенства после деления меняется на противоположный.
x ≥ 2
Графическая интерпретация решения:
Точка 2 на графике жирная, так как знак неравенства нестрогий.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на отрезке от 2 до 4. Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные.
Ответ: x ∈ [ 2 ; 4 ]
№2. Решить систему неравенств { 2 x − 1 ≤ 5 1 < − 3 x − 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2 x − 1 ≤ 5
2 x ≤ 6 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x ≤ 3
Графическая интерпретация:
Точка 3 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
1 < − 3 x − 2
3 x < − 1 − 2
3 x < − 3 | ÷ 3 , поскольку 3 > 0, знак неравенства после деления сохраняется.
x < − 1
Графическая интерпретация решения:
Точка -1 на графике выколотая, так как знак неравенства строгий.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая.
Ответ: x ∈ ( − ∞ ; − 1 )
№3. Решить систему неравенств { 3 x + 1 ≤ 2 x x − 7 > 5 − x
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
3 x + 1 ≤ 2 x
3 x − 2 x ≤ − 1
x ≤ − 1
Графическая интерпретация решения:
- Решаем второе неравенство системы
x − 7 > 5 − x
x + x > 5 + 7
2 x > 12 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x > 6
Графическая интерпретация решения:
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.
Ответ: x ∈ ∅
№4. Решить систему неравенств { x + 4 > 0 2 x + 3 ≤ x 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
x + 4 > 0
x > − 4
Графическая интерпретация решения первого неравенства:
- Решаем второе неравенство системы
2 x + 3 ≤ x 2
− x 2 + 2 x + 3 ≤ 0
Решаем методом интервалов.
− x 2 + 2 x + 3 = 0
a = − 1, b = 2, c = 3
D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16
D > 0 — два различных действительных корня.
x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1
Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.
Графическая интерпретация решения второго неравенства:
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪ .
Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные.
Ответ: x ∈ ( − 4 ; − 1 ] ∪ [ 3 ; + ∞ )
Скачать домашнее задание к уроку 8.
Решите неравенство
!!! Смотрите также подборку задач С3 (с ответами) для подготовки к ЕГЭ !!!
Список всех неравенств (С3), разобранных на сайте:
-11. (Реальный ЕГЭ, 2021) Решите неравенство:
Ответ: Решение
-10. (Реальный ЕГЭ, 2021) Решите неравенство:
Ответ: Решение
-9. (Демо ЕГЭ, 2020) Решите неравенство
Ответ: Видеорешение New*
-8. (Реальный ЕГЭ, 2019) Решите неравенство
Ответ: Решение Видеорешение New*
-7. (Реальный ЕГЭ, 2019) Решите неравенство
Ответ: Решение
-6. (Реальный ЕГЭ, 2018) Решите неравенство
Ответ: Решение Видеорешение New*
-5. (Досрочный резервный ЕГЭ, 2018) Решите неравенство
Ответ: Решение Видеорешение New*
-4. (Досрочный ЕГЭ, 2018) Решите неравенство
Ответ: Решение Видеорешение New*
-3. (Резервный ЕГЭ, 2017) Решите неравенство
Ответ: Решение
-2. (Резервный ЕГЭ, 2017) Решить неравенство
Ответ: {
}
Решение Видеорешение New*
-1. (Реальный ЕГЭ, 2017) Решить неравенство
Ответ: {
}
Решение
0. (Реальный ЕГЭ, 2017) Решить неравенство
Ответ: {
}
Решение
1. (Досрочн. ЕГЭ, 2017) Решите неравенство
Ответ: Решение Видеорешение New*
2. (Резервн. ЕГЭ, 2016) Решите неравенство
Ответ: Решение Видеорешение New*
3. (ЕГЭ, 2016) Решите неравенство
Ответ: Решение
4. (Т/Р, 2016) Решите неравенство
Ответ: Решение
5. (Досрочн. ЕГЭ, 2016) Решите неравенство
Ответ: . Решение Видеорешение New*
6. (ЕГЭ, 2015) Решите неравенство
Ответ: {
}
Решение
7. (Т/Р 2013) Решите систему неравенств
Ответ: Решение
8. (Т/Р 2013) Решите систему неравенств
Ответ: Решение
9. (Т/Р 2013) Решите систему неравенств
Ответ: {
}. Решение
10. (ДЕМО 2014) Решите систему неравенств
Ответ: Решение
11. (ЕГЭ 2013) Решите систему неравенств
Ответ: {}
Решение
12. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
13. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
14. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
15. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение Видеорешение
16. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
17. (Т/Р А. Ларина) Решите неравенство
Ответ: {
}
Решение
18. (Т/Р А. Ларина) Решите неравенство
Ответ: {
}. Решение
19. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
20. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
21. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
22. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
23. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
24. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
25. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
26. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
27. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
28. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
29. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
30. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
31. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
33. (Т/Р А. Ларина) Решите неравенство
.
Ответ: {}
Решение
34. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
35. (Т/Р А. Ларина) Решите неравенство
.
Ответ: {
}
Решение
36. (Т/Р А. Ларина) Решите неравенство
Ответ: {
}. Решение
37. (Т/Р А. Ларина) Решите неравенство
Ответ: {}
Решение
38. (Т/Р А. Ларина) Решите неравенство
Ответ: {
}
Решение
39. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
40. (Т/Р А. Ларина) Решите неравенство
.
Ответ: Решение
41. (Т/Р А. Ларина) Решите неравенство
Ответ: {
}. Решение
42. (Т/Р А. Ларина) Решите неравенство
Ответ: {
}. Решение
43. (Т/Р А. Ларина) Решите неравенство
Ответ: {
}
Решение
44. (Т/Р А. Ларина) Решите неравенство
Ответ: {
}
. Решение
45. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
46. (Т/Р А. Ларина) Решите неравенство
Ответ: {
}
Решение
47. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
48. (Т/Р А. Ларина) Решите неравенство
.
Ответ: Решение
49. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
50. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
51. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
52. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
53. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
54. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
55. (Т/Р А. Ларина) Решите неравенство
.
Ответ: Решение
56. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
57. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
58. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
59. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
60. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
61. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
62. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
63. (Т/Р А. Ларина) Решите неравенство
Ответ: {
}. Решение
64. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
65. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
66. (Т/Р А. Ларина) Решите неравенство
Ответ: (]. Решение
67. (Т/Р А. Ларина) Решите неравенство
Ответ: [)
(
]. Решение
68. (Т/Р А. Ларина) Решите неравенство
Ответ: [). Решение
69. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
70. (Т/Р А. Ларина) Решите систему неравенств
Ответ: Решение
71. (Т/Р А. Ларина) Решите систему неравенств
Ответ:
72. (Т/Р А. Ларина) Решите систему неравенств
Ответ: Решение
73. (Т/Р А. Ларина) Решите неравенство
Ответ: {
}
Решение
74. (Т/Р А. Ларина) Решите неравенство
Ответ: {
},
Решение
75. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
76. (Т/Р А. Ларина) Решите неравенство
Ответ: {}
Решение
77. (Т/Р А. Ларина) Решите неравенство
Ответ: {
}
Решение
78. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
79. (Т/Р А. Ларина) Найдите область определения функции
Ответ: {}
Решение
80. (Т/Р А. Ларина) Решите неравенство
Ответ: {
}. Решение
81. (Т/Р А. Ларина) Решите неравенство
Ответ: {
}
Решение
82. (Т/Р А. Ларина) Решите неравенство
Ответ: {
}
Решение
83. (Т/Р А. Ларина) Решите неравенство
Ответ: {
}
Решение
84. (Т/Р А. Ларина) Решите неравенство
Ответ: {}. Решение
85. (Т/Р, 2017) Решите неравенство
Ответ: Решение
86. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
87. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
88. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
89. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
90. (Т/Р А. Ларина) Решите неравенство
Ответ: {}
Решение
91. (Т/Р А. Ларина) Решите неравенство
Ответ: {}
Решение
92. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
93. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
94. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
95. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
96. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
97. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
98. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
99. (Т/Р А. Ларина) Решите неравенство
Ответ: {
}. Решение
100. (Т/Р А. Ларина) Решите неравенство
Ответ: {}
Решение
101. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
102. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
103. (Т/Р А. Ларина) Решите неравенство
Ответ: Решение
104. (Т/Р 283 А. Ларина) Решите неравенство
Ответ: Видеорешение
Рациональное неравенство — это неравенство, которое можно свести к виду [Large{dfrac{P(x)}{Q(x)}lor 0}]где (P(x),
Q(x)) — многочлены.
((lor) — один из знаков (geqslant,
leqslant, >, <))
Например, следующие неравенства являются рациональными: [dfrac1{x+1}>0,qquad x+2+dfrac{x-1}{x+3}<1,qquad x^2+x-2leqslant 0]
[{Large{text{Линейные неравенства}}}] Линейные неравенства – это неравенства вида [ax+b lor 0, qquad
lor — text{ один из знаков } geqslant, leqslant, >,
<;quad a,b — text{ числа,}]или сводящиеся к такому виду.
Область допустимых значений (x) (ОДЗ) таких неравенств — все вещественные числа ((xin mathbb{R})).
Общее правило решения линейных неравенств:
1) Для того, чтобы решить данное неравенство, необходимо привести его к виду (axlor -b), то есть перенести число (b) в правую часть.
2) Если коэффициент (a) перед (x) – положительный, то неравенство равносильно (xlor -dfrac ba), то есть после деления обеих частей неравенства на (a) знак неравенства не меняется.
3) Если коэффициент (a) перед (x) – отрицательный, то неравенство равносильно (xland -dfrac ba), то есть после деления обеих частей неравенства на (a) знак неравенства меняется на противоположный.
4) Если (a=0), то неравенство равносильно (0lor -b), что либо верно при всех значениях переменной (x) (например, если это (0>-1)), либо неверно ни при каких значениях (x) (например, если это (0leqslant -3)).
То есть ответом будут либо (xinmathbb{R}), либо (xin
varnothing).
Замечание
Заметим, что знаку (leqslant) противоположен знак (geqslant), а знаку (<) – знак (>). И наоборот.
Пример 1
Решить неравенство (5-3x>-1).
Решение. I способ
Сделаем цепочку преобразований:
[5-3x>-1 Rightarrow -3x>-1-5 Rightarrow -3x>-6
Rightarrow x<dfrac 63 Rightarrow x<2] Таким образом, ответом будет (xin(-infty;2)).
Заметим, что т.к. мы делили неравенство на (-3), то знак неравенства поменялся.
Решение. II способ
Можно перенести слагаемое (-3x) в правую часть, а (-1) – в левую:
[5-3x>-1 Rightarrow 5+1>3x Rightarrow 3x<6 Rightarrow x<2]
Пример 2
Решить неравенство ((1-sqrt2)x+2leqslant 0).
Решение
Заметим, что перед (x) находится отрицательный коэффициент. Поэтому:
[(1-sqrt2)xleqslant -2 Rightarrow xgeqslant -dfrac 2{1-sqrt2}] Преобразуем число (-dfrac 2{1-sqrt2}): домножим числитель и знаменатель дроби на сопряженное к (1-sqrt2), то есть на (1+sqrt2), чтобы избавиться от иррациональности в знаменателе:
[-dfrac 2{1-sqrt2}=-dfrac{2(1+sqrt2)}{(1-sqrt2)(1+sqrt2)}=
-dfrac{2(1+sqrt2)}{1-2}=2(1+sqrt2)]
Таким образом, ответ (xin [2+2sqrt2;+infty)).
Перейдем к квадратичным неравенствам, которые являются очень важным инструментом в решении задач.
[{Large{text{Метод интервалов}}}]
Приступим к рассмотрению общего метода для решения любого рационального неравенства, то есть неравенства вида
[(**)qquad dfrac{P(x)}{Q(x)}geqslant 0 qquad (text{на месте }geqslant
text{может стоять любой из} leqslant, <, >)]
Область допустимых значений (x) (ОДЗ) таких неравенств — все вещественные числа, кроме нулей знаменателя.
Существует два способа решения таких неравенств:
1 способ: Классический. Т.к. дробь положительна (отрицательна) тогда и только тогда, когда числитель и знаменатель дроби одного знака (разных знаков), то неравенство ((*)) равносильно совокупности: [{large{left[begin{gathered}
begin{aligned}
&begin{cases} P(x)geqslant 0\ Q(x)>0 end{cases}\
&begin{cases} P(x)leqslant 0\ Q(x)<0 end{cases}
end{aligned}
end{gathered}
right.}}]
Такой способ подойдет для решения любого неравенства, где слева стоит дробь, а справа — (0).
Но, как правило, для решения большинства рациональных неравенств он неудобен. Почему? Вы сможете убедиться в этом после того, как мы рассмотрим метод интервалов.
2 способ: Удобный. Метод интервалов (будем рассматривать этот метод на примере конкретного неравенства, чтобы было понятней).
Заметим, что первые три шага созданы для того, чтобы преобразовать неравенство к более простому виду, что поможет вам не допустить ошибку в решении подобных задач. Метод интервалов – это всего лишь удобный инструмент для решения рациональных неравенств, и если вы будете всегда пользоваться одним и тем же алгоритмом, то вероятность допустить ошибку при решении таких неравенств будет минимальной.
Данный алгоритм специально расписан подробно, чтобы у вас не возникло вопросов; всего после нескольких использований этого алгоритма вы будете решать рациональные неравенства очень быстро и без ошибок!
1 ШАГ. Необходимо перенести все слагаемые в одну часть (пусть это будет левая часть) неравенства так, чтобы в другой части неравенства остался (0), и привести эти слагаемые к общему знаменателю так, чтобы в левой части неравенства получилась дробь. Затем нужно разложить числитель и знаменатель полученной дроби, то есть многочлены (P(x), Q(x)), на множители.
Например, неравенство (dfrac1{x+1}<1) нужно переписать в виде (dfrac1{x+1}-1<0), затем привести к общему
знаменателю (dfrac1{x+1}-dfrac{x+1}{x+1}<0), затем записать в виде одной дроби левую часть: (dfrac{1-(x+1)}{x+1}<0) и
привести подобные слагаемые: (dfrac{-x}{x+1}<0).
Итак, пусть после разложения на множители неравенство приняло вид [dfrac{x^2(x-1)^3(x+1)(2x^2+3x+5)(2x-x^2-3)}{(x+1)^3(3-x)(2-3x)^2}
geqslant0]
Заметим, что любой многочлен можно (а в нашем способе НУЖНО) разложить до произведения только линейных скобок ((ax+b)) и квадратичных скобок с отрицательным дискриминантом ((ax^2+bx+c), D<0).
2 ШАГ. Рассмотрим скобки, в которых остался квадратичный трехчлен с (D<0).
(bullet) Если при (x^2) находится положительный коэффициент (a>0), то при всех значениях (x) выражение (ax^2+bx+c) положительно (не может быть равно нулю!). Т.к. мы имеем право делить неравенство на любое число/выражение, не равное (0), то разделим обе части неравенства на такие скобки (в нашем неравенстве такой скобкой является ((2x^2+3x+5))). Причем заметим, что т.к. мы делим на положительное выражение, то знак неравенства не меняется!
(bullet) Если при (x^2) находится отрицательный коэффициент (a<0), то при всех значениях (x) выражение (ax^2+bx+c) отрицательно. Т.к. мы имеем право делить неравенство на любое число/выражение, не равное (0), то разделим обе части неравенства на такие скобки (в нашем неравенстве такой скобкой является ((2x-x^2-3))). Причем заметим, что т.к. мы делим на отрицательное выражение, то знак неравенства должен измениться на противоположный!
Итак, обобщим 2 шаг: квадратичные скобки с отрицательным дискриминантом можно просто вычеркнуть, причем при вычеркивании скобок с (a>0) знак неравенства остается прежним, а вот при вычеркивании скобок с (a<0) знак неравенства меняется на противоположный столько раз, сколько было таких скобок. Лучше вычеркивать их последовательно по одной, каждый раз меняя знак неравенства на противоположный.
Таким образом, неравенство примет вид [dfrac{x^2(x-1)^3(x+1)}{(x+1)^3(3-x)(2-3x)^2}
leqslant 0]
3 ШАГ. Рассмотрим линейные скобки ((ax+b)).
Назовем скобку хорошей, если при (x) находится положительный коэффициент (такие скобки мы трогать не будем), и плохой, если при (x) находится отрицательный коэффициент (в таких скобках необходимо поменять все знаки на противоположные, то есть сделать их хорошими).
Для того, чтобы в одной плохой скобке поменять все знаки на противоположные, необходимо домножить правую и левую части неравенства на (-1). Таким образом, после одного такого действия знак неравенства сменится на противоположный. Значит, если плохих скобок четное количество, то знак неравенства не изменится, если нечетное – то знак неравенства изменится на противоположный.
Заметим, что выражение ((ax+b)^n) — это не что иное, как произведение (n) скобок ((ax+b)).
В нашем неравенстве среди плохих одна скобка ((3-x)) и две скобки ((2-3x)) (т.к. ((2-3x)^2=(2-3x)(2-3x))), то есть всего три плохих скобки, следовательно, знак неравенства изменится и неравенство примет вид: [dfrac{x^2(x-1)^3(x+1)}{(x+1)^3(x-3)(3x-2)^2}
geqslant0quad (***)]
Заметим, что множитель (x^2) — это скобка ((x-0)^2), или, что то же самое, ((x-0)(x-0)) – произведение двух одинаковых линейных скобок.
4 ШАГ. Теперь, когда левая часть неравенства состоит из произведения только хороших линейных скобок (в каких-то степенях), можно приступить к самому методу интервалов.
Его суть состоит в том, что левая часть неравенства — всюду непрерывная функция, кроме тех точек, где знаменатель дроби равен нулю. Поэтому точки, в которых эта функция равна нулю (то есть ее числитель равен нулю) и точки, в которых эта функция не существует (то есть ее знаменатель равен нулю), разбивают область определения этой функции на промежутки, причем на каждом промежутке функция принимает значения строго одного знака.
А нам как раз нужно найти те значения (x), при которых функция (geqslant 0). Причем, т.к. наша функция — рациональная, то ее область определения — это все действительные числа ((mathbb{R})), кроме нулей знаменателя. Поэтому отметим нули каждой скобки на вещественной прямой (а ноль каждой скобки – это как раз ноль числителя или знаменателя), причем нули знаменателя – выколотые, нули числителя – закрашенные (если знак неравенства нестрогий, как в примере, то есть (geqslant ) или (leqslant )) или выколотые (если знак неравенства строгий, то есть (>) или (<)).
Заметим, что если мы отметили (n) точек, то числовая прямая разобьется на (n+1) промежутков.
Расставим знак на каждом промежутке (color{red}{{Large{text{справа налево}}}}). Будем ставить “(+)”, если функция на этом промежутке принимает положительные значения, и “(-)” — если отрицательные. Нулю функция равна в закрашенных точках.
Первые три шага мы делали для того, чтобы не подставлять точки из каждого промежутка и не вычислять, какого знака будет левая часть неравенства (что бывает неудобно, если числа, которые нужно отмечать на прямой, “некрасивые”). Знаки мы будем расставлять, выявив некоторую закономерность. Какую – вы узнаете дальше.
Но в любом случае способ расстановки знаков путем подстановки чисел остается в нашем арсенале.
Т.к. все скобки – хорошие, то первый знак всегда будет “(+,)” (именно для этого мы и приводили неравенство к такому виду!). Действительно, если подставить любое число, превышающее самый большой корень (у нас самый большой корень (x=3)), то каждая скобка будет положительна, значит, и произведение таких скобок будет всегда положительно.
Если какой-то корень входит в четное количество скобок, то при переходе через него (справа налево!) знак меняться не будет. В нашем неравенстве это точки (-1, 0, dfrac23) (например, точка (-1) входит в четное количество скобок: одна в числителе ((x+1)) и три в знаменателе ((x+1)^3)).
Если точка входит в нечетное количество скобок, то при переходе через эту точку (справа налево!) знак будет меняться (в нашем неравенстве это точки (3) и (1)).
Объясним, почему так происходит. Каждая линейная скобка в нечетной степени ((x-a)^{2n+1}) имеет ровно один корень (x=a), причем, т.к. мы сделали ее хорошей, то для всех (x>a) она будет положительной, для всех (x<a) она будет отрицательной (а для (x=a), естественно, равной нулю). Значит, когда (xin (1;3)), то все скобки, кроме ((x-3)), будут оставаться положительными, и лишь эта скобка ((x-3)) станет отрицательной. Значит, их произведение также станет отрицательным. Аналогично при переходе через точку (x=1).
Каждая линейная скобка в четной степени ((x-b)^{2n}) также имеет ровно один корень (x=b), но т.к. она в четной степени, то при всех (xne b) она всегда будет положительной! И только при (x=b) она будет равна нулю. Именно поэтому при переходе через точку (x=dfrac23), т.е. на (xin(0;frac23)), скобка ((3x-2)^2) не сменит свой знак на отрицательный, поэтому вся левая часть останется по знаку такой же, как и была на ((frac23;1)) (т.е. положительной). Аналогично при переходе через точки (0, -1).
5 ШАГ. Неравенство практически решено и нам остается только записать ответ. В нашем случае, т.к. знак преобразованного ((***)) неравенства (geqslant 0) (нестрогий), то в ответ пойдут промежутки со знаком “(+,)” (где значение функции больше нуля) и закрашенные точки (где значение функции равно нулю): [xin Big(-infty;-1Big)cup left(-1;dfrac23right)cup
left(dfrac23;1right]cupBig(3;+inftyBig)]Напоминаем, что если точка не входит в ответ, то она пишется в круглой скобке “(()” или “())”, если входит в ответ – то в квадратной скобке “([)” или “(])”. Бесконечности всегда пишутся в круглых скобках.
[{Large{text{Квадратичные неравенства}}}]
Квадратичным неравенством называется любое неравенство вида [ax^2+bx+c lor 0, quad ane 0,]
или сводящееся к такому виду.
Область допустимых значений (x) (ОДЗ) таких неравенств — все вещественные числа ((xin mathbb{R})).
Квадратичные неравенства – это те же самые рациональные неравенства, следовательно, их также можно решать с помощью метода интервалов. Но давайте рассмотрим еще один способ, при помощи которого, как правило, удобнее решать квадратичные неравенства. Для этого нам понадобится вспомнить про параболу.
Замечание
Вспомним, как преобразуется квадратичный трехчлен (ax^2+bx+c) в зависимости от того, сколько корней он имеет.
Если квадратное уравнение (ax^2+bx+c=0)
(bullet) имеет два корня (x_1) и (x_2) (дискриминант (D>0)), то (ax^2+bx+c=a(x-x_1)(x-x_2)).
(bullet) имеет один корень (x_1) ((D=0)), то (ax^2+bx+c=a(x-x_1)^2).
(bullet) не имеет корней ((D<0)), то квадратный трехчлен (ax^2+bc+c) никогда не может быть равен нулю и не разлагается на линейные множители.
Шаг 1. Рассмотрим функцию (f(x)=ax^2+bx+c). Графиком такой функции является парабола.
Для того, чтобы решить квадратичное неравенство, изобразим схематично параболу: то есть определим, куда направлены ее ветви и в каких точках она пересекает ось (Ox).
Если (a>0), то ветви направлены вверх, если (a<0), то ветви направлены вниз. Корни уравнения (ax^2+bx+c=0 (*)) и есть абсциссы точек, в которых парабола пересекает ось (Ox).
Шаг 2. Таким образом, наша парабола будет одного из 6 видов:
((1)) и ((4)) — когда уравнение ((*)) имеет один корень;
((2)) и ((5)) — когда уравнение ((*)) имеет два корня;
((3)) и ((6)) — когда уравнение ((*)) не имеет корней.
Часть параболы, находящая выше оси (Ox), отвечает за (f(x)>0);
часть параболы, находящаяся ниже оси (Ox), отвечает за (f(x)<0);
точки, в которых парабола пересекает ось (Ox), отвечают за (f(x)=0).
Пример 1.
Решить неравенство (x^2+3x+2geqslant 0).
Решение
Решим уравнение (x^2+3x+2=0 Leftrightarrow x_1=-2, x_2=-1). Таким образом, неравенство можно переписать в виде: ((x+1)(x+2)geqslant
0). Ветви параболы направлены вверх, следовательно, схематично она выглядит как ((2)). Т.к. знак неравенства (geqslant), то решением неравенства будут те значения (x), для которых график находится выше оси (Ox), а именно (xin (-infty;-2]cup[-1;+infty)).
Заметим, что точки (-2, -1) входят в ответ, потому что знак “больше или равно”.
Пример 2.
Решить неравенство (11x-3x^2-6>0)
Решение
Решим уравнение (11x-3x^2-6=0 quadLeftrightarrowquad
x_1=dfrac23, x_2=3). Таким образом, неравенство можно переписать в виде: (-3(x-3)(x-frac23)>0).
1 способ. Ветви параболы направлены вниз, следовательно, схематично она выглядит как ((5)). Т.к. знак неравенства (>), то решением неравенства будут (xin left(dfrac23;3right)).
2 способ. Домножим правую и левую части неравенства на (-1), получим (3(x-3)(x-frac23)<0) (заметим, что знак сменился на противоположный). У новой параболы (Big(f(x)=3(x-3)(x-frac23)Big)) ветви направлены вверх, следовательно, схематично она выглядит как ((2)). Но знак неравенства уже (<). Решением нового неравенства, естественно, будут те же (xin left(dfrac23;3right)).
Таким образом, если в квадратичном неравенстве отрицательный знак при (x^2), то можно сначала домножить неравенство на (-1) (и не забыть поменять знак неравенства), чтобы ветви параболы всегда были направлены вверх.
Пример 3.
Решить неравенство (x^2+4x+4 geqslant 0).
Решение
Вспомнив формулу сокращенного умножения, получаем ((x+2)^2geqslant
0) (это быстрее, чем находить корни через дискриминант :)). Таким образом, парабола пересекает ось (Ox) в единственной точке (x_1=-2) и выглядит как ((1)). А т.к. нам нужны те (x), для которых график находится не ниже оси (Ox), то решением неравенства будут (xin
mathbb{R}), то есть выражение ((x+2)^2) всегда больше или равно (0).
Неравенства используются для сравнения чисел и выражений. Можно сравнивать числа и делать вывод об их расположении на числовой прямой. Неравенство 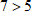
Так же можно сравнивать самые разные выражения, например, 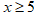
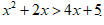
Неравенства можно обозначать четырьмя способами:
Если неравенство строгое, то граничная точка в решение не входит (поэтому ее «выкалывают» на координатной оси). У нестрого неравенства граничная точка в решение входит.
Правила преобразований неравенств
1. Любое слагаемое в неравенстве можно перенести из одной части уравнения в другую, изменив его знак на противоположный:
2. Можно умножать и делить левую и правую части уравнения на одно и то же положительное число:
3. Можно умножать и делить левую и правую части уравнения на одно и то же отрицательное число, заменяя при этом знак неравенства на противоположный:
4. Как и в уравнениях можно раскрывать скобки и упрощать выражения в обеих частях или, наоборот, раскладывать на множители.
Решение линейных неравенств
Рассмотрим пример:
1. С помощью разрешенных преобразований преобразуем неравенства так, чтобы с одной стороны было только выражение, содержащее переменную, а с другой только число:
2. Делим на коэффициент перед переменной, при необходимости меняя знак на противоположный:
Ответ:
Решение рациональных неравенств других степеней
Для решения таких неравенств применяется метод интервалов. Рассмотрим его алгоритм.
1. Переносим все слагаемые влево.
2. Раскладываем левую часть на множители.
3. Отмечаем на координатной оси нули числителя и знаменателя. Нули знаменателя всегда «выколотые» точки.
4. Определяем знак неравенства в крайнем правом промежутке (можно подставить пробную точку из каждого промежутка в преобразованное неравенство).
5. Определяем знаки в остальных промежутках, двигаясь влево. Если корень имеет нечетную кратность (то есть встречается нечетное число раз), то при переходе через него знак неравенства меняется. В случае четной кратности (корень встречается четное число раз), знак неравенства остается тем же.
6. Выбираем нужные промежутки и записываем ответ.
На практике решение выглядит следующим образом:
3. Так как пункты 1 и 2 алгоритма уже выполнены, сразу переходим к пункту 3.
Нули числителя:
Нули знаменателя: 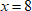
4. Отмечаем полученные точки на координатной прямой.
5. В крайнем правом промежутке можно рассмотреть точку 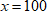
6. Определяем знаки в оставшихся промежутках. Так как корни 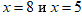
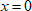
7. Так как необходимо определить, когда выражение меньше или равно нуля, то решением является множество 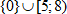
Ответ:
Посмотрите на еще одну таблицу. В ней представлены степени (frac{1}{3}):
$$left(frac{1}{3}right)^0=1;$$
$$left(frac{1}{3}right)^1=frac{1}{3};$$
$$left(frac{1}{3}right)^2=frac{1}{9};$$
$$left(frac{1}{3}right)^3=frac{1}{27};$$
$$left(frac{1}{3}right)^4=frac{1}{81};$$
$$left(frac{1}{3}right)^5=frac{1}{243};$$
Оказывается, чем в большую степень мы будем возводить (frac{1}{3}), тем МЕНЬШЕЕ значение будем получать. Показательная функция с основанием (frac{1}{3}) будет убывающей. Более того, если возводить в степень любую дробь меньшую единицы, с увеличением степени вы всегда будете получать всё меньшие и меньшие значения. Чтобы наглядно это продемонстрировать, нарисуем еще один график функции (y=(frac{1}{3})^x):
Из всего этого занудства следует очень важное общее правило:
Если основание у степени больше единицы (a>1), то показательная функция будет возрастающей, а если меньше единицы (0 lt a lt 1), то убывающей. Это ключевой момент при решении показательных неравенств!
Решение показательных (степенных) неравенств похоже на решение показательных уравнений с некоторыми оговорками. Начнем изучение с простейшего примера:
Пример 1
$$ 2^x>2^3; $$
Это неравенство решается интуитивно. Понятное дело, что чем в большую степень мы будем возводить двойку, тем большее значение будем получать. Основание больше единицы, а значит, показательная функция возрастающая!
Основания у нас одинаковые. Значит, если вместо (x) подставить любое число большее 3, мы получим верное неравенство. Решением нашего первого показательного неравенства будет:
$$ x>3;$$
Пример 2
$$3^{x+4}<3^{3x-10};$$
Основания одинаковые, большие единицы, а значит, у нас опять возрастающие функции — чем больше степень, тем больше значение показательной функции. Логично, что наше неравенство в таком случае сводится к сравнению степеней с сохранением знака неравенства:
$$x+4<3x-10;$$
$$-2x<-14;$$
При делении на отрицательное число не забываем поменять знак неравенства:
$$x>7;$$
Пример 3
$$ left(frac{1}{2}right)^x>left(frac{1}{2}right)^5;$$
Очень похожее неравенство, основания опять одинаковые, но они меньше единицы. Что это меняет? Знак неравенства!
Раз основание показательной функции меньше единицы, значит она убывающая — чем больше степень, тем меньше значение показательной функции. Поэтому для того, чтобы неравенство выполнялось, необходимо опять сравнить степени, но с противоположным знаком:
$$x<5;$$
Пример 4
$$left(frac{2}{3}right)^{2x-5}geleft(frac{2}{3}right)^{x+1};$$
Основания одинаковые и меньше единицы, значит избавляемся от основания (frac{2}{3}) и сравниваем степени, не забывая при этом изменить знак неравенства:
$$2x-5 le x+1;$$
$$x le 6;$$
Пример 5
$$2^{x+2} le 8^{2x-1};$$
Этот пример немного сложнее — здесь разные основания (слева 2, справа 8). Чтобы решить по аналогии с предыдущими примерами, нужно привести к одинаковым основаниям. Заметим, что восемь можно представить в виде степени двойки: (8=2^3). Подставим в исходное неравенство:
$$2^{x+2} le (2^3)^{2x-1};$$
Из свойства степеней: $$(a^n)^m=a^{n*m}.$$
$$2^{x+2} le 2^{3*(2x-1)};$$
Теперь основания одинаковые и больше единицы, избавляемся от них, оставляя знак неравенства неизменным:
$$x+2 le 3*(2x-1);$$
$$x+2 le 6x-3;$$
$$-5x le -5;$$
$$x ge 1.$$
Общий алгоритм
Сформулируем еще раз общие правила решения простых показательных неравенств:
- Необходимо привести показательные функции слева и справа к одинаковому основанию
- Избавляемся от оснований
- Если основание больше единицы, то знак неравенства сохраняется
- Если основание меньше единицы, то меняем знак неравенства на противоположный
- Решаем получившееся неравенство
Схема решения
$$a^{f(x)}>a^{g(x)};$$
где (a>0; ; aneq1) — некоторое положительное число, а (f(x)) и (g(x)) какие-то зависящие от (x) выражения.
Если (a>1): то (f(x)>g(x));
Если (0 lt a lt 1:) то (f(x) lt g(x)).
В принципе, схема решения простых показательных неравенств очень похожа на решение показательных уравнений. За исключением необходимости внимательно следить за основаниями и знаком неравенства.
Разберем еще несколько интересных и важных примеров.
Пример 6
$$2^{x+1} ge 4;$$
Справа от знака неравенства стоит не показательная функция, а просто число. Но его легко представить в виде степени двойки:
$$2^{x+1} ge 2^2;$$
Основания одинаковые, большие единицы. Избавляемся от них, знак неравенства сохраняем.
$$ x+1 ge 2;$$
$$x ge 1.$$
Как приводить степени к одному основанию
Пример 7
$$5^x le 3;$$
На первый взгляд, пример аналогичен предыдущему. Чтобы решить неравенство, нужно привести к одинаковому основанию. Так и есть, но вот как представить (3-ку) в виде степени (5-ки)?
Ничего сложного в этом нет. Оказывается, любое число (a) можно представить в виде степени с нужным нам основанием (b). Правда, без логарифмов тут не обойтись. Это можно сделать при помощи формулы:
$$ a=b^{log_{b}(a)}; qquad (*)$$
Например: (3=5^{log_{5}(3)};)
Кто забыл, что такое логарифмы, вам обязательно нужно посмотреть сюда.
Мы уже пользовались этой формулой в главе про показательные уравнения. На самом деле, для решения неравенств ее необязательно понимать, можно в лоб подставлять числа в формулу. Но я бы настоятельно рекомендовал разбираться во всем, чем вы пользуетесь. Поэтому подумайте самостоятельно, почему эта формула верна?
Посмотрим на правую часть формулы (*). В степени у нас стоит логарифм (log_{b}(a)). Логарифм — это число, в которое нужно возвести основание (b), чтобы получить (a). И в итоге, в правой части формулы (*) мы (b) возводим в степень, в которую нужно возвести (b), чтобы получить число (a). Так немного запутанно эта формула и работает. Но, если подумать, все не так сложно.
Возвращаемся к примеру 7. Теперь мы знаем, как (3-ку) представить в виде степени (5-ки):
$$3=5^{log_{5}(3)};$$
Подставляем в исходное неравенство
$$5^x le 5^{log_{5}(3)};$$
Наши основания одинаковые, избавляемся от них
$$x le log_{5}(3);$$
Ответ оставляем с некрасивым логарифмом. Мы его не сможем посчитать без калькулятора. На ЕГЭ именно так и поступаем.
Пример 8
$$left(frac{1}{81}right)^{-4x} < 27^{x+8};$$
Здесь привести к одному основанию несколько сложнее. Обратите внимание, что числа 27 и (frac{1}{81}) являются степенями (3-ки):
$$ 27=3^3; $$
$$ frac{1}{81}=3^{-4}; $$
Кто забыл, как работать со степенями, посмотрите главу про свойства степеней. Приведем к основанию (3) левую и правую части неравенства:
$$(3^{-4})^{-4x} < (3^3)^{x+8};$$
$$3^{16x} < 3^{3x+24};$$
Основания одинаковые, избавляемся от них:
$$16x<3x+24;$$
$$ 13x<24;$$
$$x<frac{24}{13};$$
Пример 9
$$ 5^x <-3;$$
Казалось бы, пример ничем не отличается от примера №7 — приводи себе ((-3)) к основанию (5) по формуле и решай.
Но здесь проблема кроется в определении показательной функции. Показательная функция ВСЕГДА больше нуля!
А значит, (5^x>0) и никак не может быть меньше ((-3)), какие бы (x) вы не подставляли.
Попробуйте подставить вместо (x) минус миллион, что вы получите? По определению отрицательной степени:
$$a^{-n}=frac{1}{a^n};$$
$$ 5^{-1000000}=frac{1}{5^{1000000}};$$
Это, несомненно, будет очень маленькое, но положительное число.
Итак, в этом примере корней нет. Запомните это!
Пример 10
$$ 7^x >-6;$$
Неравенство аналогичное примеру №9, но с другим знаком неравенства.
Что меняется? Теперь нас просят найти такие (x), при которых показательная функция (7^x) будет больше отрицательного числа ((-7)). Но так как показательная функция больше (0) при любых (x), то она уже точно будет больше ((-7)).
Что бы вы не подставили, всегда будете получать верное неравенство.
Ответом здесь будет любое число.
Теперь разберем пример посложнее.
Пример 11
$$ 25^{x^2-2x+10}-0,2^{2x^2-4x-80} le 0;$$
Постараемся привести данное неравенство к виду, аналогичному предыдущим примерам. Для этого перенесем вправо второе слагаемое (0,2^{2x^2-4x-80}):
$$ 25^{x^2-2x+10} le 0,2^{2x^2-4x-80};$$
Приведем к одному основанию. Советую десятичные дроби записывать в виде обыкновенных дробей, так вы сразу увидите, к какому основанию удобно привести:
$$0,2=frac{2}{10}=frac{1}{5};$$
$$ 25^{x^2-2x+10} le left(frac{1}{5}right)^{2x^2-4x-80};$$
Слева и справа в основаниях стоят числа, которые легко можно представить в виде степени (5-ки):
$$25=5^2;$$
$$ frac{1}{5}=5^{-1};$$
Подставим
$$ (5^2)^{x^2-2x+10} le (5^{-1})^{2x^2-4x-80};$$
$$ 5^{2*(x^2-2x+10)} le 5^{-1*(2x^2-4x-80)};$$
$$ 5^{2*x^2-4x+20} le 5^{-2x^2+4x+80};$$
Основания одинаковые, избавляемся от них:
$$ 2x^2-4x+20 le -2x^2+4x+80; $$
$$4x^2-8x-60 le 0;$$
Через дискриминант раскладываем квадратный многочлен на множители:
$$ 4(x+3)(x-5) le 0;$$
И решаем методом интервалов:
Замена в показательных неравенствах
Мы разобрали все виды простейших степенных неравенств. Опираясь на эти знания, можно перейти к более сложным неравенствам, которые решаются при помощи замены переменной. В ЕГЭ по профильной математике такие примеры попадаются довольно часто.
Если вы раньше решали любые уравнения или неравенства на замену переменной, то разобраться будет совсем не трудно. Давайте посмотрим на примерах:
Пример 12
$$ 4^x-29*2^x+168le 0. $$
Согласно обычной логике в показательных неравенствах, приведем все показательные функции к одинаковому основанию. Здесь это сделать довольно легко:
$$ (2^2)^x-29*2^x+168 le 0$$
$$ 2^{2x}-29*2^x+168 le 0$$
Готово. Теперь обратите внимание, что (2^{2x}=(2^x)^2), согласно свойству степеней. Подставим:
$$ (2^x)^2-29*2^x+168 le 0$$
В любом примере на замену переменной нужно найти одинаковые конструкции (выражения), зависящие от (x). В нашем примере есть такая конструкция — (2^x).
Обозначим за (t=2^x), и подставим в наше неравенство:
$$ t^2-29t+168 le 0 $$
В итоге получили обыкновенное квадратное неравенство, которое я обычно решаю при помощи универсального метода интервалов:
$$ D=29^2-4*168=841-672=169;$$
$$t_{1}=frac{29+13}{2}=21;$$
$$t_{2}=frac{29-13}{2}=8;$$
Зная корни, раскладываем квадратный многочлен на множители:
$$(t-8)(t-21) le 0;$$
Для метода интервалов рисуем числовую прямую, отмечаем нули функции (корни) и исследуем промежутки. Кто не помнит метод интервалов, настоятельно рекомендую его повторить, без него решать показательные неравенства бесполезно.
Получаем промежутки для переменной (t):
$$ t in [8;21];$$
И тут частая ошибка в том, что школьники заканчивают на этом решение. Но нас же не просят в условии задачи найти (t), нас просят найти (x)!
Поэтому обязательно нужно сделать обратную замену, чтобы вернуться к исходной переменной (x).
Для этого будем пользоваться простой логикой: раз (tin[8;21]), значит (t) может принимать такие значения, которые больше либо равны 8, но и не больше 21. Перепишем то же самое в виде системы (система, потому что эти условия должны выполняться одновременно):
$$ begin{cases}
t ge 8, \
t le 21.
end{cases}$$
Теперь нужно вспомнить, а что такое собственно (t). Это же переменная, за которую мы обозначили (2^x=t). Подставим вместо (t) (2^x).
Обратная замена:
$$ begin{cases}
2^x ge 8, \
2^x le 21.
end{cases}$$
Получили систему из двух простейших показательных неравенств, которые выше мы уже научились с вами решать.
$$ begin{cases}
2^x ge 2^3, \
2^x le 2^{log_{2}(21)}.
end{cases}$$
Основания везде одинаковые, можно от них избавиться:
$$ begin{cases}
x ge 3, \
x le log_{2}(21).
end{cases}$$
Запишем эту систему в виде промежутка
Ответ: (x in [3;log_{2}(21)].)
Как видите, все не так уж сложно. Разберем еще примеры на замену переменной в показательных неравенствах.
Пример 13
$$ 2^x+6*2^{-x} le 7$$
Этот пример тоже на замену. Хотя основания у показательных функций у нас одинаковые — двойка, но вот степень у них отличаются, а значит, делать замену пока нельзя. Нужно сделать так, чтобы одинаковым было абсолютно все — и степени, и основания.
Вспомним свойство степени с отрицательным показателем:
$$a^{-n}=frac{1}{a^n};$$
И применим его в нашем неравенстве:
$$ 2^x+6*frac{1}{2^x} le 7$$
Обозначим за (t=2^x) и подставим:
$$ t+6*frac{1}{t} le 7 $$
Для того, чтобы тут воспользоваться методом интервалов, нужно перекинуть все в левую часть и привести к общему знаменателю.
$$ frac{t^2-7t+6}{t} le 0 $$
Я не рекомендую избавляться в неравенствах от знаменателя, как вы привыкли это делать в уравнениях. В неравенствах в подавляющем большинстве случаев ни в коем случае этого делать нельзя, он тоже влияет на знак всей функции. Это одна из самых частых ошибок на ЕГЭ.
Поэтому я рекомендую всегда в неравенствах тащить знаменатель за собой, не убирать его. Подробнее про это можно почитать в теории обыкновенных неравенств.
Но я вынужден отметить, что именно в этом примере убрать знаменатель (t) можно, так как (t=2^x>0). Показательная функция у нас ВСЕГДА больше нуля, поэтому и (t>0), а значит он не влияет на знак неравенства. Однако делать мы это не будем, чтобы не запутаться. Знаменатель всегда будем оставляем на месте.
Раскладываем на множители числитель:
$$ frac{(t-1)(t-6)}{t} le 0 $$
Метод интервалов, с учетом того, что (t=2^x>0):
$$ t in[1;6];$$
Запишем промежуток в виде системы:
$$ begin{cases}
t ge 1, \
t le 6.
end{cases}$$
Вспоминаем, что (t=2^x) и делаем обратную замену:
$$ begin{cases}
2^x ge 1, \
2^x le 6.
end{cases}$$
$$ begin{cases}
2^x ge 2^0, \
2^x le 2^{log_{2}(6)}.
end{cases}$$
$$ begin{cases}
x ge 0, \
x le log_{2}(6).
end{cases}$$
Ответ: (x in [0;log_{2}(6)].)
Пример 14
$$16^{x+frac{1}{4}}-9*4^{x-frac{1}{2}}+1ge0$$
Пример очень похож на предыдущие, но перед тем, как делать замену, нам придется преобразовать левую часть неравенства. Выпишем отдельно показательные функции и постараемся привести их к одному виду. Иначе мы не сможем сделать замену. Для этого нам понадобятся свойства степеней:
$$a^{n+m}=a^n*a^m;$$
$$(a^n)^m=a^{n*m};$$
$$a^{n-m}=frac{a^n}{a^m};$$
$$16^{x+frac{1}{4}}=16^x*16^{frac{1}{4}}=16^x*2=2*16^x=2*(4^2)^x=2*(4^x)^2;$$
$$4^{x-frac{1}{2}}=frac{4^x}{4^{frac{1}{2}}}=frac{4^x}{2}=frac{1}{2}*4^x;$$
Подставим наши преобразования в исходное неравенство:
$$2*(4^x)^2-9*frac{1}{2}*4^x+1 ge 0;$$
Все готово к замене. Пусть (t=4^x):
$$2*t^2-frac{9}{2}*t+1 ge 0;$$
Домножим на (2), чтобы избавиться от знаменателя
$$4t^2-9t+2 ge 0;$$
Обыкновенное квадратное неравенство. Решаем, как обычно, методом интервалов. Для этого разложим на множители:
$$4(t-frac{1}{4})(t-2) ge 0;$$
$$left[
begin{gathered}
tle frac{1}{4}; \
tge 2, \
end{gathered}
right.$$
Обратите внимание на знак совокупности! Он означает, что нас устраивают оба промежутка, как показано на числовой прямой.
Очень важно уметь различать системы и совокупности.
Знак системы используется, когда нужно, чтобы значения (x) удовлетворяли всем неравенствам, входящим в систему. Другими словами, система — это знак пересечения решений всех неравенств.
Знак совокупности показывает, что значения (x) удовлетворяют хотя бы одному из неравенств в системе. Совокупность — это знак объединения решений.
Делаем обратную замену (t=4^x):
$$left[
begin{gathered}
4^xle frac{1}{4}; \
4^xge 2, \
end{gathered}
right.$$
$$left[
begin{gathered}
4^xle 4^{-1}; \
4^xge 4^{frac{1}{2}}, \
end{gathered}
right.$$
$$left[
begin{gathered}
xle -1; \
xge frac{1}{2}, \
end{gathered}
right.$$
Запишем получившуюся совокупность в виде промежутков.
Ответ:(xin(-infty;-1] cup [frac{1}{2};+infty).)
Теперь наших знаний достаточно, чтобы решать некоторые реальные примеры из ЕГЭ по профильной математике. Поехали:
Пример 15
$$ frac{5^x}{5^x-4}+frac{5^x+5}{5^x-5}+frac{22}{25^x-9*5^x+20} le 0$$
Перед вами настоящий пример из ЕГЭ 2016 года. Возможно, выглядит неприятно, но на самом деле, он решается очень легко. А самое главное, у нас уже есть все необходимые знания, чтобы его решить.
Обращаем внимание, что почти везде есть конструкция (5^x). Это и будет наша замена, осталось только представить (25^x=(5^x)^2):
$$ frac{5^x}{5^x-4}+frac{5^x+5}{5^x-5}+frac{22}{(5^x)^2-9*5^x+20} le 0$$
Пусть (t=5^x):
$$ frac{t}{t-4}+frac{t+5}{t-5}+frac{22}{t^2-9*t+20} le 0$$
В третьей дроби разложим знаменатель на множители при помощи дискриминанта
$$ frac{t}{t-4}+frac{t+5}{t-5}+frac{22}{(t-4)(t-5)} le 0$$
Приводим к общему знаменателю
$$ frac{t(t-5)+(t+5)(t-4)+22}{(t-4)(t-5)} le 0$$
Раскрываем скобки и приводим подобные слагаемые в числителе
$$ frac{2t^2-4t+2}{(t-4)(t-5)} le 0$$
$$ frac{2(t^2-2t+1)}{(t-4)(t-5)} le 0$$
В скобках стоит полный квадрат
$$ frac{2(t-1)^2}{(t-4)(t-5)} le 0$$
Теперь применяем метод интервалов
$$left[
begin{gathered}
t=1, \
4 lt t lt 5. \
end{gathered}
right.$$
Перепишем двойное неравенство в виде системы
$$left[
begin{gathered}
t=1, \
begin{cases}
t > 4, \
t < 5.
end{cases}. \
end{gathered}
right.$$
Делаем обратную замену (t=5^x):
$$left[
begin{gathered}
5^x=1, \
begin{cases}
5^x > 4, \
5^x < 5.
end{cases}. \
end{gathered}
right.$$
$$left[
begin{gathered}
5^x=5^0, \
begin{cases}
5^x > 5^{log_{5}(4)}, \
5^x < 5^1.
end{cases}. \
end{gathered}
right.$$
$$left[
begin{gathered}
x=0, \
begin{cases}
x > log_{5}(4), \
x < 1.
end{cases}. \
end{gathered}
right.$$
В ответе не забываем отдельную точку (x=0), она нас тоже устраивает! Если на ЕГЭ забудете точки, в зависимости от критериев, потеряете какое-то количество баллов. Отдельная точка всегда записывается при помощи фигурных скобок.
Ответ: (x in [0] cup (log_{5}(4);1).)
Пример 16
$$ frac{3}{(2^{2-x^2}-1)^2}-frac{4}{2^{2-x^2}-1}+1 ge 0$$
Тут сразу бросается в глаза одинаковая конструкция (2^{2-x^2}-1). Замену мы можем делать абсолютно любую. Поэтому ничто не мешает нам тут обозначить за (t=2^{2-x^2}-1).
Подставим в исходное неравенство
$$ frac{3}{t^2}-frac{4}{t}+1 ge 0$$
Приводим к общему знаменателю
$$frac{t^2-4t+3}{t^2} ge 0$$
$$frac{(t-3)(t-1)}{t^2} ge 0$$
Самое время для метода интервалов:
$$t in (-infty;0) cup (0;1] cup [3;+infty);$$
Нас устраивает сразу три промежутка для (t). Запишем эти промежутки в виде большой совокупности, ведь нас устраивают все три промежутка:
$$left[
begin{gathered}
t < 0; \
begin{cases}
t > 0, \
t le 1.
end{cases} ; \
tge 3, \
end{gathered}
right.$$
Обратите внимание на то, что в совокупности у нас есть еще знак системы. Действительно, во втором промежутке (t) должно быть с одной стороны больше 0, а с другой меньше 1, и это должно выполняться одновременно. Поэтому второй промежуток описывается при помощи знака системы.
Сделаем обратную замену:
$$left[
begin{gathered}
2^{2-x^2}-1< 0; \
begin{cases}
2^{2-x^2}-1 > 0, \
2^{2-x^2}-1 le 1.
end{cases} ; \
2^{2-x^2}-1ge 3, \
end{gathered}
right.$$
$$left[
begin{gathered}
2^{2-x^2}< 1; \
begin{cases}
2^{2-x^2}> 1, \
2^{2-x^2} le 2.
end{cases} ; \
2^{2-x^2}ge 4, \
end{gathered}
right.$$
$$left[
begin{gathered}
2^{2-x^2}< 2^0; \
begin{cases}
2^{2-x^2}> 2^0, \
2^{2-x^2} le 2^1.
end{cases} ; \
2^{2-x^2}ge 2^2, \
end{gathered}
right.$$
$$left[
begin{gathered}
2-x^2< 0; \
begin{cases}
2-x^2> 0, \
2-x^2 le 1.
end{cases} ; \
2-x^2ge 2, \
end{gathered}
right.$$
Разложим все квадратные неравенства по формуле разности квадратов:
$$left[
begin{gathered}
(sqrt{2}-x)(sqrt{2}+x)< 0; \
begin{cases}
(sqrt{2}-x)(sqrt{2}+x)> 0, \
(1-x)(1+x) le 0 .
end{cases} ; \
-x^2ge 0, \
end{gathered}
right.$$
Обратите внимание на последнее неравенство: так как квадрат всегда положителен, то это неравенство выполняется только, если (x=0).
И остальное решим методом интервалов. Я сразу напишу, что получается:
$$left[
begin{gathered}
xin (-infty;-sqrt{2}) cup (sqrt{2};+infty); \
begin{cases}
xin(-sqrt{2};sqrt{2}), \
xin(-infty;-1] cup [1;+infty).
end{cases} ; \
x=0, \
end{gathered}
right.$$
Для наглядности нарисуем числовую ось и отметим на ней все промежутки. Различными цветами показаны соответствующие промежутки из совокупности, а фиолетовой штриховкой показано итоговое решение. Там, где знак системы находим пересечение, там где совокупность – объединение.
Однородные показательные неравенства
Разберемся еще с одним типом показательных неравенств — однородными неравенствами. Такие неравенства часто встречаются, если в примере есть несколько показательных функций с разными основаниями, и свести их к одному основанию не представляется возможным.
Как обычно, давайте сразу будем разбираться на конкретном примере.
Пример 17
$$25^x-20^x-2*16^x le 0$$
Чем же это уравнение примечательно? Давайте попробуем по нашему старому алгоритму привести все к одинаковому основанию.
$$25^x=5^{2x};$$
$$20^x=(5*4)^x=5^x*4^x;$$
$$16^x=4^{2x};$$
Как видите, привести к одному основанию не получается. Мы никак не можем сделать одинаковые показательные функции, если основания 5 и 4. Будем работать с тем, что есть. Подставим получившееся разложение в исходное неравенство.
$$5^{2x}-5^x*4^x-2*4^{2x} le 0;$$
Так как делить неравенства на положительные числа можно, поделим получившееся неравенство на (5^{2x}). На всякий случай напомню: при делении неравенств на положительные числа полностью делится и левая, и правая части неравенства, только в этом случае преобразование будет равносильным, то есть его корни не изменятся. Делить неравенство на (5^{2x}) можно, потому что это показательная функция, а она по определению всегда строго больше нуля.
$$frac{5^{2x}-5^x*4^x-2*4^{2x}}{5^{2x}} le frac{0}{5^{2x}};$$
Разобьем левую часть на несколько дробей. То есть, поделим каждый одночлен числителя на знаменатель дроби. В правой части, очевидно, получается 0.
$$frac{5^{2x}}{5^{2x}}-frac{5^x*4^x}{5^{2x}}-2*frac{4^{2x}}{5^{2x}} le 0;$$
$$1-frac{4^x}{5^x}-2*frac{4^{2x}}{5^{2x}} le 0;$$
$$1-left(frac{4}{5}right)^x-2*left(frac{4}{5}right)^{2x} le 0;$$
$$1-left(frac{4}{5}right)^x-2*left(frac{4}{5}right)^{2x} le 0;$$
После некоторых преобразований в результате деления мы получили везде показательную функцию (left(frac{4}{5}right)^x), которую смело можно заменить на (t=left(frac{4}{5}right)^x).
$$1-t-2*t^2 le 0;$$
$$-2*t^2-t+1 le 0;$$
Разложим квадратный многочлен на множители при помощи дискриминанта, при этом не забываем про коэффициент (-2).
$$-2(t+1)(t-frac{1}{2}) le 0;$$
Решением этого квадратного неравенства будет:
$$ t in (-infty;-1]in[frac{1}{2};+infty);$$
Перепишем промежуток в виде совокупности:
$$left[
begin{gathered}
t le -1, \
t ge frac{1}{2}. \
end{gathered}
right.$$
И сделаем обратную замену. Напомню (t=left(frac{4}{5}right)^x):
$$left[
begin{gathered}
left(frac{4}{5}right)^x le -1, \
left(frac{4}{5}right)^x ge frac{1}{2}. \
end{gathered}
right.$$
$$left[
begin{gathered}
left(frac{4}{5}right)^x le -1, \
left(frac{4}{5}right)^x ge left(frac{4}{5}right)^{log_{left(frac{4}{5}right)}(frac{1}{2})}. \
end{gathered}
right.$$
$$left[
begin{gathered}
left(frac{4}{5}right)^x le -1, \
x ge log_{left(frac{4}{5}right)}(frac{1}{2}). \
end{gathered}
right.$$
Первое неравенство в совокупности не имеет решений, так как показательная функция всегда больше нуля, значит, тем более больше (-1).
Ответ: (xin(log_{left(frac{4}{5}right)}(frac{1}{2}); +infty)).
Когда нет возможности привести к одинаковому основанию все содержащиеся в неравенстве функции, попробуйте решить как однородное уравнение при помощи деления. Разные основания — это звоночек о том, что пример может решаться при помощи деления.
Рассмотрим еще один интересный пример с разными основаниями. Только это уже не однородное уравнение.
Пример 18
$$6^x-4*3^x-2^x+4 le 0$$
Обратите внимание, что у нас в неравенстве сразу 4 слагаемых. Четное количество слагаемых иногда намекает на метод группировки. Его проходят в 8м классе, но если вы не помните, то сейчас научитесь прямо на этом примере.
Первым делом сгруппируем слагаемые попарно — первое со вторым, а третье с четвертым. И вынесем общий множитель. У первого и второго слагаемых общий множитель (3^x), а у третьего и четвертого общий множитель пусть будет (-1).
$$3^x*(2^x-4)-1*(2^x-4) le 0;$$
Обратите внимание на скобки, они получились одинаковые! Теперь у нас вместо четырех слагаемых стало два, но больших. У них тоже есть общий множитель — это как раз скобка ((2^x-4)). Вынесем скобку за скобку!
$$(2^x-4)(3^x-1) le 0;$$
У нас получилось произведение двух множителей. Произведение меньше нуля может быть только в том случае, если множители имеют разные знаки. То есть, нас устраивает либо:
$$ begin{cases}
2^x-4 ge 0, \
3^x-1 le 0.
end{cases}$$
Либо:
$$ begin{cases}
2^x-4 le 0, \
3^x-1 ge 0.
end{cases}$$
Решим обе системы и объединим решения, так как нам подходят оба случая.
$$ begin{cases}
2^xge 4, \
3^x le 1.
end{cases}$$
$$ begin{cases}
2^xge 2^2, \
3^x le 3^0.
end{cases}$$
$$ begin{cases}
xge 2, \
x le 0.
end{cases}$$
Эти два неравенства в системе не имеют решений, подходящих одновременно обоим. Поэтому в первой системе нет решений. Решим вторую:
$$ begin{cases}
2^x le 4, \
3^x ge 1.
end{cases}$$
$$ begin{cases}
2^x le 2^2, \
3^x ge 3^0.
end{cases}$$
$$ begin{cases}
x le 2, \
x ge 0.
end{cases}$$
Ответ: (xin[0;2].)
Рассмотрим еще один не очень приятный пример, который, тем не менее, может встретиться на ЕГЭ.
Пример 19
$$frac{5^{2x+1}-75*0,2^{2x}-10}{x+2} le 0.$$
Неравенство неприятное, потому что в числителе дроби у нас (x) везде в степени показательной функции, а в знаменателе (x) стоит отдельно. Никак не получится сделать замену. Но обратите внимание, нас спрашивают, при каких (x) дробь будет отрицательная. А дробь отрицательна только тогда, когда у нее числитель и знаменатель имеют разные знаки. Опять, как в предыдущем примере, можем по отдельности рассмотреть числитель и знаменатель. Нас устраивает:
Либо:
$$ begin{cases}
5^{2x+1}-75*0,2^{2x}-10 ge 0, \
x+2 < 0.
end{cases}$$
Либо система с противоположными знаками:
$$ begin{cases}
5^{2x+1}-75*0,2^{2x}-10 le 0, \
x+2 > 0.
end{cases}$$
Вторые неравенства в системах имеют строгий знак, так как это — условия, накладываемые на знаменатель.
Разберемся сначала с первой системой. Постараемся привести показательные функции к одинаковым основаниям в первом неравенстве системы:
$$ begin{cases}
5^{2x}*5^1-75*left(frac{1}{5}right)^{2x}-10 ge 0, \
x+2 < 0.
end{cases}$$
$$ begin{cases}
5*25^x-75*left(frac{1}{25^{x}}right)-10 ge 0, \
x+2 < 0.
end{cases}$$
Выпишем отдельно первое неравенство и решим его, сделав замену (t=25^x>0).
$$ 5*25^x-75*left(frac{1}{25^{x}}right)-10 ge 0;$$
$$5*t-frac{75}{t}-10 ge 0;$$
$$frac{5*t^2-10*t-75}{t} ge 0;$$
Так как (t=25^x>0), то мы можем спокойно избавиться от знаменателя в дроби, ведь он всегда положительный и не влияет на знак всего выражения.
$$5*t^2-10*t-75 ge 0;$$
$$5*(t-5)(t+3) ge 0;$$
$$ tin(-infty;-3] cup [5;+infty);$$
Но так как (t>0):
$$tin[5;+infty);$$
Запишем в виде неравенства:
$$t ge 5;$$
Сделаем обратную замену
$$ 25^x ge 5;$$
$$5^{2x} ge 5^1;$$
$$2x ge 1;$$
$$xgefrac{1}{2};$$
Напоминаю, что мы решили только первое неравенство в первой системе
$$ begin{cases}
5^{2x+1}-75*0,2^{2x}-10 ge 0, \
x+2 < 0.
end{cases}$$
C учетом нашего решения, ее теперь можно переписать в виде
$$ begin{cases}
xgefrac{1}{2}, \
x < -2.
end{cases}$$
Такая система решений не имеет. Но не грустим и вспоминаем, что у нас еще одна система неравенств с противоположным случаем — когда числитель отрицательный, а знаменатель положительный:
$$ begin{cases}
5^{2x+1}-75*0,2^{2x}-10 le 0, \
x+2 > 0.
end{cases}$$
Так как отличие только в знаках неравенства, то все преобразования, которые мы делали выше, справедливы и тут. Не будем заново решать то же самое, просто возьмем решение из предыдущей системы и изменим знаки неравенства:
$$ begin{cases}
xlefrac{1}{2}, \
x > -2.
end{cases}$$
Эта система уже имеет решения. Можно, наконец, записать ответ.
Ответ: (xin(-2;frac{1}{2}].)
Мне лично не нравится рассматривать кучу случаев в подобных примерах. А что, если знаменатель будет сложнее чем в примере выше? А еще может быть не два множителя, а сразу пять или больше, тут всех случаев не рассмотришь.
Поэтому существует отличный и очень удобный метод рационализации. Я написал статью с полным его разбором. Кстати, в ЕГЭ часто встречаются примеры именно на метод рационализации, поэтому, если вы хотите сдать профиль на высокие баллы, то это прямо обязательно знать.
Инфоурок
›
Алгебра
›Презентации›Неравенства в ЕГЭ(базовый уровень)
Неравенства в ЕГЭ(базовый уровень)
Скачать материал

Скачать материал


- Сейчас обучается 25 человек из 13 регионов


- Сейчас обучается 339 человек из 69 регионов


- Сейчас обучается 138 человек из 42 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Неравенства
(ЕГЭ 17 задание база) -
2 слайд
Неравенства
Вспомним ,что такое неравенство.
Неравенство-
Это соотношения вида f(x)>g(x), f(x)<g(x) или f(x) ≥g(x), f(x)≤ g(x)
Решения неравенства- это значения переменной, обращающие его в верное числовое неравенство.
Решить неравенство- значит найти все решения или доказать, что их нет. -
3 слайд
Виды неравенств и способы их решения
1. Линейные неравенства и системы неравенств
2. Квадратные неравенства
3. Неравенства высших степеней
4. Рациональные неравенства
5. Иррациональные неравенства
6. Показательные, логарифмические неравенства и системы неравенств -
4 слайд
ТОЧКИ
А
В
С
D
ЧИСЛАlog2 10
2) 7/3
3) √26
4) (3/5)-1
-
5 слайд
Алгоритм выполнения:
Проанализировать рядом с каким из целых чисел стоит данная точка.
Проанализировать на каком интервале лежат числа из правого столбца.
Сравнить полученные интервалы и поставить в соответствие.Решение:
Рассмотрим точку А. Ее значение больше 1 и меньше 2.
Рассмотрим точку B. Ее значение больше 2 и меньше 3.
Рассмотрим точку С. Ее значение больше 3 и меньше 4.
Рассмотрим точку D. Ее значение больше 5 и меньше 6.
Вспомним что такое логарифм. -
6 слайд
Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a, чтобы получить число x.
loga x = b, где a — основание, x — аргумент, b — собственно, чему равен логарифм.
В нашем случае а = 2, x = 10.
То есть нас интересует число 2b = 10. 23 = 8 и 24 = 16, следовательно, b лежит в промежутке от 3 до 4.
Следовательно, 7/3 больше 2 и меньше 3.
Рассмотрим √26. √25 = 5, √36 = 6. Значит, √26 больше 5 и меньше 6.
То есть (3/5)-1 больше 1 и меньше 2.
Ответ: 4213. -
-
8 слайд
Алгоритм выполнения
1.Решаем по очереди каждое из неравенств (А–Г). При необходимости (для наглядности) отображаем полученное решение на координатной прямой.
2.Записываем результаты в форме, которая предложена в столбце «Решения». Находим соответствующие пары «буква–число».
А. 2–х+1 < 0,5 → 2–x+1 < 2–1 → –x+1 < –1 → –x < –2 → x > 2. Ответ: х ϵ (2; +∞). Получаем: А–3.
Б.
Корни в данном случае – это х=4 и х=5. Имеем в виду, что неравенство строгое, т.е. значения корней в промежуток для ответа не включаем. В точке х=5 перехода знака не происходит, т.к. по условию (х–5) дано в квадрате. Поскольку нам нужен промежуток, где х<0, то ответ в данном случае: х ϵ (–∞; 4).
Соответственно, имеем: Б–4. -
9 слайд
В. log4x > 1 → log4x > log44 → x > 4. Т.е.: х ϵ (4; +∞). Ответ: В–1.
Г. (х–4)(х–2) < 0. Здесь так же, как и в неравенстве Б, нужно сразу отобразить решение на координатной прямой.
Неравенство дано квадратное, его корни – х=2 и х=4. Для получения промежутков с положительными и отрицательными значениями схематически изображаем параболу, пересекающую координатную прямую в точках корней. Промежуток «внутри» параболы отрицательный, промежутки «вне» ее положительны. Т.к. в неравенстве дано «<0», то для ответа следует взять промежуток отрицательных значений. Учитываем, что неравенство строгое. Получаем: х ϵ (2; 4).
Ответ: Г–2. -
-
11 слайд
Алгоритм выполнения
Решаем последовательно неравенства А–Г, учитывая ОДЗ.
По результату (полученному простейшему неравенству) находим соответствующее графическое решение из правого столбца.
log2 (x–1) < 1 → log2 (x–1) < log2 2 → x–1 < 2 → x < 3. ОДЗ: х–1 > 0 → x > 1.
Объединяем полученный промежуток с ОДЗ, получаем: x ϵ (1; 3). Это соответствует решению №3. Ответ: А–3.ОДЗ не дает ограничений
Тогда в результате имеем: х ϵ (1; +∞). Ответ: Б–2.
Для решения требуется взять промежутки с положительным знаком. ОДЗ: х≠3. Получаем: х ϵ (1; 3)ᴗ(3; +∞). Ответ: В–4.
х2 – 4х + 3 > 0 → (x–1)(x–3) > 0. Применив метод интервалов, получим:
ОДЗ не дает ограничений. Значит, х ϵ (–∞; 1)ᴗ(3; +∞). Ответ: Г–1.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 153 389 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
Другие материалы
- 25.01.2022
- 861
- 58
Урок по теме «Квадратные уравнения»
- Учебник: «Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.
- Тема: § 8. Квадратное уравнение и его корни
- 25.01.2022
- 125
- 2







Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Основы туризма и гостеприимства»
-
Курс повышения квалификации «Финансы: управление структурой капитала»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Управление ресурсами информационных технологий»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Организация деятельности секретаря руководителя со знанием английского языка»
-
Курс профессиональной переподготовки «Методика организации, руководства и координации музейной деятельности»
-
Курс профессиональной переподготовки «Организация и управление службой рекламы и PR»
-
Скачать материал
-
25.01.2022
567
-
PPTX
692.9 кбайт -
14
скачиваний -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Требунских Лидия Владимировна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 8 лет и 3 месяца
- Подписчики: 0
- Всего просмотров: 102795
-
Всего материалов:
36