Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов).
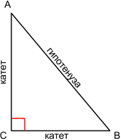
Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
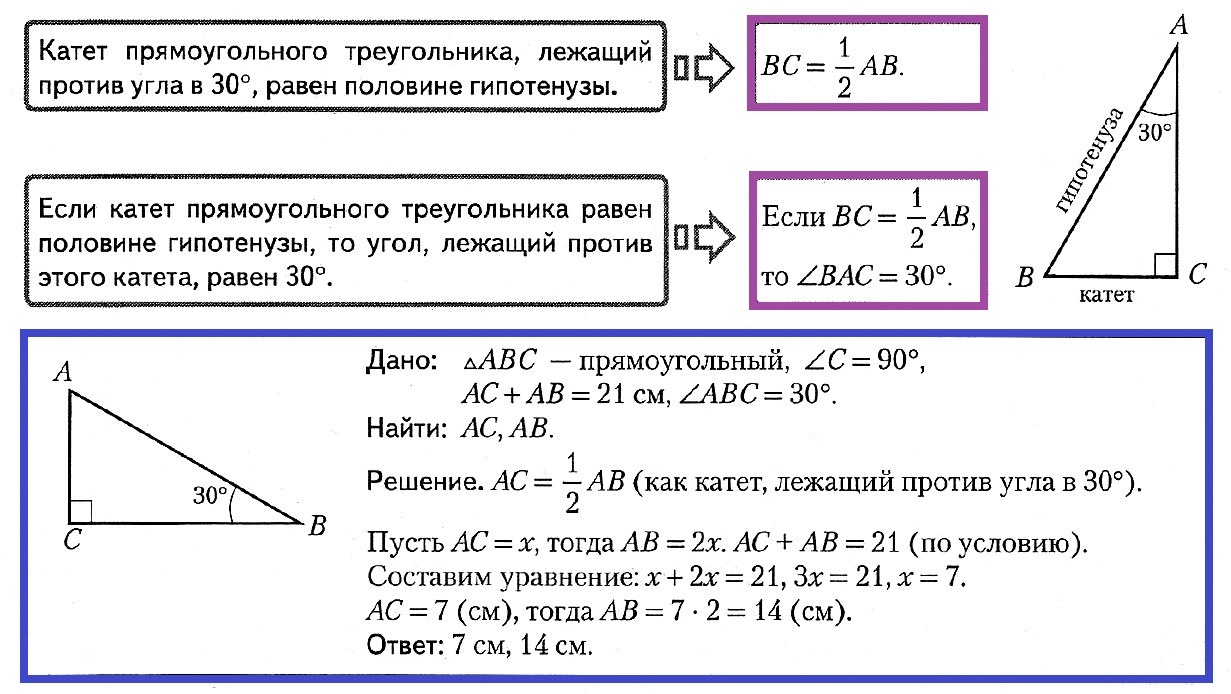
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$
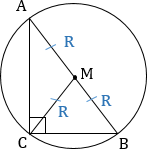
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$
7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.
1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
В прямоугольном треугольнике $АВС$ для острого угла $В$:
$sinB={AC}/{AB};$
$cosB={BC}/{AB};$
$tgB={AC}/{BC};$
$ctgB={BC}/{AC}.$
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
$sin BOA=sin BOC;$
$cos BOA=-cos BOC;$
$tg BOA=-tg BOC;$
$ctg BOA=-ctg BOC.$
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Площадь прямоугольного треугольника равна половине произведения его катетов
$S={AC∙BC}/{2}$
Пример:
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√{91}$. Найдите косинус внешнего угла при вершине $В$.
Решение:
Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то
$cosABD=-cosABC$
Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:
$cosABC={ВС}/{АВ}$
Катет $ВС$ мы можем найти по теореме Пифагора:
$ВС=√{10^2-√{91}^2}=√{100-91}=√9=3$
Подставим найденное значение в формулу косинуса
$cos ABC = {3}/{10}=0,3$
$cos ABD = — 0,3$
Ответ: $-0,3$
Пример:
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sinA={4}/{5}, AC=9$. Найдите $АВ$.
Решение:
Распишем синус угла $А$ по определению:
$sinA={ВС}/{АВ}={4}/{5}$
Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.
Применим теорему Пифагора, чтобы отыскать $«х»$
$АС^2+ВС^2=АВ^2$
$9^2+(4х)^2=(5х)^2$
$81+16х^2=25х^2$
$81=25х^2-16х^2$
$81=9х^2$
$9=х^2$
$х=3$
Так как длина $АВ$ составляет пять частей, то $3∙5=15$
Ответ: $15$
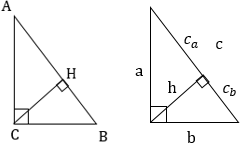
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
$CD^2=DB∙AD$
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
$CB^2=AB∙DB$
$AC^2=AB∙AD$
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
$AC∙CB=AB∙CD$
31
Июл 2013
Категория: Справочные материалы
Прямоугольный треугольник
2013-07-31
2019-09-30
Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).
Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.
Стороны, прилежащие к прямому углу, называются катетами.
Признаки равенства прямоугольных треугольников
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны (по двум катетам).
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны (по катету и острому углу).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны (по гипотенузе и катету).
Свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна 90˚.
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.
3. Теорема Пифагора:
, где
– катеты,
– гипотенуза. Видеодоказательство
4. Площадь прямоугольного треугольника с катетами
:
5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты
и гипотенузу
следующим образом:
6. Центр описанной окружности – есть середина гипотенузы.
7. Радиус описанной окружности есть половина гипотенузы
:
8. Медиана, проведенная к гипотенузе, равна ее половине
9. Радиус вписанной окружности выражается через катеты
и гипотенузу
следующим образом:
Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.
И, думаю, будет полезна таблица формул для треугольника
Автор: egeMax |
комментария 3
Печать страницы
Прямоугольный треугольник
Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).
Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.
Стороны, прилежащие к прямому углу, называются катетами .
Признаки равенства прямоугольных треугольников
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).
Свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна 90˚.
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.
3. Теорема Пифагора:
, где
– катеты,
– гипотенуза. Видеодоказательство
4. Площадь прямоугольного треугольника с катетами
:
5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты
и гипотенузу
следующим образом:
6. Центр описанной окружности – есть середина гипотенузы.
7. Радиус описанной окружности есть половина гипотенузы
:
8. Медиана, проведенная к гипотенузе, равна ее половине
9. Радиус вписанной окружности выражается через катеты
и гипотенузу
следующим образом:
Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.
Прямоугольные треугольники
Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов).
Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$
7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.
1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
В прямоугольном треугольнике $АВС$ для острого угла $В$:
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | $<1>/<2>$ | $<√2>/<2>$ | $<√3>/<2>$ |
| $cosα$ | $<√3>/<2>$ | $<√2>/<2>$ | $<1>/<2>$ |
| $tgα$ | $<√3>/<3>$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | $<√3>/<3>$ |
Площадь прямоугольного треугольника равна половине произведения его катетов
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√<91>$. Найдите косинус внешнего угла при вершине $В$.
Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то
Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:
Катет $ВС$ мы можем найти по теореме Пифагора:
Подставим найденное значение в формулу косинуса
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sinA=<4>/<5>, AC=9$. Найдите $АВ$.
Распишем синус угла $А$ по определению:
Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.
Применим теорему Пифагора, чтобы отыскать $«х»$
Так как длина $АВ$ составляет пять частей, то $3∙5=15$
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
Прямоугольный треугольник егэ теория
Прямоугольный треугольник — треугольник, имеющий прямой угол. Стороны, образующие прямой угол, называют катетами, а сторону, противолежащую к прямому углу, называют гипотенузой.
Свойства прямоугольного треугольника:
1. Катет меньше гипотенузы.
2. Квадрат гипотенузы равен сумме квадратов катетов (теорема Пифагора): с 2 = а 2 + b 2 .
3. Сумма острых углов прямоугольного треугольника равна 90°.
4. Медиана,проведенная к гипотенузе,равна половине гипотенузы (радиусу окружности, описанной около треугольника).
5. Радиус окружности, вписанной в прямоугольный треугольник ,можно вычислить по формуле: r = (a + b — c)/2.
6. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
7. Если катет прямоугольного треугольника равен 1/2 гипотенузы, то угол, лежащий против этого катета, равен 30°.
Признаки равенства прямоугольных треугольников
Два прямоугольных треугольника равны если:
• два катета одного треугольника равны двум катетам другого;
• катет и острый угол одного треугольника равны катету и острому углу другого треугольника;
• гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого треугольника;
• гипотенуза и катет одного треугольника равны гипотенузе и катету другого треугольника.
Это конспект по теме «Прямоугольные треугольники». Выберите дальнейшие действия:
источники:
http://examer.ru/ege_po_matematike/teoriya/pryamougolnie_treugolniki
http://uchitel.pro/%D0%BF%D1%80%D1%8F%D0%BC%D0%BE%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9-%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA/
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Прямоугольный треугольник. Теорема Пифагора
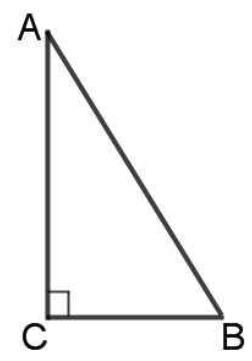
Прямоугольный треугольник – это треугольник, один из углов которого равен (90^circ) (прямой).
Сторона, лежащая напротив прямого угла, называется гипотенузой ((AB)), а две другие стороны — катетами ((AC) и (BC)).
(bullet) Катет, лежащий против угла (30^circ), равен половине гипотенузы.
Следовательно, если, например, (angle A=30^circ), то (BC=dfrac12AB).
(bullet) Сумма острых углов прямоугольного треугольника равна (90^circ): (angle A+angle B=90^circ).
Следовательно, если в прямоугольном треугольнике один из острых углов равен (45^circ), то такой треугольник является равнобедренным.
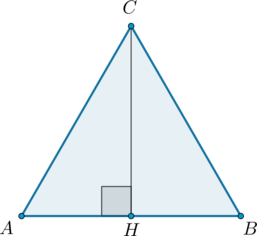
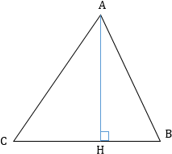
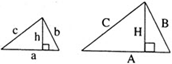
(bullet) Если в прямоугольном треугольнике (ABC) провести высоту (CH) из прямого угла, то (angle BAC=angle BCH) и (angle
ABC=angle
ACH):
(bullet) Теорема Пифагора: квадрат длины гипотенузы равен сумме квадратов длин катетов: [AB^2=AC^2+BC^2]
(bullet) (triangle ABCsim triangle AHCsim triangle BHC)
(bullet) Высота, проведенная из вершины прямого угла, есть среднее геометрическое (среднее пропорциональное) отрезков, на которые делится гипотенуза этой высотой: [CH=sqrt{AHcdot HB}]
Задание
1
#3770
Уровень задания: Равен ЕГЭ
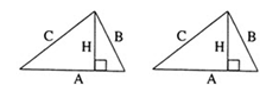
В треугольнике (ABC) угол (C) равен (90^circ), угол (A) равен (30^circ), (AB=2sqrt3). Найдите высоту (CH).
Так как катет, лежащий против угла (30^circ), равен половине гипотенузы, то (BC=0,5AB=sqrt3).
По свойству прямоугольного треугольника (angle BCH=angle
A=30^circ), следовательно, из (triangle BCH): (HB=0,5
BC=sqrt3:2).
Тогда по теореме Пифагора из (triangle BCH): [CH=sqrt{BC^2-BH^2}=sqrt{dfrac94}=1,5]
Ответ: 1,5
Задание
2
#3771
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C) равен (90^circ), (CH) – высота, угол (A) равен (30^circ). Найдите (AH), если (AB=2).
Так как катет, лежащий против угла (30^circ), равен половине гипотенузы, то (BC=0,5AB=1).
Тогда по теореме Пифагора из (triangle ABC): [AC=sqrt{AB^2-BC^2}=sqrt3] Из прямоугольного (triangle AHC): (HC=0,5AC=sqrt3:2). Тогда по теореме Пифагора [AH=sqrt{AC^2-HC^2}=1,5]
Ответ: 1,5
Задание
3
#3772
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C) равен (90^circ), (CH) – высота, угол (A) равен (30^circ). Найдите (BH), если (AB=4).
Так как катет, лежащий против угла (30^circ), равен половине гипотенузы, то (BC=0,5AB=2).
По свойству прямоугольного треугольника (angle BCH=angle
A=30^circ), следовательно, из (triangle BCH): (HB=0,5
BC=1).
Ответ: 1
Задание
4
#3773
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) ( AB=BC=AC=2sqrt3). Найдите высоту (CH).
Так как (AC=BC), то (CH) также является медианой, следовательно, (AH=0,5 AB=sqrt3). Тогда по теореме Пифагора из (triangle ACH): [CH=sqrt{AC^2-AH^2}=3]
Ответ: 3
Задание
5
#3774
Уровень задания: Равен ЕГЭ
В равностороннем треугольнике (ABC) высота (CH) равна (2sqrt3). Найдите (AB).
Так как (AC=BC), то (CH) также является медианой. Следовательно, если (AH=a), то (AB=AC=2a). Тогда по теореме Пифагора из (triangle
ACH): [AC^2=AH^2+CH^2quadRightarrowquad 4a^2=a^2+12quadRightarrowquad
a=2quadRightarrowquad AB=2a=4]
Ответ: 4
Задание
6
#3775
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) (AC=BC=4), (angle C=30^circ). Найдите высоту (AH).
Рассмотрим прямоугольный (triangle ACH). Катет, лежащий против угла (30^circ), равен половине гипотенузы, следовательно, (AH=0,5AC=2).
Заметим, что условие (BC=4) в данной задаче является лишним.
Ответ: 2
Задание
7
#3776
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) (AC=BC), высота (AH) равна (4), угол (C) равен (30^circ). Найдите (BC).
Рассмотрим прямоугольный (triangle ACH). Катет, лежащий против угла (30^circ), равен половине гипотенузы, следовательно, (4=AH=0,5AC), откуда (8=AC=BC).
Ответ: 8

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
В данной статье для вас основная теория по прямоугольному треугольнику, также мы с вами разберём несколько задач. На первый взгляд, число прототипов заданий, представленных в едином банке задач ЕГЭ, несколько пугает – их там более 300 (на момент написания этой статьи). Но практически все задания решаются в два, максимум в три действия. Многие даже в одно.
Представленные подходы к решению вполне применимы для других типов задач, в которых прямоугольный треугольник является частью другого (данного в условии) треугольника, например равнобедренного. Средства для их решения совершенно одни и те же. Постараюсь акцентировать внимание на базовых свойствах и основных методах, которые необходимы для решения.
Кстати, в большинстве пособий по подготовке к экзамену почему-то встречаются только примеры на решение прямоугольного треугольника, как будто других задач в этом разделе и не существует — странно, конечно. Теперь теория!
Прямоугольный треугольник — это треугольник, в котором один из углов прямой, то есть равен 90 градусов.
Вершина треугольника — точка, в которой сходятся две стороны треугольника.
Сторона треугольника — отрезок соединяющий две вершины треугольника.
Стороны прямоугольного треугольника имеют свои названия.
Гипотенуза — сторона прямоугольного треугольника, которая противоположна прямому углу. На рисунке.
Катеты — стороны прямоугольного треугольника, которые образуют прямой угол.
*Если длины всех трех сторон прямоугольного треугольника являются целыми числами, то такой треугольник называют Пифагоровым треугольником, а длины сторон образуют пифагорову тройку. Самый древний из известных Пифагоровых треугольников — Египетский треугольник, соотношение длин сторон которого 3:4:5.
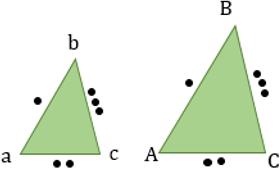
Признаки равенства прямоугольных треугольников.
1. Признак равенства прямоугольных треугольников по двум катетам.

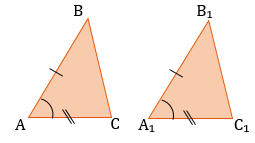
2. Признак равенства прямоугольных треугольников по катету и острому углу
Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
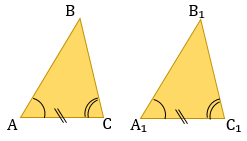
3. Признак равенства по гипотенузе и острому углу
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
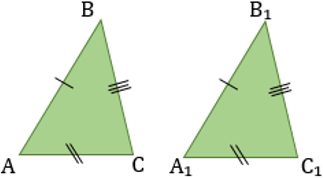
4. Признак равенства прямоугольных треугольников по катету и гипотенузе
Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
Основная теория для решения задач, смотрите здесь =>>>
Основное тригонометрическое тождество — знать его вы должны обязательно и вспомнить в любое время дня и ночи. Можно сказать что это основа для решения задач на прямоугольный треугольник. Формула «красивая» запоминается легко:
Из неё следуют следующие …
Синус в квадрате и косинус в квадрате:
*Их запоминать не нужно, всегда сможете вывести путём простейших преобразований, которые используете в уравнениях.
**Когда речь идёт об использовании этой формулы для решения прямоугольного треугольника, то перед корнем ставиться знак «+», так как углы в этом треугольнике острые, а мы знаем, что синус и косинус острого угла имеет положитльный знак.
Так же из неё получаем две другие необходимые формулы путём деления на квадрат синуса и квадрат косинуса:
Учить эти формулы не нужно, вы всегда их сможете вывести. Признаюсь сам я до сих пор их не выучил, когда нужны, вывожу их, правда устно.
Что ещё? Формулы тангенса и котангенса (выучить не сложно, выводить их будет длительнее, чем вспоминать, они просты):
Понятие синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике.
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла. Катеты — стороны, лежащие напротив острых углов.
Катет а, лежащий напротив угла альфа, называется противолежащим (по отношению к углу альфа). Другой катет b, который лежит на одной из сторон угла а, называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
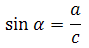
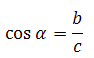
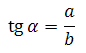
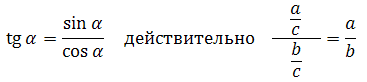
Без знания представленных определений задачи не решить. Нужно выучить!!! Проработайте определения многократно. Основная проблема в том, что учащиеся спустя время всё-таки путают в определениях синуса и косинуса — то ли прилежащий катет относится к гипотенузе, то ли противолежащий; в определениях тангенса и котангенса — то ли прилежащий катет относится к противолежащему, то ли наоборот.
По этому поводу обязательно будет статья, как быстро вспомнить эти отношения без ошибки. Постараюсь не затягивать! Вобще, темы для статей у меня в голове прибывают в геометрической прогрессии. Хочется Вам столько всего выдать, но времени маловато.
Ещё факт, который советую запомнить: синус одного острого угла в прямоугольном треугольнике равен косинусу другого острого угла в нём. И наоборот: косинус одного острого угла в прямоугольном треугольнике равен синусу другого.
Итого: основные соотношения для синуса, косинуса, тангенса и котангенса, которые пригодятся при решении задач:

В треугольнике АВС угол С равен 900, 
Если в условии нет данных о сторонах и углах, а есть только тригонометрические функции, то пользуйтесь формулами:
Сразу видно, что можно использовать формулу:
Остаётся из основного тригонометрического тождества sin2A + cos2A = 1 найти cosA:
Таким образом:
Ответ: 0,25
Дан прямоугольный треугольник АВС, угол C равен 900, 
Здесь необходимо найти тангенс другого острого угла. Как быть?
Воспользуемся формулой тангенса:
Мы знаем, что в прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла, и наоборот, то есть:
Найдём sin B.
Из основного тригонометрического тождества sin2A + cos2A = 1 найдём cos A:
Значит
Таким образом:
Ответ: 0,25
Дан прямоугольный треугольник АВС, угол C равен 900, tg A = 7/24. Найдите sin A.
Используем формулу:
Из неё мы без труда найдём cos2A, а далее используя формулу основного тригонометрического тождества sin2A + cos2A = 1, сможем определить синус:
Вычислим sin A:
Ответ: 0,28
*Обратите внимание, что мы вычислили не косинус, а квадрат косинуса, так как далее для вычислений нам нужен именно квадрат.
Дан прямоугольный треугольник АВС, C равен 900, АВ = 8, sin A = 0,5. Найдите BC.
Здесь нам дана сторона (гипотенуза) и синус угла.
Задача в одно действие, используется определение синуса:
Ответ: 4
Дан прямоугольный треугольник АВС, C равен 900, АВ = 7, tg =
В данной задаче через функцию тангенса мы можем выразить только катеты, но они нам неизвестны. Поэтому выразим её через функцию косинуса. Далее по определению косинуса, мы сможем найти АС, а затем по теореме Пифагора найдём ВС. Итак:
Следовательно:
По определению косинуса cos A = AC/АВ, значит можем найти АС:
Далее по теореме Пифагора вычислим ВС:
Таким образом, ВС = 4.
Ответ: 4
Дан прямоугольный треугольник АВС, угол C равен 900, АС = 24, ВС = 7. Найдите sin A.
Мы уже говорили, что если в задаче известны две стороны, то лучше сразу найти третью сторону по теореме Пифагора. Зная все три стороны в прямоугольном треугольнике, мы всегда без труда найдём значение любой тригонометрической функции любого угла.
По теореме Пифагора:
По определению синуса:
Ответ: 0,28
Дан прямоугольный треугольник АВС, угол C равен 900, 
По определению косинуса cos A = АС/АВ, значит:
Сторона АС нам известна, найдём cos A.
Из основного тригонометрического тождества:
Таким образом:
Ответ: 28
Если вы найдёте более рациональные пути решения подобных задач, это будет замечательно, я лишь преследовал цель показать вам основные приёмы и необходимые формулы. Способов решения каждой подобной задачи на самом деле, не менее трёх.
Решите самостоятельно:
Посмотреть решения: 27217, 27219, 27220, 27226, 27228, 27231, 27232, 27236, 27240, 27243, 27251, 27246, 27255.
В будущем мы так же будем разбирать и другие задачи на решение прямоугольного треугольника отличные от предоставленных, но теории уже касаться не буду. Надеюсь, материал был вам полезен.
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
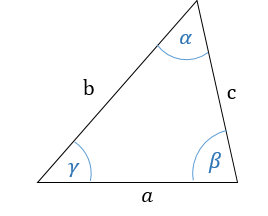
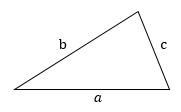
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
СВОЙСТВА ТРЕУГОЛЬНИКА:
1. Сумма углов в треугольнике равна α + β + γ = 180°.
2. Против большей стороны находится больший угол; против меньшего угла находится меньшая сторона. Отсюда следует, что если:
a < b < c, то α < β < γ и наоборот.
3. Сумма длин двух любых сторон треугольника всегда больше длины третьей стороны:
a + b > c.
Если это правило не выполняется — треугольник не существует.
4. Формулы площади треугольника:
|
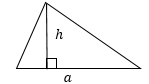
1 (через высоту) |
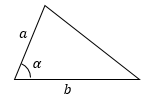
2 (через две стороны и синус угла между ними) |
3 (формула Герона) |
|
|
|
|
|
|
|
|
|
Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне. |
Площадь треугольника равна половине произведения его сторон на синус угла между ними. |
Площадь треугольника равна квадратному корню из произведения его полупериметра на разности полупериметра и каждой из его сторон. |
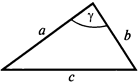
5. Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
с² = а² + b² – 2ab · cosγ
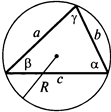
6. Теорема синусов: Отношения сторон треугольника к синусам противоположных им углов равны. Это отношение равно 2R, где R — радиус описанной окружности.
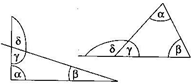
7. Внешний угол треугольника — δ, является смежным с одним из внутренних углов (сумма = 180°). Из этого следует, что внешний угол равен сумме двух внутренних, но не смежных с ним, углов треугольника (α + β = δ).
ВИДЫ ТРЕУГОЛЬНИКОВ:
Треугольники бывают:
- остроугольными (если все его углы острые),
- тупоугольными (если один из его углов тупой),
- прямоугольными (если один из его углов прямой).
Треугольник называется:
- равнобедренным, если две его стороны равны;
- равносторонним, если все три стороны равны;
- разносторонним, если все его стороны разные.
ЭЛЕМЕНТЫ ТРЕУГОЛЬНИКА:
БИССЕКТРИСА
Биссектриса ― луч, который соединяет вершину треугольника с противоположной стороной, при этом разделяя угол на две равные части.
Свойства биссектрисы треугольника:
1. Все три биссектрисы треугольника пересекаются в одной точке. Эта точка — центр вписанной в треугольник окружности.
2. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам.
3. Формулы для биссектрисы треугольника. Если а и b — стороны треугольника, γ — угол между ними, l — биссектриса треугольника, проведённая из вершины этого угла, а а’ и b’ — отрезки, на которые биссектриса делит третью сторону треугольника, то
МЕДИАНА
Медиана ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Свойства медианы треугольника:
1. Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и точкой пересечения делятся в отношении 2 к 1, считая от вершины.
- Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
- Треугольник делится тремя медианами на шесть равновеликих треугольников.
- В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
- Формула для медианы треугольника. Если стороны треугольника a и b, mc — медиана треугольника, проведённая к стороне c, то
ВЫСОТА
Высота — перпендикуляр, опущенный из вершины треугольника на противоположную сторону (точнее, на прямую, содержащую противоположную сторону).
В зависимости от типа треугольника высота может содержаться:
- внутри треугольника (для остроугольного треугольника),
- совпадать с его стороной (являться катетом прямоугольного треугольника),
- проходить вне треугольника (для тупоугольного треугольника).
Свойства высоты треугольника:
1. Все три высоты треугольника пересекаются в одной точке, которая называется ортоцентром.
2. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
3. Если в треугольнике две высоты равны, то треугольник — равнобедренный.
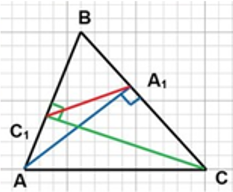
4. Если CC₁ и АА₁ — высоты треугольника АВС, то треугольник ВА₁С₁ подобен треугольнику АВС, причём коэффициент подобия равен cos B.
Сложные теоремы:
5. Если Н — точка пересечения высот треугольника AВС, а О — центр его описанной окружности, то отрезок АН вдвое больше расстояния от точки О до середины стороны ВС. То есть AH = 2OM.
6. Если Н — точка пересечения высот треугольника AВС, М — точка пересечения медиан треугольника AВС, а О — центр его описанной окружности, то точки О, H и М лежат на одной прямой (прямая Эйлера), причём точка М лежит на отрезке ОН и ОМ : МН = 1 : 2.
СРЕДИННЫЙ ПЕРПЕНДИКУЛЯР
Срединный перпендикуляр треугольника — прямая, перпендикулярная стороне треугольника и проходящая через его середину.
Все три срединных перпендикуляра треугольника пересекаются в одной точке, которая является центром описанной около треугольника окружности.
СРЕДНЯЯ ЛИНИЯ
Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника
Свойства средней линии треугольника:
- Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине:
MN||BC,MN = 1/2 BC
- В любом треугольнике три средних линии, при пересечении которых образуются 4 равных треугольника, подобных исходному с коэффициентом 1/2.
ПОДОБИЕ И РАВЕНСТВО ТРЕУГОЛЬНИКОВ
|
Подобные треугольники |
Равные треугольники |
|
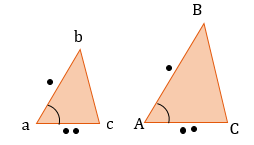
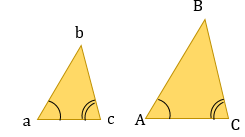
Треугольники подобны, если их углы равны. В подобных фигурах сохраняется отношение между соответствующими сторонами и другими линейными величинами (высоты, медианы, биссектрисы и периметры): Также сохраняется внутреннее отношение длин: |
Два треугольника равны, если у них соответствующие стороны равны и соответствующие углы равны (треугольники равны, если их можно совместить наложением). |
|
Признаки подобия треугольников: 1. По двум пропорциональным сторонам и углу между ними: 2. 3. По двум равным углам (тогда и третьи тоже будут равны) 4. 5. По трем пропорциональным сторонам: |
Признаки равенства треугольников: 1. По двум сторонам и углу между ними: 2. По стороне и двум прилежащим к ней углам. 3. По трем сторонам. |
ОСОБЫЕ ТРЕУГОЛЬНИКИ И ИХ СВОЙСТВА:
«Особенными», то есть обладающими какими — то дополнительными свойствами, считаются:
- равнобедренный,
- равносторонний
- прямоугольный треугольники.
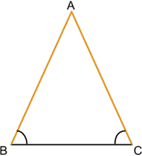
РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
Равнобедренный треугольник ― это треугольник, у которого две стороны равны (АВ = АС).
Равные стороны (АВ и АС) в таком треугольнике называются боковыми, а оставшаяся третья сторона (ВС) ― основанием.
Свойства равнобедренного треугольника:
1. Углы при основании равны (∠АВС = ∠АСВ).
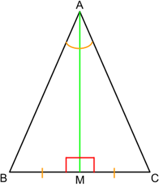
2. Медиана, проведённая к основанию, является биссектрисой и высотой. То есть она не только делит противолежащую сторону пополам (ВМ = МС), но и падает на неё под углом 90°, а кроме того делит угол, из которого выходит, пополам (∠ВАМ = ∠МАС).
Посмотрим на пример конкретной задачи. В равнобедренном треугольнике внешний угол равен 80°, необходимо найти все углы треугольника. Сразу возникает вопрос ― внешний угол при каком угле треугольника? Предположим, что это внешний угол при угле В (с нашего первого рисунка). Но в таком случае выходит, что сам ∠В = 100° (по сумме смежных углов). Значит, и ∠С = 100°, так как треугольник равнобедренный. Но тогда сумма только двух углов получается 200°, чего быть никак не может. Значит, речь идёт о внешнем угле при угле А треугольника. Тогда ∠А = 100°, а ∠В = ∠С = 40°.
РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК
Равносторонний треугольник ― треугольник, у которого все три стороны равны
Свойства равностороннего треугольника:
1. Кроме равенства сторон в таком треугольнике равны и все углы (каждый из которых по 60° ― так как 180°/3 = 60°).
2. Медиана, проведённая из любого угла, будет являться биссектрисой и высотой (другими словами, равносторонний треугольник с любой стороны является равнобедренным).
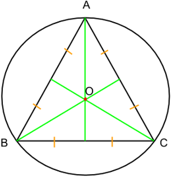
1. Центры вписанной и описанной окружностей совпадают.
2. Формулы 2 и 3 для площади треугольника превращаются в одну формулу:
— Через синус (так как все стороны равны и каждый угол равен 60°):
— Формула Герона (так как все стороны равны):
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Прямоугольный треугольник ― треугольник, у которого один угол равен 90° (собственно, это и есть прямой угол, дающий название всему треугольнику). Сторона, лежащая против такого угла, называется гипотенузой (АВ), а две другие стороны ― катетами (АС и ВС).
Свойства прямоугольного треугольника:
1. В любом прямоугольном треугольнике гипотенуза всегда больше катета (против большего угла лежит большая сторона, и наоборот).
2. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов
АВ2 = АС2 + ВС2
Теорема, обратная теореме Пифагора: Если для сторон произвольного треугольника выполняется отношение АВ2= АС2 + ВС2, то треугольник является прямоугольным.
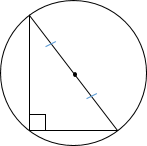
3. Центр описанной вокруг прямоугольного треугольника окружности всегда лежит на середине гипотенузы (доказательство: прямой ∠С становится вписанным, а против вписанного угла в 90° всегда лежит диаметр ― значит, гипотенуза является диаметром).
Высота, проведенная к гипотенузе, разбивает треугольник на два подобных прямоугольных треугольника, каждый из которых подобен исходному треугольнику
4. Высота, проведенная к гипотенузе, равна:
- Произведению катетов, деленному на гипотенузу
- Среднему геометрическому из произведений отрезков, на которые гипотенуза делится высотой
5. Медиана, проведенная к гипотенузе равна половине гипотенузы, то есть радиусу описанной около треугольника окружности.
6. Формулы площади прямоугольного треугольника:
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
Площадь прямоугольного треугольника равна половине произведения его катетов. |
Площадь прямоугольного треугольника равна половине произведения гипотенузы на опущенную к ней высоту. |
Площадь прямоугольного треугольника равна половине произведения его катета, гипотенузы и синуса угла между ними. |
ЗОЛОТОЙ И СЕРЕБРЯНЫЙ ТРЕУГОЛЬНИКИ:
|
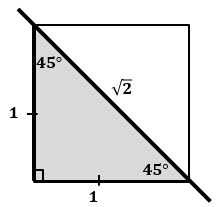
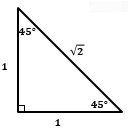
Серебряный треугольник — треугольник с углами 45°, 45° и 90° (разрубленный по диагонали квадрат) Отношение сторон в серебряном треугольнике: |
— треугольник с углами 30°, 60° и 90°. Отношение сторон в золотом треугольнике: |
Пропорциональные отрезки в прямоугольном треугольнике
Следующие соотношения позволяют найти стороны и углы прямоугольного треугольника по любым двум элементам (сторонам или стороне и углу).
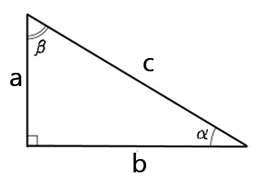
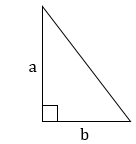
Рис. (1). Прямоугольный треугольник
Теорема Пифагора:c2=a2+b2;a2=c2−b2;b2=c2−a2.
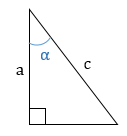
sinα=ac;cosα=bc;tgα=ab;ctgα=ba.
cos2α+sin2α=1;tgα⋅ctgα=1.
Очень важные соотношения можно получить, заметив, что
∠DCB=∠CAD;∠DBC=∠ACD.
Мы получаем три пары подобных треугольников:
ΔACD∼ΔCBD;ΔACD∼ΔABC;ΔCBD∼ΔABC.
Из подобий:
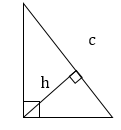
ΔACD∼ΔCBD:ACCB=CDBD=ADCD;ba=hac=bch⇒h2=ac⋅bc.
ΔACD∼ΔABC:ACAB=CDBC=ADAC;bc=ha=bcb⇒b2=c⋅bc.
ΔCBD∼ΔABC:CBAB=BDBC=CDAC;ac=aca=hb⇒a2=c⋅ac.
Из последних соотношений можно получить ещё одно важное соотношение:
ac=hb⇒h=abc.
Это же равенство можно получить, используя две формулы для вычисления площади прямоугольного треугольника:
S=12ab=12hc⇒ab=hc⇒h=abc.
Отметим ещё одно важное свойство медианы прямоугольного треугольника, проведённого к гипотенузе.
Рис. (2). Дополнительные построения
Как видно из рисунка, если мы достроим прямоугольный треугольник до прямоугольника, то окажется, что медиана (CO) — это половина диагонали прямоугольника, а следовательно, и гипотенузы.
mc=c2.
Источники:
Рис. 1. Прямоугольный треугольник. © ЯКласс.
Рис. 2. Дополнительные построения. © ЯКласс.































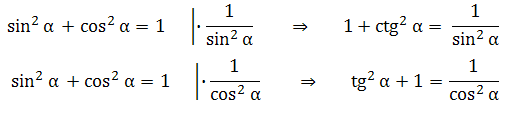
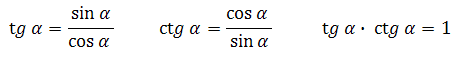
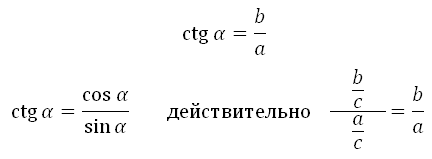
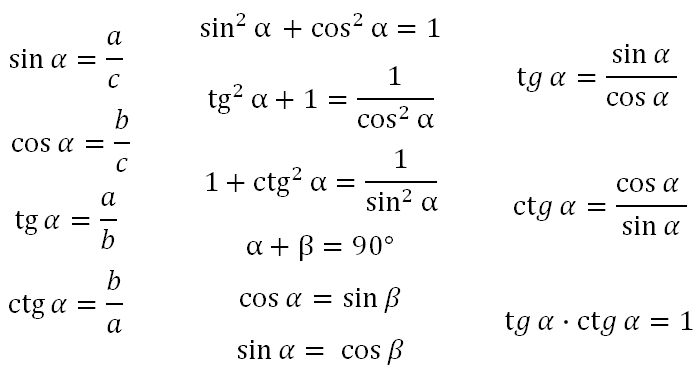















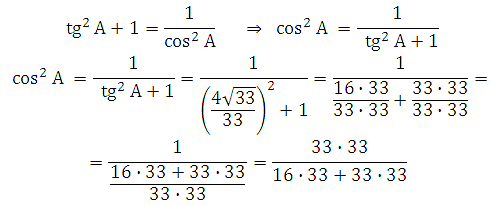































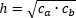




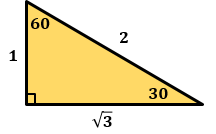 Золотой треугольник
Золотой треугольник

