25
Июл 2013
Категория: Справочные материалы
Трапеция. Свойства трапеции
2013-07-25
2016-06-15
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
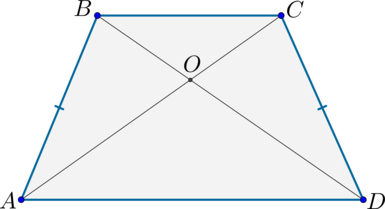
Если боковые стороны равны, трапеция называется равнобедренной.
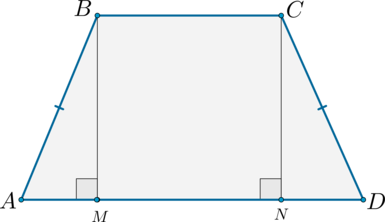
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.
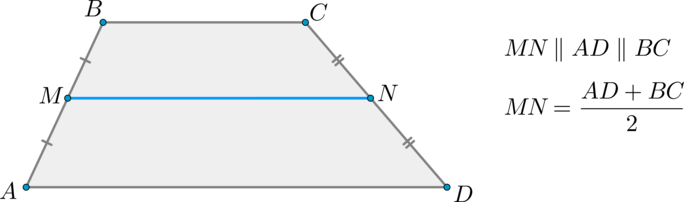
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и
, образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и
, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
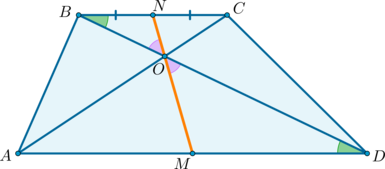
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
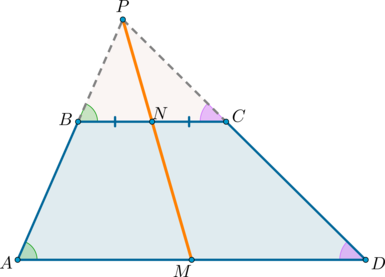
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка —
и
, то
Площадь
или
где
– средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Смотрите также площадь трапеции.
Автор: egeMax |
комментарий 431
Печать страницы
Трапеция и ее свойства
Т. А. Унегова
Определения:
Трапеция — это называется четырехугольник, у которого две стороны параллельны, а две другие — не параллельны.
Параллельные стороны называются основаниями трапеции, а непараллельные — боковыми сторонами трапеции.
Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.
Если боковые стороны равны, трапеция называется равнобедренной.
Высотой трапеции называется перпендикуляр, проведенный из любой точки одного из оснований трапеции к прямой, содержащей другое основание.
Трапеция называется вписанной в окружность, если каждая ее вершина принадлежит окружности.
Трапеция называется описанной вокруг окружности, если каждая ее сторона касается окружности.
Трапеция называется равнобедренной (равнобокой, равнобочной), если ее боковые стороны равны.
Трапеция, один из углов которой прямой, называется прямоугольной.
Теоремы о средней линии и диагоналях трапеции
Теорема 1. Средняя линия трапеции параллельна основаниям и равна их полусумме: .
Теорема 2. Диагонали трапеции делят среднюю линию трапеции на три отрезка. Средний из них равен полуразности оснований, а два крайних равны между собой: .
Теорема 3. Средняя линия треугольника, составленного из диагоналей и суммы оснований трапеции, равна средней линии трапеции: .
Теорема 4. Четыре точки: середины оснований трапеции, точка пересечения ее диагоналей и точка пересечения продолжений ее боковых сторон — лежат на одной прямой.
Эта теорема называется также «Замечательное свойство трапеции».
Теорема 5. Диагонали трапеции делят ее на четыре треугольника. Два из них, содержащие боковые стороны, равновелики (имеют равные площади), а два других, содержащие основания, подобны.
Теоремы о площади трапеции
Теорема 6. Площадь трапеции равна произведению полусуммы ее оснований на высоту: .
Теорема 7. Площадь трапеции равна произведению ее средней линии на высоту: .
Теорема 8. Площадь трапеции (как и всякого выпуклого четырехугольника) равна половине произведения ее диагоналей на синус угла между ними: , где
(Вместо
можно брать
Теорема 9. Если в трапецию можно вписать окружность, то (как и для всякого описанного многоугольника) площадь трапеции равна произведению ее полупериметра на радиус вписанной окружности: . Таким образом,
.
Теорема 10. Площадь трапеции равна площади треугольника, составленного из диагоналей и суммы оснований этой трапеции. (Сравни эту теорему и теорему 3.)
Теоремы о вписанных и описанных трапециях
Теорема 11. Если трапеция вписана в окружность, то она равнобедренная. И наоборот, если трапеция равнобедренная, то около нее можно описать окружность.
Теорема 12. Если трапеция описана около окружности, то сумма оснований трапеции равна сумме ее боковых сторон.
Задачи ЕГЭ и ОГЭ по теме: Трапеция
Задача 1.
Найдите высоту трапеции ABCD, опущенную из вершины B, если стороны квадратных клеток равны .
Решение:
Высота трапеции— это отрезок, перпендикулярный ее основаниям. Проведем высоту из вершины . Так как сторона квадратной клетки равна
, то по теореме Пифагора получаем, что
.
Ответ: 2.
Задача 2.
Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол . Найдите площадь трапеции.
Решение:
Углы ABC и
BAH — односторонние, их сумма равна
, и тогда
BAH
Из ABH найдем высоту BH. Катет, лежащий против угла в
, равен половине гипотенузы. Получаем, что BH = 3,5.
Площадь трапеции равна .
Ответ: 42.
Задача 3.
Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции ее диагональ.
Решение:
Что можно увидеть на чертеже? Можно сказать, что изображена трапеция ABCD, и в ней проведена средняя линия. А можно увидеть и другое — два треугольника, ABC и ACD, в которых проведены средние линии.
Напомним, что средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. Средняя линия треугольника параллельна третьей его стороне и равна половине этой стороны. Из ACD находим, что
Ответ: 5.
Задача 4.
Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.
Решение:
Проведем PQ — среднюю линию трапеции, PQ = 2,5 и . Отсюда получаем, что
середина отрезка AC, то есть PM — средняя линия треугольника ABC и PM = 1. Аналогично, NQ = 1.
Ответ: 0,5.
Задача 5.
Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.
Решение:
Периметр треугольника равен сумме его сторон, то есть
Периметр трапеции равен
Ответ: 23.
Задача 6.
В равнобедренной трапеции ABCD диагональ AC является биссектрисой острого угла трапеции и образует со стороной CD угол . Найдите углы трапеции.
Решение:
Пусть CAD
, тогда
CAB
и
BAD
, так как трапеция равнобедренная.
Сумма углов , откуда
Итак, , а
.
Ответ: .
Задача 7.
В равнобедренной трапеции основания равны 10 м и 24 м, боковая сторона 25 м. Найдите высоту трапеции.
Решение:
В равнобедренной трапеции проведем высоты. Получим прямоугольник и два равных прямоугольных треугольника. Тогда основание каждого треугольника равно 7 и Отсюда,
Ответ: 24.
Задача 8.
Тупой угол равнобедренной трапеции равен , а высота, проведенная из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции.
Решение:
Проведем две высоты. Они разделят трапецию на три части: прямоугольник и два равных прямоугольных треугольника с острым углом .
Каждый треугольник равнобедренный, поэтому h = 1,4.
Нетрудно видеть, что верхнее основание трапеции равно 2, а нижнее — 4,8. Отсюда площадь трапеции равна .
Ответ: 4,76.
Задача 9.
Площадь трапеции равна 60м а основания 8 м и 12 м. Найдите высоту трапеции.
Решение:
Так как площадь трапеции , то
, откуда h = 6.
Ответ: 6.
Задача 10.
В равнобедренной трапеции диагонали перпендикулярны и равны Найдите площадь трапеции.
Решение:
Проведем CE BD и DE — продолжение AD.
Так как BCDE — параллелограмм, то CE = a.
По теореме 10 получим, что .
Ответ:
Задач 11.
В трапеции ABCD с большим основанием AD диагональ AC перпендикулярна к боковой стороне CD и является биссектрисой угла A.
Найдите AD, если периметр трапеции равен 20, а угол D равен .
Решение:
По условию задачи в прямоугольном ACD
D
, следовательно,
CAD
.
Так как AC — биссектриса, то CAB
, откуда
DAB
, то есть, трапеция равнобедренная.
BCA
CAD
как накрест лежащие, поэтому
ABC — равнобедренный.
Обозначим длины боковых сторон ABC буквой x.
Тогда AB = BC = CD = x, и AD = 2x, так как в прямоугольном ACD против угла в
лежит катет, равный половине гипотенузы.
Таким образом, периметр трапеции, равный 20, составляет 5x, отсюда
x = 4 и AD = 8.
Ответ: 8.
Задача 12.
В равнобедренной трапеции ABCD с острым углом меньшее основание BC равно 2, а боковая сторона AB равна 10. Продолжения боковых сторон трапеции пересекаются в точке M. Во сколько раз площадь трапеции больше площади треугольника BCM?
Решение:
Нетрудно видеть, что BCM равносторонний и BM = 2, тогда AM = 12 и
BCM подобен
ADM c коэффициентом
.
Пусть,
, тогда
Площадь трапеции будет равна
Ответ: 35.
Задача 13.
Сумма углов при одном из оснований трапеции равна . Найдите длину отрезка, соединяющего середины оснований, если основания равны 6 и 10.
Решение:
Продолжим боковые стороны до пересечения в точке E и отметим точки F и G — середины оснований трапеции.
Так как сумма углов при основании трапеции равна , то
, поэтому EF и EG — медианы в прямоугольных треугольниках BEC и AED соответственно.
Известно, что медиана, проведенная к гипотенузе, равна ее половине, значит
Ответ: 2.
Задача 14.
Найдите радиус окружности, вписанной в равнобочную трапецию, если средняя линия трапеции равна 10, а ее площадь 24.
Решение:
Так как площадь трапеции равна , а высота трапеции равна диаметру вписанной окружности, то есть
то
, откуда
.
Ответ: 1,2.
Задача 15.
Периметр прямоугольной трапеции равен 32, а большая боковая сторона равна 10. Найдите радиус r вписанной в трапецию окружности.
Решение:
По свойствам описанной трапеции сумма ее боковых сторон равна сумме оснований, поэтому
откуда
Сторона AB равна диаметру окружности, поэтому .
Ответ: 3.
Задача 16.
Около окружности описана трапеция, сумма боковых сторон которой равна 40. Найдите длину ее средней линии.
Решение:
Длина средней линии трапеции равна полусумме оснований. Если трапеция описана вокруг окружности, то в ней сумма оснований равна сумме боковых сторон, поэтому
Ответ: 20.
Задача 17.
В окружность вписана трапеция так, что диаметр окружности служит основанием трапеции, а вершины другого основания делят полуокружность на три равные части. Найдите тупые углы трапеции. Ответ выразите в градусах.
Решение:
Так как AD — диаметр окружности, то дуга ABCD равна . Она делится на три равные части по
Вписанный угол D опирается на дугу ABC, которая равна , отсюда
и, стало быть,
Ответ: 120.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Трапеция и ее свойства» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
Свойства трапеции
Итак, что ты должен знать о свойствах трапеции…
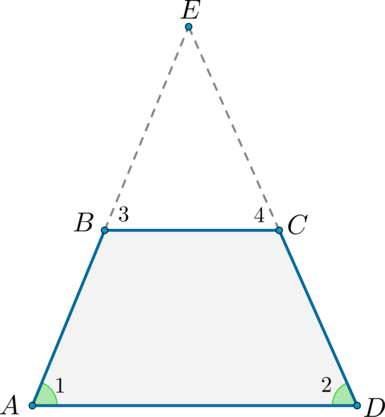
Сумма углов при каждой боковой стороне трапеции равна 180°. (у нас на рисунке ( displaystyle angle 1+angle 2=180{}^circ ) и ( displaystyle angle 3+angle 4=180{}^circ ))
Почему так?
Ну, конечно, просто потому, что основания – параллельны, а боковая сторона – секущая.
Вот и получается, что ( displaystyle angle 1) и ( displaystyle angle 2) – внутренние односторонние углы при параллельных ( displaystyle AD) и ( displaystyle BC) и секущей ( displaystyle AB).
Поэтому ( displaystyle angle 1+angle 2=180{}^circ ).
И точно так же ( displaystyle angle 3) и ( displaystyle angle 4) – внутренние односторонние углы при тех же параллельных ( displaystyle AD) и ( displaystyle BC), но секущая теперь – ( displaystyle CD).
Видишь: главное, что играет роль – это параллельность оснований. Давай разберем еще некоторые свойства трапеции.
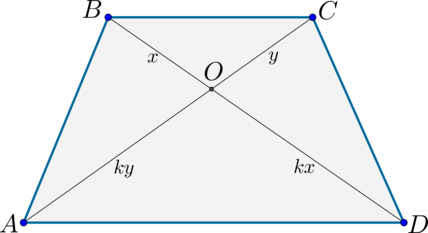
Как у всякого четырехугольника, у трапеции есть диагонали. Их две – посмотри на рисунки:
Снова порассуждаем об углах:
Опять ( displaystyle AD) и ( displaystyle BC) – параллельные, а диагональ ( displaystyle AC) – секущая. Поэтому ( displaystyle angle 1=angle 2).
А теперь рассмотрим сразу 2 диагонали и 4 угла:
( displaystyle angle 1=angle 2)
( displaystyle angle 3=angle 4)
Что из этого может следовать?
Очень важный факт:
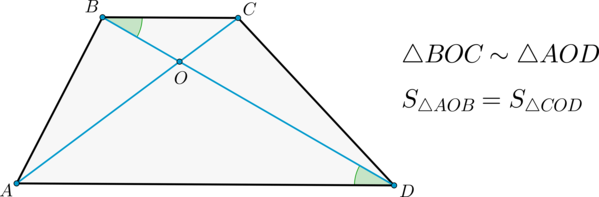
Треугольники ( displaystyle BOC) и ( displaystyle AOD) – подобны по двум углам.
Их коэффициент подобия равен отношению оснований: ( displaystyle K=frac{a}{b}).
Трапеция и её свойства
Трапеция: определение.
Трапеция — четырехугольник, две стороны которого параллельны, а две другие не параллельны.
AD, ВС — основания; AB, CD — боковые стороны.
Средняя линия — отрезок, соединяющий середины боковых сторон.
Высота трапеции — перпендикуляр, проведенный из любой точки одного основания на другое или его продолжение (расстояние между прямыми оснований).
Трaпеция встречается впервые у греческого математика Посидония (I в.). О том, что средняя линия трапеции равна половине суммы ее оснований, было известно еще древним египтянам (не позже II в. до н.э.).
Слово «трапeция» — греческое. Оно когда-то означало «столик». Этот термин и слово «трапеза» имеют общее происхождение. Слово «трапеза» дословно означает «застолье».
Свойства и признаки трапеции
Свойства трапеции
- Основания трапеции параллельны.
- Средняя линия трапеции параллельна основаниям и равна полусумме оснований.
- Сумма углов, прилегающих к боковой стороне, равна 180°.
- Средняя линия делит любой отрезок с концами, лежащими на прямых, проведенных через основания, пополам.
Признак трапеции
Если в четырехугольнике сумма углов, прилегающих к одной стороне, равна 180°, а сумма углов, прилегающих к соседней стороне, не равна 180°, то он будет трапецией.
Дополнительные свойства трапеции
1. Середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон трапеции лежат на одной прямой.
2. Треугольники, образованные боковыми сторонами и отрезками диагоналей, равновелики.
3. Треугольники, образованные основаниями и отрезками диагоналей, подобны.
Частные случаи трапеции
Равнобокая, или равнобедренная, трапеция — это трaпеция с равными боковыми сторонами (AB = CD).
Свойства равнобедренной трапеции: 1) углы при основании равны (∠A = ∠D); 2) диагонали равны (AC = BD);
Признак равнобедренной трапеции: Если ∠A = ∠D или AC = BD, то AB = CD.
Прямоугольная трапеция — это трапeция, у которой одна боковая сторона перпендикулярна основаниям.
Таблица. Трапеция и её свойства
Это конспект по теме «Трапеция и её свойства». Выберите дальнейшие действия:
- Перейти к следующему конспекту:
- Вернуться к Списку конспектов по геометрии
Трапеция ― это четырёхугольник, у которого две противоположные стороны параллельны и ОБЯЗАТЕЛЬНО не равны (потому что в этом случае эта фигура будет является параллелограммом).
Элементы трапеции:
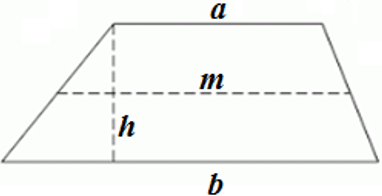
a и b ― основания трапеции, a || b;
h ― высота трапеции (расстояние между основаниями);
m ― средняя линия трапеции (отрезок, соединяющий середины боковых сторон трапеции).
Средняя линия трапеции равна полусумме оснований: $m = frac{a + b}{2}$ и параллельна им: m || a и m || b.
Виды трапеций:
1) Прямоугольная ― трапеция, имеющая прямые углы при боковой стороне:
- боковая сторона является высотой.
2) Равнобедренная ― трапеция, у которой боковые стороны равны:
- углы при основаниях равны
- длины диагоналей равны
3) Произвольная ― не является ни прямоугольной, ни равнобедренной.
Свойства трапеции:
- Сумма внутренних углов трапеции (как и любого четырехугольника) равна 360°.
- Сумма углов, прилежащих к боковой стороне, равна 180°.
- В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
- Если трапецию можно вписать в окружность, то трапеция ― равнобедренная.
- Около равнобедренной трапеции можно описать окружность.
- Треугольники BOC и AOD подобны по двум углам. (∠1=∠2, ∠3=∠4 – как накрест лежащие).
Площадь трапеции:
|
1 |
2 |
3 |
|
|
|
|
|
$S = frac{a + b}{2}cdot h$ |
S = m ∙ h, где m ― средняя линия трапеции. |
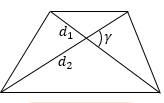
$S = frac{1}{2}d_1d_2sin gamma$ |
|
Площадь трапеции равна произведению полусуммы оснований на высоту. |
Площадь трапеции равна произведению средней линии на высоту. |
Площадь трапеции равна половине произведения диагоналей синус угла между ними. |
[{Large{text{Произвольная трапеция}}}]
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.
Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.
Теоремы: свойства трапеции
1) Сумма углов при боковой стороне равна (180^circ).
2) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.
Доказательство
1) Т.к. (ADparallel BC), то углы (angle BAD) и (angle ABC) – односторонние при этих прямых и секущей (AB), следовательно, (angle
BAD
+angle ABC=180^circ).
2) Т.к. (ADparallel BC) и (BD) – секущая, то (angle DBC=angle
BDA) как накрест лежащие.
Также (angle BOC=angle AOD) как вертикальные.
Следовательно, по двум углам (triangle BOC sim triangle AOD).
Докажем, что (S_{triangle AOB}=S_{triangle COD}). Пусть (h) – высота трапеции. Тогда (S_{triangle ABD}=frac12cdot hcdot
AD=S_{triangle ACD}). Тогда: [S_{triangle AOB}=S_{triangle ABD}-S_{triangle AOD}=S_{triangle ACD}-S_{triangle AOD}=S_{triangle
COD}]
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
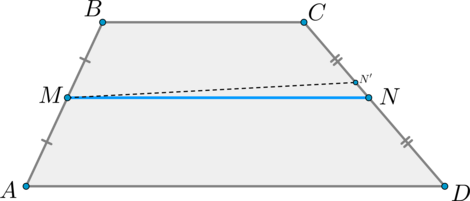
1) Докажем параллельность.
Проведем через точку (M) прямую (MN’parallel AD) ((N’in CD)). Тогда по теореме Фалеса (т.к. (MN’parallel ADparallel BC, AM=MB)) точка (N’) — середина отрезка (CD). Значит, точки (N) и (N’) совпадут.
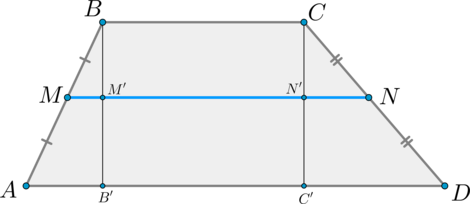
2) Докажем формулу.
Проведем (BB’perp AD, CC’perp AD). Пусть (BB’cap MN=M’, CC’cap
MN=N’).
Тогда по теореме Фалеса (M’) и (N’) — середины отрезков (BB’) и (CC’) соответственно. Значит, (MM’) – средняя линия (triangle
ABB’), (NN’) — средняя линия (triangle DCC’). Поэтому: [MM’=dfrac12 AB’, quad NN’=dfrac12 DC’]
Т.к. (MNparallel ADparallel BC) и (BB’, CC’perp AD), то (B’M’N’C’) и (BM’N’C) – прямоугольники. По теореме Фалеса из (MNparallel AD) и (AM=MB) следует, что (B’M’=M’B). Значит, (B’M’N’C’) и (BM’N’C) – равные прямоугольники, следовательно, (M’N’=B’C’=BC).
Таким образом:
[MN=MM’+M’N’+N’N=dfrac12 AB’+B’C’+dfrac12 C’D=] [=dfrac12 left(AB’+B’C’+BC+C’Dright)=dfrac12left(AD+BCright)]
Теорема: свойство произвольной трапеции
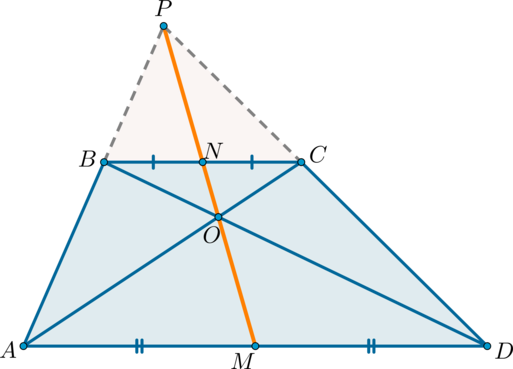
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки (P), (N) и (M) лежат на одной прямой.
Проведем прямую (PN) ((P) – точка пересечения продолжений боковых сторон, (N) – середина (BC)). Пусть она пересечет сторону (AD) в точке (M). Докажем, что (M) – середина (AD).
Рассмотрим (triangle BPN) и (triangle APM). Они подобны по двум углам ((angle APM) – общий, (angle PAM=angle PBN) как соответственные при (ADparallel BC) и (AB) секущей). Значит: [dfrac{BN}{AM}=dfrac{PN}{PM}]
Рассмотрим (triangle CPN) и (triangle DPM). Они подобны по двум углам ((angle DPM) – общий, (angle PDM=angle PCN) как соответственные при (ADparallel BC) и (CD) секущей). Значит: [dfrac{CN}{DM}=dfrac{PN}{PM}]
Отсюда (dfrac{BN}{AM}=dfrac{CN}{DM}). Но (BN=NC), следовательно, (AM=DM).
2) Докажем, что точки (N, O, M) лежат на одной прямой.
Пусть (N) – середина (BC), (O) – точка пересечения диагоналей. Проведем прямую (NO), она пересечет сторону (AD) в точке (M). Докажем, что (M) – середина (AD).
(triangle BNOsim triangle DMO) по двум углам ((angle OBN=angle
ODM) как накрест лежащие при (BCparallel AD) и (BD) секущей; (angle BON=angle DOM) как вертикальные). Значит: [dfrac{BN}{MD}=dfrac{ON}{OM}]
Аналогично (triangle CONsim triangle AOM). Значит: [dfrac{CN}{MA}=dfrac{ON}{OM}]
Отсюда (dfrac{BN}{MD}=dfrac{CN}{MA}). Но (BN=CN), следовательно, (AM=MD).
[{Large{text{Равнобедренная трапеция}}}]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию (ABCD).
Из вершин (B) и (C) опустим на сторону (AD) перпендикуляры (BM) и (CN) соответственно. Так как (BMperp AD) и (CNperp AD), то (BMparallel CN); (ADparallel BC), тогда (MBCN) – параллелограмм, следовательно, (BM = CN).
Рассмотрим прямоугольные треугольники (ABM) и (CDN). Так как у них равны гипотенузы и катет (BM) равен катету (CN), то эти треугольники равны, следовательно, (angle DAB = angle CDA).
2)
Т.к. (AB=CD, angle A=angle D, AD) – общая, то по первому признаку (triangle ABD=triangle ACD). Следовательно, (AC=BD).
3) Т.к. (triangle ABD=triangle ACD), то (angle BDA=angle CAD). Следовательно, треугольник (triangle AOD) – равнобедренный. Аналогично доказывается, что и (triangle BOC) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Рассмотрим трапецию (ABCD), такую что (angle A = angle D).
Достроим трапецию до треугольника (AED) как показано на рисунке. Так как (angle 1 = angle 2), то треугольник (AED) равнобедренный и (AE
= ED). Углы (1) и (3) равны как соответственные при параллельных прямых (AD) и (BC) и секущей (AB). Аналогично равны углы (2) и (4), но (angle 1 = angle 2), тогда (angle 3 = angle 1 = angle 2 =
angle 4), следовательно, треугольник (BEC) тоже равнобедренный и (BE = EC).
В итоге (AB = AE — BE = DE — CE = CD), то есть (AB = CD), что и требовалось доказать.
2) Пусть (AC=BD). Т.к. (triangle AODsim triangle BOC), то обозначим их коэффициент подобия за (k). Тогда если (BO=x), то (OD=kx). Аналогично (CO=y Rightarrow AO=ky).
Т.к. (AC=BD), то (x+kx=y+ky Rightarrow x=y). Значит (triangle AOD) – равнобедренный и (angle OAD=angle ODA).
Таким образом, по первому признаку (triangle ABD=triangle ACD) ((AC=BD, angle OAD=angle ODA, AD) – общая). Значит, (AB=CD), чтд.
Трапеция, подготовка к ЕГЭ по математике
- 22.12.2017
Таблицы с теорией на тему: «Трапеция» для подготовки к ЕГЭ по математике. В кратком содержании изложена вся необходимая теория для этой темы.
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Сохранить ссылку:
Комментарии (0)
Добавить комментарий
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Имя (обязательное)
E-Mail
Подписаться на уведомления о новых комментариях
Отправить