Public user contributions licensed under
cc-wiki license with attribution required
На уроке рассматривается разбор 2 задания ЕГЭ по информатике, дается подробное объяснение того, как решать подобные задачи
Содержание:
- Объяснение задания 2 ЕГЭ по информатике
- Таблицы истинности и порядок выполнения логических операций
- Решение заданий 2 ЕГЭ по информатике
- Задания для тренировки
2-е задание: «Таблицы истинности»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 3 минуты.
Проверяемые элементы содержания: Умение строить таблицы истинности и логические схемы
Типичные ошибки и рекомендации по их предотвращению:
«Игнорирование прямо указанного в условии задания требования, что заполненная таблица истинности не должна содержать одинаковых строк. Это приводит к внешне правдоподобному, но на самом деле неверному решению»
ФГБНУ «Федеральный институт педагогических измерений»
Таблицы истинности и порядок выполнения логических операций
Для логических операций приняты следующие обозначения:
| операция | пояснение | в программировании |
|---|---|---|
| ¬ A, A | не A (отрицание, инверсия) | not(A) |
| A ∧ B, A ⋅ B | A и B (логическое умножение, конъюнкция) | A and B |
| A ∨ B, A + B | A или B (логическое сложение, дизъюнкция) | A or B |
| A → B | импликация (следование) | A <= B |
| A ↔ B, A ≡ B, A ∼ B | эквиваленция (эквивалентность, равносильность) | A==B (python) A=B(pascal) |
| A ⊕ B | строгая дизъюнкция | A != B (python) A <> B (pascal) |
Егифка ©:
Отрицание (НЕ):
Таблица истинности операции НЕ
Конъюнкция (И):
Таблица истинности операции И (конъюнкция)
Дизъюнкция (ИЛИ):
Таблица истинности операции ИЛИ (дизъюнкция)
Импликация (если…, то…):
Таблица истинности операции Импликация (если…, то…)
Эквивалентность (тогда и только тогда, …):
Таблица истинности операции Эквивалентность (тогда и только тогда, …)
Сложение по модулю 2 (XOR):
| A | B | A ⊕ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Порядок выполнения операций:
- если нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», импликация, равносильность
Еще о логических операциях:
- логическое произведение X∙Y∙Z∙… равно 1, т.е. выражение является истинным, только тогда, когда все сомножители равны 1 (а в остальных случаях равно 0)
- логическая сумма X+Y+Z+… равна 0, т.е. выражение является ложным только тогда, когда все слагаемые равны 0 (а в остальных случаях равна 1)
О преобразованиях логических операций читайте здесь.
Егифка ©:
Решение заданий 2 ЕГЭ по информатике
Задание 2_11: Решение 2 задания ЕГЭ по информатике:
Логическая функция F задается выражением
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
✎ Способ 1. Электронные таблицы Excel + Логические размышления:
- Отобразим перебор всех значений использующихся в выражении переменных (всю таблицу истинности). Поскольку в выражении используются 4 переменных, то строк таблицы будет 24=16:
- Далее обе скобки исходного выражения необходимо записать в виде логического выражения, каждую — в отдельном столбце. Также в отдельном столбце добавьте формулу итоговой функции F:

xwzy
-
✎ Способ 2. Программирование:
- В результате будут выведены значения для
F=0:
Язык python:
print('x y z w') for x in 0, 1: for y in 0, 1: for z in 0, 1: for w in 0, 1: F = (not(x) or y or z) and (x or not(z) or not(w)) if not(F): print(x, y, z, w)
x y z w 0 0 1 1 0 1 1 1 1 0 0 0 1 0 0 1
xwzy
Язык pascalAbc.net:
begin writeln('x':7, 'y':7, 'z':7,'w':7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not x or y or z) and (x or not z or not w)) then writeln(x:7, y:7, z:7,w:7); end.
F=0:x y z w False False True True False True True True True False False False True False False True
false = 0, True = 1Ответ:
xwzy
-
✎ Способ 3. Логические размышления:
- Внешняя операция выражения — конъюнкция (∧). Во всех указанных строках таблицы истинности функция принимает значение 0 (ложь). Конъюнкция ложна аж в трех случаях, поэтому проверить на ложь очень затруднительно. Тогда как конъюнкция истинна (= 1) только в одном случае: когда все операнды истинны. Т.е. в нашем случае:
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w) = 1 когда: 1. (¬x ∨ y ∨ z) = 1 И 2. (x ∨ ¬z ∨ ¬w) = 1
| x | y | z | результат |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| x | z | w | результат |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | ??? | ??? | ??? | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | ??? | ??? | y | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | w | z | y | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
Результат: xwzy
🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_12: Разбор 2 задания ЕГЭ:
Миша заполнял таблицу истинности функции:
(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w)
но успел заполнить лишь фрагмент из трех различных ее строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z:
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 1 | 1 | 0 | ||
| 1 | 0 | 0 | ||
| 1 | 1 | 0 | 0 |
Определите, какому столбцу таблицы соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы.
Подобные задания для тренировки
✍ Решение:
✎ Способ 1. Логические размышления (бескомпьютерный вариант):
- Решим задание методом построения полной таблицы истинности.
- Посчитаем общее количество строк в таблице истинности и построим ее:
4 переменных -> 24 = 16 строк
(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w) 1. Избавимся от импликации: ¬(¬z ∧ ¬(x ≡ y)) ∨ ¬(y ∨ w) 2. Внесем знак отрицания в скобки (закон Де Моргана): (z ∨ (x ≡ y)) ∨ (¬y ∧ ¬w) = 0 1 часть = 0 2 часть = 0 * Исходное выражение должно быть = 0. Дизъюнкция = 0, когда оба операнда равны 0.
(z ∨ (x ≡ y)) = 0 когда z = 0 и x ≡ y = 0 ¬y ∧ ¬w = 0 когда: 1. ¬y = 0 ¬w = 0 2. ¬y = 1 ¬w = 0 3. ¬y = 0 ¬w = 1
| x | y | w | z | F |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| y | w | x | z | F |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
Результат: ywxz
✎ Способ 2. Программирование:
- В результате будут выведены значения для F=0:
Язык PascalAbc.net:
begin writeln('x':7, 'y':7, 'z':7,'w':7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not z and (x xor y)) <= not(y or w)) then writeln(x:7, y:7, z:7,w:7); end.
x y z w False True False False False True False True True False False True
false = 0, True = 1Сопоставив их с исходной таблицей, получим результат: ywxz
Язык Python:
print ('x y z w') for x in 0,1: for y in 0,1: for z in 0,1: for w in 0,1: F=(not z and not(x==y))<=(not(y or w)) if not F: print (x,y,z,w)
F=0:x y z w 0 1 0 0 0 1 0 1 1 0 0 1
Сопоставив их с исходной таблицей, получим результат:
Результат: ywxz
🎦 Доступно видео решения этого задания (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
🎦 Видео (решение 2 ЕГЭ в Excel):
📹 здесь
📹 Видеорешение на RuTube здесь
📹 Видеорешение на RuTube здесь (Программирование)
Задание 2_10: Решение 2 задания ЕГЭ по информатике:
Логическая функция F задается выражением
¬a ∧ b ∧ (c ∨ ¬d)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
🎦 (Бескомьютерный вариант) Предлагаем подробный разбор посмотреть на видео:
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_3: Решение задания 2. Демоверсия ЕГЭ 2018 информатика:
Логическая функция F задаётся выражением ¬x ∨ y ∨ (¬z ∧ w).
На рисунке приведён фрагмент таб. ист-ти функции F, содержащий все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| ??? | ??? | ??? | ??? | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Подобные задания для тренировки
✍ Решение:
-
✎ Логические размышления (бескомпьютерный вариант):
- Внешним действием (последним выполняемым) в исходном выражении является дизъюнкция:
¬x ∨ y ∨ (¬z ∧ w)
| x1 | x2 | F |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
¬x = 1 или 0, y = 1 или 0, ¬z ∧ w = 1 или 0).¬x = 0, иными словами x = 1. Значит первый столбец соответствует переменной x. | Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| x | ??? | ??? | ??? | F |
| 1 | 0 | 0 | 0 | 0 |
y = 0. Значит четвертый столбец соответствует переменной y. | Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| x | ??? | ??? | y | F |
| 1 | 1 | 1 | 0 | 0 |
¬z ∧ w должно равняться 0, чтобы функция была ложной. Конъюнкция истинна только тогда, когда оба операнда истинны (=1); в нашем случае функция должна быть ложной, но пойдем от обратного. Если ¬z = 1, т.е. z = 0, а w = 1, то это неверно для нашего случая. Значит всё должно быть наоборот: z = 1, а w = 0. Таким образом столбец второй соответствует z, а столбец третий — w. | x | z | w | y | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
Результат: xzwy
✎ Способ 2. Программирование:
Язык pascalABC.NET:
begin writeln('x ','y ','z ','w '); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not(not x or y or(not z and w)) then writeln(x:7,y:7,z:7,w:7); end.
🎦 (бескомпьютерный вариант) Подробное решение данного 2 задания из демоверсии ЕГЭ 2018 года смотрите на видео:
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_13: Разбор досрочного егэ по информатике 2019
Логическая функция F задаётся выражением
(x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 |
✍ Решение:
🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
Задания для тренировки
Задание 2_2: Задание 2 ЕГЭ по информатике:
Каждое из логических выражений F и G содержит 5 переменных. В табл. истинности для F и G есть ровно 5 одинаковых строк, причем ровно в 4 из них в столбце значений стоит 1.
Сколько строк таблицы истинности для F ∨ G содержит 1 в столбце значений?
Подобные задания для тренировки
✍ Решение:
- Поскольку в каждом из выражений присутствует 5 переменных, то эти 5 переменных порождают таблицу истинности из 32 строк: т.к. каждая из переменных может принимать оно из двух значений (0 или 1), то различных вариантов с пятью переменными будет 25=32, т.е. 32 строки.
- Из этих 32 строк и для F и для G мы знаем наверняка только о 5 строках: 4 из них истинны (=1), а одна ложна (=0).
- Вопрос стоит о количестве строк = 1 для таб. истинности F ∨ G. Данная операция — дизъюнкция, которая ложна только в одном случае — если F = 0 и одновременно G = 0
- В исходных таблицах для F и G мы знаем о существовании только одного 0, т.е. в остальных строках может быть 1. Т.о., и для F и для G в 31 строке могут быть единицы (32-1=31), а лишь в одной — ноль.
- Тогда для F ∨ G только в одном случае будет 0, когда и F = 0 и G = 0:
- Соответственно, истинными будут все остальные строки:
| № | F | G | F ∨ G |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 |
| … | … | … | 1 |
| 32 | … | … | 1 |
32 - 1 = 31
Результат: 31
Подробное объяснение данного задания смотрите на видео:
📹 здесь
Задание 2_6: Решение 2 задания ЕГЭ по информатике:
Каждое логическое выражение A и B зависит от одного и того же набора из 7 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы.
Каково максимально возможное число единиц в столбце значений таблицы истинности выражения A ∨ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 27 = 128 строк.
- В четырех из них результат равен единице, значит в остальных — 0.
- A ∨ B истинно в том случае, когда либо A = 1 либо B = 1, или и A и B = 1.
- Поскольку А = 1 только в 4 случаях, то чтобы получить максимальное количество единиц в результирующей таблице истинности (для A ∨ B), расположим все единицы т.и. для выражения A так, чтобы они были в строках, где B = 0, и наоборот, все строки, где B = 1, поставим в строки, где A = 0:
- Итого получаем 8 строк.
- Если бы в задании требовалось найти минимальное количество единиц, то мы бы совместили строки со значением = 1, и получили бы значение 4.
| A | B |
| 1 | 0 |
| 1 | 0 |
| 1 | 0 |
| 1 | 0 |
| 0 | 1 |
| 0 | 1 |
| 0 | 1 |
| 0 | 1 |
| 0 | 0 |
| … | … |
Результат: 8
Задание 2_7: Решение 2 задания ЕГЭ по информатике:
Каждое логическое выражение A и B зависит от одного и того же набора из 8 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 6 единиц.
Каково максимально возможное число нулей в столбце значений таблицы истинности выражения A ∧ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 28 = 256 строк.
- В шести из них результат равен единице, значит в остальных — 0.
- A ∧ B ложно в том случае, когда:
A ∧ B = 0 если: 1. A = 0, B = 1 2. B = 0, A = 1 3. A = 0 и B = 0
- Во всех случаях там где А=1 может стоять B=0, и тогда результат F = 0. Поскольку нам необходимо найти максимально возможное число нулей, то как раз для всех шести А=1 сопоставим B=0, и наоборот, для всех шести возможных B=1 сопоставим A=0
- Поскольку строк всего 256, то вполне возможно, что все 256 из них возвратят в результате 0
| A | B | F |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| … | … | … |
Результат: 256
Задание 2_4: 2 задание:
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Каким из приведённых ниже выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7
✍ Решение:
- В первом внешняя операция (выполняется последней) — конъюнкция. Начнем рассмотрение с нее. Соответственно, проверяем по второй строке таб. ист-ти, там где F = 1, так как в таком случае все аргументы должны быть истинными (см. таб. истинности для конъюнкции).
- Если мы подставим в нее все аргументы выражения, то функция действительно возвращает истину. Т.е. пункт первый подходит:
- Но проверим на всякий случай остальные.
- Второй пункт проверяем по первой и третьей строке, так как основная операция — дизъюнкция — ложна только в том случае, если все аргументы ложны (см. таб. истинности для дизъюнкции). Проверяя по первой строке, сразу видим, что x1 в ней равен 1. В таком случаем функция будет = 1. Т.е. этот пункт не подходит:
- Третий пункт проверяем по второй строке, так как основная операция — конъюнкция — возвратит истину только тогда, когда все операнды равны 1. Видим, что x1 = 0, соответственно функция будет тоже равна 0. Т.е. выражение нам не подходит:
- Четвертый пункт проверяем по первой и третьей строкам. В первой — x1 = 1, т.е. функция должна быть равна 1. Т.е. пункт тоже не подходит:
- Таким образом, ответ равен 1.
Результат: 1
Решение 2 задания ГВЭ по информатике смотрите на видео:
📹 здесь
Задание 2_8: Решение 2 задания ЕГЭ по информатике:
Дано логическое выражение, зависящее от 5 логических переменных:
(¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5) ∧ (x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5)
Сколько существует различных наборов значений переменных, при которых выражение истинно?
1) 0
2) 30
3) 31
4) 32
Подобные задания для тренировки
✍ Решение:
- Поскольку выражение включает 5 переменных, то таб. ист-ти состоит из 25 = 32 строк.
- Внешней операцией (последней) является конъюнкция (логическое умножение), а внутри скобок — дизъюнкция (логическое сложение).
- Обозначим первую скобку за А, а вторую скобку за B. Получим A ∧ B.
- Найдем сколько нулей существует для таб. истинности:
A B F 1. 0 0 0 2. 0 1 0 3. 1 0 0
Теперь рассмотрим каждый случай отдельно:
¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5 = 0
и
x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 = 0.
32 - 2 = 30, что соответствует номеру 2
Результат: 2
Подробное решение задания смотрите в видеоуроке:
📹 здесь
Задание 2_5: Решение 2 задания ЕГЭ по информатике:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | F |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 |
Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение x3 не совпадает с F.
Подобные задания для тренировки
✍ Решение:
- Полная таблица истинности будет иметь 26 = 64 строк (т.к. 6 переменных).
- 4 из них нам известны: в них x3 два раза не совпадает с F.
- Неизвестных строк:
64 - 4 = 60
60 + 2 = 62
Результат: 62
Задание 2_9: Решение 2 задания ЕГЭ по информатике:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 0 | 0 | 0 | |||||
| 0 | 0 | 1 | |||||
| 1 | 1 | 1 |
Каким выражением может быть F?
1) x1 ∧ (x2 → x3) ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ ¬x5 ∧ x6 ∧ x7
4) ¬x1 ∨ (x2 → ¬x3) ∨ x4 ∨ x5 ∨ x6 ∧ x7
✍ Решение:
- Рассмотрим отдельно каждый пункт и найдем последнюю операцию, которая должна быть выполнена (внешнюю).
1 пункт:
(((x1 ∧ (x2 → x3) ∧ ¬x4) ∧ x5) ∧ x6) ∧ ¬x7
2 пункт:
(((x1 ∨ (¬x2 → x3) ∨ ¬x4) ∨ ¬x5) ∨ x6) ∨ ¬x7
3 пункт:
(((¬x1 ∧ (x2 → ¬x3) ∧ x4) ∧ ¬x5) ∧ x6) ∧ x7
Результат: 4
В видеоуроке рассмотрено подробное решение 2 задания:
📹 здесь
Задание 2_1: Задание 2 ЕГЭ по информатике:
Логическая функция F задается выражением
(y → x) ∧ (y → z) ∧ z.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| ??? | ??? | ??? | F | |
| 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 1 |
| 4 | 0 | 1 | 1 | 1 |
| 5 | 1 | 0 | 0 | 0 |
| 6 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 0 | 0 |
| 8 | 1 | 1 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
- Сначала необходимо рассмотреть логическую операцию, которую мы будем выполнять в последнюю очередь — это логическое И (конъюнкция) или ∧. То есть внешнюю операцию:
(y → x) ∧ (y → z) ∧ z
(y → x) ∧ (y → z) ∧ z = 1 если: 1. (y → x) = 1 2. (y → z) = 1 3. z = 1
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| 3 | 0 | 1 | 0 | 1 |
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| _ | ??? | z | ??? | F |
| № | Перем. 1 | z | Перем. 3 | F |
|---|---|---|---|---|
| 4 | 0 | 1 | 1 | 1 |
Результат: yzx
Детальный разбор данного задания 2 ЕГЭ по информатике предлагаем посмотреть в видео:
📹 здесь
Продолжаем разбор задач из реального экзамен ЕГЭ по информатике 2022, который прошёл 20.06.22
Все задачи взяты с сайта: https://kompege.ru/variant?kim=25012688
Далее будем решать задачи из теории игр.
Разбор задач с 1 по 18 задание.
Задание 19
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две
кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах снатовится не менее 259. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 259 или больше камней.
В начальный момент в первой куче было 17 камней, во второй куче — S камней; 1 <= S <= 241. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Решение:
Решим задачу с помощью шаблона на языке программирования Python.
Введём параметр p, который будет олицетворять позицию игры (ход).
| Начальная позиция | Ход Пети | Ход Вани | Ход Пети | Ход Вани | Ход Пети | |
| p | 1 | 2 | 3 | 4 | 5 | 6 |
def F(x, y, p): if x + y >= 259 and p==3: return True if x + y < 259 and p==3: return False return F(x+1, y, p+1) or F(x*2, y, p+1) or F(x, y+1, p+1) or F(x, y*2, p+1) for s in range(1, 242): if F(17, s, 1): print(s)
Заводим функцию F. Т.к. у нас две кучи, то она принимает параметры: x — количество камней в первой куче, y — количество камней во второй куче, p-позиция игры.
Дальше описываем победу. Если x + y >= 259 и позиция равна 3 (1 Ход Вани), то возвращаем True, что означает победу.
Если, позиция уже равна 3, но камней меньше, чем должно быть для победы, то возвращаем False (проигрыш).
Если мы не вышли на первых двух условиях, то, значит, продолжаем прокручивать ходы, рекурсивно запускаем функцию F. Между запусками ставим союз ИЛИ.
В конце перебираем все возможные значения для s через цикл for, ищём те значения, которые подходят по условию задачи.
Ответ: 61
Задание 20
Для игры, описанной в предыдущем задании, найдите два нименьших значения S, при которых у Пети есть выиграшная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход.
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Решение:
def F(x, y, p): if x + y >= 259 and p==4: return True if x + y < 259 and p==4: return False if x + y >= 259: return False if p%2==0: return F(x+1, y, p+1) and F(x*2, y, p+1) and F(x, y+1, p+1) and F(x, y*2, p+1) else: return F(x+1, y, p+1) or F(x*2, y, p+1) or F(x, y+1, p+1) or F(x, y*2, p+1) for s in range(1, 242): if F(17, s, 1): print(s)
Теперь должен выигрывать Петя на своём втором ходе. Поэтому в условиях ставим позицию p=4.
Добавляется третье условие. Если кто-то выиграл, но на первых двух условиях мы не вышли из функции, то, значит, выиграл не тот, кто нам нужен, следовательно, возвращаем Fasle.
Здесь вопрос отличается от 19 задания. Здесь Петя должен побеждать при любом ходе соперника, а не при одном неудачном ходе Вани, поэтому добавляется ещё условие.
Для чётных p (это ходы Пети), возвращаем разные ходы через and, т.к. он должен побеждать в любом случае.
Для нечётных p (это ходы Вани), возвращаем ходы через or.
Ответ:
Задание 21
Для игры, описанной в задании 19, найдите мнимальное значение S, при котором одновременно выполняются два условия:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
-у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Решение:
Опять используем прошлый шаблон, но немного модернизируем.
def F(x, y, p): if x + y >= 259 and (p==3 or p==5): return True if x + y < 259 and p==5: return False if x + y >= 259: return False if p%2==1: return F(x+1, y, p+1) and F(x*2, y, p+1) and F(x, y+1, p+1) and F(x, y*2, p+1) else: return F(x+1, y, p+1) or F(x*2, y, p+1) or F(x, y+1, p+1) or F(x, y*2, p+1) def F1(x, y, p): if x>=259 and p==3: return True if x<259 and p==3: return False if x>=259: return False if p%2==1: return F1(x+1, y, p+1) and F1(x*2, y, p+1) and F1(x, y+1, p+1) and F1(x, y*2, p+1) else: return F1(x+1, y, p+1) or F1(x*2, y, p+1) or F1(x, y+1, p+1) or F1(x, y*2, p+1) for s in range(1, 242): if F(17, s, 1): print(s) print() for s in range(1, 242): if F1(17, s, 1): print(s)
Здесь Ваня должен выигрывать либо на первом своём ходе (p=3), либо на втором своём ходе (p=5).
Т.к. Ваня не должен гарантированно выиграть своим первым ходом, то мы создаём ещё одну функцию F1, похожую на основную функцию F, которая вычисляет, когда Ваня именно гарантированно выигрывает на своём первом ходе (p=3). И, затем, мы из тех чисел, которые получились в первой функции F, исключаем числа, которые получились во второй функции F1.
В первой функции получилось 111, 119, а во второй результатов нет. Получается ответ 111.
Ответ: 111
Задание 22
Ниже на четырёх языках программирования записан алгоритм. Получив на вход число x, этот алгоритм печатает два числа: L и M. Укажите наибольшее число x, при вводе которого алгоритм печатает сначала 8, а потом 21.
*На этом сайте программа приведена на одном языке.
Решение:
Будем решать методом перебора.
for i in range(0, 10000): x = i Q = 6 P = 10 K1 = 0 K2 = 0 while x <= 100: K1 = K1 + 1 x = x + P while x >= Q: K2 = K2 + 1 x = x - Q L = x + K1 M = x + K2 if L==8 and M==21: print(i)
Ответ: 71
Задание 23
Исполнитель преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Вычти 1
2. Найди целую часть от деления на 2
Первая из них уменьшает число на экране на 1, вторая заменяет число на экране на целую часть от деления числа на 2.
Программа для исполнителя — это последовательность команд.
Сколько существует программ, для которых при исходном числе 30 результатом является на число 1, и при этом траектория вычислений содержит число 12?
Траектория вычислений программы — это последователность результатов выполнения всех команд программы.
Например, для программы 122 при исходном числе 10 траектория состоит из чисел 9, 4, 2.
Решение:
Будем решать с помощью шаблона на языке Python, который был представлен в видеокурсе по подготовке к ЕГЭ по информатике.
def F(x, y): if x == y: return 1 if x < y: return 0 if x > y: return F(x-1, y) + F(x//2, y) print(F(30, 12)*F(12, 1))
Ответ: 376
Задание 24
Текстовый файл состоит из символов A, B, C, D и O. Определите максимальное количество идущих подряд пар символов вида согласная + гласная в прилагаемом файле. Для выполенения этого задания следует написать программу.
Решение:
f=open('24_10.txt') s=f.read() s=s.replace('BA', '1') s=s.replace('CA', '1') s=s.replace('DA', '1') s=s.replace('BO', '1') s=s.replace('CO', '1') s=s.replace('DO', '1') k=0 kmax=0 for i in range(0, len(s)): if s[i]=='1': k=k+1 kmax=max(k, kmax) else: k=0 print(kmax)
Ответ: 174
Задание 25
Назовём маской числа последовательность цифр, в которой также могут встречаться следующие символы:
— символ «?» означает ровно одну произвольную цифру;
— символ «*» означает любую последовательность цифр произвольной длины; в том числе «*» может задавать и пустую последовательность.
Например, маске 123*4?5 соответсвуют числа 123405 и 12300405.
Среди натуральных чисел, не превышающих 108, найдите все числа, соответствующие маске 1234*7, делящиеся на 141 без остатка.
В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, а во втором столбце — соответствующие им результаты деления этих чисел на 141.
Решение:
Здесь самый главный момент заключается в том, что есть верхняя граница 108. Т.е. самое большое число, которое нужно рассмотреть 1234[999]7 <= 108 = 100000000. Нижняя граница тоже задана, когда вместо звёздочки ни одной цифры не будет 12347.
i=12347 #Вместо звёздочки ноль разрядов if i%141==0: print(i, i//141) #Вместо звёздочки один разряд for x in '0123456789': s = '1234' + x + '7' i=int(s) if i%141==0: print(i, i//141) #Вместо звёздочки два разряда for x in '0123456789': for y in '0123456789': s = '1234' + x + y + '7' i=int(s) if i%141==0: print(i, i//141) #Вместо звёздочки три разряда for x in '0123456789': for y in '0123456789': for z in '0123456789': s = '1234' + x + y + z + '7' i = int(s) if i%141==0: print(i, i//141)
Таким образом, нужно рассмотреть, когда вместо звёздочки ноль разрядов, один разряд, два разряда и три разряда.
Каждый разряд перебираем как цифры (символы). Формируем строку s, а затем её переводим в тип int.
Когда два разряда или три разряда нужно перебирать строку с помощью вложенных циклов.
Ответ:
| 1234737 | 8757 |
| 12341307 | 87527 |
| 12342717 | 87537 |
| 12344127 | 87547 |
| 12345537 | 87557 |
| 12346947 | 87567 |
| 12348357 | 87577 |
| 12349767 | 87587 |
Задание 26
В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрёшки — подарок упаковывается в одну из коробок, та в свою очередь в другую коробоку и т.д. Одну коробку можно поместить в другую, если длина её стороны хотя бы на 3 единицы меньше длины стороны другой коробки. Определите наибольшее количество коробок, которое можно использовать для упаковки одного подарка, и максимально возможную длину стороны самой маленькой коробки, где будет находиться подарок. Размер подарка позволяет поместить его в самую маленькую коробку.
Выходные данные
В первой строке входного файла находится число N — количество коробок в магазине (натуральное число, не превышающая 10 000). В следующих N строках находятся значения длин сторон коробок (все числа натуральные, не превышающие 10 000), каждое — в отдельной строке.
Запишите в ответе два целых числа: сначала наибольшее количество коробок, которое можно использовать для упаковки одного подарка, затем максимально возможную длину стороны самой маленькой коробки в таком наборе.
Типовой пример организации данных во входном файле.
5
43
40
32
40
30
Пример входного файла приведён для пяти коробок и случая, когда минимальная допустимая разница между длинами сторон коробок, подходящих упаковки «матрёшки», составлят 3 единицы.
При таких исходных данных условию задачи удовлетворяют наборы коробок с длинами сторон 30, 40 и 43 или 32, 40 и 43 соответственно, т.е. количество коробок равно 3, а длина стороны самой маленькой коробки равна 32.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.
Решение:
f=open('26.txt') n=int(f.readline()) a=[] for i in range(n): x=int(f.readline()) a.append(x) a.sort(reverse=True) k=1 p=a[0] for i in range(1, len(a)): if p-a[i]>=3: k=k+1 p=a[i] print(k, p)
В начале считываем все числа в массив (список) a. Сортируем их в порядке убывания.
Приступаем собирать упаковку. Начинаем с самой большой упаковки. Большую упаковку точно можно взять в наш подарок. Переменная p — это размер последний коробки, которую мы взяли. Переменная k — количество коробок в подарке на текущий момент времени.
Если следующая коробка подходит по условию, то мы её берём в наш подарок. Кто-то может подумать, что может выгоднее взять не самую большую коробку, а предпоследнего размера. Но все размеры которые будут подходить для предпоследнего элемента, точно будут подходить и для последнего, и количество упаковок точно не будет меньше, если мы берём самую большую коробку.
Дубликаты не влияют на ответы.
Если мы начинаем с самой большой коробки, то в самом конце в переменной p окажется максимальный размер самой маленькой коробки.
Ответ:
Задание 27
У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 36 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории. Компания планирует открыть лабораторию в одном из пунктов. Стоимость перевозки биоматериалов равна произведению расстояния от пункта до лаборатории на количество контейнеров с пробирками. Общая стоимость перевозки за день равна сумме стоимостей перевозок из каждого пункта в лабораторию. Лабораторию расположили в одном из пунктов приёма биоматериалов таким образом, что общая стоимость доставки биоматериалов из всех пунктов минимальна.
Определите минимальную общую стоимость доставки биоматериалов из всех пунктов приёма в лабораторию.
Входные данные
Дано два входных файла (файл А и файл B), каждый из которых в первой строке содержит число N ( 1 ≤ N ≤ 10 000 000) — количество пунктов приёма биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает 1000). Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки.
В ответе укажите два числа: сначала значение искомой величины для файла A, затем — для файла B.
Типовой пример организации данных во входном файле
6
1 100
2 200
5 4
7 3
8 2
10 190
При таких исходных данных и вместимости транспортировочного контейнера, составляющей 96 пробирок, компании выгодно открыть лабораторию в пункте 2. В этом случае сумма транспортных затрат составит: 1*2 + 3*1 + 5*1 + 6*1 + 8*2.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.
Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных варантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Решение:
import math f=open('27B.txt') k=9999995 n=int(f.readline()) a=[0]*k sm=0 for i in range(n): x, y = f.readline().split() x=int(x) y=int(y) z = math.ceil(y/36) a[x] = z sm = sm + (x-1)*z # Вспомогательные суммы s1=[] s2=[] s1.append(0) s2.append(0) s1.append(0) s2.append(0) for i in range(1, k): s1[1] = s1[1] + a[i] for i in range(2, k): s1.append(s1[i-1] - a[i-1]) s2.append(s2[i-1] + a[i-1]) # Ищем минимальное значение mn=sm for i in range(2, k): sm = sm - s1[i] + s2[i] mn=min(mn, sm) print(mn)
Переменная k — это количество приёмных пунктов (Т.е. длина массива a). Превая ячейка соответсвует приёмному пункту под номером 1, вторая ячейка под номером 2 и т.д. Само значение для k мы смотрим в конце файла. Например, для файла A значение напишем 999. Всего 998 приёмных пунктов, но т.к. индексы в массиве начинаются с 0, то мы должны завести 999 ячеек. Т.е. нулевая ячейка не будет никак задействована. Для файла B устанавливаем k в 9999995.
В сами ячейки массива мы поместим для каждого приёмного пункта количество контейнеров. Их легко вычислить. Если количество пробирок не нулевое, то мы должны это количество разделить на 36 и округлить в большую сторону. Количество контейниров в нашей программе для каждого приёмного пункта — это переменная z.
Пусть лаборатория расположена в первом пункте. Тогда вычислим для неё стоимость доставки:
sm1 = a[2]*1 + a[3]*2 + a[4]*3 + … + a[m]*(m-1)
Здесь m — это последний индекс массива a (m = k-1). Пусть лаборатория будет во втором пункте, тогда:
sm2= a[3]*1 + a[4]*2 + … + a[n]*(m-2) + a[1] = sm1 — (a[2] + a[3] + a[4] + … + a[m]) + a[1]
Отсюда мы понимаем, что достаточно вычислить стоимость доставки sm1 по формуле, которую нам дали в задаче, только один раз для первого пункта. Для второго пункта вычисляем: sm2 = sm1 — (a[2] + a[3] + a[4] + … + a[m]) + a[1]. Для третьего sm3 = sm2 — (a[3] + a[4] + … + a[m]) + a[2] + a[1] и т.д.
Значит, для каждого приёмного пункта i мы должны иметь уже готовую вспомагательную сумму s1[i] = a[i] + a[i+1] + …+ a[m], а так же сумму s2, т.е. сумма элементов, которые идут левее i (само a[i] уже не берётся): s2[i] = s[1] + s[2] + … + s[i-1].
Сумму s1[i] мы должны отнимать, а s2[i] прибавлять. По мерее продвижения по нашим приёмным пунктам, s1[i] будет уменьшаться, а s2[i] увеличиваться.
Но вспомогательные суммы s1[i] и s2[i] нужно тоже вычислисть, как можно эффективней. Достаточно вычислить для s1[1] и s2[1] (для первого приёмного пункта), а дальше можно воспользоваться закономерностью: s1[2] = s1[1]-a[1], s1[3] = s1[2]-a[2]…и т.д. Так же s2[2] = s[1]+a[1], s[3] = s[2]+a[2] и т.д.
s1[0] и s2[0] не нужны, они соответсвуют a[0], а она не используется при решении задачи. Значение s1[1] вычисляем «честно» с помощью цикла. Значение s2[1] = 0 (левее нет ячеек).
В самом первом цикле вычисляется значение для переменной sm — это стоимость перевозки, если лаборатория стоит в первом пункте. В последнем цикле программы вычисляем стоимоть для всех остальных приёмных пунктов, используя вышеописанные алгоритмы. И находим минимальное значение среди всех значений для переменной sm.
Ответ:
Разбор задач с 1 по 18 задание.
Никогда не программировал, но хочешь сдать ЕГЭ по информатике? Тогда знай: к экзамену можно подготовиться за год, если грамотно организовать учебный процесс. Из этой статьи ты узнаешь все о структуре ЕГЭ по информатике в 2023 году, изменениях и типах заданий.
Изменения в ЕГЭ по информатике 2023
Последние 2 года ЕГЭ по информатике проводился в компьютерной форме, что предоставляло сдающим большое право выбора, как решать то или иное задание, благодаря чему появлялись лазейки, упрощающие решения некоторых номеров из экзамена.
В связи с этим, ФИПИ ежегодно вносят изменения в КИМ по информатике, чтобы внести больше разнообразия и избавиться от шаблонных решений. В 2023 году полностью претерпят структуру 2 задания, но это не все изменения, что ФИПИ представили в новой демоверсии ЕГЭ.
Долой переборное решение!
В блоке «Программирование» даже после перехода на компьютерную форму было два задания, в которых программа уже представлена в условии, а задача сдающего — проанализировать ее — задания №6 и 22. Но многие справедливо подумали – зачем анализировать код, если я могу его переписать и запустить переборное решение. Благодаря этому, почти все, кто знал о таком варианте решения заданий, законно получали 2 балла за них. ФИПИ такой способ решения вряд ли понравился.
Официальный список изменений выглядит следующим образом:
Задание №6 теперь мы будем относить к блоку «Алгоритмизация», так как теперь оно предоставляет нам работу с исполнителем и анализом алгоритма. В демоверсии вам предлагают проанализировать «Черепашку», которая многим знакома из ОГЭ по информатике:
Задание №22 пополняет ряды блока «Информационные модели», а также заданий, к которым прилагаются дополнительные файлы, если быть точнее — электронная таблица. В условии затрагивается новая для экзамена тема – многопоточность (довольно важная тема для многих IT-специалистов и затрагивается на определенных предметах в университете), а решение требует анализа таблицы и зависимостей процессов:
Кроме двух новых заданий, некоторые номера также претерпели изменения:
Задание №14 все еще направлено на работу с системами счисления, но теперь нужно искать неизвестную цифру числа. Такого прототипа ранее на ЕГЭ мы не видели:
Задание №12, судя по демоверсии, станет сложнее — это уже знакомый для экзамена исполнитель «Редактор», но с необычным вопросом (раньше, в основном, требовалось назвать получившуюся после обработки программой строку/сумму цифр строки):
Задание №16 на рекурсию из демоверсии намекает нам на то, что не стоит забывать про аналитическое решение. Это происходит из-за больших аргументов у функции, гораздо проще поразмыслить, что же считает функция:
Как видите, ЕГЭ по информатике в 2023 году изменился заметно. Все эти обновления нужно учитывать. Если вы не знаете, чего от вас ждут составители экзамена, даже незначительное изменение в формулировке может стоить вам нескольких баллов. А в условиях, когда от ЕГЭ зависит поступление в хороший вуз и качество образования, каждый балл важен.
Поэтому на своих занятиях по подготовке к ЕГЭ по информатике я всегда разбираю с учениками самые свежие обновления ФИПИ. Мы выясняем, как именно надо понимать задание, изучаем разные алгоритмы решения и тренируем лучшие способы их оформления — в соответствии со всеми критериями. Именно поэтому мои ученики сдают экзамен на высокий балл и поступают в тот вуз, в который изначально хотели. Помочь с этим я могу и вам — записывайтесь на курс и начните подготовку к ЕГЭ на 80+ 💪
О структуре экзамена
В ЕГЭ по-прежнему осталось 27 заданий с кратким ответом. За задания 1-25 можно получить по 1 первичному баллу, а за задания 26 и 27 — по 2 балла. Максимальный возможный результат — 29 первичных баллов.
Все задания школьникам нужно решить за 3 часа 55 минут.
На экзамене встретятся задания по программированию, логике, алгоритмизации, на работу с информационными моделями, а также на кодирование информации.
В каждом блоке есть определенные темы, которые нужно знать. Давайте посмотрим, что именно надо учить.
Программирование
Программирование встречается в шести заданиях — а именно в 16, 17, 24, 25, 26 и 27. Чтобы справиться с ними достаточно хорошо знать только один язык программирования. Нужно уметь работать с массивом, строками, файлами, знать алгоритмы сортировки и другие не менее важные алгоритмы работы с числами.
Логика
Логика встречается в заданиях 2 и 15. Чтобы успешно справиться с этими заданиями, нужно знать основные логические операции и их таблицы истинности, уметь преобразовывать и анализировать выражения.
Алгоритмизация
В данный блок входят семь заданий (5, 6, 12, 19, 20, 21 и 23). Для решения этих заданий нужно уметь работать с различными алгоритмами и исполнителями. Важно понимать теорию игр — определять выигрывающего игрока, выигрышную позицию, различать понятия заведомо проигрышной и выигрышной позиций.
Благодаря возможности использовать инструменты компьютера, многие из этих заданий также можно решать с помощью написания программы или построения электронной таблицы.
Информационные модели
С заданиями 1 и 13 ученики обычно справляются хорошо. Чтобы их решить, нужно уметь работать с графами и таблицами и знать пару простых методов. С заданием 10 проблемы возникают редко, так как от вас требуется найти количество определенных слов в текстовом документе. Задания 3, 9 и 18 требуют работы с электронными таблицами, при решении вам помогут знания про ссылки, функции и фильтры. К этому же блоку добавляется новое задание 22.
Информация и ее кодирование
Задания этого блока достаточно разнообразны. Вы встретите алгоритмы перевода чисел в различные системы счисления, условие Фано, формулы, единицы измерения информации и комбинаторику. Все это разнообразие встречается в заданиях 4, 7, 8, 11, 14, а также может пригодится в заданиях на программирование. А новый прототип задания 14 на работу с системами счисления и вовсе можно решить с помощью программы.
Шкала оценивания
На самом деле шкала перевода баллов составляется после проведения экзаменов, так как в формуле есть параметр «среднее значение». То есть то, что мы называем шкалой — это результат перевода баллов прошлого года. ФИПИ переводит баллы по формуле, а не по шкале. Поэтому шкала меняется, если меняется экзамен или массово меняются результаты его прохождения. Мы полагаем, что в 2023 году проходной балл будет 40 вторичных баллов, но это может измениться.
Какие типы заданий встретятся на ЕГЭ по информатике 2023?
На ЕГЭ 2023, как и в 2021 году, все задания будут с кратким ответом, больше не нужно писать подробные объяснения по теории игр и сдавать программный код на проверку на бумаге. Но это не значит, что все задания идентичны. Посмотрим, какие именно типы заданий встретятся на экзамене.
Задания, которые можно решить «вручную»
Хотя ЕГЭ по информатике и проходит в компьютерной форме, в КИМах по-прежнему остаются задания, которые можно решать, как на бумаге, так и на компьютере. Это задания 1, 2, 4-8, 11-15, 19-23, в них необходимо получить число или последовательность букв в ответе. Ты можешь написать программу на компьютере или использовать электронные таблицы, а затем записать в ответ получившееся значение. За каждое задание можно получить 1 балл.
Задания, которые решаются с помощью компьютера
Все такие задания бывают трех типов:
- Работа с предложенным файлом
- Создание программы
- Написание программы и получение ответа, используя предложенный файл
Разберемся с каждым типом отдельно.
Работать только с предложенным файлом нужно в заданиях 3, 9, 10, 18 и 22. Чтобы решить эти задания, нужно знать, какие функции есть у текстовых редакторов и редакторов электронных таблиц, а также теория по реляционным базам данных. За каждое задание можно получить по 1 баллу.
Создать программу понадобится в задании 25. Задача в том, чтобы написать код и получить на выходе какой-то ответ. Начальные данные, при которых нужно получить ответ, уже указаны в самом задании. За оба задания можно получить по 1 баллу.
Задания, где нужно написать программу и считать информацию из файла — это 17, 24, 26 и 27. Эффективность и способ решения, который вы использовали, не проверяется. Главное — получить верный численный ответ. За задания 17 и 24 вы можете получить по 1 баллу, а за задания 26 и 27 — по 2 первичных балла.
Обрати внимание, что в некоторых прототипах заданий 17, 24, 25, 26 и 27 программу можно не писать, если ты знаешь, как решить эти задания другим способом — это не запрещено.
Как подготовиться к ЕГЭ по информатике 2023?
Лучший способ — разобраться в каждой теме и выучить все необходимое. Как это сделать?
- Для начала оцените текущий уровень знаний. Можно пройти диагностическое тестирование или попробовать решить последнюю демоверсию экзамена. Таким образом вы поймете, что вы уже знаете, а над чем нужно еще поработать.
- Если вы не умеете программировать, советуем заняться этим с самого начала учебного года. Задания на программирование приносят минимум 8 первичных баллов из 29, это достаточно много.
- Подумайте, смогут ли вас хорошо подготовить в школе. Оцените, что из школьной программы вы уже знаете, а что предстоит изучить в течение года.
- Решите, как вам комфортнее заниматься: лично с преподавателем, в группе или онлайн.
- Регулярно занимайтесь, уделяя время и теории, и практике!
Именно по такой схеме проходят мои занятия по подготовке к ЕГЭ по информатике в MAXIMUM Education. Но вдобавок к этому я еще показываю ученикам разные ловушки экзамена: как в формулировках заданий, так и в критериях и правилах оформления решений. Я помогаю распознавать эти ловушки и обходить их стороной — только так можно гарантированно получить максимальный балл за каждое задание.
Помимо этого, я знаю много разных лайфхаков решения ЕГЭ по информатике. С их помощью найти правильный ответ можно намного быстрее — а это очень важно на экзамене, когда время ограничено. Всеми этими лайфхаками я делюсь со своими учениками и показываю, как применять на практике каждый способ.
Так что на экзамен мои ученики приходят абсолютно спокойные и уверенные в своих силах. И результаты ЕГЭ у них соответствующие: намного выше среднего балла по стране. Если и вы хотите получить 80+ на экзамене по информатике, записывайтесь на курс подготовки к ЕГЭ. Я научу вас всему, что я знаю!
Разбор варианта ЕГЭ информатика 2022
Кулабухов (Вариант 1)

-
Задание 22 -
Задание 23 -
Задание 24 -
Задание 25 -
Задание 26 -
Задание 27
Задание 15
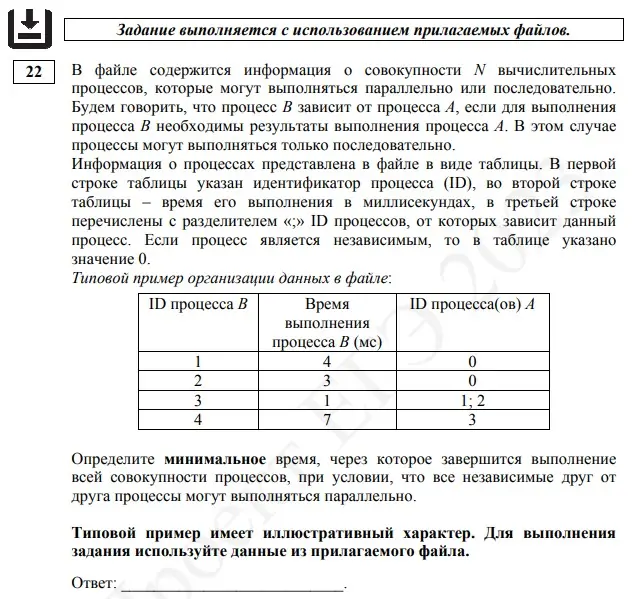
На числовой оси даны два отрезка: X = [12; 93] и Y = [54; 150]. Укажите наименьшую возможную длину такого отрезка Z, для которого логическое выражение:
(x ∈ Y) → (¬(x ∈ X) ∧ ¬(x ∈ Z) → ¬(x ∈ Y))
Тождественно истинно (то есть принимает значение 1 при любом действительном значении переменной x).
Решение:

* Обратите внимание, 93 не входит в отрезок (93;150], но по условию нам необходимы любые действительные числа, поэтому 150-93=57!!! Как-то не очень правильно 🙁
Ответ: в сборнике ответ — 57
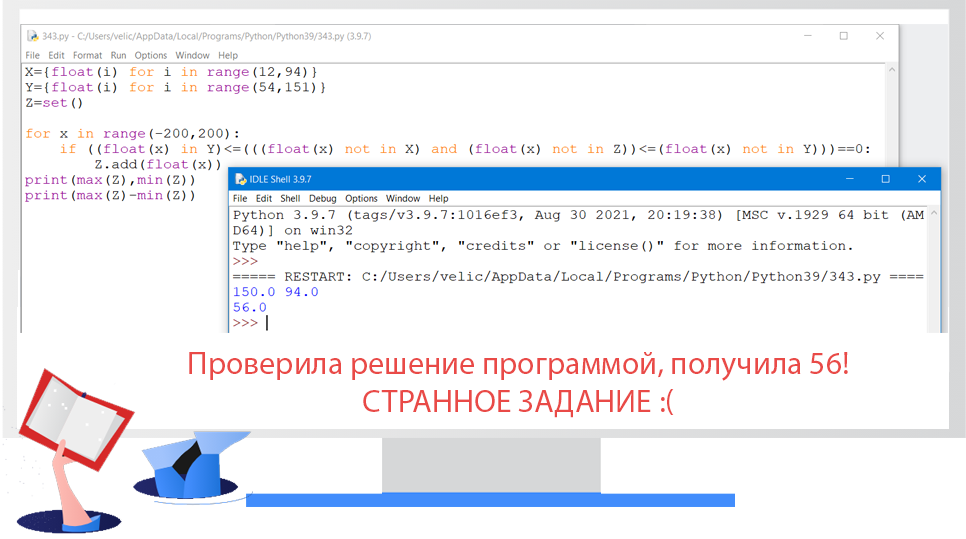
Задание 16
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими отношениями:
F(1) = 1;
F(n) = n + F(n/2), если n чётно;
F(n) = n * F(n -1), если n>1 и при этом n нечётно.
Чему равно значение функции F(37)?
Решение:
Ответ: 6993
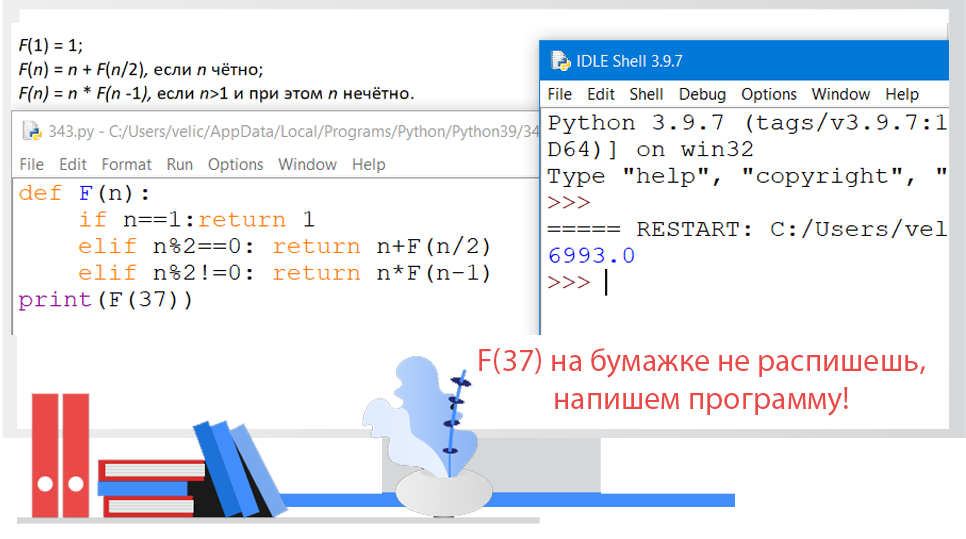
Задание 17
В файле 17_ku.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от -10 000 до 10 000 включительно. Определите и запишите в ответе сначала количество пар элементов последовательности, в которых оба числа делятся нацело на 5, затем максимальную из сумм элементов таких пар. Гарантируется, что найдется хотя бы одна такая пара. В данной задаче под парой подразумевается два идущих подряд элемента последовательности. Например, для последовательности из пяти элементов: 6; -5; 45; -10; 6 — ответ: 2 40
Решение:
Для выполнения этого задания необходимо:
- Скачать файл, создать папку и перенести его в эту папку;
- Создать файл для программы и сохранить его тоже в эту папку;
- Прочитать внимательно задание.
Ответ: 213 965
Задание 18
Квадрат разлинован на N x N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — соседнюю нижнюю. Квадрат ограничен стенами. Между соседними клетками могут быть внутренние стены. При попытке пройти сквозь стену Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежат фишки, количество которых не превышает 100. Посетив клетку, Робот забирает с собой все фишки, лежащие в этой клетке; это также относится к начальной и конечной клетками маршрута Робота.
Определите максимальное и минимальное количество фишек, которое может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа — сначала максимальное количество, затем минимальное.
Исходные данные представляют собой электронную таблицу размером N x N, каждая ячейка которой соответствует клетке квадрата. Скачать 1811.xlsx
Решение:
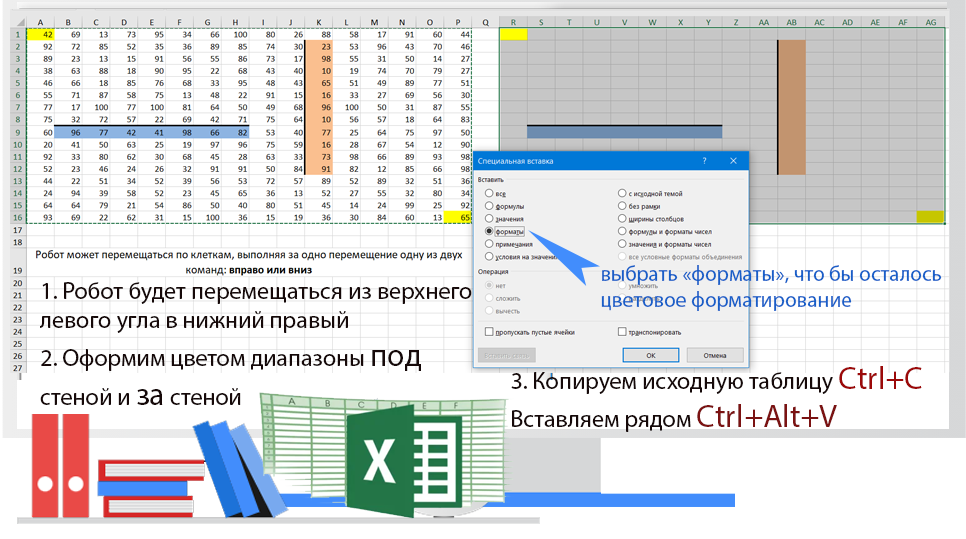
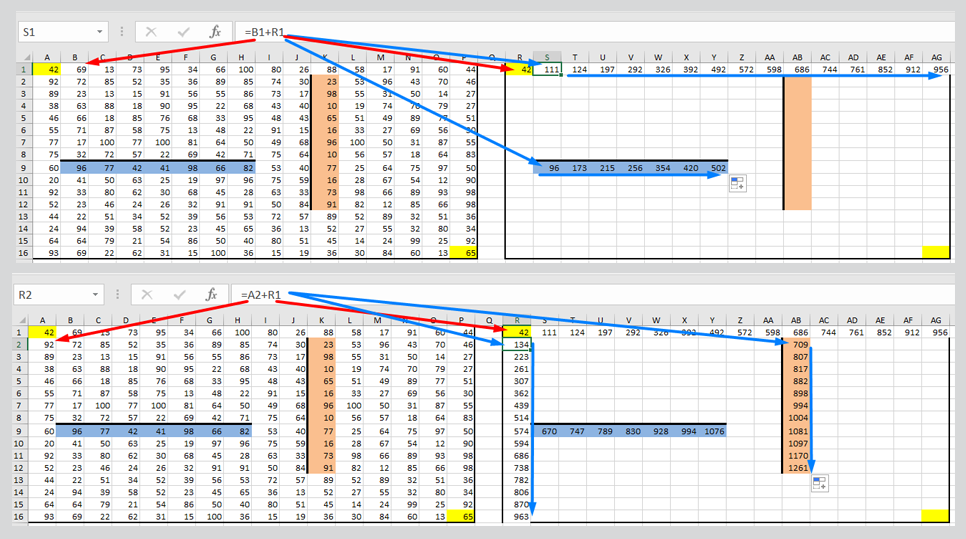
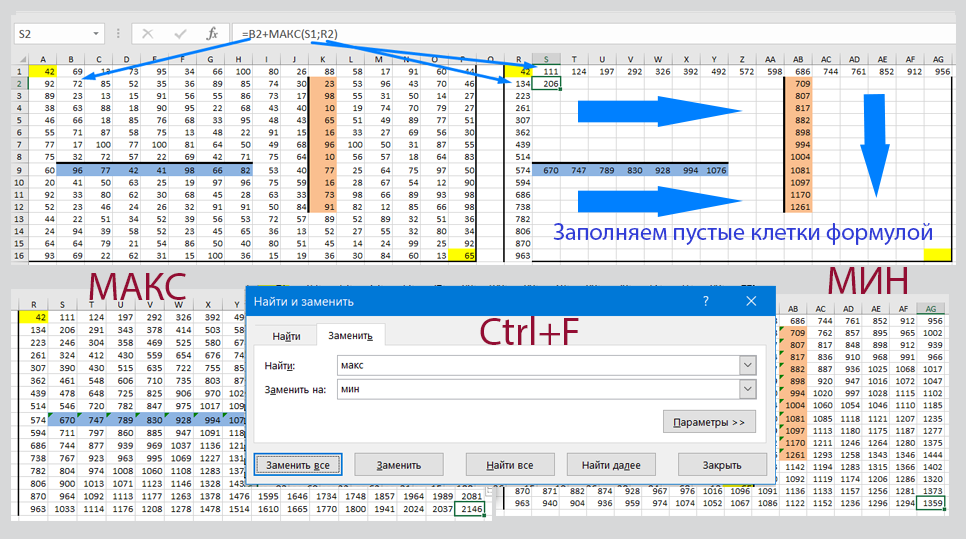
Ответ: 2146 1359
Задание 19
Два игрока, Петя и Вася, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может:
- Добавить в кучу один камень или
- Добавить в кучу три камня или
- Увеличить количество камней в куче в четыре раза.
Например, имея кучу из 20 камней, за одни ход можно получить кучу из 21, 23 или 80 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 78. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 78 или больше камней. В начальный момент в куче было S камней: 1 ≤ S ≤ 77.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретится при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Решение:

Ответ: 5
Задание 20
Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:
- Петя не может выиграть за один ход;
- Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Теперь попробуем определить значение S, при которых у Пети будет выигрышная стратегия, причём Петя не сможет выиграть первым ходом, но сможет выиграть своим вторым ходом, независимо от того, как будет ходить Ваня.

Ответ: 16 18
Задание 21
Для игры, описанной в задании 19, найдите минимальное значение S, при котором одновременно выполняются два условия:
- У Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
- У Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
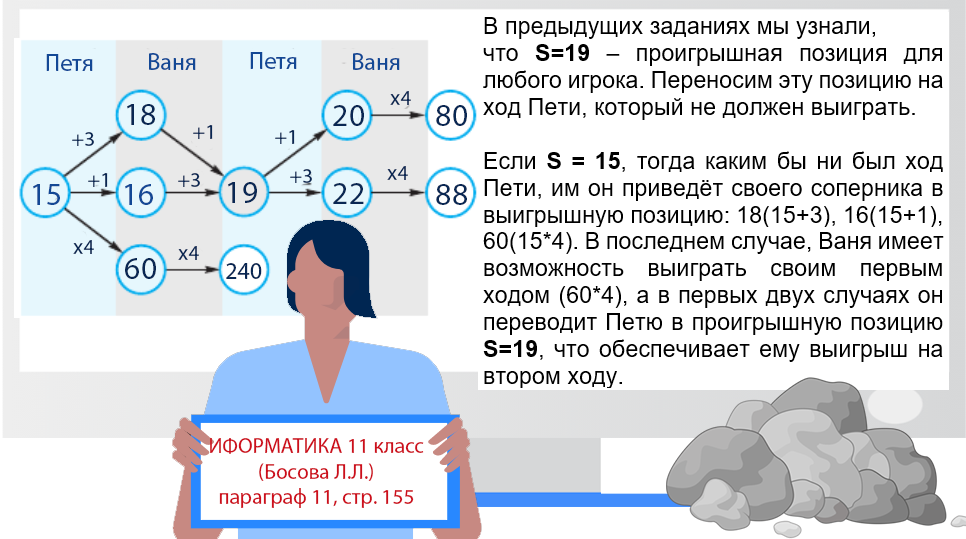
Ответ: 15
Задание 22
Ниже на четырех языках программирования записан алгоритм. Получив на вход число x, это алгоритм печатает число M. Известно, что x < 480. Укажите такое (то есть меньше 480) наибольшее число х, при вводе которого алгоритм печатает 12.
Решение:
X = int(input())
L=X
M=132
if L % 2 != 0:
M=64
while L != M:
if L >M:
L -= M
else:
M -= L
print(M)
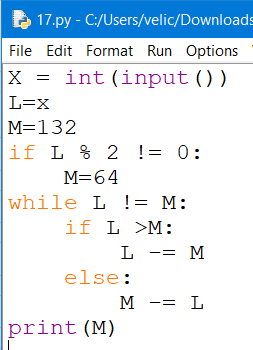
Составим программу на языке Phyton для перебора значений переменной x<480 и выполнения для каждого значения заданного алгоритма. Выведем наибольшее значение, при котором получится М=12.
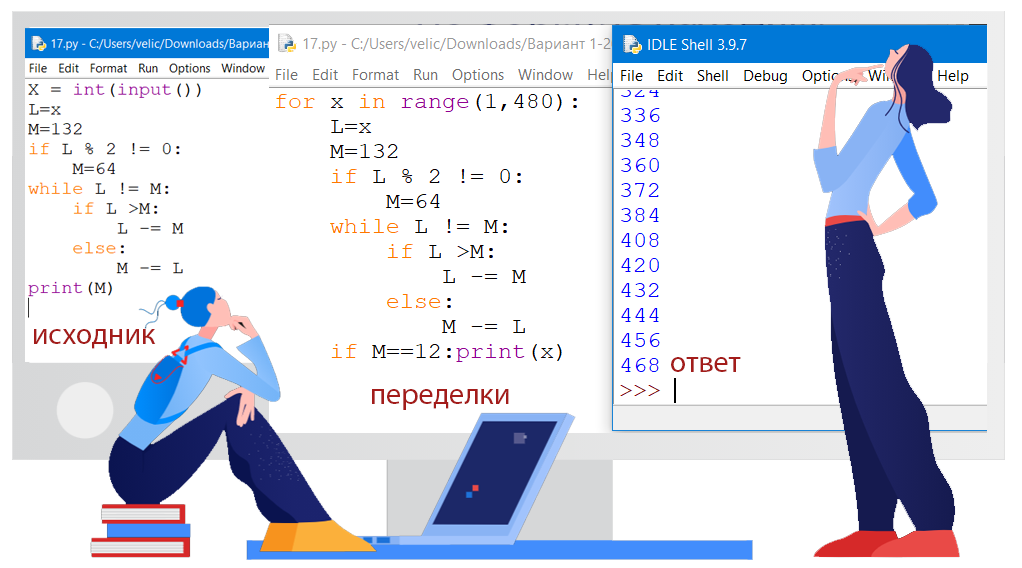
Ответ: 468
Задание 23
Исполнитель «Х125» преобразует число на экране. У исполнителя «Х125»
Есть три команды, которым присвоены номера:
- Прибавить 1
- Умножить на 2
- Умножить на 5
Первая команда увеличивает число на экране на 1, вторая в 2 раза, а третья — в 5 раз. Программа для исполнителя «Х125» — это последовательность команд.
Сколько существует программ, которые число 1 преобразуют в число 38, причем траектория вычислений содержит числа 10 и 20?
Траектория вычисления программы — это последовательность результатов выполнения всех команд программы.
Например, для программы 2231 при исходном числе 5 траектория будет состоять из чисел 10, 20, 100, 1001.
Решение:

Ответ: 36
Задание 24
Текстовый файл 24-ku.txt состоит не более чем из 106 символов A, B, C и D.
Определите, какой символ чаще всего стоит перед последовательностью символов “AD”. Если несколько символов встречаются одинаковое число раз, то в ответе запишите тот, который стоит позже в алфавите. В ответе запишите без пробелов этот символ и сколько раз он стоит перед последовательностью “AD”. Например, B25
Для выполнения этого задания следует написать программу.
Решение:
Для выполнения этого задания необходимо:
- Скачать файл, создать папку и перенести его в эту папку;
- Создать файл для программы и сохранить его тоже в эту папку;
- Прочитать внимательно задание.
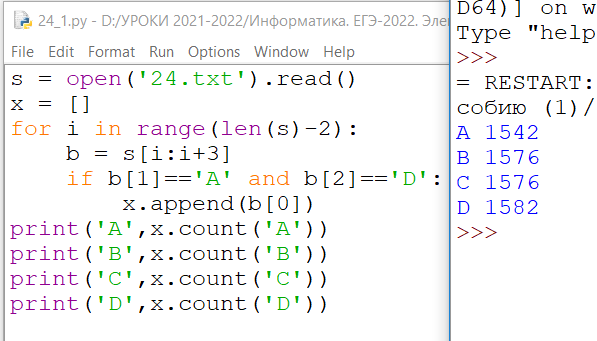

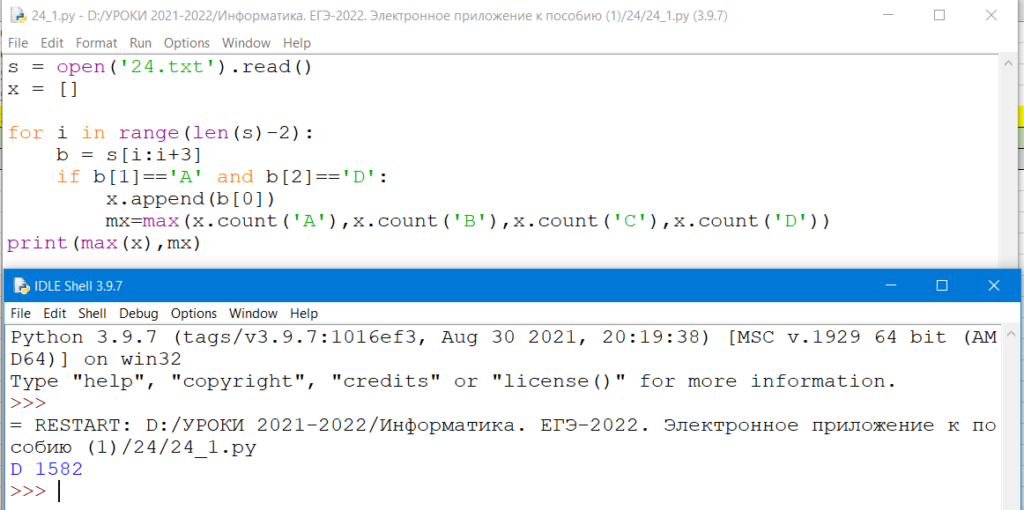
Ответ: D 1582
Задание 25
Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [50 000 000; 60 000 000], числа, имеющие ровно шесть различных натуральных делителей (не считая единицы и самого числа), среди которых есть число 911. В ответе запишите сначала количество таких чисел, а затем наименьшее из них.
Решение:
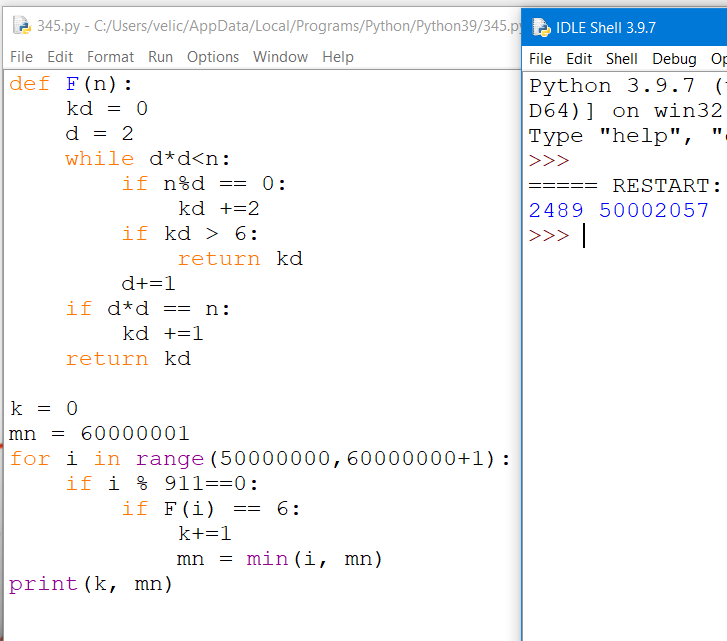
def F(n):
kd = 0
d = 2
while d*d 6:
return kd
d+=1
if d*d == n:
kd +=1
return kd
k = 0
mn = 60000001
for i in range(50000000,60000000+1):
if i % 911==0:
if F(i) == 6:
k+=1
mn = min(i, mn)
print(k, mn)
Ответ: 2489 50002057
Автор материалов — Лада Борисовна Есакова.
В компьютере вся информация представлена в двоичной системе счисления, в которой используется две цифры – 0 и 1. Собственно, и цифр как таковых у компьютера нет, а есть электрический сигнал, проходящий по электронным схемам и соединительным проводникам (шинам) компьютера, который может принимать значения “высокий уровень электрического напряжения” (принимаемый нами за 1) и “низкий уровень электрического напряжения” (принимаемый за 0). Для различных действий над этими нулями и единичками нам необходимы специальные операции, которые работают с двоичными переменными. Такие операции называются логическими операциями.
Логические операции и их аргументы принимают только два значения: 1 (“истина”) и 0 (“ложь”).
Таблица истинности выражения определяет его значения при всех возможных комбинациях исходных данных.
Количество строк в таблице истинности выражения от N переменных равно 2N.
Основные логические операции:
1). Логическое умножение (конъюнкция, логическое И). Обозначается: AND, &, /.
Таблица истинности:
|
A |
B |
А&В |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
0 |
2). Логическое сложение (дизъюнкция, логическое ИЛИ). Обозначается: OR, |, /.
Таблица истинности:
|
A |
B |
A / B |
|
1 |
1 |
1 |
|
1 |
0 |
1 |
|
0 |
1 |
1 |
|
0 |
0 |
0 |
3). Логическое отрицание (инверсия, логическое НЕ). Обозначается: NOT, ¬, .
Таблица истинности:
4). Логическое следование (импликация). Обозначается: →.
Таблица истинности:
|
A |
B |
A → B |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
1 |
|
0 |
0 |
1 |
5). Логическое равенство (эквивалентность). Обозначается: ↔, ~.
Таблица истинности:
|
A |
B |
A ~ B |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
1 |
Порядок (приоритет) выполнения логических операций:
Если в выражении нет скобок, то операции выполняются в следующем порядке:
— Логическое отрицание (инверсия, логическое НЕ);
— Логическое умножение (конъюнкция, логическое И);
— Логическое сложение (дизъюнкция, логическое ИЛИ);
— Логическое следование (импликация);
— Логическое равенство (эквивалентность).
Выбор выражения по таблице истинности
Пример 1.
Дан фрагмент таблицы истинности выражения F:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
F |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
Каким выражением может быть F?
1) (x1 ∧ x2) ∨ (x3 ∧ x4) ∨ (x5 ∧ x6)
2) (x1 ∧ x3) ∨ (x3 ∧ x5) ∨ (x5 ∧ x1)
3) (x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2)
4) (x1 ∧ x4) ∨ (x2 ∧ x5) ∨ (x3 ∧ x6)
Решение:
Все представленные варианты ответа — дизъюнкции трёх конъюнкций. Все значения F в таблице равны нулю. Дизъюнкция равна нулю, когда все слагаемые равны нулю.
Рассмотри поочерёдно все четыре выражения.
1) В первой строке таблицы x1=1 и x2=1, значит x1∧x2=1. Выражение не подходит.
2) Во второй строке таблицы x1=1 и x3=1, значит x1∧x3=1. Выражение не подходит.
3) Подставим в третье выражение поочередно значения всех строк таблицы:
Первая строка
(x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2) = (1 ∧ 0) ∨ (0 ∧ 0) ∨ (0 ∧ 1) = 0 ∨ 0 ∨ 0 = 0
Вторая строка
(x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2) = (0 ∧ 0) ∨ (0 ∧ 1) ∨ (1 ∧ 0) = 0 ∨ 0 ∨ 0 = 0
Третья строка
(x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2) = (0 ∧ 1) ∨ (1 ∧ 0) ∨ (0 ∧ 0) = 0 ∨ 0 ∨ 0 = 0
Выражение подходит.
4) В третьей строке таблицы x1=1 и x4=1, значит x1∧x4=1. Выражение не подходит.
Ответ:3
Пример 2.
Для таблицы истинности функции F известны значения только некоторых ячеек:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
F |
|
1 |
0 |
1 |
|||||
|
0 |
0 |
1 |
|||||
|
0 |
1 |
0 |
Каким выражением может быть F?
1) x1 ∧ x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ x2 ∧ ¬x3 ∧ x4 ∧ x5 ∧ x6 ∧ x7
4) x1 ∨ x2 ∨ ¬ x3 ∨ x4 ∨ x5 ∨ ¬x6 ∨ x7
Решение:
Рассмотри поочерёдно все четыре выражения.
1) Выражение является конъюнкцией переменных и их отрицаний. Конъюнкция равна единице, когда все операнды равны единице. В первой строке x6 = 0, а значит и все выражение F равно нулю, что не соответствует таблице истинности.
2) Выражение является дизъюнкцией переменных и их отрицаний. Дизъюнкция равна единице, когда хотя бы один операнд равен единице. Подставим во второе выражение поочередно значения всех строк таблицы:
Первая строка
x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7 = x1 ∨ ¬x2 ∨ x3 ∨ 0 ∨ ¬x5 ∨ 0 ∨ ¬x7 может принимать значение 1, если хотя бы один из операндов равен 1.
Вторая строка
x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7 = x1 ∨ ¬x2 ∨ x3 ∨ 1 ∨ ¬x5 ∨ x6 ∨ 1 = 1
Третья строка
x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7 = 0 ∨ ¬x2 ∨ x3 ∨ 0 ∨ ¬x5 ∨ x6 ∨ ¬x7 может принимать значение 0, если все остальные операнды равны 0.
3) Выражение является конъюнкцией переменных и их отрицаний. Конъюнкция равна единице, когда все операнды равны единице. Во второй строке x4 = 0, а значит и все выражение F равно нулю, что не соответствует таблице истинности.
4) Выражение является дизъюнкцией переменных и их отрицаний. Дизъюнкция равна единице, когда хотя бы один операнд равен единице. В третьей строке x4 = 1, значит и все выражение F равно 1, что не соответствует таблице истинности.
Ответ:2
Пример 3.
Логическая функция F задаётся выражением (¬z) ∧ x ∨ x ∧ y. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
|
Перем. 1 |
Перем. 2 |
Перем. 3 |
Функция |
|
??? |
??? |
??? |
F |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая 1-му столбцу; затем – буква, соответствующая 2-му столбцу; затем – буква, соответствующая 3-му столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение:
Выражение (¬z) ∧ x ∨ x ∧ y является дизъюнкцией двух конъюнкций:
((¬z) ∧ x) ∨ (x ∧ y) . В обеих конъюнкциях присутствует x. Т. е. при x = 0 все выражение равно 0. Это выполняется только при Перем.3 = x.
Выражение равно 1, если x =1 и выполняется хотя бы одно из условий: y = 1 или z = 0. Из четвертой строки следует, что Перем.1 = z, а Перем.2 = y.
Ответ: zyx
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задача №2. Построение таблиц истинности логических выражений. Выбор выражения, соответствующего условию.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.03.2023