Продолжаем наш видеокурс по подготовке к ЕГЭ по информатике 2022. Сегодня разоблачим второе задание!
Кто незнаком с основными логическими операциями, можете посмотреть прошлогоднюю статью по заданию 2 из ЕГЭ по информатике.
В этой статье будут раскрыты методики решения 2 задания через язык программирования Питон.
Будем перебирать для каждой логической переменной все возможные варианты в программе. А логическая переменная всего два значения может принимать: 1 или 0 (истину или ложь). Таким образом, если к примеру у нас 4 переменные, мы получим 24=16 различных комбинаций.
Кто знаком с мощнейшим методом для 2 задания из ЕГЭ по информатике, о котором я рассказывал в прошлогодней статье, тот поймёт, что мы будем применять тот же самый мощнейший метод, но автоматизированный с помощью питона.
Нам нужно будет запрограммировать логическую функцию на языке Питон. Вот таблица, которая поможет это сделать.
| Логическая операция | Представление в Питоне |
| Отрицание ¬ | not() |
| Логическое умножение ∧ | and |
| Логическое сложение ∨ | or |
| Следование A ⟶ B | not(A) or B |
| Равносильность ≡ | == |
Перейдём к практике решения задач задания 2 с помощью языка программирования Python.
Задача (Классическая)
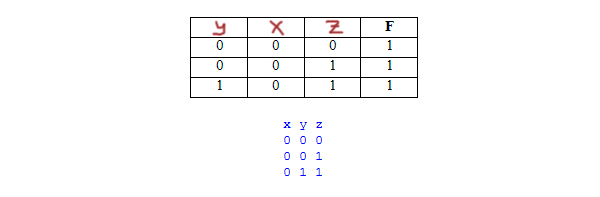
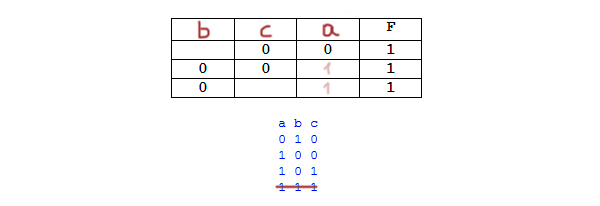
Миша заполнял таблицу истинности логической функции F
(w → z) ∧ ((y → x) ≡ (z → y)),
но успел заполнить лишь фрагмент из трёх различных её строк, даже
не указав, какому столбцу таблицы соответствует каждая из переменных
w, x, y, z.
Определите, какому столбцу таблицы соответствует каждая из переменных
w, x, y, z.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут
соответствующие им столбцы (сначала буква, соответствующая первому
столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы
в ответе пишите подряд, никаких разделителей между буквами ставить
не нужно.
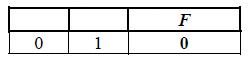
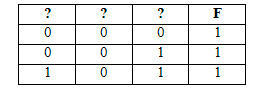
Пример. Функция F задана выражением ¬x / y, зависящим от двух
переменных, а фрагмент таблицы имеет следующий вид.
В этом случае первому столбцу соответствует переменная y, а второму
столбцу – переменная x. В ответе следует написать: yx.
Решение:
Решать задачу будем с помощью шаблона на языке Python (Питон).
print('x y z w') for x in range(0, 2): for y in range(0, 2): for w in range(0, 2): for z in range(0, 2): if (not(w) or z) and ((not(y) or x) == (not(z) or y)): print(x, y, z, w)
В задаче у нас 4 переменные, значит, формируем 4 вложенных цикла. В каждом цикле перебираем все возможные значения для конкретной переменной. Мы перебираем значения 0 и 1.
Функция должна выдавать всегда 1 (единицу, истину). Внутри всех циклов прописываем условие, которое срабатывает как раз на истину. В этом условии прописываем нашу функцию. Если наша функция будет выдавать истину, то мы распечатаем значения переменных, при которых это произошло. Если функция будет выдавать ложь, значит, ничего распечатано не будет.
Четыре вложенных цикла проверяют все возможные варианты (24 = 16 вариантов), и мы получим таблицу истинности, почти такую же, как нам и дали в условии задачи.
Так же вверху печатаем названия переменных, чтобы знать, какие значения каким переменным принадлежат.
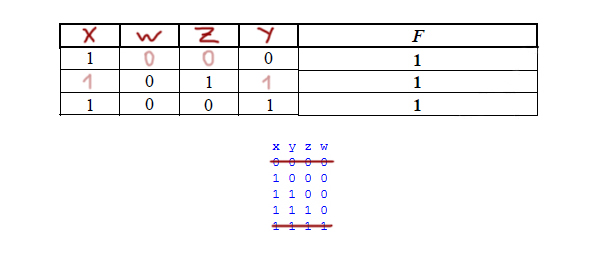
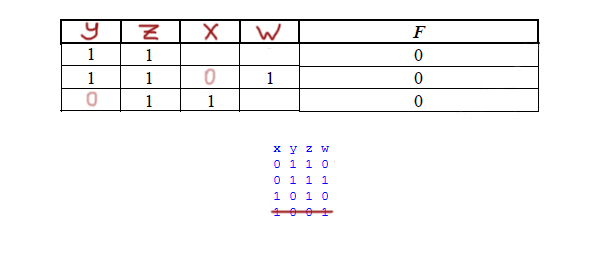
Запустим программу, и на экране распечатается табличка:
В получившийся табличке может быть больше строчек, чем в условии. Так же при поиске переменных нельзя опираться на порядок, в котором идут нули и единицы в нашей табличке. А можно опираться лишь на количество нулей и единиц в строчках или столбцах.
Можно вычеркнуть первую строчку и последнюю, потому что в таблице, которую дали в условии, в каждой строчке есть хотя бы один ноль и хотя бы одна единица.
Сразу видно, что первый столбец принадлежит переменной x, только там могут быть все единицы.
Второй столбец принадлежит переменной w, только там могут быть все нули.
У нас остались две пустые клеточки в самой таблице. Нам нужно где-то поставить единицу, а где-то ноль, потому что у нас остались столбцы с двумя единицами и одним нулём, а так же с двумя нулями и одной единицей. Если мы в третий столбец поставим единицу, а в четвёртый ноль, то первая строчка и вторая будут совпадать.
А в условии сказано, что строки не должны повторяться. Поэтому нужно ноль и единицу расставить наоборот.
Получается, что в третий столбец идёт z, а в четвёртый y
Ответ: xwzy
Посмотрим, как решать задачи второго задания из ЕГЭ по информатике, когда функция выдаёт нули в таблице истинности.
Задача (Классическая, закрепление)
Миша заполнял таблицу истинности функции (x ≡ ¬y) → ((x ∧ w) ≡ z), но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
Определите, какому столбцу таблицы соответствует каждая из переменных
w, x, y, z.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут
соответствующие им столбцы (сначала буква, соответствующая первому
столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы
в ответе пишите подряд, никаких разделителей между буквами ставить
не нужно.
Пример. Функция F задана выражением ¬x / y, зависящим от двух
переменных, а фрагмент таблицы имеет следующий вид.
В этом случае первому столбцу соответствует переменная y, а второму
столбцу – переменная x. В ответе следует написать: yx.
Решение:
Воспользуемся программой на языке Python.
print('x y z w') for x in range(0, 2): for y in range(0, 2): for w in range(0, 2): for z in range(0, 2): if not( not(( x == (not(y)) )) or ((x and w) == z) ): print(x, y, z, w)
От прошлой программы эта программа отличается только функцией!
В таблице видим, что функция должна выдавать ноль. Поэтому в условии мы функцию «оборачиваем» в not().
После == операцию not() мы заключили в скобки, чтобы не было синтаксической ошибки.
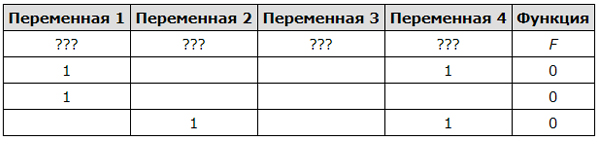
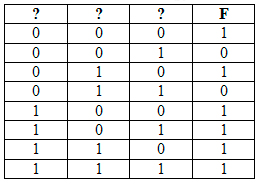
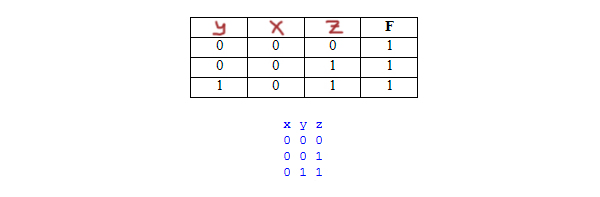
Получаем следующую таблицу истинности:
Разгадаем, где какая переменная находится.
Последнюю строку из нашей таблицы можно вычеркнуть, потому что, если мы вычеркнем другую строку, то не получится столбца, где все три единицы, а он должен быть.
Получается, что второй столбец достаётся переменной z.
В первом столбце должно быть две единицы. На эту роль подходит переменная y.
В нашей таблице нет строчки, где все единицы, значит, во второй строчке в пустом окошке выставляем ноль. И в этой строчке нулём обладает переменная x. Следовательно, в третьем столбце будет находится x.
А в последний столбец идёт переменная w по остаточному принципу.
Ответ: yzxw
А как Питон справится с более сложной функцией из примерного варианта ЕГЭ по информатике?
Задача (Сложная функция)
Логическая функция F задаётся выражением ((x → y ) ∧ (y → w)) ∨ (z ≡ ( x ∨ y)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Источник задачи сайт решу ЕГЭ: https://inf-ege.sdamgia.ru/
Решение:
Запрограммируем функцию на языке Python.
print('x y z w') for x in range(0, 2): for y in range(0, 2): for w in range(0, 2): for z in range(0, 2): if not( ((not(x) or y) and (not(y) or w)) or (z == (x or y)) ): print(x, y, z, w)
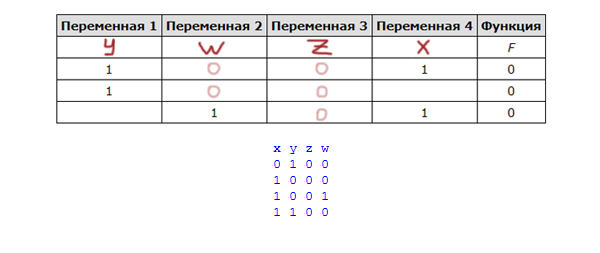
Запустим программу и расставим переменные по своим местам.
Переменная z может быть только в третьем столбце.
Во второй столбец идёт переменная w, только этот столбец может иметь одну единицу.
Посмотрим на строчку, где у w стоит единица. В этой же строчке и у x единица. Значит, x идёт в последний столбец, а y в первый столбец.
Ответ: ywzx
Тот же шаблон работает, когда у нас во втором задании три переменные.
Задача (Три переменные)
(№ 1608) Логическая функция F задаётся выражением (¬x ∧ z) ∨ (¬x ∧ ¬y ∧ ¬z)
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
Источник задачи сайт К. Ю. Полякова: https://kpolyakov.spb.ru/
Решение:
Для трёх переменных шаблон на Питоне отлично работает.
print('x y z') for x in range(0, 2): for y in range(0, 2): for z in range(0, 2): if (not(x) and z) or (not(x) and not(y) and not(z)): print(x, y, z)
Здесь и так понятно, куда какая переменная идёт.
Ответ: yxz
Посмотрим, как решать задачи из второго задания ЕГЭ по информатике, когда в таблице истинности разные значения у функции F.
Задача (Разные значения функции)
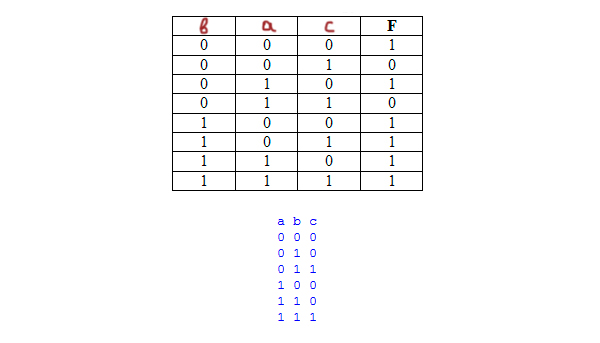
Логическая функция F задаётся выражением (¬a ∨ b ∨ ¬c) ∧ (b ∨ ¬c). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.
В ответе напишите буквы a, b, c в том порядке, в котором идут соответствующие им столбцы (без разделителей).
Источник задачи сайт К. Ю. Полякова: https://kpolyakov.spb.ru/
Решение:
Когда такая ситуация, что функция имеет различные значения в таблице, мы можем проверить, какие значения переменных дают единицу у всей функции. А потом проверить, какие значения выдают ноль у всей функции, если это потребуется.
print('a b c') for a in range(0, 2): for b in range(0, 2): for c in range(0, 2): if (not(a) or b or not(c)) and (b or not(c)): print(a, b, c)
В таблице 6 строчек, в которых главная функция превращается в единицу. Далее эти строчки и будем рассматривать. У нас тоже получилось 6 строчек.
Переменная a имеет три единицы. Это второй столбец, потому что там три единицы.
Переменная b имеет четыре единицы, значит, она расположена в первом столбце.
Переменной c достаётся последний столбец.
Ответ: bac
Ещё одна интересная задача для подготовки к ЕГЭ по информатике 2022.
Задача(С подвохом)
Логическая функция F задаётся выражением a ≡ b ∨ b → c.
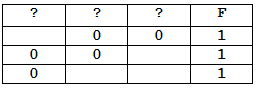
На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.
Источник задачи группа Евгения Джобса: https://vk.com/inform_web
Решение:
Подвох заключается в том, что если мы переведём бездумно функцию на язык Питон, то получится a==b or not(b) or c. Но у нас существуют приоритеты для логических операций, которые описаны в прошлогодней статье по подготовке к ЕГЭ по информатике.
В начале должно обрабатываться или, которое было изначально. Затем должно обработаться следование, а потом равносильность. А если мы переведём формулу бездумно, порядок будет не правильный.
Операцию b ∨ b можно представить, как просто b. Ведь, если b принимает значение 0, тогда будет 0 ∨ 0 = 0. Если значение будет 1, то 1 ∨ 1 = 1. Поэтому формулу можно переписать следующим образом:
a ≡ b → c
a == (not(b) or c)
В предыдущих задачах нам не приходилось думать над приоритетами, потому что везде были расставлены скобки. И в основном они уже расставлены в задачах второго задания из ЕГЭ по информатике.
Дальше решаем как обычно.
print('a b c') for a in range(0, 2): for b in range(0, 2): for c in range(0, 2): if a == (not(b) or c): print(a, b, c)
Последнюю строчку можно вычеркнуть из нашей таблицы, т.к. у нас в каждой строчке есть хотя бы один ноль.
Последний столбец занимает переменная a, т.к. только в последний столбец может влезть две единицы.
В строчке, где у a ноль, так же ноль и у переменной c. Значит, во второй столбец идёт переменная c. Если мы ноль поставим в первой строчке в первом столбце, то получится первый столбец из всех нулей. А такого у нас в таблице истинности нет.
Тогда переменная b в первом столбце.
Ответ: bca
слишком много лишних скобок ни к чему. Код очень грязный
А есть какой-нибудь простой код, который смог бы помочь с таким заданием: «Сколькими способами можно поставить в соответствие переменные w, x, y, z столбцам таблицы истинности функции F, опираясь на информацию из данного фрагмента?», или же в данном случае нужно самому подбирать комбинации?
Доброго времени суток, есть вопрос про операции в последней задаче. Вот там написано что b ∨ b можно представить как b. А если будет b ∧ b, то это можно будет представить как b? И можете объяснить почему?
Как в циклах идут переменные, это не важно. Это просто перебор всех возможных вариантов.
Володя, b ∧ b = b, эти формулы приведены в материале, на который я даю ссылку в начале статьи.
На уроке рассматривается разбор 2 задания ЕГЭ по информатике, дается подробное объяснение того, как решать подобные задачи
Содержание:
- Объяснение задания 2 ЕГЭ по информатике
- Таблицы истинности и порядок выполнения логических операций
- Решение заданий 2 ЕГЭ по информатике
- Задания для тренировки
2-е задание: «Таблицы истинности»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 3 минуты.
Проверяемые элементы содержания: Умение строить таблицы истинности и логические схемы
Типичные ошибки и рекомендации по их предотвращению:
«Игнорирование прямо указанного в условии задания требования, что заполненная таблица истинности не должна содержать одинаковых строк. Это приводит к внешне правдоподобному, но на самом деле неверному решению»
ФГБНУ «Федеральный институт педагогических измерений»
Таблицы истинности и порядок выполнения логических операций
Для логических операций приняты следующие обозначения:
| операция | пояснение | в программировании |
|---|---|---|
| ¬ A, A | не A (отрицание, инверсия) | not(A) |
| A ∧ B, A ⋅ B | A и B (логическое умножение, конъюнкция) | A and B |
| A ∨ B, A + B | A или B (логическое сложение, дизъюнкция) | A or B |
| A → B | импликация (следование) | A <= B |
| A ↔ B, A ≡ B, A ∼ B | эквиваленция (эквивалентность, равносильность) | A==B (python) A=B(pascal) |
| A ⊕ B | строгая дизъюнкция | A != B (python) A <> B (pascal) |
Егифка ©:
Отрицание (НЕ):
Таблица истинности операции НЕ
Конъюнкция (И):
Таблица истинности операции И (конъюнкция)
Дизъюнкция (ИЛИ):
Таблица истинности операции ИЛИ (дизъюнкция)
Импликация (если…, то…):
Таблица истинности операции Импликация (если…, то…)
Эквивалентность (тогда и только тогда, …):
Таблица истинности операции Эквивалентность (тогда и только тогда, …)
Сложение по модулю 2 (XOR):
| A | B | A ⊕ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Порядок выполнения операций:
- если нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», импликация, равносильность
Еще о логических операциях:
- логическое произведение X∙Y∙Z∙… равно 1, т.е. выражение является истинным, только тогда, когда все сомножители равны 1 (а в остальных случаях равно 0)
- логическая сумма X+Y+Z+… равна 0, т.е. выражение является ложным только тогда, когда все слагаемые равны 0 (а в остальных случаях равна 1)
О преобразованиях логических операций читайте здесь.
Егифка ©:
Решение заданий 2 ЕГЭ по информатике
Задание 2_11: Решение 2 задания ЕГЭ по информатике:
Логическая функция F задается выражением
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
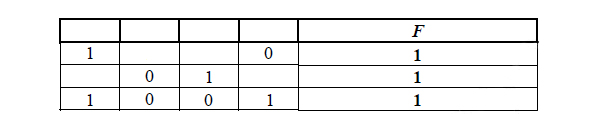
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
✎ Способ 1. Электронные таблицы Excel + Логические размышления:
- Отобразим перебор всех значений использующихся в выражении переменных (всю таблицу истинности). Поскольку в выражении используются 4 переменных, то строк таблицы будет 24=16:
- Далее обе скобки исходного выражения необходимо записать в виде логического выражения, каждую — в отдельном столбце. Также в отдельном столбце добавьте формулу итоговой функции F:

xwzy
-
✎ Способ 2. Программирование:
- В результате будут выведены значения для
F=0:
Язык python:
print('x y z w') for x in 0, 1: for y in 0, 1: for z in 0, 1: for w in 0, 1: F = (not(x) or y or z) and (x or not(z) or not(w)) if not(F): print(x, y, z, w)
x y z w 0 0 1 1 0 1 1 1 1 0 0 0 1 0 0 1
xwzy
Язык pascalAbc.net:
begin writeln('x':7, 'y':7, 'z':7,'w':7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not x or y or z) and (x or not z or not w)) then writeln(x:7, y:7, z:7,w:7); end.
F=0:x y z w False False True True False True True True True False False False True False False True
false = 0, True = 1Ответ:
xwzy
-
✎ Способ 3. Логические размышления:
- Внешняя операция выражения — конъюнкция (∧). Во всех указанных строках таблицы истинности функция принимает значение 0 (ложь). Конъюнкция ложна аж в трех случаях, поэтому проверить на ложь очень затруднительно. Тогда как конъюнкция истинна (= 1) только в одном случае: когда все операнды истинны. Т.е. в нашем случае:
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w) = 1 когда: 1. (¬x ∨ y ∨ z) = 1 И 2. (x ∨ ¬z ∨ ¬w) = 1
| x | y | z | результат |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| x | z | w | результат |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | ??? | ??? | ??? | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | ??? | ??? | y | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | w | z | y | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
Результат: xwzy
🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_12: Разбор 2 задания ЕГЭ:
Миша заполнял таблицу истинности функции:
(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w)
но успел заполнить лишь фрагмент из трех различных ее строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z:
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 1 | 1 | 0 | ||
| 1 | 0 | 0 | ||
| 1 | 1 | 0 | 0 |
Определите, какому столбцу таблицы соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы.
Подобные задания для тренировки
✍ Решение:
✎ Способ 1. Логические размышления (бескомпьютерный вариант):
- Решим задание методом построения полной таблицы истинности.
- Посчитаем общее количество строк в таблице истинности и построим ее:
4 переменных -> 24 = 16 строк
(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w) 1. Избавимся от импликации: ¬(¬z ∧ ¬(x ≡ y)) ∨ ¬(y ∨ w) 2. Внесем знак отрицания в скобки (закон Де Моргана): (z ∨ (x ≡ y)) ∨ (¬y ∧ ¬w) = 0 1 часть = 0 2 часть = 0 * Исходное выражение должно быть = 0. Дизъюнкция = 0, когда оба операнда равны 0.
(z ∨ (x ≡ y)) = 0 когда z = 0 и x ≡ y = 0 ¬y ∧ ¬w = 0 когда: 1. ¬y = 0 ¬w = 0 2. ¬y = 1 ¬w = 0 3. ¬y = 0 ¬w = 1
| x | y | w | z | F |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| y | w | x | z | F |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
Результат: ywxz
✎ Способ 2. Программирование:
- В результате будут выведены значения для F=0:
Язык PascalAbc.net:
begin writeln('x':7, 'y':7, 'z':7,'w':7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not z and (x xor y)) <= not(y or w)) then writeln(x:7, y:7, z:7,w:7); end.
x y z w False True False False False True False True True False False True
false = 0, True = 1Сопоставив их с исходной таблицей, получим результат: ywxz
Язык Python:
print ('x y z w') for x in 0,1: for y in 0,1: for z in 0,1: for w in 0,1: F=(not z and not(x==y))<=(not(y or w)) if not F: print (x,y,z,w)
F=0:x y z w 0 1 0 0 0 1 0 1 1 0 0 1
Сопоставив их с исходной таблицей, получим результат:
Результат: ywxz
🎦 Доступно видео решения этого задания (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
🎦 Видео (решение 2 ЕГЭ в Excel):
📹 здесь
📹 Видеорешение на RuTube здесь
📹 Видеорешение на RuTube здесь (Программирование)
Задание 2_10: Решение 2 задания ЕГЭ по информатике:
Логическая функция F задается выражением
¬a ∧ b ∧ (c ∨ ¬d)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
🎦 (Бескомьютерный вариант) Предлагаем подробный разбор посмотреть на видео:
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_3: Решение задания 2. Демоверсия ЕГЭ 2018 информатика:
Логическая функция F задаётся выражением ¬x ∨ y ∨ (¬z ∧ w).
На рисунке приведён фрагмент таб. ист-ти функции F, содержащий все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
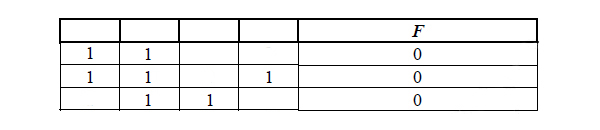
| Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| ??? | ??? | ??? | ??? | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Подобные задания для тренировки
✍ Решение:
-
✎ Логические размышления (бескомпьютерный вариант):
- Внешним действием (последним выполняемым) в исходном выражении является дизъюнкция:
¬x ∨ y ∨ (¬z ∧ w)
| x1 | x2 | F |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
¬x = 1 или 0, y = 1 или 0, ¬z ∧ w = 1 или 0).¬x = 0, иными словами x = 1. Значит первый столбец соответствует переменной x. | Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| x | ??? | ??? | ??? | F |
| 1 | 0 | 0 | 0 | 0 |
y = 0. Значит четвертый столбец соответствует переменной y. | Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| x | ??? | ??? | y | F |
| 1 | 1 | 1 | 0 | 0 |
¬z ∧ w должно равняться 0, чтобы функция была ложной. Конъюнкция истинна только тогда, когда оба операнда истинны (=1); в нашем случае функция должна быть ложной, но пойдем от обратного. Если ¬z = 1, т.е. z = 0, а w = 1, то это неверно для нашего случая. Значит всё должно быть наоборот: z = 1, а w = 0. Таким образом столбец второй соответствует z, а столбец третий — w. | x | z | w | y | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
Результат: xzwy
✎ Способ 2. Программирование:
Язык pascalABC.NET:
begin writeln('x ','y ','z ','w '); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not(not x or y or(not z and w)) then writeln(x:7,y:7,z:7,w:7); end.
🎦 (бескомпьютерный вариант) Подробное решение данного 2 задания из демоверсии ЕГЭ 2018 года смотрите на видео:
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_13: Разбор досрочного егэ по информатике 2019
Логическая функция F задаётся выражением
(x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 |
✍ Решение:
🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
Задания для тренировки
Задание 2_2: Задание 2 ЕГЭ по информатике:
Каждое из логических выражений F и G содержит 5 переменных. В табл. истинности для F и G есть ровно 5 одинаковых строк, причем ровно в 4 из них в столбце значений стоит 1.
Сколько строк таблицы истинности для F ∨ G содержит 1 в столбце значений?
Подобные задания для тренировки
✍ Решение:
- Поскольку в каждом из выражений присутствует 5 переменных, то эти 5 переменных порождают таблицу истинности из 32 строк: т.к. каждая из переменных может принимать оно из двух значений (0 или 1), то различных вариантов с пятью переменными будет 25=32, т.е. 32 строки.
- Из этих 32 строк и для F и для G мы знаем наверняка только о 5 строках: 4 из них истинны (=1), а одна ложна (=0).
- Вопрос стоит о количестве строк = 1 для таб. истинности F ∨ G. Данная операция — дизъюнкция, которая ложна только в одном случае — если F = 0 и одновременно G = 0
- В исходных таблицах для F и G мы знаем о существовании только одного 0, т.е. в остальных строках может быть 1. Т.о., и для F и для G в 31 строке могут быть единицы (32-1=31), а лишь в одной — ноль.
- Тогда для F ∨ G только в одном случае будет 0, когда и F = 0 и G = 0:
- Соответственно, истинными будут все остальные строки:
| № | F | G | F ∨ G |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 |
| … | … | … | 1 |
| 32 | … | … | 1 |
32 - 1 = 31
Результат: 31
Подробное объяснение данного задания смотрите на видео:
📹 здесь
Задание 2_6: Решение 2 задания ЕГЭ по информатике:
Каждое логическое выражение A и B зависит от одного и того же набора из 7 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы.
Каково максимально возможное число единиц в столбце значений таблицы истинности выражения A ∨ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 27 = 128 строк.
- В четырех из них результат равен единице, значит в остальных — 0.
- A ∨ B истинно в том случае, когда либо A = 1 либо B = 1, или и A и B = 1.
- Поскольку А = 1 только в 4 случаях, то чтобы получить максимальное количество единиц в результирующей таблице истинности (для A ∨ B), расположим все единицы т.и. для выражения A так, чтобы они были в строках, где B = 0, и наоборот, все строки, где B = 1, поставим в строки, где A = 0:
- Итого получаем 8 строк.
- Если бы в задании требовалось найти минимальное количество единиц, то мы бы совместили строки со значением = 1, и получили бы значение 4.
| A | B |
| 1 | 0 |
| 1 | 0 |
| 1 | 0 |
| 1 | 0 |
| 0 | 1 |
| 0 | 1 |
| 0 | 1 |
| 0 | 1 |
| 0 | 0 |
| … | … |
Результат: 8
Задание 2_7: Решение 2 задания ЕГЭ по информатике:
Каждое логическое выражение A и B зависит от одного и того же набора из 8 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 6 единиц.
Каково максимально возможное число нулей в столбце значений таблицы истинности выражения A ∧ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 28 = 256 строк.
- В шести из них результат равен единице, значит в остальных — 0.
- A ∧ B ложно в том случае, когда:
A ∧ B = 0 если: 1. A = 0, B = 1 2. B = 0, A = 1 3. A = 0 и B = 0
- Во всех случаях там где А=1 может стоять B=0, и тогда результат F = 0. Поскольку нам необходимо найти максимально возможное число нулей, то как раз для всех шести А=1 сопоставим B=0, и наоборот, для всех шести возможных B=1 сопоставим A=0
- Поскольку строк всего 256, то вполне возможно, что все 256 из них возвратят в результате 0
| A | B | F |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| … | … | … |
Результат: 256
Задание 2_4: 2 задание:
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Каким из приведённых ниже выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7
✍ Решение:
- В первом внешняя операция (выполняется последней) — конъюнкция. Начнем рассмотрение с нее. Соответственно, проверяем по второй строке таб. ист-ти, там где F = 1, так как в таком случае все аргументы должны быть истинными (см. таб. истинности для конъюнкции).
- Если мы подставим в нее все аргументы выражения, то функция действительно возвращает истину. Т.е. пункт первый подходит:
- Но проверим на всякий случай остальные.
- Второй пункт проверяем по первой и третьей строке, так как основная операция — дизъюнкция — ложна только в том случае, если все аргументы ложны (см. таб. истинности для дизъюнкции). Проверяя по первой строке, сразу видим, что x1 в ней равен 1. В таком случаем функция будет = 1. Т.е. этот пункт не подходит:
- Третий пункт проверяем по второй строке, так как основная операция — конъюнкция — возвратит истину только тогда, когда все операнды равны 1. Видим, что x1 = 0, соответственно функция будет тоже равна 0. Т.е. выражение нам не подходит:
- Четвертый пункт проверяем по первой и третьей строкам. В первой — x1 = 1, т.е. функция должна быть равна 1. Т.е. пункт тоже не подходит:
- Таким образом, ответ равен 1.
Результат: 1
Решение 2 задания ГВЭ по информатике смотрите на видео:
📹 здесь
Задание 2_8: Решение 2 задания ЕГЭ по информатике:
Дано логическое выражение, зависящее от 5 логических переменных:
(¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5) ∧ (x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5)
Сколько существует различных наборов значений переменных, при которых выражение истинно?
1) 0
2) 30
3) 31
4) 32
Подобные задания для тренировки
✍ Решение:
- Поскольку выражение включает 5 переменных, то таб. ист-ти состоит из 25 = 32 строк.
- Внешней операцией (последней) является конъюнкция (логическое умножение), а внутри скобок — дизъюнкция (логическое сложение).
- Обозначим первую скобку за А, а вторую скобку за B. Получим A ∧ B.
- Найдем сколько нулей существует для таб. истинности:
A B F 1. 0 0 0 2. 0 1 0 3. 1 0 0
Теперь рассмотрим каждый случай отдельно:
¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5 = 0
и
x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 = 0.
32 - 2 = 30, что соответствует номеру 2
Результат: 2
Подробное решение задания смотрите в видеоуроке:
📹 здесь
Задание 2_5: Решение 2 задания ЕГЭ по информатике:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | F |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 |
Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение x3 не совпадает с F.
Подобные задания для тренировки
✍ Решение:
- Полная таблица истинности будет иметь 26 = 64 строк (т.к. 6 переменных).
- 4 из них нам известны: в них x3 два раза не совпадает с F.
- Неизвестных строк:
64 - 4 = 60
60 + 2 = 62
Результат: 62
Задание 2_9: Решение 2 задания ЕГЭ по информатике:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 0 | 0 | 0 | |||||
| 0 | 0 | 1 | |||||
| 1 | 1 | 1 |
Каким выражением может быть F?
1) x1 ∧ (x2 → x3) ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ ¬x5 ∧ x6 ∧ x7
4) ¬x1 ∨ (x2 → ¬x3) ∨ x4 ∨ x5 ∨ x6 ∧ x7
✍ Решение:
- Рассмотрим отдельно каждый пункт и найдем последнюю операцию, которая должна быть выполнена (внешнюю).
1 пункт:
(((x1 ∧ (x2 → x3) ∧ ¬x4) ∧ x5) ∧ x6) ∧ ¬x7
2 пункт:
(((x1 ∨ (¬x2 → x3) ∨ ¬x4) ∨ ¬x5) ∨ x6) ∨ ¬x7
3 пункт:
(((¬x1 ∧ (x2 → ¬x3) ∧ x4) ∧ ¬x5) ∧ x6) ∧ x7
Результат: 4
В видеоуроке рассмотрено подробное решение 2 задания:
📹 здесь
Задание 2_1: Задание 2 ЕГЭ по информатике:
Логическая функция F задается выражением
(y → x) ∧ (y → z) ∧ z.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| ??? | ??? | ??? | F | |
| 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 1 |
| 4 | 0 | 1 | 1 | 1 |
| 5 | 1 | 0 | 0 | 0 |
| 6 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 0 | 0 |
| 8 | 1 | 1 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
- Сначала необходимо рассмотреть логическую операцию, которую мы будем выполнять в последнюю очередь — это логическое И (конъюнкция) или ∧. То есть внешнюю операцию:
(y → x) ∧ (y → z) ∧ z
(y → x) ∧ (y → z) ∧ z = 1 если: 1. (y → x) = 1 2. (y → z) = 1 3. z = 1
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| 3 | 0 | 1 | 0 | 1 |
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| _ | ??? | z | ??? | F |
| № | Перем. 1 | z | Перем. 3 | F |
|---|---|---|---|---|
| 4 | 0 | 1 | 1 | 1 |
Результат: yzx
Детальный разбор данного задания 2 ЕГЭ по информатике предлагаем посмотреть в видео:
📹 здесь
Характеристика задания
1. Тип ответа: запись правильной последовательности букв.
2. Структура содержания задания: дано логическое выражение и таблица истинности.
3. Уровень сложности задания: базовый.
4. Примерное время выполнения: (3) минуты.
5. Количество баллов: (1).
6. Требуется специальное программное обеспечение: не обязательно.
7. Задание проверяет умение работать с логическими переменными, выполнять логические операции, строить таблицы истинности.
Пример задания
Николай заполнял таблицу истинности логической функции (F)
но успел заполнить только фрагмент из трёх различных её строк, не указав, какому столбцу таблицы принадлежит каждая из переменных (w), (x), (y), (z).
|
(F) |
||||
|
(1) |
(1) |
(1) |
||
|
(0) |
(0) |
(1) |
||
|
(0) |
(1) |
(0) |
(1) |
Определи, какому столбцу таблицы принадлежит каждая из переменных (w), (x), (y), (z).
В ответе напиши буквы (w), (x), (y), (z) в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пиши подряд, никаких разделителей между буквами ставить не нужно.
Как решать задание?
Данное задание можно решать несколькими способами: путём логических рассуждений; использовать электронные таблицы (+) логические рассуждения; с помощью программирования.
Мы рассмотрим вариант решения с помощью языка программирования Python.
Вспомнить основные логические операции можно тут.
Правила построения таблиц истинности можно вспомнить тут.
Законы алгебры логики можно вспомнить тут.
Вспомним управляющие конструкции в Python:
|
цикл с параметром |
for переменная in диапазон:
тело цикла |
for (y) in (0), (1): тело цикла |
|
условие |
if условие then: действия, если условие истинно else: действия, если условие ложно |
if (C>D): print (‘истина‘) else: print (‘ложь‘) |
Запись логических операций на Python
|
Название операции |
Запись на Python |
|
конъюнкция |
(and) |
|
дизъюнкция |
(or) |
|
отрицание |
(not) |
|
импликация |
(<=) |
|
тождество |
(==) |
Напишем программу
Запуск программы
 |
Полученный результат необходимо сравнить с таблицей из условия |
Сопоставим полученную таблицу истинности с таблицей из условия. Нам необходимо сравнивать условие с результатами, как по строкам, так и по столбцам, отыскивая некоторые закономерности и невозможности. Заметим, что столбец (y) содержит в себе три единицы, что может быть только в третьем столбце таблицы из условия. Четвёртый столбик таблицы из условия также можем дополнить единицей, и к этому столбику подходят как (z), так и (w).
Теперь проанализируем строки. В первой строке получилось три единицы, что соответствует четвёртой строке результата программирования, дополняем нулём первую строку. В третьей строке у нас два нуля, поэтому добавляем единицу. Проверяем, чтобы сошлось по строке. Заполним второй столбец, допишем единицу. Этот столбец как раз и будет являться (x). Остаётся проанализировать столбцы (1) и (4).
Рассмотрим первую строку: (x = 0), (y = 1), (z = 0), следовательно, (z) — это четвёртый столбик, а (w) — первый.
Рис. (1). Ход решения
Ответ: (wxyz).
Источники:
Рис. 1. © ЯКласс.
Изображения. © ЯКласс.
Информатика егэ 15 задание python
Продолжаем наш видеокурс по подготовке к ЕГЭ по информатике 2022. Сегодня Разоблачим второе задание!
Кто незнаком с основными логическими операциями, можете посмотреть прошлогоднюю статью по заданию 2 из ЕГЭ по информатике.
В этой статье будут раскрыты методики решения 2 задания через язык программирования Питон.
Будем перебирать для каждой логической переменной все возможные варианты в программе. А логическая переменная всего два значения может принимать: 1 или 0 (истину или ложь). Таким образом, если к примеру у нас 4 переменные, мы получим 2 4 =16 различных комбинаций.
Кто знаком с мощнейшим методом для 2 задания из ЕГЭ по информатике, о котором я рассказывал в прошлогодней статье, тот поймёт, что мы будем применять тот же самый Мощнейший метод, но автоматизированный с помощью питона.
Нам нужно будет запрограммировать Логическую функцию на языке Питон. Вот таблица, которая поможет это сделать.
| Логическая операция | Представление в Питоне |
| Отрицание | Not() |
| Логическое умножение ∧ | And |
| Логическое сложение ∨ | Or |
| Следование A ⟶ B | Not(A) Or B |
| Равносильность ≡ | == |
Перейдём к практике решения задач задания 2 с помощью языка программирования Python.
Миша заполнял таблицу истинности логической функции F
Но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.

Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Функция F задана выражением x / y, зависящим от двух переменных, а фрагмент таблицы имеет следующий вид.
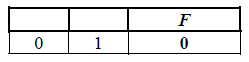
В этом случае первому столбцу соответствует переменная y, а второму столбцу – переменная x. В ответе следует написать: yx.
Решать задачу будем с помощью шаблона на языке Python (Питон).
В задаче у нас 4 переменные, значит, формируем 4 вложенных цикла. В каждом цикле перебираем все возможные значения для конкретной переменной. Мы перебираем значения 0 и 1.
Функция должна выдавать всегда 1 (единицу, истину). Внутри всех циклов прописываем условие, которое срабатывает как раз на истину. В этом условии прописываем нашу функцию. Если наша функция будет выдавать истину, то мы распечатаем значения переменных, при которых это произошло. Если функция будет выдавать ложь, значит, ничего распечатано не будет.
Четыре вложенных цикла проверяют все возможные варианты (2 4 = 16 вариантов), и мы получим таблицу истинности, почти такую же, как нам и дали в условии задачи.
Так же вверху печатаем названия переменных, чтобы знать, какие значения каким переменным принадлежат.
Запустим программу, и на экране распечатается табличка:
В получившийся табличке может быть больше строчек, чем в условии. Так же при поиске переменных нельзя опираться на порядок, в котором идут нули и единицы в нашей табличке. А можно опираться лишь на Количество нулей и единиц в строчках или столбцах.
Можно вычеркнуть первую строчку и последнюю, потому что в таблице, которую дали в условии, в каждой строчке есть хотя бы один ноль и хотя бы одна единица.
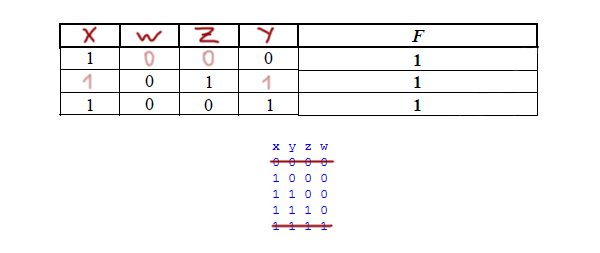
Сразу видно, что первый столбец принадлежит переменной X, только там могут быть все единицы.
Второй столбец принадлежит переменной W, только там могут быть все нули.
У нас остались две пустые клеточки в самой таблице. Нам нужно где-то поставить единицу, а где-то ноль, потому что у нас остались столбцы с двумя единицами и одним нулём, а так же с двумя нулями и одной единицей. Если мы в третий столбец поставим единицу, а в четвёртый ноль, то первая строчка и вторая будут совпадать.
А в условии сказано, что строки не должны повторяться. Поэтому нужно ноль и единицу расставить наоборот.
Получается, что в третий столбец идёт Z, а в четвёртый Y
Ответ: xwzy
Посмотрим, как решать задачи второго задания из ЕГЭ по информатике, когда функция выдаёт нули в таблице истинности.
Задача (Классическая, закрепление)
Миша заполнял таблицу истинности функции (x ≡ y) → ((x ∧ w) ≡ z), но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
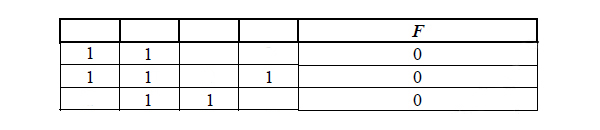
Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Функция F задана выражением x / y, зависящим от двух переменных, а фрагмент таблицы имеет следующий вид.

В этом случае первому столбцу соответствует переменная y, а второму столбцу – переменная x. В ответе следует написать: yx.
Воспользуемся программой на языке Python.
От прошлой программы эта программа отличается только функцией!
В таблице видим, что функция должна выдавать ноль. Поэтому в условии мы функцию «оборачиваем» в Not().
После == операцию Not() мы заключили в скобки, чтобы не было синтаксической ошибки.
Получаем следующую таблицу истинности:
Разгадаем, где какая переменная находится.
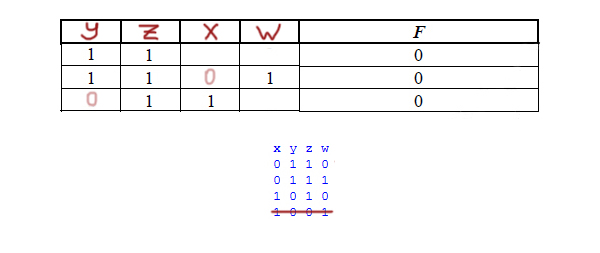
Последнюю строку из нашей таблицы можно вычеркнуть, потому что, если мы вычеркнем другую строку, то не получится столбца, где все три единицы, а он должен быть.
Получается, что второй столбец достаётся переменной Z.
В первом столбце должно быть две единицы. На эту роль подходит переменная Y.
В нашей таблице нет строчки, где все единицы, значит, во второй строчке в пустом окошке выставляем ноль. И в этой строчке нулём обладает переменная X. Следовательно, в третьем столбце будет находится X.
А в последний столбец идёт переменная W по остаточному принципу.
Ответ: yzxw
А как Питон справится с более сложной функцией из примерного варианта ЕГЭ по информатике?
Задача (Сложная функция)
Логическая функция F задаётся выражением ((x → y ) ∧ (y → w)) ∨ (z ≡ ( x ∨ y)).
Дан частично заполненный фрагмент, содержащий Неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Запрограммируем функцию на языке Python.
Запустим программу и расставим переменные по своим местам.
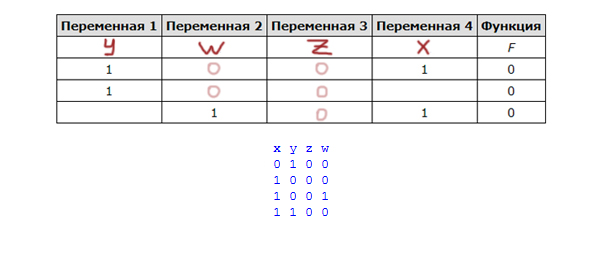
Переменная Z может быть только в третьем столбце.
Во второй столбец идёт переменная W, только этот столбец может иметь одну единицу.
Посмотрим на строчку, где у W стоит единица. В этой же строчке и у X единица. Значит, X идёт в последний столбец, а Y в первый столбец.
Ответ: ywzx
Тот же шаблон работает, когда у нас во втором задании три переменные.
(№ 1608) Логическая функция F задаётся выражением (x ∧ z) ∨ (x ∧ y ∧ z)

На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
Для трёх переменных шаблон на Питоне отлично работает.
Здесь и так понятно, куда какая переменная идёт.
Ответ: yxz
Посмотрим, как решать задачи из второго задания ЕГЭ по информатике, когда в таблице истинности разные значения у функции F.
Задача (Разные значения функции)
Логическая функция F задаётся выражением (a ∨ b ∨ c) ∧ (b ∨ c). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.
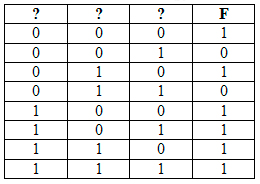
В ответе напишите буквы a, b, c в том порядке, в котором идут соответствующие им столбцы (без разделителей).
Источник задачи сайт К. Ю. Полякова: https://kpolyakov. spb. ru/
Когда такая ситуация, что функция имеет различные значения в таблице, мы можем проверить, какие значения переменных дают единицу у всей функции. А потом проверить, какие значения выдают ноль у всей функции, если это потребуется.
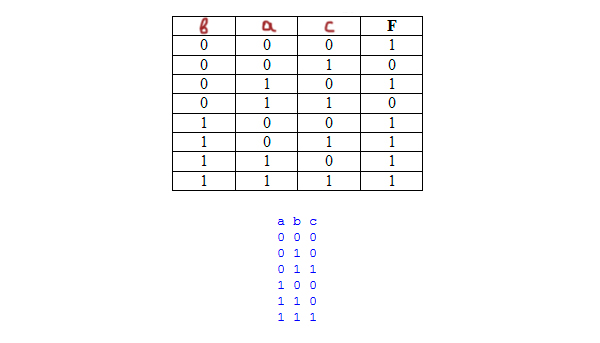
В таблице 6 строчек, в которых главная функция превращается в единицу. Далее эти строчки и будем рассматривать. У нас тоже получилось 6 строчек.
Переменная A имеет три единицы. Это второй столбец, потому что там три единицы.
Переменная B имеет четыре единицы, значит, она расположена в первом столбце.
Переменной C достаётся последний столбец.
Ещё одна интересная задача для подготовки к ЕГЭ по информатике 2022.
Логическая функция F задаётся выражением a ≡ b ∨ b → c.
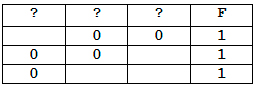
На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.
Источник задачи группа Евгения Джобса: https://vk. com/inform_web
Подвох заключается в том, что если мы переведём Бездумно функцию на язык Питон, то получится a==b or not (b) or c. Но у нас существуют приоритеты для логических операций, которые описаны в прошлогодней статье по подготовке к ЕГЭ по информатике.
В начале должно обрабатываться или, которое было изначально. Затем должно обработаться следование, а потом равносильность. А если мы переведём формулу бездумно, порядок будет не правильный.
Операцию b ∨ b можно представить, как просто b. Ведь, если b принимает значение 0, тогда будет 0 ∨ 0 = 0. Если значение будет 1, то 1 ∨ 1 = 1. Поэтому формулу можно переписать следующим образом:
A ≡ b → c
A == ( not (b) or c)
В предыдущих задачах нам не приходилось думать над приоритетами, потому что везде были расставлены скобки. И в основном они уже расставлены в задачах второго задания из ЕГЭ по информатике.
Дальше решаем как обычно.
Последнюю строчку можно вычеркнуть из нашей таблицы, т. к. у нас в каждой строчке есть хотя бы один ноль.
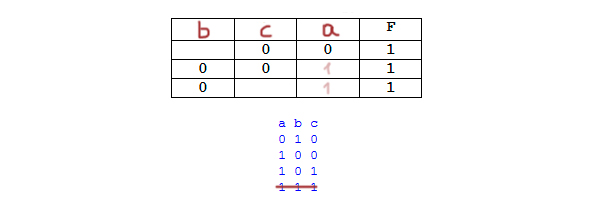
Последний столбец занимает переменная A, т. к. только в последний столбец может влезть две единицы.
В строчке, где у A ноль, так же ноль и у переменной C. Значит, во второй столбец идёт переменная C. Если мы ноль поставим в первой строчке в первом столбце, то получится первый столбец из всех нулей. А такого у нас в таблице истинности нет.
Ответ: yxz
Запрограммируем функцию на языке Python.
Code-enjoy. ru
29.05.2019 2:23:58
2019-05-29 02:23:58
Источники:
Https://code-enjoy. ru/ege_po_informatike_2022_zadanie_2_ay_da_python/
ЕГЭ информатика 15 задание разбор, теория, как решать » /> » /> .keyword { color: red; } Информатика егэ 15 задание python
Рубрика «ЕГЭ Задание 15»
Рубрика «ЕГЭ Задание 15»
Е15.20 ДЕЛ(x, А) → (ДЕЛ(x, 6) → ДЕЛ(x, 9))
ДЕЛ(x, А) → (ДЕЛ(x, 6) → ДЕЛ(x, 9)) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула ДЕЛ(x, А) → (ДЕЛ(x, 6) → ДЕЛ(x, 9)) тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)? Ответ: Демонстрационный вариант …
Е15.19 Решение задания №18 Досрочный вариант №1 ЕГЭ по информатике 2020
Решение задания №18 Досрочный вариант №1 ЕГЭ по информатике 2020 от ФИПИ. Информатика ЕГЭ 18 задание разбор. Как решать задание №18 ЕГЭ по информатике 2020 г. Для какого наименьшего целого неотрицательного числа А выражение (x + 2y < a) / (y >X) / (x > 20) тождественно истинно, т. е. принимает значение 1 при любых …
Рубрика «ЕГЭ Задание 15»
ДЕЛ(x, А) → (ДЕЛ(x, 6) → ДЕЛ(x, 9)) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула ДЕЛ(x, А) → (ДЕЛ(x, 6) → ДЕЛ(x, 9)) тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)? Ответ: Демонстрационный вариант …
Решение задания №18 Досрочный вариант №1 ЕГЭ по информатике 2020 от ФИПИ. Информатика ЕГЭ 18 задание разбор. Как решать задание №18 ЕГЭ по информатике 2020 г. Для какого наименьшего целого неотрицательного числа А выражение (x + 2y < a) / (y >X) / (x > 20) тождественно истинно, т. е. принимает значение 1 при любых …
Решение задания 18 Досрочный вариант 1 ЕГЭ по информатике 2020 от ФИПИ.
Informatikaexpert. ru
12.08.2019 13:44:24
2019-08-12 13:44:24
Источники:
Https://informatikaexpert. ru/ege/ege-zadaniya/ege-zadanie-15/page/3/
Информатика ЕГЭ 15 задание разбор, основные законы алгебры логики » /> » /> .keyword { color: red; } Информатика егэ 15 задание python
Информатика ЕГЭ 15 задание разбор
Информатика ЕГЭ 15 задание разбор
15-е задание: «Основные законы алгебры логики»
Уровень сложности — повышенный,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 5 минут.
Проверяемые элементы содержания: Знание основных понятий и законов математической логики
Плейлист видеоразборов задания на YouTube:
Задания с множествами
Элементами множества А являются натуральные числа. Известно, что выражение
Истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите наименьшее возможное значение Суммы элементов множества A .
Ответ: 12
- Введем обозначения: Выполним преобразования: Разделим выражение на две части — известную часть и неизвестную. Чтобы неизвестная часть ( А ) была непременно истинной, необходимо, чтобы известная часть была ложна: То есть получаем: Таким образом имеем пересечение (умножение) двух множеств Q и P. То есть необходимо выбрать элементы, которые встречаются в обоих множествах одновременно: Сумма элементов:
📹 Видео (аналитическое решение)
📹 Видеорешение на RuTube здесь
Элементами множества А являются натуральные числа. Известно, что выражение
Истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите наименьшее возможное значение Суммы элементов множества A .
Ответ: 18
- Введем обозначения: Выполним преобразования: Разделим выражение на две части — известную часть и неизвестную. Чтобы неизвестная часть ( А ) была непременно истинной, необходимо, чтобы известная часть была ложна: То есть получаем: Таким образом имеем пересечение (умножение) двух множеств Q и P. То есть необходимо выбрать элементы, которые встречаются в обоих множествах одновременно: Сумма элементов:
Элементами множеств А, P, Q являются натуральные числа, причём P = , Q = . Известно, что выражение
Истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите наибольшее возможное Количество элементов в множестве A .
Ответ: 7
- Введем обозначения: Выполним преобразования: Разделим выражение на две части — известную часть и неизвестную. Чтобы неизвестная часть ( А ) была непременно истинной, необходимо, чтобы известная часть была ложна: То есть получаем: Таким образом имеем разность двух множеств Q и P. То есть это новое множество, элементы которого принадлежат P, но не принадлежат Q : Количество элементов = 7
Элементами множества А являются натуральные числа. Известно, что выражение
Истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите Наименьшее возможное количество элементов множества A.
Ответ: 1
- Введем обозначения: Выполним преобразования: Разделим выражение на две части — известную часть и неизвестную. Чтобы неизвестная часть ( А ) была непременно истинной, необходимо, чтобы известная часть была ложна: То есть получаем: Таким образом имеем пересечение двух множеств Q и P : Количество элементов = 1
Задания с отрезками на числовой прямой
Отрезки на числовой прямой:
На числовой прямой даны два отрезка: P=[44,48] и Q=[23,35].
Укажите Наибольшую возможную длину отрезка А, для которого формула
Тождественно Ложна, то есть принимает значение 0 при любом значении переменной X.
Ответ: 4
- Упростим формулу, избавившись от ‘X ϵ‘: Теперь преобразуем импликацию в скобках:
✎ Решение 2 (программирование):
Внимание! этот способ подходит НЕ для всех заданий с отрезками!
Python:
PascalABC. net:
📹 Видео (аналитическое решение)
📹 Видеорешение на RuTube здесь
Отрезки на числовой прямой:
Разбор 15 (18) задания ЕГЭ по информатике, вариант 5 (ФИПИ, «ЕГЭ информатика и ИКТ, типовые экзаменационные варианты 2018», С. С. Крылов, Т. Е. Чуркина):
На числовой прямой даны два отрезка: P = [10,20] и Q = [30,40].
Укажите Наибольшую возможную длину отрезка A, для которого формула
Тождественно Истинна, то есть принимает значение 1 при любом значении переменной X.
Ответ: 10
- Упростим выражение, введя обозначения: Запишем формулу с новыми обозначениями, учитывая, что по условию она должна быть тождественно истинной: Избавимся от импликации: Используем закон Де Моргана для последующего преобразования: А — наше неизвестное, а выделенную часть формулы можно найти. Необходимо, чтобы А = 1. Значит предположим, что А = 0, тогда P ∧ Q = 1 (если P ∧ Q = 0, то А может равняться и 0 и 1, так как имеет место операция логического сложения ∨) Значит, имеем P ∧ Q = 1. Кроме того, в данном случае имеет место операция конъюнкция, которую проще вычислить, если выражение равно 1 (так как для конъюнкции существует один единственный случай истинности: 1 & 1 = 1). Таким образом имеем утверждения: Т. е. A истинно (=1) на промежутке пересечения отрезков P и Q. Отобразим отрезки на числовой прямой, чтобы найти искомое значение:
Отрезки на числовой прямой:
Вариант 6: ФИПИ, «ЕГЭ информатика и ИКТ, типовые экзаменационные варианты 2018», С. С. Крылов, Т. Е. Чуркина:
На числовой прямой даны два отрезка: P = [3, 20] и Q = [6, 12].
Укажите наибольшую возможную длину отрезка A, для которого формула
Тождественно Истинна, то есть принимает значение 1 при любом значении переменной X.
Ответ: 8
- Упростим выражение, введя обозначения: Запишем формулу с новыми обозначениями, учитывая, что по условию она должна быть тождественно истинной: Избавимся от импликации:
Далее возможно 2 способа решения.
✎ 2 способ:
После того, как мы избавились от импликации, имеем:
📹 Видео (аналитическое решение)
📹 Видеорешение на RuTube здесь
Отрезки на числовой прямой:
Вариант 7: ФИПИ, «ЕГЭ информатика и ИКТ, типовые экзаменационные варианты 2018», С. С. Крылов, Т. Е. Чуркина:
На числовой прямой даны два отрезка: P = [11, 21] и Q = [15, 40].
Укажите Наибольшую возможную длину отрезка A, для которого формула
Тождественно Истинна, то есть принимает значение 1 при любом значении переменной X.
Ответ: 19
- Упростим выражение, введя обозначения: Запишем формулу с новыми обозначениями, учитывая, что по условию она должна быть тождественно истинной: Избавимся от импликации: А — наше неизвестное, тогда как выделенную часть формулы можно найти. Введем предположение, что А = 1. Значит, А = 0 (т. е. А = 1), тогда (P ~ Q) = 1 (так как общая формула должна быть истинной по условию). Иными словами (P ~ Q) истинно для всех значений x, при которых P не равно Q (т. е. либо P = 1 и Q = 0, либо P = 0 и Q = 1). Отобразим отрезки на числовой прямой, чтобы найти искомое значение:
Задания с ДЕЛ
Поиск наибольшего А, известная часть Дел ∨ Дел = 1
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого Наибольшего натурального числа А формула
Тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной Х)?
Ответ: 8
- Введем обозначения: Перепишем исходную формулу, согласно введенным обозначениям. Укажем, что формула должна быть тождественно истинна (по условию): Избавимся от импликации: Разделим данную формулу на две части: в одной из них — искомое A, а в другой — часть формулы с X, которую можно найти: В полученной формуле необходимо, чтобы искомая часть с A в конечном счете было Истинно.
Далее можно решать задание либо с помощью кругов Эйлера, либо с помощью логических рассуждений.
Решение с помощью логических рассуждений:
Решение с помощью кругов Эйлера:
Результат: 8
✎ Решение 2 (программирование):
Python:
For A in range(1,500): OK = 1 for x in range(1,1000): OK *= ((x % 40 == 0) or (x % 64 == 0))<=(x % a== 0) if ok: print( a )
PascalABC. net:
Begin for var A := 1 to 500 do begin var ok := 1; for var x := 1 to 1000 do begin if (((x mod 40 = 0) or (x mod 64 = 0))
Результат: 8
Поиск наименьшего А, известная часть Дел ∧ Дел = 1
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого Наименьшего натурального числа А формула
Тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной Х)?
Ответ: 3
Избавимся от импликации:
✎ Решение 2 (программирование). Язык Python, Pascal:
- Из общего выражения:
For A in range(1,50): OK = 1 for x in range(1,1000): OK *= (x % A == 0)
Begin for var A := 1 to 50 do begin var ok := 1; for var x := 1 to 1000 do begin if (x mod A = 0) 0)or (x mod 42 = 0)) = false then begin ok := 0; break; end; end; if (ok = 1) then begin print(A); break; end end; end.
OK — переменная-индикатор: если находится такое А при котором, диапазон всех значений x, подставленных в выражение, возвращает истинное значение выражения, то ОК остается равным 1, т. к. используется операция умножения (до цикла ОК необходимо присвоить единице).
Следует иметь в виду, что в программировании вместо операции импликация ( -> ) можно использовать нестрогое неравенство: . Т. к. таблица истинности для операции импликация соответствует операции
Результат: 3
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого Наименьшего натурального числа А формула
Тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной Х)?
Ответ: 285
- Введем обозначения: Перепишем исходную формулу, согласно введенным обозначениям. Укажем, что формула должна быть тождественно истинна (по условию): Избавимся от импликации: Разделим данную формулу на две части: в одной из них — искомое A, а в другой — часть формулы с X, которую можно найти: Начнем с известной части — части 2 формулы. В ней находится операция конъюнкция, которую проще найти, когда все ее операнды равны 1 (единственный случай для конъюнкции: 1 ∧ 1 = 1). Вторая часть общей формулы может равняться Только1, когда A = 0 (если A = 1, то вторая часть может равнять 0, а нам нужно 1) : Т. е. получаем: Таким образом, имеем: Очевидно, что наименьшим X можем взять число 285 (15 * 19 = 285): ДЕЛ(285, 19) и ДЕЛ(285, 15) Поскольку мы ищем наименьшее A, такое что: ДЕЛ(x, A) и при этом ДЕЛ(x, 19) и ДЕЛ(x, 15), то нам необходимо найти наименьшее делимое чисел 19 и 15: A должно быть таким числом, при котором X принимает Единственно возможное (наименьшее) значение 285: Таким Наименьшим A является само число 285 .
✎ Решение 2 (программирование):
Python:
Из общего выражения:
For A in range(1,500): OK = 1 for x in range(1,1000): OK *= ((x % 19 != 0) or (x % 15 != 0))
OK — переменная-индикатор: если находится такое А при котором, диапазон всех значений x, подставленных в выражение, возвращает истинное значение выражения, то ОК остается равным 1, т. к. используется операция умножения (до цикла ОК необходимо присвоить единице).
Следует иметь в виду, что в программировании вместо операции импликация ( -> ) можно использовать нестрогое неравенство: . Т. к. таблица истинности для операции импликация соответствует операции
Задания с поразрядной конъюнкцией
Обозначим через M & n поразрядную конъюнкцию неотрицательных целых чисел M и N. Так, например, 12&6 = 11002&01102 = 01002 = 4
Для какого наименьшего неотрицательного целого числа A формула
Тождественно Ложна (то есть принимает значение 0 при любом неотрицательном значении переменной X)?
Ответ: 3
Стоит заметить, что для такого типа задач, нет универсального единственного решения. Поэтому на видео, расположенном ниже, представлено два варианта решения.
Рассмотрим один из вариантов решения:
- Удалим из формулы X&, чтобы сократить ее запись: Обратим внимание, что внешней операцией является конъюнкция — логическое умножение: Разделим общее выражение на две части относительно внешней операции. Первая часть — неизвестная, искомая, а вторая — известная, ее можно вычислить: Выполним некоторые преобразования во второй части формулы: Зная свойство импликации, преобразуем формулу (избавимся от импликации в скобках):
📹 Видео (аналитическое решение)
📹 Видеорешение на RuTube здесь
Обозначим через M & N поразрядную конъюнкцию неотрицательных целых чисел M и N. Так, например, 12&6 = 11002&01102 = 01002 = 4
Для какого наибольшего неотрицательного целого числа A формула
Тождественно Истинна (то есть принимает значение 1 при любом неотрицательном значении переменной X)?
Ответ: 38
Результат: 38
Определите Наименьшее натуральное число А из интервала [43, 55], такое, что выражение
Тождественно ложно (то есть принимает значение 0 при любом натуральном значении переменной Х)?
Ответ: 48
- Кратко изложенное решение *:
Результат: 48
Определите Набольшее натуральное число A, такое что выражение
Тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной Х)?
Ответ: 8
- Для упрощения восприятия введем обозначения: Таким образом, получим следующее выражение: Упростим выражение по свойству импликации для второй скобки: Упростим левую часть, используя свойство 2 ( Zk + Zm = Zk and m ): То есть получили z26 ∨ z13 = z8 По правилу импликации: все единичные биты двоичной записи результата (z78 ∨ A) должны входить во множество единичных битов двоичной записи z8. Рассмотрим: Для А единичными битами должны быть общие единичные биты для z8 (10002). Т. е. в нашим случае — это один бит — 3-й:
Результат: 8
Задания на поиск наибольшего или наименьшего числа А
Поиск наибольшего или наименьшего числа А:
Для какого наибольшего целого числа А формула
Тождественно Истинна, то есть принимает значение 1 при любых целых неотрицательных X и Y?
Ответ: 99
Важно: Поскольку используется метод полного перебора, то возможна ситуация, когда транслятор будет работать слишком медленно. Но работоспособность представленного алгоритма проверена на онлайн компиляторах.
Begin for var A := 200 downto -100 do begin var OK := 1; for var x := 0 to 100 do for var y := 0 to 100 do if ((x
For A in range(200,-100,-1): OK = 1 for x in range(0,100): for y in range(0,100): OK *= ((x<=9) <= (x*x<=a)) and((y*y<=a) <= (y<=9)) if ok: print(a) break
✎ Способ 2 (теоретическое решение):
- Условно разделим исходное выражение на части:
(импликация 0 → 0 = 1)
📹 Видео (аналитическое решение)
📹 Видеорешение на RuTube здесь
Поиск наибольшего или наименьшего числа А:
Укажите Наименьшее значение А, при котором выражение
Истинно для любых целых положительных значений X и Y.
Ответ: 101
Важно: Поскольку используется метод полного перебора, то возможна ситуация, когда транслятор будет работать слишком медленно. Но работоспособность представленного алгоритма проверена на онлайн компиляторах.
Begin for var A := -100 to 200 do begin var OK := 1; for var x := 1 to 100 do for var y := 1 to 100 do if ((y+3*x20)or(y>40)) = false then begin OK := 0; break; end; if OK = 1 then begin print(A); break end; end; end.
For A in range(-100,200): OK = 1 for x in range(1,100): for y in range(1,100): OK *= (y+3*x 20) or (y > 40) if OK: print(A) break
✎ Способ 2 (теоретическое решение):
- Определим основные части выражения, выделив отдельно неизвестную часть — с А, и, так сказать, известную часть, то есть остальную. Поскольку основными операциями являются операции дизъюнкции (логического сложения) и порядок их выполнения не важен, то последней, внешней, операцией будем выполнять дизъюнкцию слева, т. к. она объединяет неизвестную и известную часть. Сначала важно рассмотреть вторую часть выражения, известную, так как от нее будет зависеть значение A. Если вторая часть истинна, то А может быть как = 1, так и = 0. Такой вариант нам не подходит: Соответственно, рассмотрим вариант, когда вторая часть ложна, тогда часть выражения с неизвестным А будет обязательно истинной, т. е.: Дизъюнкция ложна, когда оба операнда ложны, т. е. из второго пункта имеем: Для того, чтобы перекрыть все x и все y, возьмем наибольшие из возможных значений: X = 20, Y = 40. Выразим А: Поскольку требуется найти наименьшее значение А, то имеем А = 101 .
📹 Видео (аналитическое решение)
📹 Видеорешение на RuTube здесь
Поиск наибольшего и наименьшего числа A:
Для какого наибольшего целого неотрицательного числа А выражение
(48 ≠ y + 2x) ∨ (A Показать решение:
- Разделим общее выражение на две части. Выделим неизвестную часть красным: Неизвестная часть должна быть истинной, она обязательно будет истинна, если известная часть — ложь: Т. е. 48 ≠ y + 2x = 0 или Y + 2x = 48. На графике это уравнение представляет линию. Из условия имеем два ограничения:(x > 0) and (y > 0). Отобразим линию для 1-й четверти, соответствующей положительным X и Y:
✎ Решение 2 (программное):
Python:
For A in range(200,0,-1): OK = 1 for x in range(0,100): for y in range(0,100): OK *= (48!=y+2*x) or(A
📹 Видео (аналитическое решение)
📹 Видеорешение на RuTube здесь
Поиск наибольшего и наименьшего числа A:
Разбор 15 (18) задания ЕГЭ вариант № 3, 2019 Информатика и ИКТ Типовые экзаменационные варианты (10 вариантов), С. С. Крылов, Т. Е. Чуркина:
Для какого наименьшего целого числа А формула
(y + 5x 4) ∨ (y Показать решение:
- Общая идея такова:
Необходимо упростить формулу так, чтобы последняя операция (внешняя) выполнялась со скобкой, в которой находится искомое A. После чего разделить формулу на две части, в одной из которых находится искомое. Избавимся от импликации, это даст нам возможность опустить общие скобки во второй части формулы: Разделим формулу на две части таким образом, чтобы внешняя операции отделяла часть, в которой находится искомое A: Формула по условию должна быть истинной (=1). Внешняя операция — дизъюнкция — истинна аж в трех случаях: a=1 b=0, a=0 b=1, a=1 b=1. Если мы допустим, что первая часть истинна, то вторая, искомая часть, может быть как истинной, так и ложной. Поэтому такой вариант не подходит. Допустим, что первая часть ложна, тогда вторая, искомая часть, Должна быть только истинной: С учетом, что в первой части формулу находится операция дизъюнкция, которая ложна только в одном случае (a=0 b=0), то выпишем утверждения, получившиеся из первой части: Кроме того, имеем еще одно утверждение второй части: Отобразим получившиеся уравнения прямых на плоскости:
✎ Решение 2 (программное):
Python:
For A in range(-100,100): OK = 1 for x in range(0,100): for y in range(0,100): OK *= (y+5*x<=34)<=((y-x >4)or(y<=a)) if ok: print( a ) break
Begin for var A := -100 to 100 do begin var OK := true; for var x := 0 to 100 do begin for var y := 0 to 100 do begin OK := (y + 5 * x 4) or (y
Поиск наибольшего и наименьшего числа A:
Укажите Наименьшее целое значение А при котором выражение
(2y + 5x 100) ∨ (3x – 2y > 70)
Истинно для любых целых положительных значений X и Y.
Ответ: 171
- ✎ Решение (программное):
Python:
For A in range(-200,200): OK = 1 for x in range(1,100): for y in range(1,100): OK *= (2*y + 5*x < a) or (2*x + 4*y >100) or (3*x — 2*y > 70) if OK: print( A ) break
Begin for var A := -200 to 200 do begin var OK := true; for var x := 1 to 100 do begin for var y := 1 to 100 do begin OK := (2*y + 5*x < a) or (2*x + 4*y >100) or (3*x — 2*y > 70); if OK = false then break; end; if OK = false then break; end; if OK then begin print(A); break; end; end; end.
📹 Видео (аналитическое решение)
📹 Видеорешение на RuTube здесь
Поиск наибольшего и наименьшего числа A:
Укажите Наибольшее целое значение А при котором выражение
(3y – x > A) ∨ (2x + 3y Показать решение:
- ✎ Решение 1 (теоретическое):
✎ Решение 2 (программное):
Python:
For A in range(200,-200,-1): OK = 1 for x in range(1,100): for y in range(1,100): OK *= (3*y-x>A) or (2*x+3*y
Рубрики:
Здравствуйте! Понравилось Ваше объяснение задач. Всё очень просто и доступно. Вопрос по подобной задаче (у Вас 18_4) из решу егэ. Объяснение оттуда не очень меня удовлетворяет. Помогите, пожалуйста! Вот задача:
На числовой прямой даны два отрезка: P = [8, 39] и Q = [23, 58].
Выберите из предложенных отрезков такой отрезок A, что логическое выражение
((x ∈ P) ∨ (x ∈ А)) → ((x ∈ Q) ∨ (x ∈ А))
Тождественно истинно, то есть принимает значение 1 при любом значении переменной х.
Для какого наибольшего целого числа А формула
Тождественно Истинна, то есть принимает значение 1 при любых целых неотрицательных X и Y?
Плейлист видеоразборов задания на YouTube:
Тождественно истинна то есть принимает значение 1 при любом натуральном значении переменной х.
Labs-org. ru
23.06.2019 7:04:58
2019-06-23 07:04:58
Источники:
Https://labs-org. ru/ege-15-practice/
02 задание ЕГЭ информатика (Питон)
print(«x y z»)
for x in range (2):
for y in range (2):
for z in range (2):
if ((not(z) and x) or (x and y))==0:
print(x,y,z)
print(«x y z»)
for x in range (2):
for y in range (2):
for z in range (2):
if (not(x) and y and z) or (not(x) and y and not(z)) or (not(x) and not(y) and not(z)):
print(x,y,z)
Логическая функция F задаётся выражением ¬((?∨?)→(?∧?))∧(?→?). Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
print(‘a b c d’)
for a in range(2):
for b in range(2):
for c in range(2):
for d in range(2):
if (not ((a or b) <= (c and d))) and (a <= d):
print(a, b, c, d)
from itertools import product
def condition(x, y, z, w):
return (not ((x or y) <= (z and w))) and (x <= w)
print(‘a b c d’)
rec = list(product(’01’, repeat=4))
for a in rec:
if condition(int(a[0]), int(a[1]), int(a[2]), int(a[3])) == 1:
print(int(a[0]), int(a[1]), int(a[2]), int(a[3]))