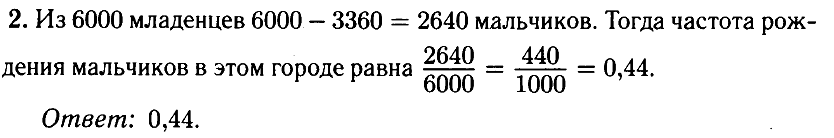Практика по заданию №2 ЕГЭ 2022 по математике профильного уровня — классическое определение вероятности.
Для выполнения задания №2 необходимо умение решать простейшие задачи по теории вероятностей.
Практика
Примеры заданий:
1. В чемпионате по гимнастике участвуют 56 спортсменок: 27 из Норвегии, 15 из Дании, остальные из Швеции. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Швеции.
2. Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 46 спортсменов, среди которых 28 спортсменов из России, в том числе Дмитрий Тоснин. Найдите вероятность того, что в первом туре Дмитрий Тоснин будет играть с каким либо спортсменом из России.
3. Научная конференция проводится в 4 дня. Всего запланировано 80 докладов – первые два дня по 12 докладов, остальные распределены поровну между третьим и четвёртым днями. На конференции планируется доклад профессора М. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
4. Фабрика выпускает сумки. В среднем на 150 качественных сумок приходится 14 сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
5. В сборнике билетов по химии всего 15 билетов, в 6 из них встречается вопрос по теме «Кислоты». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме «Кислоты».
Связанные страницы:
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?
2
В летнем лагере на каждого участника полагается 40 г сахара в день. В лагере 181 человек. Сколько килограммовых упаковок сахара понадобится на весь лагерь на 5 дней?
3
Каждый день во время конференции расходуется 90 пакетиков чая. Конференция длится 3 дня. Чай продаётся в пачках по 50 пакетиков. Сколько пачек чая нужно купить на все дни конференции?
4
Каждый день во время конференции расходуется 80 пакетиков чая. Конференция длится 4 дня. Чай продаётся в пачках по 100 пакетиков. Сколько пачек чая нужно купить на все дни конференции?
5
Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.
Источник: Досрочный ЕГЭ по математике (Центр) 30.03.2018
Пройти тестирование по этим заданиям
За это задание ты можешь получить 1 балл. На решение дается около 5 минут. Уровень сложности: базовый.
Средний процент выполнения: 66.7%
Ответом к заданию 2 по математике (профильной) может быть целое число или конечная десятичная дробь.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
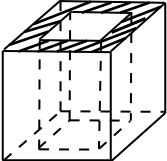
Из единичного куба вырезана правильная четырёхугольная призма со стороной основания $0{,}7$ и боковым ребром $1$. Найдите площадь поверхности получившейся фигуры (cм. рис.).
Решение
Поверхность оставшейся части куба состоит из боковой поверхности куба, площадь которой равна 4·1·1=4, боковой поверхности призмы, площадь которой равна 4·0,7·1=2.8, и двух равных фигур (см. заштрихованную фигуру на рисунке), площадь каждой из которых равна 1·1 — 0,7·0,7 = 0.51. Таким образом, площадь поверхности оставшейся части куба равна 4 + 2.8 + 2 · 0.51 = 7.82.
Ответ: 7.82
Задача 2
Если каждое ребро куба увеличить на $1$ (см. рис.), то площадь его поверхности увеличится на $42$. Найдите ребро куба.
Решение
Пусть ребро куба равно $x$. Площадь поверхности куба равна $6x^2$. Если ребро куба увеличить на $1$, то оно станет равным $(x + 1)$, а площадь поверхности $6(x + 1)^2$. Так как площадь поверхности при этом увеличится на $42$, то $6(x + 1)^2 — 6x^2 = 42$, откуда $12x + 6 = 42, 12x = 36, x = 3$.
Ответ: 3
Задача 3
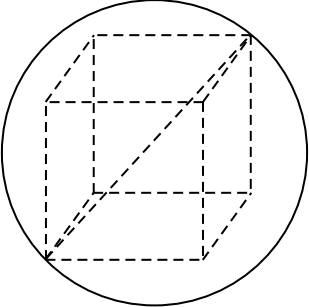
Куб вписан в шар радиуса $2√ 3$. Найдите объём куба.
Решение
Так как диагональ куба, вписанного в шар, равна диаметру шара, то $√3a = 2R$, где $a$ — ребро куба, $R = 2√3$ — радиус шара. Тогда $a√3 = 4√3, a = 4$. Объём куба равен $a^3 = 64$.
Ответ: 64
Задача 4
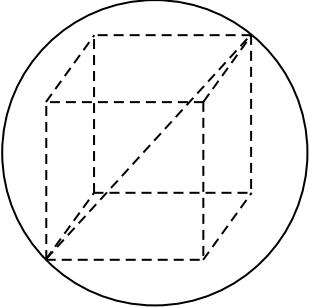
Куб вписан в шар радиуса $1{,}5√ 3$. Найдите объём куба.
Решение
Так как диагональ куба, вписанного в шар, равна диаметру шара, то $√3a = 2R$, где $a$ — ребро куба, $R = 1.5√3$ — радиус шара. Тогда $√3a = 3√3, a = 3$. Объём куба равен $a^3 = 27$.
Ответ: 27
Задача 5
Объём куба равен $64$ (см. рис.). Найдите площадь его поверхности.
Решение
Пусть ребро куба равно $x$. По условию объём куба равен $64$, тогда $x^3=64$, откуда $x=4$. Площадь грани куба равна $x^2=16$. Площадь поверхности куба равна $6x^2=6⋅16=96$.
Ответ: 96
Задача 6
Длина окружности основания цилиндра равна $6$. Площадь боковой поверхности равна $21$. Найдите высоту цилиндра.
Решение
Площадь боковой поверхности цилиндра вычисляется по формуле $S_{бок} = 2πRH$, где $R$ — радиус основания, $H$ — высота цилиндра. По условию $2πR = 6, S_{бок} = 21$, тогда $H = 21 : 6 = 3.5$.
Ответ: 3.5
Задача 7
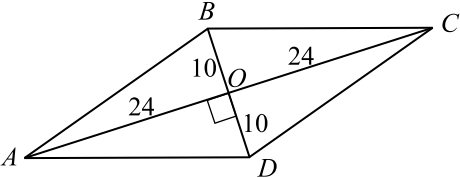
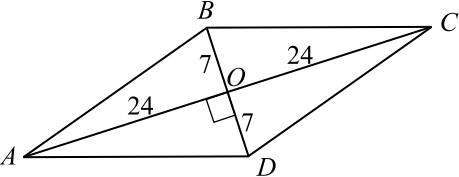
В основании прямой призмы лежит ромб с диагоналями, равными $20$ и $48$ (см. рис.). Площадь её поверхности равна $1272$. Найдите боковое ребро этой призмы.
Решение
Так как диагонали ромба перпендикулярны и точкой пересечения делятся пополам, то сторону ромба найдём из прямоугольного треугольника $AOD$ по теореме Пифагора.
$AD = √{AO^2 + OD^2} = √{24^2 + 10^2} = 26$.
Площадь ромба $S_{осн} = {1}/{2}d_1 · d_2$, где $d_1$ и $d_2$ — диагонали ромба. $S_{осн} = {1}/{2} · 48 · 20 = 480$. Пусть боковое ребро призмы равно $x$. Площадь поверхности призмы равна $S = S_{бок} + 2S_{осн} = 1272$, откуда $S_{бок} = 1272 — 960 = 312$. Так как $S_{бок} = 4 · 26 · x$, то $104x = 312$, откуда $x = 3$.
Ответ: 3
Задача 8
В основании прямой призмы лежит ромб с диагоналями, равными $14$ и $48$ (см. рис.). Площадь её поверхности равна $1232$. Найдите боковое ребро этой призмы.
Решение
Так как диагонали ромба перпендикулярны и точкой пересечения делятся пополам, то сторону ромба найдём из прямоугольного треугольника $AOD$ по теореме Пифагора.
$AD = √{AO^2 + OD^2} = √{24^2 + 7^2} = 25$.
Площадь ромба $S_{осн} = {1}/{2}d_1 · d_2$, где $d_1$ и $d_2$ — диагонали ромба. $S_{осн} = {1}/{2} · 48 · 14 = 336$. Пусть боковое ребро призмы равно $x$. Площадь поверхности призмы равна $S = S_{бок} + 2S_{осн} = 1232$, откуда $S_{бок} = 1232 — 672 = 560$. Так как $S_{бок} = 4 · 25 · x$, то $100x = 560$, откуда $x = 5.6$.
Ответ: 5.6
Задача 9
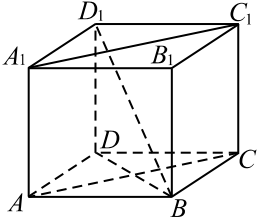
В правильной четырёхугольной призме $ABCDA_1B_1 C_1 D_1$ ребро $AA_1$ равно $24$, а диагональ $BD_1$ равна $26$ (см. рис.). Найдите площадь сечения призмы плоскостью, проходящей через точки $A$, $A_1$ и $C$.
Решение
Сечением призмы плоскостью, проходящей через точки $A, A_1$ и $C$, является прямоугольник $AA_1C_1C$, площадь которого равна $S = AA_1 · AC$. Выразим катет $BD$ из прямоугольного треугольника $BDD_1 : BD = √{BD_1^2 — DD_1^2} = √{26^2 — 24^2} = √{(26 — 24)(26 + 24)} = 10$. Так как $BD = AC$, то $S = 24 · 10 = 240$.
Ответ: 240
Задача 10
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен $7$.
Решение
$V_{цилиндра}=S_{осн}⋅ H$, $V_{конуса}={1} / {3} S_{осн}⋅ H$. По условию конус
и цилиндр имеют общее основание и общую высоту, значит,
$V_{цилиндра}=3V_{конуса}=21$.
Ответ: 21
Задача 11
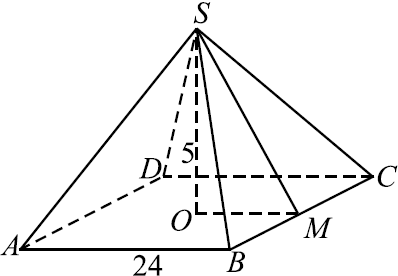
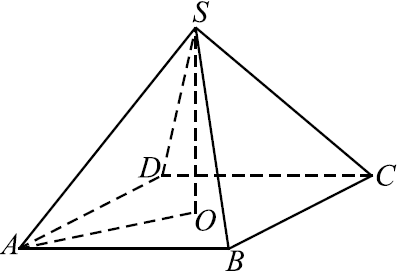
Найдите площадь поверхности правильной четырёхугольной пирамиды, стороны основания которой равны $24$ и высота равна $5$ (см. рис.).
Решение
Площадь $S$ поверхности правильной четырёхугольной пирамиды $SABCD$ равна сумме площади основания $S_{осн}$ и площади боковой поверхности $S_{бок}: S = S_{осн} + S_{бок} = AB^2 + 4S_{SBC}. SM$ — апофема.
$S_{осн} = AB^2 = 576, SM$ найдём по теореме Пифагора как гипотенузу прямоугольного треугольника $SOM: SM = √{SO^2 + OM^2} = √{SO^2 + ({1}/{2}AB)^2} = √{5^2 + 12^2} = 13$.
$S_{бок} = 4S_{SBC} = 4·{1}/{2}·24·13 = 4·156=624. $
$S = 576 + 624 = 1200$.
Ответ: 1200
Задача 12
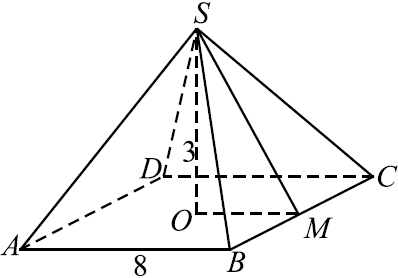
Найдите площадь поверхности правильной четырёхугольной пирамиды, стороны основания которой равны $8$ и высота равна $3$ (см. рис.).
Решение
Площадь $S$ поверхности правильной четырёхугольной пирамиды $SABCD$ равна сумме площади основания $S_{осн}$ и площади боковой поверхности $S_{осн} + S_{бок} = AB^2 + 4S_{SBC}$
$SM$ — апофема.
$S_{осн} = AB^2 = 64$
$SM$ найдём по теореме Пифагора как гипотенузу прямоугольного треугольника $SOM: SM = √{SO^2 + OM^2} = √{SO^2 + ({1}/{2}AB)^2} = √{3^2 + 4^2} = 5$.
$S_{бок} = 4S_{SBC} = 4·{1}/{2}·8·5 = 80$
$S_{осн} + S_{бок} = 64 + 80 = 144$
Ответ: 144
Задача 13
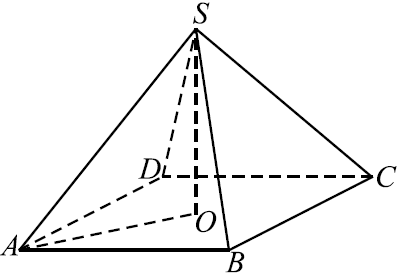
В правильной четырёхугольной пирамиде высота равна $3$, объём равен $32$ (cм. рис.). Найдите боковое ребро этой пирамиды.
Решение
Объём пирамиды вычисляется по формуле $V = {1}/{3}·S_{осн}·H$, где $H = 3$ — высота пирамиды. Площадь основания равна $S_{осн} = 3{V}/{H} = {3·32}/{3} = 32$, откуда длина стороны квадрата, лежащего в основании пирамиды, равна $√{32} = 4√2$. Диагональ квадрата $AC = 8$.
Боковое ребро $SA$ найдём как гипотенузу прямоугольного треугольника $AOS$, где $SO$ — высота пирамиды. $AS = √{SO^2 + OA^2} = √{SO^2 + ({1}/{2}AC)^2} = √{3^2 + 4^2} = 5$.
Ответ: 5
Задача 14
В правильной четырёхугольной пирамиде высота равна $9$, объём равен $864$ (cм. рис.). Найдите боковое ребро этой пирамиды.
Решение
Объём пирамиды вычисляется по формуле $V = {1}/{3}·S_{осн}·H$, где $H = 9$ — высота пирамиды. Площадь основания равна $S_{осн} = 3{V}/{H} = {3·864}/{9} = 288$, откуда длина стороны квадрата, лежащего в основании пирамиды, равна $√{288} = 12√2$. Диагональ квадрата $AC = 24$.
Боковое ребро $SA$ найдём как гипотенузу прямоугольного треугольника $AOS$, где $SO$ — высота пирамиды. $AS = √{SO^2 + OA^2} = √{SO^2 + ({1}/{2}AC)^2} = √{9^2 + 12^2} = 15$.
Ответ: 15
Задача 15
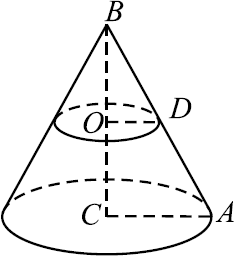
Площадь основания конуса равна $27$. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной $2$ и $4$, считая от вершины (см. рис.). Найдите площадь сечения конуса этой плоскостью.
Решение
Пусть $CA = R$ — радиус основания конуса, сечение конуса плоскостью, параллельной плоскости основания конуса — круг, радиус которого $OD = r$.
$OD ‖ AC$, следовательно, $△ABC ∼ △DBO$ по первому признаку подобия ($∠ACB = ∠DOB = 90°, ∠ABC$ — общий). По условию $BO = 2, OC = 4$, значит, $BC = 6$, откуда ${BO}/{BC} = {OD}/{AC} = {1}/{3}, {πr^2}/{πR^2} = {1}/{9}$. Значит, площадь сечения конуса плоскостью, параллельной плоскости основания конуса, в $9$ раз меньше плоскости основания конуса, то есть равна $27 : 9 = 3$.
Ответ: 3
Задача 16
Если каждое ребро куба увеличить на 3, то его площадь поверхности увеличится на 126. Найдите ребро куба.
Решение
$S_1=6а^2$
$ S_2=6(a+3)^2$
$ 6(a+3)^2-6а^2=126$
$ 6(а^2+6а+9)-6а^2=126$
$ 6а^2+36а+54-6а^2=126$
$ 36а=126-54$
$ 36а=72$
$ а=2$.
Ответ: 2
Рекомендуемые курсы подготовки
ЕГЭ Профиль №2. Теоремы о вероятностях событий
Скачать файл в формате pdf.
ЕГЭ Профиль №2. Теоремы о вероятностях событий
| Задача 1. На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем. |
| Задача 2. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства. |
| Задача 3. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из не пристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся. |
| Задача 4. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза. |
| Задача 5. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98? |
| Задача 6. Вероятность того, что на тесте по биологии учащийся О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач. |
| Задача 7. Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание. Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5. Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей. |
| Задача 8. Чтобы поступить в институт на специальность «Международные отношения» абитуриент должен набрать на ЕГЭ не менее 67 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Менеджмент» нужно набрать не менее 67 баллов по каждому из трёх предметов — математика, русский язык и обществознание. Вероятность того, что абитуриент Т. получит не менее 67 баллов по математике — равна 0,6, по русскому языку — 0,5, по иностранному языку — 0,8 и по обществознанию — 0,9. Найдите вероятность того, что Т. сможет поступить на одну из двух упомянутых специальностей. |
| Задача 9. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятность того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19.
Ответ
ОТВЕТ: 0,38. |
|
| Задача 10. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
Ответ
ОТВЕТ: 0,392. |
|
| Задача 11. Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Ответ
ОТВЕТ: 0,0545. |
|
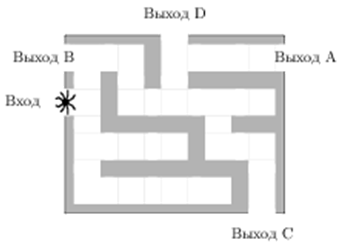
| Задача 12. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу D.
Ответ
ОТВЕТ: 0,0625. |
 |
| Задача 13. Какова вероятность того, что последние три цифры номера случайно выбранного паспорта различны?
Ответ
ОТВЕТ: 0,72. |
|
| Задача 14. Какова вероятность того, что в случайном телефонном номере три последние цифры одинаковые?
Ответ
ОТВЕТ: 0,01. |
|
| Задача 15. При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше 810 г, равна 0,96. Вероятность того, что масса окажется больше 790 г, равна 0,82. Найдите вероятность того, что масса буханки больше 790 г, но меньше 810 г.
Ответ
ОТВЕТ: 0,78. |
|
| Задача 16. При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше 810 г, равна 0,98. Вероятность того, что масса окажется больше 790 г, равна 0,83. Найдите вероятность того, что масса буханки больше 790 г, но меньше 810 г.
Ответ
ОТВЕТ: 0,81. |
Уважаемый посетитель!
Если у вас есть вопрос, предложение или жалоба, пожалуйста, заполните короткую форму и изложите суть обращения в текстовом поле ниже. Мы обязательно с ним ознакомимся и в 30-дневный срок ответим на указанный вами адрес электронной почты
Статус Абитуриент Студент Родитель Соискатель Сотрудник Другое
Филиал Абакан Актобе Алагир Алматы Алушта Анапа Ангарск Архангельск Армавир Асбест Астана Астрахань Атырау Баку Балхаш Барановичи Барнаул Белая Калитва Белгород Бельцы Берлин Бишкек Благовещенск Бобров Бобруйск Борисов Боровичи Бронницы Брянск Бузулук Чехов Челябинск Череповец Черкесск Дамаск Дербент Димитровград Дмитров Долгопрудный Домодедово Дубай Дубна Душанбе Екатеринбург Электросталь Елец Элиста Ереван Евпатория Гана Гомель Гродно Грозный Хабаровск Ханты-Мансийск Хива Худжанд Иркутск Истра Иваново Ижевск Калининград Карабулак Караганда Каракол Кашира Казань Кемерово Киев Кинешма Киров Кизляр Королев Кострома Красноармейск Краснодар Красногорск Красноярск Краснознаменск Курган Курск Кызыл Липецк Лобня Магадан Махачкала Майкоп Минеральные Воды Минск Могилев Москва Моздок Мозырь Мурманск Набережные Челны Нальчик Наро-Фоминск Нижневартовск Нижний Новгород Нижний Тагил Ногинск Норильск Новокузнецк Новосибирск Новоуральск Ноябрьск Обнинск Одинцово Омск Орехово-Зуево Орел Оренбург Ош Озёры Павлодар Пенза Пермь Петропавловск Подольск Полоцк Псков Пушкино Пятигорск Радужный Ростов-на-Дону Рязань Рыбинск Ржев Сальск Самара Самарканд Санкт-Петербург Саратов Сергиев Посад Серпухов Севастополь Северодвинск Щербинка Шымкент Слоним Смоленск Солигорск Солнечногорск Ставрополь Сургут Светлогорск Сыктывкар Сызрань Тамбов Ташкент Тбилиси Терек Тихорецк Тобольск Тольятти Томск Троицк Тула Тверь Тюмень Уфа Ухта Улан-Удэ Ульяновск Ургенч Усть-Каменогорск Вёшенская Видное Владимир Владивосток Волгодонск Волгоград Волжск Воркута Воронеж Якутск Ярославль Юдино Жлобин Жуковский Златоуст Зубова Поляна Звенигород
Тип обращения Вопрос Предложение Благодарность Жалоба
Тема обращения Поступление Трудоустройство Обучение Оплата Кадровый резерв Внеучебная деятельность Работа автоматических сервисов университета Другое
* Все поля обязательны для заполнения
Я даю согласие на обработку персональных данных, согласен на получение информационных рассылок от Университета «Синергия» и соглашаюсь c политикой конфиденциальности
ЕГЭ по математике Профиль. Задание 2: Уметь строить и исследовать простейшие математические модели. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».
ЕГЭ Профиль. Задание № 2.
АЛГОРИТМ ВЫПОЛНЕНИЯ
Задание № 2 проверяет умение использовать элементы теории вероятностей при решении прикладных задач. Для его выполнения понадобится производить действия с дробями и совершать простые вычисления. Задание представляет собой текстовую задачу, которая решается с помощью базовых арифметических операций. В ответе необходимо указать целое или дробное число, записанное в виде конечной десятичной дроби.
План выполнения:
- Внимательно прочитайте задачу.
- Выявите число всех элементарных событий и число благоприятствующих событий, не пропустив ни одного из всех возможных исходов и не включая ни одного лишнего.
- При решении задачи на классическое определение вероятности установите, зависимы (совместны) или независимы (несовместны) элементарные события.
- Выполните на черновике необходимые вычисления.
- Запишите полученное число в поле ответа КИМ и бланк ответов № 1.
Задачи на классическое
определение вероятности
Задача № 2 (1). В коробке лежит 40 шаров: 20 чёрных, 4 жёлтых и 16 зелёных. Наугад из коробки достают один шар. Найдите вероятность того, что этот шар будет жёлтым.
Решение:
Ответ: 0,1.
Задача № 2 (2). Участников шахматного турнира разбивают на пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шахматистов, среди которых 11 спортсменов из России, в том числе Пётр Орлов. Найдите вероятность того, что Пётр Орлов будет играть с шахматистом из России.
Решение:
Ответ: 0,4.
Задача № 2 (3). У Дениса в копилке лежит 6 рублёвых, 3 двухрублёвых, 2 пятирублёвых и 4 десятирублёвых монеты. Денис наугад достал из копилки одну монету. Найдите вероятность того, что оставшаяся в копилке сумма составит более 60 рублей.
Решение:
Ответ: 0,4.
Задачи на использование теорем
о вероятностях событий
Задача № 2 (4). Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы в течение года равна 0,2. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Решение:
Ответ: 0,96.
Задача № 2 (5). При проверке на вирусное заболевание делают анализ крови. Если анализ выявляет вирус, то результат является положительным. У больных анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на заболевание, действительно больны. Найдите вероятность того, что результат анализа у пациента будет положительным. Ответ округлите до сотых.
Решение:
Ответ: 0,05.
Задача № 2 (6). На экзамене по истории ученик отвечает на один вопрос из списка. Вероятность того, что это вопрос по теме «Крепостное право», равна 0,2. Вероятность того, что это вопрос по теме «Февральская революция», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене ученику достанется вопрос по одной из этих двух тем.
Решение:
Ответ: 0,35.
Тренировочные задания с самопроверкой
№ 2.1. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 5 очков. Ответ округлите до сотых.
Открыть ОТВЕТ
№ 2.2. В некотором городе на 6000 появившихся на свет младенцев приходится 3360 девочек. Найдите частоту рождения мальчиков в этом городе.
Открыть ОТВЕТ
№ 2.3. Вероятность того, что на тесте по математике ученица Настя верно решит не менее 12 задач, равна 0,84. Вероятность того, что Настя решит больше 11 задач, равна 0,96. Найдите вероятность того, что Настя решит ровно 12 задач.
Открыть ОТВЕТ
№ 2.4. Склад освещается двумя фонарями с лампами. Вероятность перегорания лампы одного фонаря в течение одного месяца равна 0,4. Найдите вероятность того, что в течение месяца хотя бы одна лампа не перегорит.
Открыть ОТВЕТ
№ 2.5. Вероятность того, что батарейка бракованная, равна 0,05. Покупатель в магазине выбирает случайную упаковку, в которой две такие батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Открыть ОТВЕТ
Вы смотрели: ЕГЭ по математике Профиль. Задание 2: Уметь строить и исследовать простейшие математические модели. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.
Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».
Просмотров:
17 273
Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 11. Найдите объём куба.
Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 25. Найдите объём куба.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 19. Найдите объем шара.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 188. Найдите объем конуса.
Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна (27sqrt{2}) Найдите площадь боковой поверхности конуса.
Цилиндр и конус имеют общие основание и высоту. Объём цилиндра равен 162. Найдите объём конуса.
В цилиндрическом сосуде уровень жидкости достигает 25 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2,5 раза больше диаметра первого? Ответ дайте в сантиметрах.
Дано два цилиндра. Объём первого цилиндра равен 5. У второго цилиндра высота в 2,5 раза меньше, а радиус основания в 3 раза больше, чем у первого. Найдите объём второго цилиндра.
В сосуд, имеющий форму правильной треугольной призмы, налили 1100 см(^3) воды и полностью в неё погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 29 см. Чему равен объём детали? Ответ выразите в см(^3).
В сосуде, имеющем форму конуса, уровень жидкости достигает 0,25 высоты. Объём жидкости равен 5 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?