Скачать материал

Скачать материал




- Сейчас обучается 29 человек из 17 регионов




Описание презентации по отдельным слайдам:
-
1 слайд
26.02.2019
РЕШЕНИЯ ЗАДАЧ ЕГЭ
ПО ИНФОРМАТИКЕ И ИКТ С ИСПОЛЬЗОВАНИЕМ ПОНЯТИЯ «ВЫИГРЫШНОЙ СТРАТЕГИИ»ПФУНТ Ольга Леонидовна,
учитель информатики
высшей категории
МАОУ «СОШ№5» городского округа г. Стерлитамак РБ -
2 слайд
Часть 2 экзаменационной работы содержит 4 задания, первое из которых повышенного уровня сложности, остальные 3 (в том числе задание 26)- задания высокого уровня сложности. Задания этой части подразумевают запись развернутого ответа в произвольной форме.
-
3 слайд
Спецификация
контрольных измерительных материалов
для проведения в 2019 году
единого государственного экзамена
по информатике и ИКТ
(максимальный балл -3 балла) -
4 слайд
.
В задаче от ученика требуется выполнить 3 задания. Их трудность возрастает. Количество баллов в целом соответствует количеству выполненных заданий.
Ошибка в решении, не искажающая основного замысла, например, арифметическая ошибка при вычислении количества камней в заключительной позиции, при оценке решения не учитывается. -
-
6 слайд
.
Теория:
Выигрышные и проигрышные позиции
все позиции в простых играх делятся на выигрышные и проигрышные;
выигрышная позиция – это такая позиция, в которой игрок, делающий первый ход, может гарантированно выиграть при любой игре соперника, если не сделает ошибку; при этом говорят, что у него есть выигрышная стратегия – алгоритм выбора очередного хода, позволяющий ему выиграть
если игрок начинает играть в проигрышной позиции, он обязательно проиграет, если ошибку не сделает его соперник; в этом случае говорят, что у него нет выигрышной стратегии; таким образом, общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для соперника
выигрышные и проигрышные позиции характеризуются так:
позиция, из которой все возможные ходы ведут в выигрышные позиции – проигрышная;
позиция, из которой хотя бы один из последующих возможных ходов ведет в проигрышную позицию — выигрышная, при этом стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную (для оппонента) позицию.
Кто выиграет при стратегически правильной игре?
для того чтобы определить, какой из игроков выиграет при стратегически правильной игре, необходимо ответить на вопросы:
Может ли какой-либо из игроков выиграть, независимо от ходов других игроков?
Что должен сделать игрок с выигрышной стратегией первым ходом, чтобы он смог выиграть, независимо от действий ходов игроков? -
7 слайд
.
Стратегия игрока определяет его действие в любой момент игры и для каждого возможного течения игры.
Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
В описании выигрышной стратегии не следует включать ходы играющего, не являющиеся для него безусловно выигрышными. -
8 слайд
.
Методы решения :выигрышную стратегию в несложных играх, достаточно использовать метод перебора всех возможных вариантов ходов игроков;
для решения задач 26 задания чаще всего для этого применяется метод построения деревьев; -
9 слайд
Пример:
Игра: В кучке лежит 5 спичек; два игрока убирают спички по очереди, причем за 1 ход можно убрать 1 или 2 спички; выигрывает тот, кто оставит в кучке 1 спичку(победное число)
Вопросы:
1) «Может ли первый игрок выиграть, независимо от действий второго?»
2) «Может ли второй игрок выиграть, независимо от действий первого?» -
-
11 слайд
Вопросы:
1) «Может ли первый игрок выиграть, независимо от действий второго?»
2) «Может ли второй игрок выиграть, независимо от действий первого?»
Ответы:
1) «да»; действительно, убрав всего одну спичку первым ходом, 1-ый игрок всегда может выиграть на следующем ходу
2) «нет», потому что если первый игрок сначала убрал одну спичку, второй всегда проиграет, если первый не ошибется -
-
13 слайд
2019 год (две кучи камней)
-
14 слайд
2019 год (две кучи камней)
Задание1
а) Укажите все такие значения числа S, при которых Петя может выиграть за один ход
б)Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна -
15 слайд
2019 год (две кучи камней)
Задание2
Укажите такое значения числа S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются следующие условия:
а) Петя не может выиграть за один ход
б)Петя может выиграть своим вторым ходом, независимо от того, как будет ходить Ваня. -
16 слайд
2019 год (две кучи камней)
Задание3
Укажите такое значение числа S, при которых :
а) у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети
б)У Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом -
-
18 слайд
Дерево партий (заготовки)
-
19 слайд
Дерево партий в виде ориентированного графа
-
20 слайд
2018 год (одна куча)
-
-
-
-
24 слайд
2018 год
На каждом шаге мы рассматриваем все возможные ходы Пети и только один лучший ход Вани. Например, в позиции S = 15 Ваня может сделать ход «+1» и получить 16 камней в куче, но тогда он проиграет (Петя следующим ходом удвоит число камней и получит 32 камня). Этот ход мы не рассматриваем, потому что мы хотим доказать, что у Вани есть выигрышная стратегия – ему достаточно хода «*2», после которого он выиграет. В то же время нужно рассмотреть все возможные ответы Пети, чтобы доказать, что у него нет шансов на выигрыш при правильной игре Вани. В этом суть теории игр – добиться лучшего результата -
-
-
27 слайд
Стратегия игры ФИШКИ
-
28 слайд
Демо-вариант 2018 года, проект) Два игрока, Петя и Ваня играют в следующую игру. На столе в кучке лежат фишки. На лицевой стороне каждой фишки написано двузначное натуральное число, обе цифры которого находятся в диапазоне от 1 до 4. Никакие две фишки не повторяются. Игра состоит в том, что игроки
поочередно берут из кучки по одной фишке и выкладывают в цепочку на стол лицевой стороной вверх таким образом, что каждая новая фишка ставится правее предыдущей и ближайшие цифры соседних фишек совпадают. Верхняя часть всех выложенных фишек направлена в одну
сторону, то есть переворачивать фишки нельзя. Например, из фишки, на которой написано 23, нельзя сделать фишку, на которой написано 32. Первый ход делает Петя, выкладывая на стол любую фишку из кучки. Игра заканчивается, когда в кучке нет ни одной фишки, которую можно добавить в цепочку. Тот, кто добавил в цепочку последнюю фишку, выигрывает, а его противник проигрывает. Будем называть партией любую допустимую правилами последовательность ходов игроков, приводящую к завершению игры. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит указать, какую фишку он должен выставить в любой ситуации, которая ему может встретиться при различной игре противника.
Пример. Пусть на столе в кучке лежат фишки: 11, 12, 13, 21, 22, 23
Пусть первый ход Пети 12. Ваня может поставить 21, 22 или 23. Предположим, он ставит 21. Получим цепочку 12-21. Петя может поставить 11 или 13. Предположим, он ставит 11. Получим цепочку 12-21-11. Ваня может поставить только фишку со значением 13. Получим цепочку 12-21-11-13. Перед Петей в кучке остались только фишки 22 и 23, то есть нет фишек, которые он мог бы добавить в цепочку. Таким образом, партия закончена, Ваня выиграл.
Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}. -
29 слайд
Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.
Задание 1.
б) Пусть Петя первым ходом пошел 42. У кого из игроков есть выигрышная стратегия в этой ситуации? Укажите первый ход, который должен сделать выигрывающий игрок, играющий по этой стратегии. Приведите пример одной из партий, возможных при реализации выигрывающим игроком этой стратегии. -
30 слайд
Задание 1 б
среди фишек есть две особые – 22 и 44 («дубли») они служат для того, чтобы передать ход сопернику; если выставить дубль, оказавшись в проигрышной позиции, то эта проигрышная позиция «переходит» к сопернику
Рассмотрим ситуацию, когда игроки не используют дубли -
31 слайд
Задание 1 б
Во всех партиях выигрывает Ваня -
32 слайд
Задание 1 б
Если Петя выставит дубль 44, то выиграет Петя -
33 слайд
Стратегия Буквы
Правила игры -
34 слайд
Два игрока, Петя и Ваня играют в следующую игру. Задан некоторый набор символьных цепочек («слов»), в котором ни одно слово не является началом другого (выполняется условие Фано). Игра начинается с пустой строки, в конец которой игроки по очереди дописывают буквы, по одной букве за ход так, чтобы полученная цепочка на каждом шаге была началом одного из заданных слов. Первый ход делает Петя. Выигрывает тот, кто первый составит слово из заданного набора
Пример. Пусть заданы слова {МАК, МЫЛО, РАМА, РАК}. На первом ходу Петя может написать букву М или Р. Пусть он написал букву М. В ответ Ваня может написать А или Ы. В первом случае получается МА, и Петя, дописав букву К, получает слово МАК из заданного набора и выигрывает. Во втором случае получается МЫ, Петя вынужден дописать Л и Ваня выиграет вторым ходом, дописав О и получив слово МЫЛО.
-
35 слайд
Пример.
Задание 1.
а) Определите, у кого из игроков есть выигрышная стратегия для набора слов {ВАРЕНЬЕ, КОРОВА}. Опишите эту стратегию. Определите, сколько различных партий может быть сыграно при этой стратегии и какое слово будет получено в каждом случае.
Решение:
Для набора слов {ВАРЕНЬЕ, КОРОВА} выигрышная стратегия есть у Пети.
Выигрышная стратегия Пети состоит в том, чтобы написать первую букву В. Далее остается только одно допустимое слово – ВАРЕНЬЕ, и Петя выиграет, так как в этом слове 7 букв и он допишет последнюю букву, имеющую нечётный номер.
При выбранной стратегии возможна только одна партия.
В результате этой партии получится слово ВАРЕНЬЕ. -
36 слайд
Игра Баше (учебник Информатика и ИКТ Семакин И.Г., 9класс)
-
37 слайд
Ресурсы
http://kpolyakov.spb.ru/school/ege/gen.php?action=viewAllEgeNo&egeId=26&cat87=on -
38 слайд
http://kpolyakov.spb.ru/school/ege.htm
-
-
-
41 слайд
Решу ЕГЭ
https://inf-ege.sdamgia.ru/test?theme=290
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 153 421 материал в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 05.03.2019
- 542
- 3


Рейтинг:
3 из 5
- 04.03.2019
- 229
- 0
- 04.03.2019
- 330
- 0

- 04.03.2019
- 261
- 0

- 04.03.2019
- 763
- 8
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
-
Курс повышения квалификации «Организация работы по формированию медиаграмотности и повышению уровня информационных компетенций всех участников образовательного процесса»
-
Курс повышения квалификации «Сетевые и дистанционные (электронные) формы обучения в условиях реализации ФГОС по ТОП-50»
-
Курс повышения квалификации «Использование компьютерных технологий в процессе обучения в условиях реализации ФГОС»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»
-
Курс профессиональной переподготовки «Управление в сфере информационных технологий в образовательной организации»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Современные языки программирования интегрированной оболочки Microsoft Visual Studio C# NET., C++. NET, VB.NET. с использованием структурного и объектно-ориентированного методов разработки корпоративных систем»
Слайд 1
Дерево игры Поиск выигрышной стратегии Учитель информатики и ИКТ МБОУ СОШ № 7 г. Оха Сахалинской области Сергиенко Татьяна Геннадьевна
Слайд 2
В простых играх можно найти выигрышную стратегию, просто перебрав все возможные варианты ходов соперников. Полный перебор вариантов реально выполнить только для очень простых игр; например, в шахматах сделать это за приемлемое время не удается (дерево игры очень сильно разветвляется, порождая огромное количество вариантов) Что нужно знать :
Слайд 3
Все позиции в простых играх делятся на выигрышные и проигрышные Выигрышная позиция – это такая позиция, в которой игрок, делающий первый ход, может гарантированно выиграть при любой игре соперника, если не сделает ошибку; при этом говорят, что у него есть выигрышная стратегия – алгоритм выбора очередного хода, позволяющий ему выиграть
Слайд 4
Если игрок начинает играть в проигрышной позиции, он обязательно проиграет, если ошибку не сделает его соперник; в этом случае говорят, что у него нет выигрышной стратегии; таким образом, общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для соперника
Слайд 5
выигрышные и проигрышные позиции можно охарактеризовать так: позиция, из которой все возможные ходы ведут в выигрышные позиции – проигрышная для соперника; позиция, из которой хотя бы один из возможных ходов ведет в проигрышную позицию – выигрышная для соперника, при этом стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную (для соперника) позицию.
Слайд 6
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу два камня или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 17 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 25. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 25 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 24 . Задача
Слайд 7
За один ход игрок может добавить в кучу два камня или увеличить количество камней в куче в два раза. Выиграть ходом +2 можно только из S = 23 или 24. Увеличив число камней в 2 раза, он получит число, большее 24 при S от 13 (26) до 24 (48), причём числа 23 и 24 тоже войдут в этот промежуток. Следовательно , выигрышными для первого хода Пети будут все значения S от 13 до 24 . S = 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24 1. При каких S: 1а) Петя выигрывает первым ходом;
Слайд 8
S = 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24 Для ответа на этот вопрос нужно найти позицию, из которой все возможные ходы ведут к выигрышу Вани за 1 ход. Ваня выиграет первым ходом, если после первого хода Пети S = 11 или 12, т.к. любой его ход в этом случае будет выигрышным. 11 + 2 = 13 12 + 2 = 14 11 * 2 = 22 12 * 2 = 24, т.е. при S = 11 или 12 Ваня выиграет первым ходом. 1. При каких S : 1б) Ваня выигрывает первым ходом?
Слайд 9
Петя может выиграть своим вторым ходом на основе Ваниных выигрышных вариантов, т.е. попав в позицию, которая заведомо могла быть выигрышной для Вани, но стала для него проигрышной, т.к. ход Пети. 11 – 2 = 9 11 на 2 не делится, пропускаем 12 – 2 = 10 12 / 2 = 6 Следовательно, при S = 6 , 9 , 1 0 Петя может выиграть своим вторым ходом. 2. Назовите три значения S, при которых Петя может выиграть своим вторым ходом?
Слайд 10
Ваня выиграет своим первым или вторым ходом, если оба его хода приведут в промежуток S от 13 до 24 или S = 6 , 9 , 10 . 6 – 2 = 4 4 * 2 = 8 (не входит ни в один промежуток) 9 – 2 = 7 7 * 2 = 14 (подходит) 10 – 2 = 8 8 * 2 = 16 (подходит) Следовательно, при S = 7 или 8 Ваня выиграет своим первым ходом. 3. При каком S Ваня выигрывает своим первым или вторым ходом?
Слайд 11
Остается построить таблицу возможных вариантов игры из позиции S = 7 и 8 . К расным цветом выделим позиции, в которых игра заканчивается.
Слайд 12
Начальная позиция 1-й ход Пети (все варианты) 1-й ход Вани (ход по стратегии) 2-й ход Пети (все варианты) 2-й ход Вани (ход по стратегии) 7 9 11 13 15 26 22 24 44 18 20 22 40 36 — 14 16 18 20 36 32 — 28 — — 8 10 12 14 16 28 24 26 48 20 22 24 44 40 — 16 18 20 22 40 36 — 32 — —
Слайд 13
Спасибо за внимание!
30 июня 2022
В закладки
Обсудить
Жалоба
Анализ алгоритмов логической игры и разработка выигрышной стратегии
Разбор заданий 19, 20, 21 КЕГЭ по информатике.
В презентации представлен алгоритм решения задач №19 (базового уровня), №20 (повышенного уровня), №21 (высокого уровня).
19-21kege.pdf
Автор: Глотова О.С.
Решение заданий по теме
Поиск выигрышной стратегии
Цель работы:
подготовка учащихся к сдаче государственного экзамена в форме ЕГЭ
Задача работы:
рассмотреть решение типичных задач уровня сложности С3
С3 (высокий уровень).
Рекомендованное время – 30 минут.
Указания по оцениванию
Правильное указание выигрывающего игрока и его ходов со строгим доказательством правильности (с помощью или без помощи дерева игры)
Баллы
3
Правильное указание выигрывающего игрока, стратегии игры, приводящей к победе, но при отсутствии доказательства ее правильности.
2
При наличии в представленном решении одного из пунктов:
1
- Правильно указан выигрывающий игрок и его первый ход, рассмотрены все возможные варианты второго игрока, но неверно определены дальнейшие действия.
- Правильно указан выигрывающий игрок и его первый ход, но описание выигрышной стратегии неполно и рассмотрены несколько (больше одного, но не все) вариантов ответов второго игрока.
Задание не выполнено или в представленном решении полностью отсутствует описание элементов выигрышной стратегии, и отсутствует анализ вариантов первого-второго ходов играющих (даже при наличии правильного указания выигрывающего игрока)
0
Максимальный балл
3
№ 1.
Два игрока играют в следующую игру. На координатной плоскости стоит фишка.
Игроки ходят по очереди. В начале игры фишка находится в точке с координатами (5,2) . Ход состоит в том, что игрок перемещает фишку из точки с координатами (x,y) в одну из трех точек: или в точку с координатами (x+3,y) , или в точку с координатами (x,y+3) , или в точку с координатами (x,y+4) . Выигрывает игрок, после хода которого расстояние от фишки до точки с координатами (0,0) больше 13 единиц. Кто выигрывает при безошибочной игре обоих игроков – игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
Анализ задачи
1) Из каждой ситуации в этой игре возможны 3 продолжения.
2) По теореме Пифагора расстояние от начала координат до точки с координатами (0,0)
определяется по формуле:
3) Условие равносильно условию
4) Составим таблицу:
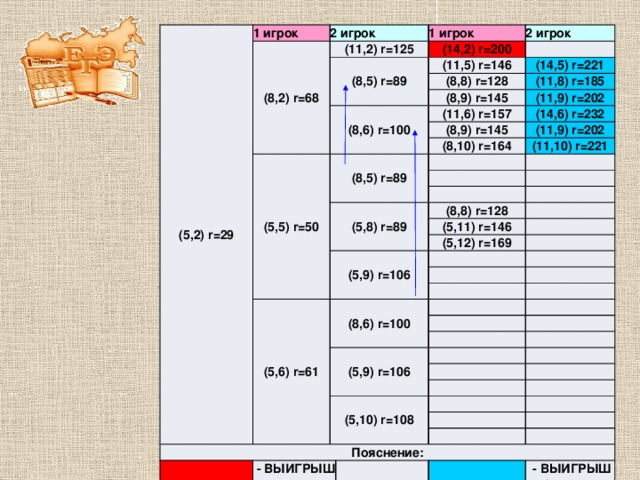
(5,2) r=29
1 игрок
2 игрок
(8,2) r=68
(11,2) r=125
1 игрок
(8,5) r=89
2 игрок
(14,2) r=200
(11,5) r=146
(14,5) r=221
(8,8) r=128
(8,6) r=100
(11,8) r=185
(8,9) r=145
(11,9) r=202
(11,6) r=157
(5,5) r=50
(14,6) r=232
(8,5) r=89
(8,9) r=145
(11,9) r=202
(8,10) r=164
(11,10) r=221
(5,8) r=89
(8,8) r=128
(5,9) r=106
(5,11) r=146
(5,12) r=169
(5,6) r=61
(8,6) r=100
(5,9) r=106
(5,10) r=108
Пояснение:
— ВЫИГРЫШ 1 игрока
— ВЫИГРЫШ 2 игрока
Ответ: 2 игрок выигрывает вторым ходом. Если он сводит ситуацию к положению (8,5) или (8,6).
Но он может свести к этому положению в любом случае:
(8,2)→(8,5) или (8,2) →(8,6),
(5,5) →(8,5)
(5,6) →(8,6)
№ 2.
Два ребенка играют в игру: перед ними стоят 2 вазы с конфетами, в первой – 1 конфета, во второй – 3 конфеты. У каждого ребенка неограниченное количество конфет. Дети ходят по очереди. Ход состоит в том, что игрок или увеличивает в 2 раза число конфет в какой-то вазе, или добавляет 3 конфеты в одну из них. Выигрывает ребенок, после хода которого число конфет в обеих вазах превышает 15 штук. Кто выигрывает при безошибочной игре обоих игроков – игрок, делающий первый ход. Или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
Анализ задачи
Из каждой ситуации в этой игре возможны 4 продолжения.
Составим таблицу:
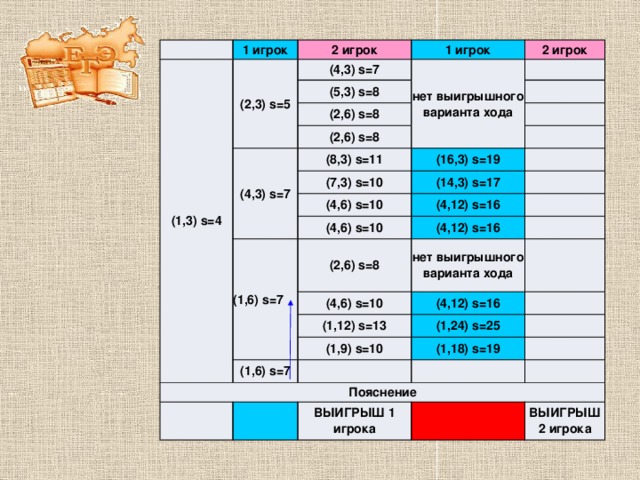
1 игрок
(1,3) s=4
(2,3) s=5
2 игрок
1 игрок
(4,3) s=7
2 игрок
нет выигрышного варианта хода
(5,3) s=8
(2,6) s=8
(4,3) s=7
(2,6) s=8
(8,3) s=11
(16,3) s=19
(7,3) s=10
(14,3) s=17
(4,6) s=10
(1,6) s=7
(4,6) s=10
(4,12) s=16
(4,12) s=16
(2,6) s=8
нет выигрышного варианта хода
(4,6) s=10
(4,12) s=16
(1,12) s=13
Пояснение
(1,6) s=7
(1,9) s=10
(1,24) s=25
(1,18) s=19
ВЫИГРЫШ 1 игрока
ВЫИГРЫШ 2 игрока
Ответ: 1 игрок выигрывает вторым ходом, если он сводит ситуацию к положению (4,3), а это он может сделать, т. к. первый ход его. В этом случае как бы ни пошел второй игрок (выигрыша у второго не будет), у первого после этого всегда будет выигрышный ход.
№ 3.
Два игрока играют в следующую игру. Имеются 3 кучки камней, содержащих соответственно 2, 3, 4 камня. За один ход разрешается или удвоить количество камней в какой-нибудь кучке, или добавить по 2 камня в каждую из трех куч. Предполагается. Что у каждого игрока имеется неограниченный запас камней. Выигрывает то игрок, после чьего хода в какой-нибудь кучке становится не менее15 камней или во всех трех кучках суммарно становится не менее 25 камней. Игроки ходят по очереди. Выясните, кто выигрывает при правильной игре, – первый или второй игрок.
Анализ задачи
Из каждой ситуации в этой игре возможны 4 продолжения.
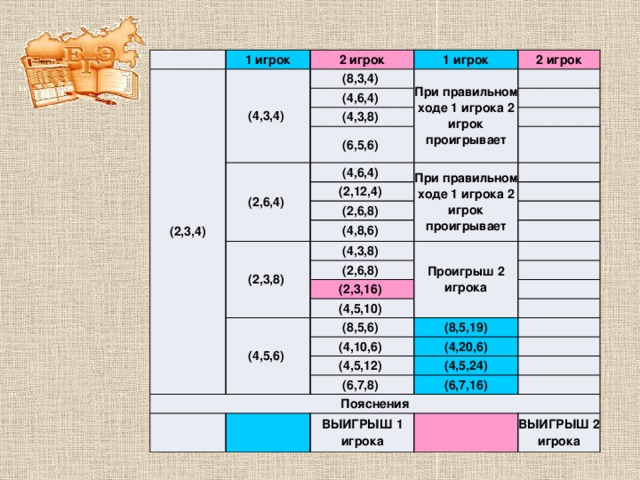
Составим таблицу:
1 игрок
(2,3,4)
2 игрок
(4,3,4)
1 игрок
(8,3,4)
(4,6,4)
2 игрок
При правильном ходе 1 игрока 2 игрок проигрывает
(4,3,8)
(6,5,6)
(2,6,4)
(4,6,4)
При правильном ходе 1 игрока 2 игрок проигрывает
(2,12,4)
(2,6,8)
(2,3,8)
(4,8,6)
(4,3,8)
Проигрыш 2 игрока
(2,6,8)
(2,3,16)
(4,5,10)
(4,5,6)
(8,5,6)
(4,10,6)
(8,5,19)
(4,20,6)
(4,5,12)
Пояснения
(6,7,8)
(4,5,24)
(6,7,16)
ВЫИГРЫШ 1 игрока
ВЫИГРЫШ 2 игрока
Ответ: 1 игрок выигрывает вторым ходом, если он сводит ситуацию к положению (4,5,6), а это он может сделать, т. к. первый ход его. В этом случае как бы ни пошел второй игрок (выигрыша у второго не будет), у первого после этого всегда будет выигрышный ход.
Теория Игр
Выигрышные стратегии
Что нужно знать
- в простых играх можно найти выигрышную стратегию, просто перебрав все возможные варианты ходов соперников
- полный перебор вариантов реально выполнить только для очень простых игр; например, в шахматах сделать это за приемлемое время не удается
- все позиции в простых играх делятся на выигрышные и проигрышные
Что нужно знать
- выигрышная позиция – это такая позиция, в которой игрок, делающий первый ход, может гарантированно выиграть при любой игре соперника, если не сделает ошибку; при этом говорят, что у него есть выигрышная стратегия – алгоритм выбора очередного хода, позволяющий ему выиграть
- если игрок начинает играть в проигрышной позиции, он обязательно проиграет, если ошибку не сделает его соперник; в этом случае говорят, что у него нет выигрышной стратегии; таким образом, общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для соперника
.
Что нужно знать
- выигрышные и проигрышные позиции можно охарактеризовать так:
- позиция, из которой все возможные ходы ведут в выигрышные позиции – проигрышная ; позиция, из которой хотя бы один из возможных ходов ведет в проигрышную позицию — выигрышная , при этом стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную (для соперника) позицию
- позиция, из которой все возможные ходы ведут в выигрышные позиции – проигрышная ;
- позиция, из которой хотя бы один из возможных ходов ведет в проигрышную позицию — выигрышная , при этом стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную (для соперника) позицию
Задача 1
Задача 1
- Игра состоит в том, что игроки поочередно берут из кучки по одной фишке и выкладывают в цепочку на стол лицевой стороной вверх таким образом, что каждая новая фишка ставится правее предыдущей и ближайшие цифры соседних фишек совпадают.
- Пример. Пусть на столе в кучке лежат фишки: 11, 12, 13, 21, 22, 23
- Пусть первый ход Пети 12. Ваня может поставить 21, 22 или 23. Предположим, он ставит 21. Получим цепочку 12-21. Петя может поставить 11 или 13. Предположим, он ставит 11. Получим цепочку 12-21-11. Ваня может поставить только фишку со значением 13. Получим цепочку 12-21-11-13. Перед Петей в кучке остались только фишки 22 и 23, то есть нет фишек, которые он мог бы добавить в цепочку. Таким образом, партия закончена, Ваня выиграл.
Задача 1
- Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.
- Задание 1.
- а) Приведите пример самой короткой партии, возможной при данном наборе фишек. Если таких партий несколько, достаточно привести одну.
- б) Пусть Петя первым ходом пошел 42. У кого из игроков есть выигрышная стратегия в этой ситуации? Укажите первый ход, который должен сделать выигрывающий игрок, играющий по этой стратегии. Приведите пример одной из партий, возможных при реализации выигрывающим игроком этой стратегии.
Задача 1 (задание 1)
- Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.
- а)
- меньше всего фишек заданного набора начинается с цифры 1 (только 12 и 14), поэтому самой короткой партией, вероятно, будет партия, которая заканчивается на цифре 1 (фишкой 21 или 41), при этом фишки 12 и 14 должны быть выставлены;
12 – 21 – 14 – 41 и 14 – 41 – 12 – 21
- В ответе достаточно привести одну из них.
Задача 1 (задание 1)
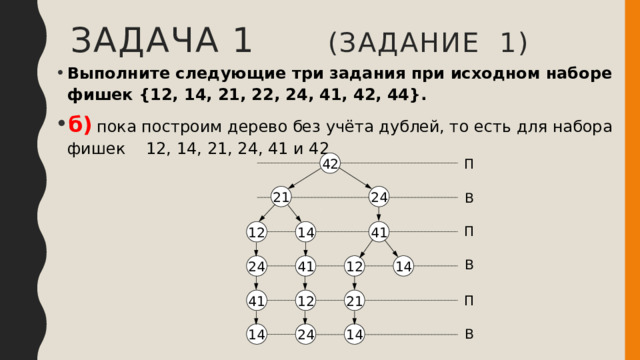
- Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.
- б) пока построим дерево без учёта дублей, то есть для набора фишек 12, 14, 21, 24, 41 и 42
42
П
21
24
В
П
41
12
14
В
24
41
12
14
П
12
41
21
В
14
24
14
Задача 1 (задание 1)
- Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.
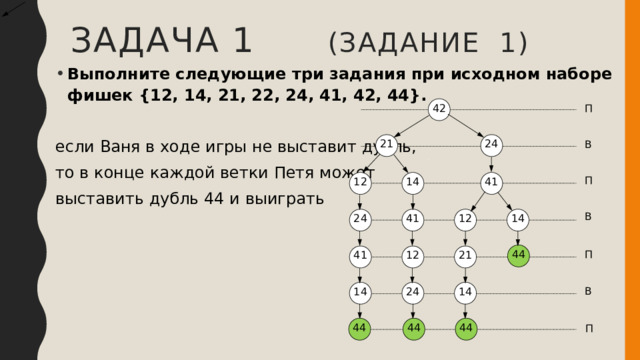
если Ваня в ходе игры не выставит дубль,
то в конце каждой ветки Петя может
выставить дубль 44 и выиграть
П
42
21
24
В
П
41
14
12
В
41
24
12
14
44
П
21
41
12
В
14
14
24
44
44
44
П
Задача 1 (задание 1)
- Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.
42
П
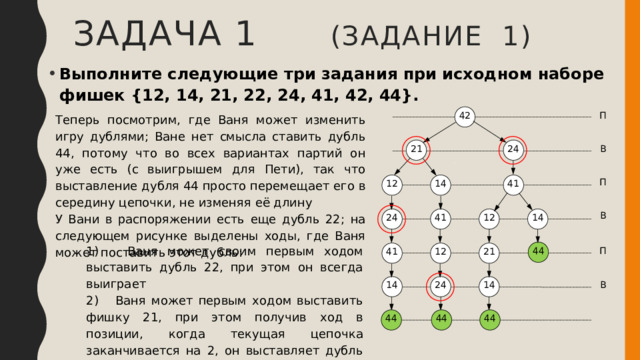
Теперь посмотрим, где Ваня может изменить игру дублями; Ване нет смысла ставить дубль 44, потому что во всех вариантах партий он уже есть (с выигрышем для Пети), так что выставление дубля 44 просто перемещает его в середину цепочки, не изменяя её длину
У Вани в распоряжении есть еще дубль 22; на следующем рисунке выделены ходы, где Ваня может поставить этот дубль:
21
24
В
П
14
12
41
В
24
14
12
41
1) Ваня может своим первым ходом выставить дубль 22, при этом он всегда выиграет
2) Ваня может первым ходом выставить фишку 21, при этом получив ход в позиции, когда текущая цепочка заканчивается на 2, он выставляет дубль 22 и выигрывает
44
П
41
21
12
В
14
24
14
44
44
44
Задача 1 (задание 2)
- Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.
- Задание 2
- Пусть Петя первым ходом пошел 44. У кого из игроков есть выигрышная стратегия, позволяющая в этой ситуации выиграть своим четвертым ходом? Постройте в виде рисунка или таблицы дерево всех партий, возможных при реализации выигрывающим игроком этой стратегии. На рёбрах дерева указывайте ход, в узлах – цепочку фишек, получившуюся после этого хода.
Задача 1 (задание 2)
- Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.
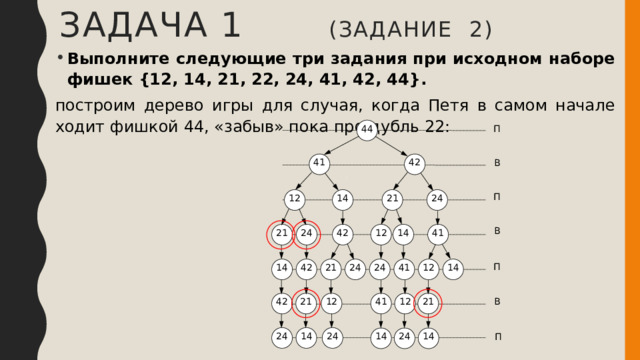
построим дерево игры для случая, когда Петя в самом начале ходит фишкой 44, «забыв» пока про дубль 22:
П
44
41
42
В
П
21
12
14
24
В
12
41
42
14
21
24
П
24
42
14
24
21
14
12
41
В
42
21
12
41
21
12
14
24
24
14
24
14
П
Задача 1 (задание 2)
- Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.
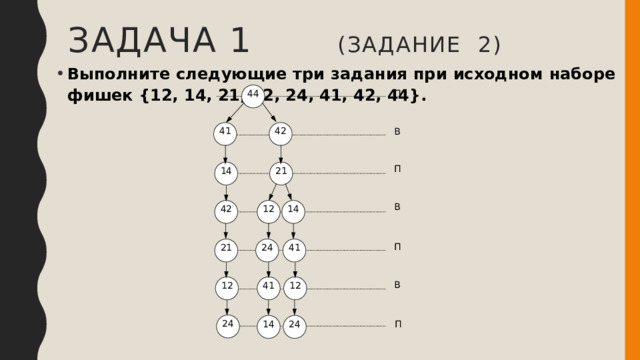
- по дереву видим, что при игре без дубля 22 выигрывает Петя своим третьим или четвёртым ходом
- Ваня может изменить ход игры дублем 22 только в выделенных узлах, поэтому
- если Ваня походит фишкой 41, Петя должен ответить ходом 14
- если Ваня походит фишкой 42, Петя должен ответить ходом 21
Задача 1 (задание 2)
- Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.
44
П
41
42
В
П
14
21
В
14
42
12
П
21
41
24
В
12
12
41
24
24
14
П
Задача 1
- Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.
- Задание 3
- Укажите хотя бы один способ убрать 2 фишки из исходного набора так, чтобы всегда выигрывал не тот игрок, который имеет выигрышную стратегию в задании 2. Приведите пример партии для набора из 6 оставшихся фишек.
Задача 1 (задание 3)
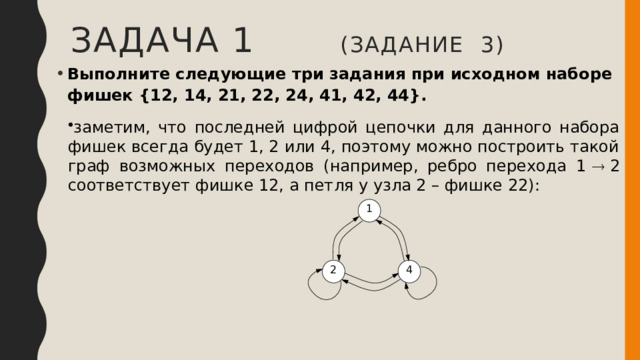
- Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.
- заметим, что последней цифрой цепочки для данного набора фишек всегда будет 1, 2 или 4, поэтому можно построить такой граф возможных переходов (например, ребро перехода 1 2 соответствует фишке 12, а петля у узла 2 – фишке 22):
1
2
4
Задача 1 (задание 3)
- Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.
если убрать два дубля, то всегда будут выставлены 4 или все 6 фишек, поскольку 4 и 6 – чётные числа, то всегда выиграет Ваня, потому что он делает все ходы с чётными номерами; например, при первом ходе Пети 12 возможны партии:
12 – 21 – 14 – 41 или 12 – 24 – 41 – 14 – 42 – 21.
Задача 2
Задача 2
- Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
- а) добавить в кучу один камень или
- б) увеличить количество камней в куче в два раза .
- Игра завершается в тот момент, когда количество камней в куче становится не менее 24. Если при этом в куче оказалось не более 38 камней, то победителем считается игрок, сделавший последний ход. В противном случае победителем становится его противник. Например, если в куче был 21 камень и Петя удвоит количество камней в куче, то игра закончится и победителем будет Ваня. В начальный момент в куче было S камней, 1
Задача 2
- Задание 1. а) При каких значениях числа S Петя может выиграть в один ход? Укажите все такие значения и соответствующие ходы Пети.
- б) У кого из игроков есть выигрышная стратегия при S = 22, 21, 20? Опишите выигрышные стратегии для этих случаев.
- Задание 2 . У кого из игроков есть выигрышная стратегия при S = 11, 10? Опишите соответствующие выигрышные стратегии.
- Задание 3 . У кого из игроков есть выигрышная стратегия при S = 9? Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход; в узлах – количество камней в позиции.
Задача 2 (задание 1)
- а)
- Сложность состоит в том, что Петя проиграет, если в результате его хода количество камней станет больше, чем 38. Он может сделать ход «+1» или «*2». Ходом «+1» он сможет получить 24 камня в куче (и таким образом выиграет!) из позиции S = 23.
- Теперь проверим ход «*2». Для выигрыша Пети количество камней в результате этого хода должно стать от 24 до 38, поэтому Петя выиграет этим ходом при S от 12 до 19.

Задача 2 (задание 1)
- б)
- При S = 22 возможные ходы дают кучи в 23 и 44 камня. В первом случае (S = 23) противник оказывается в выигрышной позиции (см. предыдущий пункт), во втором случае тот, кто ходит, проигрывает, потому что 44 38. Поэтому позиция S = 22 – проигрышная, Петя проиграет, у Вани есть выигрышная стратегия: в случае S = 23 сделать ход «+1» .
- При S = 21 Петя может перевести игру в позицию S = 22, она, как мы только что показали, проигрышная для Вани. Поэтому у Пети есть выигрышная стратегия.
- При S = 20 ходом «+1» Петя переведет игру в выигрышную (для Вани) позицию, а при ходе «*3» он сразу проиграет, получив 40 38 камней. Поэтому выигрышная стратегия есть у Вани.
Задача 2 (задание 2)
- При S = 11 или S = 10 Петя может ходом «*2» перевести игру в позиции S = 22 и S = 20, обе они, как мы показали в предыдущем пункте, проигрышные. Поэтому выигрышную стратегию имеет Петя.
Задача 2 (задание 3)
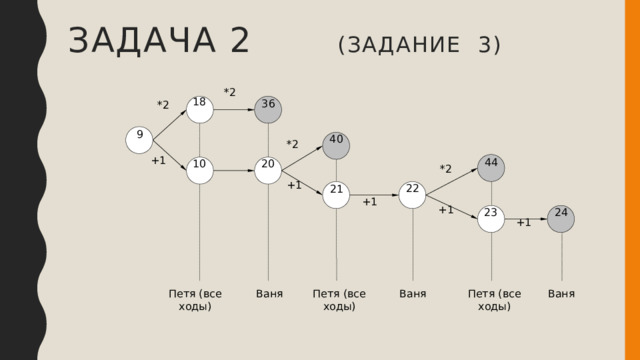
- При S = 9 возможно 2 хода: ход «+1» приводит к позиции S = 10, она выигрышная (см. предыдущий пункт); ход «*2» приводит к позиции S = 18, она тоже выигрышная (см. первый пункт). Таким образом, все возможные ходы ведут в выигрышные для соперника позиции, и позиция S = 9 – проигрышная (для Пети). Выигрышную стратегию имеет Ваня.
Задача 2 (задание 3)
*2
18
36
*2
9
40
*2
+1
44
10
20
*2
+1
22
21
+1
+1
23
24
+1
Петя (все ходы)
Петя (все ходы)
Петя (все ходы)
Ваня
Ваня
Ваня
Задача 2 (задание 3)
или записать в виде таблицы
Петя
9
Ваня
9*2=18
9+1=10
Петя
18*2=36
Ваня
10*2=20
Петя
20*2=40
Ваня
20+1=21
21+1=22
22+1=23
22*2=44
23+1=24
1
Дерево игры (ЕГЭ С3) Выигрышные игровые стратегии
2
Цель задания: сформировать умение построить дерево игры по заданному алгоритму и обосновать выигрышную стратегию. Что нужно знать: правила построения дерева игры (то есть перечисления всех возможных ходов игроков); правила исключения из рассмотрения тех ходов, которые являются ошибочными (по правилам игра ведется безошибочно обоими игроками); правила поиска в построенном дереве выигрышной стратегии, то есть наличия такой вершины («переломного момента игры»), после посещения которой, один из игроков проигрывает всегда (при безошибочной игре соперника).
3
В кучке лежит 5 спичек. Два игрока убирают спички по очереди, причем за 1 ход можно убрать 1 или 2 спички. Выигрывает тот, кто оставит в кучке 1 спичку.
4
Кто же выиграет при правильной игре? Для этого нужно ответить на вопросы: 1.«Может ли первый игрок выиграть, независимо от действий второго?» 2.«Может ли второй игрок выиграть, независимо от действий первого?»
5
ЕГЭ С3_ Два игрока играют в следующую игру. Имеются три кучи камней, содержащих соответственно 2, 3, 4 камня. За один ход разрешается или удвоить количество камней в какой-нибудь куче, или добавить по два камня в каждую из трех куч. Предполагается, что у каждого игрока имеется неограниченный запас камней. Выигрывает тот игрок, после чьего хода в какой- нибудь куче становится > 15 камней или во всех трех кучах суммарно становится > 25 камней. Игроки ходят по очереди. Выяснить, кто выигрывает при правильной игре, — первый или второй игрок.
6
Решение: cтарт 2, 3, 4 4, 3, 4 2, 6, 42, 3, 84, 5, 6 I II 8, 3, 4 4, 6, 4 4, 3, 8 6, 5, 6 4, 6, 4 2,12, 4 2, 6, 8 4, 8, 6 4, 3, 8 2, 6, 8 2, 3,16 4, 5, 10 8, 5, 6 4, 10, 6 4, 5, 12 6, 7, 8 Проигрыш I игрока Ход (2, 3, 
7
8
ЕГЭ С3_3_ 2006 Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 5, а во второй — 3 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или удваивает число камней в какой-то куче, или добавляет 4 камня в какую-то кучу. Выигрывает игрок, после хода которого в одной из куч становится не менее 22 камней. Кто выигрывает при безошибочной игре обоих игроков -игрок, делающий первый ход, или игрок, делающий второй ход? Как должен ходить выигрывающий игрок? Ответ обоснуйте.
9
10
ЕГЭ С3_2_ 2006 Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 4, а во второй — 3 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче или добавляет 2 камня в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 24 камней. Кто выигрывает при безошибочной игре обоих игроков — игрок, делающий первый ход или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
11
12
Демо 2008
13
14
ЕГЭ С3_ Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 6, а во второй — 5 камней. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок увеличивает или в 2 раза, или в 3 раза число камней в какой-то куче. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 48 камней. Кто выигрывает при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
15
16
ЕГЭ С3_ Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 3, а во второй — 6 камней. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или удваивает число камней в какой-то куче, или добавляет 2 камня в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 24 камней. Кто выигрывает при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
17
18
ЕГЭ 2009
19
На уроке рассмотрен разбор 19, 20, 21 задания ЕГЭ по информатике: дается подробное объяснение и решение задания
Содержание:
- Объяснение заданий 19, 20 и 21 ЕГЭ по информатике
- Теория игр. Поиск выигрышной стратегии
- Решение 19, 20, 21 заданий ЕГЭ по информатике
- Игра с двумя кучами камней или табличка
- Задания для тренировки 19, 20, 21 заданий ЕГЭ (взяты из КИМ и сборников прошлых лет)
- Игра с одной кучей камней
- Игра с набором слов
Объяснение заданий 19, 20 и 21 ЕГЭ по информатике
19-е задание: «Анализ алгоритма логической игры»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 6 минут.
Проверяемые элементы содержания: Умение анализировать алгоритм логической игры
20-е задание: «Поиск выигрышной стратегии»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 6 минут.
Проверяемые элементы содержания: Умение найти выигрышную стратегию игры
21-е задание: «Дерево игры для выигрышной стратегии»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 10 минут.
Проверяемые элементы содержания: Умение построить дерево игры по заданному алгоритму и найти выигрышную стратегию
До ЕГЭ 2021 года — эти задания были объединены в задание № 26 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«Для пункта 2 или 3 в представленной стратегии рассмотрены не все возможные ходы проигрывающего игрока, которые он может сделать при игре выигрывающего игрока по выигрышной стратегии.
Для пункта 3 представлено дерево игры, содержащее лишние ветви, не относящиеся к выигрышной стратегии.
Дерево, являющееся частью ответа на пункт 3, представлено с использованием ссылок на
фрагменты, являющиеся решениями других пунктов задания.
В задании спрашивается, в частности, кто выиграет, а в ответе не указан в явном виде выигрывающий игрок. На все вопросы, поставленные в задании, должны быть даны чёткие ответы. Ответ на вопрос о выигрышной стратегии в стиле «Может выиграть первый игрок, но если он неправильно пойдёт, то выиграет второй» является ошибочным, поскольку выигрышная стратегия одного игрока не оставляет возможности победы другому игроку»
ФГБНУ «Федеральный институт педагогических измерений»
* Некоторые изображения и примеры страницы взяты из материалов презентации К. Полякова
Теория игр. Поиск выигрышной стратегии
Для решения 19 задания необходимо вспомнить следующие темы и понятия:
- для того чтобы найти выигрышную стратегию в несложных играх, достаточно использовать метод перебора всех возможных вариантов ходов игроков;
- для решения задач 19 задания чаще всего для этого применяется метод построения деревьев;
- если от каждого узла дерева отходят две ветви, т.е. возможные варианты хода, то такое дерево называется двоичным (если из каждой позиции есть три варианта продолжения, дерево будет троичным).
- все позиции в простых играх делятся на выигрышные и проигрышные;
- выигрышная позиция – это такая позиция, в которой игрок, делающий первый ход, обязательно выиграет при любых действиях соперника, если не допустит ошибки; при этом говорят, что у данного игрока есть выигрышная стратегия – алгоритм выбора очередного хода, позволяющий ему выиграть;
- если игрок, делающий первый ход, находится в проигрышной позиции, то он обязательно проиграет, если ошибку не сделает его оппонент; в этом случае говорят, что у данного игрока нет выигрышной стратегии; таким образом, общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для оппонента;
- выигрышные и проигрышные позиции характеризуются так:
- позиция, из которой все возможные ходы ведут в выигрышные позиции – проигрышная;
- позиция, из которой хотя бы один из последующих возможных ходов ведет в проигрышную позицию — выигрышная, при этом стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную (для оппонента) позицию.
- для того чтобы определить, какой из игроков выиграет при стратегически правильной игре, необходимо ответить на вопросы:
- Может ли какой-либо из игроков выиграть, независимо от ходов других игроков?
- Что должен сделать игрок с выигрышной стратегией первым ходом, чтобы он смог выиграть, независимо от действий ходов игроков?
Выигрышная стратегия
Выигрышные и проигрышные позиции
Кто выиграет при стратегически правильной игре?
Рассмотрим пример:
Игра: в кучке лежит 5 спичек; играют два игрока, которые по очереди убирают спички из кучки; условие: за один ход можно убрать 1 или 2 спички; выигрывает тот, кто оставит в кучке 1 спичку
Решение:
- Будем использовать метод построения дерева. Первый играющий может убрать одну спичку (в этом случае их останется 4) или сразу 2 (останется 3), эти два варианта отобразим при помощи дерева:
- если первый игрок оставил 4 спички, второй может своим ходом оставить 3 или 2; а если после первого хода осталось 3 спички, второй игрок может выиграть, взяв две спички и оставив одну:
- если осталось 3 или 2 спички, то 1-ый игрок (в обеих ситуациях) выиграет своим ходом:
- если первый игрок своим первым ходом взял две спички, то второй сразу выигрывает; если же он взял одну спичку, то своим вторым ходом он может выиграть, независимо от хода второго игрока;
- итак, убрав всего одну спичку первым ходом, 1-ый игрок всегда может выиграть на следующем ходу;
- тогда как второй игрок не может выиграть, независимо от действий первого: потому что, если первый игрок сначала убрал одну спичку, второй всегда проиграет.
проанализируем стратегию игры:
Ответ: при правильной игре (стратегии игры) выиграет первый игрок; для этого ему достаточно своим первым ходом убрать одну спичку.
Решение 19, 20, 21 заданий ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Игра с двумя кучами камней или табличка
19_8:
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 59. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 59 или больше камней.
В начальный момент в первой куче было 5 камней, во второй куче – S камней; 1 ≤ S ≤ 53.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Задание 20 ЕГЭ.
Найдите минимальное значение S, при котором у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Задание 21 ЕГЭ.
Найдите два значения S, при которых одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Найденные значения запишите в ответе в порядке возрастания.
✍ Решение:
- Нарисуем таблицу, в первом столбце которой будем откладывать количество камней в первой куче, а в первой строке — количество камней во второй куче. Получим матрицу. Поскольку в первой куче количество начинается с 5, то это и будет первым значением в таблице. Во второй куче начнем с наибольшего возможного числа — 53. Таблица пригодится для решения заданий 20 и 21:
- Для начала найдем все выигрышные позиции для первой строки таблицы, т.е. для первого хода. Обозначим их плюсами (
+): - Для того, чтобы получить наименьшее значение
S, в качестве первого хода Пети необходимо увеличивать в два раза вторую кучу. Т.е. для решения задания необходимо найти такое наименьшееS, при котором Петя походил неверно, и попал своим ходом в выигрышную позицию для своего соперника, т.е. в ячейку с плюсом:
Выигрышные позиции для первой строки ищем по принципу увеличения количества камней S в 2 два раза: 5 + S*2 >=59. Получим S>=27
S = 14 1 ход Петя: 14*2 = (5,28) 2 ход Ваня: 28*2 = (5,56), Сумма = 61, Выигрыш!
Ответ: 14
✎ Задание 20:
- Проанализируем таблицу, и для каждой строки найдем выигрышные позиции с одного хода. Т.е. которые позволят игроку, оказавшемуся «на них», выиграть за один ход (получить суммарно 59 и более камней):
- Найдем проигрышные позиции: те, которые ведут только в выигрышные позиции для соперника (ведут только в плюсы)
- В задании требуется найти минимальное
S, котором выиграет Петя, но выиграет он НЕ первым своим ходом, а вторым. То есть в нашем случае необходимо найтиS, которое может перевести соперника в проигрышную позицию. То есть в минус. Для первой строки (так как первым будет ходить Петя) таких значений два: - Наименьшее S = 24
При заполнении таблицы выигрышными позициями можно проследить закономерность «узора», а заполнять позиции по аналогии.
Проигрышные позиции: (6,26) (8,25) (10,24) (12,23) (14,22)
- Для решения этого задания найдем выигрышные позиции со второго хода, т.е. которые могут перевести соперника в проигрышную позицию (с минусом):
- Чтобы выиграл Ваня, но выиграл не первым ходом, а вторым, необходимо, чтобы Петя находился в такой позиции, которая ведет его только на выигрышные позиции со второго хода:

Ответ: 23 25
>19_9:
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя.
За один ход игрок может убрать из одной из куч один камень или уменьшить количество камней в куче в два раза (если количество камней в куче нечётно, остаётся на 1 камень больше, чем убирается).
Например, пусть в одной куче 6, а в другой 9 камней; такую позицию мы будем обозначать (6, 9). За один ход из позиции (6, 9) можно получить любую из четырёх позиций: (5, 9), (3, 9), (6, 8), (6, 5).
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не более 20. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой в кучах будет 20 или меньше камней. В начальный момент в первой куче было 10 камней, во второй куче – S камней, S > 10.
Найдите значение S, при котором Ваня выигрывает своим первым ходом при любой игре Пети?
Задание 20 ЕГЭ.
Найдите минимальное и максимальное значение S, при котором у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Задание 21 ЕГЭ.
Найдите значение S, при котором одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
✍ Решение (Excel):
✎ Задание 19:
- В столбце
Аотложим значения — количество камней в первой куче. Начнем с ячейкиА2, в которую внесем начальное количество камней, т.е. 10. Автозаполнением продлим значения вниз до 0: - В строке 1 таблицы (начиная с ячейки
B1) отложим значения для второй кучи. Поскольку в задании говорится, что победа будет достигнута при S<=20, и достигнуть этого значения более сильной командой можно уменьшив кол-во камней во второй куче в два раза, начиная с числа 40: 40/20. То есть возьмем значение больше 40, примерно 45. Используем автозаполнение до значения 11: - Из двух команд, которые могут выполнять игроки, выберем наиболее сильную, т.е. благодаря которой можно быстрее достичь выигрышного диапазона и попасть в значения S<=20. Это команда уменьшения количества камней в два раза, т.е.
/2. - Для каждой из ячеек полученной таблицы рассчитаем значение, полученное в результате уменьшения в два раза той кучи камней, в которой большее количество камней (так как это даст меньший результат). Например, для ячейки
С5, в которой игрок имеет в первой куче 7 камней, а во второй куче 44 камня, мы бы выполнили действие 44/2+7. Т.е. уменьшили вдвое вторую кучу, т.к. в ней больше камней. Еще необходимо обращать внимание на четность и нечетность значений (в Excel это функцияЕНЕЧЁТ— возвращает ИСТИНУ, если значение нечетно). - Чтобы автоматизировать процесс необходимо использовать формулу, в которой найдем максимальное значение из двух вариантов:
Минимальное из (ЕСЛИ(ЕНЕЧЁТ(1-я куча)то(1-я куча+1)/2+2-я куча,иначе1-я куча/2+2-я куча);ЕСЛИ(ЕНЕЧЁТ(2-я куча)то(2-я куча+1)/2+1-я куча,иначе2-я куча/2+1-я куча)).
B2:= МИН(ЕСЛИ(ЕНЕЧЁТ($A2);($A2+1)/2+B$1;$A2/2+B$1);ЕСЛИ(ЕНЕЧЁТ(B$1);(B$1+1)/2+$A2;B$1/2+$A2))
$ будем использовать для фиксации столбца А и строки 1 при копировании формулы.
Ответ: 21
✎ Задание 20:
- Продолжаем работать с той же таблицей, что и в задании 19. Выделим все проигрышные позиции (из которых можно походить только в выигрышные позиции для соперника, т.е. в выделенные ячейки):
- Петя может выиграть свои вторым ходом, если он не может выиграть первым ходом, но может выполнить ход в позицию, проигрышную для соперника (в ячейку, выделенную красным). Такие позиции назовем выигрышные позиции со второго хода. Найдем минимальное и максимальное значение
Sпри таком первом ходе Пети:
При S=44 Пете необходимо уменьшить 2-ю кучу вдвое (44/2 = 22), чтобы оказаться в проигрышной позиции для соперника.
Ответ: 22 44
✎ Задание 21:
- Выделим все такие выигрышные позиции со второго хода:
- Далее придерживаемся следующей логики: Ваня сможет выиграть свои первым или вторым ходом, но при этом не гарантированно первым ходом, если у Пети будет возможность выполнить ходы только в позиции выигрышные со второго хода. Найдем такое S:
При S = 24 Петя сможет уменьшить кучи на один камень, и тогда оказывается в выделенной зеленой области — выигрышные позиции со второго хода для Вани, либо уменьшить количество камней вдвое, и тогда Ваня оказывается в выигрышной позиции с первого хода (розовая область).
Ответ: 24
19_7: с экзамена ЕГЭ 2020г. (со слов учащегося):
Два игрока, Петя и Ваня, играют в следующую игру. На табличке написаны два значения. Оба игрока в свой ход могут заменить одно из значений на сумму обеих (по своему выбору). Первый ход делает Петя. Игра считается законченной когда сумма обеих значений равняется не меньше 56. То есть выигрывает игрок, получивший 56 или более в сумме. Начальное значение (10, S).
Найдите максимальное S при котором Петя не может выиграть первым ходом.
Задание 20 ЕГЭ.
У кого из игроков есть выигрышная стратегия при начальном значении (9, 15).
Задание 21 ЕГЭ.
У кого из игроков есть выигрышная стратегия при начальном значении (3,7)? Опишите эту стратегию и изобразите дерево всех возможных партий
при этой стратегии
.
Типовые задания для тренировки
✍ Решение:
- Задание 19.
Максимальное S при котором Петя НЕ может выиграть своим первым ходом S = 22. Петя проиграет, если в сумме получится 55 и меньше. Первое значение = 10, необходимо найти второе значение, при этом максимальное. Схематично отобразим варианты ходов:
(10,22) - ход Пети - (10+22, 22) - итог суммы обеих значений таблички: 32 + 22 = 54 (<56)
Для того, чтобы сделать сумму большей, Петя заменит первое значение на сумму, так как оно меньше второго значения (10<22)
В начальной позиции (9, 15) выигрышная стратегия есть у Вани. Для себя отобразим схематично выигрышную партию Вани:
Зеленым цветом выделены выигрышные ходы.
В начальной позиции (3, 7) выигрышная стратегия есть у Вани. Изобразим дерево всех возможных партий при этой стратегии (раз говорится «при этой стратегии» имеем в виду, выигрышную стратегию Вани):

Дерево для выигрышной стратегии Вани: для Вани отображены только ходы по стратегии, для Пети — все возможные ходы. Зеленым цветом — выигрышный ход, красная обводка — ход по стратегии.
Решение подобного задания в Excel смотрите на видео:
📹 Видео
📹 Видеорешение на RuTube здесь
19_6:
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) два камня или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 44.
Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, что в кучах всего будет 44 или больше камней.
В начальный момент в первой куче было 5 камней, во второй куче – S камней; 1 ≤ S ≤ 38.
Задание 19 ЕГЭ.
При каких S: 1а) Петя выигрывает первым ходом; 1б) Ваня выигрывает первым ходом?
Задание 20 ЕГЭ.
Назовите одно любое значение S, при котором Петя может выиграть своим вторым ходом.
Задание 21 ЕГЭ.
Назовите значение S, при котором Ваня выигрывает своим первым или вторым ходом.
✍ Решение:
- Нарисуем таблицу, в первом столбце которой будем откладывать количество камней в первой куче, а в первой строке — количество камней во второй куче. Получим матрицу. Поскольку в первой куче количество начинается с 5, то это и будет первым значением в таблице. Во второй куче начнем с наибольшего возможного числа — 38:
- Далее будем рассуждать так: Петя может выиграть первым ходом, выполнив команду *2 (увеличить количество камней в куче в два раза), если вместо S (кол-во камней во второй куче), мы будем изменять значение, начиная от 20, до последнего возможного по условию значения 38:
Задание 19 а):
5 + 20*2 = 45 (>44) * 5 - кол-во камней в первой куче, оно не меняется по условию
+ означает выигрышную позицию с первого хода:Ответ 1 а):
S = [20;38] (На ЕГЭ пояснить ходы, например: (5; 20) -> (Ход Пети)-> (5;40); 40 + 5 = 45)
Задание 19 б):
+). Отметим такие позиции, учитывая, что это первый ход Пети, и кол-во камней в первой куче должно быть 5. Найденные позиции будут проигрышными позициями (-):S = 19 (На ЕГЭ пояснить ходы, например: (5; 19) -> (Ходы Пети): (5;21),(5;28);(7;19);(7;28). Везде следующим ходом выиграет Ваня, см. предыдущ. пункт)
Задание 20:
2+):
S = 16, 17 или 18 (На ЕГЭ пояснить ходы, ссылаясь на объяснения в предыдущих пунктах)
Задание 21:
+), либо в позицию выигрышную со второго хода или n-го хода (2+). Это позиция при S = 14:
Ответ 3: S = 14 (На ЕГЭ пояснить ходы, ссылаясь на объяснения в предыдущих пунктах)
📹 YouTube здесь
Видеорешение на RuTube здесь
Задания для тренировки 19, 20, 21 заданий ЕГЭ (взяты из КИМ и сборников прошлых лет)
Игра с одной кучей камней
19_3: Демоверсия ЕГЭ 2018 информатика:
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 29 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 28.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Задание 19 ЕГЭ
а) Укажите такие значения числа S, при которых Петя может выиграть в один ход.
б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.
Задание 20 ЕГЭ
Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причем:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Для указанных значений S опишите выигрышную стратегию Пети.
Задание 21 ЕГЭ
Укажите значение S, при котором:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На ребрах дерева указывайте, кто делает ход; в узлах — количество камней в позиции
Дерево не должно содержать партий, невозможных при реализации выигрывающим игроком своей выигрышной стратегии. Например, полное дерево игры не является верным ответом на это задание.
✍ Решение:
-
Задание 19.
- а) Петя может выиграть, если S = 15, … 28
15, ..., 28 - выигрышные позиции с первого хода
S = 14 Петя: 14 + 1 = 15 выигрышная позиция (см. п. а). Выигрывает Ваня Петя: 14 * 2 = 28 выигрышная позиция (см. п. а). Выигрывает Ваня 14 - проигрышная позиция
Задание 20.
S = 7 Петя: 7 * 2 = 14 проигрышная позиция (см. п. 1 б). Выигрывает Петя S = 13 Петя: 13 + 1 = 14 проигрышная позиция (см. п. 1 б). Выигрывает Петя 7, 13 - выигрышные позиции со второго хода
Задание 21.
S = 12 Петя: 12 + 1 = 13 Ваня: 13 + 1 = 14 проигрышная позиция (см. п. 1 б). Выигрывает Ваня вторым ходом!
В таблице изображено дерево возможных партий (и только их) при описанной стратегии Вани. Заключительные позиции (в них выигрывает Ваня) подчеркнуты. На рисунке это же дерево изображено в графическом виде.
Дерево всех партий, возможных при стратегии Вани:
* красный круг означает выигрыш
19_4: Досрочный егэ по информатике 2018, вариант 1. Задание 19:
Два игрока, Паша и Вася, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Паша. За один ход игрок может добавить в кучу один или четыре камня или увеличить количество камней в куче в пять раз. Игра завершается в тот момент, когда количество камней в куче становится не менее 69.
Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 69 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 68.
а) Укажите все такие значения числа S, при которых Паша может выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающий ход для каждого указанного значения S.
б)Укажите такое значение S, при котором Паша не может выиграть за один ход, но при любом ходе Паши Вася может выиграть своим первым ходом. Опишите выигрышную стратегию Васи.
Задание 20 ЕГЭ.
Укажите 2 таких значения S, при которых у Паши есть выигрышная стратегия, причём Паша не может выиграть за один ход и может выиграть своим вторым ходом независимо от того, как будет ходить Вася. Для каждого указанного значения S опишите выигрышную стратегию Паши.
Задание 21 ЕГЭ.
Укажите хотя бы одно значение S, при котором у Васи есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Паши, и у Васи нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Для указанного значения S опишите выигрышную стратегию Васи. Постройте дерево всех партий, возможных при этой выигрышной стратегии Васи (в виде рисунка или таблицы).
Типовые задания для тренировки
✍ Решение:
-
19.
а) S ≥ 14. При количестве камней в куче от 14 и выше Паше необходимо увеличить их количество в пять раз, тем самым получив 70 или более камней.
S ≥ 14 выигрышные позиции
б) S = 13. Паша своим первым ходом может сделать 14, 17 или 65 камней, после этого Вася увеличивает количество в пять раз, получая 70, 85 или 325 камней в куче.
S = 13 Паша 1 ход: 13 + 1 = 14 Паша 1 ход: 13 + 4 = 17 Паша 1 ход: 13 * 5 = 65 Ваня 1 ход: [14, 17, 65] * 5 = S ≥ 14 Ваня выигрывает 13 - проигрышная позиция
20. S = 9, 12. Для данных случаев Паше необходимо прибавить 4 камня к куче из 9 камней, либо 1 камень к куче из 12, и получить кучу из 13 камней.
После чего игра сводится к стратегии, описанной в пункте 1б.
S = 13 Паша 1 ход: 9 + 4 = 13 Паша выигрывает Паша 1 ход: 12 + 1 = 13 Паша выигрывает 9, 12 - выигрышные позиции со второго хода
21. S = 8. Своим первым ходом Паша может сделать количество камней в куче 9, 12 или 40. Если Паша увеличивает кол-во в пять раз, тогда Вася выигрывает своим первым ходом, увеличивая количество камней в пять раз.
Для случая 9 и 12 камней Вася использует стратегию, указанную в п.2.
S = 8 Паша 1 ход: 8 + 1 = 9 Ваня Выигрывает (см. п.2) Паша 1 ход: 8 + 4 = 12 Ваня Выигрывает (см. п.2) Паша 1 ход: 8 * 5 = 40

Аналитическое решение 19 задания смотрите на видео:
📹 YouTube здесь
Видеорешение на RuTube здесь
19_1:
Два игрока, Паша и Валя, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Паша. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Например, имея кучу из 7 камней, за один ход можно получить кучу из 14 или 8 камней. У каждого игрока, чтобы сделать ход, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 28. Если при этом в куче осталось не более 44 камней, то победителем считается игрок, сделавший последний ход. В противном случае победителем становится его противник. Например, если в куче было 23 камня, и Паша удвоит количество камней в куче, то игра закончится и победителем будет Валя. В начальный момент в куче было S камней, 1≤ S ≤ 27.
Задание 19 ЕГЭ
а) При каких значениях числа S Паша может выиграть в один ход? Укажите все такие значения и соответствующие ходы Паши.
б) У кого из игроков есть выигрышная стратегия при S = 26, 25, 24? Опишите выигрышные стратегии для этих случаев.
Задание 20 ЕГЭ
У кого из игроков есть выигрышная стратегия при S = 13, 12? Опишите соответствующие выигрышные стратегии.
Задание 21 ЕГЭ
У кого из игроков есть выигрышная стратегия при S = 11? Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На ребрах дерева указывайте, кто делает ход; в узлах — количество камней в позиции.
✍ Решение:
а) Паша имеет выигрышную стратегию и может выиграть за один ход, если S = 27: тогда ему достаточно добавить один камень, чтобы игра закончилась при 28 камнях в куче; или если S = 14, 15, 16, 17, 18, 19, 20, 21, 22 (44/2 = 22 и 28/2 = 14, т.е. от 14 до 22): тогда необходимо удвоить кучу.
S=27 Паша: 27 + 1 = 28 - Выигрыш! 27 - выигрышная позиция
б) При S = 26 выигрышная стратегия есть у Вали. Паша делает ход первым, у него есть возможность либо удвоить количество камней в куче, и тогда количество превысит 44, — выигрывает Валя; либо увеличить количество на один камень, станет 27 камней: следующая Валя, — она может положить один камень и выиграть.
S=26 Паша: 26 * 2 = 52 Валя выигрывает! или: Паша: 26 + 1 = 27 Валя: 27 + 1 = 28 - Выигрыш! 26 - проигрышная позиция
При S = 25 выигрышная стратегия есть у Паши. Удваивать количество камней нет смысла, т.к. количество превысит 44, значит, Паша добавит один камень, их станет 26, следующая Валя, — она может либо добавить камень (станет 27 камней, следующим ходом выиграет Паша) либо удвоить — и сразу проиграть, т.к. станет более 44 камней.
S=25 Паша: 25 + 1 = 26 Валя: 26 ... проигрышная позиция (см. выше) Паша выигрывает! 25 - выигрышная позиция
При S = 24 выигрышная стратегия есть у Вали. Паша делает ход первым: удваивать кучу нет смысла, т.к. в ней станет более 44, значит, Паша добавит один камень, их станет 25; следующая — Валя: она может только добавить один камень (станет 26 камней, следующим ходом Паша оказывается в проигрышной позиции, см. пункт при S = 26).
S=24 Паша: 24 + 1 = 25 Валя: 25 ... выигрышная позиция (см. выше) Валя выигрывает! 24 - проигрышная позиция
Задание 20 ЕГЭ:
При S = 13 или S = 12 выигрышная стратегия есть у Паши. Паша удваивает количество и в куче остается 26 или 24 камня. Это проигрышная позиция для того, кто ходит (см. п. 1 б), а следующий ход за Валей.
Задание 21 ЕГЭ:
При S = 11 выигрышная стратегия есть у Вали. Паша делает первый ход: в куче остается либо 22, либо 12 камней. Обе эти позиции выигрышные для того, кто ходит. При S = 12 последовательность игры описана в пункте 2, а при S = 22 — в пункте 1а.
Дерево возможных партий:
* Для Вали отображены только ходы по стратегии
** красный круг означает выигрыш
*** фиолетовый круг — конец игры (проигрыш)
Подробное объяснение 19 задания ЕГЭ смотрите на видео (аналитическое решение):
📹 YouTube здесь
Видеорешение на RuTube здесь
Игра с двумя кучами камней или табличка
19_5:
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 73.
Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, что в кучах всего будет 73 камня или больше.
Задание 1.
Для каждой из начальных позиций (6, 33), (8, 32) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.
Задание 2.
Для каждой из начальных позиций (6, 32), (7, 32), (8, 31) укажите, кто из игроков имеет выигрышную стратегию.
Задание 3.
Для начальной позиции (7, 31) укажите, кто из игроков имеет выигрышную стратегию. Постройте дерево всех партий, возможных при указанной вами выигрышной стратегии. Представьте дерево в виде рисунка или таблицы.
✍ Решение:
- Задание 1. В начальных позициях (6, 33), (8, 32) выигрышная стратегия есть у Вани.
- Задание 2. В начальных позициях (6, 32), (7, 32) и (8, 31) выигрышная стратегия есть у Пети.
- Задание 3. В начальной позиции (7, 31) выигрышная стратегия есть у Вани.

Видео решения 19 задания с двумя кучами (аналитическое решение):
📹 YouTube здесь
Видеорешение на RuTube здесь
Игра с набором слов
19_2: 2017 год (один из вариантов со слов выпускника):
Петя и Ваня играют в игру: есть набор слов, необходимо последовательно называть буквы этих слов. Побеждает тот игрок, который называет последнюю букву любого слова из набора. Петя ходит первым.
Например, есть набор слов {Волк, Информатика, Страшно}; для заданного набора слов Петя своим первым ходом может назвать букву В, И или С. Если Петя выберет букву В, то победит Ваня (следующие ходы: Петя — В, Ваня — О, Петя — Л, Ваня — К).
Задание 1
А) Даны 2 слова (набора букв) {ИКЛМНИКЛМНХ, НМЛКИНМЛКИ}. Определить выигрышную стратегию.
Б) Даны 2 слова {ТРИТРИТРИ…ТРИ, РИТАРИТАРИТАРИТА…РИТА}. В первом слове 99 букв, во втором 164. Определить выигрышную стратегию.
Задание 2
Необходимо поменять две буквы местами из набора пункта 1А в слове с наименьшей длинной так, чтобы выигрышная стратегия была у другого игрока. Объяснить выигрышную стратегию.
Задание 3
Дан набор слов {Ворона, Волк, Волна, Производная, Прохор, Просо}. У кого из игроков есть выигрышная стратегия? Обосновать ответ и написать дерево всех возможных партий для выигрышной стратегии.
✍ Решение:
- Если поменять местами во втором слове (НМЛКИНМЛКИ) буквы Н и И, то получится следующий набор слов:
{ИКЛМНИКЛМНХ, ИМЛКННМЛКИ}Для данного набора выигрышная стратегия есть у Вани. Петя в любом случае должен будет выбрать букву И, а Ваня следующим ходом может перевести игру в проигрышную позицию для Пети, т.е. перейти на второе слово, назвав букву М. Такая стратегия приведет Ваню к выигрышу, так как последнюю букву слова — И — запишет именно он.
- Выигрышная стратегия есть у Вани, так как при любом выборе Пети, Ваня может перевести игру в проигрышную позицию для Пети, т.е. «перейти» на слово с четным количеством букв. Такая стратегия позволит Ване написать последнюю букву и тем самым выиграть игру.
А) Для выигрыша Пете достаточно выбрать первую букву слова с нечетным количеством букв, тогда последний ход делает Петя. При исходном наборе слов выигрышная стратегия есть у Пети. Она заключается в том, что своим первым ходом он должен выбрать букву И (слово ИКЛМНИКЛМНХ из 11 букв). Ване придется выбрать букву К. Таким образом, они последовательно будут называть буквы первого слова, пока Петя не выберет последнюю букву Х. На этом игра закончится выигрышем Пети. При данной стратегии возможна только одна партия. Заключением партии будет написано слово ИКЛМНИКЛМНХ.
Б) При исходном наборе слов выигрышная стратегия есть у Пети. Она заключается в том, чтобы выбрать слово с нечетным количеством букв, т.к. при такой стратегии последнюю букву в любом случае записывает Петя. Т.о., Петя должен выбрать букву Т, т.к. в первом слове 99 букв.
Дерево возможных партий:
* Для Вани отображены только ходы по стратегии
** Красный круг означает выигрыш
Подробней с решением задания про слова ознакомьтесь в видеоуроке (аналитическое решение):
📹 YouTube здесь
Видеорешение на RuTube здесь