-
Абитуриентам
Одним из главных принципов уникальной «системы Физтеха», заложенной в основу образования в МФТИ, является тщательный отбор одаренных и склонных к творческой работе представителей молодежи. Абитуриентами Физтеха становятся самые талантливые и высокообразованные выпускники школ всей России и десятков стран мира.
- Приемная комиссия
- Физтех-центр
- ЗФТШ
- Школы
- Олимпиады и конференции
- Студентам
- Аспирантам
- Выпускникам

- О Физтехе
- Образование
- Наука и инновации
- Новости науки
- МФТИ
- Образование
- Институтские кафедры
- Кафедра высшей математики
- Экзамены (контроль успеваемости)
- Осенний семестр (зимняя сессия)
- Весенний семестр (летняя сессия)
- О контроле знаний студентов
- Варианты экзаменационных контрольных
- Вступительные экзамены по математике
Если вы заметили в тексте ошибку, выделите её и нажмите Ctrl+Enter.
На Физтехе лучше всего я выучил дифференциальные уравнения. Потому что феерично сдавал их аж четыре раза.
Система обучения в МФТИ уникальна тем, что можно сдать экзамен, абсолютно ничего не делая весь семетр, и не сдать, посетив все лекции и семинары и зная предмет достаточно хорошо. И мне это чертовски нравилось. Мой незамысловатый подход к учебе (скорее обход учебы) гарантировал безудержное веселье почти на каждом экзамене.
Были истории карнавального успеха, когда удавалось обмануть всех и получать хорошие оценки, не зная даже названия предмета. Были не менее феерические провалы, когда я палился в последний момент, или же отвечал долго, уверенно и правильно, но из-за странных заскоков преподавателей получал пересдачи.
Да и у кого из физтехов таких историй не было?
Бакалавриат обошелся мне в 12 пересдач, не считая зачетов. Самые долгие отношения случились с аналитической геометрией в первом семестре (сдал с 4-го раза) и с дифференциальными уравнениями в четвертом (тоже с 4-го раза).
Диффуры и матан на втором курсе у моей группы вел преподаватель по фамилии Ждановский. Многие мои одногруппники его недолюбливали, но мне он очень импонировал своим живым чувством юмора, а также тем, что не чурался пообщаться со студентами на отвлеченные темы. На какой-то из пар он сказал мне, что на Физтехе я занимаю чужое место. Мы с интересом подискутировали на эту тему, и я понял, что концептуально он в чем-то прав. Еще я понял, что сдать задания будет непросто.
Я не знаю, как сейчас в МФТИ принимают экзамены, поэтому на всякий случай уточню: год изучения диффуров венчали письменный и устный экзамены. За устный можно получить не больше, чем за письменный, то есть, если я напишу письменный на итоговый «удовл», то на устном могу получить или три, или пересдачу. Если суммы баллов на письменном не хватит даже для трояка, то это автоматическая пересдача.
В обратную сторону это не работает. Если написать на «отлично», то можно получить за устный и 5, и 4, и 3, и пересдачу.
По ходу семестра надо сдать несколько заданий. Если не сдать, то из результата письменного экзамена вычитается какое-то количество баллов.
По счастью, Ждановский любил футбол, и задания по матану я сдал во многом благодаря четырем голам, забитым мной ФАЛТу на Матче века. Пришел на сдачу прямиком с коробки, как только отыграла моя команда, прямо в форме. Увы, на диффуры это правило не распространилось, поэтому на письменном экзамене меня ожидало снятие баллов за плохую работу в семестре.
Надо сказать, что свое первое в жизни дифференциальное уравнение я решил ровно за день до письменного экзамена. Таким образом, чтобы наскрести на тройку, нужно было сесть на экзамене рядом с нужными людьми и аккуратненько все списать, что я неоднократно проделывал и ранее, и потом.
Экзамен мы писали всем потоком. Я спрятался за спинами однокурсников где-то в середине Большой химической аудитории, чтобы случайно не попасться на глаза Ждановскому.
Пока другие преподаватели копошились в листочках с заданиями и занимались рассадкой прибывших в аудиторию студентов, он суетливо ходил вдоль первого ряда, пересчитывал студентов и хмурил брови. Наконец, когда весь наш поток расселся, он остановился и пробасил на всю аудиторию: «Заварин!».
Сто с лишним человек затаили дыхание. Я спрятался под партой.
Секундная пауза. Тишина.
— Заварин!!! — громче и требовательней гаркнул Ждановский. Я понял, что сопротивление бесполезно, и вяло поднял руку.
— Я здесь.
— На первый ряд! — торжественно изрек он.
Аудитория содрогнулась от смеха. Аудитория ликовала. Спускаясь к первому ряду, я чувствовал себя гладиатором, выходящим на бой со львами. Вслед неслось улюлюканье и громовые раскаты хохота.
Усевшись на первый ряд, я заметил направленный на меня из-под толстенных очков безразличный взгляд Беклемишева, хмурое лицо Ивановой и жизнерадостную улыбку Ждановского. Совершенно очевидно, что при таких обстоятельствах шансов списать, а значит, написать контрольную хотя бы на «удовл» у меня не было.
В итоге за этот экзамен я кое-как наскреб 10 баллов (из 50), из которых 8 с меня списали за несданные задания. Пороговый балл на тройбас был 12 или 13, поэтому я даже порадовался, что не сдавал эти задания в семестре.
В общем, это было абсолютно справедливо: ничего не знаешь, не смог обхитрить препода — извольте на пересдачу. То есть, обижаться и расстраиваться совершенно не было повода — сам ведь виноват.
…
Оставшиеся в той сессии шесть экзаменов я кое-как спихнул, подработки свернул до начала экзаменов, а оставшиеся мудро приберег на лето. Квновский сезон также взял летнюю паузу. Сессия закончилась, и у меня была ровно неделя, чтобы подготовиться к пересдаче. Что ж, всю неделю я добросовестно посвятил диффурам. На мой взгляд, за такой большой срок можно расшарить вообще любую дисциплину, так что, к пересдаче я подходил сверхготовым.
Чтобы допуститься непосредственно к самой пересдаче, надо было написать дебильник — решить пять не самых сложных задач. Дальше эти задачи проверяет кто-то из преподавателей, потом он выходит из аудитории к ожидающим в коридоре своей участи студентам и оглашает список из 4-5 фамилий. Эти студенты либо отправляются на следующую пересдачу, если завалили дебильник, либо тянут билет и готовятся отвечать, скорее всего, этому же преподавателю.
Вышел какой-то препод, назвал мою фамилию в компании с еще четырьмя ребятами, и скрылся за дверьми аудитории. Пока мы направлялись следом, один парень тихо произнес: «Нам пиз*ец,..» и, поймав мой недоуменный взгляд, добавил: «Это Умнов-младший».
Умного-младшего мои знакомые в основном люто ненавидели. По учебным делам я с ним не сталкивался, поэтому никакого мнения на этот счет у меня не было.
Зато вот благодаря пересдаче появилось. Мы расселись на одном из рядов, возле Умнова стопочкой лежали наши дебильники и зачетки.
— Значит так, ребята. Я считаю, что все эти пересдачи — это профанация. Если студент получает пересдачу, значит, он не учился весь семестр, значит, такой студент Физтеху не нужен, — с этими словами он подвинул к нам стопку наших зачеток. — Я вам всем уже выставил двойки в ведомость.
Сказать, что мы немного подофигели — значит ничего не сказать. Настолько, что даже не попробовали внятно оспорить это решение. На вопрос, можно ли проапеллировать к результатам проверки дебильников, Умнов презрительно фыркнул и сказал, что даже не стал их проверять.
На самом деле, в данной ситуации мало что можно сделать. Если уж преподаватель хочет завалить студента, то что может ему помешать? Теоретически можно было бы обратиться к кому-нибудь там на кафедре и как-то оспорить это решение. Тогда Умнов проверил бы дебильник и, возможно, даже допустил бы студента к ответу. И что? Отвечать-то все равно пришлось бы ему.
Так что, я пожал плечами, забрал зачетку и вышел из аудитории, вспоминая, как примерно за полгода до этого я сидел на какой-то паре, когда в кабинет ворвалась студентка и начала вопить что-то нечленораздельное и махать руками. Забежав в соседнюю аудиторию, я увидел, как на полу лежит весь измазанный мелом мужик, пускает слюни и смотрит ничего не выражающим взглядом куда-то в потолок.
Группа этого преподавателя сидела за партами, пребывая в небольшом шоке. Я крикнул, чтобы они вызвали скорую, позвал одногруппника, и мы вдвоем на своих закорках потащили мужика вниз, к выходу из Главного корпуса. Вынесли на улицу аккурат к подъехавшей скорой.
Возможно, мы спасли ему жизнь. Возможно, конкретно в данном случае время ничего не решало, и случившийся с ним приступ серьезной угрозы для жизни не представлял. Как бы то ни было, мы сделали то, что должен был сделать любой другой адекватный человек.
Я курил в туалете возле аудитории, в которой только что получил пересдачу, смотрел из окна на стройку рядом с Физтехом и думал, что наши усилия не пропали даром, раз уж этот человек (нет, это был не Альберт Эйнштейн) оказался жив и достаточно здоров для того, чтобы отправлять студентов на пересдачи со скоростью пулемета.
…
До следующей пересдачи было два дня, их я тоже посвятил чертовым дифференциальным уравнениям. Я даже помнил, что и на какой странице написано в учебнике Романко. Человек-диффур просто.
Дебильник я написал на максимум, и меня позвал к себе стремительно лысеющий дедушка, у которого были какие-то проблемы с одним глазом, из-за чего он немного походил на Терминатора. Позднее я узнал, что его фамилия Егоров, и ни один человек не смог сказать мне про него ни одного плохого слова. Все утверждали, что он адекватный и местами даже веселый человек, кроме того, еще и достаточно халявный преподаватель.
Что же, тем ценнее оказалась следующая история.
У Егорова есть фишка: переворачивать листок с ответом на билет, чтобы студент написал все на чистой стороне листа. Я всегда хорошо готовился к пересдачам (когда-то ведь надо начинать учиться), поэтому, в отличие от основных экзаменов не брал с собой шпоры, бомбы и прочие приятные мелочи.
В этот раз, как уже отмечал выше, я был просто отцом диффуров. Поэтому гордо написал билет заново прямо при нем, не отходя от кассы. Егоров одобрительно посмотрел на меня одним глазом, дал дополнительный вопрос и пошел спрашивать других сдающих.
Нас сидело человек семь и, возможно, это был единственный случай, когда я отвечал лучше всех остальных. Парни сильно плавали на простых вещах, палились за списыванием с телефонов, один со слезами на глазах уговаривал поставить ему три.
Егоров был милостив. После двух-трех ответов (даже неправильных) он по очереди отпускал ребят с трояками.
И вот я остался один. Начался четвертый час экзамена. За это время я ответил на семь или восемь вопросов, решил пару задач и доказал несколько теорем. При этом, вообще не понимал, зачем я все это делаю. «Он что, тянет меня на хор?». К черту эти условности, меня никогда не интересовало, какие оценки будут стоять в моей зачетке. Идеальный вариант еще в начале первого семестра мне виделся таким: мне сразу проставляют тройки по всем предметам всех курсов и отдают диплом.
Короче говоря, где-то на девятом-десятом вопросе я сломался и не ответил. Ну, как бы, тяжеловато четыре часа подряд говорить только о дифференциальных уравнениях. Не то чтобы это моя любимая тема.
Я честно признался, что не знаю ответа на этот вопрос, но готов ответить на любой другой. Егоров пробормотал грустное «Не сомневаюсь, Сергей, не сомневаюсь…», полистал мою зачетку, а потом выдал шедевральное:
— Знаете, Сергей, я преподаю на Физтехе уже почти сорок лет. И по своему опыту могу совершенно ответственно заявить, что Вы могли бы учиться здесь на отлично. Ну, может, с четверками. Но я листаю зачетку и вижу там тройки, а это значит, что Вы ленитесь. А за лень надо наказывать. Поэтому я поставлю Вам пересдачу.
Согласно официальным правилам института, три двойки по одному предмету — это отчисление. Немного дурацкая причина для вылета, правда?
— Хм… Я просто уточнить. Вы мне ставите два за то, что я слишком хорошо ответил?
— Да.
Я не стал выпрашивать у него тройку (никогда этого не делал) или ругаться (я не особо конфликтный). Пока он искал ведомость и что-то туда записывал, я просто представлял, что у него на плече сидит огромный пиратский попугай.
И клювом выдалбывает ему второй глаз.
Егоров оторвался от ведомости и спросил, сколько баллов у меня было за письменный экзамен.
— Два.
— Я понимаю, что два. Я имею ввиду, по 50-балльной шкале.
— Два. Из пятидесяти.
— Это как? — растерялся Егоров.
— Просто я на тот момент вообще ничего не знал, плюс с меня еще и баллы за несданные задания сняли.
— Так Вы еще и задания не сдали?! А чем Вы занимались весь семестр? Подождите… Вы что, хотите сказать, что выучили дифференциальные уравнения за неделю?! — он пораженно вытаращил на меня глаз.
— Йохохо, — тихо пробубнил я в ответ.
…
Августовская пересдача по диффурам — возможно, самое мерзкое в плане учебы среди всего, что я видел на Физтехе.
На пересдачу поначалу пришла только Иванова. Мне не доводилось что-либо ей сдавать, но, насколько я понял из рассказов знакомых, она человек настроения. Мой сосед в первом семестре написал письменный экзамен по матанализу на твердый «отл». Вполне заслуженно — он действительно учил и отлично шарил этот предмет. На устном попал к Ивановой и получил пересдачу. В то же время, иногда люди получали у нее тройки-четверки просто так, под аккомпанемент ее шуточек-прибауточек.
В тот день, по всей видимости, она была не в духе и мощно загнобила пришедших на пересдачу. Не помню дословно, что именно она говорила. Но в ход точно шли обороты типа «тупицы», «идиоты» и «скорее бы вас всех отчислили». Особенно на орехи доставалось девушкам, которые поступили на Физтех, только чтобы найти себе мужа. И то, непонятно, кому нужны такие «никчемные дуры».
Некоторые девушки аж заплакали. Все подавленно молчали. Достаточно гнетущая атмосфера, хотя вроде как экзамен — это всегда праздник (я так объяснял в деканате свои пересдачи). Ну если студент действительно тупой и не тянет — пересдача и отчисление. Окей, никаких вопросов. Но зачем оскорблять?
Вообще, организовано было все очень по-дурацки. По правилам кафедры вышмата, если студент сдает дебильник, но получает двойку при устном ответе, то на следующей пересдаче он может дебильник не писать. Это был как раз мой случай, и в деканате мне сказали сделать именно так.
Но, как оказалось, в ведомости Егоров то ли забыл, то ли специально не указал, что я ему отвечал устно. Иванова развела руками и предложила либо дождаться его, либо написать дебильник еще раз. Немного стремный выбор. Если случайно накосячить — отчисление. Если Егоров не придет в итоге, то написать дебильник мне уже никто не даст — тоже отчисление. Я решил, что лучше рассчитывать на себя. Тем более, за неделю до пересдачи шестое чувство подсказало мне, что все может пойти не так, и лучше на всякий случай заботать все задачи.
Собственно, Егоров пришел чуть позже. Но в лучших традициях самого себя, сказал, что считает это правило каким-то корявым и ничего засчитывать мне не будет. Так что, если бы я решил действовать согласно официально принятым правилам пересдачи, то эта история закончилась бы белорусским военкоматом, еще более бессмысленным и беспощадным, чем кафедра вышмата Физтеха.
Я написал дебильник на максимум, в стиле колобка ушел от Ивановой, украв свою зачетку с преподского стола, получил заветный трояк у другого преподавателя, и моя улыбка в тот день была способна осветить и Москву, и ближайшее Подмосковье. В деканате я танцевал танец победителя, а потом еще примерно неделю праздновал это событие.
В общем, пересдачи нужны для того, чтобы их получать. Ни в школе, ни в университете я не мог заставить себя серьезно относиться к учебе. Поэтому, когда случались подобные истории, я искренне радовался им — в моем понимании полученный благодаря высшему образованию такого рода опыт намного ценнее недополученных теоретических знаний.
Оригинал записи в блоге Сергея Заварина
Поделиться
Твитнуть
Поделиться
В данной статье разобран пример вступительного экзамена по математике в МФТИ (бакалавриат). Если вас интересует разбор вступительного экзамена по физике, вы можете найти его на этой странице. Все решения выполнены профессиональным репетитором по математике и физике, осуществляющим подготовку абитуриентов к вступительным экзаменам в МФТИ (ФизТех).
Разбор вступительного экзамена по математике в МФТИ
Используем формулу «синус двойного угла»:
Переносим слагаемые, находящиеся справа от знака равенства, в левую сторону, меняя при этом их знак на противоположный, и выносим за скобки:
Преобразуем теперь выражение, стоящее в скобках, используя формулу «косинус двойного угла»:
Произведение равно нулю, если хотя бы один из множителей равен нулю. То есть возможны два случая:
1) .
2)
Умножим обе части последнего уравнения на и введём замену
:
Примечание. Последнее уравнение является квадратным и решается по стандартному алгоритму с помощью дискриминанта.
Возвращаемся к исходной переменной. Получаем, что либо (это уравнение не имеет решений в действительных числах, так как
), либо
. Из последнего уравнения получаем
.
Ответ: .
Преобразуем выражение с суммой кубов:
В скобках заменим член на разность
. От этого равенство не нарушится. В результате получим:
Итак, исходную систему можно представить в следующем виде:
Теперь используем замену: и
. Тогда система принимает вид:
Теперь складываем почленно оба уравнения и приходим к следующему уравнению:
Корень этого уравнения угадывается автоматически: . Других корней не будет, так как справа стоит возрастающая функция, поскольку она является суммой возрастающих функций, поэтому нулевое значение она может принимать только при каком-то одном значении
.
Итак, , значит
. Возвращаясь к исходным переменным, получаем следующую систему:
В результате приходим к окончательному ответу: и
.
В общем виде уравнение прямой может быть записано следующим образом: . Известно, что эта прямая проходит через точку
, то есть имеет место равенство:
(1)
Кроме того, прямая касается графика функции . Значит уравнение
должно иметь ровно один корень. Введём замену . Тогда последнее условие эквивалентно тому, что дискриминант квадратного уравнения
(2)
равен нулю, и корень при этом неотрицателен. То есть получаем:
Таким образом с учётом уравнения (1) приходим к следующей системе:
Решая эту систему методом подстановки, получаем следующие результаты: ( и
) или (
и
). При
и
уравнение (2) имеет один неотрицательный корень
. При
и
уравнение (2) имеет один неотрицательный корень
.
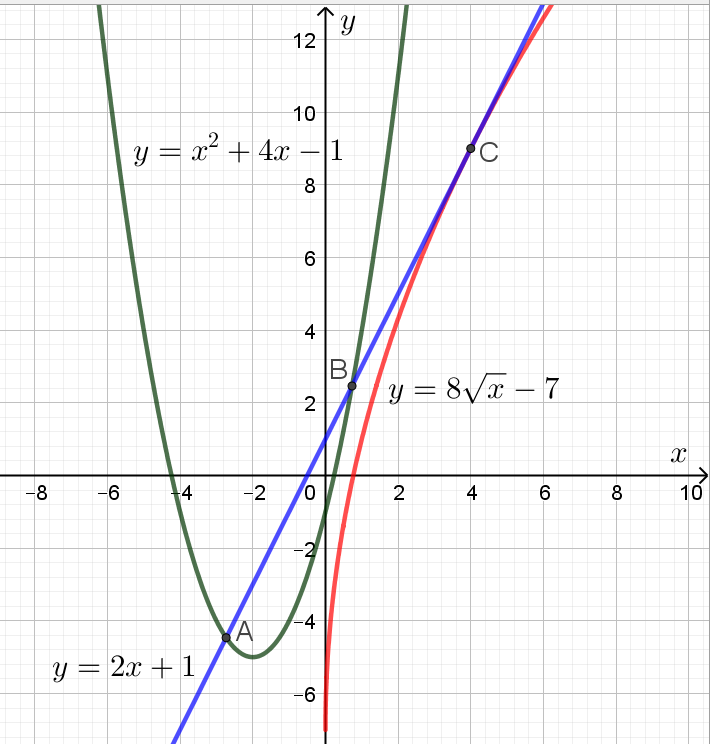
То есть из двух прямых и
нужно выбрать такую, которая пересекает график функции
в двух различных точках.
- Решаем сперва уравнение:
Дискриминант последнего уравнения положителен. Значит, оно имеет два различных корня. Этот случай нам подходит.
- Решаем теперь уравнение:
Дискриминант этого уравнения равен нулю. Значит, решение в этом случае будет одно. Этот случай нам не подходит.
Ответ: .
Примечание. Для наглядности изобразим ситуацию на графике, хотя делать это необязательно, поскольку в задании этого не требуют:
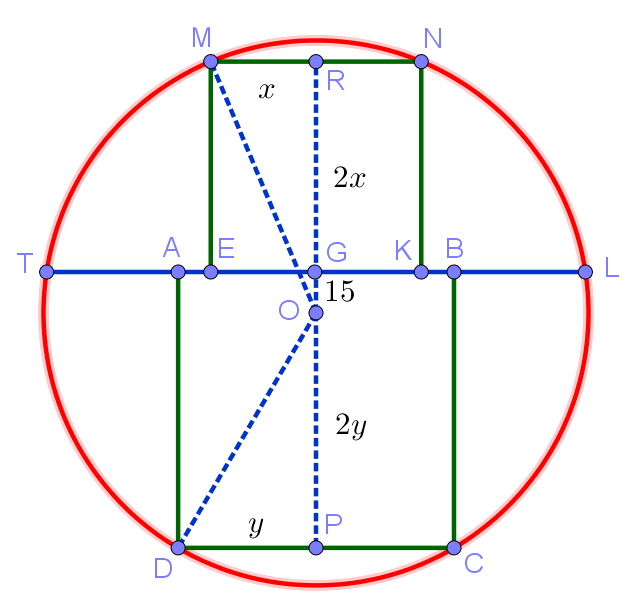
4. Хорда окружности, удалённая от центра на расстояние 15, разбивает окружность на два сегмента, в каждый из которых вписан квадрат. Найдите разность сторон этих квадратов.
Пусть радиус окружности равен . Рассмотрим прямоугольные треугольники OMR и ODP. С учётом введённых на рисунке обозначений распишем теорему Пифагора для этих треугольников:
Вычтем почленно второе уравнение из первого:
Преобразуем полученное выражение, используя формулу «разность квадратов»:
Поделим обе части этого уравнения на и обозначит разность
за
. В результате приходим к следующему уравнению:
Искомая разность сторон квадратов в наших обозначениях будет равна .
Ответ: 24.
Введём замену: . Тогда неравенство принимает вид:
Теперь, используя стандартные свойства логарифмов, представим логарифмическое выражение слева от знака неравенства следующим образом:
Введём ещё одну замену: . Тогда после умножения обеих частей неравенства на положительное число
неравенство принимает вид:
Последовательно возвращаемся к исходной переменной :
Окончательно получаем следующий ответ:
Пусть в первую бочку долили кг воды, а во вторую —
кг. Пусть в первой бочке находится
кг, а во второй
кг соли.
Тогда изначально в первой бочке процентное содержание соли составляло:
а после доливания воды оно стало равно:
Аналогично, во второй бочке изначально процентное содержание соли составляло:
а после доливания воды оно стало равно:
Тогда справедливы равенства:
(3)
(4)
Из уравнения (3) выражаем , из уравнения (4) выражаем
, а из уравнения
выражаем
. Мы ищем минимальное значение суммы
. Проще всего найти его, используя неравенство Коши:
Итак, наименьшее количество воды, которое могло быть долито в обе бочки вместе равно 80 кг.
Этот случай реализуется при , когда неравенство Коши преобразуется в равенство. То есть при
. Подставляя это в выражение
, получаем после преобразований, что
. Отрицательный корень мы в расчёт не берём.
Ответ: 80 кг.
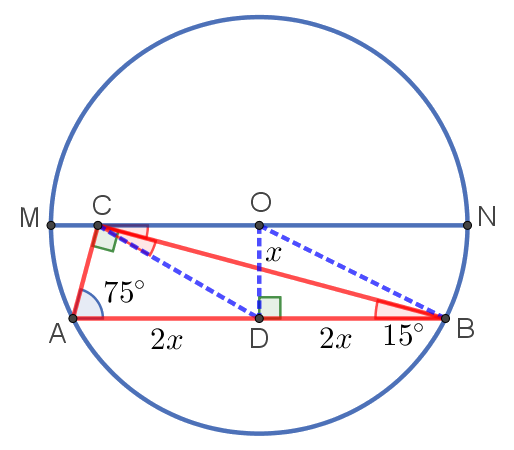
7. Вершина прямого угла C прямоугольного треугольника ABC расположена на диаметре окружности, параллельном хорде AB. Найдите площадь треугольника ABC, если ∠BAC = 75°, а радиус окружности равен 10.
Выполним следующие дополнительные построения:
- проведём высоту OD к хорде AB. Тогда D — середина AB, так как OD — высота и медиана, проведённая к основанию равнобедренного треугольника AOB;
- проведём отрезок CD. Он является медианой прямоугольного треугольника ACB, проведённой из вершины прямого угла. Значит, CD = AD = BD.
Переходим к решению:
- сумма углов в любом треугольнике равна 180°. Значит, ∠CBA = 15°;
- так как CD = BD, то треугольник CDB — равнобедренный и ∠CBD = ∠DCB = 15°;
- ∠CBD = ∠BCO = 15°, поскольку они являются накрест лежащими при параллельных прямых и секущей. Значит, ∠DСO = 30°;
- значит, в прямоугольном треугольнике COD против угла в 30° лежит катет OD, который равен половине гипотенузы CD. Пусть DO = x, а CD = AD = DB = 2x;
- из теоремы Пифагора для треугольника ODB получаем, что
, то есть
;
- тогда искомая площадь треугольника ABC равна половине произведения его высоты, проведённой к стороне AB, которая по длине равна x, на основание AB, которое по длине равно 4x. То есть искомая площадь равна
.
Ответ: 40.
выполняется для всех значений .
Преобразуем данное неравенство, раскрыв в нём скобки и использовав основное тригонометрическое тождество. В результате после всех преобразований получаем следующее неравенство:
Ведём замену , причём
. Тогда получим следующее неравенство:
Задача свелась к тому, чтобы найти все значения параметра , при котором последнее неравенство выполняется при всех
.
Для решения этой задачи представим последнее неравенство в виде:
Легко видеть, что при любых значениях
, так как дискриминант соответствующего квадратного уравнения отрицателен, и ветви соответствующей параболы направлены вверх. Поэтому мы можем разделить обе части последнего неравенства на положительное выражение
, при этом знак неравенства не поменяется:
(5)
Исследуем функцию на возрастание. Для этого определим при каких значениях
её производная положительна:
Так как , а
, то на промежутке
данная функция возрастает. Поэтому неравенство (5) будет выполняться при любом
при условии, что
, то есть
.
Ответ: .
Подготовка к вступительному экзамену по математике в МФТИ
Если вам требуется подготовка к вступительному экзамену по математике в МФТИ, обращайтесь к опытному профессиональному репетитору в Москве Сергею Валерьевичу. Возможны как очные, так и удаленный занятия через интернет с использованием интерактивной доски. Как показывает практика, в условиях ограниченности во времени именно занятия с репетитором обеспечивают наиболее эффективную подготовку к вступительным экзаменам. Подробную информацию о занятиях с репетитором вы можете найти на этой странице. Успехов вам в подготовке к экзаменам!
Сегодня сдал экзамен по уравнениям математической физики на 4. Казалось бы обычный экзамен, но не совсем. Это был последний раз, на котором самая жесткая на Физтехе кафедра, кафедра высшей математики, могла на меня повлиять. В связи с этим хочется вспомнить былое…
1. Сергей Васильевич Резниченко. Хуевые у вас лекции, если честно. Но зато предмет (теория вероятностей) очень важный и нужный, буду пользоваться им всю жизнь. Вы заложили фундамент — остальные преподаватели мои знания лишь развивали. Вы принимали у меня самый первый экзамен на Физтехе, по математическому анализу. Вы поставили (уже на другом экзамене) мне первую и единственную за 2 курса тройку — причем по теории вероятностей, которую я сейчас знаю от и до. Вы жесткий, но по-своему справедливый преподаватель.
2. Андрей Леонидович Степанов. Андрюша, как мы его звали, был аспирантом и вел у нас семинары по мат.анализу на 1ом курсе. Недавно видел его и очень мило поговорил о жизни. Хороший парень — многого казалось бы не требовал, но знал я немало. Задачи перед письменным экзаменом по крайней мере решать умел.
3. Владимир Иванович Зубов. Очень мягкий и интеллигентный преподаватель, доктор наук, классичяеский советский интеллигент. Я всегда писал его контрольные на четверки, но мнения он обо мне был хорошего. Помню такой случай:
— Вы все задачи решили, — спросил меня Зубов перед просмотром тетрадки с заданием.
— Конечно все!
— Почему конечно?
— Ну вы же все равно задание не засчитаете, если там задач хватать не будет.
— Ну прямо бальзам на душу, хоть делать задание полностью я вас научил.
4. Вера Юльевна Дубинская. Жена Сергея Васильевича Резниченко, этим и знаменита — вела семинары по теорверу. Добрая тетечка пятидесяти лет, проблем с ней не было.
5. Андрей Юрьевич Семенов. 2 раза ему сдавал аналитическую геометрию. В первом семестре поставил четверку и предложил прийти через полгода за пятеркой. Я пришел — и получил!
6. Илья Юрьевич Ждановский. Сдавал ему матан во втором семестре. Спросил меня формулу Грина из программы следующего семестра, я не ответил и он поставил мне 5, продублировав оценку за письменную работу.
7. Максим Викторович Балашов. Максимкой нас пугали старшекурсники-раздолбаи, а на самом деле очень хороший преподаватель. Вел семинары на 2 курсе по мат.анализу и дифф.уравнениям. Объясняет стремительно: на доске он пишет быстрее, чем я в тетради, но зато понимает свой предмет глубоко, я даже одно время думал, что глубже и невозможно. Я ошибался, но об этом позже. Еще Максимке спасибо стоит сказать за то, что однажды видя, что я списываю на экзамене не сказал об этом моему экзаменатору. А еще на диффурах, когда другой мой экзаменатор спросил его: «Как Сидоровский знает предмет?» Он ответил, что между 4 и 5, хотя мог бы назвать и более плохие оценки.
8. Валерий Николаевич Седов. Принимал у меня мат.анализ в четвертом семестре. Спросил 2 вопроса и поняв, что я недоучил, поставил мне 4. Спасибо ему за это!
9. Григорий Евгеньевич Иванов. Вел лекции целых 2 года, правда посещал я их всего один семестр =) Добрый преподаватель, но нахаляву ставит только 4, не представляю как ему надо отвечать на 5? У меня ни разу не получилось… ох уж эти его теоретические задачки…
10. Вера Тимофеевна Петрова. Не самый шарящий преподаватель, видимо потому что женщина. Однажды очень лояльно проверила мою контру по мат.анализу и ни разу не взяла к себе на экзамен на аналит.геометрии — спасибо Вам за это, Вера Тимофеевна! Я кстати честно пытался ходить на ваши лекции — не многие преподаватели могут этим похвастаться =)
11. Александр Александрович Абрамов. Живая легенда советской математики! Читал лекции по дифференциальным уравнениям, но я посетил только одну… Стыдно.
12. Геннадий Валентиновия Мухин. Вел самый нужный мне нынче предмет, стохастические процессы. Именно от него я впервые услышал столь привычные теперь термины как ошибка первого рода, критерий Колмогорова-Смирнова, неравенство Крамера-Рао… Я, конечно, попал на раздачу халявы от него, получив пять. Но Геннадий Валентинович, теперь-то я знаю Ваш предмет — другие преподы заставили-таки меня его выучить =)
13. Михаил Иванович Карлов. Сегодня взял мою зачетку, покрутил-повертел, да и отправил меня сдавать халявщику. А ведь ровно полгода назад он безжалостно отправил меня пересдавать Теорию Функции Комплексной Переменной. Лектор он очень прикольный и веселый, часто пугает студентов военкоматом. =)
14. Лариса Алексеевна Леонтьева. Принимала у меня ГОС-экзамен. Как и любая женщина в математике не шарит, но зато с пытливым умом, поэтому пыталась меня поймать на неточностях. не получилось, так как ей активно мешал…
15. Валентин Петрович Михайлов. Одни из самых добрых воспоминаний останутся у меня именно от этого замечательного «великорусского деда» с явным вологодским акцентом. Когда Леонтьева на ГОС-экзамене его спросила: «Ну что поставим Сидоровскому, все-таки наверно 5?» Он ответил: «Однозначно 5!» Было очень приятно, что такой заслуженный математик оценил мои знания. А еще он у нас вел лекции по УМФ, но я опять же посетил лишь самую первую. Я, наверное, мудак…
16. Валентин Анатольевич Гущин. Мой последний экзаменатор на Физтехе по математике поставил мне сегодня 4. И правильно: мой роман с математикой завершился на мажорной ноте.
17. Роман Викторович Константинов. Рискну предположить, что сейчас это самый эрудированный математик в России. Знает вообще все! А о том чего говорит, что не знает может рассказывать пары напролет =) Писал на доске в 1.5 раза быстрее Балашова, махал руками в 5 раз активнее. На семинарах ничего не было понятно, но какие-то знания остались. А еще спасибо, что я чудом Вам сдал на пересдаче ТФКП на 4. Одна из самых заслуженных моих четверок за всю историю.
________________________________
________________________________
Вот и весь список преподавателей, которые у меня вели занятия или принимали экзамен по математике в МФТИ. Сколько же сил потрачено, сколько бомб написано, сколько нового узнано…
Спасибо всем!
Московский Физико-Технический Институт (государственный университет)МФТИ |
Проходные баллы в МФТИ
Показать только с
|
0 |
Доступные ЕГЭ
|

|
Пожалуйста, подождите. Идет загрузка…
Прикладная математика и информатика
Бакалавриат | 01.03.02
|
Подразделение: Физтех-школа прикладной математики и информатики Проходные баллы:
|

|
||||||
|
|
|
Подразделение: Физтех-школа прикладной математики и информатики Проходные баллы:
|

|
||||||
|
|
Прикладные математика и физика
Бакалавриат | 03.03.01
|
Подразделение: Физтех-школа аэрокосмических технологий Проходные баллы:
|

|
||||||
|
|
|
Подразделение: Физтех-школа бизнеса высоких технологий Проходные баллы:
|

|
||||||
|
|
|
Подразделение: Физтех-школа аэрокосмических технологий Проходные баллы:
|

|
||||||
|
|
|
Подразделение: Физтех-школа аэрокосмических технологий Проходные баллы:
|

|
||||||
|
|
|
Подразделение: Физтех-школа прикладной математики и информатики Проходные баллы:
|

|
||||||
|
|
|
Подразделение: Физтех-школа радиотехники и компьютерных технологий Проходные баллы:
|

|
||||||
|
|
|
Подразделение: Физтех-школа физики и исследований им. Ландау Проходные баллы:
|

|
||||||
|
|
|
Подразделение: Физтех-школа электроники, фотоники и молекулярной физики Проходные баллы:
|

|
||||||
|
|
|
Подразделение: Физтех-школа прикладной математики и информатики Проходные баллы:
|

|
||||||
|
|
|
Подразделение: Физтех-школа биологической и медицинской физики Проходные баллы:
|

|
||||||
|
|
|
Подразделение: Институт нано-, био-, информационных, когнитивных и социогуманитарных наук и технологий Проходные баллы:
|

|
||||||
|
|
Информатика и вычислительная техника
Бакалавриат | 09.03.01
|
Подразделение: Высшая школа программной инженерии Проходные баллы:
|

|
||||||
|
|
|
Подразделение: Физтех-школа прикладной математики и информатики Проходные баллы:
|

|
||||||
|
|
|
Подразделение: Физтех-школа аэрокосмических технологий Проходные баллы:
|

|
||||||
|
|
|
Подразделение: Физтех-школа прикладной математики и информатики Проходные баллы:
|

|
||||||
|
|
Электроника и наноэлектроника
Бакалавриат | 11.03.04
|
Подразделение: Физтех-школа электроники, фотоники и молекулярной физики Проходные баллы:
|

|
||||||
|
|
Техническая физика
Бакалавриат | 16.03.01
|
Подразделение: Физтех-школа аэрокосмических технологий Проходные баллы:
|

|
||||||
|
|
Биотехнология
Бакалавриат | 19.03.01
|
Подразделение: Физтех-школа бизнеса высоких технологий Проходные баллы:
|

|
||||||
|
|
|
Подразделение: Физтех-школа биологической и медицинской физики Проходные баллы:
|

|
||||||
|
|
Системный анализ и управление
Бакалавриат | 27.03.03
|
Подразделение: Физтех-школа бизнеса высоких технологий Проходные баллы:
|

|
||||||
|
|
|
Подразделение: Физтех-школа прикладной математики и информатики Проходные баллы:
|

|
||||||
|
|
Экономика
Бакалавриат | 38.03.01
|
Подразделение: Физтех-школа бизнеса высоких технологий Набор экзаменов:
Проходные баллы:
|

|
||||||||
|
|
Компьютерная безопасность
Специалитет | 10.05.01
|
Подразделение: Физтех-школа радиотехники и компьютерных технологий Проходные баллы:
|

|
||||||
|
|
Пожалуйста, подождите. Идет загрузка…
Загрузить еще
Пожалуйста, подождите. Идет загрузка…
|
Вопрос: Добрый день! Крик души |
| 19 марта в 12:00 | |||
|
|||
| 23 марта в 16:00 | |||
|
|||
Вопрос: Добрый день! Крик души
Я впл, март на дворе, а я не уверена в какой вуз мне поступать
В прошлом году сдавала русский 91 балл
В этом году будут ещё результаты по обществознанию и литературе
Я хочу на…
| 19 марта в 12:00 | ||
|
||
| 23 марта в 16:00 | ||
|
||



![Rendered by QuickLaTeX.com [ 4t^2-2sqrt{3}t-6=0Leftrightarrowleft[ begin{array}{l} t_1 = -frac{sqrt{3}}{2} \ t_2=sqrt{3}. end{array} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-8e85e67c476157c1f85c10a768fe9a26_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} x^3+y^3=19 \ (xy+8)(x+y)=2. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e7bc49f8e253669ff9ba49d9426f85af_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} (x+y)((x+y)^2-3xy)=19 \ (xy+8)(x+y)=2. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-178655bc3fda7ef894fc3bbd7840314d_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} a(a^2-3b)=19 \ a(b+8)=2 end{cases}Leftrightarrow begin{cases} a^3-3ab = 19 \ 3ab+24a=6. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-5c997b7d3fe4081ba0adee4f624d29fa_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} x+y = 1 \ xy=-6. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-4a755b8f09270e84f7dc7d2a2b347511_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} k+b = 3 \ 16-7k-kb=0. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-f6bc14d85bd685587ec8be4ccf4a0b59_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} x^2 = R^2-(2x+15)^2 \ y^2 = R^2 - (2y-15)^2. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-4d914f9a98f6f9b06171fc2db0fd713e_l3.png)
![Rendered by QuickLaTeX.com [ =40sqrt{left(frac{m+3}{m-1}-1right)(m-1)}= ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-f3a93b14138c23455fa41a3e86698c39_l3.png)
![Rendered by QuickLaTeX.com [ y'=-frac{t^2+6t-29}{(t^2-6t+11)^2}>0Leftrightarrow ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-8059bcd31ba16c4f55ea4f68984b4b4a_l3.png)