Высшая школа экономики примеры вступительных экзаменов - Помощь в подготовке к экзаменам и поступлению

Поступление в лицей НИУ ВШЭ
в 9 класс. Русский язык.

— Тренировочные варианты, разработанные на основе ДЕМО.
— Советы по подготовке и сдаче вступительных.

До экзамена осталось:

Вебинары по математике и русскому языку:
Темы вебинаров по математике: «Текстовые задачи» (2 веба), «Логические задачи», «Геометрия»(2 веба), «Параметры» (2 веба), Функции (1веб).
Темы вебинаров по русскому языку: «Словообразование», «Этимология».
Стоимость вебинаров по математике: 4000 р.
Стоимость вебинаров по русскому языку: 1200 р.
Вебинары можно приобрести в записи. Чтобы узнать подробности, напишите в ватсап по номеру 89252093897

Важно: Мы не являемся сотрудниками лицея ВШЭ (подробнее в разделе «О нас») . Мы не продаём и не распространяем задания, которые будут на реальном экзамене в 2022 году.

Подготовка с репетитором к поступлению В Лицей ВШЭ
Проходные баллы прошлых лет
Тренировочные варианты 2022
Реальные варианты 2021
Тренировочные варианты 2021
Решение демоварианта 2019
Решение демоварианта 2018
Математика 10 класс
Математика 9 класс
Контакты

Важно! Мы не являемся сотрудниками Лицея ВШЭ (подробнее в разделе «о нас»). Никаких реальных вариантов мы не продаем и не распространяем! Подборка заданий и все задания в сборниках составлена нами, реальные задания составлены со слов учеников и публикуются в ознакомительных целях ПОСЛЕ экзамена!

Подготовка к поступлению В Лицей ВШЭ

Как поступить в лицей ВШЭ

Пробуйте себя на вступительных в другие лицеи и школы. Это будет хорошей тренировкой перед поступлением в Лицей ВШЭ и также запасным вариантом. Помните, что поступают всего 17%, каждый год более 1000 человек не поступает в 9 класс. Можно выбрать несколько вариантов из следующих лицеев: Лицей 1535, Лицей Плеханова, Лицей Финансового университета, Школа «Покровский квартал» и множество других достойных лицеев и школ.
Важно регулярно писать пробники в формате вступительных. Многие поступившие в лицей считают это одной из важнейших причин своего поступления. Пробники можно писать дома, выделяя для этого определенное время, либо в более приближенных к экзамену условиях. Это поможет вам скорректировать свою подготовку и понять слабые места.
При подготовке нужно сконцентрироваться на понимании тем, а не на нарешивании определенных задач. Задания ежегодно меняются, а темы остаются неизменными. Задания составлены так, что без понимания их решить будет очень трудно.
Список тем на экзамене:
— орфография (правописание приставок, корней, суффиксов, окончаний, орфограммы на стыке приставки и корня; слитное, раздельное, дефисное написание слов)
— работа с текстом (понимание смысловой и грамматической организации текста);
— морфемика, словообразование, этимология;
— словосочетания, типы связи в словосочетаниях;
— синтаксис и пунктуация (синтаксис простого и сложного предложений, обособленные члены предложения и пунктуация при них, грамматически не связанные члены предложения и пунктуация при них);
— фразеология;
— средства выразительности.
Самая большая проблема на экзамене – мелкие ошибки. Не стоит их недооценивать на пробниках, думая, что на экзамене с вами такого не случится. Ошибки стоит детально прорабатывать, а на экзамене лучше сосредоточиться на решении 6-7 заданий и их тщательной проверке, чем пытаться решить как можно больше.
Экзамен не стоит недооценивать. Экзамен сложный из-за его атмосферы и уровня. Вы будете соревноваться с лучшими учениками Москвы. Конкурс очень большой и нервы выдерживают не у каждого. Готовиться нужно тщательно и сильно заранее (в идеале хотя бы за 3 месяца). Подготовиться к экзамену за 2 недели не получится даже у отличников.

Проходные баллы прошлых лет

В этом списке не учитываются баллы учеников, поступивших по ходатайству. Эти случаи Лицей ВШЭ рассматривает индивидуально.
* Обычный проходной балл в 2019 году 13,5, но по спискам зачисленных можно увидеть, что из резервного списка в Лицей поступили с 11,5 баллами. Основной список Резерв
** Обычный проходной балл в 2019 году на мат. направление был 26, но по спискам зачисленных можно увидеть, что из резервного списка в Лицей поступили с 25 баллами. Основной список Резерв

Тренировочные варианты 2022

*Задания составлены аналогично демовариантам

Реальные варианты 2021

*Задания составлены со слов учеников

Тренировочные варианты 2021

*Задания составлены аналогично демовариантам

направление «Универсальное»

Разбор официальной демоверсии 2019

Разбор официальной демоверсии 2018

Источник

Лицей НИУ ВШЭ

Место в рейтинге школ Москвы

Общая информация по набору

Адрес	Большой Харитоньевский переулок, д. 4 м. Сретенский бульвар
Сайт	https://school.hse.ru//
Рейтинг	2 место (2016 год), 1 место (2017 год), 1 место (2019 год) среди школ Москвы 40 место среди школ России— конкурентоспособность выпускников (2019 год)
Обучение	С 9 по 11 классы
Прием	9, 10 классы (11 возможен добор)
Вступительные экзамены	Математика,русский язык, иностранный язык

Подготовка к поступлению в лицей НИУ ВШЭ с Лицей-гуру

Основное направление – подготовка к поступлению в лицей НИУ «Высшая школа экономики» (ВШЭ).
В рамка курса прорабатываются темы в соответствие со структурой экзамена в ВШЭ:

Уравнения, вычисления — 0,5 балла
Задача на проценты — 0,5 балла
Иррациональные числа и выражения — 0,5 балла
Графики функций — 0,5 балла
Логическая задача — 1 балл
Преобразования — 1 балл
Геометрическая задача — 1 балл
Текстовая задача — 1 балл
Параметры — 2 балла
Нестандартная задача 2 балла

При обучении используются внутренние методички ВШЭ и методички для подготовки к поступлению в ВШЭ, программа углубляется и обогащается за счет материалов из методичек других ведущих математических лицеев, а так же включен разбор большого количества вариантов прошлых лет.

Мы делаем основной упор на понимание тем, а не на натаскивание на определенный тип задач. Ежегодно задачи меняются и предугадать, что будет в этот раз – невозможно. Поэтому мы даем углубленную программу текущего класса с запасом по сложности.

Перед сдачей экзамена в лицей ВШЭ мы очень рекомендуем посещать пробные контрольные раз в месяц или чаще, это один из важнейших аспектов поступления, т.к. тренирует концентрацию, стрессоустойчивость ученика, выявляет проблемные темы и развивает способность рассчитывать время вступительного экзамена.

Т.к в лицей ВШЭ конкурс очень высок, в среднем около 5 – 8 человек на место, желательно выбрать несколько вариантов для поступления – например, школа «Покровский квартал», школа 109, Лицей 1535, Лицей Плеханова, Предуниверситарий МИФИ (1511) и др. Программа поможет подготовиться к поступлению и в эти учебные заведения, а посещение экзаменов так же будет полезно для тренировки.

Очень часто ученики 8-9 классов при написании экзамена в ВШЭ и другие лицеи теряют значительную часть баллов из-за невнимательности и вычислительных ошибок. На наших курсах мы стараемся решить данную проблему за счет домашних заданий с автоматической проверкой на нашей специальной платформе. Когда ученик отправляет домашнюю работу на проверку, ему сразу приходит результат, и он может самостоятельно найти ошибку в задании. Таким образом, развивается навык самопроверки, важный при подготовке к экзамену в Лицей ВШЭ. Каждое домашнее задание по структуре напоминает вступительный вариант экзамена, т.к. включает в себя сразу много тем – на повтор уже пройденных ранее, закрепление текущей темы + логические и текстовые задачи.

История Лицея

Лицей при НИУ ВШЭ открылся совсем недавно, в сентябре 2013 года. Изначально набирали только учеников в 10 класс, затем открылся набор и в 9 класс, а в 2017 году проводился дополнительный набор и в 11 класс. Не смотря на столь юный «возраст» лицей занимает 1 или 2 место в рейтинге школ Москвы последние 4 года.

Учебный процесс

Учебный процесс совсем не похож на стандартный в общеобразовательных школах.

В 9 классе всего две специализации: универсальная и математическая. В универсальной все предметы изучаются на примерно одном уровне углубленности. В математических классах уделяется особое внимание всем естественно-научным предметам: математике, физике, химии, информатике, биологии. Часть предметов ученики могут выбрать для изучения по своему желанию.

В 10 «классах» уже 10 специализаций:

«Экономика и математика»,
«Экономика и социальные науки»,
«Гуманитарные науки»,
«Дизайн»,
«Востоковедение»,
«Информатика, инженерия и математика»,
«Юриспруденция»,
«Психология»,
«Математика»,
«Естественные науки»

«Классах» в кавычках, потому что как таковых классов нет, есть группы по 6-20 человек, которые на каждом предмете разные. Каждый ученик составляет себе индивидуальный план, какие предметы и углубленно или на базовом уровне он хочет изучать. Конечно, есть и обязательные предметы для изучения: математика, русский язык и хотя бы один иностранный язык.

Есть большое количество разнообразных кружков и факультативов: начиная от современных молодежных культур до изучения китайских иероглифов. Но обучение на этих факультативах идет очень серьезное — с учетом посещаемости, сдачей зачетов и экзаменов.

Прием в Лицей НИУ ВШЭ

Прием осуществляется в 9 и 10 классы.

При подаче заявления для поступления его необходимо сопроводить эссе на 400 слов, в котором должен быть ответ на вопрос: «Почему я хочу учиться в лицее НИУ ВШЭ».

Сами вступительные испытания представляют собой комплексный тест из двух этапов. На первом этапе проверяются школьные знания по русскому языку, математике и иностранному языку. На втором этапе проводятся испытания по профильным предметам выбранного направления ( при подаче заявления на поступление можно указать два желаемых профиля).

Еще варианты вступительных экзаменов в лицей НИУ ВШЭ

Лицей-гуру

Курсы по подготовке к экзаменам

Источник

Поступление в лицей НИУ ВШЭ – это заветная мечта многих школьников и их родителей. Но поступить туда не просто, для этого нужно пройти конкурсный отбор, включающий в себя тестирование по профильным предметам, в том числе по математике. Ко мне, как к репетитору по математике и физике, часто обращаются родители абитуриентов с просьбой помочь подготовиться к тестированию по математике в лицей НИУ ВШЭ. В данной статье представлен разбор варианта вступительного тестирования по математике в лицей ВШЭ. Предложите своему ребёнку выполнить данные задания самостоятельно. Узнайте, вдруг ему тоже требуется помощь профессионального репетитора для подготовки к этому вступительному испытанию.

Разбора заданий вступительного тестирования в лицей при ВШЭ

1. Найдите значение выражения

$[ left(4u-4v+frac{v^2}{u}right):left(2-frac{v}{u}right) ]$

при , .

Упростим сперва выражение, находящееся в левых скобках:

$[ 4u-4v+frac{v^2}{u} = frac{4u^2-4uv+v^2}{u} = frac{(2u-v)^2}{u}. ]$

Выражение, стоящее в правых скобках, может быть также преобразовано к виду:

$[ 2-frac{v}{u} = frac{2u-v}{u}. ]$

Тогда после деления результата первого действия на результат второго мы получаем:

$[ frac{(2u-v)^2}{u} : frac{2u-v}{u} = frac{(2u-v)^2cdot u}{ucdot (2u-v)} = 2u-v. ]$

Подставляем в полученное выражение данные из условия. В результате получаем:

2. Вычислите значение выражения:

$[ left(frac{sqrt{2}+sqrt{3}}{sqrt{2}}-frac{sqrt{3}-5}{sqrt{3}}right)cdotfrac{sqrt{30}}{3+5sqrt{2}}. ]$

Начнём с упрощения выражения, стоящего в скобках. Как видите, общий знаменатель равен: . Тогда получается следующее выражение:

$[ frac{sqrt{3}(sqrt{2}+sqrt{3})}{sqrt{6}}-frac{sqrt{2}(sqrt{3}-5)}{sqrt{6}} = ]$

$[ = frac{sqrt{6}+3-sqrt{6}+5sqrt{2}}{sqrt{6}} = frac{3+5sqrt{2}}{sqrt{6}}. ]$

Далее полученные выражение умножаем на дробь, записанную справа от знака умножения:

$[ frac{3+5sqrt{2}}{sqrt{6}}cdot frac{sqrt{30}}{3+5sqrt{2}} = frac{sqrt{5}cdotsqrt{6}}{sqrt{6}} = sqrt{5}. ]$

Пусть искомое число процентов равно . Тогда после уменьшения на процентов останется $frac{100-n}{100}y$ . При этом при уменьшении на 52% получится . Тогда полученные после этих преобразований число равно:

$[ frac{0.48x}{frac{100-n}{100}y}= frac{48x}{(100-n)y}. ]$

По условию это число составляет 240% от исходного числа $frac{x}{y}$ . Следовательно, имеет место уравнение:

$[ frac{48x}{(100-n)y} = 2.4frac{x}{y}. ]$

Так как понятно, что $frac{x}{y}ne 0$ , обе части уравнения можно разделить на $frac{x}{y}$ . Тогда для в результате получаем:

$[ frac{48}{100-n} = 2.4Rightarrow 100-n = 20Leftrightarrow n = 80. ]$

То есть число было уменьшено на 80%.

4. Найдите наибольшее значение функции

$[ y = 6x+5-frac{x^2}{4}. ]$

Представлена квадратичная функция с коэффициентами $a=-frac{1}{4}$ , и . Графиком этой квадратичной функции является парабола. Ветви этой параболы направлены вниз, поскольку коэффициент .

Следовательно, наиболее значение эта функция принимает в вершине соответствующей параболы. Абсцисса вершины параболы вычисляется по формуле:

$[ x_0=-frac{b}{2a} = -frac{6}{2cdotleft(-frac{1}{4}right)} = 12. ]$

Тогда легко находится ордината вершины. Она и будет являться наибольшим значением данной функции:

$[ y_0 = 6x_0+5-frac{x_0^2}{4} = 6cdot 12 +5 -frac{12^2}{4} = 41. ]$

5. Найдите сумму квадратов корней уравнения .

Сперва разделим обе части этого уравнения на 2. Тогда получится следующее уравнение: $x^2+41x+frac{81}{2}=0$ . Зачем мы это сделали? Чтобы коэффициент при стал равен 1.

Теперь можно воспользоваться теоремой Виета. Пусть и — корни данного квадратного уравнения. Тогда имеем:

$[ begin{cases} x_1+x_2=-41 \ x_1x_2 = frac{81}{2}. end{cases} ]$

Умножим на 2 обе части второго уравнения, а в первом уравнении обе части возведём в квадрат и раскроем скобки. В результате получаем:

$[ begin{cases} x_1^2+2x_1x_2+x_2^2= 1681\ 2x_1x_2 = 81. end{cases} ]$

Теперь вычтем почленно второе уравнение системы из первого и в результате получим требуемый ответ:

6, Решите неравенство

$[ frac{3-10x}{sqrt{3-4x-4x^2}}>0. ]$

Начнём с определения области допустимых значений данного неравенства. Известно, что выражение, стоящее в знаменателе дроби, не может быть равно 0, а выражение, стоящее под знаком корня, не может быть отрицательным. Следовательно, область допустимых значений данного неравенства определяется следующим условием: .

Для всех , удовлетворяющих этому условию, исходное неравенство эквивалентно следующему: . Получается, что исходное сложное неравенство эквивалентно следующей системе неравенств:

$[ begin{cases} 3-4x-4x^2> 0\ 3-10x>0. end{cases} ]$

Решаем первое неравенство системы методом интервалов. Второе неравенство решается элементарным образом. В результате приходим к следующей системе:

$[ begin{cases} -frac{3}{2}<x<frac{1}{2}\ x<frac{3}{10}. end{cases} ]$

Ответом к заданию будет пересечение промежутков, служащих решением каждого из неравенств данной системы. Итак, ответ: $xinleft(-frac{3}{2};frac{3}{10}right)$ .

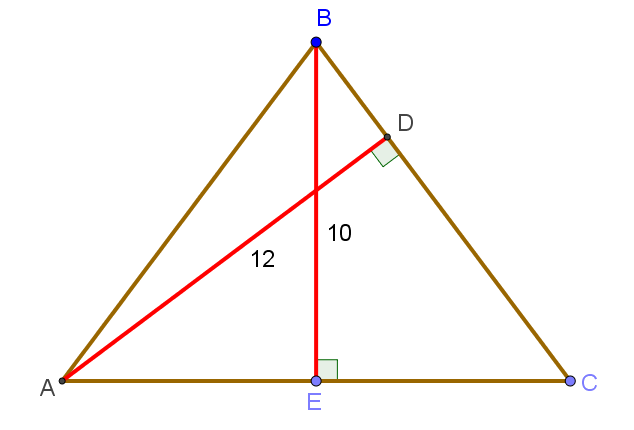
7. Найдите площадь равнобедренного треугольника ABC, если высота, опущенная на основание, равна 10, а высота, опущенная на боковую сторону, равна 12.

Пусть в равнобедренном треугольнике ABC с основанием AC проведена высота BE длиной 10 и высота AD длиной 12:

Введём следующие обозначения. Пусть и . Известно, что площадь треугольника вычисляется путём умножения длины его высоты на половину длины основания, к которому эта высота проведена. Тогда площадь треугольника ABC с одной стороны равна , а с другой стороны — . То есть $a = frac{5}{6}b$ .

Поскольку высота BE проведена в равнобедренном треугольнике ABC к основанию AC, то она является также и медианой этого треугольника. Следовательно, $EC = frac{1}{2}b$ . Тогда по теореме Пифагора для прямоугольного треугольника BEC получаем:

$[ 10^2+left(frac{b}{2}right)^2 = a^2Leftrightarrow 400 + b^2 = 4a^2. ]$

С учётом найденной ранее связи между и получаем:

$[ 400 + b^2 = 4timesleft(frac{5}{6}bright)^2Rightarrow b = 15. ]$

Тогда искомая площадь треугольника равна 75.

Пусть разность данной арифметической прогрессии равна . Обращаем сразу внимание на то, что третий член арифметической прогрессии получается вычитанием удвоенной разности этой прогрессии из пятого её члена. В cвою очередь, седьмой член арифметической прогрессии получается добавлением удвоенной разности этой прогрессии к пятому её члену.

Аналогично, девятый член арифметической прогрессии получается вычитанием удвоенной разности этой прогрессии из одиннадцатого её члена. А тринадцатый член арифметической прогрессии получается добавлением удвоенной разности этой прогрессии к одиннадцатому её члену.

С учётом этих обстоятельств получаем:

$[ a_3+a_7+a_9+a_{13} = a_5-2d+a_5+2d+ ]$

$[ + a_{11}-2d+a_{11}+2d =2(a_5+a_{11}) = 30. ]$

9. Из пункта А в пункт В выехал велосипедист, который приедет в В через 2 часа, одновременно с ним из В в А вышел пешеход, который придет в А через 6 часов. Через какое время они встретятся?

Здесь в варианте вступительного тестирования по математике в лицей ВШЭ предлагается решить задачу на движение. Пусть скорость пешехода равна . Тогда скорость велосипедиста равна , ведь он движется в 3 раза быстрее пешехода. Тогда скорость сближения велосипедиста и пешехода равна , что в 4 раза больше скорости пешехода. Значит, в сумме они преодолеют расстояние от A к В (то есть встретятся), спустя промежуток времени, который в четыре раза меньше того времени, которое требуется пешеходу, чтобы дойти из пункта A в пункт B. То есть через $frac{6}{4} = 1.5$ часа.

10. Взяли 5 листов бумаги, один из них разрезали на 5 частей, один из полученных снова на 5 и так далее. Какое число листов можно таким образом получить? 2015, 2016, 2017 или 2018?

Если записать в ряд количество листков, которые получаются в результате всех этих действий на каждой итерации, то получится арифметическая прогрессия с разностью 4. Значит, может получиться только число, которое при уменьшении на 5 делилось бы нацело на 4. Из всех предложенных это число 2017.

Задание с полным решением из вступительного экзамена в лицей НИУ ВШЭ

Дано уравнение .

а) Найдите наименьшее целое значение параметра , при котором уравнение имеет корни разных знаков.

Начнём с того, что параметр , в противном случае уравнение имело бы только один корень. Разделим обе части уравнения на . В результате приходим у следующему уравнению:

$[ x^2-frac{3}{p+4}x+frac{p}{p+4} = 0. ]$

Как узнать при каких значениях корни этого уравнения будут различны по знаку? Нужно вспомнить, что графиком соответствующей квадратичной функции является парабола, ветви которой направлены вверх. Причём эта парабола пересекает вертикальную ось в точке с ординатой $c=frac{p}{p+4}$ . Следовательно, корни будут различны по знаку, если свободный член отрицателен. То есть имеет место неравенство:

$[ frac{p}{p+4}<0Leftrightarrow pin(-4;0). ]$

Итак, наименьшее целое значение из полученного промежутка — это число -3.

б) Найдите длину промежутка, в который может попасть значение параметра , чтобы уравнение имело хотя бы один корень.

Полученное нами уравнение имеет два корня в том случае, если его дискриминант положителен, то есть выполнено неравенство:

$[ left(-frac{3}{p+4}right)^2-frac{4p}{p+4}>0Leftrightarrow frac{9-4p(p+4)}{(p+4)^2}>0. ]$

Последнее неравенство выполняется при $pinleft(-frac{9}{2};-4right)cup left(-4;frac{1}{2}right)$ .

Один корень будет, когда дискриминант равен нулю, то есть при $p=-frac{9}{2}$ и $p=frac{1}{2}$ , а также при , поскольку в этом случае уравнение становится линейным.

Из всего вышесказанного заключаем, что промежуток, в который может попасть значение параметра , чтобы уравнение имело хотя бы один корень, — это промежуток $left[-frac{9}{2};frac{1}{2}right]$ . Длина этого промежутка равна $frac{1}{2}-left(-frac{9}{2}right) = 5$ .

в) Найдите сумму всех значений , при которых уравнение имеет ровно 1 корень.

Корень будет один, если , и когда дискриминант равен 0, то есть при $p=frac{1}{2}$ и $p=-frac{9}{2}$ . Тогда искомая сумма равна -8.

Телефон репетитора для подготовки к вступительному тестированию по математике в лицей НИУ ВШЭ, Сергея Валерьевича

Сайт для подготовки к вступительному тесту по математике в лицей ВШЭ

Понравилась статья? Возможно, вам будет интересна также следующая:

Разбор комплексного теста по математике в лицей ВШЭ

Источник

Лицей НИУ ВШЭ

Общая информация по набору

Последние новости по набору

Подготовка к поступлению в лицей НИУ ВШЭ с Лицей-гуру

История Лицея

Учебный процесс

Прием в Лицей НИУ ВШЭ

Еще варианты вступительных экзаменов в лицей НИУ ВШЭ

Лицей-гуру

Курсы по подготовке к экзаменам

Разбора заданий вступительного тестирования в лицей при ВШЭ

Задание с полным решением из вступительного экзамена в лицей НИУ ВШЭ