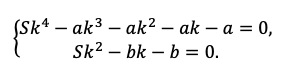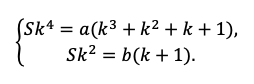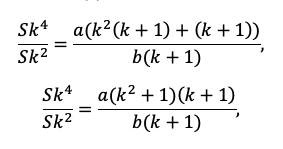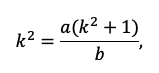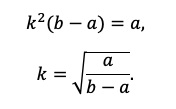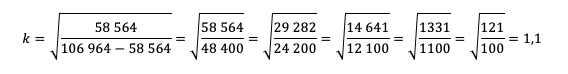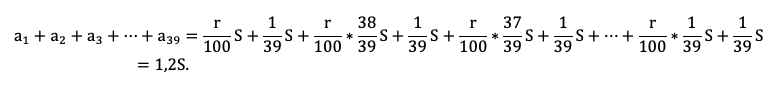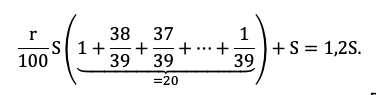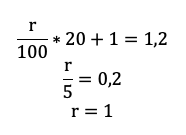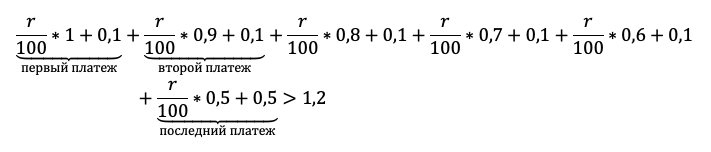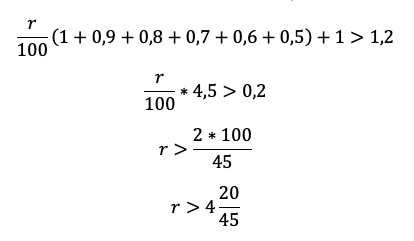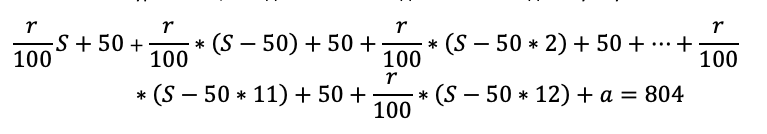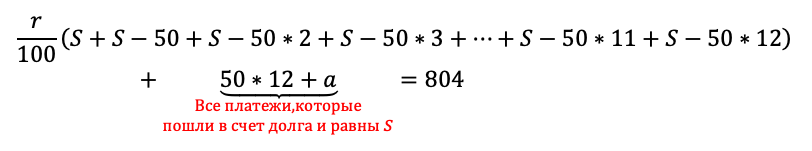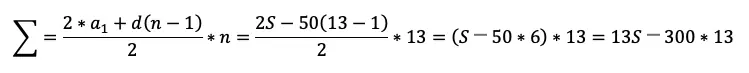Яковлев экономические задачи егэ

• Что будет на марафоне

• В программе Марафона:

• Как занимаемся?

• А теперь – 3 лайфхака решения задачи 15

• Онлайн-курсы:

Марафон по «Экономическим» + Лайфхаки по задаче 15 в письме!

Приветствуем, дорогие старшеклассники!

Кто хочет научиться решать любые «экономические» задачи? Читаем в письме о лайфхаках для их решения. И регистрируемся на наш Марафон! Сейчас действует специальная скидка!

ЗАРЕГИСТРИРОВАТЬСЯ

к оглавлению ▴

Что будет на марафоне

Марафон по «экономической» задаче № 15. 3 дня по 3 часа.

9, 11, 12 февраля. С 13 до 16 часов по московскому времени.

Эта задача оценивается в 2 первичных балла. И на ЕГЭ надо решить ее без ошибок!

Хорошая новость: задачи 15 на ЕГЭ довольно стандартны. На Марафоне научим решать все типы задач 15!

Плохая новость: в задаче 15 приходится много считать без калькулятора. На Марафоне будем учиться упрощать вычисления везде, где только возможно.

к оглавлению ▴

В программе Марафона:

1. «Экономические» задачи. Первый тип задач на кредиты.

2. «Экономические» задачи. Второй тип задач на кредиты (да, их всего два типа!). Вывод формулы для переплаты – обязательно.

3. Комбинированные задачи (оба типа в одной).

4. «Экономические» задачи на оптимальный выбор, в том числе с применением производной.

5. Приемы быстрого счета в экономических задачах. Как обойтись без сложных «столбиков»?

6. И главное. Будем учиться грамотному оформлению решений.

В общем, все, что нужно, чтобы гарантированно получить за задачу 15 полный балл на ЕГЭ по математике.

Решим не менее 40 задач № 15. Это больше, чем вы сможете сами за месяц учебы.

Каждый день – домашнее задание. На следующий день – разбор и новые задачи.

к оглавлению ▴

Как занимаемся?

Работаем на нашей онлайн-платформе.

Она специально разработана программистами ЕГЭ-Студии для качественного онлайн-обучения.

Это не Zoom, где вы видите только голову преподавателя. Это трансляции из нашей ЕГЭ-Студии. Полный эффект присутствия на реальном уроке!

Каждый день мы будем начинать с основных моментов теории.

Перед началом марафона, 14 марта, мы разместим в нашей Онлайн-системе Теоретический материал, который надо прочитать, и первый тест, который надо пройти.

Будем решать задачи. Много задач. Это главное. Разберем все непонятные моменты.

Вы получите образцы правильного решения задачи 15.

Будут ДЗ и контрольные.

И на следующий день разбор этих контрольных.

Мы создадим специальную группу в WhatsApp, где каждый из вас сможет задать вопрос по любой задаче 15 Профильного ЕГЭ.

Как всегда, будет видеозапись занятий. Если что-то непонятно — можно будет позже посмотреть еще раз и задать вопросы.

Вы можете задавать вопросы или предлагать свое решение задачи! Можно общаться, как в настоящем школьном классе.

Марафон ведет преподаватель ЕГЭ-Студии с опытом работы более 20 лет Александр Еремеевич Нижарадзе. Методика и подбор задач – Анна Малкова.

Не пропусти Марафон!

к оглавлению ▴

А теперь – 3 лайфхака решения задачи 15

1. Есть всего две схемы решения задач на кредиты.

Первая схема: кредит погашается равными платежами (аннуитет). Или дана информация о платежах.

Вторая схема: равномерно (или известным образом) уменьшается сумма долга. Это схема с дифференцированными платежами.

В задачах первого типа обычно применяется формула для суммы геометрической прогрессии. В задачах второго типа – формула суммы арифметической прогрессии.

И первое, что надо сделать, когда решаете «экономическую» задачу, – определить, к какому типу она относится.

2. Есть отличная формула для величины переплаты по кредиту (в задачах второго типа, с дифференцированными платежами):

Здесь р – процент, начисляемый банком, n – количество платежных периодов, П – величина переплаты, S – сумма долга.

Конечно, на ЕГЭ формулу лучше вывести. На Марафоне выведем!

3. Основная сложность задачи 15 – вычисления. Например, в условии дано, что банк начисляет 12,5 процентов годовых. Тогда долг увеличивается в k=1,125 раза. А если надо посчитать k в квадрате или в четвертой степени? Откроем секрет: проще записать эту дробь как обыкновенную, то есть 1,125 = 9/8. И сразу станет проще! Возможно, и вычисления «в столбик» не понадобятся.

Остальные лайфхаки – на Марафоне по «экономическим» задачам.

к оглавлению ▴

Онлайн-курсы:

Когда нужна выстроенная, проверенная программа подготовки с опытными преподавателями. Кому нужна подготовка здесь и сейчас. С нуля до самых сложных тем. Есть учебник, тренажер задач, еженедельные онлайн-занятия и много всего! Оформите бесплатный демодоступ. Подготовка по предметам:

Математика

Физика

Информатика

Русский

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице ««Экономические» задачи на ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из Рубрики: Новости.

Публикация обновлена:
10.03.2023

Мы используем файлы cookie, чтобы персонализировать контент, адаптировать и оценивать результативность рекламы, а также обеспечить безопасность. Перейдя на сайт, вы соглашаетесь с использованием файлов cookie.

• Главная

  
  

• Теория ЕГЭ

  
  

• Математика — теория ЕГЭ

  
  

• 
  Экономические задачи повышенного уровня сложности ЕГЭ по математике

Экономические задачи повышенного уровня сложности ЕГЭ по математике

02.03.2016

Замечательное краткое пособие по теме экономических задач.

В методичке приведена необходимая теория, а так же рассмотрены основные типы экономических задач, которые встречаются в ЕГЭ по математике.

Кулабухов Сергей Юрьевич

Смотреть в PDF:

Или прямо сейчас: cкачать в pdf файле.

Сохранить ссылку:

Комментарии (1)
Добавить комментарий

Комментарии  

0


#1
андрей
01.03.2017 02:15

С праздником Весны

Цитировать

Обновить список комментариев

Добавить комментарий

Комментарии без регистрации. Несодержательные сообщения удаляются.

Имя (обязательное)

E-Mail

Подписаться на уведомления о новых комментариях

Отправить

Курс ведёт: Андрей Юрьевич Иванов, кандидат технических наук, преподаватель ЧОУ «Школа Экспресс» Санкт-Петербурга.

Задания №15 в ЕГЭ-2023 по математике профильного уровня — «экономические» задачи на вклады, проценты, кредиты, оптимизацию (номер задания тот же, что и в ЕГЭ-2022). Нумерация выпусков продолжает порядок разборов 2022 года.

Уровень сложности 2 (из 3).

Ответом к заданию является развернутый ответ (полная запись решения с обоснованием выполненных действий).

Как эффективно работать с видеоразборами

№ 5. Решение задачи о кредитах (банковских процентах).

Методика комплексного анализа и выбор оптимального решения. Время решения 13 — 15 минут.

№ 6. Решение задачи о кредитах (банковских процентах).

Методика комплексного анализа и выбор оптимального решения. Время решения 9 — 11 минут.

---

В части с развернутым ответом в ЕГЭ по профильной математике есть уникальный номер, к которому школьник почти готов сразу после освоения материала для первых 12-ти заданий. Речь об экономической задаче под номером 17 в ЕГЭ по математике. Конечно, поготовиться придется, но, если повезет с прототипом, баллы можно урвать почти даром!

Прототипы для 17-го номера делятся на три большие группы: 

• банковские задачи, 
• на ценные бумаги,
• задачи на оптимальный выбор. 

В этой статье мы расскажем, как научить ученика структурировать условие любой банковской задачи, как составить по этим данным математическую модель и найти решение. Расскажем, на что обратить внимание ученика, чтобы школьник не потерял баллы из-за неверного оформления.

Главная трудность — школьник плохо понимает условие, ведь с кредитами и вкладами он пока не сталкивался.

• Как работает процент по кредиту?
• На какую сумму начисляется?
• Из каких частей состоит платеж?
• Как уменьшается долг?

На все эти вопросы вам придется ответить. Это отличная возможность показать пользу уроков математики, ведь 17-ый номер — едва ли не самая прикладная задача за весь школьный курс! 

Например, можно рассказать о том, какие бывают образовательные кредиты. Вы в курсе, что их дают с 14 лет, а платеж первые годы может быть ничтожным? Школьник об этом точно не знает.

С чего начать разбор экономической (банковской) задачи в ЕГЭ по математике

Экзамен немного утрирует реальную ситуацию, в жизни кредит работает сложнее. Однако грустно упускать возможность рассказать школьнику что-то из реальности! Если у вас есть опыт с кредитованием, самое время им поделиться. Если нет, то воспользуйтесь нашим:

• Например, расскажите, что клиенту придется сверх купить страховку на случай потери работоспособности, ведь банк не хочет терять прибыль даже если на заемщика кирпич упадет. Ваши ученики знают, как работает страховка?
• Расскажите о механизме аннуитетного платежа: как часть денег банк забирает себе в качестве дохода, то есть на погашение процентов за пользование кредитом; а на вторую часть уменьшает ваш долг. В реальности это разделение считается по специальной формуле, и совсем не в пользу заемщика.
• Например, по нашему опыту, в ипотеке на 10 лет из 20 тысяч ежемесячного платежа на первых порах всего 5 000 рублей идет в счет уменьшения долга, а 15 000 — забирает себе банк! Но каждый раз платеж чуть ребалансируется, и в счет долга идет чуть больше. Так в последних платежах через 10 лет в счет процентов идет буквально пара сотен, а все остальное гасит долг. 

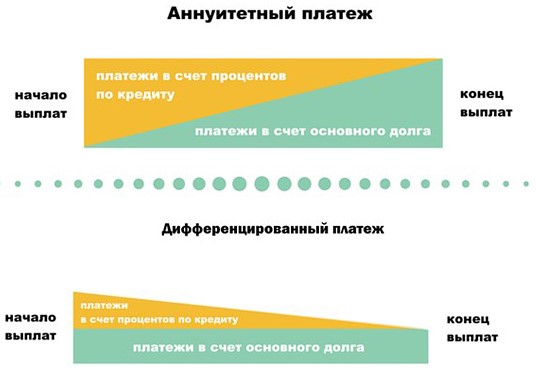
Хорошая новость в том, что в экзаменационных задачах подобной вакханалии не бывает. Долг и проценты или гасятся равномерно, или по заранее известному алгоритму, достаточно просто внимательно прочитать условие.

Еще одно частое упрощение в ЕГЭ — процент там обычно не годовой, а ежемесячный! То есть своим платежом заемщик гасит набежавший за этот месяц процент и уменьшает долг на заданную величину. Удобно.

Мы предлагаем научить школьника упорядочивать данные банковской задачи в ЕГЭ по математике с помощью таблицы. Табличка — не единственный способ решить 17-ый номер, кто-то использует последовательности, кто-то — считает прикладным методом как заправский бухгалтер. Однако наш метод универсален, а значит вы дадите школьнику один алгоритм на все типы банковских задач. Согласитесь, работать с одним алгоритмом проще, чем подбирать разные по ситуации.

Тип 1. Равные платежи

Особенность этого типа заданий в том, что заемщик всегда вносит одинаковые суммы.

В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r.

Очевидно, что эта схема должна оказаться у школьника в тетради. Ведь вы же знаете: того, чего нет в тетради, и на уроке-то не было!

Заполняем всю табличку. Учитываем обе ситуации из условия. Для наглядности каждую выделим жирной рамкой.

Теперь остался еще один непростой шаг — перейти от структурированных данных к математической модели. Дайте ученику возможность увидеть, что уже почти составил ее.

Мы получили два уравнения, которые подсветили в табличке оранжевым. Объединим их в систему и решим!

Напомните выпускнику о культуре вычислений! Порой эти задачи составлены так, что неудачная последовательность действий сделает их нерешаемыми без калькулятора. Потому не надо спешить делать первое попавшееся действие, пусть школьник тренируется думать на пару ходов вперед.

Например, разделим одно уравнение на другое, ведь так мы избавимся от одной неизвестной S:

Наше решение не зависит от суммы кредита, S сокращается. 

По сути, мы получили уравнение с одной неизвестной, ведь платежи a и b знаем из условия. Выразим k:

Пожалуй, все, проще уже некуда. Подставляем значения!   

Тут можно обратить внимание ученика на то, как составители экзамена на самом деле заботятся о нем! Ведь будь задачка хоть чуть-чуть другой, посчитать без калькулятора было бы невозможно.

Вспоминаем, что k=1+r/100, а найти нам надо r.

Ответ: 10%.

Не забудьте после решения расставить акценты в задаче:

Чтобы решить задачу и получить 3 балла, мы:
— Воспользовались простым алгоритмом упорядочивания данных,
— Составили математическую модель,
— Нашли удобный способ решить ее, ВСЕ!
Это и есть алгоритм решения банковской задачи.

Тип 2. Равномерно убывающий долг

В прошлой задаче заемщик платил одинаковую сумму каждый месяц. Тут ему нужно уменьшать долг на одну и ту же величину. То есть за месяц пользования деньгами банк начислил на них процент, клиент теперь должен чуть больше. Своим платежом он оплатит банку проценты, чтобы заем стал таким, как ДО их начисления. А сверху внесет сумму, которая как раз и пойдет на то самое РАВНОМЕРНОЕ уменьшение долга.  

15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
(Считайте, что округления при вычислении платежей не производятся.)

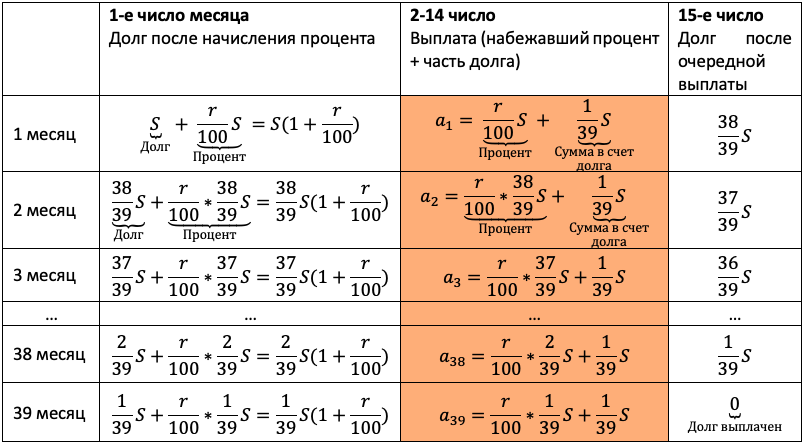
Тут главный элемент в задаче — равномерно убывающий долг. Если мы взяли сумму S на 39 месяцев, и каждый месяц долг должен быть меньше на одинаковую величину, то что это за величина? Пусть правильный ответ 1/39 S даст ученик.

Проиллюстрируйте школьнику, как здорово работает наш алгоритм. Пусть выпускник проговаривает пункты вслух, а вы их выполняйте. Следите, чтобы каждый шаг подопечный фиксировал в тетради:

Продолжаем заполнять табличку. Пусть дальше пробует выпускник, ведь пока сам не попробуешь, не научишься:

Осталось увязать добытую информацию в уравнение или неравенство. Обратите внимание подопечного на то, что ненужных подробностей в задачах ЕГЭ не бывает! Единственная информация в задаче, которую мы до сих пор не использовали — общая сумма выплат. По условию она на 20% больше суммы кредита, то есть равна 1,2S:

Приведем подобные, вынесем общий множитель за скобку:

Решение в итоге снова не зависит от того, какую сумму взяли в долг. Разделим обе части на S и упростим выражение:

Ответ: 1%.

И снова все по нашему алгоритму, ничего нового, кроме него, мы не используем! Не забудьте излучать восторг, иначе школьник не проникнется мощью вашего метода решения.

Тип 3. Долг, убывающий согласно табличке

Задача похожа на прошлую. Разница лишь в том, что кроме процентов нам каждый месяц придется гасить не равную долю долга, а долю согласно таблице.

15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг(в млн рублей)	1	0,9	0,8	0,7	0,6	0,5	0

Найдите наименьшее значение r, при котором общая сумма выплат будет больше 1,2 млн рублей.

Протестируем нашу универсальную табличку в третий раз, доверьте это непростое занятие школьнику. Пусть процессом командует он! По ответам будет ясно, ловит ли он суть.

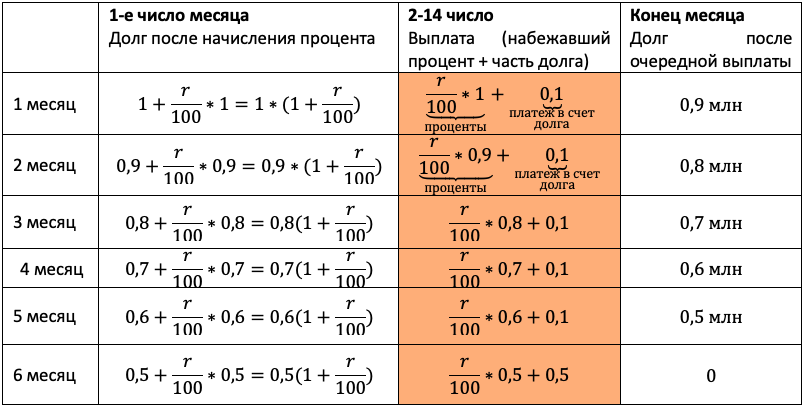
Отличие от прошлого типа будет лишь в том, что в третий столбец мы будем записывать не равномерно убывающий долг, а перенесем остаток долга из таблицы условия. Чтобы не таскать по решению нули, считать будем в миллионах:

Чтобы долг убывал согласно табличке, нам снова каждый раз придется гасить набежавшие проценты и первые 5 месяцев добавлять сверху 0,1 млн. После останется погасить весь остаток.

Акцентируйте внимание на механизме погашения, для школьника он не всегда очевиден.

«По условию нам снова дана общая сумма выплат, значит достаточно просуммировать оранжевый столбец, и уравнение готово», — вероятно, подумает школьник. Подловите его! Уравнение в этой задаче — прямой путь потерять балл! Сумма выплат должна быть БОЛЬШЕ 1,2 млн. Отразим это в модели с помощью неравенства:

Подопечный должен быть уверен в каждом символе в бланке ответа. Даже не пригодившиеся промежуточные вычисления с ошибкой приведут к катастрофе.

Приведем подобные и вынесем общие множители за скобку:

Последний шаг – не забыть, что по условию процент должен быть целым и округлить в верную сторону.

Ответ: 5%.

Правильная математическая модель — это суперважно! К ней проверяющие обязательно придерутся.

Тип 4. Погашение кредита в два этапа.

По сути, это та же прошлая задача, но месяцев больше

В 2017-2018 учебном году составителей экзамена посетило вдохновение, на свет родился вот этот тип банковских задач. Школьники были в шоке, и от страха завалили 17-ый номер. Хотя всего-то нужно было догадаться воспользоваться знаниями об арифметической прогрессии и достать из условия одно немного неочевидное дано!

15-го декабря планируется взять кредит в банке на 13 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 12-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 13-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 804 тысячи рублей?

И снова пусть по возможности командует школьник. По крайней мере он уже точно в курсе, что происходит первые 13 месяцев.

Последовательно начисляем процент на остаток долга – считаем выплату – фиксируем остаток долга после выплаты. Сумму кредита возьмем за S.

Научите школьника не спешить с вычислениями. Например, вместо того чтобы написать S-600, мы пишем S-50*12, потому что так удобнее: нам сразу ясно, что речь идет о двенадцатом месяце. Да и потом вычисления будут проще, если мы оставим маленькие числа.

Осталось составить уравнение, и модель готова. В задаче нам снова дали сумму всех выплат:

Как обычно, сгруппируем отдельно слагаемые с r/100, отдельно слагаемые без них:

Вот именно последняя группировка всех платежей в счет долга и оказалась неочевидной. Без нее в задаче остается одна лишняя неизвестная величина, которая рушит все решение.

Осталось привести уравнение к решаемому виду. Для этого надо просуммировать то, что получилось в скобках. Если внимательно приглядеться, то видно, что это сумма арифметической прогрессии:

Посчитаем эту сумму:

Подставляем выражение для суммы в уравнение, заметим, что по условию r=2:

Мы сокращали дробь, пока это было возможно, и в итоге довольно просто получили ответ даже без калькулятора. Ваш подопечный должен научиться также!

Ответ: 700 тысяч.

Зачем использовать формулу суммы прогрессии, если можно посчитать вручную? Все верно, можно. Но это только в данном случае кредит взяли всего на 13 месяцев. А бывают прототипы, когда срок – 21 и больше месяцев. В какой-то момент считать вручную станет совсем долго и неудобно, потому воспользоваться формулой суммы – более универсальный метод.

Чем закончить разбор экономической (банковской) задачи № 17 в ЕГЭ по математике

Чтобы у ученика окончательно сложилась картинка занятия, пробегитесь еще раз по основным выводам:

• Повторите алгоритм заполнения таблицы и решения задачи (да, пятый раз);
• Повторите типы задач и механизм распределения платежа на проценты и долг;
• Напомните, как важно считать культурно и быть уверенным в каждой циферке в бланке;
• Проговорите, что математическая модель должна точно отражать условие задачи.

Как показывает практика, чем больше повторяешь, тем больше шансов, что в голове выпускника останется хоть что-то.

За что дают баллы?

Знание критериев оценивания экономической (банковской) задачи № 17 в ЕГЭ по математике поможетученику чувствовать себя увереннее, ведь выставление баллов — это не какая-то магия и не вредность экспертов. Все правила игры прописаны в нормативных документах.

17-ый номер стоит 3 балла. Чтобы узнать, как их присуждают, мы залезли в методические рекомендации для членов предметных комиссий.

Согласно пояснениям из документа, для получения одного балла мало просто обоснованно составить математическую модель по задаче, надо предложить правильный метод ее анализа. 

Два балла получит школьник, который ошибся в вычислениях или не обосновал появление математической модели в решении. Например, согласно методическим рекомендациям, решение на 2 балла выглядит так:

А вот отсутствие промежуточных вычислений хоть и усложняет проверку, но баллы не снимает.

Идеально выполненная первая часть ЕГЭ по профильной математике принесет школьнику всего 62 тестовых балла. Добавим сюда пару ошибок по невнимательности, и останутся совсем крохи — баллов 50, не больше. Для поступления на бюджет мало, а значит необходимо планировать делать вторую часть! Чем раньше школьник это осознает, тем проще будет с ним работать. А банковская задача поможет получить дополнительные баллы с минимальными усилиями.

Однако кредиты – не единственный прототип 17-го номера, и в следующий раз мы расскажем, как научить школьника решать задачи на оптимальный выбор и ценные бумаги.