3 июня 2022
В закладки
Обсудить
Жалоба
Вариант собран по заданиям прошедшего ЕГЭ 2 июня.
Ответы прилагаются.
rm-ege2022-pro.pdf
Каждое из заданий 1–11 считается выполненными верно, если экзаменуемый дал верный ответ в виде целого числа или конечной десятичной дроби. Каждое верно выполненное задание оценивается 1 баллом.
Каждое из заданий 12–18 считается выполненными верно, если экзаменуемый дал верный ответ и предоставил обоснованное решение. Задания 12, 14, 15 оценивается 2 баллами, задания 13, 16 – 3 баллами, 17, 18 – 4 баллами соответственно. При неточностях баллы могут быть снижены.
Источник: yagubov.ru
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.
Варианты составлены в соответствии с демоверсией 2023 года
Тренировочные варианты ЕГЭ 2023 по математике (профиль)
| vk.com/pezhirovschool | |
| Вариант 1 | решения |
| Вариант 2 | решения |
| Вариант 3 | решения |
| Вариант 4 | решения |
| Вариант 5 (с ответами) | |
| Вариант 6 (с ответами) | |
| Вариант 7 (с ответами) | |
| Вариант 8 (с ответами) | |
| egemath.ru | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| вариант 12 | скачать |
| вариант 13 | скачать |
| вариант 14 | скачать |
| вариант 15 | скачать |
| вариант 16 | скачать |
| вариант 17 | скачать |
| вариант 18 | скачать |
| вариант 19 | скачать |
| вариант 20 | скачать |
| time4math.ru | |
| вариант 1-2 | ответы |
| вариант 3-4 | ответы |
| вариант 5-6 | ответы |
| вариант 7-8 | |
| yagubov.ru | |
| вариант 33 (сентябрь) | ege2023-yagubov-prof-var33 |
| вариант 34 (октябрь) | ege2023-yagubov-prof-var34 |
| вариант 35 (ноябрь) | ege2023-yagubov-prof-var35 |
| вариант 36 (декабрь) | ege2023-yagubov-prof-var36 |
| вариант 37 (январь) | ege2023-yagubov-prof-var37 |
| вариант 38 (февраль) | ege2023-yagubov-prof-var38 |
| math100.ru (с ответами) | |
| variant 179 | скачать |
| variant 180 | скачать |
| variant 181 | скачать |
| variant 182 | скачать |
| variant 183 | скачать |
| variant 184 | скачать |
| variant 185 | скачать |
| variant 186 | скачать |
| variant 187 | скачать |
| variant 188 | скачать |
| variant 189 | скачать |
| variant 190 | скачать |
| variant 191 | скачать |
| variant 192 | скачать |
| variant 193 | скачать |
| variant 194 | скачать |
| variant 195 | скачать |
| variant 196 | скачать |
| variant 197 | скачать |
| variant 198 | скачать |
| variant 199 | скачать |
| variant 200 | скачать |
| variant 201 | скачать |
| variant 202 | скачать |
| variant 203 | скачать |
| variant 204 | скачать |
| variant 205 | скачать |
| alexlarin.net | |
| Вариант 397 | проверить ответы |
| Вариант 398 | проверить ответы |
| Вариант 399 | проверить ответы |
| Вариант 400 | проверить ответы |
| Вариант 401 | проверить ответы |
| Вариант 402 | проверить ответы |
| Вариант 403 | проверить ответы |
| Вариант 404 | проверить ответы |
| Вариант 405 | проверить ответы |
| Вариант 406 | проверить ответы |
| Вариант 407 | проверить ответы |
| Вариант 408 | проверить ответы |
| Вариант 409 | проверить ответы |
| Вариант 410 | проверить ответы |
| Вариант 411 | проверить ответы |
| Вариант 412 | проверить ответы |
| Вариант 413 | проверить ответы |
| vk.com/ege100ballov | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| vk.com/math.studying | |
| Вариант 1 | ответы |
| vk.com/marsel_tutor | |
| Вариант 1 | разбор |
| Вариант 2 | конспект / разбор |
| Вариант 3 | конспект / разбор |
| Вариант 4 | конспект / разбор |
| Вариант 5 | конспект / разбор |
| Вариант 6 | разбор |
| vk.com/shkolkovo_easy_math | |
| Вариант 1 | решение |
| Вариант 2 | решение |
| Вариант 3 | решение |
| Вариант 5 | решение |
| Вариант 6 | решение |
| vk.com/mathlearn_ru | |
| вариант 1 | разбор |
| vk.com/ekaterina_chekmareva | |
| Вариант 1 | ответы |
| Вариант 2 | ответы |
| Вариант 3 | ответы |
| Вариант 4 | ответы |
| Вариант 5 | ответы |
| Вариант 6 | ответы |
| Вариант 7 | ответы |
| Вариант 8 | ответы |
Структура варианта КИМ ЕГЭ 2023 по математике профильного уровня
Экзаменационная работа состоит из двух частей и включает в себя 18 заданий, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях. Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Задания части 1 предназначены для определения математических компетентностей выпускников образовательных организаций, реализующих программы среднего (полного) общего образования на базовом уровне. Задание с кратким ответом (1–11) считается выполненным, если в бланке ответов № 1 зафиксирован верный ответ в виде целого числа или конечной десятичной дроби.
Задания 12–18 с развёрнутым ответом, в числе которых 5 заданий повышенного уровня и 2 задания высокого уровня сложности, предназначены для более точной дифференциации абитуриентов вузов.
Примеры заданий:
1. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 22 спортсмена из России, в том числе Игорь Чаев. Найдите вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России.
2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу
3. На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?
в) Найдите наибольшее возможное значение суммы получившихся чисел.
Смотрите также:
Тренировочные варианты профильного ЕГЭ 2023 по математике с ответами.
Математика 36 вариантов ЕГЭ 2023 ФИПИ школе Ященко профильный уровень 🔥
Таблица соответствия заданий ЕГЭ 2023 по математике профильного уровня по сравнению с ЕГЭ 2022
Федеральный институт ПИ в очередной раз славно потрудился и порадовал изменениями номеров заданий первой части в ЕГЭ по профильной математике.
Цитата от ФИПИ:
«В структуру части 1 КИМ внесены изменения, позволяющие участнику экзамена более эффективно организовать работу над заданиями за счет перегруппировки заданий по тематическим блокам…».
Итак, «новое» от перегруппировщиков:
| 2023 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 2022 | 3 | 5 | 2 | 10 | 1 | 4 | 6 | 7 | 8 | 9 | 11 |
| Планиметрия | Стереометрия | Вероятность | Вероятность | Уравнения | Выражения | Смысл производной | Прикладная физическая | Текстовая | График функции | Исследование функции |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Уравнения | Стереометря | Неравенства | Экономическая | Планиметрия | Параметры | Числа и их свойства |
Планируемые изменения в КИМ ЕГЭ 2023 года
Планируемые изменения в КИМ ЕГЭ 2023 года
Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2023 года по МАТЕМАТИКЕ Профильный уровень
ФИПИ Демовариант по математике профиль ЕГЭ 2023 года
Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2023 года по Русскому языку
ФИПИ Демовариант по Русскому языку ЕГЭ 2023 года Проект
Критерии оценивания ЕГЭ для апелляции
Критерии оценивания 2 части ЕГЭ по математике профильного уровня ФИПИ

ЕГЭ по математике 2022 основная волна 02.06.2022
Решение заданий вариантов ЕГЭ по математике профильного уровня основной волны 2 июня 2022 года
ОГЭ по математике 2022
Решение заданий вариантов ОГЭ по математике основной волны 23 мая 2022 года
Досрочный ЕГЭ по математике 2022
Решение заданий вариантов досрочного ЕГЭ по математике основной волны профильного уровня 18 марта 2022 года
Математика 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко профильный уровень
Математика 50 вариантов заданий ЕГЭ 2022 Ященко
Таблица соответствия заданий ЕГЭ 2022 профильного уровня по сравнению с ЕГЭ 2021
| Стало | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Было | 5 | 4 | 6 | 9 | 8 | 7 | 10 | 11 | — | 4 | 12 | 13 | 14 | 15 | 17 | 16 | 18 | 19 |
| Баллы | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 3 | 2 | 2 | 3 | 4 | 4 |
Демонстрационный вариант ЕГЭ 2022 года ФИПИ КИМ по математике профильного уровня (Проект). Критерии, ответы
Решение заданий демонстрационного варианта ЕГЭ 2022 года ФИПИ по математике профильного уровня

Демонстрационный вариант ЕГЭ 2022 года ФИПИ КИМ по математике базового уровня (Проект). Ответы

ЕГЭ по математике профильного уровня 07.06.2021 основная волна
Решение заданий вариантов ЕГЭ по математике 2021 года основной волны профильного уровня 7 июня
ЕГЭ по математике 2021 профильного уровня резервный день
Решение заданий вариантов ЕГЭ по математике 2021 года резервного дня
Открытые варианты КИМ ЕГЭ 2021
Открытый вариант КИМ ЕГЭ по математике 2021 (профильная)

Решение открытого варианта КИМ ЕГЭ по математике 2021 (профильного уровня) ФИПИ
Открытый вариант КИМ ЕГЭ по русскому языку 2021

Открытый вариант КИМ ЕГЭ по физике 2021

Открытый вариант КИМ ЕГЭ по информатике 2021

Открытый вариант КИМ ЕГЭ по обществознанию 2021

Математика 50 вариантов заданий ЕГЭ 2021 Ященко
Математика 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко профильный уровень
Демонстрационный вариант ЕГЭ 2021 года ФИПИ КИМ по математике профильного уровня (Проект). Критерии, ответы

Решение заданий демонстрационного варианта ЕГЭ 2021 года ФИПИ по математике профильного уровня
Демонстрационный вариант ЕГЭ 2021 года ФИПИ КИМ по математике базового уровня (Проект). Ответы

Демонстрационный вариант ОГЭ 2021 года ФИПИ КИМ по математике (Проект). Критерии, ответы

Открытые варианты досрочного (отменённого) ЕГЭ 2020
Открытые варианты досрочного (отменённого) ЕГЭ 2020 по математике профильного уровня
Открытые варианты досрочного (отменённого) ЕГЭ 2020 по информатике
Открытые варианты досрочного (отменённого) ЕГЭ 2020 по физике
Открытые варианты досрочного (отменённого) ЕГЭ 2020 по обществознанию
Математика 50 вариантов заданий 2020 Ященко профильный уровень ЕГЭ
Математика 36 вариантов заданий 2020 Ященко профильный уровень ЕГЭ
Математика 36 вариантов ОГЭ 2020 ФИПИ Ященко
Демонстрационный вариант ЕГЭ 2020 года ФИПИ КИМ по математике
Демонстрационный вариант ОГЭ 2020 года ФИПИ КИМ по математике
Досрочный егэ по математике 2019 профильный уровень 29-03-2019
Демонстрационный вариант КИМ ЕГЭ 2019 года ФИПИ по математике Профильный уровень
Демонстрационный вариант КИМ ЕГЭ 2018 года по математике Профильный уровень
Решение заданий и ответы вариантов Дальнего Востока Москвы и других регионов реального ЕГЭ от 2 июня 2022 года по математике (профильный уровень). Основная волна КИМ, ДВ, МСК Дальневосточный, Владивосток, профиль.

Задание 1.
Найдите корень уравнения sqrt{22-3x}=2.
ИЛИ
Найдите корень уравнения 7−6−х = 343.
Задание 2.
В чемпионате по гимнастике участвуют 70 спортсменок: 14 из Сербии, 23 из Хорватии, остальные из Словении. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Сербии.
ИЛИ
В соревнованиях по толканию ядра участвуют спортсмены из четырёх стран: 6 из Черногории, 7 из Сербии, 8 из Хорватии и 9 из Словении. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из Словении.
ИЛИ
В сборнике билетов по химии всего 60 билетов, в 3 из них встречаются вопрос по теме «Белки». Найдите вероятность того что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме «Белки».
ИЛИ
На чемпионате по прыжкам в воду выступают 20 спортсменов, среди них 7 спортсменов из Германии и 9 спортсменов из США. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что двенадцатым будет выступать спортсмен из Германии.
Задание 3.
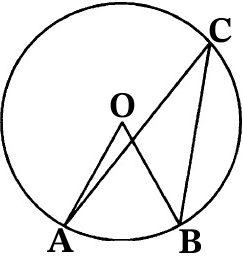
Отрезки АС и ВD – диаметры окружности с центром О. Угол АОD равен 108°. Найдите вписанный угол АСВ. Ответ дайте в градусах.
ИЛИ
Найдите центральный угол АОВ, если он на 67 градусов больше острого вписанного угла АСВ, опирающегося на ту же дугу. Ответ дайте в градусах.
ИЛИ
Треугольник ABC вписан в окружность с центром О. Угол ВАС равен 32°. Найдите угол ВОС. Ответ дайте в градусах.
Задание 4.
Найдите значение выражения sqrt{2}sinfrac{7pi}{8}cosfrac{7pi}{8}.
ИЛИ
Найдите значение выражения frac{10sin38°}{sin19°cdot sin71°}.
ИЛИ
Найдите значение выражения frac{7sin154°}{cos77°cdot cos13°}.
Задание 5.
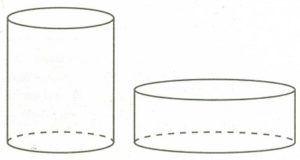
Объем первого цилиндра равен 6 кубических метров. У второго цилиндра высота в 2 раза меньше, а радиус основания – в 3 раза больше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
ИЛИ
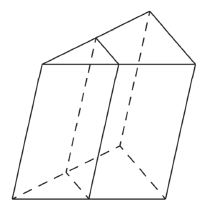
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.
ИЛИ
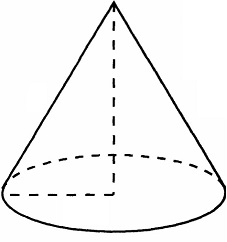
Во сколько раз уменьшится объем конуса, если его высота уменьшится в 12 раз, а радиус основания не изменится?
Задание 6.
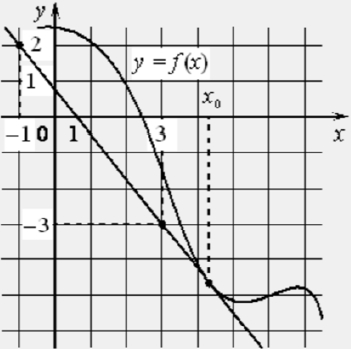
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
ИЛИ
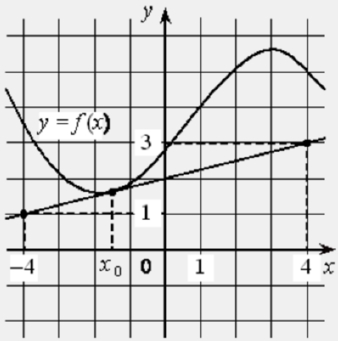
На рисунке изображены график функции 𝑦 = 𝑓(𝑥) и касательная к нему в точке с абсциссой 𝑥0. Найдите значение производной функции 𝑓(𝑥) в точке 𝑥0.
Задание 7.
В ходе распада радиоактивного изотопа его масса уменьшается по закону , где m0 – начальная масса изотопа, t – время, прошедшее от начального момента, Т – период полураспада. В начальный момент времени масса изотопа 20 мг. Период его полураспада составляет 10 мин. Найдите, через сколько минут масса изотопа будет равна 5 мг.
ИЛИ
Водолазный колокол, содержащий v = 2 моль воздуха при давлении p1 = 2,4 атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления p2 в атмосферах. Работа, совершаемая водой при сжатии воздуха, вычисляется по формуле ‚ где α = 13,5 Дж/моль·К – постоянная, Т = 300 К – температура воздуха. Найдите, какое давление p2 будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 16200 Дж. Ответ дайте в атмосферах.
ИЛИ
Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением а = 6500 км/ч2. Скорость v (в км/ч) вычисляется по формуле ‚ где l – пройденный автомобилем путь (в км). Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 130 км/ч.
Задание 8.
Теплоход проходит по течению реки до пункта назначения 216 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 23 часа после отплытия из него.
ИЛИ
От пристани A к пристани B, расстояние между которыми равно 176 км, отправился с постоянной скоростью первый теплоход, а через 5 часов после этого следом за ним, со скоростью на 5 км/ч большей, отправился второй. Найдите скорость второго теплохода, если в пункт B он прибыл одновременно с первым. Ответ дайте в км/ч.
ИЛИ
Катер в 8:40 вышел из пункта А в пункт В, расположенный в 48 км от А. Пробыв 40 минут в пункте В, катер отправился назад и вернулся в пункт А в 16:20 того же дня. Найдите собственную скорость катера (в км/ч), если известно, что скорость течения реки 2 км/ч.
Задание 9.
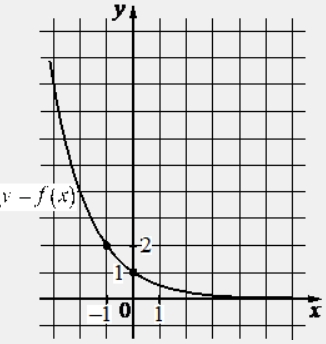
На рисунке изображён график функции вида f(x) = ax. Найдите значение f(–4).
ИЛИ
На рисунке изображён график функции вида f(x) = loga x. Найдите значение f(8).
ИЛИ
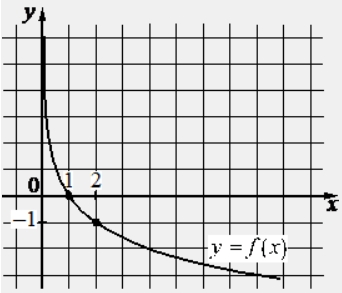
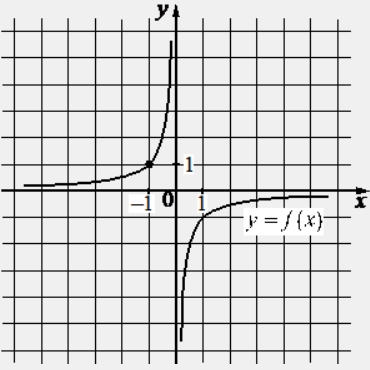
На рисунке изображён график функции вида f(x)=frac{k}{x}. Найдите значение f(10).
Задание 10.
Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые 3 раза попал в мишени, а последние 2 промахнулся. Результат округлите до сотых.
ИЛИ
Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
ИЛИ
Игральную кость бросили два раза. Известно, что три очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 8».
ИЛИ
Помещение освещается фонарем с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,3. Лампы перегорают независимо друг от друга. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
ИЛИ
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,05. Перед упаковкой каждая батарейка проходит систему контроля качества. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Задание 11.
Найдите точку минимума функции y = x3 – 16x2 + 64x + 17.
ИЛИ
Найдите наименьшее значение функции
y=11+frac{7sqrt{3}}{18}pi-frac{7sqrt{3}}{3}x-frac{14sqrt{3}}{3}cosx
на отрезке [0;frac{pi}{2}].
ИЛИ
Найдите точку минимума функции y = x2 – 28x + 96lnx – 5.
Задание 12.
а) Решите уравнение 2cos2x – 3sin(–x) – 3 = 0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [frac{5pi}{2};4pi].
ИЛИ
а) Решите уравнение sin2x – 2sin(–x) – cos(–x) – 1 = 0.
б) Найдите все корни уравнения, принадлежащие отрезку [2pi;frac{7pi}{2}].
ИЛИ
а) Решите уравнение 5^{2log_{2}^{2}(sinx)}=frac{5}{5^{log_{2}(sinx)}}.
б) Найдите все корни уравнения, принадлежащие отрезку [pi;frac{5pi}{2}].
Задание 13.
Точка M – середина бокового ребра SC правильной четырёхугольной пирамиды SABCD, точка N лежит на стороне основания BC. Плоскость α проходит через точки M и N параллельно боковому ребру SA.
а) α пересекает ребро SD в точке L. Докажите, что BN : NC = DL : LS.
б) Пусть BN : NC = 1 : 2. Найдите отношение объёмов многогранников, на которые плоскость α разбивает пирамиду.
ИЛИ
В кубе ABCDA1B1C1D1 отмечены середины M и N отрезков AB и AD соответственно.
а) Докажите, что прямые B1N и CM перпендикулярны.
б) Найдите расстояние между этими прямыми, если B1N = 3√5.
ИЛИ
В основании пирамиды SABCD лежит трапеция ABCD с большим основанием AD. Диагонали пересекаются в точке O. Точки M и N – середины боковых сторон AB и CD соответственно. Плоскость α проходит через точки M и N параллельно прямой SO.
а) Докажите, что сечение пирамиды SABCD плоскостью α является трапецией.
б) Найдите площадь сечения пирамиды SABCD плоскостью α, если AD = 10, BC = 8, SO = 8, а прямая SO перпендикулярна прямой AD.
ИЛИ
В прямоугольном параллелепипеде ABCDA1B1C1D1 на диагонали BD1 отмечена точка N так, что BN:ND1 = 1:2. Точка O – середина отрезка CB1.
а) Докажите, что прямая NO проходит через точку A.
б) Найдите объём параллелепипеда ABCDA1B1C1D1, если длина отрезка NO равна расстоянию между прямыми BD1 и CB1 и равна √2.
Задание 14.
Решите неравенство frac{6}{5^{x}–125}le frac{1}{5^{x}–25}.
ИЛИ
Решите неравенство 5^{x}+frac{125}{5^{x}–126}ge 0.
Задание 15.
В июле 2026 года планируется взять кредит на три года в размере 900 тыс. рублей. Условия его возврата таковы:
– каждый январь долг будет возрастать на 30% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
– платежи в 2027 и 2028 годах должны быть равными;
– к июлю 2029 года долг должен быть выплачен полностью.
Известно, что сумма всех платежей после полного погашения кредита будет равна 1482,3 тыс. рублей. Сколько рублей составит платёж 2029 года?
ИЛИ
В июле 2026 года планируется взять кредит на три года в размере 800 тыс. рублей. Условия его возврата таковы:
– каждый январь долг будет возрастать на 10% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
– платежи в 2027 и 2028 годах должны быть равны;
– к июлю 2029 года долг должен быть выплачен полностью.
Известно, что сумма всех платежей после полного погашения кредита равна 971,8 тыс. рублей. Сколько рублей составит платёж в 2027 году?
ИЛИ
В июле 2026 года планируется взять кредит на три года в размере 800 тыс. рублей. Условия его возврата таковы:
– каждый январь долг будет возрастать на 10% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
– платежи в 2027 и 2028 годах должны быть равными;
– к июлю 2029 года долг должен быть выплачен полностью.
Известно, что платёж в 2029 году составит 833,8 тыс. рублей. Сколько рублей составит платёж в 2027 году?
ИЛИ
В июле 2026 года планируется взять кредит в размере 880 тыс. руб.
Условия возврата таковы:
– каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
– с февраля по июнь необходимо выплатить часть долга;
– в июле 2027, 2028 и 2029 годов долг остается равным 880 тыс. руб.
– суммы выплат 2030 и 2031 годов равны;
– к июлю 2031 года долг будет выплачен полностью.
Найдите разницу между первым и последним платежами.
ИЛИ
В июле 2026 года планируется взять кредит на три года в размере 700 тысяч рублей. Условия его возврата таковы:
– каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– платёж в 2027 и 2028 годах должен быть по 400 тыс. рублей;
– к июлю 2029 года долг должен быть выплачен полностью.
Найдите сумму всех платежей после полного погашения кредита.
ИЛИ
В июле 2026 года планируется взять кредит на три года в размере 900 тыс. рублей. Условия его возврата таковы:
– каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
– платежи в 2027 и 2028 годах должны быть равными;
– к июлю 2029 года долг должен быть выплачен полностью.
Найдите сумму всех платежей после полного погашения кредита, если известно, что платёж в 2029 году равен 1027,2 тыс. рублей?
ИЛИ
В июле 2026 года планируется взять кредит на три года. Условия его возврата таковы:
– каждый январь долг будет возрастать на 30% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
– платежи в 2027 и 2028 годах должны быть по 300 тыс. рублей;
– к июлю 2029 года долг должен быть выплачен полностью.
Какую сумму планируется взять в кредит, если известно, что платёж в 2029 году равен 860,6 тыс. рублей?
ИЛИ
В июле 2026 года планируется взять кредит на три года. Условия его возврата таковы:
– каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
– платежи в 2027 и 2028 годах должны быть по 500 тыс. рублей;
– к июлю 2029 года долг должен быть выплачен полностью.
Известно, что сумма всех платежей после полного погашения кредита равна 1235,2 тыс. рублей. Какую сумму планируется взять в кредит?
Задание 16.
Биссектриса ВВ1 и высота СС1 треугольника АВС пересекают описанную окружность в точках М и N. Известно, что угол ВСА = 85° и угол ABC равен 40°.
а) Докажите, что CN = ВМ.
б) Пусть МN и ВС пересекаются в точке D. Найти площадь треугольника ВDN, если его высота BH равна 7.
ИЛИ
На стороне BC параллелограмма ABCD отмечена точка М такая, что треугольник АМС – равнобедренный, так, что AM = MC.
а) Докажите, что центр окружности, вписанной в треугольник АMD лежит на диагонали параллелограмма. б) Найдите радиус окружности, вписанной в треугольник АMD, если известно, что AB = 7, BC = 21, а ∠DAB = 60°.
ИЛИ
В параллелограмме ABCD угол BAC вдвое больше угла CAD. Биссектриса угла BAC пересекает отрезок BC в точке L. На продолжении стороны CD за точку D выбрана такая точка E, что AE = CE.
а) Докажите, что AL·BC = AB·AC.
б) Найдите EL, если AC = 8, тангенс ∠BCA = frac{1}{2}.
ИЛИ
На стороне острого угла с вершиной A отмечена точка B. Из точки B на биссектрису и другую сторону угла опущены перпендикуляры BC и BD соответственно.
а) Докажите, что AC2 + CB2 = AD2 + DB2 .
б) Прямые AC и BD пересекаются в точке T найдите отношение AT:TC, если cos∠ABC = frac{3}{8}.
Задание 17.
Найдите все значения 𝑎, при каждом из которых уравнение
х2 – 2х – 6а + а2 = |6х – 2а|
имеет 2 различных решения.
ИЛИ
Найдите все значения a, при каждом из которых уравнение
|х2 + а2 – 7x – 5a| = х + а
имеет 4 различных решения.
ИЛИ
Найдите все значения a, при каждом из которых уравнение
a2 – 4x2 + 8|x| – 4 = 0
имеет ровно два различных корня.
ИЛИ
Найдите все значения a, при каждом из которых уравнение
– 2x2 + 9|x| + a2 – 6a + ax – 3x = 0
имеет меньше 4 различных решения.
Задание 18.
С натуральным трёхзначным числом проводят следующую операцию: из числа вычитают его сумму цифр, и полученный результат делят на 3.
а) Может ли результатом выполнения операции быть число 300?
б) Может ли результатом выполнения операции быть число 151?
в) Сколько различных результатов можно получить, если применить данную операцию для всех трёхзначных чисел от 100 до 600?
ИЛИ
С натуральным трёхзначным числом производят следующую операцию: к нему прибавляют цифру десятков, умноженную на 10, а затем к получившейся сумме прибавляют 3.
а) Могло ли в результате такой операции получиться число 224?
б) Могло ли в результате такой операции получиться число 314?
в) Найдите наибольшее отношение получившегося числа к исходному.
ИЛИ
Есть четыре коробки: в первой коробке 101 камень, во второй – 102, в третьей – 103, а в четвёртой коробке камней нет. За один ход берут по одному камню из любых трёх коробок и кладут в оставшуюся. Сделали некоторое количество таких ходов.
а) Могло ли в первой коробке оказаться 97 камней, во второй – 102, в третье – 103, а в четвёртой – 4?
б) Могло ли в четвёртой коробке оказаться 306 камней?
в) Какое наибольшее число камней могло оказаться в первой коробке?
ИЛИ
По кругу расставлено N различных натуральных чисел, каждое из которых не превосходит 305. Сумма любых четырёх идущих подряд чисел делится на 4, а сумма любых трёх идущих подряд чисел нечётна.
а) Может ли N быть равным 160?
б) Может ли N быть равным 89?
в) Найдите наибольшее значение N.
ИЛИ
По кругу расставлено N различных натуральных чисел, каждое из которых не превосходит 400. Сумма любых четырёх идущих подряд чисел делится на 3, а сумма любых трёх идущих подряд не делится на 3.
а) Может ли N быть равным 360?
б) Может ли N быть равным 149?
в) Найдите наибольшее значение N.
ИЛИ
На доске написано N различных натуральных чисел, каждое из которых не превосходит 99. Для любых двух написанных на доске чисел a и b, таких, что a < b, ни одно из написанных чисел не делится на b − a, и ни одно из написанных чисел не является делителем числа b − a.
а) Могли ли на доске быть написаны какие-то два числа из чисел 18, 19 и 20?
б) Среди написанных на доске чисел есть 17. Может ли N быть равно 25?
в) Найдите наибольшее значение N.
Источники заданий варианта: беседы vk.com и telegram, Школа Пифагора, Ягубов РФ.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.1 / 5. Количество оценок: 29
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
- 29.03.2022
Начинаем собирать реальные варианты ЕГЭ 2022 года по профильной математике. Все варианты собираются и публикуются после проведения экзамена.
- Смотреть реальные варианты ЕГЭ 2022 по всем предметам
ОБНОВЛЕНО 05.06.2022
Все возможные варианты с досрочного ЕГЭ 2022 по математике и с основной волны, которая прошла 02.06.2022. Смотрим, разбираем. Все варианты будут сопровождаться видеоуроками, на которых будут разобраны примеры решения, правильные ответы и т.д.
- Другие варианты ЕГЭ по профильной математике (включая Статград)
Есть вопросы? Пишите их ниже! Обсудим, решим, ответим.
- Вариант досрочного ЕГЭ 2022 по профильной математике от 28.03.2022
- Открытый вариант от ФИПИ ЕГЭ 2022 по профильной математике (аналог досрочного варианта) от 28.04.2022
Один из вариантов досрочного реального ЕГЭ 2022 по математике
Варианты с основной волны от 2 июня 2022
Вариант в формате PDF
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Видеоразборы заданий ЕГЭ 2022 по профилю с основной волны