Ященко егэ 2021 математика профиль 15 вариант 15 задание - Помощь в подготовке к экзаменам и поступлению

Задание 1

В школе 400 учеников, из них 30 % — ученики начальной школы. Среди учеников средней и старшей школы 30 % изучают французский язык. Сколько учеников в школе изучают французский язык, если в начальной школе французский язык не изучается?

Ответ: 84

Задание 2

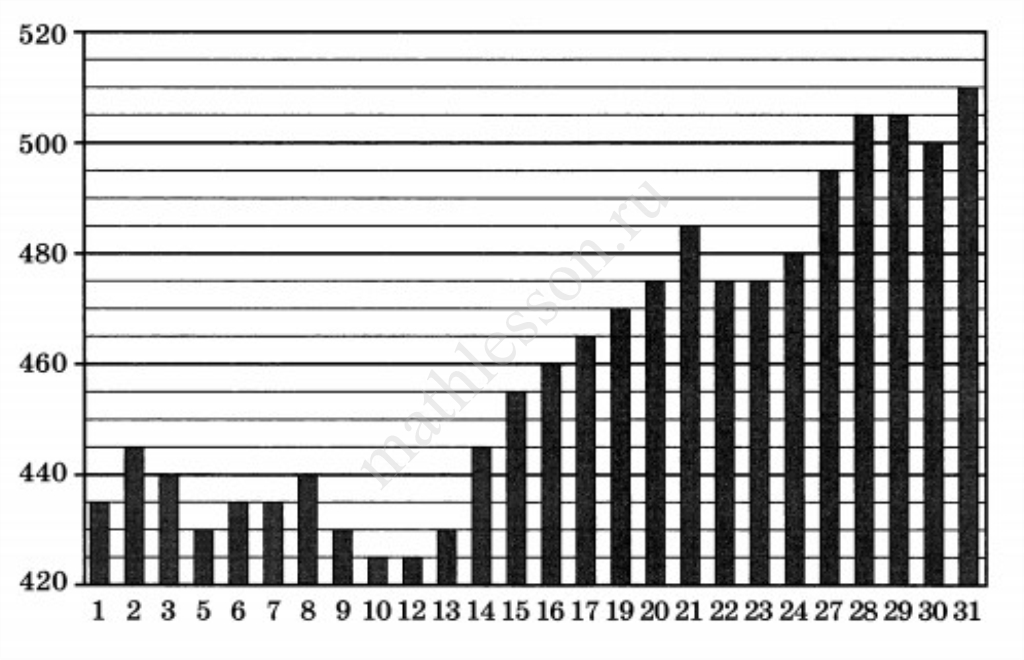
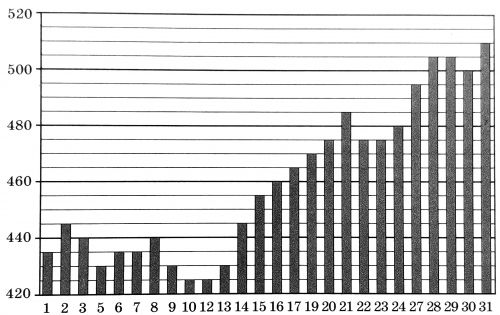
На диаграмме показана цена пшеницы на момент закрытия биржи во все торговые дни мая 2019 года. По горизонтали указаны числа месяца, по вертикали — цена 100 бушелей пшеницы в долларах США.

Определите по диаграмме наибольшую цену в долларах США 100 бушелей пшеницы с 14 по 24 мая.

Ответ: 485

Задание 3

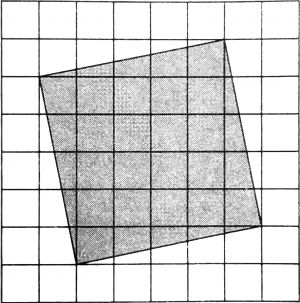
На клетчатой бумаге с размером клетки 1×1 изображён квадрат. Найдите его площадь.

Ответ: 26

Задание 4

На заводе делают электрические лампочки. 5 % всех изготовленных лампочек неисправны. Система контроля качества выявляет все неисправные лампочки, но по ошибке бракует еще 1 % исправных лампочек. Все забракованные лампочки отправляются в переработку, а остальные — в продажу. Найдите вероятность того, что случайно выбранная изготовленная лампочка отправится в переработку.

Ответ: 0,0595

Задание 5

Найдите корень уравнения $${log}_3(x + 6) = {log}_3(10-x)-1.$$

Ответ: -2

Задание 6

Один из углов прямоугольного треугольника равен $$66{}^circ$$. Найдите угол между высотой и биссектрисой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

Ответ: 21

Задание 7

Прямая $$y = 8x+11$$ параллельна касательной к графику функции $$y = x^2 + 7x-7.$$ Найдите абсциссу точки касания.

Ответ: 0,5

Задание 8

Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 25. Найдите объём куба.

Ответ: 200

Задание 9

Найдите значение выражения $$frac{{left(5sqrt{3}right)}^2}{10}$$

Ответ: 7,5

Задание 10

Рейтинг R интернет-магазина вычисляется по формуле $$R=r_p-frac{r_p-r_{ex}}{{left(K+1right)}^m},$$ где $$m=frac{0,02K}{r_p+0,1},$$ $$r_p$$ — средняя оценка покупателями, $$r_{ex} $$- оценка магазина, данная экспертами, $$K$$ — число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 15, их средняя оценка равна 0,3, а оценка экспертов равна 0,38.

Ответ: 0,31

Задание 11

Из пункта А в пункт В, расстояние между которыми 30 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 1 час позже автомобилиста. Ответ дайте в км/ч.

Ответ: 20

Задание 12

Найдите точку минимума функции $$y=frac{162}{x}+2x+7$$

Ответ: 9

Задание 13

а) Решите уравнение $$2{{cos }^4 x }+3{{sin }^2 x } — 2= 0.$$

б) Найдите все корни этого уравнения, принадлежащие отрезку $$[-frac{7pi }{2}; -frac{5pi }{2}]$$

Ответ: а) $$pi n, frac{pi }{4}+frac{pi }{2}n, n in Z$$; б) $$-frac{13pi }{4}, -3pi, -frac{11pi }{4}$$

Задание 14

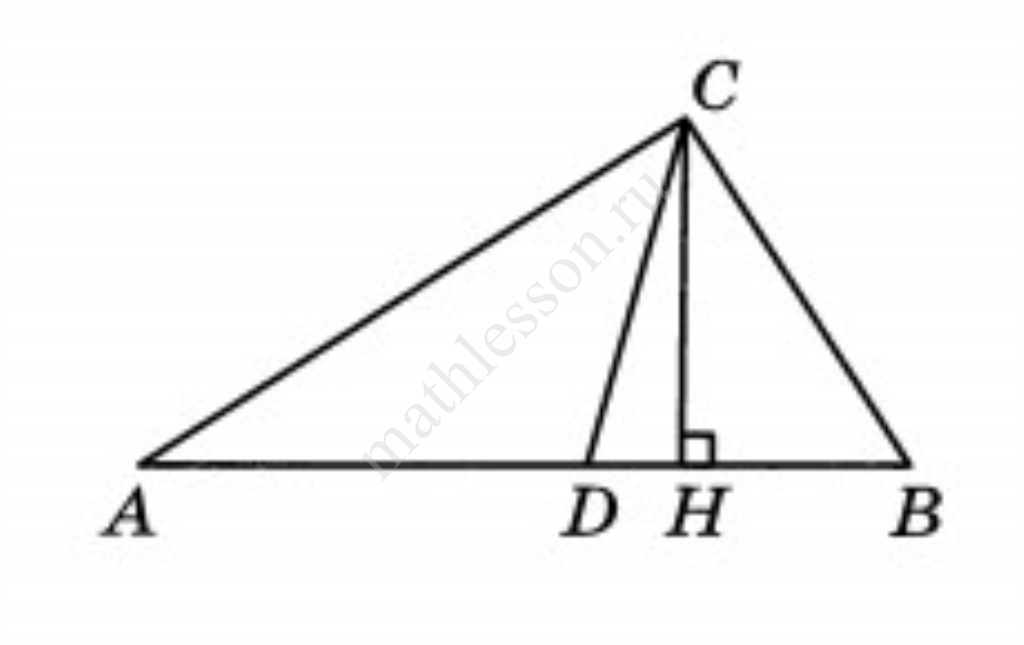
Основанием пирамиды FABC является правильный треугольник АВС со стороной 36. Все боковые рёбра пирамиды равны 30. На рёбрах FB и FC отмечены соответственно точки К и N так, что $$BK = CN = 20.$$ Через точки К и N проведена плоскость $$alpha $$, перпендикулярная плоскости АВС.

а) Докажите, что плоскость$$ alpha $$ делит медиану AM в отношении $$2 : 7.$$

б) Найдите расстояние от точки В до плоскости $$alpha $$

Ответ: $$4sqrt{3}$$

Задание 15

Решите неравенство $${log}^2_{0,2}{left(x-3right)}^8+8{log}_5{left(x-3right)}^4le 32$$

Ответ: $$[3-sqrt{5}; 2,8]cup [3,2; 3+sqrt{5}]$$

Задание 16

В треугольнике АВС известно, что $$AC = 10$$ и $$AB = BC= 14.$$

а) Докажите, что средняя линия треугольника, параллельная стороне АС, пересекает окружность, вписанную в треугольник АВС.

б) Найдите отношение длин отрезков, на которые окружность делит среднюю линию, параллельную стороне АС.

Ответ: 1:3:1

Задание 17

15 декабря планируется взять кредит в банке на сумму 600 тысяч рублей на $$(n+1)$$ месяц. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 3 % по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца с 1-го по n-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;

— 15-го числа n-го месяца долг составит 200 тысяч рублей;

— к 15-му числу $$(n + 1)$$-го месяца кредит должен быть полностью погашен.

Найдите n, если известно, что общая сумма выплат после полного погашения кредита составит 852 тысячи рублей.

Ответ: 20

Задание 18

Найдите все значения а, при каждом из которых неравенство $$(4left|xright|-a-3)(x^2-2x-2-a)le 0$$ имеет хотя бы одно решение из промежутка [-4; 4].

Ответ: [-3; 22]

Задание 19

а) Может ли потребоваться 5 автобусов модели А?

б) Найдите наименьшее возможное количество детей в группе, если известно, что их больше 150.

в) Найдите наибольшее возможное количество детей в группе.

Ответ: а) да; б) 180; в) 546

Источник

Решение и ответы заданий Варианта №15 из сборника ЕГЭ 2023 по математике (профильный уровень) И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ профиль для 11 класса. Полный разбор.

Задание 1.
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 33.

Задание 2.
Высота конуса равна 18, а длина образующей равна 30. Найдите площадь осевого сечения этого конуса.

Задание 3.
При изготовлении подшипников диаметром 62 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,986. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 61,99 мм, или больше, чем 62,01 мм.

Задание 4.
Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.

Задание 5.
Найдите корень уравнения sqrt{9-8x}=-x. Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Задание 6.
Найдите значение выражения frac{2^{log_{9}3}}{2^{log_{9}243}}.

Задание 7.
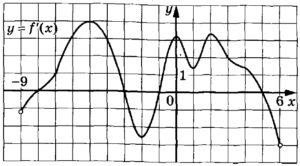
На рисунке изображён график у = f′(x) – производной функции f(x), определённой на интервале (–9; 6). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.

Задание 8.
Груз массой 0,25 кг колеблется на пружине. Его скорость v меняется по закону v=v_{0}cos frac{2pi t}{T}, где t – время с момента начала колебаний, Т = 2с – период колебаний, v₀ = 1,6 м/с. Кинетическая энергия Е (в джоулях) груза вычисляется по формуле E=frac{mv^{2}}{2}, где m – масса груза в килограммах, v – скорость груза в м/с². Найдите кинетическую энергию груза через 56 секунд после начала колебаний. Ответ дайте в джоулях.

Задание 9.
Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв 45 минут в пункте В, баржа отправилась назад и вернулась в пункт А в 16:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость баржи равна 7 км/ч.

Задание 10.
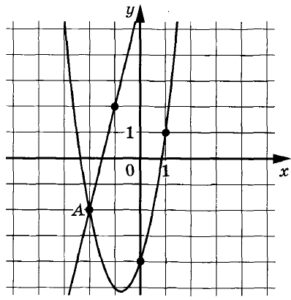
На рисунке изображены функций графики f(x) = ах² + bх + с и g(x) = kx + d, которые пересекаются в точках А и В. Найдите абсциссу точки В.

Задание 11.
Найдите наибольшее значение функции у = х⁵ + 5х³ – 140х на отрезке [–8; –1].

Задание 12.
а) Решите уравнение sin2x + cos2x = 1.
б) Найдите все корни этого уравнения, принадлежащие отрезку [-frac{7pi }{2}; –2pi].

Задание 13.
В правильной призме ABCDA₁B₁C₁D₁ с основанием ABCD боковое ребро равно √3 , а сторона основания равна 2. Через точку А₁ перпендикулярно плоскости AB₁D₁ проведена прямая l.

а) Докажите, что прямая l пересекает отрезок АС и делит его в отношении 3:1.
б) Найдите угол между прямыми l и СВ₁.

Задание 14.
Решите неравенство 7^{log_{frac{1}{7}}log_{frac{1}{2}}(–x)}< 2^{log_{frac{1}{2}}log_{frac{1}{7}}(–x)}.

Задание 15.
В июле 2025 года планируется взять кредит в банке на сумму 300 тыс. рублей на 6 лет. Условия его возврата таковы:
– в январе 2026, 2027 и 2028 годов долг возрастает на 20 % по сравнению с концом предыдущего года;
– в январе 2029, 2030 и 2031 годов долг возрастает на r% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
– к июлю 2031 года кредит должен быть полностью погашен.
Известно, что общая сумма выплат после полного погашения кредита составит 498 тысяч рублей. Найдите r.

Задание 16.
Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.

а) Докажите, что ∠AOB = ∠COD = 90°.
б) Найдите отношение большего основания трапеции к меньшему, если известно, что АВ = CD, а площадь четырёхугольника с вершинами в точках касания окружности со сторонами трапеции составляет frac{12}{49} площади трапеции ABCD.

Задание 17.
Найдите все такие значения а, при каждом из которых неравенство

–1 ≤ sinx(a – cos2x) ≤ 1

верно при всех действительных значениях х.

Задание 18.
Отношение трёхзначного натурального числа к сумме его цифр – целое число.

а) Может ли это отношение быть равным 34?
б) Может ли это отношение быть равным 84?
в) Какое наименьшее значение может принимать это отношение, если первая цифра трёхзначного числа равна 4?

Источник варианта: Сборник ЕГЭ 2023. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 0 / 5. Количество оценок: 0

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Разбираем все типы задач № 15 из сборника: 30 тренировочных вариантов ЕГЭ под редакцией И. В. Ященко» – 2021.
Подробно объясняем ход решения и показываем оформление задач.
Полное название сборника:
«Математика. Профильный уровень. Единый Государственный Экзамен. Готовимся к итоговой аттестации. 2021 год. 30 вариантов».
Как правило, задания из таких сборников немного сложнее, чем реальные задачи ЕГЭ. Зато, решая такие задачи, вы сможете отлично подготовиться к любым возможным неожиданностям на экзамене.
В задании 15 вариантов ЕГЭ вам встретятся всевозможные неравенства: показательные, логарифмические, иррациональные, комбинированные.

Задача 15, Вариант 1

Решите неравенство

$displaystyle3^{lg x}+6 frac{2}{3} cdot 3^{0,5 lg x} cdot 2^{0,5 (lg x - 6)} leq 2^{lg x}$

Посмотреть решение

Задача 15, Вариант 3

Решите неравенство $displaystyle frac{log_{frac{1}{4}}(3x+1)}{log_{frac{1}{4}}(6x-1)} , textless , 2$

Посмотреть решение

Задача 15, Вариант 5

Решите неравенство $displaystyle (2+sqrt{3})^{frac{6-5x}{x}} leq (2-sqrt{3})^{-x}.$

Посмотреть решение

Задача 15, Вариант 12

Следующая задача – типичная. Такие задания очень любят давать в реальных вариантах Профильного ЕГЭ по математике.

Решите неравенство $displaystyle frac{2^x+8}{2^x-8}+frac{2^x-8}{2^x+8} leq frac{5 cdot 2^{x+3}-72}{4^x-64}$

Посмотреть решение

Задача 15, Вариант 17

В апреле 2020 года И. В. Ященко, автор книги, задачи из которой мы сейчас разбираем, и составитель задач ЕГЭ, дал интервью, в котором пообещал, что на реальном ЕГЭ иррациональных неравенств в задаче 15 не будет, однако не исключил, что они могут встретиться в тренировочных и контрольных работах. Как видим, в сборнике ««30 тренировочных вариантов под редакцией И. В. Ященко», 2021 год, такие неравенства есть.

Решите неравенство $displaystyle sqrt{2 - log_{frac{1}{2}x}} cdot frac{(x-1)(x+7)}{x+2} geq 0$

Посмотреть решение

Задача 15, Вариант 24
И наконец, еще одна типичная для ЕГЭ задача.

Решите неравенство $displaystyle lg frac{4-x}{x-15}+log_{0,1}(x-4)geq log_{frac{1}{10}} ((x-15)^2)$

Посмотреть решение

Больше интересных задач: на нашем канале на Ютьюбе и на онлайн-курсе Анны Малковой.
Успеха вам на экзамене!

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Решаем задачи из сборника : 30 тренировочных вариантов ЕГЭ под редакцией И. В. Ященко» – 2021. Все задачи №15 (Неравенства)» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

В школе 400 учеников, из них 30% — ученики начальной школы. Среди учеников средней и старшей школы 30% изучают французский язык. Сколько учеников в школе изучают французский язык, если в начальной школе французский язык не изучается?

Определите по диаграмме наибольшую цену в долларах США 100 бушелей пшеницы с 14 по 24 мая.

На клетчатой бумаге с размером клетки (1times1) изображён квадрат. Найдите его площадь.

На заводе делают электрические лампочки. 5% всех изготовленных лампочек неисправны. Система контроля качества выявляет все неисправные лампочки, но по ошибке бракует еще 1% исправных лампочек. Все забракованные лампочки отправляются в переработку, а остальные — в продажу. Найдите вероятность того, что случайно выбранная изготовленная лампочка отправится в переработку.

Найдите корень уравнения (log_{3}{(x+6)}=log_{3}{(10-x)}-1 )

Один из углов прямоугольного треугольника равен 66°. Найдите угол между высотой и биссектрисой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

Прямая (y=8x+11) параллельна касательной к графику функции (y=x^2+7x-7). Найдите абсциссу точки касания.

Найдите значение выражения (dfrac{(5sqrt{3})^2}{10})

Рейтинг R интернет-магазина вычисляется по формуле (R=r_{пок}-dfrac{r_{пок}-r_{экс}}{(K+1)^m}), где (m=dfrac{0{,}02K}{r_{пок}+0{,}1}), (r_{пок}) – средняя оценка магазина покупателями, (r_{экс}) – оценка магазина, данная экспертами, (K) – число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 15, их средняя оценка равна 0,3, а оценка экспертов равна 0,38.

Найдите точку минимума функции (y=dfrac{162}{x}+2x+7)

а) Решите уравнение (2cos^4x+3sin^2x-2=0)

б) Найдите все корни этого уравнения, принадлежащие отрезку (left[-dfrac{7pi}{2};-dfrac{5pi}{2}right])

Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)

1. 2πn, n∈Z	2. π/6+2πn, n∈Z	3. π/4+2πn, n∈Z	4.π/3+2πn, n∈Z
5. π/2+2πn, n∈Z	6. 2π/3+2πn, n∈Z	7. 3π/4+2πn, n∈Z	8. 5π/6+2πn, n∈Z
9. π+2πn, n∈Z	10. -π/6+2πn, n∈Z	11. -π/4+2πn, n∈Z	12. -π/3+2πn, n∈Z
13. -π/2+2πn, n∈Z	14. -2π/3+2πn, n∈Z	15. -3π/4+2πn, n∈Z	16. -5π/6+2πn, n∈Z

б)

17. -7π/2	18. -10π/3	19. -13π/4	20. -19π/6
21. -3π	22. -17π/6	23. -11π/4	24. -8π/3
25. -5π/2	26. -7π/3	27. -9π/4	28. -13π/6
29. -2π

Основанием пирамиды (FABC) является правильный треугольник (ABC) со стороной 36. Все боковые рёбра пирамиды равны 30. На рёбрах (FB) и (FC) отмечены соответственно точки (K) и (N) так, что (BK=CN=20). Через точки (K) и (N) проведена плоскость (alpha), перпендикулярная плоскости (ABC).

а) Докажите, что плоскость (alpha) делит медиану (AM) в отношении (2:7).

б) Найдите расстояние от точки (B) до плоскости (alpha).

Решите неравенство (log^2_{0{,}2}{(x-3)^8}+8log_{5}{(x-3)^4}leqslant32)

В треугольнике (ABC) известно, что (AC=10) и (AB=BC=14).
а) Докажите, что средняя линия треугольника, параллельная стороне (AC), пересекает окружность, вписанную в треугольник (ABC).
б) Найдите отношение длин отрезков, на которые окружность делит среднюю линию, параллельную стороне (AC).

Ответ запишите в виде несократимого отношения без пробелов, например «4:13:5».

15 декабря планируется взять кредит в банке на сумму 600 тысяч рублей на n+1 месяц. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3 % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по n-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— 15-го числа n-го месяца долг составит 200 тысяч рублей;
— к 15-му числу (n+1)-го месяца кредит должен быть полностью погашен. Найдите n, если известно, что общая сумма выплат после полного погашения кредита составит 852 тысячи рублей.

Найдите все значения (a), при каждом из которых неравенство ((4|x|-a-3)(x^2-2x-2-a)leqslant0 ) имеет хотя бы одно решение на промежутке ([-4;4]).

Группу детей можно перевезти автобусами модели А или автобусами модели Б. Известно, что в автобусе модели А количество мест больше 30, но меньше 40, а в автобусах модели Б — больше 40, но меньше 50. Если всех детей рассадить в автобусы модели А, то все места будут заняты. Если всех детей рассадить в автобусы модели Б, то все места также будут заняты, но потребуется на один автобус меньше.
а) Может ли потребоваться 5 автобусов модели А?
б) Найдите наименьшее возможное количество детей в группе, если известно, что их больше 150.
в) Найдите наибольшее возможное количество детей в группе.

Введите ответ в форме строки «да;123;1234». Где ответы на пункты разделены «;», и первый ответ с маленькой буквы.

Источник


3221	Стрелок в тире стреляет по мишени до тех пор, пока не поразит её. Известно, что он попадает в цель с вероятностью 0,2 при каждом отдельном выстреле. Сколько патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не менее 0,4? Решение	Стрелок в тире стреляет по мишени до тех пор, пока не поразит её ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 10

2607	В магазине в одной коробке лежат вперемешку ручки с чёрными, синими или красными чернилами одинаковые на вид. Покупатель случайным образом выбирает одну ручку. Вероятность того, что она окажется чёрной, равна 0,37, а того, что она окажется синей, равна 0,45. Найдите вероятность того, что ручка окажется красной Решение	В магазине в одной коробке лежат вперемешку ручки ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 2 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 10 Задание 4

2554	Две трубы, работая одновременно, наполняют бассейн за 18 часов 40 минут, а одна первая труба наполняет бассейн за 40 часов. За сколько часов наполняет бассейн одна вторая труба? Решение	Две трубы, работая одновременно, наполняют бассейн за 18 часов 40 минут ! 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 5 Задание 11

2553	Найдите точку максимума функции y=-(x^2+196)/x Решение График	Найдите точку максимума функции y= -(x^2 + 196) / x ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 11 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 5 Задание 12

2551	У Миши в копилке есть 2-рублёвые, 5-рублёвые и 10-рублёвые монеты. Если взять 10 монет, то среди них обязательно найдётся хотя бы одна 2-рублёвая. Если взять 15 монет, то среди них обязательно найдётся хотя бы одна 5-рублёвая. Если взять 20 монет, то среди них обязательно найдётся хотя бы одна 10-рублёвая. a) Может ли у Миши быть 30 монет? б) Какое наибольшее количество монет может быть у Миши? в) Какая наибольшая сумма рублей может быть у Миши? Решение	У Миши в копилке есть 2-рублёвые, 5-рублёвые и 10-рублёвые монеты ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 18 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 5 Задание 19

2550	В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 сторона основания AB равна 4, а боковое ребро AA1 равно 5sqrt3. На ребре DD1 отмечена точка M так, что DM:MD1=3:2. Плоскость alpha параллельна прямой A1F1 и проходит через точки M и E. а) Докажите, что сечение призмы ABCDEFA1B1C1D1E1F1 плоскостью alpha — равнобедренная трапеция. б) Найдите объём пирамиды, вершиной которой является точка F, а основанием — сечение призмы ABCDEFA1B1C1D1E1F1 плоскостью alpha Решение	В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 сторона основания AB равна 4 ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 13 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 5 Задание 14

2549	а) Решите уравнение sin^4(x/4)-cos^4(x/4)=cos(x-pi/2) б) Найдите все корни этого уравнения, принадлежащие отрезку [-(3pi)/2; pi]. Решение График	Решите уравнение sin^4(x/4) -cos^4(x/4) = cos(x-pi/2) ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 12 #36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 5 Задание 13

2548	Решите неравенство (20.5^(x+2)-0.52^(x+2)). (2log_{0.5)^2(x+2)-0.5log_{2}(x+2)) <= 0. Решение График	Решите неравенство (20.5^(x+2)- 0.52^(x+ 2)) (2log^2_{0.5)(x+2)- 0.5log_{2}(x+ 2)) <= 0 ! 36 вариантов ФИПИ Ященко 2022 Вариант 15 Задание 14 #36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 5 Задание 15