Решение 21 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023
Скачать сборник в pdf
В треугольнике АВС угол С равен 46°, AD и BE – биссектрисы, пересекающиеся в точке О. Найдите угол АОВ. Ответ дайте в градусах.
В кубе ABCDA₁B₁C₁D₁ найдите угол между прямыми DC₁ и BD. Ответ дайте в градусах.
В классе 16 учащихся, среди них два друга – Юра и Борис. Класс случайным образом разбивают на 4 равные группы. Найдите вероятность того, что Юра и Борис окажутся в одной группе.
Комната освещается тремя лампами. Вероятность того, что в течение года лампа перегорит, равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Найдите корень уравнения (dfrac1{2x-3}=dfrac18)
Найдите значение выражения (4^{1-2log_{0,5} 3 })
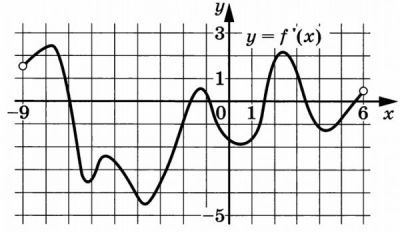
На рисунке изображён график (y = f ‘ (x)) – производной функции (f(x)), определённой на интервале ((-9; 6)). Найдите количество точек минимума функции (f(x)), принадлежащих отрезку ([-8; 5]).
Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением (a) в км/ч². Скорость (v) (в км/ч) вычисляется по формуле (v=sqrt{2la}), где (l) — пройденный автомобилем путь (в км). Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав 0,8 км, приобрести скорость 100 км/ч. Ответ дайте в км/ч².
Катер в 8:40 вышел из пунтка А в пункт В, расположенный в 48 км от А. Пробыв 40 минут в пункте В, катер отправился назад и вернулся в пункт А в 16:20 того же дня. Найдите собственную скорость катера (в км/ч), если известно, что скорость течения реки 2 км/ч.
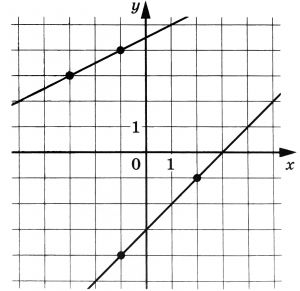
На рисунке изображены графики двух функций вида (y=kx+b), которые пересекаются в точке (A(x_0;y_0)). Найдите (x_0).
Найдите наименьшее значение функции (y=4sin x -6x+7) на отрезке (left[-dfrac{3pi }{2};0right])
а) Решите уравнение (2sin^2left(dfrac{pi}2-xright)+sin2x=0).
б) Найдите все корни этого уравнения, принадлежащие отрезку (left[ 3pi; dfrac{9pi}{2}right]).
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 3π | 18. 19π/6 | 19. 13π/4 | 20. 10π/3 |
| 21. 7π/2 | 22. 11π/3 | 23. 15π/4 | 24. 23π/6 |
| 25. 4π | 26. 25π/6 | 27. 17π/4 | 28. 13π/3 |
| 29. 9π/2 |
В правильной шестиугольной пирамиде SABCDEF сторона основания AB равна 2, а боковое ребро SA равно 8. Точка М – середина ребра AB. Плоскость α перпендикулярна плоскости ABC и содержит точки M и D. Прямая SC пересекает плоскость α в точке K.
a) Докажите, что KM = KD.
б) Найдите объем пирамиды CDKM.
Решите неравенство (x^2log_{64} (3-2x) geqslant log_2 left(4x^2-12x+9right) )
В июле 2022 года планируется взять кредит на пять лет в размере 1050 тыс. рублей. Условия его возврата таковы:
– каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
– в июле 2023, 2024 и 2025 годов долг остаётся равным 1050 тыс. рублей;
– выплаты в 2026 и 2027 годах равны;
– к июлю 2027 года долг будет выплачен полностью.
На сколько тысяч рублей последняя выплата будет больше первой?
Две окружности касаются внутренним образом в точке С. Вершины А и В равнобедренного прямоугольного треугольника АВС с прямым углом С лежат на меньшей и большей окружностях соответственно. Прямая АС вторично пересекает большую окружность в точке Е, а прямая ВС вторично пересекает меньшую окружность в точке D.
а) Докажите, что прямые AD и BE параллельны.
б) Найдите АС, если радиусы окружностей равны 3 и 4.
Найдите все значения параметра (a), при которых система (begin{cases} sqrt{16-y^2}=sqrt{16-a^2x^2}\ x^2+y^2=8x+4yend{cases}) имеет ровно два различных решения.
На доске было написано несколько различных натуральных чисел. Эти числа разбили на три группы, в каждой из которых оказалось хотя бы одно число. К каждому числу из первой группы приписали справа цифру 3, к каждому числу из второй группы — цифру 7, а числа из третьей группы оставили без изменений.
а) Могла ли сумма всех этих чисел увеличиться в 8 раз?
б) Могла ли сумма всех этих чисел увеличиться в 17 раз?
в) В какое наибольшее число раз могла увеличиться сумма всех этих чисел?
Введите ответ в форме строки «да;да;12:34». Где ответы на пункты разделены «;», первые два ответа с маленькой буквы, а третий в виде несократимой дроби через двоеточие «:».
Задание 1
Найдите корень уравнения $$0,5^{4-5х}=64.$$
Ответ: 2
Скрыть
Представим число $$0,5=frac{1}{2}=2^{-1},$$ а число $$64=2^6,$$ получаем такое уравнение:
$$2^{-1(4-5x)}=2^6,$$
и, так как основания у степеней равны, то можно перейти к их равенству:
$$-(4-5x)=6$$
$$5x=6+4$$
$$x=2$$
Задание 2
Фабрика выпускает сумки. В среднем 2 сумки из 120 имеют скрытые дефекты.
Найдите вероятность того, что купленная сумка окажется без дефектов. Результат округлите до сотых.
Ответ: 0,98
Скрыть
m — число благоприятствующих этому событию исходов, то есть число исходов, когда купленная сумка окажется без дефектов. Это число равно количеству сумок без дефектов:
$$m=120–2=118$$
n – общее число всевозможных исходов, оно равно общему количеству сумок:
$$n=120$$
$$Р(А)=frac{m}{n}=frac{118}{120}=0,9833….$$
Результат округляем до сотых:
$$Р(А)=0,98$$
Задание 3
Периметр прямоугольной трапеции, описанной около окружности, равен 100, её большая боковая сторона равна 37. Найдите радиус окружности.
Ответ: 6,5
Скрыть
Радиус окружности будет равен половине стороны AD, т.к. AD по длине совпадает с диаметром окружности. Найдем сторону AD. Воспользуемся свойством четырехугольника вписанного в окружность. Для длин его сторон можно записать такое равенство:
$$AD+CB=DC+AB$$ (1)
Далее, по условию задания нам дана длина стороны CB=37 и периметр трапеции:
$$AD+CB+DC+AB=100$$
Из условия (1) следует, что
$$AD+CB=frac{100}{2}=50$$
откуда
$$AD=50-CB=50-37=13$$
и радиус окружности:
$$R=frac{AD}{2}=frac{13}{2}=6,5$$
Задание 4
Найдите значение выражения $$(sqrt{3}-sqrt{13})(sqrt{3}+sqrt{13}).$$
Ответ: -10
Скрыть
Вычислим выражение, используя правило
$$(a-b)(a+b)=a^2-b^2,$$
получим:
$$(sqrt{3}-sqrt{13})(sqrt{3}+sqrt{13})-(sqrt{3})^2-(sqrt{13})^2=3-13=-10$$
Задание 5
Цилиндр и конус имеют общие основание и высоту. Объём цилиндра равен 162. Найдите объём конуса.
Ответ: 54
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 6
На рисунке изображён график $$у=f'(x)$$ — производной функции $$f(x),$$ определённой на интервале $$(-4; 7).$$ В какой точке отрезка $$[-2; 2]$$ функция $$f(x)$$ принимает наименьшее значение?
Ответ: 2
Скрыть
Известно, что если производная $$f’(x)$$ принимает отрицательные значения, то в этих точках функция $$f(x)$$ убывает. Из рисунка видно, что на интервале $$[-2; 2]$$ производная всюду принимает отрицательные значения, следовательно, на этом интервале функция $$f(x)$$ убывает и наименьшее значение будет достигнуто на правой границе интервала со значением $$2.$$
Задание 7
Для сматывания кабеля на заводе используют лебёдку, которая равноускоренно наматывает кабель на катушку. Угол, на который поворачивается катушка,
изменяется со временем по закону $$varphi=omega t+frac{beta t^2}{2},$$ где t — время в минутах, $$omega=60^{circ}/мин$$ — начальная угловая скорость вращения катушки, а $$beta=6^{circ}/мин^2$$ — угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки $$varphi$$ достигнет $$3375^{circ}.$$ Определите время после начала работы лебёдки, не позже которого рабочий должен проверить её работу. Ответ выразите в минутах.
Ответ: 25
Скрыть
По условию задания нам даны параметры:
$$beta=6^{circ}/мин; omega=60^{circ}/мин; varphi=3375^{circ}$$
Подставляем их в формулу изменения угла:
$$3375=60t+frac{6}{2}t^2$$
Решаем квадратное уравнение:
$$3t^2+60t-3375=0$$
$$t^2+20t-1125=0$$
$$D=b^2-4ac=400+4cdot1125=4900=70^2$$
$$t_1=frac{-b+sqrt{D}}{2a}=frac{-20+70}{2}=25$$
$$t_2=frac{-b-sqrt{D}}{2a}=frac{-20-70}{2}=-45$$
Так как время наматывания не должно быть отрицательным, подходит только один корень $$t=25$$ минут.
Задание 8
Первая труба наполняет резервуар на 54 минуты дольше, чем вторая. Обе трубы наполняют этот же резервуар за 36 минут. За сколько минут наполняет этот резервуар одна вторая труба?
Ответ: 54
Скрыть
Пусть вторая труба наполняет резервуар за $$x$$ минут, тогда первая будет наполнять этот же резервуар за $$x+54$$ минуты. Условно примем объем резервуара за 1. Тогда первая труба будет наполнять его со скоростью $$frac{1}{x+54},$$ а вторая со скоростью $$frac{1}{x}.$$ И так как обе трубы заполняют этот резервуар за 36 минут, то можно записать уравнение:
$$frac{1}{x}+frac{1}{x+54}=frac{1}{36}$$
Преобразуем это выражение:
$$frac{x+54+x}{xcdot(x+54)}=frac{1}{36}$$
$$36cdot(2x+54)=x^2+54x$$
$$62x+1944=x^2+54x$$
$$x^2-18x-1944=0$$
$$D=324+776=8100=90^2$$
$$x_1=frac{-b+sqrt{D}}{2a}=frac{18+90}{2}=54$$
$$x_2=frac{-b-sqrt{D}}{2a}<0$$
то есть вторая труба будет наполнять этот резервуар 54 минуты.
Задание 9
На рисунке изображён график функции $$f(x)=kx+b.$$ Найдите $$f(-18).$$
Ответ: -7
Скрыть
Для того чтобы найти $$f(-18)$$ нам необходимо знать уравнение прямой, то есть значение коэффициентов k и b.
Прямая проходит через точки $$(3;-1)$$ и $$(-4;-3).$$ Подставим их координаты в уравнение прямой:
$$-1=3k+b$$ (1)
$$-3=-4k+b$$ (2)
Вычтем из (1) уравнения (2):
$$-1-(-3)=3k+b-(-4k+b)$$
Раскроем скобки:
$$-1+3=3k+b+4k- b$$
Приведем подобные слагаемые в обеих частях уравнения:
$$2=7k$$
Найдем k:
$$k=frac{2}{7}$$
Найдем b из (1), подставив в него значение коэффициента $$k = frac{2}{7}:$$
$$-1=3cdotfrac{2}{7}+b$$
$$-1=frac{6}{7}+b$$
$$b=-1-frac{6}{7}$$
$$b=-frac{13}{7}$$
Получим следующее уравнение прямой:
$$f(x)=frac{2}{7}cdot x-frac{13}{7}$$
Найдем $$f(-18):$$
$$f(-18)=frac{2}{7}cdot(-18)-frac{13}{7}$$
$$f(-18)=-frac{36}{7}-frac{13}{7}$$
$$f(-18)=-frac{49}{7}$$
$$f(-18)=-7$$
Задание 10
В ящике четыре красных и два синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер достанут третьим по счёту?
Ответ: 0,2
Скрыть
Первые два фломастера, которые мы вытащим должны быть красные
$$P_{иск}=frac{4}{6}cdotfrac{3}{5}cdotfrac{2}{4}=0,2$$
Задание 11
Найдите точку минимума функции $$y=x^2-28x+96ln x-5.$$
Ответ: 8
Скрыть
Функция будет иметь точку минимума в своей точке экстремума. Найдем эти точки. Вычислим производную функции и приравняем ее нулю, получим:
$$y’=2x-28+96cdotfrac{1}{x}=0, xneq0$$
Вычисляем точки экстремума функции:
$$2x^2-28x+96=0$$
$$x^2-14+48=0$$
$$D=196-192=4=2^2$$
$$x_1=frac{-b+sqrt{D}}{2a}=frac{14+2}{2}=8$$
$$x_2=frac{-b-sqrt{D}}{2a}=frac{14-2}{2}=6$$
Известно, что в точке минимума производная функции меняет свой знак с минуса на плюс. Определим знаки производной в окрестностях наших точек экстремума:
Получаем точку минимума функции $$x=8.$$
Задание 12
а) Решите уравнение $$cos 2x-sqrt{2}cos(frac{pi}{2}+x)+1=0.$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[-5pi;-frac{7pi}{2}].$$
Ответ: $$а)-frac{pi}{4}+2pi n,nin Z;-frac{3pi}{4}+2pi m,min Z;$$ $$б)-frac{19pi}{4};-frac{17pi}{4}$$
Скрыть
а) $$cos 2x-sqrt{2}cos(frac{pi}{2}+x)+1=0$$
$$cos^2 x-sin^2 x+sqrt{2}sin x+1=0$$
$$1-sin^2 x-sin^ 2+sqrt{2}sin x+1=0$$
$$-2sin^2 x+sqrt{2}sin x+2=0$$
Введём замену: $$sin x=t$$
$$-2t^2+sqrt{2}t+2=0$$
$$D=(sqrt{2})^2-4cdot2cdot(-2)=2+16=18$$
$$t_{1}=frac{-sqrt{2}+sqrt{18}}{-4}=frac{-sqrt{2}+3sqrt{2}}{-4}=frac{2sqrt{2}}{-4}=-frac{sqrt{2}}{2}$$
$$t_{2}=frac{-sqrt{2}-sqrt{18}}{-4}=frac{-sqrt{2}-3sqrt{2}}{-4}=frac{-4sqrt{2}}{-4}=sqrt{2}$$
Обратная замена:
$$sin x=-frac{sqrt{2}}{2}$$
$$x=-frac{pi}{4}+2pi n, nin Z$$
$$x=-frac{3pi}{4}+2pi n, nin Z$$
и
$$sin x=sqrt{2}$$
корней нет, т. к. $$sin xin [-1;1]$$
б) Отбор корней на отрезке $$[-5pi;-frac{7pi}{2}]$$
$$x_1=-5pi+frac{pi}{4}=-frac{19pi}{4}$$
$$x_2=-4pi+frac{pi}{4}=-frac{17pi}{4}$$
Задание 13
В правильной треугольной пирамиде $$SABC$$ сторона основания $$АВ$$ равна $$6,$$ а боковое ребро $$SA$$ равно $$7.$$ На рёбрах $$АВ$$ и $$SC$$ отмечены точки $$К$$ и $$М$$ соответственно, причём $$АК:КВ=SM:МС=1:5.$$ Плоскость $$alpha$$ содержит прямую $$КМ$$ и параллельна прямой $$ВС.$$
а) Докажите, что плоскость $$alpha$$ параллельна прямой $$SA.$$
б) Найдите угол между плоскостями $$alpha$$ и $$SBC.$$
Ответ:
Скрыть
а) Пусть плоскость α пересекает ребро SB в точке L. Поскольку прямая ВС параллельна плоскости α, прямые LM и ВС параллельны, а значит,
$$frac{SL}{LB}=frac{SM}{MC}=frac{AK}{KB}$$
Следовательно, прямые KL и SA параллельны. Таким образом, плоскость α, содержащая прямую KL, параллельна прямой SA.
б) Пусть точка Н — середина ребра ВС. Тогда медианы АН и SH треугольников ABC и SBC соответственно являются их высотами, а значит, плоскость ASH перпендикулярна прямой ВС. Следовательно, плоскость ASH перпендикулярна плоскости α, параллельной прямой ВС, и плоскости SBC, содержащей прямую ВС.
Поскольку плоскость α параллельна прямой SA, лежащей в плоскости ASH, искомый угол равен углу между прямой SA и плоскостью SBC. Таким образом, угол между плоскостями α и SBC равен углу ASH. В треугольнике ASH имеем:
$$AS=7, АН=3sqrt{3}$$
$$SH=sqrt{SB^2-BH^2}=sqrt{SB^2-frac{BC^2}{4}}=2sqrt{10}.$$
По теореме косинусов
$$cosangle ASH=frac{SA^2+SH^2-AH^2}{2SAcdot SH}$$
$$cosangle ASH=frac{49+40-27}{2cdot7cdot2sqrt{10}}=frac{31sqrt{10}}{140}$$
и угол ASH, равен:
$$angle ASH=arccosfrac{31sqrt{10}}{140}$$
Задание 14
Решите неравенство $$log_{0,5}(12-6x)geqlog_{0;5}(x^2-6x+8)+log_{0,5}(x + 3).$$
Ответ: $$[-2;2)$$
Скрыть
ОДЗ неравенства:
$$Rightarrow xin (-3;2)$$
Преобразуем неравенство:
$$log_{0,5}(12-6x)geqlog_{0,5}(x^2-6x+8)+log_{0,5}(x+3)$$
$$log_{0,5} 6(2-x)geqlog_{0,5}((x-4)(x-2))+log_{0,5}(x+3)$$
$$log_{0,5} 6(2-x)geqlog_{0,5}((4-x)(2-x))+log_{0,5}(x+3)$$
Логарифм произведения равен сумме логарифмов множителей:
$$log_{0,5}6+log_{0,5}(2-x)geqlog_{0,5}(4-x)+log_{0,5}(2-x)+log_{0,5}(x+3)$$
$$log_{0,5} 6geqlog_{0,5}(4-x)+log_{0,5}(x+3)$$
Сумма логарифмов равна логарифму произведения подлогарифмических выражений:
$$log_{0,5} 6geqlog_{0,5} ((4-x)(x+3))$$
Так как основание логарифмического неравенства 0 < 0,5 < 1, то логарифмическое неравенство равносильно неравенству:
$$6leq(4-x)(x+3)$$
$$6leq4x+12-x^2-3x$$
$$6-4x-12+x^2+3xleq0$$
$$x^2-x-6leq0$$
Решим неравенство методом интервалов, найдем нули квадратного трехчлена:
$$x^2-x-6=0$$
$$D=(-1)^2-4cdot1cdot(-6)=25$$
$$x_{1,2}=frac{1pm5}{2}$$
$$x_1=-2; x_2=3$$
$$xin (-2;3)$$
Учитывая ОДЗ неравенства, найдем его решение:
$$xin [-2;2)$$
Задание 15
15 января планируется взять кредит в банке на некоторый срок (целое число месяцев). Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
На сколько месяцев планируется взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 20 % больше суммы, взятой в кредит? (Считайте, что округления при вычислении платежей не производятся.)
Ответ: 39
Скрыть
Пусть сумма кредита равна S, а кредит планируется взять на n месяцев. По условию, долг перед банком по состоянию на 15-е число должен уменьшаться до нуля равномерно:
$$S;frac{S(n-1)}{n};cdots;frac{2S}{n};frac{S}{n};0$$
Первого числа каждого месяца долг возрастает на 1%, значит, последовательность размеров долга на 1-е число каждого месяца такова:
$$1,01S;frac{1,01S(n-1)}{n};cdots;frac{2,02S}{n};frac{1,01S}{n}$$
Следовательно, выплаты должны быть следующими:
$$0,01S+frac{S}{n};frac{0,01S(n-1)}{n};cdots;frac{0,02S}{n}+frac{S}{n};frac{0,01S}{n}+frac{S}{n}$$
Всего следует выплатить
$$S+0,01S(frac{n}{n}+frac{n-1}{n}+cdots+frac{2}{n}+frac{1}{n})=S(1+frac{0,01(n+1)}{2})$$
Общая сумма выплат на 20 % больше суммы, взятой в кредит, поэтому
$$frac{0,01(n+1)}{2}=0,2Rightarrow n=39$$
Задание 16
Точка $$О$$ — центр вписанной в треугольник $$АВС$$ окружности. Прямая $$ВО$$ вторично пересекает описанную около этого треугольника окружность в точке $$Р.$$
а) Докажите, что $$angle РОА=angle РАО.$$
б) Найдите площадь треугольника $$АРО,$$ если радиус описанной около треугольника $$АВС$$ окружности равен $$6,$$ $$angle BAC=75^{circ}, angle ABC=60^{circ}.$$
Ответ: $$9sqrt{2}$$
Скрыть
а) Поскольку точка О — центр вписанной в треугольник ABC окружности, лучи АО и ВО являются биссектрисами углов треугольника ABC. Угол РОА является внешним углом треугольника АОВ. Следовательно,
$$angle POA=angle BAO+angle ABO=frac{1}{2}angle BAC+frac{1}{2}angle ABC$$
Углы РАС и РВС равны, поскольку опираются на одну и ту же дугу окружности, описанной около треугольника ABC, поэтому
$$angle PAO=angle PAC+angle OAC=angle PBC+angle OAC=frac{1}{2}angle ABC+frac{1}{2}angle BAC$$
Таким образом, $$angle POA=angle PAO$$.
б) Пусть R = 6 — радиус окружности, описанной около треугольника ABC.
Поскольку $$angle POA=angle PAO,$$ треугольник АРО равнобедренный, следовательно,.
$$OP=AP=2Rsinangle ABP=2Rsin 30^{circ}=6$$
Таким образом, площадь треугольника АРО равна
$$frac{APcdot OPcdotsinangle APO}{2}=frac{AP^2cdotsinangle ACB}{2}=frac{AP^2cdotsin 45^{circ}}{2}=9sqrt{2}$$
Задание 17
Найдите все значения $$a$$, при каждом из которых уравнение $$frac{left|3xright|-2x-2-a}{x^2-2x-a}=0$$ имеет ровно два различных корня.
Ответ: $$-2<a<-1; -1<a<0; 0<a<3; 3<a<8; a>8$$
Задание 18
В ящике лежит 76 фруктов, масса каждого из которых выражается целым числом граммов. В ящике есть хотя бы два фрукта различной массы, а средняя масса всех фруктов равна 100 г. Средняя масса фруктов, масса каждого из которых меньше 100 г, равна 85 г. Средняя масса фруктов, масса каждого из которых больше 100 г, равна 124 г.
а) Могло ли в ящике оказаться поровну фруктов массой меньше 100 г и фруктов массой больше 100 г?
б) Могло ли в ящике оказаться меньше 8 фруктов, масса каждого из которых равна 100 г?
в) Какую наибольшую массу может иметь фрукт в этом ящике?
Ответ: нет, нет, 676 гр.
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Решение заданий варианта №21 из сборника ОГЭ 2023 по математике И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.
ЧАСТЬ 1
Задание 1-5.
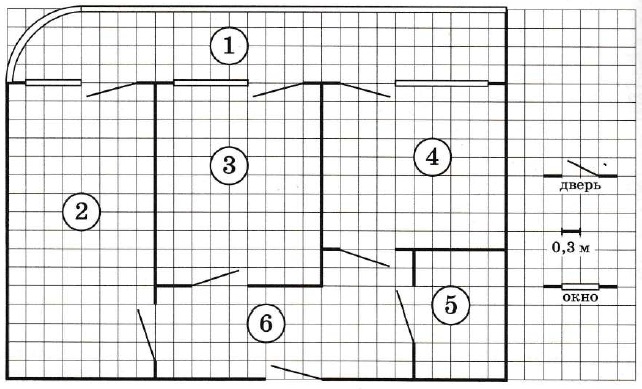
Задание 6.
Найдите значение выражения frac{9}{16}:(-frac{3}{40})+4,7.
Задание 7.
Одно из чисел √28, √33, √38, √47 отмечено на прямой А.
Какое это число?
1)√28 2)√33 3)√38 4)√47
Задание 8.
Найдите значение выражения frac{(a^{4})^{-3}}{a^{-15}} при а = 2.
Задание 9.
Найдите корень уравнения (х + 10)2 = (5 – х)2.
Задание 10.
В магазине канцтоваров продаётся 200 ручек: 31 красная, 25 зеленых, 38 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или черной.
Задание 11.
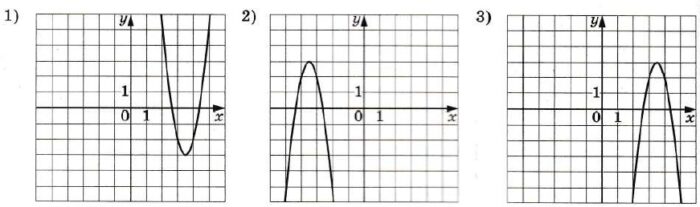
Установите соответствие между формулами, которыми заданы функции, и графиками этих функций.
ФОРМУЛЫ
А) у = –4х2 – 28х – 46
Б) у = 4х2 – 28х + 46
С) у = –4х2 + 28х – 46
ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.
Задание 12.
Центростремительное ускорение при движении по окружности (в м/с2) вычисляется по формуле a = ω2R, где ω – угловая скорость (в с-1), R – радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус R, если угловая скорость равна 9 с-1, а центростремительное ускорение равно 243 м/с2. Ответ дайте в метрах.
Задание 13.
Укажите решение неравенства (х + 2)(х – 7) > 0
Задание 14.
В течение 20 банковских дней акции компании дорожали ежедневно на одну и ту же сумму. Сколько стоила акция компании в последний день этого периода, если в 9-й день акция стоила 888 рублей, а в 13-й день – 940 рублей?
Задание 15.
Сторона треугольника равна 29, а высота, проведённая к этой стороне, равна 12. Найдите площадь этого треугольника.
Задание 16.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 38º, угол CAD равен 33º. Найдите угол ABD. Ответ дайте в градусах.
Задание 17.
Диагональ прямоугольника образует угол 47° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Задание 18.
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Задание 19.
Какие из следующих утверждений верны?
1) Основания любой трапеции параллельны.
2) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
3) Все углы ромба равны.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
ЧАСТЬ 2
Задание 20.
Решите уравнение x6 = –(12 – 8x)3.
Задание 21.
Два велосипедиста одновременно отправились в 208-километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым.
Задание 22.
Постройте график функции у = х2 – 4|х| – х и определите, при каких значениях m прямая у = m имеет с графиком не менее одной, но не более трёх общих точек.
Задание 23.
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 6:13:17. Найдите радиус окружности, если меньшая из сторон равна 18.
Задание 24.
Основания ВС и АD трапеции АВСВ равны соответственно 5 и 45, BD = 15. Докажите, что треугольники СВD и ВDА подобны.
Задание 25.
Биссектрисы углов А и В параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если ВС = 6, а расстояние от точки K до стороны АВ равно 6.
Источник варианта: Сборник ОГЭ 2023 по математике. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 1
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Ответы к 36 вариантам профильного ЕГЭ по математике. Сборник ЕГЭ-2023 «Типовые экзаменационные варианты».
Вариант 1
1) 5,5
2) 2048
3) 0,06
4) 0,89
5) -0,2
6) 0,5
7) 5

9) 2
10) -4
11) -2910
Вариант 2
1) 7,5
2) 4
3) 0,12
4) 0,91
5) -0,9
6) 0,2
7) 1

9) 16
10) -8
11) 12,25
Вариант 3
1) 2,5
2) 30
3) 0,37
4) 0,375
5) -2,5
6) 4
7) 2

9) 14
10) 32
11) 204
Вариант 4
1) 1,5
2) 12
3) 0,24
4) 0,125.
5) 0,375
6) 125
7) 8

9) 18
10) -56
11) -10,9
Вариант 5
1) 99,5
2) 12
3) 0,004 /или/ -0,004
4) 0,9409
5) -0,5
6) 2
7) -19

9) 17
10) 16
11) -52
Вариант 6
1) 55
2) 18
3) 0,006 /или/ -0,006
4) 0,8464
5) -5,5
6) 3
7) -4

9) 24
10) -1
11) -6
Вариант 7
1) 0,2
2) 10
3) 0,2
4) 0,56
5) -0,4
6) -1
7) 9

9) 55
10) 6
11) 0,5
Вариант 8
1) 0,4
2) 5
3) 0,125
4) 0,46
5) -7
6) -1
7) 7

9) 11
10) 0,25
11) 17
Вариант 9
1) 3
2) 15 625
3) 0,01
4) 0,28
5) -12
6) 144
7) -1

9) 20
10) -3
11) 9
Вариант 10
1) 0,6
2) 150
3) 0,28
4) 0,17
5) -2,6
6) 625
7) -18

9) 9
10) 253
11) -23,25
Вариант 11
1) -0,7
2) 72
3) 0,25
4) 0,043
5) -0,2
6) -5
7) -1

9) 17,5
10) 78
11) 6,75
Вариант 12
1) 0,75
2) 24
3) 0,55
4) 0,02
5) -1,5
6) -4
7) 4

9) 13,5
10) -23
11) 6,25
Вариант 13
1) 8
2) 48
3) 0,4
4) 0,6
5) -9
6) 0,5
7) 4

9) 9
10) -0,5
11) 77
Вариант 14
1) 14
2) 40,5
3) 0,28
4) 0,78
5) -2
6) 0,04
7) 39

9) 24
10) 0,4
11) 37
Вариант 15
1) 11,55
2) 432
3) 0,014
4) 0,06
5) -9
6) 0,25
7) 2

9) 3
10) 2,5
11) 208
Вариант 16
1) 12
2) 192
3) 0,29
4) 0,02
5) -8
6) 0,125
7) 4

9) 1
10) -15
11) 5
Вариант 17
1) 10
2) 80
3) 0,08
4) 0,2
5) -2,5
6) 216
7) -2

9) 18
10) 16
11) -24
Вариант 18
1) 35
2) 10
3) 0,2
4) 0,24
5) -0,2
6) 3,5
7) 28

9) 21
10) 2,25
11) -15
Вариант 19
1) 2,5
2) 7,28
3) 0,25
4) 0,22
5) -1,5
6) 1
7) 0,2

9) 135
10) 2
11) -34
Вариант 20
1) 6
2) 7,68
3) 0,75
4) 0,27
5) -4,5
6) 10
7) -0,25

9) 52
10) 27
11) 0
Вариант 21
1) 113
2) 60
3) 0,2
4) 0,973
5) 5,5
6) 324
7) 2

9) 14
10) 15
11) 7
Вариант 22
1) 0,75
2) 45
3) 0,3
4) 0,9744
5) 11
6) -7,5
7) 7

9) 5
10) 3,4
11) 1,2
Вариант 23
1) 62
2) 25
3) 0,25
4) 0,3
5) -2
6) 80
7) 6

9) 75
10) 28
11) 18
Вариант 24
1) 78
2) 20
3) 0,2
4) 0,82
5) 0
6) 28
7) 6

9) 10
10) -28
11) -2
Вариант 25
1) 37
2) 135
3) 0,18
4) 3
5) 0,8
6) 0,4
7) -0,2

9) 1 35
10) -0,4
11) 14
Вариант 26
1) 53
2) 72
3) 0,38
4) 5
5) -4
6) -0,3
7) -0,75

9) 28
10) -13
11) 1
Вариант 27
1) 29
2) 315
3) 0,14
4) 0,03
5) 4
6) 2,72
7) 6

9) 77
10) 76
11) -3
Вариант 28
1) 6
2) 176
3) 0,375
4) 0,012
5) -1
6) -3
7) -3

9) 6
10) -5
11) 38
Вариант 29
1) 60
2) 18
3) 0,24
4) 0,2
5) 3
6) 4
7) 4

9) 6,4
10) 67
11) -21
Вариант 30
1) 64
2) 4
3) 0,28
4) 0,6
5) 4
6) 8
7) 14

9) 22
10) 3
11) -8
Вариант 31
1) 6,5
2) 54
3) 0,98
4) 0,2
5) 2
6) -10
7) 2

9) 54
10) -7
11) 8
Вариант 32
1) 30
2) 27
3) 0,024
4) 0,15
5) -2
6) 91
7) 3

9) 12
10) 13
11) -9
Вариант 33
1) 72,5
2) 47
3) 0,28
4) 0,097
5) -5
6) 65
7) 3

9) 48
10) -2,5
11) 26
Вариант 34
1) 68
2) 76
3) 0,16
4) 0,068
5) 6
6) 16
7) 6

9) 64
10) -0,25
11) -1
Вариант 35
1) 21
2) 200
3) 0,56
4) 0,9
5) -2
6) 7,5
7) 0,5

9) 20
10) 0,75
11) 9
Вариант 36
1) 35
2) 88
3) 0,12
4) 12
5) -5
6) 2,5
7) 5,5

9) 756
10) -0,5
11) 30
Перейти к содержимому

Читать онлайн и скачать сборник в формате PDF: Скачать
* Еще больше пособий ЕГЭ и ОГЭ
* Учебные материалы
Поделиться:
Наверх

Скачать бесплатно сборник Ященко И.В. ЕГЭ 2023 профильный уровень математика 11 класс 36 тренировочных вариантов с ответами и решением.
Скачать сборник Ященко ЕГЭ 2023 в PDF
Аннотация к сборнику «ЕГЭ 2023. Математика. Профильный уровень. Типовые экзаменационные варианты. 36 вариантов» Серия подготовлена разработчиками контрольных измерительных материалов (КИМ) единого государственного экзамена.
Ященко ЕГЭ 2023 математика профиль 36 вариантов
В сборнике представлены: -36 типовых экзаменационных вариантов, составленных в соответствии с проектом демоверсии КИМ ЕГЭ по математике профильного уровня 2023 года; — инструкция по выполнению экзаменационной работы; — ответы ко всем заданиям; — решения и критерии оценивания заданий 12-18.
Выполнение заданий типовых экзаменационных вариантов предоставляет обучающимся возможность самостоятельно подготовиться к государственной итоговой аттестации, а также объективно оценить уровень своей подготовки.
Учителя могут использовать типовые экзаменационные варианты для организации контроля результатов освоения школьниками образовательных программ среднего общего образования и интенсивной подготовки обучающихся к ЕГЭ. Под редакцией И. В. Ященко.
-
Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением
-
Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Ответы к пособию для подготовки ЕГЭ-2023 по математике. Профильный уровень. Типовые экзаменационные варианты. Под редакцией И. В. Ященко. 36 вариантов.
| Вариант 1 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 5.5 | 10 | -4 |
| 2 | 2048 | 11 | -2910 |
| 3 | 0.06 | 12 | 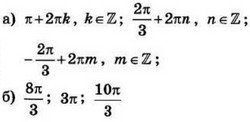 |
| 4 | 0.89 | 13 | б) 24 |
| 5 | -0.2 | 14 | 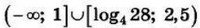 |
| 6 | 0.5 | 15 | 400 тыс. рублей |
| 7 | 5 | 16 | б) 14.2 |
| 8 | 5.832 | 17 | (-4; -3) ∪ (-3; -1) ∪ (-1; 0) |
| 9 | 2 | 18 | а) да; б) нет; в) 205 |
| Вариант 2 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 7.5 | 10 | -8 |
| 2 | 4 | 11 | 12.25 |
| 3 | 0.12 | 12 | 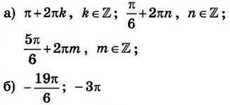 |
| 4 | 0.91 | 13 | б) 26 |
| 5 | -0.9 | 14 | 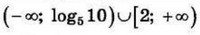 |
| 6 | 0.2 | 15 | 210 тыс. рублей |
| 7 | 1 | 16 | б) 29.7 |
| 8 | 0.216 | 17 | (0; 0.8) ∪ (0.8; 3.2) ∪ (3.2; 4) |
| 9 | 16 | 18 | а) да; б) нет; в) 195 |
| Вариант 3 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 2.5 | 10 | 32 |
| 2 | 30 | 11 | 204 |
| 3 | 0.37 | 12 | 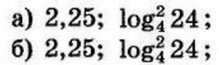 |
| 4 | 0.375 | 13 | б) 180 |
| 5 | -2.5 | 14 | 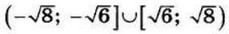 |
| 6 | 4 | 15 | 7.28 млн рублей |
| 7 | 2 | 16 | б) 32 |
| 8 | 51.2 | 17 | 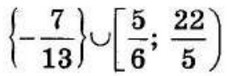 |
| 9 | 14 | 18 | а) да; б) да; в) 2295 |
| Вариант 4 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 1.5 | 10 | -56 |
| 2 | 12 | 11 | -10.9 |
| 3 | 0.24 | 12 |  |
| 4 | 0.125 | 13 | б) 40 |
| 5 | 0.375 | 14 | 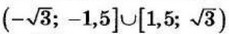 |
| 6 | 125 | 15 | 8 937 тыс. рублей |
| 7 | 8 | 16 | 42.16 |
| 8 | 281.25 | 17 | 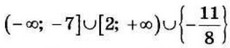 |
| 9 | 18 | 18 | а) да; б) нет; в) 897 |
| Вариант 5 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 99.5 | 10 | 16 |
| 2 | 12 | 11 | -52 |
| 3 | 0.004 или -0.004 | 12 | 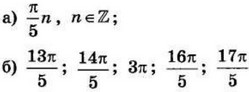 |
| 4 | 0.9409 | 13 | 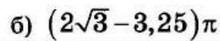 |
| 5 | -0.5 | 14 | 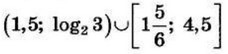 |
| 6 | 2 | 15 | 8.4 млн рублей |
| 7 | -19 | 16 | б) 9.1 |
| 8 | 60 | 17 | 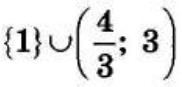 |
| 9 | 17 | 18 | а) нет; б) нет; в) 36 |
| Вариант 6 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 55 | 10 | -1 |
| 2 | 18 | 11 | -6 |
| 3 | 0.006 или -0.006 | 12 | 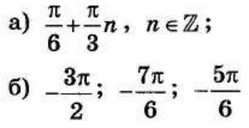 |
| 4 | 0.8464 | 13 | 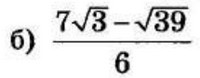 |
| 5 | -5.5 | 14 | 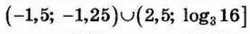 |
| 6 | 3 | 15 | 5.65 млн рублей |
| 7 | -4 | 16 | 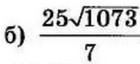 |
| 8 | 30 | 17 | 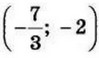 |
| 9 | 24 | 18 | а) нет; б) нет; в) 57, 58, 59, 60, 61 |
| Вариант 7 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 0.2 | 10 | 6 |
| 2 | 10 | 11 | 0.5 |
| 3 | 0.2 | 12 | 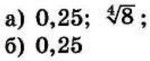 |
| 4 | 0.56 | 13 | б) 3 |
| 5 | -0.4 | 14 | 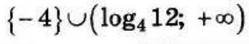 |
| 6 | -1 | 15 | 8 млн рублей |
| 7 | 9 | 16 | б) 6√2 |
| 8 | 0.6 | 17 | 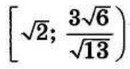 |
| 9 | 55 | 18 | а) да; б) нет; в) 79 |
| Вариант 8 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 0.4 | 10 | 0.25 |
| 2 | 5 | 11 | 17 |
| 3 | 0.125 | 12 | 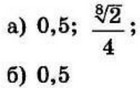 |
| 4 | 0.46 | 13 | 6√3 |
| 5 | -7 | 14 | 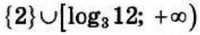 |
| 6 | -1 | 15 | 13 млн рублей |
| 7 | 7 | 16 | 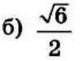 |
| 8 | 1.8 | 17 | 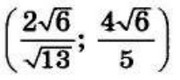 |
| 9 | 11 | 18 | а) да; б) нет; в) 73 |
| Вариант 9 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 3 | 10 | -3 |
| 2 | 15 625 | 11 | 9 |
| 3 | 0.01 | 12 | 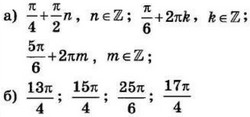 |
| 4 | 0.28 | 13 | 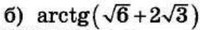 |
| 5 | -12 | 14 | (-∞; -1) |
| 6 | 144 | 15 | 7 млн рублей |
| 7 | -1 | 16 | 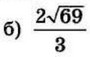 |
| 8 | 756 | 17 | 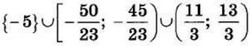 |
| 9 | 20 | 18 | а) да; б) нет; в) 176 |
| Вариант 10 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 0.6 | 10 | 253 |
| 2 | 150 | 11 | -23.25 |
| 3 | 0.28 | 12 | 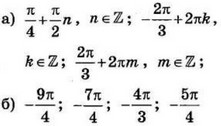 |
| 4 | 0.17 | 13 | 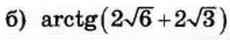 |
| 5 | -2.6 | 14 | (-∞; -2) |
| 6 | 625 | 15 | 4 млн рублей |
| 7 | -18 | 16 | 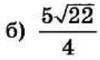 |
| 8 | 220.5 | 17 | 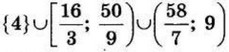 |
| 9 | 9 | 18 | а) нет; б) нет; в) 1933 |
| Вариант 11 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | -0.7 | 10 | 78 |
| 2 | 72 | 11 | 6.75 |
| 3 | 0.25 | 12 | 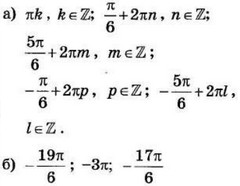 |
| 4 | 0.043 | 13 | б) 80√3 |
| 5 | -0.2 | 14 | (-∞; 0] ∪ [2; 3] |
| 6 | -5 | 15 | 600 тыс. рублей |
| 7 | -1 | 16 | 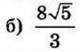 |
| 8 | 50 | 17 | {-5} ∪ (-1; 0) |
| 9 | 17.5 | 18 | а) да; б) нет; в) 97 |
| Вариант 12 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 0.75 | 10 | -23 |
| 2 | 24 | 11 | 6.25 |
| 3 | 0.55 | 12 | 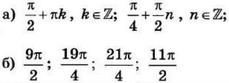 |
| 4 | 0.02 | 13 | б) 150 |
| 5 | -1.5 | 14 | (-∞; 0) ∪ (log53; 1) |
| 6 | -4 | 15 | 750 тыс. рублей |
| 7 | 4 | 16 | 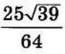 |
| 8 | 40 | 17 | 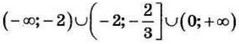 |
| 9 | 13.5 | 18 | а) да; б)нет; в) 85 |
| Вариант 13 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 8 | 10 | -0.5 |
| 2 | 48 | 11 | 77 |
| 3 | 0.4 | 12 | а) -2; -1 б) -1 |
| 4 | 0.6 | 13 | б) 5√3 |
| 5 | -9 | 14 | (1; 3] |
| 6 | 0.5 | 15 | 37 |
| 7 | 4 | 16 | б) 120/13 |
| 8 | 33 | 17 | [4√3; 12] |
| 9 | 9 | 18 | а) да; б) нет; в) 23/20 |
| Вариант 14 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 14 | 10 | 0.4 |
| 2 | 40.5 | 11 | 37 |
| 3 | 0.28 | 12 | 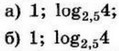 |
| 4 | 0.78 | 13 | 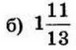 |
| 5 | -2 | 14 | [-3; -1) |
| 6 | 0.04 | 15 | 3 |
| 7 | 39 | 16 | б) 4 |
| 8 | 23 | 17 | 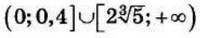 |
| 9 | 24 | 18 | 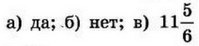 |
| Вариант 15 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 11.55 | 10 | 2.5 |
| 2 | 432 | 11 | 208 |
| 3 | 0.014 | 12 | 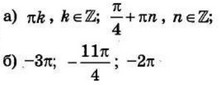 |
| 4 | 0.06 | 13 | 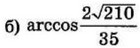 |
| 5 | -9 | 14 | (-1; 0) |
| 6 | 0.25 | 15 | 16 |
| 7 | 2 | 16 | б) 6 |
| 8 | 0.32 | 17 | 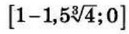 |
| 9 | 3 | 18 | а) да; б) нет; в) 26 |
| Вариант 16 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 12 | 10 | -15 |
| 2 | 192 | 11 | 5 |
| 3 | 0.29 | 12 | 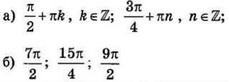 |
| 4 | 0.02 | 13 | 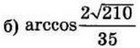 |
| 5 | -8 | 14 | (-∞; -0.5) |
| 6 | 0.125 | 15 | 19 |
| 7 | 4 | 16 | б) 8 |
| 8 | 1.16 | 17 | 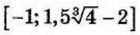 |
| 9 | 1 | 18 | а) да; б) нет; в) 80 |
| Вариант 17 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 10 | 10 | 16 |
| 2 | 80 | 11 | -24 |
| 3 | 0.08 | 12 | 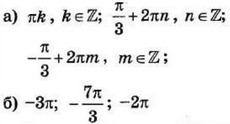 |
| 4 | 0.2 | 13 | б) 45° |
| 5 | -2.5 | 14 | 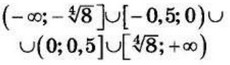 |
| 6 | 216 | 15 | 29 |
| 7 | -2 | 16 | б) 5/3 |
| 8 | 175 | 17 | -1/2; 2 |
| 9 | 18 | 18 | а) нет; б) да; в) 306 |
| Вариант 18 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 35 | 10 | 2.25 |
| 2 | 10 | 11 | -15 |
| 3 | 0.2 | 12 | 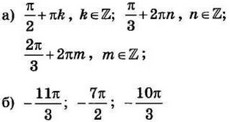 |
| 4 | 0.24 | 13 | б) arctg 0.5 |
| 5 | -0.2 | 14 | 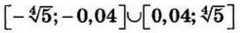 |
| 6 | 3.5 | 15 | 24 |
| 7 | 28 | 16 | б) 2.4 |
| 8 | 43.75 | 17 | 1; 9 |
| 9 | 21 | 18 | а) нет; б) да; в) 552 |
| Вариант 19 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 2.5 | 10 | 2 |
| 2 | 7.28 | 11 | -34 |
| 3 | 0.25 | 12 | 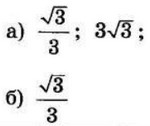 |
| 4 | 0.22 | 13 | б) 0.3√30 |
| 5 | -1.5 | 14 | (-∞; -1] ∪ [2; +∞) |
| 6 | 1 | 15 | 1300 тыс. рублей |
| 7 | 0.2 | 16 | б) 71° |
| 8 | 115 | 17 | 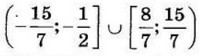 |
| 9 | 135 | 18 |  |
| Вариант 20 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 6 | 10 | 27 |
| 2 | 7.68 | 11 | 0 |
| 3 | 0.75 | 12 | 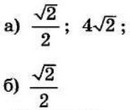 |
| 4 | 0.27 | 13 | б) arctg 2 |
| 5 | -4.5 | 14 | [-5; 0) ∪ (0; 2.5] |
| 6 | 10 | 15 | 2541 тыс. рублей |
| 7 | -0.25 | 16 | 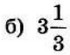 |
| 8 | 220 | 17 | 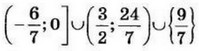 |
| 9 | 52 | 18 | а) 42; б) положительных; в) 24 |
| Вариант 21 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 113 | 10 | 15 |
| 2 | 60 | 11 | 7 |
| 3 | 0.2 | 12 | 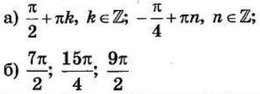 |
| 4 | 0.973 | 13 | 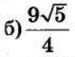 |
| 5 | 5.5 | 14 | 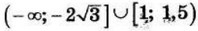 |
| 6 | 324 | 15 | 500 тыс. рублей |
| 7 | 2 | 16 | б) 4.8 |
| 8 | 6250 | 17 | 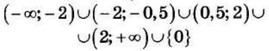 |
| 9 | 14 | 18 | 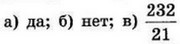 |
| Вариант 22 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 0.75 | 10 | 3.4 |
| 2 | 45 | 11 | 1.2 |
| 3 | 0.3 | 12 | 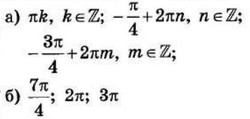 |
| 4 | 0.9744 | 13 |  |
| 5 | 11 | 14 | 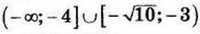 |
| 6 | -7.5 | 15 | 20 |
| 7 | 7 | 16 | б) 7.5 |
| 8 | 1.3 | 17 | [1; 9) |
| 9 | 5 | 18 | а) да; б) нет; в) 10 |
| Вариант 23 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 62 | 10 | 28 |
| 2 | 25 | 11 | 18 |
| 3 | 0.25 | 12 | 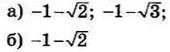 |
| 4 | 0.3 | 13 | 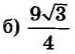 |
| 5 | -2 | 14 | (-∞; -1) ∪ {0} ∪ (0.5; +∞) |
| 6 | 80 | 15 | 35 700 рублей |
| 7 | 6 | 16 | 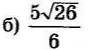 |
| 8 | 60 | 17 |  |
| 9 | 75 | 18 | а) 7; б) 15; в) 14 |
| Вариант 24 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 78 | 10 | -28 |
| 2 | 20 | 11 | -2 |
| 3 | 0.2 | 12 | 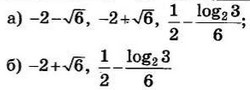 |
| 4 | 0.82 | 13 | 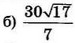 |
| 5 | 0 | 14 | 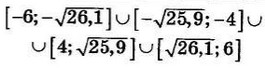 |
| 6 | 28 | 15 | 53 820 рублей |
| 7 | 6 | 16 | 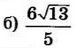 |
| 8 | 30 | 17 | 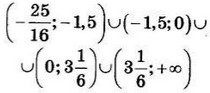 |
| 9 | 10 | 18 | а) 12; б) 15; в) 6 |
| Вариант 25 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 37 | 10 | -0.4 |
| 2 | 135 | 11 | 14 |
| 3 | 0.18 | 12 | 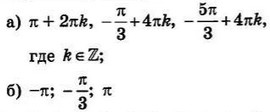 |
| 4 | 3 | 13 | б) 36 |
| 5 | 0.8 | 14 | 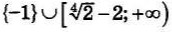 |
| 6 | 0.4 | 15 | 1 080 000 рублей |
| 7 | -0.2 | 16 | 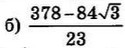 |
| 8 | 6 | 17 | 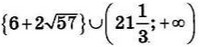 |
| 9 | 35 | 18 | а) нет; б) 21; в) 82 |
| Вариант 26 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 53 | 10 | -13 |
| 2 | 72 | 11 | 1 |
| 3 | 0.38 | 12 | 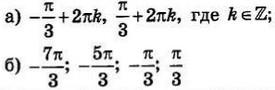 |
| 4 | 5 | 13 | б) 189 |
| 5 | -4 | 14 | (-0.5; 0.5) ∪ (0.5; 624.5) |
| 6 | -0.3 | 15 | 1 706 400 рублей |
| 7 | -0.75 | 16 | б) 91(5√2 — 7) |
| 8 | 96 | 17 | 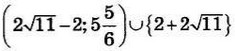 |
| 9 | 28 | 18 | а) нет; б) 36; в) 182 |
| Вариант 27 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 29 | 10 | 76 |
| 2 | 315 | 11 | -3 |
| 3 | 0.14 | 12 | 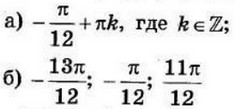 |
| 4 | 0.03 | 13 | б) 45° |
| 5 | 4 | 14 | (-1; 0) ∪ {log53} |
| 6 | 2.72 | 15 | 54 925 рублей |
| 7 | 6 | 16 | б) 8 |
| 8 | 7 | 17 | [0; 1.5) ∪ [2; +∞) |
| 9 | 77 | 18 | а) да; б) нет; в) 16 |
| Вариант 28 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 6 | 10 | -5 |
| 2 | 176 | 11 | 38 |
| 3 | 0.375 | 12 | 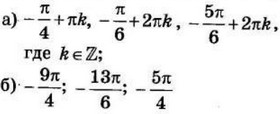 |
| 4 | 0.012 | 13 | 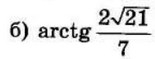 |
| 5 | -1 | 14 |  |
| 6 | -3 | 15 | 78 125 рублей |
| 7 | -3 | 16 | б) 18 |
| 8 | 28 | 17 | 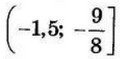 |
| 9 | 6 | 18 | а) да; б) нет; в) 12 |
| Вариант 29 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 60 | 10 | 67 |
| 2 | 18 | 11 | -21 |
| 3 | 0.24 | 12 | 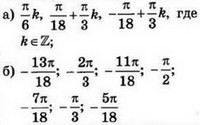 |
| 4 | 0.2 | 13 | б) 36 + 30√2 |
| 5 | 3 | 14 | [2; 5) |
| 6 | 4 | 15 | 126 694.4 рубля |
| 7 | 4 | 16 | б) 1 |
| 8 | 6.5 | 17 | 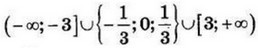 |
| 9 | 6.4 | 18 | а) да; б) нет; в) 2805 |
| Вариант 30 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 64 | 10 | 3 |
| 2 | 4 | 11 | -8 |
| 3 | 0.28 | 12 | 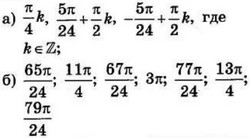 |
| 4 | 0.6 | 13 | 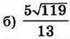 |
| 5 | 4 | 14 | (0; 5] |
| 6 | 8 | 15 | 1-й объект — 7 человек 2-й объект — 23 человека; 43 150 рублей |
| 7 | 14 | 16 | б) 50 |
| 8 | 9.6 | 17 | 4 < a ≤ 16 |
| 9 | 22 | 18 | а) да; б) нет; в) 2220 |
| Вариант 31 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 6.5 | 10 | -7 |
| 2 | 54 | 11 | 8 |
| 3 | 0.98 | 12 | 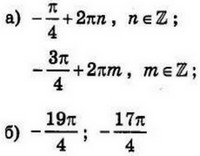 |
| 4 | 0.2 | 13 | 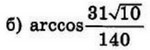 |
| 5 | 2 | 14 | [-2; 2) |
| 6 | -10 | 15 | 39 |
| 7 | 2 | 16 | б) 9√2 |
| 8 | 25 | 17 | 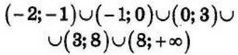 |
| 9 | 54 | 18 | а) нет; б) нет; в) 676 г. |
| Вариант 32 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 30 | 10 | 13 |
| 2 | 27 | 11 | -9 |
| 3 | 0.024 | 12 | 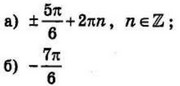 |
| 4 | 0.15 | 13 | 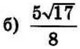 |
| 5 | -2 | 14 | (-2; 1) ∪ (1; 2) |
| 6 | 91 | 15 | 1.6 млн рублей |
| 7 | 3 | 16 | б) 27√3 |
| 8 | 17 | 17 | 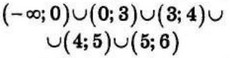 |
| 9 | 12 | 18 | а) нет; б) нет; в) 240 г |
| Вариант 33 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 72.5 | 10 | -2.5 |
| 2 | 47 | 11 | 26 |
| 3 | 0.28 | 12 | 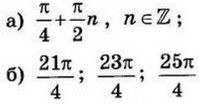 |
| 4 | 0.097 | 13 | б) 13√6 |
| 5 | -5 | 14 | 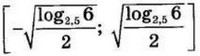 |
| 6 | 65 | 15 | 2.58 |
| 7 | 3 | 16 | б) 5 : 7 |
| 8 | 8 | 17 | 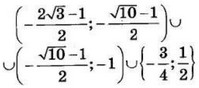 |
| 9 | 48 | 18 | а) нет; б) нет; в) 3 |
| Вариант 34 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 68 | 10 | -0.25 |
| 2 | 76 | 11 | -1 |
| 3 | 0.16 | 12 | 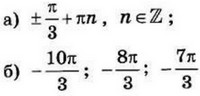 |
| 4 | 0.068 | 13 | б) 48.5 |
| 5 | 6 | 14 | 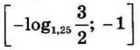 |
| 6 | 16 | 15 | 4.05 |
| 7 | 6 | 16 | б) 10 : 11 |
| 8 | 633 | 17 | 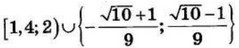 |
| 9 | 64 | 18 | а) да; б) нет; в) 5 |
| Вариант 35 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 21 | 10 | 0.75 |
| 2 | 200 | 11 | 9 |
| 3 | 0.56 | 12 | 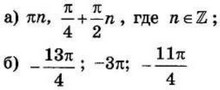 |
| 4 | 0.9 | 13 | б) 4√3 |
| 5 | -2 | 14 | [3 — √5; 2.8] ∪ [3.2; 3 + √5] |
| 6 | 7.5 | 15 | 20 |
| 7 | 0.5 | 16 | б) 1 : 3 : 1 |
| 8 | 0.31 | 17 | [-3; 22] |
| 9 | 20 | 18 | а) да; б) 180; в) 546 |
| Вариант 36 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 35 | 10 | -0.5 |
| 2 | 88 | 11 | 30 |
| 3 | 0.12 | 12 | 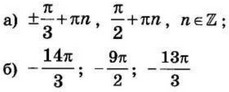 |
| 4 | 12 | 13 | б) 6√3 |
| 5 | -5 | 14 | 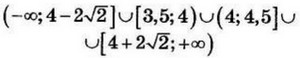 |
| 6 | 2.5 | 15 | 3 |
| 7 | 5.5 | 16 | б) 4 : 5 : 4 |
| 8 | 1.728 | 17 | (-∞; 4 — 2√2] ∪ ∪ [3.5; 4) ∪ ∪ (4; 4.5] ∪ ∪ [4 + 2√2; +∞) |
| 9 | 756 | 18 | а) да; б) 270; в) 17 |