По теме: методические разработки, презентации и конспекты
Проверочная работа при подготовке к ЕГЭ, 11 класс
Проверочная работа составлена в двух вариантах. Рекомендуется проводить после повторения тем «Показательная функция» и «Логарифмическая функция». 11 класс…
Анализ результатов проверочной работы по подготовке к ЕГЭ по обществознанию (11класс)
Назначение работы.Единый государственный экзамен (ЕГЭ) представляет собой форму объективной оценки качества подготовки лиц, освоивших образовательныепрограммы среднего общего образования, с испол…
Методическая разработка проверочной работы по подготовке к Всероссийской проверочной работе, 11 класс
Веселова Татьяна Андреевна, учитель географии ГБОУ лицея №150 Калининского района Санкт-Петербурга.Данная методическая разработка позволит учителю подготвоить учащихся 11-х классов к итоговой ат…
9 класс. Подготовка к ОГЭ. Задание № 20. Задания для подготовки и проверочная работа.
В данной методической разработке представлены 12 заданий из сборника подготовки к ОГЭ, 9 класс «Анализ геометрических высказываний» (задание № 20). Эти задания можно разобрать в классе…
Организация и подготовка к Всероссийским проверочным работам. (из опыта работы)
МБОУ «Ивановская ООШ»…
Практика работы по подготовке к Всероссийской проверочной работе по русскому языку
Здесь можно узнать о формах организации учебной деятельности при подготовке учащихся 5-8-х классов к ВПР, познакомиться с электронными ресурсами, которые помогут успешно подготовиться к ВПР…
Проверочные работы для подготовки к ЕГЭ «ПЛАНИМЕТРИЯ»
1. Проверочная рработа по теме «Треугольник».2. Проверочная работа по теме :»Четырехугольник»3. Проверочная работа по теме : «Окружность».Материалы взяты с сайта «Ре…
Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
В основании правильной треугольной призмы ABCA1B1C1 лежит треугольник со стороной 6. Высота призмы равна 4. Точка N — середина ребра A1C1.
а) Постройте сечение призмы плоскостью BAN.
б) Найдите периметр этого сечения.
2
В правильной четырехугольной пирамиде PABCD, все ребра которой равны 4, точка K ― середина бокового ребра AP.
а) Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной прямым PB и BC.
б) Найдите площадь сечения.
Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 1.
3
На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E : EA = 5 : 3, на ребре BB1 — точка F так, что B1F : FB = 5 : 11, а точка T − середина ребра B1C1. Известно, что AD = 10, AA1 = 16.
а) Докажите, что плоскость EFT проходит через вершину D1.
б) Найдите площадь сечения параллелепипеда плоскостью EFT.
4
На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E = 6EA. Точка T — середина ребра B1C1. Известно, что AD = 12, AA1 = 14.
а) Докажите, что плоскость ETD1 делит ребро BB1 в отношении 4 : 3.
б) Найдите площадь сечения параллелепипеда плоскостью ETD1.
5
Основанием прямой четырехугольной призмы ABCDA’B’C’D’ является квадрат ABCD со стороной высота призмы равна
Точка K — середина ребра BB’. Через точки K и С’ проведена плоскость α, параллельная прямой BD’.
а) Докажите, что сечение призмы плоскостью α является равнобедренным треугольником.
б) Найдите периметр треугольника, являющегося сечением призмы плоскостью α.
Источник: ЕГЭ по математике 2015. Досрочная волна, резервная волна (часть С)
Пройти тестирование по этим заданиям
Тренажёр по геометрии. Стереометрия в задачах ЕГЭ.

Тест предназначен для учащихся 11 классов для проверки уровня подготовки к государственной итоговой аттестации по геометрии, в нём содержатся задачи по разделу «Стереометрия». В тесте 9 задач из Открытого банка. Ответом для каждого задания служит целое число или десятичная дробь.
Для подготовки к ЕГЭ.
Работа предназначена для закрепления знаний по стереометрии. Состоит из 9 заданий. Ответом для каждого задания служит целое число или десятичная дробь. Желаю удачи!
Количество вопросов в тесте:
9
Вариант 1 8. Стереометрия
1.Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
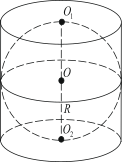
2. Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.
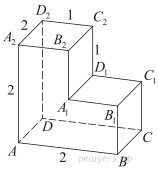
3. Найдите угол CAD2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
4. Площадь боковой поверхности цилиндра равна , а диаметр основания — 8. Найдите высоту цилиндра.
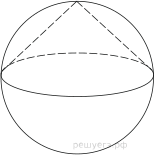
5. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 112. Найдите объём конуса.
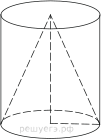
6. Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
7. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
8. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
9. Радиусы двух шаров равны 32 и 60. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.
10. Объем конуса равен 10. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Вариант 2 8. Стереометрия
1. Диаметр основания конуса равен 42, а длина образующей равна 75. Найдите высоту конуса.
2. Гранью параллелепипеда является ромб со стороной 4 и острым углом 30°. Одно из ребер параллелепипеда составляет с этой гранью угол в 30° и равно 6. Найдите объем параллелепипеда.
3. Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A1, B1, C1, D1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 9, а боковое ребро равно 10.
4. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 4 и 16. Найдите ребро равновеликого ему куба.
5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
6. В правильной четырехугольной пирамиде точка
— центр основания,
вершина,
,
Найдите длину отрезка
7. Гранью параллелепипеда является ромб со стороной 1 и острым углом 45°. Одно из ребер параллелепипеда составляет с этой гранью угол в 45° и равно 5. Найдите объем параллелепипеда.
8. Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 1:1, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.
9. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 112. Найдите объём конуса.
10.Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
Вариант 3 8. Стереометрия
1. На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла C2C3B2.
2. Найдите угол CAD2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
3. Найдите угол многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
4. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
6. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 0,5 и 16. Найдите ребро равновеликого ему куба.
7. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 24. Найдите объем пирамиды.
8. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 6. Найдите объем пирамиды.
9. Объем правильной четырехугольной пирамиды SABCD равен 116. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.
10. В прямоугольном параллелепипеде известно, что Найдите длину ребра
Вариант 4 8. Стереометрия
1. Найдите квадрат расстояния между вершинами и
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
2. В прямоугольном параллелепипеде известно, что Найдите длину ребра
3. Площадь боковой поверхности цилиндра равна 18, а диаметр основания равен 9. Найдите высоту цилиндра.
4. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в три раза?
5. Найдите объём многогранника, вершинами которого являются точки правильной треугольной призмы площадь основания которой равна 9, а боковое ребро равно 8.
6. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 2 и 3. Объем призмы равен 18. Найдите ее боковое ребро.
7. Найдите объем многогранника, вершинами которого являются точки ,
,
,
,
,
,
правильной шестиугольной призмы , площадь основания которой равна 4, а боковое ребро равно 3.
8. Конус описан около правильной четырехугольной пирамиды со стороной основания 3 и высотой 13. Найдите его объем, деленный на π.
9. Диагональ куба равна 13. Найдите площадь его поверхности.
10. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 48 и высота равна 7.
Вариант 5 8. Стереометрия
1. Диагональ куба равна 1. Найдите площадь его поверхности.
2. Найдите объем пирамиды, высота которой равна 6, а основание – прямоугольник со сторонами 3 и 4.
3. В правильной треугольной призме ABCA1B1C1 стороны оснований равны 2, боковые рёбра равны 5. Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер AB, AC, A1B1 и A1C1.
4. Найдите квадрат расстояния между вершинами и
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
5. В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ выразите в см.
6. В сосуд, имеющий форму правильной треугольной призмы, налили 2300 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найдите объем детали. Ответ выразите в см3.
7. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.
8. В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.
9. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы
.
10.Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
Вариант 6 8. Стереометрия
1. В правильной треугольной пирамиде SABC точка K – середина ребра BC, S – вершина. Известно, что SK = 4, а площадь боковой поверхности пирамиды равна 54. Найдите длину ребра AC.
2. Найдите угол ABD многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
3. Во сколько раз увеличится объем куба, если его ребра увеличить в пятнадцать раз?
4. Найдите объем многогранника, вершинами которого являются точки ,
,
,
,
,
,
,
правильной шестиугольной призмы , площадь основания которой равна 6, а боковое ребро равно 2.
5. Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A1, B1, C1, D1 правильной шестиугольной призмыABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 2.
6. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60°. Одно из ребер параллелепипеда составляет с этой гранью угол в 60° и равно 2. Найдите объем параллелепипеда.
7. Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара.
8. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
9. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
10. Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.
Вариант 7 8. Стереометрия
1. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
2. Найдите объем части конуса, изображенной на рисунке. В ответе укажите
3. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.
4. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
5. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
6. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
7. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
8. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
9. Найдите объем части конуса, изображенной на рисунке. В ответе укажите
10. Найдите объем части конуса, изображенной на рисунке. В ответе укажите
Вариант 8 8. Стереометрия
1. Объем одного куба в 729 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
2. В правильной четырехугольной пирамиде точка
— центр основания,
вершина, , Найдите длину отрезка
3. В правильной треугольной пирамиде SABC точка R — середина ребра BC, S — вершина. Известно, что AB = 1, а SR = 2. Найдите площадь боковой поверхности.
4. В правильной треугольной пирамиде SABC точка N — середина ребра BC, S — вершина. Известно, что AB = 1, а площадь боковой поверхности равна 3. Найдите длину отрезка SN.
5. В правильной треугольной пирамиде SABC точка L — середина ребра BC, S — вершина. Известно, что SL = 2, а площадь боковой поверхности равна 3. Найдите длину отрезка AB.
6. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, объем пирамиды равен 1. Найдите длину отрезка MS.
7. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, MS = 1. Найдите объем пирамиды.
8. В правильной треугольной пирамиде медианы основания пересекаются в точке Объем пирамиды равен
,
Найдите площадь треугольника
9. В прямоугольном параллелепипеде известно, что , , Найдите длину ребра
10. Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.
Вариант 9 8. Стереометрия
1. Найдите расстояние между вершинами и
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
2. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
3. Высота конуса равна 6, образующая равна 10. Найдите площадь его полной поверхности, деленную на
4. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
5. Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 1:1, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.
6. Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
7. Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.
8. Объём куба равен 12. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.
9. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
10. В правильной четырёхугольной пирамиде высота равна 2, боковое ребро равно 5. Найдите её объём.
Вариант 10 8. Стереометрия
1. Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A1, B1, C1, D1 правильной шестиугольной призмыABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 2.
2.Высота конуса равна 12, образующая равна 15. Найдите его объем, деленный на
3. В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SO = 4, AC = 6. Найдите боковое ребро SC.
4. В правильной четырехугольной пирамиде точка О — центр основания,
вершина, , Найдите длину отрезка
5. В правильной четырехугольной пирамиде точка
— центр основания,
вершина, , Найдите длину отрезка
6. ЗВ правильной треугольной пирамиде SABC точка R — середина ребра BC, S — вершина. Известно, что AB = 1, а SR = 2. Найдите площадь боковой поверхности.
7. В правильной треугольной пирамиде SABC точка N — середина ребра BC, S — вершина. Известно, что AB = 1, а площадь боковой поверхности равна 3. Найдите длину отрезка SN.
8. В правильной треугольной пирамиде SABC точка L — середина ребра BC, S — вершина. Известно, что SL = 2, а площадь боковой поверхности равна 3. Найдите длину отрезка AB.
9. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, объем пирамиды равен 1. Найдите длину отрезка MS.
10. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, MS = 1. Найдите объем пирамиды.
|
8. Стереометрия |
||||
|
Вариант 1
|
Вариант 2
|
Вариант 3
|
Вариант 4
|
Вариант 5
|
|
Вариант 6
|
Вариант 7
|
Вариант 8
|
Вариант 9
|
Вариант 10
|
34 вопроса. Ответы прилагаются.
st.docx
st.pdf
1. Раздел геометрии, в котором изучаются фигуры и их свойства в пространстве
А) Планиметрия
Б) Аналитическая геометрия
В) Стереометрия
2. Евклидову плоскость можно представить, как
А) ограниченную поверхность, состоящую из прямоугольников
Б) гладкую ровную поверхность крышки стола, продолженную неограниченно во все стороны
В) бесконечную волнообразную поверхность
3. Выберете вариант, в котором перечислены все пространственные фигуры
А) Овал, параллелограмм, парабола
Б) Квадрат, круг, равносторонний треугольник
В) Цилиндр, сфера, пирамида
4. Укажите основные (неопределяемые) понятия стереометрии
А) угол, прямая, луч
Б) точка, прямая, плоскость
В) точка, прямая, окружность
5. Продолжите первую аксиому стереометрии «Через три точки, не лежащие на одной прямой…
А) нельзя провести плоскость
Б) можно провести бесконечное число плоскостей
В) можно провести три различные плоскости
Г) можно провести плоскость и притом только одну
6. Продолжите вторую аксиому стереометрии «Если две точки прямой лежат в данной плоскости,
А) то эта прямая пересекает эту плоскость
Б) то эта прямая параллельна этой плоскости
В) то эта прямая перпендикулярна этой плоскости
Г) то и вся эта прямая лежит в этой плоскости
7. Продолжите 3ю аксиому стереометрии «Если две различные плоскости имеют одну общую точку
А) то эти плоскости имеют бесконечное число общих точек, лежащих на одной прямой
Б) то эти плоскости больше не имеют общих точек
В) то эти плоскости имеют ещё одну общую точку
Г) такого быть не может
8. Установите соответствия между условиями и заключениями аксиом стереометрии
А) Через три точки, не лежащие на одной прямой…
Б) Если две точки прямой лежат в данной плоскости, …
В) Если две различные плоскости имеют одну общую точку, …
1. … то эти плоскости имеют бесконечное число общих точек, лежащих на одной прямой.
2. …можно провести плоскость и притом только одну
3. …то и вся эта прямая лежит в этой плоскости
9. Установите соответствия между взаимным расположением прямых в пространстве
А) Две прямые в пространстве называются параллельными, если…
Б) Две прямые в пространстве называются скрещивающимися, если…
В) Две прямые в пространстве называются пересекающимися, если…
1. они не лежат в одной плоскости
2. они лежат в одной плоскости и пересекаются
3. они лежат в одной плоскости и не пересекаются
10. Две прямые в пространстве называются параллельными, если…
А) они не лежат в одной плоскости
Б) они лежат в одной плоскости и не пересекаются
В) они лежат в одной плоскости и пересекаются
11. Две прямые в пространстве называются скрещивающимися, если…
А) они не лежат в одной плоскости
Б) они лежат в одной плоскости и не пересекаются
В) они лежат в одной плоскости и пересекаются
12. Установите соответствия между взаимным расположением прямой и плоскости в пространстве
А) Прямая лежит в данной плоскости
Б) Прямая пересекает плоскость
В) Прямая параллельна плоскости
Г) Прямая перпендикулярна плоскости
13. Установите соответствия
А) Пересекающиеся прямые
Б) Параллельные прямые
В) Скрещивающиеся прямые
14. Через какие две прямые нельзя провести одну плоскость?
А) Скрещивающиеся
Б) Параллельные
В) Пересекающиеся
Г) Перпендикулярные
15. Прямая называется перпендикулярной плоскости, если…
А) угол между прямой и плоскостью равен 0о
Б) она пересекает эту плоскость
В) она перпендикулярна любой прямой, лежащей в этой плоскости
16. Сколько плоскостей можно провести через прямую и точку, не лежащую на ней?
А) Ни одной
Б) Одну
В) Две
Г) Бесконечное множество
17. Сколько плоскостей можно провести через прямую и точку, лежащую на ней?
А) Ни одной
Б) Одну
В) Две
Г) Бесконечное множество
18. Сколько плоскостей можно провести через три точки, лежащие на одной прямой?
А) Ни одной
Б) Одну
В) Две
Г) Бесконечное множество
19. Сколько плоскостей можно провести через три точки, не лежащие на одной прямой?
А) Ни одной
Б) Одну
В) Три
Г) Бесконечное множество
20. Как называются прямые в пространстве, которые лежат в одной плоскости и не пересекаются?
А) Перпендикулярные
Б) Параллельные
В) Скрещивающиеся
Г) Таких прямых не существует
Ответы
1. В
2. Б
3. В
4. Б
5. Г
6. Г
7. А
8. А-2, Б-3, В-1
9. А-3, Б-1, В-2
10. Б11. А
12. А-3, Б-4, В-1, Г-2
13. А-3, Б-1, В-2
14. А
15. В
16. Б
17. Г
18. Г
19. Б
20. Б
Параллельность в пространстве
- Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек.
- Если две прямые на плоскости перпендикулярны к третьей прямой, то они параллельны.
- Если две прямые в трехмерном пространстве перпендикулярны к одной плоскости, то они параллельны.
- Если прямая a, не лежащая в плоскости $α$, параллельна некоторой прямой $b$, которая лежит в плоскости $α$, то прямая a параллельна плоскости $α$.
- Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым, лежащим в другой плоскости, то такие плоскости параллельны.
Перпендикулярность в пространстве
- Две прямые называются перпендикулярными, если угол между ними равен $90°$.
- Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.
- Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то заданные плоскости перпендикулярны.
- Теорема о трех перпендикулярах: если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна и самой наклонной.
- Если из одной точки проведены к плоскости перпендикуляр и наклонные, то:
- Перпендикуляр короче наклонных.
- Равные наклонные имеют равные проекции на плоскости.
- Большей наклонной соответствует большая проекция на плоскости.
Скрещивающиеся прямые
- Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются.
- Через две скрещивающиеся прямые проходит единственная пара параллельных плоскостей.
- Расстояние между скрещивающимися прямыми – это расстояние от некоторой точки одной из скрещивающихся прямых до плоскости, проходящей через другую прямую параллельно первой прямой.
- Угол между скрещивающимися прямыми – это острый угол между двумя пересекающимися прямыми, которые соответственно параллельны заданным скрещивающимся прямым.
Многогранники
Введем общие обозначения
$P_{осн}$ — периметр основания;
$S_{осн}$ — площадь основания;
$S_{бок}$ — площадь боковой поверхности;
$S_{п.п}$ — площадь полной поверхности;
$V$ — объем фигуры.
| Название | Определение и свойства фигуры | Обозначения и формулы объема, площади |
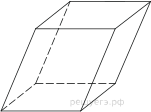
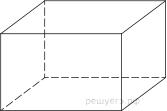
| Прямоугольный параллелепипед | 1. Все двугранные углы прямоугольного параллелепипеда – прямые. 2. Противоположные грани попарно равны и параллельны. 3. Диагонали прямоугольного параллелепипеда равны. 4. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты). $B_1D^2=AD^2+DC^2+C_1C^2$ |
$V=a·b·c$, где $a, b$ и $с$ – длина, ширина и высота. $S_{бок}=P_{осн}·c=2(a+b)·c$ $S_{п.п}=2(ab+bc+ac)$. |
| Куб | 1. Противоположные грани попарно параллельны. 2. Все двугранные углы куба – прямые. 3. Диагональ куба в $√3$ раз больше его ребра. $B_1 D=АВ√3$ |
Пусть $а$ — длина ребра куба, $d$ — диагональ куба, тогда справедливы формулы: $V=a^3={d^3}/{3√3}$. $S_{п.п}=6а^2=2d^2$ $R={a√3}/{2}$, где $R$ — радиус сферы, описанной около куба. $r={a}/{2}$, где $r$ — радиус сферы, вписанной в куб. |
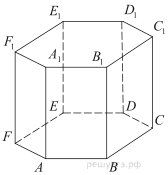
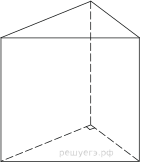
| Призма |
Призма – это многогранник, состоящий из двух равных многоугольников, расположенных в параллельных плоскостях, и $n$-го количества параллелограммов.
|
$S_{бок}=P_{осн}·h$ $S_{п.п}=S_{бок}+2S_{осн}$ $V=S_{осн}·h$ |
| Пирамида |
|
Формулы вычисления объема и площади поверхности правильной пирамиды. $h_a$ — высота боковой грани (апофема) $S_{бок}={P_{осн}·h_a}/{2}$ $S_{п.п}=S_{бок}+S_{осн}$ $V={1}/{3} S_{осн}·h$ |
| Усеченная пирамида |
|
$V={h(F+f+√{Ff})}/{3}$ Где $F,f$ — площади оснований; $h$ — высота (расстояние между основаниями); Для правильной ус. пирамиды $S_{бок}={(P+p)·a}/{2}$, где $P$ и $p$ – периметры оснований; $а$ – апофема. |
| Цилиндр |
|
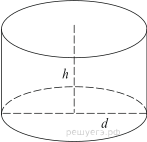
$S_{бок.пов.}=2πR·h$ $S_{полной.пов.}=2πR(R+h)$ $V=πR^2·h$ |
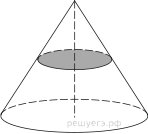
| Конус |
|
$S_{бок.пов.}=πR·l$ $S_{полной.пов.}=πR^2+πR·l=πR(R+l)$ $V={πR^2·h}/{3}$ |
| Усеченный конус |
|
$S_{бок}=πl(R+r)$ $S_{п.п.}=π(R^2+r^2+l(R+r))$ $V={πH(R^2+r^2+Rr)}/{3}$ Где $R$ и $r$ – радиусы оснований; $Н$ — высота усеченного конуса. |
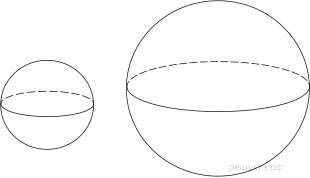
| Сфера, шар |
|
$S_{п.п}=4π·R^2=π·d^2$, где $R$ — радиус сферы, $d$ — диаметр сферы $V={4π·R^3}/{3}={π·d^3}/{6}$, где $R$ — радиус шара, $d$ — диаметр шара. |
Тетраэдр
Радиус описанной сферы тетраэдра.
Вокруг тетраэдра можно описать сферу, радиус которой находим по формуле, где $R$ — радиус описанной сферы, $a$ — ребро тетраэдра.
$R={a√6}/{4}$
Радиус вписанной в тетраэдр сферы.
В тетраэдр можно вписать сферу, радиус вписанной сферы находим по формуле, приведенной ниже.
Где $r$ — радиус вписанной в тетраэдр сферы,
$a$ — ребро тетраэдра.
$r={a√6}/{12}$
Составные многогранники
Задачи на нахождение объема составного многогранника:
- Разделить составной многогранник на несколько параллелепипедов.
- Найти объем каждого параллелепипеда.
- Сложить объемы.
Задачи на нахождение площади поверхности составного многогранника.
— Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:
$S_{полн.пов.}=P_{осн}·h+2S_{осн}$
Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.
— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.
Пример:
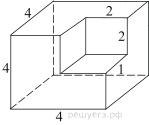
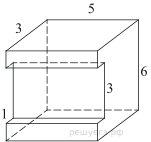
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
Представим данный многогранник как прямую призму с высотой равной $12$.
$S_{полн.пов.}=P_{осн}·h+2S_{осн}$
$P_{осн}=8+6+6+2+2+4=28$
Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:
$S_1=6·6=36$
$S_2=2·4=8$
$S_осн=36+8=44$
Далее подставим все данные в формулу и найдем площадь поверхности многогранника
$S_{полн.пов.}=28·12+2·44=336+88=424$
Ответ: $424$
— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.
Задачи на нахождение расстояния между точками составного многогранника.
В данных задачах приведены составные многогранники, у которых двугранные углы прямые. Надо соединить расстояние между заданными точками и достроить его до прямоугольного треугольника. Далее остается воспользоваться теоремой Пифагора для нахождения нужной стороны.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Задачи на нахождение угла или значения одной из тригонометрических функций обозначенного в условии угла составного многогранника.
Так как в данных задачах приведены составные многогранники, у которых все двугранные углы прямые, то достроим угол до прямоугольного треугольника и найдем его значение по тригонометрическим значениям.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$:
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Связь между сторонами правильного n-угольника и радиусами описанной и вписанной окружностей
$АВ=a_n$ — сторона правильного многоугольника
$R$ — радиус описанной окружности
$r$ — радиус вписанной окружности
$n$ — количество сторон и углов
$a_n=2·R·sin{180°}/{n}$;
$r=R·cos{180°}/{n}$;
$a_n=2·r·tg{180°}/{n}$.
Формула нахождения градусной меры угла в правильном многоугольнике:
$α={(n-2)·180°}/{n}$
Формулы площадей треугольников и многоугольников, которые могут находиться в основании многогранников
В основании лежит треугольник
1. $S={a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне а
2. $S={a·b·sinα}/{2}$, где $a, b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
3. $S=p·r$, где $r$ — радиус вписанной окружности
4. $S={a·b·c}/{4R}$, где $R$ — радиус описанной окружности
5. Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ — катеты прямоугольного треугольника.
В основании лежит четырехугольник
Прямоугольник
$S=a·b$, где $а$ и $b$ — смежные стороны.
Ромб
$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба
$S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
Трапеция
$S={(a+b)·h}/{2}$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
Площади правильных многоугольников:
1. Для равностороннего треугольника $S={a^{2}√3}/{4}$, где $а$ — длина стороны.
2. Квадрат
$S=a^2$, где $а$ — сторона квадрата.
3. Правильный шестиугольник
Шестиугольник разделим на шесть правильных треугольников и найдем площадь как:
$S=6·S_{треугольника}={6·a^{2}√3}/{4}={3·a^{2}√3}/{2}$, где $а$ — сторона правильного шестиугольника.
14. Задачи по стереометрии
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи по стереометрии формата ЕГЭ
Задание
1
#3868
Уровень задания: Равен ЕГЭ
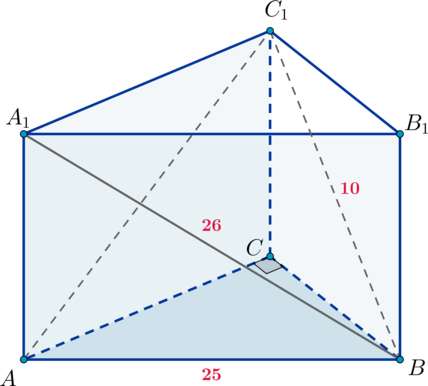
Основанием прямой треугольной призмы (ABCA_1B_1C_1) является прямоугольный треугольник (ABC), причем (angle C=90^circ). Диагонали боковых граней (AA_1B_1B) и (BB_1C_1C) равны соответственно (26) и (10), (AB=25).
а) Докажите, что (triangle BA_1C_1) – прямоугольный.
б) Найдите объем пирамиды (AA_1C_1B).
а) Так как (BB_1perp (A_1B_1C_1)), (B_1C_1perp A_1C_1), то по теореме о трех перпендикулярах (BC_1perp A_1C_1) (как наклонная). Следовательно, (triangle A_1C_1B) – прямоугольный.
б) Заметим, что (BCperp AC) и (BCperp CC_1), следовательно, по признаку (BCperp (AA_1C_1)). Следовательно, (BC) – высота пирамиды (BAA_1C_1) с основанием (AA_1C_1).
Так как (triangle AA_1C_1) прямоугольный, то [V_{BAA_1C_1}=dfrac{frac12cdot AA_1cdot A_1C_1cdot BC}3] По теореме Пифагора [begin{aligned}
&A_1C_1=sqrt{26^2-10^2}=sqrt{16cdot 36}=24\[1ex]
&AA_1=sqrt{26^2-25^2}=sqrt{1cdot 51}=sqrt{51}\[1ex]
&BC=sqrt{10^2-51}=sqrt{49}=7 end{aligned}] Тогда [V_{BAA_1C_1}=dfrac{frac12cdot 24cdot sqrt{51}cdot 7}3=28sqrt{51}]
Ответ:
б) (28sqrt{51})
Задание
2
#6924
Уровень задания: Равен ЕГЭ
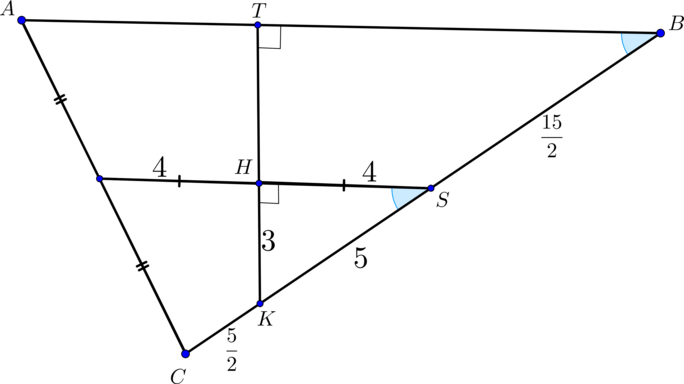
(ABCA_1B_1C_1) — прямая треугольная призма, (AB=16, BC=15,
AA_1=8), (cosangle ABC=0,8). (M, N) – середины ребер (AC) и (B_1C_1) соответственно. (K,P) – такие точки на ребрах (BC) и (B_1C_1) соответственно, что (CK=B_1P=dfrac{1}{6}BC).
а) Построить сечение призмы плоскостью (alpha), параллельной прямой (MN) и проходящей через точки (K) и (P).
б) Найти площадь сечения призмы плоскостью (alpha).
а) 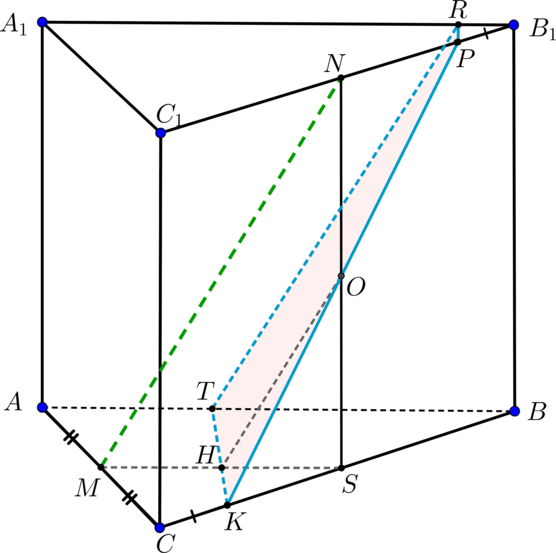
Если прямая (MNparallel alpha Rightarrow MN) параллельна некоторой прямой, лежащей в (alpha). Проведем (NSperp BC, NScap
KP=O). В плоскости (MNS) проведем (OHparallel MN Rightarrow
MH=HS). Тогда прямая (KHcap AB=T). Так как плоскости (ABC) и (A_1B_1C_1) параллельны, то (alpha) пересечет плоскость (A_1B_1C_1) по прямой, параллельной (KT). Следовательно, проведем (PRparallel
KT). Таким образом, (TRPK) – искомое сечение (трапеция).
б) Заметим, что (CK=dfrac{1}{6} cdot 15=dfrac{5}{2} Rightarrow
KS=5). Т.к. (MS) – средняя линия треугольника (ABC Rightarrow MS=8
Rightarrow HS=4). Так как (angle HSK=angle ABC), то по теореме косинусов (HK=sqrt{16+25-2cdot 4cdot 5cdot frac45}=3). Таким образом, по обратной теореме Пифагора треугольник (HKS) – прямоугольный, следовательно, (angle H =90^circ). Таким образом, по теореме о трех перпендикулярах, из того, что (NSperp (ABC),
HSperp KT Rightarrow
OHperp KT).
Проведем (PH_1 perp KT). Из подобия треугольников (HOK) и (H_1PK) следует, что (PH_1=2OH). Т.к. (OS=dfrac{1}{2}NS=4, HS=4 Rightarrow
OH=4sqrt2). Таким образом найдена высота трапеции (PH_1=8sqrt2).
Найдем основания трапеции (KT) и (PR).
(sin angle KSH = dfrac{3}{5}=sin angle B=dfrac{KT}{KB}
Rightarrow KT=dfrac{15}{2}).
(bigtriangleup PRB_1 sim bigtriangleup KTB Rightarrow
PR=dfrac{3}{2}).
Таким образом, (S_{TRPK} = dfrac{1}{2}cdot
left(dfrac{15}{2}+dfrac{3}{2}right)cdot 8sqrt2 = 36sqrt2)
Ответ:
б) (36sqrt2)
Задание
3
#2300
Уровень задания: Равен ЕГЭ
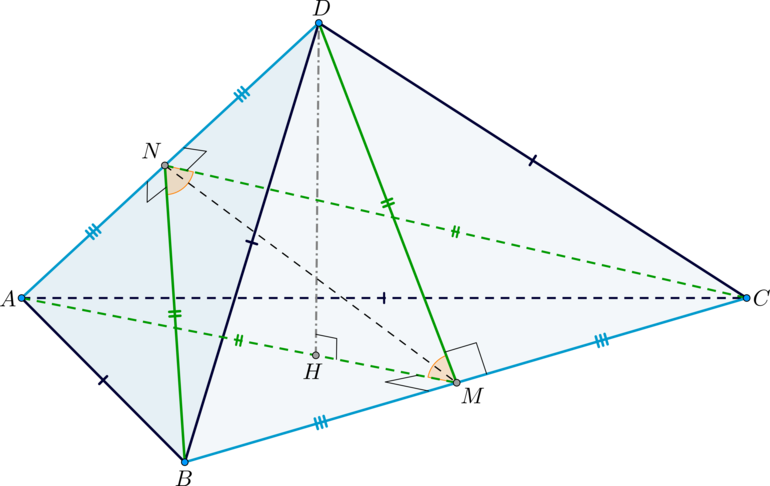
В треугольной пирамиде (DABC) двугранные углы при ребрах (AD) и (BC) равны. Известно также, что (AB=BD=DC=AC=sqrt{15}).
а) Докажите, что (AD=BC).
б) Найдите объем пирамиды, если двугранные углы при (AD) и (BC) равны по (60^circ).
а) Рассмотрим пирамиду (DABC), (AB=BD=DC=CA), (angle
(BAD,CAD)=angle (BAC,BDC)).
Т.к. (triangle ABD) и (triangle ACD) – равнобедренные, причем (AD) – общее основание, то высоты к основаниями попадут в одну точку – в середину стороны (AD), точку (N). То есть (BNperp AD), (CNperp AD). Таким образом, (angle BNC) – линейный угол двугранного угла (angle(BAD,CAD)).
Аналогичным образом строится угол (angle AMD) – линейный угол двугранного угла (angle (BAC,BDC)), где (M) – середина (BC). Таким образом, (angle BNC=angle AMD).
Т.к. (triangle ABD=triangle ACD) по трем сторонам, то (BN=CN). Аналогично (AM=DM). Значит, (triangle AMD) и (triangle BNC) – равнобедренные и подобные (по двум пропорциональным сторонам и углу между ними).
Заметим, что плоскости ((AMD)) и ((BNC)) имеют две общие точки – это точки (N) и (M). Следовательно, они пересекаются по прямой (MN). Отрезок (NM) – это высота в (triangle AMD) и (triangle BNC) к основаниям (AD) и (BC) соответственно. Следовательно, эти треугольники равны. Следовательно, (AD=BC), чтд.
б) Из пункта а) также следует, что (AM=DM=BN=CN). Т.к. двугранные углы равны (60^circ), то (triangle AMD) и (triangle BNC) – равносторонние.
Пусть (AM=DM=BN=CN=AD=BC=x).
Проведем высоту пирамиды (DH). Т.к. (DMperp BC), то по теореме о трех перпендикулярах (HMperp BC). Таким образом, точка (H) должна лежать на (AM), причем на середине, т.к. (triangle AMD) – равносторонний.
(DH=frac{sqrt3}2cdot AD=frac{sqrt3}2x). Найдем по теореме Пифагора (x) из (triangle ABM):
(AM=x), (BM=frac x2), (AB=sqrt{15}), следовательно, (x=2sqrt3).
Таким образом, [V_{DABC}=frac13cdot DHcdot S_{ABC}=dfrac13cdot
frac{sqrt3}2xcdot frac12x^2=6]
Ответ:
б) (6)
Задание
4
#1265
Уровень задания: Равен ЕГЭ
Дан правильный тетраэдр (SABC), (H) – такая точка на высоте (SO), что (OH:HS=1:3). Плоскость (alpha) проходит через точки (A) и (H) параллельно медиане (BM) треугольника (ABC) и пересекает ребро (CS) в точке (P).
а) Докажите, что (CP:PS=2:3).
б) Найдите угол между плоскостями (alpha) и (ABC).
а)
Правильный тетраэдр — это правильная треугольная пирамида, у которой все ребра равны. Пусть ребро пирамиды равно (a).
Т.к. пирамида правильная, то высота (SO) падает в точку пересечения медиан (bigtriangleup ABC). Рассмотрим плоскость (BSM), точка (H) лежит в этой плоскости. Т.к. плоскость (alpha) параллельна (BM), то она пересекает плоскость (BSM) по прямой, параллельной (BM).
Проведем (RTparallel BM, Hin RT). Тогда по теореме Фалеса (dfrac{SH}{HO}=dfrac{ST}{TM}=dfrac{3}{1}).
Прямая (AT) пересечет (CS) в точке (P). (bigtriangleup APR) – сечение пирамиды плоскостью (alpha).
Напишем теорему Менелая для (bigtriangleup CSM) и прямой (AP):
[dfrac{CP}{PS}cdot dfrac{ST}{TM}cdot dfrac{MA}{AC}=1] Из этого равенства находим, что (dfrac{CP}{PS}=dfrac{2}{3})
б) Докажем, что линия пересечения плоскостей (alpha) и (ABC) параллельна прямой (BM). Пусть это не так: пусть (l) – линия пересечения (alpha) и (ABC) и (lcap BM=Z). Тога прямая (BMcap
alpha=Z), следовательно, не может быть параллельна (alpha). Получили противоречие, следовательно, (lparallel BM). Заметим, что прямая (l) проходит через точку (A).
Построим линейный угол двугранного угла между (alpha) и (ABC). Т.к. (HOperp ABC), проведем (OKperp l), следовательно, по теореме о трех перпендикулярах (HKperp l). Таким образом, (angle HKO) – искомый угол.
1) Найдем (HO).
(BO=dfrac{2}{3}cdot BM=dfrac{2}{3}cdot
dfrac{sqrt3}{2}a=dfrac{a}{sqrt3})
Тогда (SO=sqrt{a^2 -dfrac{a^2}{3}}=sqrt{dfrac{2}{3}}a
Rightarrow HO=dfrac{1}{4}SO=dfrac{sqrt2a}{4sqrt3})
2) Найдем (OK).
(BMperp AC, BMparallel l Rightarrow ACperp l). Т.к. (OKperp l
Rightarrow OKparallel AC). Таким образом, (OMAK) – параллелограмм, следовательно, (OK=MA=dfrac{1}{2}a).
Треугольник (HOK) – прямоугольный, следовательно, (mathrm{ctg},angle
HKO=dfrac{OK}{HO}=sqrt6)
Тогда (angle HKO= mathrm{arcctg},sqrt6).
Ответ:
б) (mathrm{arcctg},sqrt6)
Задание
5
#3059
Уровень задания: Равен ЕГЭ
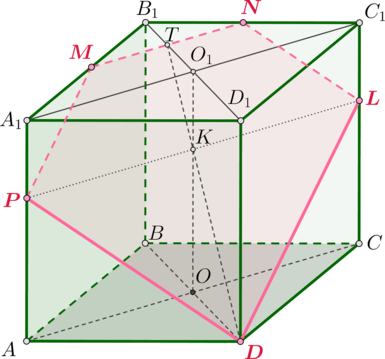
Дана правильная четырехугольная призма (ABCDA_1B_1C_1D_1), стороны основания которой равна (4), а боковые ребра равны (5).
а) Постройте сечение призмы плоскостью (DMN), где (M) и (N) – середины отрезков (A_1B_1) и (B_1C_1).
б) Найдите угол между данным сечением и плоскостью (ABC).
(Задача от подписчиков)
а) Из условия следует, что призма прямая и основаниями являются квадраты.
(MN) – средняя линия в (triangle A_1B_1C_1), следовательно, (MNparallel A_1C_1). Тогда плоскость (DMN) пересечет плоскость (A_1C_1CA) по прямой (l), параллельной (A_1C_1) (в противном случае (l) пересечет (A_1C_1) в некоторой точке (K), которая будет лежать и на (A_1C_1), и в плоскости (DMN), следовательно, должна будет лежать и на (MN), что невозможно, так как (MN) не пересекает (A_1C_1)).
Таким образом, найдем точку, в которой плоскость (DMN) пересекает плоскость (A_1C_1CA).
Пусть плоскость (B_1D_1DB) пересекает (MN) в точке (T). Тогда (DTin
(DMN)). Если (O) и (O_1) – точки пересечения диагоналей оснований, то прямые (DT) и (OO_1) лежат в плоскости (B_1D_1DB). Пусть точка их пересечения – точка (K). Тогда (K) – искомая точка пересечения плоскости (DMN) и плоскости (A_1C_1CA).
Проведем через точку (K) прямую (l) параллельно (A_1C_1). Пусть она пересекла (AA_1) в точке (P), (CC_1) в точке (L). Таким образом, получили сечение (DPMNL) призмы плоскостью (DMN).
б) Заметим, что (KOperp (ABC)), следовательно, так как (ODperp
AC), то и (KDperp AC) по теореме о трех перпендикулярах. Значит, (angle KDO) равен углу между плоскостями (DMN) и (ABC).
По теореме Фалеса [dfrac{A_1M}{MB_1}=dfrac11=dfrac{O_1T}{TB_1}
quadRightarrowquad O_1T=TB_1.] (triangle TO_1Ksim triangle DOK), следовательно, [dfrac{O_1T}{OD}=dfrac12=dfrac{O_1K}{OK}] Следовательно, (OK=frac23OO_1=frac23AA_1=frac23cdot
5=frac{10}3).
(OD=frac12 BD=frac12cdot sqrt2AB=2sqrt2.)
Тогда [mathrm{tg},angle KDO=dfrac{OK}{OD}=dfrac56sqrt2
quadRightarrowquad
angle KDO=mathrm{arctg},dfrac56sqrt2.]
Ответ:
б) (mathrm{arctg},dfrac56sqrt2)
Задание
6
#3064
Уровень задания: Равен ЕГЭ
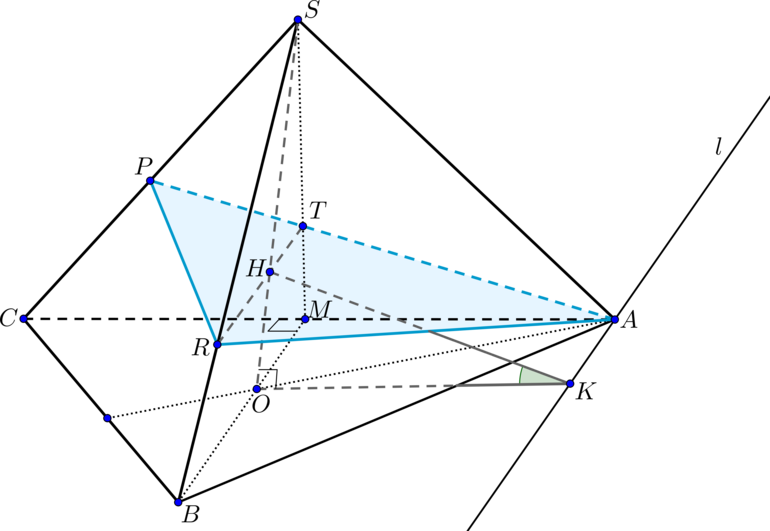
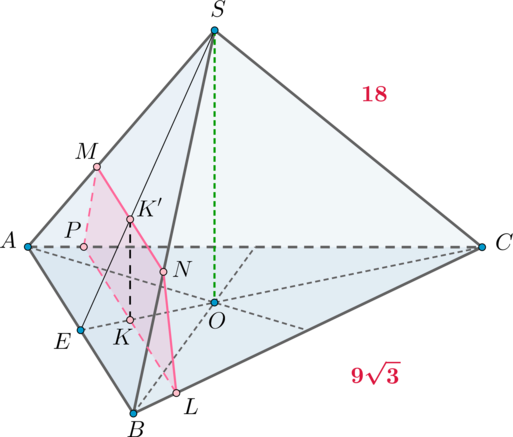
В правильной треугольной пирамиде (SABC) с основанием (ABC) на медиане основания (CE) взята точка (K) так, что (CK:KE=8:1). Через точку (K) проведена плоскость (alpha), которая перпендикулярна прямой (CE) и пересекает боковые ребра (SA) и (SB) в точках (M) и (N) соответственно.
а) Докажите, что (MN:AB=2:3).
б) Найдите объем пирамиды, вершиной которой является точка (C), а основанием – сечение пирамиды (SABC) плоскостью (alpha), если известно, что (AB=9sqrt3), (SA=18).
(Задача от подписчиков)
а) Пусть (SO) – высота пирамиды, (O) – точка пересечения медиан. Следовательно, [dfrac{CO}{OE}=dfrac21] Так как по условию (CK:KE=8:1), то можно обозначить (CK=8x), (KE=x). Тогда (CE=9x). Следовательно, (CO=frac23CE=6x), (OE=3x), (OK=2x).
Так как (CE) перпендикулярна плоскости (alpha), то нужно построить две пересекающиеся прямые в плоскости (alpha), которым (CE) будет перпендикулярна.
Первая прямая: так как (CEperp AB), то проведем через точку (K) прямую (PLparallel AB). Тогда (CEperp PL) ((Pin AC, Lin BC)).
Вторая прямая: так как (SOperp (ABC)), то (SOperp CE). Следовательно, проведем (KK’parallel SO), тогда (KK’perp CE) ((K’in SE)).
Следовательно, (alpha) проходит через точки (P, L, K’).
Заметим, что (alpha) пересечет плоскость (ASB) по прямой, параллельной (AB) (в противном случае (alpha) будет иметь общую точку с (AB), что невозможно, так как (ABparallel PL
quadRightarrowquad ABparallel alpha)).
Следовательно, (MNparallel AB) и проходит через (K’).
Из подобия (triangle K’EKsim triangle SEO): [dfrac{SE}{K’E}=dfrac{OE}{KE}=dfrac31 quadRightarrowquad K’E=
dfrac13SE
quadRightarrowquad SK’=dfrac23SE.] Из подобия (triangle
MSNsim triangle ASB): [dfrac{MN}{AB}=dfrac{SK’}{SE}=dfrac23.]
б) Рассмотрим пирамиду (CPMNL). (CK) – высота этой пирамиды, (PMNL) – трапеция ((MNparallel ABparallel PL)).
Следовательно, [V=dfrac13cdot CKcdot dfrac{MN+PL}2cdot KK’] Так как (BC=9sqrt3), то (CE=sqrt{BC^2-EB^2}=frac{27}2). Следовательно, [CK=dfrac89CE=12.] Из подобия (triangle PCLsim triangle ACB): [dfrac{PL}{AB}=dfrac{CK}{CE}=dfrac89quadRightarrowquad PL=
8sqrt3.] Из пункта а) [MN=dfrac23AB=6sqrt3.] Из подобия (triangle
EK’Ksim triangle ESO): [KK’=dfrac13SO=dfrac13sqrt{SC^2-CO^2}=dfrac13sqrt{18^2-9^2}=
3sqrt3.] Следовательно, [V=dfrac13cdot 12cdot dfrac{6sqrt3+8sqrt3}2cdot 3sqrt3=252.]
Ответ:
б) 252
Задание
7
#3063
Уровень задания: Равен ЕГЭ
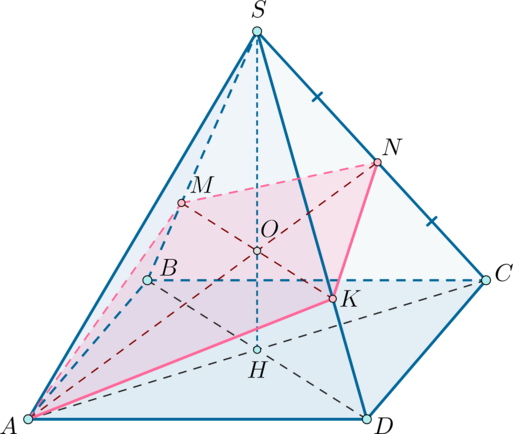
Дана правильная четырехугольная пирамида (SABCD) с вершиной (S), стороны основания которой равны (6sqrt2), а боковые ребра равны (21).
а) Постройте сечение пирамиды плоскостью, проходящей через точку (A) и середину ребра (SC) параллельно прямой (BD).
б) Найдите площадь построенного сечения.
(Задача от подписчиков)
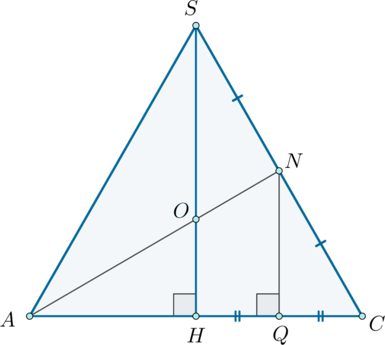
а) Пусть (N) – середина ребра (SC), (SH) – высота пирамиды (падает в точку пересечения диагоналей основания).
Необходимо построить прямую, лежащую в плоскости сечения и параллельную (BD). Рассмотрим плоскость (ASC). Прямая (AN) пересекает (SH) в точке (O). Теперь рассмотрим (BSD). Проведем в этой плоскости через точку (O) прямую, параллельную (BD). Пусть она пересечет ребра (SB) и (SD) в точках (M) и (K) соответственно. Таким образом, (AMNK) – искомое сечение.
б) Заметим, что по теореме о трех перпендикулярах (так как (OHperp
(ABC), AHperp BD)) (AOperp BD). Так как (BDparallel MK), то (AOperp MK), следовательно, (ANperp MK). Следовательно, у четырехугольника (AMNK) диагонали взаимно перпендикулярны. Значит, его площадь можно найти как [S=dfrac12 ANcdot MK.]
Заметим сразу, что (BD=AC=ABsqrt2=12).
Рассмотрим плоскость (ASC).
По теореме Менелая: [dfrac{SN}
{NC}cdot dfrac{CA}{AH}cdot dfrac{HO}{OS}=1 quadRightarrow
quad dfrac{HO}{OS}=dfrac12 quadRightarrowquad OS=2OH
quadRightarrowquad dfrac{SO}{SH}=dfrac23.] (это нам понадобится позже для поиска (MK))
Проведем (NQperp AC). Тогда из подобия (triangle SHC) и (triangle
NQC): [dfrac{SH}{NQ}=dfrac{SC}{NC}=2 quadRightarrowquad
NQ=dfrac12SH=dfrac12sqrt{SC^2-HC^2}=dfrac12sqrt{21^2-6^2}=
dfrac12sqrt{81cdot 5}] (Q) – середина (HC), следовательно, (AQ=frac34AC=frac34cdot 12=9). Тогда по теореме Пифагора [AN=sqrt{AQ^2+NQ^2}=sqrt{dfrac{81cdot 5}4+81}=dfrac{27}2.]
Рассмотрим (BSD). Так как (triangle MSKsim triangle BSD), то [dfrac{MK}{BD}=dfrac{SO}{SH}=dfrac23 quadRightarrowquad
MK=dfrac23BD=dfrac23cdot 12=8.] Следовательно, площадь сечения равна [S=dfrac12cdot 8cdot dfrac{27}2=54.]
Ответ:
б) 54

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ